Approaches for determining cardiac bidomain conductivity values: progress and challenges

Abstract

Modelling the electrical activity of the heart is an important tool for understanding electrical function in various diseases and conduction disorders. Clearly, for model results to be useful, it is necessary to have accurate inputs for the models, in particular the commonly used bidomain model. However, there are only three sets of four experimentally determined conductivity values for cardiac ventricular tissue and these are inconsistent, were measured around 40 years ago, often produce different results in simulations and do not fully represent the three-dimensional anisotropic nature of cardiac tissue. Despite efforts in the intervening years, difficulties associated with making the measurements and also determining the conductivities from the experimental data have not yet been overcome. In this review, we summarise what is known about the conductivity values, as well as progress to date in meeting the challenges associated with both the mathematical modelling and the experimental techniques.

1 Introduction

In 2014, Henriquez [29] commented, in relation to the conductivities that are necessary inputs to models of cardiac electrical behaviour, that “Understanding all the factors that affect the microscopic and macroscopic electrical properties and performing the measurements in vivo over a range of conditions remains an open challenge to the field”. This is still true today and it provides the impetus for this review to discuss what these challenges are and why it is essential for models to use accurate values for the cardiac electrical conductivities, as well as to gather together the information that is currently known about the conductivities. The state of the art in terms of measuring the conductivities will also be presented, in addition to suggestions about the way the field might move forward in the future.

It has been shown that values for the bidomain conductivities play a significant role in the modelling and simulation of many bioelectric phenomena and that differences in published conductivity values can lead to divergent predictions from mathematical models utilising such values [16, 34, 41, 55, 60, 84]. Hence, an accurate determination of conductivity values is of fundamental importance to researchers who undertake electrophysiological simulations with the aim of understanding aspects of cardiac electrophysiology that are not amenable to experimental study. Such studies include models of ST segment deviation, electrical conduction defects and cardiac defibrillation.

At present, only three fully experimentally derived sets of four bidomain conductivities for ventricular tissue are available in the literature [13, 86, 87] and these are inconsistent [89] and produce different results in simulations [41, 55]. They also do not fully represent the three dimensional anisotropy that has been shown [11, 32] to exist in cardiac tissue, as there are no separate values for the two directions that are orthogonal to the cardiac fibres. In addition, they were found in different types of animal tissue, with different experimental (in vitro and in vivo) conditions, using different mathematical assumptions.

Ideally, what is required is sets of six bidomain conductivities (two domains, three directions) found in human ventricular tissue in vivo, for different positions in the ventricle, in different subjects and for different diseases and conditions. Even more ambitiously, Sadleir and Henriquez [93] suggest that a “method of continuously monitoring cardiac properties over time, would be of great benefit in monitoring interventions such as ablation and cellular therapies ... [and] may also lead to a deeper understanding of the role of tissue structure in the initiation and maintenance of cardiac arrhythmias”.

The accurate determination of the six conductivity values presents a considerable challenge both from experimental and computational points of view. Firstly, the measurements must be made using very small electrode spacings [74], around the size of the space constant of the tissue, which is of the order of 500 μm [50]. This introduces considerable technical challenges, both in constructing the electrode array and in deploying it [77]. Secondly, a method for determining the conductivities from the measurements must be designed. This relies on a mathematical model, a solution technique for this model and, generally, an inverse method for retrieving the conductivities, a mathematically ill-posed problem that involves considerable computational difficulties [93].

Efforts, in the 40 years since the four conductivity sets [13, 86, 87] mentioned above were found, have produced experimental and computer modelling methods that have been able to find the bulk conductivities (monodomain) in three directions [11, 30], theoretical methods that have been able to estimate the six conductivities from cell properties [9, 26, 96] and experimental plus mathematical methods that have been shown, in silico, to be able to retrieve the six conductivities [43].

The structure of this paper is as follows. Section 2 presents an overview of cardiac tissue microstructure and how it is modelled using the bidomain model. Then, Section 3 presents literature values for conductivities. In Section 4, two modelling studies examine the effect of differing conductivity values on simulation outputs. Experimental techniques for determining conductivities are reviewed in Section 5, and challenges and future work are discussed in the final section.

2 Modelling

2.1 Cardiac tissue microstructure

The microstructure of cardiac tissue is composed of cells that are, by volume, predominantly myocytes. See Fig. 1 for a confocal microscopic image of rabbit left ventricular tissue [26], showing myocytes (black) with their nuclei (blue), and extracellular space and cell membranes (green).

Fig. 1

Confocal microscopic image of left ventricular myocardium from rabbit. Nuclei are labelled in blue. The extracellular space and cell membranes including the transverse tubular system are labelled in green. The majority of the tissue is occupied by myocytes. The image describes an area of 204 × 204 μm². Pixel sizes are 0.2 × 0.2 μm² (image data from [26])

Cardiac tissue also contains large numbers of fibroblasts, as well as fluids [12]. Fibroblasts are not modelled explicitly in the standard bidomain model (Section 2.2). They perform an important role in the maintenance of the extracellular matrix that supports the cardiac tissue, but their role in electrical conduction is not well-understood [92].

Experimental studies have shown that myocytes have an approximate length of 100 μm and are arranged in fibres in a laminar structure that consists of branching layers or sheets that are around four myocardial cells thick [68, 69]. Although these sheets of cardiac fibres connect with one another, there are cleavage planes between them, stopping direct coupling of myocytes [32]. The sheets of fibres also rotate relative to one another between the epicardium and the endocardium [71, 103]. In addition, it is known [96] that the electrical connection between cardiac cells occurs via low-resistance gap junction channels.

Based on these structural differences in cardiac tissue, LeGrice et al. [68] suggested that conduction would not be isotropic in all directions transverse to the cardiac fibres, and in fact would be less in the direction normal to the sheets. This was later established to be correct by the work of Hooks et al. [32] and Caldwell et al. [11], who showed that cardiac tissue is orthotropic and it is necessary to use three different values (corresponding to three mutually orthogonal directions) at any point to describe the conductivity.

The following papers can be consulted for a more comprehensive description of cardiac tissue microstructure and electrical properties [12, 32, 68, 69], including differences in tissue properties by type (e.g. atrial, ventricular, Purkinje). In addition, the following excellent reviews [12, 29] give a more detailed description of the bidomain model than the one that will be given in the next section, since the main focus of this review is the cardiac conductivities themselves.

2.2 Bidomain model

In 1969, Otto Schmitt [95] proposed a continuum model of cardiac tissue, based on the idea of representing the tissue as two spatially interpenetrating domains. One domain consists of the space within the cardiac cells, the so-called intracellular space, and the other consists of the interstitial space outside of the cells, but within the tissue, the so-called extracellular space. The two spaces are everywhere separated by the cell membrane. These ideas were then formulated into partial differential equation models by Arthur and Geselowitz [1] and Tung [107], becoming known as the bidomain equations. The basic idea is that, at each point in the domain of the model, the potentials in the intracellular space and the extracellular space are governed by Ohm’s law and that the current that leaves one space must enter the other space. Mathematically, these ideas can be formulated as:

$$ \begin{array}{@{}rcl@{}} \nabla \cdot \mathbf{M}_{i} \nabla \phi_{i} &= -I_{m} \\ \nabla \cdot \mathbf{M}_{e} \nabla \phi_{e} &= I_{m} \end{array} $$

(1)

where ϕ_p (p = i or e) is the potential, (i=intracellular, e=extracellular), the conductivity tensors M_p are discussed below, and $I_{m}=\frac {\beta }{R} (\phi _{i}-\phi _{e})$ is the transmembrane current per unit volume. Here, β is the surface to volume ratio of the cells and R is the membrane resistance.

The fact that cardiac tissue consists of sheets of fibres of cardiac cells results in current flowing along the direction of the fibres (longitudinal, l) more easily than it can across the sheets of fibres (transverse, t) or between the sheets (normal, n) [32]. So, in general, the conductivity tensors can be written as:

$$ \mathbf{M}_{p} = \mathbf{A} \mathbf{G}_{p} \mathbf{A}^{T} $$

(2)

where A represents the local direction of the fibres and G_p is a diagonal matrix, containing the longitudinal (g_pl), transverse (g_pt), and normal tissue conductivities (g_pn) along the diagonal.

If it is assumed that the electrical potentials do not change with time, for example, during the ST segment of the electrocardiogram (ECG), it is possible to simplify Eq. 1 by introducing the transmembrane potential ϕ_m = ϕ_i − ϕ_e and combining Eq. 1 into the so-called passive bidomain equation [34]:

$$ \nabla \cdot (\mathbf{M}_{i} + \mathbf{M}_{e}) \nabla \phi_{e} = -\nabla \cdot \mathbf{M}_{i} \nabla \phi_{m}. $$

(3)

This generalised Poisson equation governs the extracellular potential distribution that is induced by the spatial distribution in transmembrane potentials. This transmembrane potential distribution arises due to the differences in plateau potentials between normal and ischaemic tissue [107].

On the other hand, if we wish to model the propagation of the wavefront through the cardiac tissue, then some form of time dependence must be introduced into Eq. 1. This is generally achieved by assuming a time-varying transmembrane current of the form:

$$ I_{m} = \beta \left (C_{m} \frac{\partial \phi_{m}}{\partial t} + I_{\text{ion}} \right ) $$

(4)

where C_m is the membrane capacitance and I_ion is the ionic current, as modelled via an individual cell model of the electric current. After some manipulation of Eq. 1, it can be shown that:

$$ \nabla \cdot \mathbf{M}_{i} \nabla \phi_{m} + \nabla \cdot \mathbf{M}_{i} \nabla \phi_{e} = \beta \left (C_{m} \frac{\partial \phi_{m}}{\partial t} + I_{\text{ion}} \right ), $$

(5)

which along with Eq. 3 represents the active bidomain model.

3 Literature values for conductivities

3.1 Four conductivity sets

As mentioned in “Introduction”, only three fully experimentally determined datasets for four bidomain conductivities in ventricular tissue exist; that is, values for {g_pq,p = i,e, q = l,t}. These are the values given in Table 1 for Clerc [13], Roberts and Scher [87] and Roberts et al. [86]; hereafter, these three sets will be referred to as the Clerc and Roberts sets of conductivity values. These values are sometimes used in modelling studies, or in lieu of accurate conductivity values researchers sometimes tune the conductivities to ensure that the conduction velocities are in the range 30–80 cm/s [12, 29]. When the Clerc and Roberts values are used in modelling studies, it is customary [32] to set the normal conductivities equal to the transverse conductivities; that is, g_in = g_it and g_en = g_et.

Table 1 Bidomain four conductivity data (in mS/cm) found in (E experimental or T theoretical) studies or used (U) in the indicated studies

In addition to these studies, Table 1 lists eight other conductivity sets that are either experimentally (E) or theoretically (T) determined, along with a selection of studies that used (U) particular values. Where known, the tissue type is listed. Two of these studies, those by Kleber and Riegger [61] and Weidmann [110], list values for g_il and g_el only, while the studies by Le Guyader et al. [65, 66] use atrial tissue.

It can be seen that, even within the E group at the top of the table, there is a wide range of values for a particular conductivity, with variations in the ranges (in mS/cm), g_il 1.6–4.5, g_el 1.2–6.3, g_it 0.19–0.6 and g_et 0.8–2.4. Explanations for this variation [102] include the fact that different animal species were used, as well as different experimental techniques and mathematical models. For example, Clerc [13] used in vitro calf trabecula bundles, injected current longitudinally and transversely, measured extracellular and intracellular potentials and then used 1D cable theory to derive the conductivities. Roberts and Scher [87] and Roberts et al. [86] used a completely different approach that involved mapping the propagation of the wavefront in vivo in canine hearts after epicardial stimulation. The two Roberts studies then used different assumptions to find the conductivities.

The second group of conductivities, marked T in Table 1, come from theoretical geometrical models of cardiac tissue, where the researchers extrapolate from models of cellular processes to produce estimates of tissue scale properties such as conductivities. Of note among this group are the values for g_it that are one or two orders of magnitude smaller than the other g_it values in the table. Explanations for this from the authors include the gap junction conductivities are higher than those used in the model [62, 101]; the gap junctions may be located more towards the sides of the cells [101], or the model may neglect to include a cellular mechanism that enhances the conductivity in the transverse direction [28]. Another possibility is that the other literature values for g_it are too high, perhaps, in the case of Clerc’s [13] study, due to the non-alignment of the probe with the transverse direction, or in general, due to the influence of the measuring conditions [62].

3.2 Six conductivity sets

Although no one has yet been able to directly measure all six bidomain conductivity values, a few datasets do exist in the literature and these are listed in Table 2. The first group is marked as partly experimental (PE) and the tissue type is given. However, out of the five PE studies, only two [30, 106] list all six conductivities, with the other three listing either the three intracellular conductivities [9] or the three extracellular conductivities [26, 96]. The latter three studies used confocal microscopy image data of rabbit ventricular tissue to obtain conductivity data for normal and (in two cases [26, 96]) infarcted tissue.

Table 2 Bidomain six conductivity data (in mS/cm) found in (PE partly experimental or T theoretical) studies or used (U) in the indicated studies

In two of these studies [26, 96], the authors constructed conductivity models based on the 3D reconstructions of the microstructure of the tissue, from which they calculated electric fields under the assumption that the only current flowing was in the extracellular space. The extracellular conductivity tensors were computed based on the image intensities.

The values of Hooks [30] are based on suggestions that are made in [31], with relative intracellular longitudinal and transverse values derived from heart surface potential measurements made in a rat left ventricle. The set of six conductivity values of Trew et al. [106] was found in vivo for porcine free wall tissue, which may explain why the values are generally higher than others in Table 2 [106].

The middle group, marked T in Table 2, are theoretical in a different way from those marked T in Table 1. Those by Johnston [39] are based on the experimental results of Hooks et al. [32] that found that the ratio of the bulk conductivities g_il + g_el : g_it + g_et : g_in + g_en was approximately 4:2:1, as well as the result of Caldwell et al. [11] that suggested that the same is true for the conduction velocities. Mathematical manipulations then produced a set of conductivities that is dependent on the value of the ratio g_il/g_el and the value of g_it (which was taken to be the mean of the Clerc and Roberts set of g_it values). Taking g_il/g_el = 0.6,1 and 1.6 then led to three sets of conductivities [41]. The other set by Johnston et al. [42] in Table 2 comes from a survey of the literature. The final set in the T category in Table 2 are those used by MacLachlan et al. [72], which were based on the theoretical work by Foster and Schwan [22]. The fact that there is only one set of six conductivities marked U (used) in Table 2 is probably indicative of the fact that the majority of studies use the four conductivity sets with the normal conductivities taken to be equal to the transverse conductivities.

As with the values in Table 1, there is no real consistency among the values listed for each of the six conductivities. However, the ranges for g_il,g_el and g_et are much smaller in this case, and the values for g_en are reasonably similar. The least consistent values are g_it and g_in. Finally, based on Tables 1 and 2, it would seem to be the case that, in each domain (p = i,e), g_pl > g_pt > g_pn, consistent with information that is known about cardiac electrical conduction [32].

3.3 Possible reasons for differences in conductivity values

As mentioned above, possible reasons for the discrepancies between sets of conductivity values could be experimental conditions (including in vitro and in vivo), mathematical models and methods used to determine the conductivities from data, and different assumptions for theoretical studies. Another reason might be intrinsic biological variability. The final reason may be related to tissue type—firstly, the tissue position within the atria or ventricle, and secondly, the animal species used. From Tables 1 and 2, it can be seen that the conductivities listed pertain to a range of animals—calf, rabbit, mouse, rat, sheep, pig and dog. Given that there are structural differences between the species, as well as differences in action potentials [18, 21, 36, 108], it is perhaps not surprising that different values for conductivities might be found, irrespective of other factors.

3.4 Conductivity ratios

Quite a number of studies [39, 44, 56, 57, 89] have examined ratios of conductivities, rather than their individual values. One reason for this is because the form of the passive bidomain Eq. 3 means that it is the ratio of the conductivities, and not the individual conductivities, that affects the potentials that are produced. The other reason is to attempt to find a parameter that is consistent between the three Clerc and Roberts sets of conductivities.

One study of this type is the study by Roth [89], which considered space constants in the q = l,t directions:

$$ \lambda_{q} = \sqrt{\frac{R}{\beta}\left( \frac{g_{iq} g_{eq}}{g_{iq}+g_{eq}}\right)}, $$

(6)

as well as two parameters α and 𝜖, defined as:

$$ \alpha= \frac{g_{il}}{g_{el}}, ~~~~~~ \epsilon=1-\frac{g_{el}/g_{et}}{g_{il}/g_{it}}. $$

(7)

Roth found [89] that for each of the Clerc and Roberts studies the value of 𝜖 was in the range 0.7–0.8. After non-dimensionalising the conductivities relative to g_il, Roth was able to suggest a “nominal” set of relative bidomain conductivities, using 𝜖 = 0.75,α = 1 and λ_l/λ_t = 2.5, giving ${g}_{il}^{\prime }=1,{g}_{el}^{\prime }=1,{g}_{it}^{\prime }=0.1,{g}_{et}^{\prime }=0.4$, where the prime indicates non-dimensionalisation with respect to g_il.

Values for α and 𝜖, for the various studies, are listed in the right-hand columns of Table 1. It can be seen that α varies from 0.3–2.8, whereas 𝜖 is generally in the range 0.6–0.9, except for two studies [66, 105] where it is 0.3, one where it is 0 [74] and two where it is almost 1 [28, 62]. Values for the g_il/g_it and g_el/g_et ratios are also given in Tables 1 and 2. Almost all of these studies are consistent with previous work using a geometrical model [33, 102] that has suggested that g_il/g_it > g_el/g_et, which then leads to 𝜖 > 0 as:

$$ \frac{g_{il}}{g_{it}} > \frac{g_{el}}{g_{et}} \Rightarrow \frac{g_{el}/g_{et}}{g_{il}/g_{it}}<1 \Rightarrow \epsilon > 0. $$

(8)

Given that there are six conductivities in Table 2, the additional ratios g_it/g_in and g_et/g_en are also listed. The results indicate that g_it/g_in > g_et/g_en. In other words, it appears that the intracellular domain is more anisotropic than the extracellular domain. This is consistent with theoretical work [39] that found g_it/g_in ≈ 4 and g_et/g_en ≈ 2. The same study also suggests that g_en/g_in ≈ 14 and g_et/g_it ≈ 6, indicating that the ratio of extra- to intracellular conductivity is much greater in the normal direction than in the transverse direction.

3.5 Conductivity changes in disease

The conductivities that are presented in Tables 1 and 2 are for normal cardiac tissue; however, a number of studies have shown [34, 61, 99, 101] that the conductivities are sensitive to ischaemia, hypoxia, myocardial perfusion and blood volume [100].

3.5.1 Conductivity changes in ischaemia

There are physical changes that take place during ischaemia that are likely to impact the conductivity values [101] and these changes can be grouped into three main phases. There is an initial phase, which is then followed by an early phase (approximately 5–20 min after onset). In both these phases, there is a reduction in g_el [101]. There is also a reduction in g_et in the early phase [33]. Finally, in the late phase (approximately 15–30 min after onset), there is a sharp reduction in intracellular conductivity due to the closing of the gap junctions [99].

There is some debate about the mechanism for the initial drop in g_el: either the collapse of capillaries because of reduced blood flow [61], or decreased hydrostatic pressure leading to increased flow of fluid into the capillaries from the extracellular space. On the other hand, it is generally agreed that the effects on g_el and g_et in the early phase are caused by fluid moving from the extracellular space into the myocytes [33].

It is difficult to quantify these reductions in the various domains and directions and this has been done somewhat differently for the l and t directions in a few studies (Table 3). Given the lack of any literature on reductions in the normal direction, Johnston and Johnston [48] simply set the normal reductions to be the same as the transverse reductions, and based their reductions on those of Hopenfeld et al. [34]. In the summary table for the various approaches (Table 3), the values given for early- and late-stage ischaemia are fractional reductions in the corresponding bidomain conductivities and these are applied in the ischaemic region, while the normal bidomain conductivities are used in the remainder of the tissue.

Table 3 Fractional reductions f_pq,p = i,e, q = l,t,n for bidomain conductivities in ischaemic tissue, corresponding to conductivities g_pq in the remainder of the tissue. A value of 0 indicates no change in the conductivity

3.5.2 Conductivity changes in infarcted tissue

The study by Schwab et al. [96], discussed in Section 3.2, also used confocal microscopy and modelling to look at changes in conductivities adjacent to an infarct, and it was found that there was an increase in the volume fraction of fibroblasts, along with a corresponding decrease in the myocyte volume fraction. An increase in the density of gap junctions proximal to the fibroblasts and myocytes was also found in the infarcted tissue, leading to an increase in g_el and a decrease in the anisotropy ratio. A later microscopy study [26], which considered three regions within 200 μm, 250–750 μm and 1000–1250 μm of the infarction border, found marked increases in the three intracellular conductivities, in the range 42–171%, compared with normal tissue.

4 The effect of conductivities on model output

There are a number of aspects associated with the conductivity values that can affect simulation results. Firstly, there is the choice of whether a bidomain or a monodomain model, in which the intra- and extracellular conductivities are equal, is used. Then, it is sometimes assumed that the tissue is isotropic, that is the conductivities are the same in all directions, or that there are equal anisotropy ratios (g_il/g_el = g_it/g_et). In addition to these, the assumption is often made that the transverse and normal conductivity values are equal [32]. Some studies have examined the effect of these assumptions on the output of models of cardiac ischaemia [53, 59, 72], for example, and demonstrated that the conclusions that would be drawn from the results are different, depending on the assumptions that are made.

Apart from these assumptions, there is the fact that groups of researchers use different sets of conductivities (Tables 1 and 2). Some studies [41, 55, 58] have compared the output of simulations for various conductivity sets from these tables and again showed that the choice of conductivity set can have a significant effect on the conclusions that may be drawn.

This will be demonstrated in this section by comparing the output produced by six different conductivity sets, in three different simulation studies, ischaemia, activation and defibrillation. The six conductivity sets used include the three Clerc and Roberts sets, as well as those of Stinstra et al. [101], MacLachlan et al. [72] and Hooks [30]. In the first four studies, normal direction conductivities are not available, so it will be assumed that conductivities in the normal and transverse directions are equal. Other parameters used in these studies are β = 2000 cm^− 1 [74], R = 9100 Ω cm² [110] and C_m = 1μF cm^− 2 [81].

4.1 ST segment shifts due to subendocardial ischaemia

During the ST segment of the ECG, the cardiac tissue is isoelectric and so the passive bidomain Eq. 3 can be used to study the epicardial potentials. In this study, the formulation will be presented in the context of the half-ellipsoid model of the left ventricle, introduced in [54]. In this geometry, the epicardium is represented by the surface:

$$ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} + \frac{z^{2}}{c^{2}} = 1 $$

(9)

for z ≥ 0, with a = b = 3 cm and c = 5 cm. The endocardium is represented by the same surface except a = b = 2 cm and c = 4 cm. Cardiac tissue occupies the space between the two surfaces, with the fibres within the tissue rotating from the epicardium to the endocardium. The region within the inner surface is filled with blood and the potential within the blood ϕ_b is governed by Laplace’s equation. Boundary conditions for the governing Eq. 3 are derived from the fact that the entire outer surface of the geometry is insulated and that there is continuity of potential and current between the extracellular space and the blood at the tissue–blood interface. Further details of the model and implementation of the finite volume method solution are available in reference [54].

Figure 2 shows the “epicardial” potential distributions (in mV), on the surface of the ellipsoidal model, for the six conductivity sets considered. For these simulations, an ischaemic region is placed on the endocardial surface that extends for 50% of the thickness of the tissue. The region also extends from − 25^∘≤ ϕ ≤ 25^∘ and from 30^∘≤ 𝜃 ≤ 60^∘ in the polar and azimuthal directions, respectively. Conductivities in the ischaemic region are assumed to be the same as in healthy tissue and the difference in plateau potentials is set at − 30 mV. Fibre rotation is included in the model, with the fibres rotating through 120^∘ anticlockwise moving from the epicardium to the endocardium. The fibres on the epicardium are offset by an angle of 45^∘ from the vertical. Finally, the potential is set to 0 at the base of the ellipse, where ϕ = 180^∘.

Fig. 2

Epicardial surface potential distributions (in mV), arising from a region of subendocardial ischaemia, using the indicated conductivity data. All plots use the same scale, indicated at the top of the figure. The black contour lines are spaced at 0.1 mV and the white contour line is the zero potential line contour

The differences in the epicardial potential distributions in Fig. 2 are quite significant. Firstly, the data of Roberts and Scher [87] (panel (c)) shows no positive potential (except for the region near where the potential is earthed, which is not visible in the figure), whereas all the other datasets show both positive and negative potentials. The data of Clerc [13] (panel (a)) show a smaller range in potential compared with the other datasets. The remaining four datasets (panels (b), (d), (e) and (f)) all show similar potential distributions, except that the magnitudes of the potentials vary, and, hence, so do the potential gradients across the surfaces. Finally, the path of the zero contour line (shown in white) exhibits a significantly different behaviour in panels (a), (b) and (f) compared with panels (d) and (e).

4.2 Activation time maps

Activation time maps are commonly used to describe the propagation of the depolarisation wave front through cardiac tissue. This is modelled using the active bidomain Eq. 5 in the same geometry as described in the previous section for the ischaemia study, with the addition of a simple Purkinje fibre system, with ten evenly spaced strands, running from the apex of the endocardial surface to the base of the ventricle. Boundary conditions are also the same as those of the previous section, with the addition of a stimulating current. At t = 0, a stimulus is applied to the model at the apex of the endocardium. This model is also solved using the finite volume method and full details of its implementation are available elsewhere [4, 5].

Figure 3 shows the activation times (in ms) and, here, the different conductivity sets fall into two distinct categories of activation time maps. Panels (a), (b), (c) and (f) all show an epicardial breakthrough on the apex of the ventricle, whereas panels (d) and (e) show epicardial breakthrough along a ring around the ventricle at about the height of the endocardial apex. The data of Roberts and Scher [87] (panel (c)) give rise to the fastest activation times (less than 100 ms) and the greatest amplitude of the waves in the contour lines, starting from the apex and progressing towards the base. Panels (f), (b) and (a) then follow in overall activation times. In panels (d) and (e), propagation continues after the initial breakthrough around the ring, towards the apex and the base. In both cases, the total activation time exceeds 200 ms, with the data of Stinstra et al. [101] taking the longest time to complete the activation.

Fig. 3

Activation time maps (in ms) on the epicardial surface, arising from a point stimulation at the apex of the endocardium, using the indicated conductivity data. All plots use the same contour scale, indicated at the top of the figure. The black contour lines are spaced at 10 ms

4.3 A simple defibrillation model

A simple model for defibrillation of the heart can be created by considering a heart situated in a fluid bath with electrode paddles attached to opposite sides of the bath, as shown in Fig. 4. The heart has a realistic canine geometry, obtained from MRI data, and includes realistic fibre orientation taken from diffusion weighted images (SCIRun Tutorial, http://www.scirun.org). The bath and ventricles are filled with a fluid having the same electrical properties as blood. The governing equations are Eq. 1 and Laplace’s equation in the blood, and these are solved using the finite element method as implemented in SCIRun (http://www.scirun.org). The boundary conditions are that the outside of the bath, apart from the electrodes, is insulated, and there is continuity of potential and current between the tissue and the bath. The two electrodes are set at fixed potentials, one of which is 0.

Fig. 4

Model geometry used for the defibrillation study. The heart (red surface) is contained in a bath (blue boundary) with electrodes (green) positioned as shown

Finally, Table 4 shows the necessary potential differences to be applied between the two electrodes in Fig. 4 to obtain the defibrillation threshold of subjecting 95% of the extracellular tissue to a potential gradient of 6 V/cm or greater [35]. The values range from 171 V for the data of Roberts and Scher [87] up to 214 V for the data of Clerc [13]. This gives a range of 43 V, or approximately 20% of the upper potential difference. This is a significant difference since the results from this type of simulation can be used in the design of defibrillators and changes in potential difference can affect the longevity or power requirements of implantable defibrillators.

Table 4 Voltages (V) required to obtain the defibrillation threshold, using conductivity data from the indicated studies

4.4 Quantifying the effect of conductivity variations

Until recently, most studies that have attempted to quantify the effect of uncertainty in the bidomain conductivities, on the outputs of simulations, have done so by varying one conductivity value at a time [6, 38, 60, 94]. For example, Keller et al. [60] showed that the cardiac conductivities have a significant effect on forward-calculated ECGs, and Barone et al. [6] performed a sensitivity study on the placement and number of measurement sites that are required to determine the monodomain conductivities. Johnston [38] used the technique in the design of an electrode array to measure cardiac conductivities (Section 5.1.6). Sanchez et al. [94] showed that left ventricle activation and the ECG were sensitive to some of the cardiac conductivities in a realistic anatomical–physiological model of the heart used to study cardiac resynchronisation therapy.

A number of authors have used this approach to examine the effect that variations in the conductivity values can have on simulations of ischaemia [33, 34, 84, 85, 97]. These studies have shown that the occurrence of epicardial ST depression or elevation is affected by the anisotropy ratio of the cardiac conductivity values, among other factors.

In later work in slab and half-ellipsoidal models of the ventricle, Johnston and colleagues [42, 47, 48, 52] were able to simultaneously quantify the effect of all six of the conductivity values on the epicardial potentials during the ST segment of the ECG, produced by non-transmural ischaemic regions. The studies used uncertainty quantification and sensitivity analysis techniques, such as Gaussian Process emulators and Partial Least Squares. This work found that the model outputs were most consistently sensitive to the value of the intracellular longitudinal conductivity g_il and are not sensitive to the transverse conductivities. This result is in accord with earlier work [44], using a different approach, which concluded that it is the ratio g_il/g_it that is the key parameter for explaining the effect of different conductivity sets on epicardial potential distributions that are generated by subendocardial ischaemia.

5 Experimental techniques for determining conductivities

A number of different approaches have been proposed for determining the bidomain conductivity values from experimental measurements; these will be summarised in this section. There are two main types of challenges associated with this work: one is related to the precision of the experimental measurements, and the other concerns the mathematical models and methods that are required to retrieve the conductivity values from the experimental measurements [93]. A majority of the proposed techniques are for determining the four longitudinal and transverse conductivities {g_il,g_el,g_it,g_et}, which for the remainder of the manuscript will be referred to as the four conductivities.

None of the following methods has yet been used to fully experimentally determine either a set of four or six conductivity values in ventricular tissue (Le Guyader et al. [65, 66] use atrial tissue). In many cases, the methods are only validated using synthetic data. In others, only bulk conductivities are found, and in some cases, bidomain conductivities are found from these under various different assumptions.

5.1 Methods for retrieving the four conductivities

5.1.1 Graham and Kilpatrick

The approach proposed by Graham and Kilpatrick [25] uses point stimulation and maps the propagation of electrical activity across the tissue. An array with electrode separations of around 1.5 mm is used and a 2D simulation using the active bidomain model (Eq. 5) is performed, with the conductivities found by minimising the difference between the measured potentials and the model output. The approach was validated using synthetic data to which noise was added.

5.1.2 Barone, Veneziani, Yang and colleagues

More recently, Yang et al. [111, 112] have analysed a numerical approach that is similar to that of Graham and Kilpatrick [25], but applied to different data. In this case, the data are potential measurements produced by multiple stimuli, using the monodomain model in a real ventricle geometry or the bidomain model in 2D. The transmembrane potential is measured directly using optical mapping and microelectrodes are used to measure the extracellular potentials. Then, the variational data assimilation method minimises the difference between the model output and measurements. The technique is validated using noisy potentials and it is demonstrated that the method is able to retrieve monodomain conductivities [6]. This study also examines the number of measurement sites that would be required as well as their positions. Later work [7] uses a similar approach to estimate space-dependent cardiac monodomain conductivities; in this study, the approach is validated using experimental imaging data.

5.1.3 Barr and Plonsey

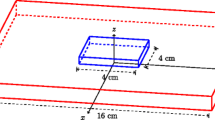
Most of the other proposed methods are based on the four-electrode technique [73]; that is, a probe with four co-linear equally spaced electrodes is used, current is applied to the outer electrodes and potential is measured at the inner electrodes (Fig. 5). Plonsey and Barr [74] showed that, under the assumption of equal anisotropy ratios (g_il/g_el = g_it/g_et), it is theoretically possible to retrieve the four conductivities, provided the measurements are made with the electrodes aligned along the cardiac fibres and then at right angles to them, and made with particular electrode spacings. The requirements are that the electrode spacing is small (around the size of the space constant - Eq. 6) to extract the extracellular conductivities, and much larger than that to find the intracellular conductivities. The rationale for this two-phase protocol is that, for the larger electrode spacing, some of the current is diverted from the extracellular space into the intracellular space [74].

Fig. 5

Schematic diagram for the four-electrode probe

Barr and Plonsey [8] also proposed a variant of this approach, a single vertical probe that contains a mixture of extracellular electrodes and optical transmembrane sensors, some of which are only 50 μm apart. The analysis showed that it is theoretically possible to retrieve the four conductivities, provided that it is assumed that there are equal anisotropy ratios and a two-phase protocol similar to that above is used. This work did not need to take into account the effect of fibre rotation, as a single vertical probe forms an axis of rotation for the cardiac fibres [73]. This is not the case, however, for a multi-probe electrode array that is inserted into the tissue [51].

5.1.4 Le Guyader, Savard and Trelles

Le Guyader, Savard and Trelles performed two experimental studies in atrial tissue [65, 66] using another variant of the four-electrode technique, with electrode spacings of around the size of the space constant. Instead of changing the orientation of the probe, their method used an eight-electrode probe with two sets of four electrodes at right angles to one another and an AC current with low and higher frequencies to re-direct some of the current into the intracellular domain. They then used a minimisation technique, along with a first pass at low frequency to fit the extracellular conductivities, and then a second pass at higher frequencies, to fit the remainder of the parameters. These studies [65, 66] were able to retrieve two sets of four conductivities for canine atrial tissue (see Table 1).

Their later work [67] presented two different models that could be used to analyse the experimental potentials. The first was the standard bidomain model with a membrane capacitance and the second had an added intracellular capacitance to represent the intercalated discs. The models were solved over the full domain using a fast Fourier transform technique.

5.1.5 Henriquez and Sadleir

In 2006, Sadleir and Henriquez [93] published an extension of the four-electrode technique, which used two different sized 5×5 square electrode arrays placed on the tissue surface. In this case, the two-phase approach was to be implemented by using one array with 5- or 10-μm electrode spacings, as well as one with 2.5-mm spacings. In silico simulations with added noise, using a 2D model solved in CardioWave [83], demonstrated that the method was able to retrieve the four bidomain conductivities as well as the angle of the array to the fibre direction. It is worth noting that 5–10-μm electrode spacings are smaller than the size of the cardiac myocytes and so a continuum description of the tissue, such as the bidomain model, may not be valid.

5.1.6 Johnston, Johnston and Kilpatrick

In the same year as Sadleir and Henriquez’ paper [93] appeared, Johnston et al. [50, 51] published two papers with a related four-electrode approach for finding the four conductivities, as well as the fibre rotation angle through the tissue. The first paper [51] presented a new 3D mathematical model and solution technique for finding the electric potential in a slab of cardiac tissue. An advantage of this solution technique is that it is not necessary for the potential to be calculated over the whole domain, as it could just be calculated at the required points (for example, at the electrodes).

The second paper [50] again proposed the use of a 5×5 electrode array, except in this case each needle contained two electrodes and the array was to be inserted into the tissue (Fig. 6). The electrode spacing was 500 μm between probes and 300 μm between electrodes on a probe, and different subsets of the electrodes were to be used in a two-pass approach. These sets were “closely spaced” and “widely spaced” and were to be used to retrieve the extracellular conductivities, and the intracellular conductivities plus fibre rotation angle, respectively. Using sets of in silico simulations with added noise, with an iterative inversion technique involving Tikhonov regularisation [104] and a modified Shor’s algorithm solver [98], it was demonstrated that it is possible to retrieve the four conductivities and the fibre rotation angle.

Fig. 6

Two-layer multi-electrode array used to retrieve four conductivity values [50]. Subsets of the electrodes are used in the two-pass protocol

5.2 Methods for retrieving the six conductivities

5.2.1 Caldwell, Hooks, Trew and colleagues

The work of Caldwell, Hooks, Trew and colleagues has been instrumental in establishing that cardiac tissue is electrically orthotropic (anisotropic), with three distinct propagation directions, through their experimental work using in vivo porcine ventricular tissue [11, 30, 32]. In the first study [31], tissue was reconstructed using confocal microscopy and simulations were performed using finite element modelling, whereas later work [11, 30, 32, 106] used intramural mapping and a matching computer model. An 11-needle array of plunge needles with 1–4-mm electrode spacings and 137 recording sites was designed, fabricated and then used.

In addition to confirming the anisotropic nature of the tissue, it was established that the bulk conductivities in the l : t : n directions were approximately in the ratio 4:2:1 [11, 32]. However, the method was not able to separate the six bidomain conductivities from the bulk conductivities.

Trew et al. [106] used a 4 mm × 4 mm × 1 mm electrode array of plunge needles of 400-μm diameter with 325 electrodes to again record intramural electrograms in the porcine LV free wall. The tissue was imaged and a computer model was constructed using the three intracellular conductivities that produced conduction velocities that best matched the recorded values. The three extracellular conductivities were then found using the previous experimental results for the sums of the bulk conductivities [32].

5.2.2 Costa, Frank and colleagues

Costa et al. [19] have proposed a method that is designed to iteratively retrieve all three bulk conductivities from 1D cable simulations, by tuning them to match conduction velocities. Once these conductivities are found, the bidomain conductivities are calculated using fixed values for g_il and the anisotropy ratios, and the fact that the monodomain conductivities are taken to be 0.5 times the harmonic mean of the intra- and extracellular conductivities.

5.2.3 Johnston and Johnston

In 2013, Johnston and Johnston presented [37, 38, 43] a new approach to find all six bidomain conductivities, along with the fibre rotation angle. The mathematical model and inversion technique were extensions of their previous work [51] (Section 5.1.6). The new multi-electrode array was again based on a 5×5 grid, this time with three electrodes per needle and a 500-μm electrode spacing (Fig. 7). New subsets of electrodes, corresponding to closely spaced sets of electrodes for the first pass to find the extracellular conductivities and widely spaced sets of electrodes for the second pass to find the intracellular conductivities and fibre rotation angle, were investigated. The accuracy of retrieval for various simulated noise levels was presented [40, 45, 46], and it was found that the three extracellular conductivities could be retrieved extremely accurately; even with added noise of up to 40%, relative errors are around 2% on average. The fibre rotation angle and g_il can also be retrieved quite accurately, with around 8% error for 40% noise. Both g_it and g_in are more challenging to retrieve, with errors that are generally less than twice the added noise.

Fig. 7

The 2 mm × 2 mm × 2 mm multi-electrode array of Johnston and Johnston [46], comprised three electrodes per needle, which is used for making the potential measurements. Source and sink electrodes are red and are marked with an “S”. The spacing between the electrodes and also between the needles is 500 μm. a The “closely spaced” electrodes on the needles in the inner square (green plus red) are used in the first pass. b All the electrodes are used in the second pass

It is worth noting that it is assumed, in this modelling, that the electrode array is aligned with the cardiac fibres, which may present practical challenges, although there are techniques that can be used to deal with this [75] or histology can be used. Another associated challenge is related to the manufacture of the electrode array, which is of overall size 2 mm × 2 mm × 2 mm, with 500-μm spacing between the electrodes. Another potential limitation relates to the mathematical model, which assumes that the cardiac tissue is a flat slab; however, this may not be a problem because of the small volume of tissue that is considered. One final assumption is that the array can be inserted into the tissue without causing significant injury currents [70].

5.2.4 Barr, Pollard and Smith

A group of manuscripts by Barr, Pollard and Smith [76, 77, 80, 82] has presented a new plan for direct conductivity measurements in vivo. The approach uses multi-site interstitial stimulation, at multiple frequencies, using very small stimulating electrodes and electrode spacings with micro-electrical-mechanical systems (MEMS) fabricated blocks. They demonstrate theoretically that a set of eight equally spaced electrodes with 25-μm gaps, which are stimulated by pairs of electrodes that are separated by 75, 125 and 175 μm, is sufficient to retrieve the six resistivities (inverses of conductivities). A two-pass approach is again used, with frequencies below 100 Hz used to retrieve the extracellular resistivities and frequencies between 200 and 4000 Hz are used to retrieve the intracellular resistivities. The resistivities are found using a look-up table, where the resistivities are varied until the best match with the measured potentials is found. Simulations, under the assumption of equal normal and transverse resistivities, indicate that 10% fluctuations in voltage readings lead to errors of less than 5% in resistivity values. Fibre rotation was ignored in these simulations as the effective penetration depth associated with the array was only 25–50 μm [77]. Another assumption that was made was that the MEMS array was aligned with the fibre direction on the tissue surface.

5.3 Recent work

5.3.1 Barr, Pollard and Waits

A relatively recent series of manuscripts by Barr, Pollard and Waits [78, 79, 109] analyses experiments with a four-electrode probe that is stimulated at multiple frequencies, with wide (1 mm) and fine (250 μm) electrode separation and examines the complex spectra (resistivity and reactivity) that are produced. Pollard and Barr [79] suggest that spectra resolution using finely spaced electrodes may provide a way of separating the extracellular and intracellular contributions to the resistivity because the current is unable to cross the membrane at low frequencies. This work considers the considerable technical challenges that are associated with small electrode spacings and high impedances and also measures the total tissue resistivity for rabbit ventricular epicardium. Practical issues include [23, 78] temperature maintenance, calibration, water vapour saturation of tissue, time limits on protocols, tissue conditioning and methods for positioning the array.

5.3.2 Kwon, Sanchez and colleagues

Recent modelling and experimental work, using ovine skeletal muscle, by Kwon, Sanchez and colleagues [63, 64], is worthy of note despite its application being to progression of neuromuscular diseases. In these models, the object is to allow for anisotropy in both the resistivity and reactivity of the tissue. The approach uses a variant of the four-electrode technique that does not require the alignment of the array with the fibres and it has been validated using numerical simulations and in situ experiments. In the first study [64], a printed circuit board containing two concentric circles of monopolar electrodes was used. Then, the number of needle insertions required was reduced from 12 to 6 in the second study [63] by using multipolar needles. At present, this approach is applicable to measuring materials with different anisotropies in two dimensions only.

6 Challenges and future work

One thing to bear in mind in relation to the bidomain model is that the six conductivities are not the only inputs to the model. For example, depending on what is being modelled, it is necessary to have values for β,R,C_m, the blood conductivity g_b and the fibre rotation angle (Section 2.2). Commonly used values for these appear to be g_b = 6.7 mS/cm [91], β = 2000 cm^− 1 [74], R = 9100 Ω cm² [110], C_m = 1 μF cm^− 2 [27] and a fibre rotation angle of 120^∘ [71]. However, a range of other values is used in the literature; for example, Clayton et al. [12] state that typical values for β used in tissue models are in the range 1000–5000 cm^− 1 and for C_m 1–10 μF cm^− 2.

In addition to finding accurate conductivity values, it is obviously necessary to find accurate values for the above parameters as well. The method of Johnston and Johnston (Section 5.2.3) is able to retrieve the fibre rotation angle as well as the conductivities (under the assumption that there is a linear change in fibre rotation through the tissue, which seems to be consistent with experimental data [71]). It would also be informative to perform sensitivity analyses and quantify the effect of the above parameters on model outputs, as has been already done for the fibre rotation angle in models of ischaemia [47, 49].

The methods presented in Section 5 use the standard bidomain model (or sometimes the monodomain model), but a number of extensions to this have been developed, particularly to model diseased and damaged tissue. One reason that this is necessary is that it has been shown, using confocal microscopy, that the volume fractions of myocytes and fibroblasts change in infarcted hearts [96] and the conductivity values change near the boundary of the infarcted tissue (Section 3.5.2).

One method to deal with this is the extended bidomain model [92], which includes electrical coupling between fibroblasts and also between fibroblasts and myocytes. A variant on this approach is the modified bidomain model [20], which alternates healthy and fibrotic tissue at the microscopic scale and then homogenises this to produce a macroscopic scale model with altered conductivities. See [24] for a comparison of re-entrant behaviour in fibrotic tissue, using continuous models, discrete microstructural models and hybrid models.

In recent years, more complex models are being introduced to try to more faithfully represent various cardiac electrophysiological diseases and disorders. However, for precision medicine, these models are only useful if their inputs are accurate, or, at least, the degree of uncertainty can be quantified. This review has presented the state of the art in relation to the six bidomain conductivity values that are required in the standard bidomain model (Section 2.2) and highlighted the significant challenges for the scientific and engineering communities that determining them presents.

However, it is not just a matter of determining one consistent set of six conductivity values. The fact that changes in conductivity values can make significant differences to the outputs of simulations and hence to conclusions that might be drawn from them, as shown in simulations here (Section 4), means that it is necessary to establish whether the bidomain conductivity values are dependent on the position in the heart, or on tissue type, and how they change in disease.

Finally, if personalised medicine is being considered, it is also necessary to establish whether the conductivities vary between subjects. If so, it is important to determine how that may affect simulations that are used for clinical decisions, or, as suggested by Sadleir and Henriquez [93] and quoted in Section 1, how these changes may be harnessed to monitor clinical interventions.