Analytically Supported Hybrid Photonic–plasmonic Crystal Design Using Artificial Neural Networks

Abstract

An analytical and numerical study of hybrid photonic–plasmonic crystals is presented. The proposed theoretical model describes a system composed of a dielectric photonic crystal on a metallic thin film. To show the validity and usefulness of the model, four particular structures are analyzed: a one-dimensional crystal and three lattices of two-dimensional crystals. The model can calculate the photonic band structure of photonic–plasmonic crystals as a function of structural characteristics, showing two partial bandgaps for a square lattice, and complete bandgaps for triangular lattices. Furthermore, using a particular high-symmetry path, a full bandgap emerges in rectangular lattices, even with a small refractive index contrast. Using the analytical model, a dataset is generated to train an artificial neural network to predict the center and width of the bandgap, that is, the forward design. In addition, an artificial neural network is trained to tune the optical response, that is, to perform the inverse design. The analytical results are consistent with the physics of the system studied and are supported by numerical simulations. Moreover, the prediction accuracy of the artificial neural networks is better than 95%. Overall, this paper reports a useful tool for tuning the optical properties of hybrid photonic–plasmonic crystals with potential applications in waveguides, nanocavities, mirrors, etc.

Introduction

Photonic crystals are media whose refractive index is periodically modulated in space. This variation in the refractive index produces bandgaps in the photonic band structure, which physically results in the inhibition of light propagation in the medium for some frequencies ranges. Such an optical effect can be applied in various photonic devices, including filters, reflectors, and waveguides [1,2,3].

On the other hand, surface plasmon polaritons (SPPs) are electromagnetic excitations arising at a dielectric–metal interface. The optical properties of these electromagnetic excitations are of great interest, especially in technologies involving photonic devices [4].

As for waveguides based on photonic crystals, it is possible to use them in plasmonic devices. There is experimental evidence of an analogous photonic bandgap effect in periodic arrays of gold nanoparticles [5]. In addition, there are experimental observations of waveguiding of SPPs through bent linear defects fabricated in periodic arrays of gold nanoparticles [6,7,8]. Similarly, these periodic arrays can be used as mirrors to modify the propagation of SPPs [9].

Furthermore, experimental studies have analyzed the influence of different characteristics of plasmonic crystals in the photonic bandgap. Such characteristics are the lattice period or lattice constant, filling fraction and crystal orientation effect [10, 11]. These experimental results suggest that the propagation of SPPs can be controlled through the appropriate characteristics of the plasmonic crystal.

Metallic photonic crystals have proven to be efficient in producing bandgaps; however, this effect can also be achieved with dielectric photonic crystals. Numerical and experimental studies have shown the possibility of using dielectric ridge stacks as one-dimensional plasmonic crystals to open bandgaps in the SPPs dispersion relation [12]. The results of this last work suggest the application of these structures as a mechanism to control SPPs propagation.

In two-dimensional arrays, dielectric photonic crystals have been numerically analyzed to implement them as cavities [13, 14]. The results obtained from numerical studies show that these hybrid structures, photonic–plasmonic crystals, are capable of opening bandgaps in the dispersion relation. This suggests that they can be applied in a wide range of plasmonic devices such as nanocavities, nanolasers, reflectors or waveguides [13, 14].

On the other hand, several theoretical analyses have been developed for modeling the optical response of these plasmonic systems. Some of these studies are based on the multiple-scattering dipole approach [15], on the Lippmann-Schwinger integral equation method [16], and on the homogeneous form of the reduced Rayleigh equation [17].

As for conventional photonic crystals, one way to know their optical properties is to calculate their photonic band structure. There are several methods to do so, where one of the most widely used is the plane-wave expansion method (PWEM). Although this method is effective for calculating the band structure of dielectric photonic crystals, it also works for calculating the band structure of frequency-dependent media. For example, the PWEM has been applied to calculate the band structure of a silicon photonic crystal deposited over an aluminum film [18].

Another way to calculate the photonic band structure of these optical devices is based on the perturbation theory. From the band structure of a dielectric photonic crystal, perturbation theory is applied to analyze the effect of a frequency-dependent dielectric function [19]. However, this method is effective when the variation of the dielectric function is less than 1% [3].

In an opposite direction, the inverse design consists in the retrieval of the suitable structure for a particular desired optical response [20]. However, it sometimes requires a search for different system characteristics, starting from a random design, and comparing the result with the target response [21]. This search, called optimization, is performed iteratively and need being carried out too many times to achieve the desired result [21].

In contrast to the above, machine learning algorithms, such as artificial neural networks (ANNs), are efficient tools to design photonic structures [20, 21]. ANNs can be applied in two different ways. The first is to use the structural parameters to predict the optical response, to avoid the optimization loop, which can sometimes be computationally expensive. This process is known as forward design [21]. The second approach to the ANNs is using the inverse design mentioned before. The aim is to predict the structural properties of the photonic system from the desired optical response [20, 21].

In this work, an analytical model based on PWEM is proposed to calculate the photonic band structure of hybrid photonic–plasmonic crystals (PhPl crystals). These hybrid structures are composed of a dielectric photonic crystal, whose dielectric function is not frequency-dependent, supported on a thin film of gold or silver. Since the dielectric functions of gold and silver are frequency-dependent, a nonlinear eigenvalue equation is needed to solve the corresponding Helmholtz equation.

From the general model, the photonic band structure of four particular systems is studied to test the proposed model and show its usefulness. The analyzed photonic devices are experimentally feasible, since they are composed of a dielectric photonic crystal formed by a periodic array of PMMA structures supported on a thin metallic film.

Using the analytical model, a dataset was constructed to train the machine learning algorithms. These algorithms are used to predict the optical response of a hybrid PhPl crystal without the need to run a computationally expensive code (forward design). Furthermore, the algorithms are useful to build a dataset larger than the first one to train a second ANN.

With the last dataset, this second ANN was trained to predict the structural parameters for a given specific optical response (inverse design); that is, this ANN is a useful tool to tune the optical response. To validate the results obtained from this ANN, the predicted value is compared to the results obtained with the analytical model, and both are supported by numerical simulations.

Analytical Model

The PWEM is a widely used tool to solve the wave equation for photonic crystals. In this method, both the electric field and the inverse of dielectric functions are expressed as Fourier series

$$\begin{aligned} \mathbf {E}(\mathbf {r})&= \sum _{\mathbf {G}} \mathcal {E}_{\mathbf {k}n}(\mathbf {G}) e^{i(\mathbf {k} + \mathbf {G})\cdot \mathbf {r}}, \end{aligned}$$

(1)

$$\begin{aligned} \frac{1}{\epsilon (\mathbf {r})}&= \sum _{\mathbf {G}} \xi (\mathbf {G})e^{i\mathbf {G}\cdot \mathbf {r}}, \end{aligned}$$

(2)

where $\mathcal {E}_{\mathbf {k}n}(\mathbf {G})$ and $\xi (\mathbf {G})$ are the Fourier coefficients of the expansion [1,2,3]. Inserting both equations into the Helmholtz one, the master equation for photonic crystals is obtained for a TM polarized electromagnetic wave

$$\begin{aligned} -\sum _{\mathbf {G'}}\xi (\mathbf {G} - \mathbf {G'}) (\mathbf {k} + \mathbf {G'}) \times \left\{ (\mathbf {k} + \mathbf {G'}) \times \mathcal {E}_{\mathbf {k}n}(\mathbf {G'}) \right\} = \frac{\omega _{\mathbf {k}n}^2}{c^2} \mathcal {E}_{\mathbf {k}n}(\mathbf {G}), \end{aligned}$$

(3)

where $\mathbf {G}$ and $\mathbf {G'}$ are the reciprocal vectors, $\mathbf {k}$ is the wave vector, and $\omega _{\mathbf {k}n}$ are the eigenfrequencies [1, 2].

This equation can be expressed as a matrix equation as follows:

$$\begin{aligned} \mathbf {\hat{\Xi }}' \mathbf {\hat{K}} \mathcal {E} = \hat{\mathbf {M}} \mathcal {E} = \frac{\omega ^2}{c^2} \mathcal {E}, \end{aligned}$$

(4)

where $\mathbf {\hat{\Xi }}'$ is a matrix constructed with the coefficients $\xi$, $\hat{\mathbf {K}}$ is a matrix formed by the vectors $\mathbf {k}$ and $\mathbf {G}$, and $\mathcal {E}$ is a vector constructed with the coefficients $\mathcal {E}_{\mathbf {k}n}$. The last equation is an eigenvalue equation and can be considered as solved when the eigenvalues of the matrix $\hat{\mathbf {M}}$ are found [1,2,3].

When the dielectric function is non-dependent on the frequency, the eigenfrequencies are obtained by solving Eq. (4). However, if the dielectric function is frequency-dependent, as it is the case for SPPs, solving the equation is not straightforward since it is a nonlinear eigenvalue equation.

The analytical model is based on the PWEM; however, the problem to be solved is a nonlinear eigenvalue equation. The key to solving this equation is to find how the inverse of the dielectric function depends on the frequency over a given range of wavelengths. The above allows to convert the nonlinear eigenvalue problem into a linear eigenvalue problem to solve Eq. (4).

Let be a dielectric–metal interface that supports typical SPP propagation. The effective refractive index is defined as [4]

$$\begin{aligned} n_{eff} = \sqrt{\frac{\epsilon _d\epsilon _m}{\epsilon _d + \epsilon _m}}, \end{aligned}$$

(5)

so that the inverse of the dielectric function is

$$\begin{aligned} \frac{1}{\epsilon _{eff}(\omega )} = \frac{\epsilon _d + \epsilon _m}{\epsilon _d\epsilon _m}, \end{aligned}$$

(6)

where $\epsilon _d$ and $\epsilon _m$ are the dielectric functions of dielectric and metallic media, respectively.

Fig. 1

Physical system composed of a dielectric photonic crystal supported on a gold or silver thin film

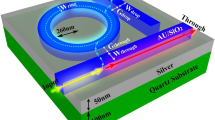
The system under analysis is a photonic crystal made up of two dielectrics: one with permittivity $\epsilon _a$ and the other with permittivity $\epsilon _b$. Both dielectric functions are considered to be non-dependent on the frequency. This photonic crystal is supported on a metallic thin film as shown in Fig. 1, so there are two interfaces in a unit cell. In this work, the base is the repeating element; that is, the interface formed by the dielectric b and the metallic thin film.

Figure 2 shows a unit cell of a rectangular lattice with three different bases for one of the dielectrics: an arbitrary shape, a rectangular shape, and a circular shape base.

Fig. 2

Rectangular lattice with an arbitrary shape base (left), rectangular base (center) and circular base (right)

For the interface represented by the white zone in the unit cell, the effective dielectric function is described by $\epsilon _1 = \epsilon _a \epsilon _m/(\epsilon _a + \epsilon _m)$, while for the interface represented by the gray zone, the effective dielectric function is described by $\epsilon _2 = \epsilon _b \epsilon _m/ (\epsilon _b + \epsilon _m)$. In general, the inverse of the effective dielectric function throughout the unit cell is given by

$$\begin{aligned} \begin{aligned} \frac{1}{\epsilon _{eff}(\omega )}&= \frac{1}{\epsilon _1(\omega )} + \left[ \frac{1}{\epsilon _2(\omega )} - \frac{1}{\epsilon _1(\omega )} \right] F(\mathbf {r}) \\&= \frac{1}{\epsilon _1(\omega )} + \Delta \xi F(\mathbf {r}), \end{aligned} \end{aligned}$$

with $F(\mathbf {r}) = 1$, if $\mathbf {r}$ is within the gray zone, and $F(\mathbf {r}) = 0$ otherwise. It is important to note that the quantity $\Delta \xi$ in the second term does not depend on the frequency.

This way, the Fourier coefficients $\xi$ are given by

$$\begin{aligned} \xi (\mathbf {G}) = \frac{1}{\epsilon _1(\omega )}\delta ^2(\mathbf {G}) + \frac{1}{A_0}\Delta \xi \mathcal {F} (\mathbf {G}), \end{aligned}$$

(7)

where $A_0$ is the unit cell area, and $\mathcal {F}(\mathbf {G})$ is the Fourier transform of $F(\mathbf {r})$. The coefficient depends on the geometry of the base and the symmetry of the crystal lattice, since $\mathbf {G}$ is defined by the crystal lattice vectors.

Thus, the matrix $\mathbf {\hat{\Xi }}'(\omega )$ in Eq. (4) has two terms: one frequency-dependent and one frequency-independent, so that it can be written as

$$\begin{aligned} \mathbf {\hat{\Xi }}'(\omega ) = \mathbf {\hat{\Xi }}_0(\omega ) + \mathbf {\hat{\Xi }}, \end{aligned}$$

(8)

where $\mathbf {\hat{\Xi }}$ is constructed by terms of $\frac{1}{A_0}\Delta \xi \mathcal {F}(\mathbf {G})$ and $\mathbf {\hat{\Xi }}_0(\omega )$ is given by

$$\begin{aligned} \mathbf {\hat{\Xi }}_{0}(\omega ) = \frac{1}{\epsilon _1(\omega )} \mathbf {\hat{1}} = \frac{1}{\epsilon _1(\omega )} \begin{pmatrix} 1 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 1 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 1 \end{pmatrix}, \end{aligned}$$

(9)

Considering this, Eq. (4) becomes

$$\begin{aligned} \left( \frac{1}{\epsilon _1(\omega )} \mathbf {\hat{1}} + \mathbf {\hat{\Xi }}\right) \mathbf {\hat{K}} \mathbf {\mathcal {E}} = \frac{\omega ^2}{c^2} \mathbf {\mathcal {E}}. \end{aligned}$$

(10)

The inverse of the dielectric function described by Eq. (6) for dielectric–gold or dielectric–silver interfaces can be approximated, over a suitable frequency range, by a function given as follows:

$$\begin{aligned} \frac{1}{\epsilon _{eff}(\omega )} \approx \frac{1}{\epsilon _d} + \gamma _1\left( \frac{\omega }{c} - b\right) ^{-2} + \gamma _2\left( \frac{\omega }{c} - b\right) ^{-1} + \gamma _3\left( \frac{\omega }{c} - b\right) , \end{aligned}$$

(11)

where parameters $\gamma _i$ and b are determined as a function of the dielectric constants $\epsilon _d$ and $\epsilon _m$. With the change of variable $\alpha =\omega /c - b$, the inverse of the dielectric functions $1/\epsilon _1 (\omega )$ and $1/\epsilon _2 (\omega )$ are

$$\begin{aligned} \frac{1}{\epsilon _1}&= \frac{1}{\epsilon _a} + \gamma _1\alpha ^{-2} + \gamma _2\alpha ^{-1} + \gamma _3\alpha , \end{aligned}$$

(12)

$$\begin{aligned} \frac{1}{\epsilon _2}&= \frac{1}{\epsilon _b} + \gamma _1\alpha ^{-2} + \gamma _2\alpha ^{-1} + \gamma _3\alpha . \end{aligned}$$

(13)

Fig. 3

Inverse of dielectric function for two different dielectric–gold interfaces

As an example, Fig. 3 shows the inverse of dielectric function data for an air–gold interface (black circles), and for a PMMA–gold interface (black squares), in the range of wavelengths 548.6-1937 nm. In both cases, the inverse of the dielectric function was calculated using Johnson & Christy data of permittivity for gold [22]. The continuous lines are the data fitted to the Eq. (11).

This way, Eq. (10) is expressed by

$$\begin{aligned} \left( \gamma _1\alpha ^{-2}\mathbf {\hat{1}} + \gamma _2\alpha ^{-1}\mathbf {\hat{1}} + \frac{1}{\epsilon _a} \mathbf {\hat{1}} + \mathbf {\hat{\Xi }} + \gamma _3\alpha \mathbf {\hat{1}} \right) \mathbf {\hat{K}} \mathbf {\mathcal {E}} = \left( b^2 + 2b\alpha + \alpha ^2\right) \mathbf {\mathcal {E}}, \end{aligned}$$

(14)

ordering the terms

$$\begin{aligned} \left[ \alpha ^{-2}\gamma _1\mathbf {\hat{K}} + \alpha ^{-1}\gamma _2\mathbf {\hat{K}} + \left( \frac{1}{\epsilon _a}\mathbf {\hat{K}} + \mathbf {\hat{\Xi }}\mathbf {\hat{K}} - b^2 \mathbf {\hat{1}} \right) + \alpha \left( \gamma _3\mathbf {\hat{K}} - 2b\mathbf {\hat{1}}\right) \right] \mathbf {\mathcal {E}} = \alpha ^2 \mathbf {\mathcal {E}}. \end{aligned}$$

(15)

With $\mathbf {\hat{A}} = \gamma _1\mathbf {\hat{K}}$, $\mathbf {\hat{B}} = \gamma _2\mathbf {\hat{K}}$, $\mathbf {\hat{C}} = (\frac{1}{\epsilon _a}\mathbf {\hat{1}} + \mathbf {\hat{\Xi }})\mathbf {\hat{K}} - b^2 \mathbf {\hat{1}}$ and $\mathbf {\hat{D}} = \gamma _3\mathbf {\hat{K}} - 2b\mathbf {\hat{1}}$, Eq. (15) is rewritten as

$$\begin{aligned} \left( \alpha ^{-2}\mathbf {\hat{A}} + \alpha ^{-1}\mathbf {\hat{B}} + \mathbf {\hat{C}} + \alpha \mathbf {\hat{D}} \right) \mathbf {\mathcal {E}} = \alpha ^2 \mathbf {\mathcal {E}}. \end{aligned}$$

(16)

Now, the problem has become a nonlinear eigenvalue equation. However, it can be solved with an extended matrix $\mathbf {\hat{M}}_{ext}$ to treat it as a linear eigenvalue problem [23, 24]. This extended matrix acts over an extended vector $\mathbf {\mathcal {E}}_{ext}$ as follows:

$$\begin{aligned} \mathbf {\hat{M}}_{ext} \mathbf {\mathcal {E}}_{ext} = \begin{pmatrix} \mathbf {\hat{0}} &{} \mathbf {\hat{1}} &{} \mathbf {\hat{0}} &{} \mathbf {\hat{0}} \\ \mathbf {\hat{0}} &{} \mathbf {\hat{0}} &{} \mathbf {\hat{1}} &{} \mathbf {\hat{0}} \\ \mathbf {\hat{0}} &{} \mathbf {\hat{0}} &{} \mathbf {\hat{0}} &{} \mathbf {\hat{1}} \\ \mathbf {\hat{A}} &{} \mathbf {\hat{B}} &{} \mathbf {\hat{C}} &{} \mathbf {\hat{D}} \end{pmatrix} \begin{pmatrix} \alpha ^{-2}\mathbf {\mathcal {E}} \\ \alpha ^{-1}\mathbf {\mathcal {E}} \\ \mathbf {\mathcal {E}} \\ \alpha \mathbf {\mathcal {E}} \end{pmatrix} = \begin{pmatrix} \alpha ^{-1}\mathbf {\mathcal {E}} \\ \mathbf {\mathcal {E}} \\ \alpha \mathbf {\mathcal {E}} \\ \left( \alpha ^{-2}\mathbf {\hat{A}} + \alpha ^{-1}\mathbf {\hat{B}} + \mathbf {\hat{C}} + \alpha \mathbf {\hat{D}} \right) \mathcal {E} \end{pmatrix} = \alpha \begin{pmatrix} \alpha ^{-2}\mathbf {\mathcal {E}} \\ \alpha ^{-1}\mathbf {\mathcal {E}} \\ \mathbf {\mathcal {E}} \\ \alpha \mathbf {\mathcal {E}} \end{pmatrix} . \end{aligned}$$

(17)

To obtain the eigenfrequencies $\omega$, it is sufficient to find the eigenvalues of the matrix $\mathbf {\hat{M}}_{ext}$, simplifying enormously the mathematical problem.

Particular Structures

The proposed dielectric photonic crystal consists of PMMA pillars of either rectangular or elliptical cross sections immersed in air. It is worth mentioning that square and circular cross sections are considered particular cases of rectangular and elliptical cross sections. The refractive index of PMMA has small variations in the 550-2000 nm range and does not represent a significant change in the PMMA-gold dispersion relation if its dielectric function is assumed to be constant.

Fig. 4

SPPs dispersion relation for a PMMA-gold interface

Figure 4 shows the SPPs dispersion relation for a PMMA-gold interface. The dashed line is the dispersion relation considering a frequency-dependent PMMA dielectric function, as in reference [25]. The solid gray line is the dispersion relation considering a constant PMMA dielectric function. The value of the dielectric functions is $\epsilon _{PMMA} = \epsilon _b = 2.2$ for PMMA, taking the value of PMMA dielectric function at $\lambda =633$ nm [25], and $\epsilon _{air} = \epsilon _a = 1$ for air, such that the dielectric constants contrast is $\epsilon _b/\epsilon _a$ = 2.2.

Fig. 5

Inverse of dielectric function for four different dielectric-gold and dielectric-silver interfaces

As an example, Fig. 5 shows the inverse of dielectric function data for an air–gold interface, represented by black circles, and for a PMMA–gold interface, represented by black squares, in the wavelength range 548.6-1937 nm. The black diamonds and black triangles are the inverse of dielectric function data for an air–silver and a PMMA–silver interfaces, respectively, in the range of wavelengths from 331.50 to 1937 nm. For all the interfaces, the inverse of the dielectric function is calculated using Johnson & Christy data of permittivity for gold and silver [22]. The solid and dashed lines are the inverse of dielectric function data fitted to Eq. (11).

The wavelength ranges for data fitting were chosen to avoid the maximum value of the effective refractive index, since, near that value, SPPs propagation is considerably attenuated. The maximum value of the effective refractive index for a dielectric–gold interface is located at approximately 520 nm, while for a dielectric–silver interface it occurs approximately at 340 nm.

The data fit parameters for the dielectric–gold interface are $\gamma _1=0.115218$, $\gamma _2=0.266632$, $\gamma _3=-0.002649$ and $b=12.368228$. For the dielectric–silver interface, the data fit parameters are $\gamma _1=0.153906$, $\gamma _2=0.901489$, $\gamma _3=-0.003654$ and $b=19.361642$.

In the case of a dielectric–gold interface, the fit of the data of the inverse of the effective refractive index has an asymptotic behavior at $b=12.368228$, which is equivalent to a wavelength of approximately 508 nm. For a dielectric–silver interface, the asymptotic behavior is found at $b=19.361642$, corresponding to a wavelength of approximately 324 nm.

To solve Eq. (17) for the four chosen different crystal lattices as a function of the lattice length and base size for two bases with different geometries, a python code was written.

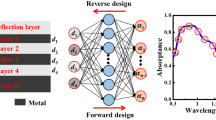
Machine Learning Algorithms

Various machine learning algorithms were trained to predict bandgap properties (optical properties) as a function of crystal parameters (forward design) and to determine the structural features for a target optical response (inverse design). These algorithms were linear and polynomial regression, k-nearest neighbors (KNN), decision tree and artificial neural networks (ANN). The polynomial regression, KNN and decision tree algorithms were implemented using scikit-learn library [26].

For forward design, all the algorithms perform optimally predicting the optical response with high accuracy. However, the best results in predicting the physical characteristics of the PhPl crystal from a target optical response were obtained using ANN for triangular and rectangular lattices.

Table 1 Parameters to generate data for the three lattices and two bases

The datasets necessary to train the algorithms were generated using the analytical model. To calculate the photonic band structure as a function of the lattice and the base sizes, these quantities were varied as shown in Table 1. With the band structure information, the bandgap width $\Delta \lambda$, and the bandgap center $\lambda _c$, were calculated for all the parameters.

The filling fractions $f_x$ and $f_y$, in x and y directions, respectively, are defined as $f_x=d_x/a$ and $f_y=d_y/a$, for the square and triangular lattices, and $f_x=d_x/a_x$ and $f_y=d_y/a_y$ for the rectangular lattice. The parameters $d_x$ and $d_y$ are the characteristic sizes of the base. For a rectangular base, they are the lengths of the sides in x and y directions, and for an elliptical base, they are the lengths of the axes of the ellipse in x and y directions, respectively, as shown in Fig. 6. As mentioned above, the square and circular bases are particular cases of the rectangular and elliptical bases, when $d_x = d_y = d$.

Fig. 6

Three two-dimensional lattices with rectangular and elliptical bases

For the square lattice, the lattice size is varied in steps of 50 nm. The step of the filling fraction variation was 0.05 for the elliptical base and 0.1 for the rectangular base. On the other hand, for the triangular lattice, the variation of the lattice size is the same as the square lattice, 50 nm. The variation of the filling fraction for the elliptical base was 0.043. For a rectangular base, the step of variation was 0.036. In the case of the rectangular lattice, the lattice size in x-direction is varied in steps of 50 nm, while the size in y-direction is varied in steps of 0.1, from 1.2$a_x$ to 1.8$a_x$. The step of the filling fraction for both the elliptical and the rectangular bases was 0.05.

To train the algorithms, polynomial regression from 1 to 15 degrees was tested, KNN was used with a range of nearest neighbors from 1 to 30, the decision tree algorithm was used with a maximum depth of 1 to 30, and ANN was implemented by testing various architectures.

On the other hand, for triangular and rectangular lattices, an ANN was trained to predict the optical response ($\Delta \lambda$ and $\lambda _c$) as a function of the lattice size (a), and base size ($d_x$ and $d_y$). This ANN architecture is shown in Fig. 7.

Fig. 7

ANN architecture to predict the optical response of triangular lattice

This ANN has five hidden layers, where the first and fifth layers have 100 neurons, the second and fourth layers have 200 neurons and the third layer has 300 neurons.

The ANN was trained with 12486 samples, 70% of which were used to training, 15% to testing, and 15% was used for cross-validation. The optimizer used was Adam, with a learning rate of 0.004, the loss function used was mean square error, and the metric used was accuracy. In addition, a batch size of 6000 and 200 epochs were used.

For the rectangular lattice, the input features are $a_x$, $a_y$, $d_x$ and $d_y$. Figure 8 shows the ANN architecture for the rectangular lattice.

Fig. 8

ANN architecture to predict the optical response for the rectangular lattice

The architecture of the hidden layers of this ANN is the same as for the previous case.

This ANN was trained with 10416 samples, split into 70%, 15%, and 15% for training, testing, and cross-validation, respectively. In this case, the same optimizer was used, but with a learning rate of 0.01. Again, the loss function was mean square error, and the metric used was accuracy. The batch size was 500, and the number of epochs was 500.

Using both ANNs, more datasets of optical response data were generated as a function of crystal characteristics. With the new datasets, further ANNs were trained to develop the inverse design of the PhPl crystals. With the above, the crystal characteristics were predicted from the optical response. In this case, the input features are the optical response $\Delta \lambda$ and $\lambda _c$. The output are the characteristics of the PhPl crystal, a and f for the triangular lattice, and $a_x$, $a_y$ and f for rectangular lattice.

The ANNs architectures for predicting crystal parameters from the optical response of the triangular and rectangular lattices are shown in Figs. 9 and 10, respectively. Both ANNs have 15 hidden layers, each with 500 neurons.

Fig. 9

ANN architecture to predict the crystal parameters of a triangular lattice

To train the ANN for the triangular lattice, 12126 samples, split into 70%, 15%, and 15%, were used for training, testing, and cross-validation, respectively. In addition, an Adam optimizer with a learning rate of 0.003 was used. The loss function and metric used were mean square error and cosine similarity, respectively. In this case, a batch size of 4000 and 400 epochs were used to train the algorithm.

Fig. 10

ANN architecture to predict the crystal parameters of a rectangular lattice

On the other hand, the ANN for the rectangular lattice was trained with 308050 samples, split in 90%, 5%, and 5%, for train, test, and cross-validation, respectively. The optimizer used was Adam with a learning rate of 0.0015. As above, the loss function and metric used were mean square error and cosine similarity, respectively. Finally, a batch size of 10,000 and 100 epochs were used.

The ANNs were implemented using Keras with the TensorFlow backend. All hyperparameters were chosen to obtain a maximum accuracy. Also, to avoid underfitting and improve the ANN training performance, it was noted that the only geometry needed to be considered was bases with circular and square shapes, for the triangular lattice; and elliptical and rectangular shapes, for the rectangular lattice.

Results

One-dimensional PhPl Crystal

The one-dimensional PhPl crystal formed by layers of air and PMMA on a gold or silver thin film, as shown in Fig. 11

Fig. 11

The one-dimensional PhPl crystal formed by stacks of air and PMMA on a thin metallic film

Figure 12 shows the band structure of a one-dimensional dielectric–gold PhPl crystal.

Fig. 12

Band structure of a one-dimensional PhPl crystal for $a=300$ nm and $f=0.5$. Au case

The lattice constant is $a=300$ nm and the filling fraction is $f= 0.5$. With these parameters, it has a bandgap with width $\Delta \lambda =179.74$ nm and centered at $\lambda _c=787.22$ nm. The bandgap is represented with a gray fringe in the band structure.

To test the validity of the model, the band structure of a one-dimensional PhPl crystal with two different filling fractions was calculated. The first value is $f=0$, which corresponds to a pure air–gold interface.

Fig. 13

Band structure of a one-dimensional PhPl crystal for $a=300$ nm and $f=0$. Au case

The agreement shown in Fig. 13 between the band structure of the PhPl crystal for $f=0$, represented by blue and red lines, and the dispersion relation of the SPPs in an air–gold interface, represented by the black circles, is evident.

Fig. 14

Band structure of a one-dimensional PhPl crystal for $a=300$ nm and $f=1$. Au case

On the contrary, for $f=1$, the physical system is a PMMA–gold interface, since the unit cell is completely covered by the PMMA layer. Figure 14 shows the corresponding band structure. As above, the blue and red lines are the band structure of the PhPl crystal, while the black circles are the dispersion relation of the SPPs in a PMMA-gold interface. Again, there is a total agreement between the band structure and the dispersion relation.

For a PhPl crystal with a lattice constant of $a=300$ nm and a filling fraction $f=0.5$, but composed of a PMMA structure supported on a silver thin film, the photonic band structure is shown in Fig. 15.

Fig. 15

Band structure of a one-dimensional PhPl crystal for $a=300$ nm and $f=0.5$. Ag case

In this case, the center and width of the bandgap are $\lambda =782.09$ nm and $\Delta \lambda =181.78$, respectively.

Comparing the dielectric–silver PhPl crystal with the dielectric–gold PhPl crystal one, there is a small difference between the bandgap characteristics of both when using the same parameters. This is because the effective refractive indexes of a dielectric–gold interface and a dielectric–silver interface are similar in the electromagnetic spectrum where the bandgap arises.

To understand how the optical response is modified as a function of crystal parameters, the band structure was calculated for different lattice constants and filling fractions for a dielectric-gold PhPl crystal.

Fig. 16

Bandgap center as a function of a and f for one-dimensional dielectric-gold PhPl crystal

Figure 16 shows the behavior of the bandgap center as a function of lattice constant and filling fraction. As it is shown in the plot, the bandgap center increases monotonically as the lattice constant and filling fraction do too. This result is consistent with the one reported in reference [12], where it is observed that the center of the bandgap is red shifted as the filling fraction increases.

On the other hand, the bandgap width as a function of the lattice constant and filling fraction is shown in Fig. 17. In this case, $\Delta \lambda$ increases as the lattice constant does. However, as a function of the filling fraction, it increases until it reaches a maximum near $f=0.44$, and then it decreases to zero. This result is consistent with the one reported in reference [12], where it is concluded that the maximum width of the bandgap is close to $f=0.42$ for SiO$_2$ ridges.

Fig. 17

Bandgap width as a function of a and f for one-dimensional dielectric–gold PhPl crystal

Two-dimensional PhPl Crystals

As it was mentioned above, three different two-dimensional lattices were analyzed. For each case, the optical response (the bandgap width $\Delta \lambda$ and center $\lambda _c$) was studied as a function of the lattice constant a, and the base sizes $d_x$ and $d_y$. Then, an ANN was trained to predict the PhPl crystal parameters for the desired optical response. For all the cases, numerical simulations were obtained to corroborate the analytical results. The simulations are shown only for the triangular and the rectangular lattices.

Square Lattice

For a square lattice with a 300-nm lattice constant and an elliptical base with 165 nm for the major axis, and 132 nm for the minor one, the band structure is shown in Fig. 18.

Fig. 18

Band structure of a dielectric-gold PhPl crystal for a square lattice with an elliptical base. This band structure corresponds to a lattice constant of $a=$ 300 nm, with $d_x=165$ nm and $d_y=132$ nm

In this case, the major axis is in the x-direction, while the minor axis is in the y-direction. For the square lattice, there are two partial bandgaps. The first is on the $\Gamma -\mathrm {X}$ orientation, which has a width of 90.30 nm and is centered at 696.19 nm. The second is on the $\mathrm {M}-\Gamma$ orientation, with a width of 72.55 nm and center at 573.64 nm.

Note that bands 2 and 3 (black and red curves, respectively) coincide at the $\Gamma$ point with a value of 0.57, which is equivalent to a wavelength of about 526.32 nm. Moreover, the upper bands cluster near this same value, that is, near the fitting parameter b of Eqs. (12) and (13) for a dielectric–gold interface. This means that the bandgap is within the wavelength range in which the data fitting was made.

Fig. 19

Band structure of a dielectric–silver PhPl crystal for a square lattice with an elliptical base. This band structure corresponds to a lattice constant of $a=$ 300 nm, $d_x=165$ nm and $d_y=132$ nm

Using the same parameters as above, the band structure of a dielectric-silver PhPl crystal is shown in Fig. 19. The bandgap in the $\Gamma -\mathrm {X}$ orientation is centered at 689.94 nm and has a width of 92.37 nm. The bandgap in the $\mathrm {M}-\Gamma$ orientation is centered at 549.22 nm and has a width of 84.26 nm.

Fig. 20

Band structure of a square lattice with an elliptical base. This band structure corresponds to a lattice constant of $a=300$ nm, $d_x=165$ nm and $d_y=132$ nm, but with a dielectric constants contrast of $\epsilon _b/\epsilon _a=9$

In this case, the characteristics of the bandgap in the $\Gamma -\mathrm {X}$ orientation are similar to the dielectric–gold PhPl crystal. However, characteristics of both bandgaps in the $\mathrm {M}-\Gamma$ orientation are remarkably different. This is due to the difference of the effective refractive indexes in that range of the electromagnetic spectrum.

As in the previous case, for a dielectric-silver PhPl crystal, the upper bands cluster near parameter b of the fitting equation. This means that the dielectric-silver PhPl crystal can be used over a wider range of wavelengths.

On the other hand, one of the reasons of the existence of two partial bandgaps for both cases is a low contrast of dielectric constants. For example, in a PhPl crystal with the same dimensions but with a dielectric constants contrast of $\epsilon _b/\epsilon _a=9$, there are two complete bandgaps, as it is shown in Fig. 20.

In this case, one of the bandgaps has a width of $\Delta \lambda =243.76$ nm and is centered at $\lambda _c=966.93$ nm. The other bandgap has a width of $\Delta \lambda =38.22$ nm and is centered at $\lambda _c=711.9$ nm. In addition, as the contrast of the dielectric constants increases, the width and center of the bandgap also increase.

As in the one-dimensional case, the center and width of the bandgap were calculated for a square lattice with rectangular and elliptical bases. Furthermore, the geometry of the base cross section does not represent a significant difference in the structure of the band, the key parameter being the filling fraction.

Fig. 21

Bandgap center as a function of a and f for square lattice and with an elliptical base

Figures 21 and 22 show heat maps of the center and width of the bandgap in the $\Gamma -\mathrm {X}$ orientation, respectively, as a function of the lattice constant a and filling fraction f. As in the one-dimensional case, the center of bandgap is an increasing function of the lattice constant and the filling fraction. Furthermore, the bandgap width increases up to a maximum near $f=0.38$, decreasing after that.

Fig. 22

Bandgap width as a function of a and f for square lattice and with an elliptical base

Having the above into account, to tune the bandgap center and width for a square lattice, it is necessary adjusting both the lattice constant and filling fraction. However, the relationship to tune the optical response from the structural properties is not obvious; therefore, machine learning algorithms were necessary to be used. Furthermore, it is possible obtaining a complete bandgap by varying the dielectric constants contrast.

Regarding the machine learning algorithms, the optimal results for the forward design were obtained for polynomial regression of degree 6, for 4 nearest neighbors and, in the case of the decision tree algorithm, for a maximum depth of 15. In all three cases, the prediction accuracy is greater than 99%.

On the contrary, for the inverse design, the best performances were obtained for a polynomial regression of degree 13, for 30 nearest neighbors in the case of the KNN algorithm, and a maximum depth of 7 for the decision tree algorithm. In this case, the prediction accuracy is not as high as in forward design, since the accuracy is less than 78%.

Table 2 shows the performance results of the machine learning algorithms for the square lattice. Within it, the performance of the algorithms can be compared, being observed that the polynomial regression generalizes better the predictions for the forward design, while KNN does better for the inverse design.

Table 2 Machine learning algorithms results for square lattice

The algorithms results were tested using a lattice constant $a = 300,$ and base sizes $d_x = 100$ nm and $d_y = 150$ nm. With these parameters, the partial bandgap in $\Gamma -\mathrm {X}$ orientation is centered at $\lambda _c = 674.446$ nm and has a width of $\Delta \lambda = 82.113$ nm.

Table 3 Results comparison between theoretical model and machine learning algorithms

The results obtained with machine learning algorithms are shown in Table 3. As it can be seen, the machine learning algorithms predict correctly the optical properties as a function of crystal parameters, where the minimum discrepancy between results is obtained with KNN for both bandgap center and bandgap width.

This means that the algorithms are able to understand the relationship between the structural parameters and the optical response, with which it is possible to calculate the properties of the bandgap without the need to calculate the complete band structure.

Triangular Lattice

Unlike the square lattice, the triangular lattice presents a complete bandgap even at low dielectric constants contrast, as it is shown in Fig. 23.

Fig. 23

Band structure of a dielectric–gold PhPl crystal for a triangular lattice with an elliptical base, with $a=330$ nm, $d_x=130$ nm and $d_y=100$ nm

This band structure corresponds to a lattice constant of 330 nm, with an elliptical base whose major axis is $d_x=130$ nm, while the minor axis is $d_y=100$ nm. The bandgap has a width of 42.82 nm and is centered at $\lambda _c=631.33$ nm.

To compare the results provided by the model with experimental results, the bandgap properties were calculated for a triangular lattice with a lattice constant $a = 400$ nm and with a base diameter $d = 200$ nm, as in reference [6]. In that case, the base corresponds to a circular gold structure.

Fig. 24

Band structure of a dielectric–silver PhPl crystal for a triangular lattice with an elliptical base, with $a=330$ nm, $d_x=130$ nm and $d_y=100$ nm

In the experimental data of Bozhevolnyi et al., a high reflectivity is reported at $\lambda = 782$ nm, suggesting that this wavelength is within the bandgap. In addition, it is mentioned that the intensity of the reflected SPPs practically vanishes at $\lambda = 815$ nm; that is, this wavelength does not belong to the bandgap. With the same parameters, the model calculates a bandgap centered at $\lambda _c = 774.041$ nm with a width of $\Delta \lambda = 52.141$ nm. Although it is not the same physical system, the results are consistent.

The photonic band structure of a dielectric–silver PhPl crystal with the same lattice constant and base size is shown in Fig. 24. The bandgap is centered at $\lambda _c=620.16$ nm with a width of $\Delta \lambda =40.98$ nm. Comparing this PhPl crystal with a dielectric–gold PhPl crystal, the significant change is in the bandgap center. The difference between both bandgap centers is about 11 nm.

The experimental results reported by Kitson, Barnes and Sambles, show the existence of a bandgap in a triangular array of circular silver structures on a film of the same material. This triangular lattice has a period $a = 300$ nm and the structures have a diameter $d = 200$ nm. The reported bandgap is centered at $\lambda _c = 634.527$ nm and has a width $\Delta \lambda = 29.211$ nm [5].

Fig. 25

Bandgap width as a function of a and f for triangular lattice and with an elliptical base

Using these same parameters in the theoretical model, the calculated bandgap is centered at $\lambda _c = 638.626$ nm and has a width $\Delta \lambda = 41.285$ nm. Although the bases are different in composition, the calculated theoretical result is consistent with that reported experimentally in reference [5], showing that the lattice constant and the size of the base are determining parameters in the properties of the bandgap.

As in the previous cases, the center of the bandgap is red shifted when the lattice constant and the filling fraction are increased. On the other hand, Fig. 25 shows the bandgap width as a function of lattice size and filling fraction. In this case, a complete bandgap arises for filling fractions larger than 0.3 and less than 0.85 and reaches its maximum near $f=0.44$. Furthermore, the bandgap width is a monotonically increasing function of the lattice constant. For the wavelength interval used, the maximum width is $\Delta \lambda =99.56$ nm.

This behavior of the bandgap properties is consistent with the results reported in references [10, 11]. In that case, the PhPl crystals consist of gold columns in a triangular array on a thin film of the same material, and it is experimentally verified that the bandgap broadens and is red-shifted when the filling fraction increases.

Regarding the algorithms used in the forward design, for polynomial regression the best performance was obtained with degree 5, for KNN it was obtained with 6 nearest neighbors, and for the decision tree, it was obtained with a maximum depth of 15. With respect to the ANN, an accuracy of 1 is obtained to predict the optical response as a function of plasmonic crystal characteristics with the architecture described above.

Table 4 Machine learning algorithms results for triangular lattice

Table 4 shows the performance results of the machine learning algorithms for the triangular lattice. As in the previous lattice, for the accuracy reported in the table, the algorithms are more accurate in the forward design than in the inverse design.

ANNs exhibit high precision in obtaining the structural properties for a target optical response. This means that this algorithm adequately learns the relationship between the optical response and the structural properties, which allows tuning the optical response of the PhPl crystals.

For triangular lattices, the optical response was predicted using the algorithms with the same crystal parameters: a lattice constant $a = 300$ nm, and a base with major axis $d_x = 100$ nm and minor axis $d_y = 150$ nm. The analytical model with these parameters predicts a bandgap centered at $\lambda _c = 588.724$ nm, with a width of $\Delta \lambda = 25.198$ nm. The prediction and comparison of the machine learning algorithms are given in Table 5. As it can be seen, the prediction of the optical response for all the algorithms is close to the calculations using the analytical model, which is consistent with the accuracy reported above.

Table 5 Results comparison between theoretical model and machine learning algorithms of triangular lattice for forward design

For the inverse design, the best performance was obtained with ANN, where the cosine similarity is greater than 0.98 to predict the PhPl crystal characteristics for a particular optical response. As an example, for a bandgap width of $\Delta \lambda =20$ nm, centered at $\lambda _c=633$ nm, the algorithms predicts the parameters shown in Table 6.

Table 6 Results comparison between theoretical model and machine learning algorithms of triangular lattice for inverse design

Fig. 26

Band structure of a dielectric–gold PhPl crystal for a triangular lattice with a circular base, with $a=329.968$ nm and $d=126.149$ nm

As it can be seen from the data provided for the ANN, the bandgap width is $\Delta \lambda =19.505$ nm and is centered at $\lambda _c=620.884$ nm. Figure 26 shows the photonic band structure of this crystal. In this case, the difference between the predicted and the actual bandgap width is 0.495 nm. Concerning the bandgap centers, the difference between predicted and the actual ones is 12.12 nm.

To support both the results obtained with the analytical model and those obtained with the ANNs, numerical simulations were performed using the COMSOL Multiphysics ® software. It is worth mentioning that the numerical simulations were performed for all orientations; however, for illustrative purposes, only the numerical simulations for the PhPl crystal in the $\Gamma -\mathrm {M}$ orientation are shown. The PhPl crystal has a lattice constant of $a=329.968$ nm, a base diameter $d=126.149$ nm and is oriented in the $\Gamma -\mathrm {M}$ orientation.

Fig. 27

Numerical simulation of incident electric field at $\lambda =605$ nm in a PhPl crystal, at an allowed frequency

Figure 27 shows a numerical simulation of an incident SPPs at $\lambda =605$ nm in a dielectric–gold PhPl crystal. This wavelength corresponds to an allowed frequency. Figure 28 shows a numerical simulation of an incident electric field at $\lambda =633$ nm in a PhPl crystal, that is, at a frequency within the photonic bandgap.

Fig. 28

Numerical simulation of incident electric field at $\lambda =633$ nm in a PhPl crystal, at a frequency within the bandgap

Figure 29 shows a numerical simulation of an incident electric field at $\lambda =690$ nm in a PhPl crystal. This wavelength corresponds to an allowed frequency in the partial photonic bandgap in the $\Gamma -\mathrm {M}$ orientation.

Fig. 29

Numerical simulation of incident electric field at $\lambda =690$ nm in a PhPl crystal, at an allowed frequency

The normalized absolute value of the electric field at $\lambda =633$ nm, that is, within the bandgap, is compared to the normalized absolute value of the electric field at the two allowed wavelengths in the $\Gamma -\mathrm {M}$ orientation, 605 and 690 nm. This is shown in Fig. 30, where the blue line corresponds to 605 nm, the black line corresponds to 633 nm, and the red line corresponds to 690 nm. The vertical dashed gray line marks where the PhPl crystal begins.

Fig. 30

Comparison of the normalized absolute value of the electric field for three different wavelengths

For all the three wavelengths, before entering to the PhPl crystal, the field intensity increases due to reflections on the PhPl crystal. After that, for all the three wavelengths, the electric field intensity decreases as it enters the PhPl crystal, since SPPs intensity decays exponentially, as it is shown in the graph. However, the electric field corresponding to the wavelength within the bandgap, 633 nm, decreases faster than the other wavelengths.

The imaginary part of the effective refractive index is larger at 605 nm than at the other two wavelengths, then larger attenuation would be expected. However, the PhPl crystal is tuned to have a bandgap centered at 633 nm; thus, the field intensity decreases faster for this case, corroborating the physics behind the proposed analytical model.

Rectangular Lattice

In this case, the theoretical model was used to analyze the band structures of dielectric–gold and dielectric–silver PhPl crystals in a rectangular lattice, with elliptical and rectangular bases.

Fig. 31

Band structure of a dielectric–gold PhPl crystal in a rectangular lattice with $a_x=300$ nm, $a_y=480$ nm and $d=235$ nm

Figure 31 shows the photonic band structure of a dielectric–gold PhPl crystal in a rectangular lattice with a circular base, where this base is considered a particular case of an elliptical base. The lattice constant in x-direction is $a_x=300$ nm, in y-direction is $a_y=480$ nm and the diameter of the cross section is $d=235$ nm.

Using the same parameters, the band structure of a dielectric–silver PhPl crystal was calculated; it is shown in Fig. 32.

Fig. 32

Band structure of a dielectric–silver PhPl crystal in a rectangular lattice with $a_x=300$ nm, $a_y=480$ nm and $d=235$ nm

In both cases, two partial bandgaps arise in the fitting range: one in $\Gamma -\mathrm {X}$ orientation and the other in the $\mathrm {Y}-\Gamma$ orientation. The former has a width of $\Delta \lambda =90.95$ nm and is centered at $\lambda _c=747.09$ nm, while the latter has a width of $\Delta \lambda =222.11$ nm and is centered at $\lambda _c=1242.28.$ nm.

In addition, the first band of the band structure of both PhPl crystals is similar because the effective refractive indexes are similar in that frequency range. The above means that the dielectric–gold and dielectric–silver PhPl crystals have almost the same optical response in that range of the electromagnetic spectrum. However, the third band presents significant differences, since the inverse of the effective refractive index has a wider fitting range. Besides, the dielectric–silver PhPl crystal can operate over a wider frequency range.

On the other hand, as shown above, for a square lattice with a low contrast of dielectric constants (in particular $\epsilon _b/\epsilon _a$ = 2.2), there were no complete bandgaps. However, using the theoretical model to analyze a rectangular lattice, and considering an analogous orientation to the square lattice (in this case $\Gamma -\mathrm {X}-\mathrm {S}-\Gamma$), a complete bandgap can be found for some ratios $a_y/a_x$ and filling fractions f.

Figure 33 shows the photonic band structure of a rectangular PhPl crystal with $a_x=300$ nm, $a_y=465$ nm and $d=230$ nm. For these parameters, the bandgap center and width are $\lambda _c = 714.12$ nm and $\Delta \lambda =36.49$ nm, respectively. With this lattice, it is possible to have a complete bandgap even with a small refractive index contrast considering a $\Gamma - \mathrm {X} - \mathrm {S} -\Gamma$ path.

Fig. 33

Band structure of a rectangular plasmonic crystal with $a_x=300$ nm, $a_y=465$ nm and $d=230$ nm

To get a clearer picture of the bandgap formation, a heat map of the bandgap width as a function of the lattice

Fig. 34

Bandgap width as a function of a and f for rectangular lattice and with an elliptical base

side ratio $r_a=a_y/a_x$ and the filling fraction f is shown in Fig. 34. This graph corresponds to a lattice constant of $a_x=300$ nm, with a variation of the lattice constant $a_y$. This variation was between 20% to 180% of the lattice constant $a_x$.

In the heat map, it is possible to observe that the bandgap appears when the ratio $r_a = a_y/a_x$ is between 1.26 and 1.8. In addition to this, to have a complete bandgap, the filling fraction must have values between 0.1 and 0.6. In this particular case, the maximum width, $\Delta \lambda =59.79$ nm, is obtained for $r_a=1.5$ and $f=0.33$.

As in previous lattices, machine learning algorithms help in establishing the relationship between structural features and optical response. The optimal performance of the machine learning algorithms for forward design was obtained with a polynomial of degree 12, for the KNN algorithm with 3 nearest neighbors, and a maximum depth equal to 30 for the decision tree algorithm.

For the inverse design, the best performances were obtained for a polynomial regression of degree 14, the KNN algorithm with 30 neighbors, and a maximum depth of 10 for the decision tree algorithm. However, the accuracy of the prediction did not reach 70%. On the other hand, ANNs performed best with the architectures described above. The accuracy of the machine learning algorithms for the rectangular lattice is shown in Table 7.

Table 7 Machine learning algorithms results for rectangular lattice

As in the previous lattice, the optical response was predicted with the same crystal parameters for all four algorithms: lattice constants $a_x = 300$ nm, $a_y = 480$ nm, $d_x = 100$ nm and $d_y = 240$ nm. The analytical model with these parameters calculates a bandgap centered at $\lambda _c = 655.245$ nm and width $\Delta \lambda = 26.011$ nm. The prediction and comparison of the machine learning algorithms are given in Table 8.

Table 8 Results comparison between theoretical model and machine learning algorithms of rectangular lattice for forward design

The four algorithms predict an optical response very similar to the one calculated by the theoretical model, which was an expected fact since they all exhibit high precision for the forward design; however, with KNN and ANN the predictions are more accurate with the mentioned parameters.

The algorithms were applied to predict the structural parameters from a target bandgap centered at $\lambda _c = 633$ nm and with width $\Delta \lambda = 20$ nm. The results are shown in Table 9. The predictions of the polynomial regression, KNN and ANN algorithms are very similar to each other. Furthermore, the properties of the bandgap calculated from the predictions are very close to those of the target optical response, where the discrepancy is larger in the width of the bandgap.

Table 9 Results comparison between theoretical model and machine learning algorithms of rectangular lattice for inverse design

The results obtained with the analytical model are consistent with the results obtained with the ANNs. Both results are supported by numerical simulations. As for the previous case, the numerical simulations were performed for all orientations; however, for illustrative purposes, only the numerical simulations for the PhPl crystal in a particular orientation are shown, in this case in the $\Gamma -\mathrm {X}$ orientation.

The simulated PhPl crystal has lattice constants $a_x=279.96$ nm and $a_y=339.85$ nm in x and y directions, while the base is an ellipse with axes $d_x=173.28$ nm and $d_y=206.72$ nm. With these structural parameters, the bandgap center and width calculated with the analytical model are $\lambda _c=640.88$ nm and $\Delta \lambda = 10.09$ nm, respectively.

Fig. 35

Numerical simulation of incident electric field at $\lambda =620$ nm in a rectangular PhPl crystal, at an allowed frequency

Figure 35 shows the electric field intensity of SPPs incident at $\lambda =620$ nm, that is, at an allowed frequency. On the contrary, Fig. 36 shows the electric field intensity of SPPs incident at $\lambda = 670$ nm, a frequency within the bandgap in the $\Gamma -\mathrm {X}$ orientation.

Fig. 36

Numerical simulation of incident electric field at $\lambda =670$ nm in a rectangular PhPl crystal, at a frequency within the bandgap

Additionally, Fig. 37 shows the electric field intensity of SPPs incident at $\lambda = 750$ nm, that is, at an allowed frequency, in the same orientation.

Fig. 37

Numerical simulation of incident electric field at $\lambda =750$ nm in a rectangular PhPl crystal, at an allowed frequency

As in the triangular lattice, the SPPs are reflected in the PhPl crystal, causing the electric field intensity to increase before penetrating into the array. In Fig. 36, the extinction of SPPs electric field is evident when impinging at a frequency within the bandgap. For other wavelengths, the SPPs impinge on the PhPl crystal, propagate through it and decay exponentially, as expected. To show clearly this fact, the normalized electric field intensities of SPPs for the three wavelengths are compared in Fig. 38.

Fig. 38

Comparison of the normalized absolute value of the electric field for three different wavelengths

From the plot, it is clear that the electric field intensity for the wavelength within the bandgap decreases faster than the electric field intensities for the allowed wavelengths. The curves in Fig. 38 reveal the field enhancement due to reflections in the PhPl crystal and the exponential decay of the electric field as it propagates into it. The above reinforces the consistent agreement between the obtained results with the analytical model and those obtained using the ANNs.

Conclusions

A general theoretical model based on PWEM is proposed to study and calculate the photonic band structure of dielectric-gold and dielectric-silver PhPl crystals. The validity and usefulness of the model are shown for several particular structures in one and two dimensions, from which the theoretical results allow to infer that the dielectric-gold and dielectric-silver crystals respond quite similarly in the approximate range of 600-2000 nm. However, for wavelengths below 550 nm, the dielectric-silver PhPl crystal is a better choice, since it exhibits less propagation attenuation than the dielectric-gold PhPl crystal.

In addition to the theoretical model, computational tools, based mainly on ANNs, are developed to calculate the center and width of the bandgap of these hybrid PhPl systems. These tools are useful in tuning the optical response since they are able to find and learn the relationship between structural features and bandgap properties. Also, with the above it is possible to avoid the execution of codes that can be computationally expensive, which would imply making the design and fabrication process of these structures more efficient.

Both the results obtained with the analytical model and those obtained with the computational tools are consistent with the physics inherent to the systems studied, both are supported by numerical simulations, and both are successfully compared, when possible, to experimental results from the literature. In general, the tools proposed in this work are integrated together to study systems that could be implemented experimentally and applied in new PhPl devices.