1 Introduction

Since the early 1990s, a large number of constitutive models for unsaturated soils have been proposed [1, 2, 4, 5, 10, 13, 18, 19, 23,24,25, 27, 30, 34, 35, 38,39,40,41, 43, 45,46,47,48]. The influence of matric suction (\(s\)) on the stiffness and strength of unsaturated soils and the elastoplastic volume decrease upon wetting can be well reflected in the early models. However, the influence of the degree of saturation (\(S_{r}\)) on the yield curves of unsaturated soils is not directly considered in the early models. The variation of degree of saturation is usually incorporated in the framework of hydraulic hysteresis. Wheeler et al. [37] presented an elastoplastic constitutive model that fully couples hydraulic hysteresis with the mechanical behavior of unsaturated soils. The influence of degree of saturation on load–collapse (LC) yield surface and the influence of specific volume (\(v\)) on the suction-increase/decrease (SI/SD) yield surfaces have been included in this model. Wheeler’s model has been further developed by many researchers [12, 19, 24, 25, 28, 33, 42]. These hydromechanical models are able to capture the coupling feature of unsaturated soils. However, the coupling movement of LC yield surface is usually related to volumetric strain increment in those models. This makes it difficult to judge the mechanical state of unsaturated soils. Besides, the coupling parameters should be carefully chosen when yielding at the corner two yield surface. This two reason makes those models difficult to implement.

Hence, some researchers pay more attention on the influence of void ratio on hydraulic hysteresis. The coupling movement of soil–water characteristic curve (SWCC) with volumetric strain increment is expressed in another way. Gallipoli et al. [7] modeled the variation of degree of saturation of a deformable unsaturated soil in \(\left( {S_{r} ,s,v} \right)\) space. This hydraulic model has been further developed by some researchers [9, 26, 32, 36, 44]. Especially, considering the change of pore-size distribution (PSD), this model was further developed by Hu et al. [9] to give the expression of the main wetting and main drying surfaces. Different air-entry suctions are used to define the two surfaces. The elastic hydraulic behavior can be represented by scanning lines between the main drying surface and the main wetting surface. The influence of void ratio on soil–water characteristic curve (SWCC) as well as the hydraulic hysteresis behavior can be well reflected by this model. Unfortunately, the mechanical part is absent in the model of Hu et al. [9].

The concept of “state boundary hypersurface” was used by Wheeler and Sivakumar [38]. The state boundary hypersurface is defined by a single equation relating several state variables. The state variables can be either stress variables or strain variables. The state boundary hypersurface can be used to build an elastoplastic constitutive model, with elastic behavior when the soil state lies inside the state boundary hypersurface and plastic behavior when the state boundary hypersurface is reached.

In this paper, the concept of “state boundary hypersurface” is adopted and is called “hypersurface” for short. To overcome the above limitations, the degree of saturation is taken as a state variable to rebuild a mechanical hypersurface. In this way, the influence of saturation on yield surface can be expressed in a full form rather than an incremental form. It becomes much easier to judge the mechanical state of Sect. 1, unsaturated soils. Hence, there are two kinds of hypersurfaces used in this paper, the hydraulic hypersurface and the mechanical hypersurface. In Sect. 2, considering the evolution of PSD, a general equation for hydraulic hypersurface is given. Then, two hydraulic hypersurfaces are used with a mechanical hypersurface to establish a constitutive model for unsaturated soils. The performance of the model is assessed by comparisons with experimental data from literatures in Sect. 3. The discussion and conclusion are given in Sect. 4 and Sect. 5, respectively.

2 Framework of state boundary hypersurface

2.1 Hydraulic hypersurface

Experimental data showed that SWCC dependents on void ratio [7]. In other words, the degree of saturation varies with both matric suction and void ratio.

$$ S_{r} = S_{r} \left( {e,s} \right) $$
(1)

where \(S_{r}\) is the degree of saturation, \(e\) is the void ratio, and \(s\) is the matric suction.

Therefore, the increment of degree of saturation can be divided into two parts

$$ dS_{r} = \frac{{\partial S_{r} }}{\partial s}ds + \frac{{\partial S_{r} }}{\partial e}de $$
(2)

where \(\frac{{\partial S_{r} }}{\partial s}\) and \(\frac{{\partial S_{r} }}{\partial e}\) are the partial differences of degree of saturation with respect to matric suction and void ratio, respectively.

The void space of a soil may be regarded as a set of connected pores that are randomly distributed with the pore radius \(r\). The smaller pores are potentially occupied with water, and the rest by air. Hence, the degree of saturation can be expressed by

$$ S_{r} = F\left( r \right) = 1 - G\left( s \right) $$
(3)

where \(F\left( r \right)\) is the distribution function of pore radius, representing the proportion of the volume of pores with radius less than \(r\) to the total pore volume. This function can be used to describe PSD. \(G\left( s \right)\) is the distribution function of matric suction. The inner-connections of pores are ignored here for simplicity. This assumption is reasonable because the inner-connections of pores can be equivalent to several smaller pores, which can also be included in \(F\left( r \right)\).

According to the capillary law [6] and Eq. 2, the relationship between the probability density function of pore radius and the probability density function of matric suction can be expressed by

$$ rf\left( r \right) = sg\left( s \right) $$
(4)

where \(f\left( r \right)\) is the probability density function of pore radius, and \(f\left( r \right)dr\) represents the volume percentage of pores with radius from \(r\) to \(r + dr\). \(g\left( s \right)\) is the probability density function of matric suction. \(f\left( r \right)\) and \(g\left( s \right)\) are the derivatives of \(F\left( r \right)\) and \(G\left( s \right)\), respectively.

The evolution of PSD is important in analyzing the variation of degree of saturation [9]. The incremental form of evolution of PSD caused by deformation is analyzed below. If we assume that the size of all pores is equally reduced by consolidation. The volume percentage of pores with radius from \(r\) to \(r + dr\) equals to the volume percentage of pores from radius from \(r^{\prime}\) to \(r^{\prime} + dr^{\prime}\)(Fig. 1).

$$ \tilde{f}_{i} \left( {r^{\prime}} \right)dr^{\prime} = f_{i - 1} \left( r \right)dr $$
(5)

where \(\tilde{f}_{i} \left( {r^{\prime}} \right)\) is the probability density function of pore radius when assuming all the pores are equally reduced by consolidation.

Fig. 1
figure 1

Evolution of probability density function of pore radius

Full size image

Hence, the pore radius change ratio of loading step \(i\) is given by

$$ \eta_{i} = \frac{{r^{\prime}}}{r} = \left( {\frac{e + de}{e}} \right)^{1/3} $$
(6)

where \(r^{\prime}\) is the assumed pore radius after loading step \(i\).

Considering Eq. (5) and Eq. (6), the relationship between \(\tilde{f}_{i} \left( {r^{\prime}} \right)\) and \(f_{i - 1} \left( r \right)\) is given by

$$ \tilde{f}_{i} \left( {r^{\prime}} \right) = f_{i - 1} \left( {r^{\prime}/\eta_{i} } \right)/\eta_{i} $$
(7)

Thus, the assumed distribution function of pore radius is given by

$$ \tilde{F}_{i} \left( r \right) = F_{i - 1} \left( {r/\eta_{i} } \right) $$
(8)

where \(\tilde{F}_{i} \left( r \right)\) is the distribution function of pore radius when assuming all the pores are equally reduced by consolidation.

However, the assumption that the size of all pores is equally reduced by consolidation is not consistent with experimental results. As plotted in Fig. 2, the experimental data of Tanaka et al. [31] on Osaka Clay show an additional left shifting of PSD when assuming that the size of all pores is equally reduced by consolidation. This discrepancy suggests that the pores are not only compressed, but also breakdown into small pores as pressure increases. The stress effects on PSD and SWCC were discussed in [3, 17, 44], where the hydromechanical coupling feature of unsaturated soils can be well reflected. However, the obtained SWCC is complex when both mean net stress and matric suction are included. Hence, it is better to only included void ratio and matric suction in a hydraulic framework Eq. 1. According to the experimental results of Tanaka et al. [31] on Osaka Clay, a shifting left is added to the assumed PSD.

$$ F_{i} \left( r \right) = F_{i - 1} \left( {\frac{r + d\chi }{{\eta_{i} }}} \right) $$
(9)

where \(d\chi\) indicates the amount of shifting of PSD during compression. As will be confirmed letter, \(d\chi\) is given in the following form

$$ d\chi = - \frac{h - 1}{{3e}}rde $$
(10)

where \(h\) is a constant, \(h \ge 1\). The value of \(h\) indicates the amount of PSD shifting. \(h = 1\) indicates that all the pores are equally reduced and there is no additional left shifting of PSD.

Fig. 2
figure 2

PSD for Osaka Clay under compaction. a experimental PSD obtained by mercury intrusion porosimetry (MIP) b calculated PSD under the assumption that the size of all pores is equally reduced by consolidation [31]

Full size image

According to Eq. 9 and Eq. 10, the variation of degree of saturation caused by variation of void ratio is given by

$$ \frac{{\partial S_{r} }}{\partial e}de = \frac{{\partial S_{r} }}{\partial r}\frac{\partial r}{{\partial e}}de = - f_{i - 1} \left( r \right)\frac{hr}{{3e}}de $$
(11)

where \(f_{i - 1} \left( r \right)\) is the probability density function of pore radius in loading step \(i - 1\).

The PSD is more difficult to obtain compared with SWCC. Therefore, according to Eq. 4, Eq. 11 can be expressed by

$$ \frac{{\partial S_{r} }}{\partial e}de = - sg_{i - 1} \left( s \right)\frac{h}{3e}de $$
(12)

where \(g_{i - 1} \left( s \right)\) is the probability density function of matric suction in loading step \(i - 1\).

Finally, the increment of degree of saturation caused by variation of matric suction and void ratio is given by

$$ dS_{r} = \frac{{\partial S_{r} }}{\partial s}ds + \frac{{\partial S_{r} }}{\partial e}de = - g_{i - 1} \left( s \right)ds - \frac{h}{3e}sg_{i - 1} \left( s \right)de $$
(13)

Besides, according to Eq. 9 and Eq. 10, the evolution of PSD distribution function for loading step \(i\) is given by

$$ F_{i} \left( r \right) = F_{i - 1} \left( {r\alpha_{i} } \right) $$
(14)

where \(\alpha_{i} = 1 - \frac{h}{3e}de\).

To give an expression of the PSD variation from a reference state, Eq. 14 can be expressed by

$$ F_{i} \left( r \right) = F_{i - 1} \left( {r\alpha_{i} } \right) = F_{i - 2} \left( {r\alpha_{i} \alpha_{i - 1} } \right) = \cdots = F_{0} \left( {r\alpha_{i} \alpha_{i - 1} \cdots \alpha_{1} } \right) $$
(15)

where \(F_{0} \left( r \right)\) is the distribution function of pore radius of the reference state.

If we remark \(t_{i} = \alpha_{i} \alpha_{i - 1} \cdots \alpha_{1}\), it is easy to obtain that

$$ t_{i} = \left( {\frac{{e_{i} }}{{e_{0} }}} \right)^{ - h/3} $$
(16)

where \(e_{i}\) is the void ratio after loading step \(i\) and \(e_{0}\) is the void ratio of the reference state.

According to Eq. 15, 16, the evolution of the distribution function of pore radius from a reference state can be given by

$$ F_{i} \left( r \right) = F_{0} \left( {rt_{i} } \right) $$
(17)
$$ f_{i} \left( r \right) = t_{i} f_{0} \left( {rt_{i} } \right) $$
(18)

where \(f_{0} \left( r \right)\) is the probability density function of pore radius of the reference state.

According to Eq. 3, the evolution of the distribution function of matric suction can be given by

$$ G_{i} \left( s \right) = G_{0} \left( {s/t_{i} } \right) $$
(19)
$$ g_{i} \left( s \right) = g_{0} \left( {s/t_{i} } \right)/t_{i} $$
(20)

where \(G_{0} \left( s \right)\) and \(g_{0} \left( s \right)\) are the distribution function and probability density function of matric suction of the reference state, respectively.

Considering Eq. 3 and Eq. 19, the variation of degree of saturation with matric suction and void ratio is given by

$$ S_{r} = 1 - G_{i} \left( s \right) = 1 - G_{0} \left[ {s\left( {\frac{e}{{e_{0} }}} \right)^{h/3} } \right] $$
(21)

Equation 26 gives a general expression of the variation of degree of saturation with matric suction and void ratio and \(S_{r,0} = 1 - G_{0} \left( s \right)\) represents the SWCC curve of the reference state.

Noteworthy, the relationship of \(D_{50}\) and the void ratio can be deduced from Eq. 17.

$$ 0.5 = F_{i} \left( {D_{50} /2} \right) = F_{0} \left( {t_{i} D_{50} /2} \right) $$
(22)

where \(D_{50}\) is the diameter of pore where 50% of the total cumulative porosity percentage is attained.

Hence, the relationship between \(D_{50}\) and \(e\) is given by

$$ D_{50} = \left( {\frac{e}{{e_{0} }}} \right)^{h/3} D_{50,0} $$
(23)

where \(D_{50,0}\) is the value of \(D_{50}\) of the reference state.

Equation 23 indicates a linear relationship between \(D_{50} - e\) in a log–log plot and the slope is \(h/3\). The experimental data [31] of Osaka Clay Ma13 shows a value of \(h = 1.28 \times 3 = 3.84\) Fig. 3. With the value of \(h\), the model is capable to predict the PSD shifting of Osaka Clay Ma13 under different pressure. Noteworthy that the y axis in Fig. 2 is \(dV/d\log D_{p}\), not the probability density function of pores \(f\left( r \right)\). If we express the PSD in another way

$$ \left\{ \begin{array}{ll} l\left( {\log D_{p} } \right) = dV/d\log D_{p} \hfill \\ L\left( {\log D_{p} } \right) = \int\limits_{ - \infty }^{{\log D_{p} }} {l\left( {\log x} \right)d\log x} \hfill \\ \end{array} \right. $$
(24)

where \(L\left( {\log D_{p} } \right)\) represent the volume of pores with diameter smaller than \(D_{p}\), \(dV\) is the increment of volume of pores. Therefore,

$$ L\left( {\log D_{p} } \right) = eF\left( {D_{p} /2} \right) $$
(25)
Fig. 3
figure 3

Relation between \(D_{50}\) and \(e\) in log–log plot [31]

Full size image

Considering Eq. 17 and Eq. 24, the evolution of PSD in terms of \(l\left( {\log D_{p} } \right)\) can be represented by

$$ l_{i} \left( {\log D_{p} } \right) = \frac{{e_{i} }}{{e_{0} }}l_{0} \left( {\log D_{p} - \frac{h}{3}\log \frac{{e_{i} }}{{e_{0} }}} \right) $$
(26)

where \(l\left( {\log D_{p} } \right)\) is derivative of \(L\left( {\log D_{p} } \right)\), \(l_{i} \left( {\log D_{p} } \right)\) is the value of \(l\left( {\log D_{p} } \right)\) in loading step \(i\).

Take the PSD of Osaka Clay Ma13 [31] at 0 kPa as a reference state, the PSD of Osaka Clay Ma13 under 78 kPa, 2544 kPa and 10,042 kPa can be obtained by Eq. 26. As added in Fig. 2 a, the predicted PSD curves show reasonable good fit to the experimental data. Actually the assumption of all pores are equally reduced by compression is a special situation of the model with \(h = 1\).

Noteworthy, the relationship of air-entry suction and void ratio can also be deduced from Eq. 21.

$$ s_{ae} = \left( {\frac{e}{{e_{0} }}} \right)^{ - h/3} s_{ae,0} $$
(27)

where \(s_{ae}\) is the air-entry suction with respect to void ratio \(e\), \(s_{ae,0}\) is the value of \(s_{ae}\) in the reference state.

Equation 27 indicates a linear relationship between \(s_{ae}\) and \(e\) in log–log plot and the slope is \(- h/3\). This deduction is consistent with the experimental data presented in the paper of Huang et al. [11] on touchet loam, Columbia sandy loam and unconsolidated sand Fig. 4.

Fig. 4
figure 4

Relation between \(s_{ae}\) and \(e\) in log–log plot [11]

Full size image

Equation 23 indicates a liner relationship between \(D_{50} - e\) in log–log plot Fig. 3; Eq. 26 indicates the amount of shifting of PSD in terms of \(l\left( {\log D_{p} } \right)\) Fig. 2a; Eq. 27 indicates a liner relationship between \(s_{ae} - e\) in log–log plot Fig. 4. These three equations are all basically derive from Eq. 10, therefore, the correctness of Eq. 10 is guaranteed.

Furthermore, if we remark \(\lambda_{s} = - \frac{{\partial S_{r} }}{\partial \ln s}\) and \(\lambda_{e} = - \frac{{\partial S_{r} }}{\partial \ln e}\), the degree of saturation increment is given by

$$ dS_{r} = - \lambda_{s} d\ln s - \lambda_{e} d\ln e $$
(28)

Considering the general expression of the variation of degree of saturation with matric suction and void ratio given by Eq. 21, the following relation can be obtained

$$ \lambda_{e} = \frac{h}{3}\lambda_{s} $$
(29)

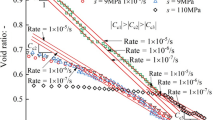
Equation 10 and Eq. 29 show that \(h\) is an interesting parameter. In the micro scope, it indicates the amount of PSD shifting. In the macro scope, it indicates the variation of degree of saturation with void ratio. Besides, in a wide range of matric suction, experimental results show a linear relationship between \(S_{r} - \ln s\). According to Eq. 28 and Eq. 29, there may be a linear relationship between \(S_{r} - \ln e\). This deduction is consistent with the experimental results of Sun et al. on Pearl Clay [28], which shows a linear relationship between \(S_{r}\) and \(\ln e\) when the soil is loaded at constant matric suction Fig. 5.

Fig. 5
figure 5

Relation between \(S_{r}\) and \(e\) for loading at constant matric suction on Pearl Clay [28]

Full size image

Equation 21 gives a general expression of the variation of degree of saturation with matric suction and void ratio. Any form of SWCC at a reference state can be extended to be a hypersurface in the \(\left( {e,s,S_{r} } \right)\) space to describe the variation of degree of saturation with matric suction and void ratio. This form of surface is called hydraulic hypersurface which defines the plastic hydraulic boundary of unsaturated soils. For example, if we adopt the Fredlund and Xing’s [6] SWCC to describe the hydraulic hypersurface.

$$ S_{r,0} = 1 - G_{0} \left( s \right) = \left\{ {\ln \left[ {\exp \left( 1 \right) + \left( {s/a} \right)^{n} } \right]} \right\}^{ - m} $$
(30)

where \(a\) is the air-entry matric suction. \(m,n\) are the shape parameters of SWCC.

Extending the SWCC given by Eq. 30 to the \(\left( {e,s,S_{r} } \right)\) space by Eq. 21. The hydraulic hypersurface is given by

$$ S_{r} = \left\{ {\ln \left[ {\exp \left( 1 \right) + \left( {s/a} \right)^{n} \left( {e/e_{0} } \right)^{hn/3} } \right]} \right\}^{ - m} $$
(31)

Considering hydraulic hysteresis, two air-entry value are used to build the main wetting and the main drying hydraulic hypersurface.

$$ S_{r} = \left\{ {\begin{array}{*{20}l} {\left\{ {\ln \left[ {\exp \left( 1 \right) + \left( {s/a_{d} } \right)^{n} \left( {e/e_{0} } \right)^{{hn/3}} } \right]} \right\}^{{ - m}} } & {{\text{main}}\,{\text{drying}}} \\ {\left\{ {\ln \left[ {\exp \left( 1 \right) + \left( {s/a_{w} } \right)^{n} \left( {e/e_{0} } \right)^{{hn/3}} } \right]} \right\}^{{ - m}} } & {{\text{ main}}\,{\text{weting}}} \\ \end{array} } \right.{\text{ }} $$
(32)

where \(a_{d}\) and \(a_{w}\) are the air-entry matric suction for the main drying hypersurface and the main wetting hypersurface, respectively. The shape parameters \(m,n\) are assumed to be the same for the main drying hypersurface and the main wetting hypersurface.

The hydraulic part of the constitutive model is plotted in Fig. 6. The main drying hypersurface and the main wetting hypersurface Eq. 32 define the plastic hydraulic boundary of unsaturated soils. The elastic hydraulic behavior can be expressed by scanning lines between the two hydraulic hypersurfaces. The hydraulic scanning behavior can be caused by either the variation of matric suction or by the variation of void ratio between the two hydraulic hypersurfaces. Considering Eq. 29, the hydraulic scanning line is given by

$$ dS_{r} = - \kappa_{s} d\ln s - \frac{h}{3}\kappa_{s} d\ln e $$
(33)

where \(\kappa_{s}\) is the partial derivative of \(S_{r}\) over \(\ln s\), \(\frac{h}{3}\kappa_{s}\) is the partial derivative of \(S_{r}\) over \(\ln e\).

Fig. 6
figure 6

The hydraulic part of the constitutive model in \(\left( {e,s,S_{r} } \right)\) space.

Full size image

The parameter \(\kappa_{s}\) is regarded as a constant in this paper, which gives a linear type of hydraulic scanning lines. Though a nonzero \(\kappa_{s}\) leads to a problem regarding the smooth transition between the unsaturated soil and saturated conditions[15], this limitation can be overcome as long as the variation of degree of saturation is strictly fixed by two smooth hydraulic hypersurfaces.

3 Mechanical hypersurface

The hydraulic part of the constitutive model is illustrated in Sect. 2.2. The variation of degree of saturation with matric suction and void ratio is governed by hydraulic hypersurfaces and hydraulic scanning lines. There should be a mechanical part to make a complete constitutive model.

The LC yield surface moves inward as degree of saturation increase and outward as degree of saturation decrease [37]. This phenomenon indicates that the normal consolidation line (NCL) moves inward as degree of saturation increases Fig. 7a. This coupling behavior has been modeled by many researchers [8, 14,15,16, 37]. However, most of the models related the LC yield curve movement with plastic degree of saturation increment Eq. 34. The location of LC yield surface is given in an incremental form. This makes it is difficult to judge the mechanical state of unsaturated soils. Besides, the coupling parameters should be carefully chosen when yielding at the corner of SD/SI and LC yield curve.

$$ df_{LC} = df_{LC} \left( {dS_{r}^{p} , \cdots } \right) $$
(34)

where \(df_{LC}\) is the increment of LC yield curve, \(dS_{r}^{p}\) is the increment of plastic degree of saturation.

Fig. 7
figure 7

Mechanical behavior of unsaturated soils. a Inward movement of NCLs with increase in saturation; b Mechanical scanning lines

Full size image

The coupling movements of LC yield curve with degree of saturation have been considered in another way in this paper. A type mechanical hypersurface is proposed in the \(\left( {S_{r} ,p^{*} ,e} \right)\) space. Similar to the hydraulic hypersurface, it is reasonable to assume the existence of mechanical hypersurface to define the plastic mechanical boundary of unsaturated soils. In this way, the location of the LC yield surface is given in a total form.

$$ f_{LC} = f_{LC} \left( {S_{r} , \cdots } \right) $$
(35)

where \(f_{LC}\) is the function of LC yield curve.

The coupling parameters between LC curves and SD/SI curves are now become shape parameters of the mechanical hypersurface, where the mechanical state of the unsaturated soils can be easily obtained. In this paper, the shape of the mechanical hypersurface is given by

$$ e_{p} = e_{m} + \alpha \left( {1 - S_{r} } \right) - \lambda \ln p^{*} $$
(36)

where \(e_{p}\) define the mechanical boundary of unsaturated soils in \(\left( {S_{r} ,p^{*} ,e} \right)\) space., \(e_{m}\) is the value of \(e_{p}\) for a saturated soil under low confining stress \(\left( {S_{r} = 1,p^{*} = 1} \right)\), \(\alpha\) is a shape parameter to take account the influence of degree of saturation on NCLs. \(\lambda\) is the slope of NCLs and is assumed to be a constant for all degree of saturations, \(p^{*}\) is the effective stress for unsaturated soil and is given by [37]

$$ p^{*} = \left( {p - u_{a} } \right) + sS_{r} $$
(37)

where \(\left( {p - u_{a} } \right)\) is the mean net stress.

The mechanical elastic behavior can be expressed by scanning lines below the mechanical hypersurface. The scanning line is given by

$$ de = - \frac{{\kappa dp^{*} }}{{p^{*} }} - \beta dS_{r} $$
(38)

where \(\kappa\) is the partial derivative of \(e\) over \(\ln p^{*}\); \(\beta\) is the partial derivative of \(e\) over \(S_{r}\).

The shape of the mechanical scanning lines is plotted in Fig. 7b. The shape of the mechanical scanning lines varies with confining stress. This is because the shape parameter \(\beta\) varies with confining stress to give an appropriate amount of wetting collapse. A reduction in matric suction (wetting) for a given confining stress will lead to a reduction in effective stress, in the same time may also induce an irrecoverable volumetric compression (collapse). Adding parameter \(\beta\) in the mechanical scanning line is to consider the additional influence of saturation on void ratio, such as wetting collapse. Wetting collapse is usually accompanied with SD yielding (reached the main wetting hydraulic hypersurface), and irrecoverable increment of saturation is accompanied by an irrecoverable volumetric compression according to Eq. 38. As the confining stress is increased, the amount of collapse increases and may reach a maximum then followed by decreasing values [1]. The value of \(\beta\) may show similar tendency with confining stress \(\beta = \beta \left( {p - u_{a} } \right)\). For example, a value of 0.45 is used for \(\beta\) when the soil is wetted at a medium stress level of 50 kPa (Test No. 12 listed in Table 5, 6). The wetting collapse behavior of bentonite–kaolin mixture is well predicted in Fig. 13g. At lower confining stress level of 10 kPa (Test No. 10, No. 11 and No.13 listed in Table 5, 6), a zero \(\beta\) is used to predict the elastic expansion during wetting Fig. 13a, e and i which is the same as most existing models. More experimental data are needed to calibrated the relation between the new parameter \(\beta\) and the confining stress.

The mechanical hypersurface and the mechanical scanning lines composite the mechanical part of the constitutive model (Fig. 8). It is more convenient to judge the mechanical state of unsaturated soils when taking degree of saturation as a state variable to build the mechanical hypersurface. The mechanical hypersurface defines the plastic mechanical boundary of unsaturated soils. The elastic mechanic behavior can be represented by mechanical scanning lines below the mechanical hypersurface. Besides, the mechanical hypersurface given by Eq. 36 suggests that the compression curve for saturated soils obtained from wetting at different mean net stress is the same. This is consistent with the experimental results of sun et al. [29].

Fig. 8
figure 8

The mechanical part of the constitutive model in \(\left( {S_{r} ,p^{*} ,e} \right)\) space

Full size image

4 Hydromechanical modeling

The hydraulic part and the mechanical part of the constitutive model are given in Sect. 2.1 and Sect. 2.2, respectively. These two parts are used together to build a hydromechanical constitutive model for unsaturated soils. The hydraulic hypersurfaces and the mechanical hypersurface are given by Eq. 32 and Eq. 36, respectively. The hydraulic scanning line and the mechanical scanning line are given by Eq. 33 and Eq. 38, respectively. Hence, a hydromechanical model is proposed based on those hypersurfaces and scanning lines.

As listed in Table 1, the plastic behavior and elastic behavior can be represented by the hypersurfaces and scanning lines. Two hydraulic hypersurfaces define the plastic hydraulic boundary. The elastic hydraulic behavior of unsaturated soils can be represented by scanning lines between these two hydraulic hypersurfaces. The mechanical hypersurface defines the plastic mechanical boundary. The elastic mechanical behavior of unsaturated soils can be represented by scanning lines below the mechanical hypersurfaces.

Table 1 A hydromechanical model for unsaturated soils
Full size table

The implementation of model can be started from assuming the state lies inside the scanning zone; then, the increment of effective stress, void ratio and degree of saturation can be obtained by

$$ \left\{ \begin{array}{lll} dS_{r} = - \kappa_{s} d\ln s - \frac{h}{3}\kappa_{s} d\ln e \hfill \\ de = - \frac{{\kappa dp^{*} }}{{p^{*} }} - \beta dS_{r} \hfill \\ dp^{*} = d\left( {p - u_{a} } \right) + sdS_{r} + S_{r} ds \hfill \\ \end{array} \right. $$
(39)

There are three unknown variables \(\left( {dS_{r} ,de,dp^{*} } \right)\) and three independent equations in Eq. 39. By solving the linear equations given in Eq. 39, a trial degree of saturation and a trial void ratio can be written as

$$ \left\{ \begin{array}{ll} S_{r,trial} = S_{r} + dS_{r} \hfill \\ e_{trial} = e + de \hfill \\ \end{array} \right. $$
(40)

The updated soil hydraulic state \(\left( {e + de,s + ds,S_{r,trial} } \right)\) should be located between the two hydraulic hypersurfaces. Besides, the updated soil mechanical state \(\left( {S_{r} + dS_{r} ,p^{*} + dp^{*} ,e_{trial} } \right)\) should be located below the mechanical hypersurface. Therefore, the following statements are used.

If \(e_{trial} > e_{p}\), the mechanical hypersurface instead of the mechanical scanning line is used to recalculate the increments. The increment of void ratio is given by

$$ e + de = e_{p} \left( {S_{r} + dS_{r} ,p^{*} + dp^{*} } \right) $$
(41)

If \(S_{r,trail} > S_{r,d}\), the main drying hydraulic hypersurface instead of the hydraulic scanning line is used to recalculate the increments. The increment of degree of saturation is given by

$$ S_{r} + dS_{r} = S_{r,d} \left( {e + de,s + ds} \right) $$
(42)

If \(S_{r,trail} < S_{r,w}\), the main wetting hydraulic hypersurface instead of the hydraulic scanning line is used to recalculate the increments. The increment of degree of saturation is given by

$$ S_{r} + dS_{r} = S_{r,w} \left( {e + de,s + ds} \right) $$
(43)

Noteworthy that, Eq. 39 is a system of linear equations to solve the increments of effective stress, void ratio and degree of saturation. Once one or two of the hypersurfaces are reached, the increments are determined by a system of nonlinear equations, where an iterative algorithm is required.

Once the satisfied degree of saturation and void ratio at the updated state is obtained, the subsequent degree of saturation and void ratio can be easily calculated by repeating the above procedure. With mechanical hypersurface, the influence of degree of saturation on LC yield curve has been considered in a full form rather than in an incremental form. Thus, it is much easier to judge the mechanical state of unsaturated soil, and it is much easier to implement the constitutive model (only three equations are needed).

A total of eleven parameters are needed for the proposed model, including six hydraulic parameters \(\left( {a_{d} ,a_{w} ,m,n,h,\kappa_{s} } \right)\) and five mechanical parameters \(\left( {e_{m} ,\alpha ,\lambda ,\kappa ,\beta } \right)\). The parameters \(a_{d} ,a_{w} ,m,n,h\) can be determined by wetting–drying cycles on the main drying/wetting hypersurface. The parameter \(\kappa_{s}\) can be determined by wetting–drying tests in the hydraulic scanning zone. The parameters \(e_{m} ,\alpha ,\lambda\) can be determined by loading tests on the mechanical hypersurface. The parameters \(\kappa ,\beta\) can be determined by unloading test in the mechanical scanning zone. Especially, wetting collapse tests should be conducted to determine parameter \(\beta\).

5 Comparison of model predictions with experimental results

In this section, several experimental results are compared with model predictions to demonstrate its usefulness. A total of 13 tests are used to validate the model. Three (No. 1 – No. 3) experiment data (municipal Boom clay [20], Speswhite kaolin [32] and clayey silty sand [21]) are used to validate the rationality of hydraulic hypersurface. The other ten experiments (No. 4 –No. 13) are used to validate the rationality of the proposed hydromechanical model. This ten tests are isotropic loading/unloading tests conducted by Sharma [22] on bentonite–kaolin.

6 Validation of hydraulic hypersurface

In this subsection, the influence of void ratio on SWCC is validated against experimental datasets. The soils types and model parameters for hydraulic hypersurfaces are listed in Table 2.

Table 2 Model parameters for hydraulic hypersurfaces
Full size table

Comparisons between the model predictions and experimental data of the hydraulic hypersurface for soils No. 1 to No. 3 are plotted in Fig. 9. It can be seen from Fig. 9 that the hydraulic hypersurface given by Eq. 32 shows good fit with experimental data sets. In addition, Fig. 9c indicates that the model is able to describe main drying hydraulic hypersurface in a wide suction range, from 0.01 kPa to \(1 \times 10^{6}\) kPa.

Fig. 9
figure 9

Measured and predicted main hydraulic drying/wetting curves for: a No. 1, municipal Boom clay; b No. 2, Speswhite kaolin; cNo. 3 clayey silty sand

Full size image

7 Validation of the hydromechanical model

Sharma [22] has conducted several isotropic loading/unloading tests on bentonite–kaolin. Those tests are carefully conducted with measurement of specific volume \(v\), degree of saturation \(S_{r}\), mean net stress \(p - u_{a}\) and matric suction \(s\). These tests are used to validate the proposed model. The model parameters for bentonite–kaolin are listed in Table 3.

Table 3 Model parameters for bentonite–kaolin under mechanical cycling [22]
Full size table

The stress paths of the experiments (No. 4– No. 9) are listed in Table 4. The tests include loading/unloading tests under different matric suction levels. The test results and model predictions for unsaturated soils (No. 4– No. 7) are plotted in Fig. 10. Model predictions of the specific volume (\(v = e + 1\)) and degree of saturation with applied mean net stress in Fig. 10 show reasonable agreement with experimental data. The used model parameters are the same except little discrepancy in the value of \(e_{m}\). The parameters \(a_{d}\) and \(\beta\) are not used, because neither main drying nor wetting collapse occurred during those tests.

Table 4 Stress path for bentonite–kaolin under mechanical cycling [22]
Full size table
Fig. 10
figure 10

Comparisons between the measured and predicted results for bentonite–kaolin mixture: a specific volume for No. 4; b degree of saturation for No. 4; c specific volume for No. 5; d degree of saturation for No. 5; e specific volume for No. 6; f degree of saturation for No. 6; g specific volume for No. 7; h degree of saturation for No. 7; Note: Model predictions are plotted in solid lines, the width of the line indicates the mechanical state of unsaturated soils, thin line for elastic state and thick line for plastic state; the color of the line indicates the hydraulic state of unsaturated soils, black for elastic state, blue for wetting state and red for drying state (not existed). This notification is also applicable to Fig. 11 and Fig. 13

Full size image

The test results and model predictions for unsaturated soils (No. 8– No. 9) are plotted in Fig. 11. Predictions of the specific volume and degree of saturation in Fig. 11 show reasonable agreement with experimental data. The initial states for No. 8 and No. 9 are similar. The two loading–unloading stages for No. 8 and No. 9 are the same. However, there is an additional wetting–drying cycle c–d–e for No. 9, where a significant increase in the degree of saturation occurred due to hydraulic hysteresis. During the second isotropic loading stage e–f, yield occurred at a mean net stress lower than the value of 100 kPa previously applied. This phenomenon identifies the inward movement of LC yield surface with increase in degree of saturation. The inward movement of LC yield surface was not occurred for No. 8 which had not been subjected to a wetting–drying cycle.

Fig. 11
figure 11

Comparisons between the measured and predicted results for bentonite–kaolin mixture: a void ratio for No. 8; b degree of saturation for No. 8; c void ratio (with mean net stress) for No. 9; d degree of saturation (with mean net stress) for No. 9; (e) void ratio (with matric suction) for No. 9; f degree of saturation (with matric suction) for No. 9

Full size image

The parameters listed in Table 2 show little discrepancy except in \(e_{m}\). This indicates the correctness of the proposed model. The mechanical hypersurface (\(e_{m} = 2.46\)) and the hydraulic hypersurface are plotted in Fig. 12. The grid lines in Fig. 12a indicate the NCLs in the \(e - \ln p^{*}\) plane. The grid lines in Fig. 12b indicate the SWCCs in the \(S_{r} - \ln s\) plane. The two hypersurface can reflect the influence of degree of saturation on NCLs and the influence of void ratio on SWCCs.

Fig. 12
figure 12

The state boundary hypersurface of bentonite–kaolin during mechanical cycles [22]: a mechanical hypersurface; b Main wetting hydraulic hypersurface

Full size image

Sharma [22] had also conducted several hydraulic cycling tests on bentonite–kaolin. These tests are also used to validate the proposed model. The model parameters for bentonite–kaolin are listed in Table 5.

Table 5 Model parameters for bentonite–kaolin under hydraulic cycling [22]
Full size table

The stress paths of the experiments (No. 10– No. 13) are listed in Table 6. The tests are wetting–drying tests under different mean net stress levels. The test results and model predictions for bentonite–kaolin (No. 10–No. 13) are plotted in Fig. 13.

Table 6 Stress path for bentonite–kaolin under hydraulic cycling [22]
Full size table
Fig. 13
figure 13

Comparisons between the measured and predicted results for bentonite–kaolin mixture: a specific volume (with matric suction) for No. 10; b degree of saturation (with matric suction) for No. 10; c specific volume (with mean net stress) for No. 10; d degree of saturation (with mean net stress) for No. 10; e specific volume for No. 11; f degree of saturation for No. 11; g specific volume for No. 12; h degree of saturation for No. 12; i specific volume for No. 13; j degree of saturation for No. 13

Full size image

As shown in Fig. 13, the model predictions show good agreement with experimental data. Especially, wetting collapse occurred for No. 12, where an irreversible increase of volumetric strain is accompanied by an irreversible increase of degree of saturation. This phenomenon identifies the shape of the mechanical scanning lines proposed in Sect. 2.2. However, there are two points needed to be noticed. Firstly, the model parameters listed in Table 5 show little discrepancy with the parameters listed in Table 3, the reason will be discussed in the discussion section. Secondly, the predicted degree of saturation for No.13 Fig. 10 j does not fit well with the experimental data in the d-e stage. This is caused by the using a constant slope of the hydraulic scanning line, it is better to let the value of \(\kappa_{s}\) tends to zero as \(S_{r}\) approaches 1. Future work may give a more detailed description of the hydraulic scanning lines.

8 Discussion

Based on state boundary hypersurfaces and scanning lines, the proposed hydromechanical model can capture some important features of unsaturated soils. The variation of degree of saturation caused by the variation of matric suction and by the variation of void ratio can be well reflected in the model. Especially, by mechanical hypersurface Eq. 33, the influence of degree of saturation on LC yield surface is expressed in a full form rather than an incremental form. This makes it much easier to judge the mechanical state of the unsaturated soil and much easier to implement the constitutive model. However, there are two questions needed to be discussed here.

One question is that the model parameters listed in Table 5 show little discrepancy with the parameters listed in Table 3. The three mechanical shape parameters \(\alpha ,\lambda ,\kappa\) show different values in the mechanical cycling tests and in the hydraulic cycling tests. This may be caused by choosing the effective stress as a stress variable to build the mechanical surface and the mechanical scanning lining line.

The mechanical cycling and the hydraulic cycling show different values of shape parameters of mechanical hypersurface and mechanical scanning line. This may indicate that the variation of void ratio caused by the variation of mean net stress is not equal to that caused by the variation of matric suction in the context of effective stress. In other words

$$ \left( {de} \right)_{{p - u_{a} }} = \frac{{\overline{\lambda }\left[ {d\left( {p - u_{a} } \right) + sdS_{r} } \right]}}{{p^{*} }} \ne \left( {de} \right)_{s} = \frac{{\overline{\lambda }\left( {sdS_{r} + S_{r} ds} \right)}}{{p^{*} }} $$
(44)

where \(\overline{\lambda }\) is the slope of curve of \(e - p^{*}\) in semi-log plot.

The experimental data of No. 10 on bentonite–kaolin [22] may validate this assumption. The variation of void ratio with effective stress of No. 10 is plotted in Fig. 14. As can be seen in Fig. 14, a wetting–drying cycle (blue dots) is followed by a mechanical loading stage (black dots). The slope of \(e - \ln p^{*}\) in the wetting–drying stage is similar to the value of \(\kappa\) and \(\lambda\) listed in Table 5. The slope of \(e - \ln p^{*}\) in the mechanical loading stage is similar to the value of \(\lambda\) listed in Table 3. Besides, the slope of \(e - \ln p^{*}\) in the mechanical loading stage shows a deeper slope than that in the wetting–drying stage. This indicates that in the context of effective stress, mean net stress contributes more to soil deformation. The effective stress may be modified to give a general expression to describe deformation. Otherwise, the deformation of unsaturated soil should be control separately by two stress variables, such as mean net stress and matric suction. In this case, two more parameters may be needed to build the model, the mechanic scanning lines and the mechanic hypersurface may be given by

$$ de = \frac{{\kappa_{a} d\left( {p - u_{a} } \right)}}{{\left( {p - u_{a} } \right)}} + \frac{{\kappa_{b} ds}}{s} + \beta dS_{r} $$
(45)
$$ e_{p} = e_{m} - \alpha S_{r} - \lambda_{a} \ln \left( {p - u_{a} } \right) - \lambda_{b} \ln s $$
(46)
Fig. 14
figure 14

The variation of void ratio with effective stress for No. 10 on bentonite–kaolin [22]

Full size image

Of course, the reasonability of Eq. 45 and Eq. 46 needs to be validated by experimental data.

The other question is that this model is limited to isotropic loading case. Deviatoric loading tests are beyond the scope of this paper. However, if more triaxial experimental data available, this model can be extended to deviatoric stress state. The mechanical hypersurface may be expressed as

$$ e_{p} = e_{p} \left( {p^{*} ,q,S_{r} } \right)\,or\,e_{p} = e_{p} \left( {p - u_{a} ,s,q,S_{r} } \right) $$
(47)

The shear strain may be obtained by associated or nonassociated flow rule. Of course, the premise of proposing an extended model is that there are relevant experimental data with measurements of \(\left( {p - u_{a} ,s,q,S_{r} ,e} \right)\) datasets.

9 Conclusion

A general expression of the hydraulic hypersurface is proposed (Eq. (21)) based on the evolution of PSD. Two different air-entry suction is used for the main drying hydraulic hypersurface and the main wetting hydraulic hypersurface. The elastic hydraulic behavior can be expressed by scanning lines between the two hydraulic hypersurfaces. Besides, through mechanical hypersurface Eq. 33, the influence of degree of saturation on LC yield curve is expressed in total form instead of in incremental form. It becomes much easier to judge the mechanical state of unsaturated soils. The elastic mechanical behavior can be expressed by scanning lines below the mechanical hypersurface. Based on these hypersurfaces and scanning lines, an elastoplastic hydromechanical constitutive model for unsaturated soils is proposed. A large number of experimental data were used to validate the model. The model is open to improvement when more triaxial experiment data are available.