A unified mechanical and retention model for saturated and unsaturated soil behaviour

Abstract

The coupled mechanical and water retention elasto-plastic constitutive model of Wheeler, Sharma and Buisson (the Glasgow coupled model, GCM) predicts unique unsaturated isotropic normal compression and unsaturated critical state planar surfaces for specific volume and degree of saturation when soil states are at the intersection of mechanical (M) and wetting retention (WR) yield surfaces. Experimental results from tests performed by Sivakumar on unsaturated samples of compacted speswhite kaolin confirm the existence and form of these unique surfaces. The GCM provides consistent representation of transitions between saturated and unsaturated conditions, including the influence of retention hysteresis and the effect of plastic volumetric strains on retention behaviour, and it gives unique expressions to predict saturation and de-saturation conditions (air-exclusion and air-entry points, respectively). Mechanical behaviour is modelled consistently across these transitions, including appropriate variation of mechanical yield stress under both saturated and unsaturated conditions. The expressions defining the unsaturated isotropic normal compression planar surfaces for specific volume and degree of saturation are central to the development of a relatively straightforward methodology for determining values of all GCM parameters (soil constants and initial state) from a limited number of laboratory tests. This methodology is demonstrated by application to the experimental data of Sivakumar. Comparison of model simulations with experimental results for the full set of Sivakumar’s isotropic loading stages demonstrates that the model is able to predict accurately the variation of both specific volume and degree of saturation during isotropic stress paths under saturated and unsaturated conditions.

1 Introduction

Wheeler et al. [51] developed a coupled elasto-plastic constitutive model for unsaturated soils, which represents both mechanical behaviour and water retention behaviour, including the coupling between them. The model, originally presented solely for isotropic stress states, has subsequently been extended to general stress states (e.g. Lloret-Cabot et al. [24]) and is referred to hereafter as the Glasgow coupled model (GCM). In the model, a single yield surface represents mechanical behaviour, with plastic volumetric strains $d\varepsilon_{\text{v}}^{\text{p}}$ and plastic deviatoric strains dε ^p_q occurring during yielding on this surface. Two other yield surfaces represent water retention behaviour, with plastic changes of degree of saturation dS ^p_r occurring during yielding on either of these surfaces. Coupled movements of the three yield surfaces represent the influence of plastic changes of degree of saturation on mechanical behaviour and the influence of plastic volumetric strains on water retention behaviour.

In this paper, it is shown that the GCM predicts unique expressions for specific volume v and degree of saturation S _r for stress states involving simultaneous mechanical yielding (occurrence of plastic compression) and wetting retention yielding (occurrence of plastic increases of S _r). These expressions for v and S _r facilitate significantly the use and interpretation of the model, including determination of model parameter values from experimental test data.

A major challenge of constitutive models for unsaturated soils is the correct representation of transitions between unsaturated and saturated conditions. The challenge of properly modelling such transitions is intimately linked to consistent consideration of retention hysteresis and to the choice of stress state variables, with particular difficulties for conventional models expressed in terms of net stresses (excess of total stress over pore air pressure) and suction (difference between pore air pressure and pore water pressure), because de-saturation during drying will not occur at zero suction and subsequent re-saturation on wetting will occur at a different value of suction. This paper shows how the GCM is able to provide consistent representation of transitions between unsaturated and saturated states, through the use of non-conventional stress state variables and proper consideration of retention hysteresis. The model gives unique expressions to predict saturation and de-saturation conditions, which account for both retention hysteresis and the influence of plastic volumetric strains on retention behaviour, and it provides consistent modelling of mechanical behaviour across these transitions.

2 The Glasgow coupled model (GCM)

The stress variables used in the GCM are “Bishops’s stress” tensor σ ^* _ij (sometimes also called “average soil skeleton stress”, Jommi [19]) and “modified suction” s ^*. The stress tensor σ ^* _ij is similar to the effective stress expression proposed by Bishop in 1959 [4] but with his weighting factor χ replaced by the degree of saturation (as suggested in Schrefler [36]). For the restricted range of stress states that apply in the triaxial test, it is sufficient to consider only mean Bishop’s stress p ^*, deviator stress q and modified suction s ^*, defined as follows:

$$p^{*} = p - S_{\text{r}} u_{\text{w}} - \left( {1 - S_{\text{r}} } \right)u_{\text{a}} = \bar{p} + S_{\text{r}} s$$

(1)

$$q = \sigma_{1} - \sigma_{3}$$

(2)

$$s^{*} = n\left( {u_{\text{a}} - u_{\text{w}} } \right) = ns$$

(3)

where p is mean total stress, u _w is pore water pressure, u _a is pore air pressure, σ ₁ and σ ₃ are, respectively, major and minor principal total stresses, and n is porosity. $\bar{p}$ and s are mean net stress and matric suction, respectively, where $\bar{p}$, q and s are the stress variables used in many more conventional mechanical constitutive models for unsaturated soils, such as the Barcelona basic model (BBM) of Alonso et al. [1]. The stress variables p ^*, q and s ^* are work-conjugate with volumetric strain increment dε _v, deviatoric strain increment dε _q and decrement of degree of saturation −dS _r, respectively (Houlsby [18]).

Elastic components of dε _v, dε _q and –dS _r are given by:

$$d\varepsilon_{\text{v}}^{\text{e}} = \frac{{\kappa dp^{*} }}{{vp^{*} }}$$

(4)

$$d\varepsilon_{\text{q}}^{\text{e}} = \frac{dq}{3G}$$

(5)

$$- dS_{\text{r}}^{\text{e}} = \frac{{\kappa_{\text{s}} ds^{*} }}{{s^{*} }}$$

(6)

where κ is the elastic swelling index, giving the gradient of elastic swelling lines in the v:ln p ^* plane (mechanical behaviour), G is the elastic shear modulus (mechanical behaviour), and κ _s is the gradient of elastic scanning curves in the S _r:ln s ^* plane (water retention behaviour).

The model includes three yield surfaces in p ^*:q:s ^* space: a mechanical (M) yield surface to represent mechanical behaviour (originally referred to as the loading collapse (LC) yield surface in Wheeler et al. [51]) and wetting retention (WR) and drying retention (DR) yield surfaces to represent water retention behaviour (originally referred to as, respectively, the suction decrease (SD) and suction increase (SI) yield surfaces). Plastic volumetric strains and plastic deviatoric strains occur during yielding on the M surface, whereas plastic changes of degree of saturation occur during yielding on WR or DR surfaces. The renaming of the yield surfaces from the original terminology used in [51] is to make explicit the fact that the M surface is the only one of the three describing mechanical yielding (and this can occur during loading, wetting or drying, see Lloret-Cabot et al. [25]), whereas the other two describe retention behaviour. This contrasts with the BBM, where both LC and SI yield surfaces represent mechanical behaviour (Alonso et al. [1]).

The equations of M, WR and DR surfaces are given, respectively, by:

$$q^{2} - M^{2} p^{*} \left( {p_{0}^{*} - p^{*} } \right) = 0$$

(7)

$$s_{1}^{*} - s^{*} = 0$$

(8)

$$s^{*} - s_{2}^{*} = 0$$

(9)

where M is a soil constant and p ^*₀ , s ^*₁ and s ^*₂ are hardening parameters defining the current positions of the M, WR and DR yield surfaces, respectively (Fig. 1). Equation 7 indicates that constant s ^* cross sections of the mechanical yield surface are elliptical in shape (of aspect ratio M) and the size p ^*₀ of these cross sections does not vary with s ^*. Equations 8 and 9 indicate that the WR and DR surfaces form vertical walls in p ^*:q:s ^* space (Fig. 1).

Fig. 1

Yield surfaces in Glasgow coupled model (GCM)

Associated flow rules are assumed on all three yield surfaces. This means that yielding on the M surface alone corresponds to:

$$\frac{{d\varepsilon_{\text{q}}^{\text{p}} }}{{d\varepsilon_{\text{v}}^{\text{p}} }} = \frac{{2\eta^{*} }}{{M^{2} - \left( {\eta^{*} } \right)^{2} }}\;\; {\text{and}}\;\;dS_{\text{r}}^{\text{p}} = 0$$

(10)

where η ^* = q/p ^*. Similarly, yielding on the WR surface alone corresponds to:

$$d\varepsilon_{\text{q}}^{\text{p}} = d\varepsilon_{\text{v}}^{\text{p}} = 0\;\;{\text{and}}\;\;dS_{\text{r}}^{\text{p}} > 0$$

(11)

and yielding on the DR surface alone corresponds to:

$$d\varepsilon_{\text{q}}^{\text{p}} = d\varepsilon_{\text{v}}^{\text{p}} = 0\;\;{\text{and}}\;\;dS_{\text{r}}^{\text{p}} < 0$$

(12)

The hardening law giving movements of the M yield surface includes a direct component of movement caused by plastic volumetric strain (due to yielding on the M surface), but also a second (coupled) component of movement caused by any plastic changes of S _r due to yielding on WR or DR surfaces:

$$\frac{{dp_{0}^{*} }}{{p_{0}^{*} }} = \frac{{vd\varepsilon_{\text{v}}^{\text{p}} }}{\lambda - \kappa } - k_{1} \frac{{dS_{\text{r}}^{\text{p}} }}{{\lambda_{\text{s}} - \kappa_{\text{s}} }}$$

(13)

where λ and κ are the gradients of normal compression lines and swelling lines, respectively, in the v:ln p ^* plane for isotropic loading and unloading tests involving no plastic changes of S _r (such as saturated tests), λ _s and κ _s are the gradients of main wetting/drying curves and scanning curves, respectively, in the S _r:ln s ^* plane (see Fig. 2a) for retention tests involving no plastic volumetric strains, and k ₁ is a coupling parameter.

Fig. 2

Modelling retention behaviour and treatment of saturated conditions

Similarly, the hardening law giving movements of the WR or DR yield surfaces includes a direct component of movement caused by plastic change of S _r (due to yielding on the WR or DR surface) and a second (coupled) component of movement caused by any plastic volumetric strains due to yielding on the M surface:

$$\frac{{ds_{1}^{*} }}{{s_{1}^{*} }} = \frac{{ds_{2}^{*} }}{{s_{2}^{*} }} = - \frac{{dS_{\text{r}}^{\text{p}} }}{{\lambda_{\text{s}} - \kappa_{\text{s}} }} + k_{2} \frac{{vd\varepsilon_{\text{v}}^{\text{p}} }}{\lambda - \kappa }$$

(14)

where k ₂ is a second coupling parameter. Equation 14 ensures that the movements of the DR and WR yield surfaces are such that the ratio of s ^*₂ to s ^*₁ (the spacing of the DR and WR surfaces when plotted in terms of ln s ^*) remains constant:

$$\frac{{s_{2}^{*} }}{{s_{1}^{*} }} = R$$

(15)

where R is a soil constant.

The special cases of the hardening laws during yielding on only a single yield surface (M , WR or DR) are given by inserting the relevant condition from Eqs. 10, 11 or 12 (dS ^p_r  = 0 or dε ^p_v  = 0) into Eqs. 13 and 14.

When the soil reaches a saturated condition (S _r = 1), further elastic increases of S _r are prevented (Eq. 6 no longer applies for decreases of s ^*) and further plastic increases of S _r are prevented (dε ^p_q  = dε ^p_v  = dS ^p_r  = 0 replaces Eq. 11 for states on the WR yield surface alone). In addition, the consistency condition on the WR yield surface is removed, so that the stress state can pass beyond the WR surface. This is illustrated in Fig. 2, with Fig. 2a showing water retention behaviour (for conditions of no plastic volumetric straining), including a saturated point X, and Fig. 2b showing the corresponding positions of the yield curves when the stresses are at point X. While the soil is saturated, the M yield surface is still operative, and Eq. 13 (with dS ^p_r  = 0) recovers the conventional modified Cam clay hardening law (Roscoe and Burland [35]). Also, while the soil is saturated, Eq. 14 (with dS ^p_r  = 0) is still used to determine coupled movements of the WR and DR surfaces caused by plastic volumetric strain. This represents changes of air-entry value caused by plastic volumetric strain.

The model predicts the occurrence of critical states that correspond to the apex of the elliptical cross sections of the M yield surface, and hence it predicts a unique critical state line in the q:p ^* plane:

$$q = Mp^{*}$$

(16)

The assumption of a unique critical state line in the q:p ^* plane has been demonstrated for a range of compacted non-expansive fine-grained soils (e.g. Gallipoli et al. [16], Lloret-Cabot et al. [24]).

3 Derivation and validation of expressions for v and S _r

3.1 Isotropic normal compression states

Due to the coupled movements of the yield surfaces, there is a very wide variety of isotropic stress paths that will ultimately arrive at the intersection between M and WR surfaces (point A in Fig. 3). For example, if yield occurs first on the M surface, this will cause a coupled movement of the WR surface, which after a while will typically bring the WR surface to the stress point. Similarly, if yield occurs first on the WR surface, this will cause a coupled inward movement of the M surface, which after a while will typically bring the M surface into the stress point. More generally, any stress paths where plastic volumetric strains and plastic increases of S _r occur simultaneously correspond to this intersection of M and WR surfaces. Inspection of the literature indicates that this behaviour applies to the majority of published experimental data for normal compression states. This is because the occurrence of plastic compression typically observed during isotropic (or one-dimensional) loadings at constant suction reduces porosity and, when such reduction is sufficiently large, irreversible increases of S _r are also observed, even though suction remains constant during the test (e.g. [8, 10, 13, 14, 22, 28–30, 32–34, 37, 41, 42, 44, 45, 47, 49, 51]). This type of response is also very often observed in available experimental data showing collapse compression behaviour on wetting (e.g. [13, 14, 22, 28–30, 32–34, 37, 41, 42, 44, 51]). In this case, the plastic increases of S _r caused when decreasing suction tend to reduce the stability of the soil skeleton [51] and this loss of stability may potentially result in volumetric compression [25]. From a theoretical point of view, a proper representation of this coupling between variations of volumetric strains (mechanical behaviour) and variations of degree of saturation or suction (retention behaviour) during loading and wetting paths has been the focus of a large number of constitutive relationships proposed in the literature (e.g. [1, 3, 9, 12–15, 20, 21, 23–27, 31, 34, 39, 40, 46, 48, 49, 51–53]), because they potentially play a critical role in the geotechnical response of boundary value problems involving unsaturated soils (e.g. [2, 5–7, 11, 17, 22, 38, 43]).

Fig. 3

Positions of various points relative to the yield surfaces

What can now be shown is that the model predicts unique expressions for v and S _r for these isotropic normal compression states at the intersection of M and WR surfaces.

Combining Eqs. 13 and 14 gives the following expressions for dε ^p_v and −dS ^P_r in terms of the movements of the M and WR yield surfaces:

$$d\varepsilon_{\text{v}}^{\text{p}} = \frac{{\left( {\lambda - \kappa } \right)}}{{v\left( {1 - k_{1} k_{2} } \right)}}\left( {\frac{{dp_{0}^{*} }}{{p_{0}^{*} }} - k_{1} \frac{{ds_{1}^{*} }}{{s_{1}^{*} }}} \right)$$

(17)

$$- dS_{\text{r}}^{\text{p}} = \frac{{\left( {\lambda_{\text{s}} - \kappa_{\text{s}} } \right)}}{{\left( {1 - k_{1} k_{2} } \right)}}\left( {\frac{{ds_{1}^{*} }}{{s_{1}^{*} }} - k_{2} \frac{{dp_{0}^{*} }}{{p_{0}^{*} }}} \right)$$

(18)

Equations 4 and 17, for the elastic and plastic components of volumetric strain, can be combined, in order to give the total volumetric strain increment and hence the total increment of v:

$$dv = - \frac{{\kappa dp^{*} }}{{p^{*} }} - \frac{{\left( {\lambda - \kappa } \right)}}{{\left( {1 - k_{1} k_{2} } \right)}}\left( {\frac{{dp_{0}^{*} }}{{p_{0}^{*} }} - k_{1} \frac{{ds_{1}^{*} }}{{s_{1}^{*} }}} \right)$$

(19)

For an isotropic stress state at the intersection between M and WR surfaces (p ^*₀  = p ^* and s ^*₁  = s ^*) and an isotropic stress increment remaining at this intersection (dp ^*₀  = dp ^* and ds ^*₁  = ds ^*), Eq. 19 simplifies to:

$$dv = - \lambda^{*} \frac{{dp^{*} }}{{p^{*} }} + k_{1}^{*} \frac{{ds^{*} }}{{s^{*} }}$$

(20)

where

$$\lambda^{*} = \frac{{\lambda - k_{1} k_{2} \kappa }}{{1 - k_{1} k_{2} }}$$

(21)

$$k_{1}^{*} = k_{1} \frac{{\left( {\lambda - \kappa } \right)}}{{\left( {1 - k_{1} k_{2} } \right)}}$$

(22)

Integration of Eq. 20 indicates that the model predicts that values of v for isotropic normal compression states at the intersection of M and WR yield surfaces are given by the following unique expression:

$$v = N^{*} - \lambda^{*} \ln p^{*} + k_{1}^{*} \ln s^{*}$$

(23)

where λ ^* and k ^*₁ are soil constants given by Eqs. 21 and 22 and N ^* is an additional soil constant. Equation 23 represents a planar surface in v:ln p ^*:ln s ^* space, as shown in Fig. 4.

Fig. 4

Isotropic normal compression planar surface for v (Sivakumar [41])

A similar procedure for the variation of S _r shows that the model predicts that values of S _r for isotropic normal compression states at the intersection of M and WR yield surfaces are given by:

$$S_{\text{r}} = \varOmega^{*} - \lambda_{\text{s}}^{*} \ln s^{*} + k_{2}^{*} \ln p^{*}$$

(24)

where λ ^*_s and k ^*₂ are soil constants given by:

$$\lambda_{\text{s}}^{*} = \frac{{\lambda_{\text{s}} - k_{1} k_{2} \kappa_{\text{s}} }}{{1 - k_{1} k_{2} }}$$

(25)

$$k_{2}^{*} = k_{2} \frac{{\left( {\lambda_{\text{s}} - \kappa_{\text{s}} } \right)}}{{\left( {1 - k_{1} k_{2} } \right)}}$$

(26)

and Ω ^* is an additional soil constant. Equation 24 represents a planar surface in S _r:ln p ^*:ln s ^* space, as shown in Fig. 5.

Fig. 5

Isotropic normal compression planar surface for S _r (Sivakumar [41])

3.2 General states

Expressions for v and S _r for any general stress state (see point B in Fig. 3) can now be derived by considering an elastic stress path from A (coordinates p ^*₀ , 0, s ^*₁ ) to B (coordinates p ^*, q, s ^*):

$$v = N^{*} - \lambda^{*} \ln p_{0}^{*} + k_{1}^{*} \ln s_{1}^{*} + \kappa \ln \left( {\frac{{p_{0}^{*} }}{{p^{*} }}} \right)$$

(27)

$$S_{\text{r}} = \varOmega^{*} - \lambda_{\text{s}}^{*} \ln s_{1}^{*} + k_{2}^{*} \ln p_{0}^{*} - \kappa_{\text{s}} \ln \left( {\frac{{s^{*} }}{{s_{1}^{*} }}} \right)$$

(28)

Equations 27 and 28 provide general expressions for v and S _r for any stress state (p ^*, q, s ^*) when the current locations of the M and WR yield surfaces are given by p ^*₀ and s ^*₁ , respectively.

For the particular case of isotropic stress states at the intersection between M and DR surfaces (point C in Fig. 3), p ^* = p ^*₀ , s ^* = Rs ^*₁ and Eqs. 27 and 28 give:

$$v = N^{*} - k_{1}^{*} \ln R - \lambda^{*} \ln p^{*} + k_{1}^{*} \ln s^{*}$$

(29)

$$S_{\text{r}} = \varOmega^{*} + \left( {\lambda_{\text{s}}^{*} - \kappa_{\text{s}} } \right)\ln R - \lambda_{\text{s}}^{*} \ln s^{*} + k_{2}^{*} \ln p^{*}$$

(30)

3.3 Critical states

The model predicts that critical states can correspond to any points at the apex of the M yield surface, such as points D, E and F in Fig. 3. In practice, however, it will normally happen that critical states correspond to the intersection with the WR yield surface (i.e. point D in Fig. 3), because yielding on the M surface will cause coupled movement of the WR surface that will be sufficient to bring the WR surface to the stress point prior to arrival at a critical state.

Expressions for v and S _r for critical states corresponding to the intersection of M and WR yield surfaces (point D in Fig. 3) can be derived from the general expressions of Eqs. 27 and 28 by inserting p ^*₀  = 2p ^* (based on the elliptical shape of constant s ^* cross sections of the M surface) and s ^*₁  = s ^*. This gives:

$$v = \varGamma^{*} - \lambda^{*} \ln p^{*} + k_{1}^{*} \ln s^{*}$$

(31)

$$S_{\text{r}} = \varPsi^{*} - \lambda_{\text{s}}^{*} \ln s^{*} + k_{2}^{*} \ln p^{*}$$

(32)

where Γ ^* and Ψ ^* are given by:

$$\varGamma^{*} = N^{*} - \left( {\lambda^{*} - \kappa } \right)\ln 2$$

(33)

$$\varPsi^{*} = \varOmega^{*} + k_{2}^{*} \ln 2$$

(34)

Equations 31 and 32 define two unique critical state planar surfaces, in v:ln p ^*:ln s ^* and S _r:ln p ^*:ln s ^* spaces, respectively. Comparison with Eqs. 23 and 24 indicates that these critical state surfaces for v and S _r are predicted to be parallel to the corresponding normal compression surfaces.

3.4 Experimental validation for isotropic normal compression states

Experimental data from the tests of Sivakumar [41] on compacted speswhite kaolin are used to investigate the validity of the model predictions of unique planar surfaces for v and S _r for both isotropic normal compressions states and critical states.

Experimental results are taken from 15 constant suction isotropic loading tests performed by Sivakumar [41] on unsaturated samples at three different values of suction s (100, 200 and 300 kPa). In each unsaturated test, the isotropic loading was preceded by an initial equalisation stage, as the sample was wetted from a substantially higher as-compacted value of suction. In all cases, plastic increases of degree of saturation occurred during the equalisation stage and plastic volumetric strains and increases of S _r occurred during the isotropic loading stage, consistent with soil states at the intersection of M and WR yield surfaces.

Figures 4 and 5 show experimental values of v and S _r from each isotropic loading unsaturated test that corresponded to soil states at the intersection of M and WR yield surfaces plotted in v:ln p ^*:ln s ^* and S _r:ln p ^*:ln s ^* spaces, respectively, together with the corresponding best-fit planar surfaces obtained by least-squares multiple regression. The gradients and intercepts of these best-fit surfaces gave values for λ ^*, k ^*₁ , λ ^*_s , k ^*₂ , N ^* and Ω ^* (see Eqs. 23 and 24), which are listed in Table 1.

Table 1 Gradients and intercepts of best-fit isotropic normal compression planar surfaces for v and S _r

A clearer view of the quality of fit shown in the three-dimensional representation presented in Fig. 4 is provided by re-plotting the experimental data and best-fit surface for v in a pair of orthogonal two-dimensional views in Fig. 6, using a form of plotting where the best-fit surface is reduced to a single straight line in each of the two views. Figure 7 provides an equivalent representation for S _r. Inspection of Figs. 6 and 7 indicates that the two planar surfaces (for v and S _r) provide excellent fits to the experimental data.

Fig. 6

Orthogonal two-dimensional views of isotropic normal compression planar surface for v (Sivakumar [41])

Fig. 7

Orthogonal two-dimensional views of isotropic normal compression planar surface for S _r (Sivakumar [41])

3.5 Experimental validation for critical states

Each of the experimental tests of Sivakumar [41] involved shearing to failure after the isotropic loading stage. Figures 8 and 9 show the experimental critical state values of v and S _r plotted in v:ln p ^*:ln s ^* and S _r:ln p ^*:ln s ^* spaces, respectively, together with the corresponding best-fit planar surfaces obtained by least-squares multiple regression. The gradients and intercepts of these best-fit surfaces gave values for λ ^*, k ^*₁ , λ ^*_s , k ^*₂ , Γ ^* and Ψ ^* (see Eqs. 31 and 32), which are listed in Table 2.

Fig. 8

Critical state planar surface for v (Sivakumar [41])

Fig. 9

Critical state planar surface for S _r (Sivakumar [41])

Table 2 Gradients and intercepts of best-fit critical state planar surfaces for v and S _r

Figures 10 and 11 show pairs of orthogonal two-dimensional views of the critical state results, presented in suitable form so that, in each view, the fitted planar surface is reduced to a single straight line. Inspection of Figs. 10 and 11 shows that the experimental critical state results for v and S _r show a degree of scatter, but approximate to planar surfaces in v:ln p ^*:ln s ^* and S _r:ln p ^*:ln s ^* spaces, respectively.

Fig. 10

Orthogonal two-dimensional views of critical state planar surface for v (Sivakumar [41])

Fig. 11

Orthogonal two-dimensional views of critical state planar surface for S _r (Sivakumar [41])

Tables 1 and 2 include the two sets of experimentally determined values of λ ^*, k ^*₁ , λ ^*_s and k ₂ ^* from isotropic normal compression states and critical states, respectively. Inspection of these tables show that the two different sets of values of λ ^* and k ^*₁ (giving the gradients of the planar surfaces for v) show good consistency. The values of λ ^*_s and k ^*₂ (giving the gradients of the planar surfaces for S _r) show larger differences between the two sets.

Figure 12 shows a pair of orthogonal two-dimensional representations of the isotropic normal compression and critical state data for v. The continuous lines in Fig. 12 represent the best-fit planar surface to the experimental isotropic normal compression data, whereas the dashed lines represent the form of the critical state surface for v predicted by the model (Eqs. 31 and 33), if values of N ^*, λ ^* and k ^*₁ determined from the isotropic normal compression planar surface are employed. Inspection of the experimental critical state values of v shows that the two planar surfaces for v are approximately parallel, as predicted by the model, but that the vertical spacing between the critical state and isotropic normal compression surfaces for v is significantly over-predicted by the model. The over-prediction of the spacing between the two planar surfaces for v is a consequence of the assumed elliptical shape of constant s ^* cross sections of the M yield surface [24] which could be adjusted following similar developments with constitutive models for saturated soils. For example, Wheeler et al. [50] show that incorporation of evolving plastic anisotropy in an elasto-plastic constitutive model for saturated clays (by means of an inclined yield curve with evolving inclination) reduces the predicted spacing between critical state line and isotropic normal compression line in the v:ln p′ plane and p′ is the saturated mean effective stress.

Fig. 12

Orthogonal two-dimensional views of planar surfaces for v (Sivakumar [41])

Figure 13 shows an equivalent pair of orthogonal two-dimensional representations of the isotropic normal compression and critical state data for S _r. Values of Ω ^*, λ ^*_s and k ^*₂ determined from the isotropic normal compression planar surface (the solid lines) are employed here to plot the dashed lines, which represent the form of the critical state surface predicted by the model (Eqs. 32 and 34). Inspection of Fig. 13 shows that the vertical spacing between the critical state and isotropic normal compression surfaces for S _r predicted by the model provides a reasonable match to the experimental data, although there is significant scatter.

Fig. 13

Orthogonal two-dimensional views of planar surfaces for S _r (Sivakumar [41])

4 Modelling transitions between unsaturated and saturated behaviour

The GCM covers both unsaturated states (S _r < 1) and saturated states (S _r = 1). For saturated states, the GCM recovers naturally the incremental mechanical constitutive relationships of the modified Cam clay model for saturated soils. This is a direct consequence of using Bishop’s stress σ ^* _ij as a stress state variable of the model because, by definition, σ ^* _ij becomes the saturated effective stress σ ^′ _ij when S _r = 1, which does not occur for the conventional net stress state variable $\bar{\sigma }_{ij}$ unless s = 0 (see Eq. 1).

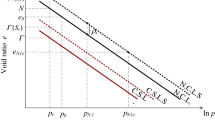
For isotropic stress states on the M yield surface, as S _r reaches 1 the GCM response for v should converge to the conventional saturated normal compression line, NCL:

$$v = N - \lambda \ln p'$$

(35)

where λ and N are, respectively, the gradient and intercept of the saturated NCL in the v:ln p′ plane. Manipulation of Eqs. 23 and 24, defining the unsaturated isotropic normal compression planar surfaces for v and S _r, shows that for the unsaturated normal compression surface for v (given by Eq. 23) to converge to the saturated NCL (Eq. 35) at S _r = 1 (as given by Eq. 24), it is necessary that κ _s = 0. This restriction on the value of κ _s is a consequence of a small inconsistency in the GCM model highlighted by Raveendiraraj [32], which is associated with any occurrence of plastic volumetric strains while the soil is fully saturated (or fully dry), as illustrated in Fig. 14.

Fig. 14

Demonstration of irreversible elastic changes of S _r if κ _s > 0

Figure 14 shows a wetting stress path ABC, followed by a loading–unloading cycle CDE (not seen in the figure) while the soil is saturated and then a drying path EFG. The loading–unloading cycle is such that during CDE plastic volumetric strain occurs, due to yielding on the M surface, whereas for simplicity it is assumed that no plastic volumetric strains occur during either AB or FG, while the soil is unsaturated. As a consequence of the plastic volumetric strain occurring while the soil is saturated, coupled movements of the WR and DR yield surfaces occur and this means that the water retention curves translate from the positions shown by the fine continuous lines in Fig. 14 to those shown by the fine dashed lines. As a consequence, whereas the soil reaches a saturated state at a value of modified suction s ^*_B during wetting, de-saturation occurs at a higher value of modified suction s ^*_F during subsequent drying. This means that elastic increases of S _r occur over the range of modified suction s ^*_F to s ^*_B during the wetting path (plastic changes of S _r also occur), but that elastic decreases of S _r do not occur between s ^*_B and s ^*_F during the drying path. This means that elastic changes of S _r have not been reversible over the range of modified suction s ^*_B to s ^*_F , which contravenes a basic tenet of elastic behaviour.

The predicted irreversibility of elastic changes of S _r introduces inconsistency into the model, by incorporating permanent distinction between the effects of past plastic volumetric strains occurring at saturated states and those occurring at unsaturated states (Raveendiraraj [32]). A simple way to overcome this problem is by assuming κ _s = 0, but inevitably this may result in slight deterioration in the representation of water retention behaviour. This sacrifice is, however, surprisingly small, because experimental values of κ _s determined from tests on compacted fine-grained soils are typically very small (e.g. [24–26]). It is therefore recommended that κ _s = 0 is assumed when the GCM is used in situations where transitions between unsaturated and saturated conditions occur (reducing by one the number of soil constants within the model).

With κ _s = 0, Fig. 15 shows a three-dimensional view (in v:ln p ^*:ln s ^* space) of both the unsaturated isotropic normal compression planar surface for v corresponding to the intersection of M and WR yield surfaces and the saturated isotropic normal compression line (which forms a planar surface parallel to the ln s ^* axis in this three-dimensional space). The intersection of the two surfaces defines a “saturation line” corresponding to the transition from unsaturated to saturated conditions. Figure 16 shows the equivalent surfaces for S _r (in S _r:ln p ^*:ln s ^* space), with the intersection between unsaturated and saturated surfaces corresponding to the same saturation line as in Fig. 15. Also shown in Figs. 15 and 16 is a typical stress path ASB involving transition from unsaturated to saturated conditions at point S.

Fig. 15

Isotropic normal compression planar surfaces for v for unsaturated and saturated conditions

Fig. 16

Isotropic normal compression planar surfaces for S _r for unsaturated and saturated conditions

4.1 Derivation of expressions for saturation and de-saturation lines

Adopting κ _s = 0, Eqs. 21 and 22 remain unchanged, and Eqs. 25 and 26 become:

$$\lambda_{\text{s}}^{*} = \frac{{\lambda_{\text{s}} }}{{1 - k_{1} k_{2} }}$$

(36)

$$k_{2}^{*} = k_{2} \frac{{\lambda_{\text{s}} }}{{\left( {1 - k_{1} k_{2} } \right)}}$$

(37)

Putting S _r = 1 in Eq. 24, which defines the unsaturated normal compression planar surface for S _r, with λ ^*_s and k ^*₂ given by Eqs. 36 and 37, produces an expression for the saturation line shown in Figs. 15 and 16:

$$\ln s^{*} = \frac{{\varOmega^{*} - 1}}{{\lambda_{s}^{*} }} + k_{2} \ln p^{*}$$

(38)

Inserting the expression for the saturation line of Eq. 38 in the expression for the unsaturated normal compression planar surface for v (Eq. 23) gives an expression for the saturated NCL:

$$v = N^{*} - \frac{{k_{1} \left( {\lambda - \kappa } \right)}}{{\lambda_{s} }}\left( {1 - \varOmega^{*} } \right) - \lambda \ln p_{{}}^{*}$$

(39)

Comparing Eq. 39 with the standard expression for the saturated NCL (Eq. 35), and remembering p ^* = p′ when S _r = 1, shows that the intercepts Ω ^*, N ^* and N are related:

$$\varOmega^{*} = 1 - \frac{{\left( {N^{*} - N} \right)\lambda_{s} }}{{k_{1} \left( {\lambda - \kappa } \right)}}$$

(40)

The saturation line defined by Eq. 38 represents the combinations of s ^* and p ^* at which transitions from unsaturated to saturated conditions will occur if the stress state is isotropic and at the intersection between M and WR yield surfaces. With κ _s = 0, transitions from unsaturated to saturated conditions can only occur while on the WR yield surface, but it is not necessary for the stress state to be on the M yield surface or for the stress state to be isotropic at the point of transition from unsaturated to saturated conditions. Given that changes of p ^* or q do not produce elastic changes of S _r, it is straightforward to use Eq. 38 to derive a generalised expression for transition from unsaturated to saturated conditions, applicable to any isotropic or anisotropic stress states, including those not on the M yield surface, by considering an elastic stress path along the WR yield surface from the intersection with the M yield surface at q = 0. This generalised expression for transition from unsaturated to saturated conditions under any stress state takes the form:

$$\ln s^{*} = \frac{{\varOmega^{*} - 1}}{{\lambda_{\text{s}}^{*} }} + k_{2} \ln p_{0}^{*}$$

(41)

This can be rewritten as:

$$s^{*} = \exp \left( {\frac{{\varOmega^{*} - 1}}{{\lambda_{\text{s}}^{*} }}} \right)\left( {p_{0}^{*} } \right)^{{k_{2} }}$$

(42)

The general expression for the saturation line, corresponding to transition from unsaturated to saturated conditions (sometimes known as the air-exclusion point), defined by Eqs. 41 or 42, is illustrated in Fig. 17 (in both a log–log plot and a linear plot). Note that Eqs. 41 and 42 and Fig. 17 show that the saturation value of s ^* is uniquely dependent on the position of the M yield surface (i.e. the value of p ^*₀ ).

Fig. 17

Predicted saturation and de-saturation lines

Transitions in the reverse direction, from saturated to unsaturated conditions, must occur on the DR yield surface if κ _s = 0, but it is not necessary for the stress state at the point of de-saturation to be on the M surface. This transition from saturated to unsaturated conditions occurs on a “de-saturation line” defined by:

$$s^{*} = R\,\exp \left( {\frac{{\varOmega^{*} - 1}}{{\lambda_{\text{s}}^{*} }}} \right)\left( {p_{0}^{*} } \right)^{{k_{2} }}$$

(43)

where R is the soil constant defining the fixed ratio of s ^*₂ to s ^*₁ (see Eq. 15).

Figure 17 shows the form of the de-saturation line defined by Eq. 43, corresponding to transition from saturated to unsaturated conditions (sometimes known as the air-entry point).

Figure 17 illustrates that the GCM includes the influences of both retention hysteresis and plastic volumetric straining on transitions between saturated and unsaturated conditions. The difference between the saturation and de-saturation values of s ^* (at the same value of p ^*₀ ) shows the influence of retention hysteresis, whereas the variation of both saturation and de-saturation values of s ^* with p ^*₀ shows the influence of plastic volumetric strains on air-exclusion and air-entry points.

4.2 Mechanical yielding under saturated and unsaturated conditions

Figure 18 illustrates how the GCM provides consistent modelling of mechanical yielding under both saturated and unsaturated conditions. The figure shows a wetting–drying cycle ABCDEF involving transitions between unsaturated and saturated conditions during both wetting and drying (at points B and E, respectively). The stress path starts on the WR yield surface at A, but remains inside the M yield surface throughout. The stress path shown in Fig. 18 in both the s ^*:p ^* plane (Fig. 18a) and the conventional s:$\bar{p}$ plane (Fig. 18b) happens to represent a wetting–drying cycle performed at constant $\bar{p}$, but the discussion presented in this section would apply equally well to any general wetting–drying path remaining inside the M yield surface.

Fig. 18

Variation of mechanical yield stress during a wetting–drying cycle

Also shown in Fig. 18a is the variation of mechanical yield stress p ^*₀ predicted by the GCM during the wetting–drying cycle, representing the coupled movement of the M yield surface. The value of p ^*₀ reduces during the initial unsaturated section AB of the wetting path, due to the coupled inward movement of the M surface caused by the plastic increases of S _r during yielding on the WR surface (see Eq. 13). However, during the final saturated section BC of the wetting path, the value of p ^*₀ remains constant, as there are no longer any plastic increases of S _r to produce further coupled movement of the M surface. During drying path CDEF, the stress path passes back inside the WR surface at point D, but de-saturation only occurs when the stress path reaches the DR surface at E. The value of p ^*₀ therefore remains constant during the initial saturated section CDE of the drying path and then increases during the final unsaturated section EF (see Eq. 13).

Figure 18b shows the variation of mechanical yield stress predicted by the GCM during the wetting–drying cycle ABCDEF re-plotted in the conventional s:$\bar{p}$ plane. The variation of mechanical yield stress during the unsaturated section AB of the wetting path is equivalent to the LC yield curve in conventional models such as the BBM. From B to C, however, with the soil in a saturated condition, the variation of mechanical yield stress for the GCM plots as a 45° line in the s:$\bar{p}$ plane, consistent with yield at a constant value of saturated mean effective stress ($p^{\prime} = p - u_{\text{w}} = \bar{p} + s$). During the drying path CDEF, the variation of mechanical yield stress follows a 45° line until the soil de-saturates at E, and then from E to F it forms a curve again. The qualitative form of variation of mechanical yield stress shown in Fig. 18b is exactly what would be expected for a soil under unsaturated and saturated conditions, where saturation occurs at a nonzero air-exclusion value of suction (point B) and de-saturation occurs at a nonzero air-entry value of suction (point E) that is higher than the air-exclusion value because of hysteresis in the retention behaviour. This variation of mechanical yield stress emerges naturally from the GCM, whereas it would be very difficult to achieve in any mechanical model expressed in terms of net stresses and suction.

5 Determination of model parameter values

With κ _s = 0, the GCM involves 10 soil constants: λ, κ, N, M, G, N ^*, k ₁, k ₂, λ _s and R. The first 5 constants are the modified Cam clay parameters required for modelling of mechanical behaviour under saturated conditions, whereas the other 5 constants are required to extend the modelling to include mechanical behaviour under unsaturated conditions, water retention behaviour and the coupling between them. The values of the 10 constants must be determined for a given soil if the model is to be used in numerical simulations of single-element laboratory tests or geotechnical boundary value problems where both saturated and unsaturated conditions occur. In addition, the initial state of the soil must be specified for any numerical simulation, including appropriate variation of this initial state with position (e.g. with depth) in a boundary value problem.

5.1 Soil constants

The values of soil constants λ, κ and N can be determined from conventional isotropic loading and unloading stages performed in a triaxial apparatus on saturated samples. The value of M can be determined from experimental critical state data for saturated and unsaturated samples plotted in the q:p ^* plane (see Eq. 16), and the value of G can be measured in triaxial shear tests on saturated or unsaturated samples (ideally involving unload–reload stages).

It might appear that the values of soil constants λ _s and R would best be determined from conventional water retention curves (measured, for example, in a pressure plate test) plotted in the S _r:ln s ^* plane, with λ _s given by the gradient of the main drying and main wetting curves and R calculated from the spacing of the main drying curve and the main wetting curve. However, this procedure would often give misleading values for λ _s and R, because conventional water retention tests will often involve plastic volumetric strains, and under these conditions the GCM predicts that the gradients and spacing of the main drying and main wetting curves do not correspond simply to λ _s and R. A better alternative is therefore to use experimental data from isotropic loading under unsaturated conditions (at a minimum of two different values of suction) to define the unsaturated isotropic normal compression planar surfaces for v and S _r corresponding to the intersection of M and WR yield surfaces, and to use the gradients and intercepts of these surfaces to determine the values of the soil constants k ₁, k ₂, λ _s and N ^*.

When plotted in v:ln p ^*:ln s ^* space, the intercept of the experimental unsaturated normal compression surface for v gives the value of the soil constant N ^* directly (Eq. 23). With values of λ and κ already determined from tests on saturated samples, the two gradients λ ^* and k ^*₁ of the experimental unsaturated normal compression surface for v (see Eq. 23) can then be used to determine values for the soil constants k ₁ and k ₂, by combining Eqs. 21 and 22 to give:

$$k_{1} = \frac{{k_{1}^{*} }}{{\lambda^{*} - \kappa }}$$

(44)

$$k_{2} = \frac{{\lambda^{*} - \lambda }}{{k_{1}^{*} }}$$

(45)

The corresponding experimental unsaturated normal compression surface for S _r (see Eq. 24) can then be used to determine the value of the soil constant λ _s. With κ _s = 0 and values already determined for the soil constants λ, κ, N, N ^*, k ₁ and k ₂, Eqs. 40, 36 and 37 show that the intercept Ω ^* and the two gradients, λ ^*_s and k ^*₂ , of the unsaturated normal compression surface for S _r all depend solely on the value of λ _s. Least-squares fitting of Eq. 24 to the experimental data defining the planar surface in S _r:ln p ^*:ln s ^* space, with the value of λ _s as the sole degree of freedom, can be used to determine a value for λ _s.

The procedure described above for determining the values of N ^*, k ₁, k ₂ and λ _s allows three degrees of freedom (the values of N ^*, k ₁ and k ₂) for fitting the intercept and the two gradients of the unsaturated normal compression surface for v, but only a single degree of freedom (the value of λ _s) for fitting the intercept and the two gradients of the unsaturated normal compression surface for S _r. If this results in poor fitting of the experimental data defining the unsaturated normal compression surface for S _r, it may be appropriate to perform iterative adjustment of parameter values, to improve the fit of the surface for S _r, while slightly compromising the fit of the surface for v.

The final soil constant R is required only if the GCM is to be used for simulations involving yielding on both WR and DR retention yield surfaces. The value of R can be determined by comparing experimental values of v for isotropic stress states at the intersection of DR and M yield surfaces with Eq. 29 (with κ _s = 0). Suitable experimental tests would include drying of samples starting in normally consolidated saturated states.

The methodology for determining the values of λ, κ, N, N ^*, k ₁, k ₂ and λ _s was applied to the experimental results of Sivakumar [41], including saturated and unsaturated tests, resulting in the values shown in Table 3.

Table 3 Values of soil constants for model simulations

5.2 Initial state

The initial state of the soil must be specified for any numerical simulation. For the GCM, this initial state is represented by initial values of the stress variables σ ^* _ij and s ^* (p ^*, q and s ^* are sufficient for the case of a triaxial test) and initial values of the hardening parameters p ^*₀ and s ^*₁ (or s ^*₂ ).

For simulations of laboratory tests, it is likely that the initial state will be known in terms of initial values of conventional stress variables, $\bar{p}$, q and s, and initial values of v and S _r. These can be combined to give initial values of p ^*, q and s ^* (Eqs. 1 and 3). With the values of soil constants already determined, the general expressions for v and S _r of Eqs. 27 and 28 can be combined (using κ _s = 0 and Eqs. 21, 22, 36 and 37) to give expressions for the initial values of the hardening parameters p ^*₀ and s ^*₁ in terms of the initial values of p ^*, v and S _r (the initial value of s ^* is not involved, because of the assumption κ _s = 0):

$$\ln p_{0}^{*} = \frac{{N^{*} - v - \kappa \ln p^{*} }}{\lambda - \kappa } + \frac{{k_{1}^{{}} \left( {\varOmega^{*} - S_{\text{r}} } \right)}}{{\lambda_{\text{s}} }}$$

(46)

$$\ln s_{1}^{*} = \frac{{\varOmega^{*} - S_{\text{r}} }}{{\lambda_{\text{s}} }} + \frac{{k_{2}^{{}} \left( {N^{*} - v - \kappa \ln p^{*} } \right)}}{\lambda - \kappa }$$

(47)

where Ω ^* is given by Eq. 40.

Having calculated initial values of p ^*₀ and s ^*₁ from Eqs. 46 and 47, these should be checked to ensure that the initial stress state does not fall outside any of the yield surfaces. If this condition is not satisfied, it will be necessary to adjust slightly the initial value of S _r or v (accepting that it will not then perfectly match the experimental value) in order to adjust the values of p ^*₀ and s ^*₁ (Eqs. 46 and 47) such that the initial stress state now falls on or inside the relevant yield surface. Similar adjustment of the initial value of v or S _r may be required if experimental evidence suggests that the initial stress state lies exactly on one of the yield surfaces. To bring the initial stress state exactly on to one of the yield surfaces, through adjustment of the initial value of S _r or v, it will normally be necessary to employ an iterative procedure, because the initial stress state is normally known in terms of the conventional stress parameters $\bar{p}$, q and s (rather than p ^*, q and s ^*), and adjustment of the initial value of S _r or v will then lead to a change of the initial value of p ^* or s ^* (see Eqs. 1 and 3).

The methodology for determining initial state described above was applied to the tests of Sivakumar [41], for the initial state corresponding to the start of the isotropic loading stage of those tests performed at a suction of 300 kPa ($\bar{p} = 50$ kPa, q = 0, s = 300 kPa). The corresponding average initial experimental values of v and S _r measured for this group of tests were 2.210 and 0.597, respectively. Experimental evidence suggested that the initial state was on the WR yield surface, but not necessarily on the M yield surface (plastic increase of S _r but no plastic volumetric strain (no collapse compression) occurred during the preceding wetting from the much higher as-compacted value of suction). The procedure to calculate the initial values of p ^* and s ^* and the initial values of the hardening parameters p ^*₀ and s ^*₁ (using Eqs. 46 and 47) therefore included iterative adjustment of the initial value of S _r to ensure that the initial state fell exactly on the WR yield surface (s ^* = s ^*₁ ). The values of soil constants used in this process were those previously determined and are shown in Table 3. The resulting initial value of S _r was 0.562 (rather than the average experimental value of 0.597), and the full calculated initial state conditions are given in Table 4.

Table 4 Initial state for model simulations

For simulations of boundary value problems, the initial state will typically vary with depth within a given soil layer. To represent this, the variations with depth of initial stress state and stress history in terms of net stresses $\bar{\sigma }_{ij}$ and suction s will first need to be estimated, using similar procedures to those employed for boundary value problems involving saturated conditions. This information will then need to be combined with the relevant GCM model equations, and the values of the 10 GCM constants for the particular soil (typically determined from laboratory test data), to estimate the variation with depth of the initial stress state in terms of Bishop’s stresses σ ^* _ij and modified suction s ^* and the variation with depth of the initial values of the hardening parameters p ^*₀ and s ^*₁ .

Once the initial state of a boundary value problem has been specified, it is useful to express the incremental mechanical and water retention relationships of the GCM, in terms of the increments of strains Δε and the increments of matric suction Δs (see [23, 24]) because, together, they define an initial value problem that can be integrated over time at each Gauss or integration point within each finite element (i.e. local level). This is the common procedure used in the literature for finite element analysis involving unsaturated soils [5, 38, 43], because these two increments (i.e. Δε, Δs) can be easily approximated at the corresponding integration points, once the nodal displacements and pore fluid pressures increments have been found from the discretised global equations.

6 Simulations of experimental data of Sivakumar (1993)

Validation of the GCM was undertaken by performing model simulations of the experimental tests of Sivakumar [41] performed on saturated and unsaturated samples of compacted speswhite kaolin at suctions of 0, 100, 200 and 300 kPa. Model simulations of initial equalisation stages and isotropic loading stages are discussed here, whereas model simulations of subsequent shearing stages are discussed elsewhere ([24, 26]). Model simulations were performed using the set of values for soil constants shown in Table 3.

All simulations commenced from the same initial state A, corresponding to the end of the initial equalisation stage for those samples tested at a suction of 300 kPa, as shown in Table 4. For tests conducted at suctions of 200 or 100 kPa, the simulations commenced with an initial wetting stage, AB or AC, respectively (at $\bar{p}$ = 50 kPa) from s = 300 kPa to the required value of s, to represent the remainder of the initial equalisation stage for these tests. For tests conducted at zero suction, the simulations were designed to replicate the stress path followed by Sivakumar [41] in the initial equalisation stage of his tests on saturated samples. This required initial isotropic unloading AD (at s = 300 kPa) from $\bar{p} = 50$ kPa to $\bar{p} = 40$ kPa, followed by wetting DE (at $\bar{p} = 40$ kPa) from s = 300 kPa to s = 0, and then finally isotropic unloading EF (at s = 0) from $\bar{p} = 40$ kPa to $\bar{p} = 25$ kPa. These procedures ensured that simulations performed at all four values of suction employed consistent initial states at the start of the subsequent isotropic loading stages, with differences of v and S _r that were consistent with model predictions.

Figures 19 and 20 show experimental variations of v against p ^* and $\bar{p}$, respectively (with stresses on both linear and logarithmic scales), from the isotropic loading stages performed at all four different values of suction, plotted together with the corresponding model simulations. Variations of S _r are presented in Fig. 21 against p ^*. In Figs. 19, 20 and 21, model simulations of the initial equalisation stages from the common starting point A are indicated by dashed lines, simulations of constant suction isotropic loading stages are indicated by thick solid lines and experimental results for isotropic loading stages are indicated by symbols joined by thinner solid lines.

Fig. 19

Model predictions and experimental variations of v against p ^* (Sivakumar [41]): a linear scale; b logarithmic scale

Fig. 20

Model predictions and experimental variations of v against $\bar{p}$ (Sivakumar [41]): a linear scale; b logarithmic scale

Fig. 21

Model predictions and experimental variations of S _r against p ^* (Sivakumar [41]): a linear scale; b logarithmic scale

Inspection of Figs. 19 and 21 shows that the GCM simulations capture the observed changes of v and S _r during the equalisation stages of the tests conducted at suctions of 200, 100 kPa and 0, relative to the common starting point A of the simulations. As a consequence, the predicted values of v and S _r at the start of the isotropic loading stages of these tests (points B, C and F) show reasonable agreement with the corresponding experimental values (predicted values of v at C and F are slightly too high and slightly too low, respectively).

In particular, the model simulations correctly predict, at a qualitative level, the complex pattern of swelling and collapse compression reported by Sivakumar [41] during wetting DE to zero suction in the tests conducted on saturated samples. During the first part of this wetting, from D to Y (see Fig. 19), the soil state is on the WR yield surface but inside the M yield surface, and elastic swelling is predicted (due to the decrease of p ^*). Coupled inward movements of the M yield surface occur, such that yield on the M surface commences at Y, and then collapse compression is predicted from Y to S, where the soil reaches a saturated state (at a nonzero air-exclusion value of suction). From S to E, with the soil in a saturated condition, the model prediction shows elastic swelling, due to the reduction of p ^* (where p ^* = p′ in this saturated condition), as suction is reduced from the air-exclusion value to a final value of zero. Sivakumar [41] observed the same qualitative pattern of behaviour in his experimental tests, with initial wetting-induced swelling followed by wetting-induced collapse compression and then finally more wetting-induced swelling. Conventional models expressed in terms of net stresses and suction (such as the BBM) would be unable to predict the final phase of wetting-induced swelling.

Inspection of Fig. 19 shows that the GCM simulations provide an excellent match to the experimental positions of the normal compression lines at the four different values of suction in the v:ln p ^* plane. This is a consequence of selecting the values of the model parameters λ, N, N ^*, k ₁ and k ₂ to fit the saturated isotropic NCL and the unsaturated isotropic normal compression planar surface in v:ln p ^*:ln s ^* space. The fact that the GCM simulations for v at the four different values of suction also match well the experimental normal compression lines when plotted in the v:$\ln \bar{p}$ plane (see Fig. 20) indicates that the model has also been able to provide adequate modelling of the variation of S _r, given that conversion of experimental and predicted values of p ^* to corresponding values of $\bar{p}$ involves the experimental and predicted values of S _r (see Eq. 1).

Figure 21 shows that the GCM predictions for the variations of S _r at the three nonzero values of suction provide a reasonable match to the experimental results, but the match is not as good as for the corresponding variations of v (see Fig. 19). This is a consequence of allowing 3 degrees of freedom (the values of N ^*, k ₁ and k ₂) when fitting the experimental data defining the unsaturated normal compression surface for v, but only 1 degree of freedom (the value of λ _s) when fitting the data defining the normal compression surface for S _r. It would have been possible to improve the fit of the predicted variations of S _r, by adjusting some of the model parameter values, but this would have been at the expense of slight deterioration in the fit of the predicted values of v.

A significant conclusion arises from comparison of Figs. 19b and 20b: whereas a clear pattern emerges from the experimental normal compression lines for different values of suction when plotted in the v:ln p ^* plane, no such pattern is apparent when the same experimental curves are plotted in the v:$\ln \bar{p}$ plane. In the v:ln p ^* plane (Fig. 19b), the constant suction experimental normal compression lines corresponding to unsaturated conditions (at suctions of 100, 200 kPa and 300 kPa) approximate to straight parallel lines, whereas the saturated normal compression line forms a straight line of lower gradient. This pattern is perfectly represented by the GCM, which predicts that constant s isotropic normal compression lines corresponding to unsaturated conditions approximate to straight parallel lines of gradient λ ^* in the v:ln p ^* plane (the GCM would predict perfectly straight parallel lines of gradient λ ^* if s ^* were held constant (see Eq. 23), rather than s), whereas the GCM predicts a saturated isotropic normal compression line of lower gradient λ. In contrast, when the same experimental curves are re-plotted in the v:$\ln \bar{p}$ plane (Fig. 20b), the variation of normal compression line gradient with suction appears complex and without clear pattern. Despite this, the GCM manages to predict well the complex form of the various normal compression lines in the v:$\ln \bar{p}$ plane, because the GCM is developed in the v:ln p ^* plane, where the experimental results show a logical pattern, and only then transferred to the v:$\ln \bar{p}$ plane. This provides a strong argument in favour of developing models that employ mean Bishop’s stress p ^* as a stress state variable, rather than mean net stress $\bar{p}$.

Various previous authors have proposed mechanical constitutive models that involve relatively complex relationships attempting to represent variations of a virgin compression index λ with suction (Alonso et al. [1]; Wong and Mašín [52]), with degree of saturation (Zhou and Sheng [53]) or with both s and S _r (Alonso et al. [3]). The evidence presented in Fig. 19b suggests that such complexity may be overcome by developing models that use p ^* as stress state variable and fully account for the coupling between mechanical and water retention behaviour.

7 Conclusions

The Glasgow coupled model (GCM) predicts that isotropic normal compression states and critical states in experimental tests involving plastic volumetric strains and plastic increases of S _r will correspond to points at the intersection of M and WR yield surfaces. For these states, the model predicts unique unsaturated isotropic normal compression and unsaturated critical state planar surfaces for specific volume v (in v:ln p ^*:ln s ^* space) and also unique isotropic normal compression and critical state planar surfaces for degree of saturation S _r (in S _r:ln p ^*:ln s ^* space). Experimental results from the tests of Sivakumar [41] on unsaturated samples of compacted speswhite kaolin provide confirmation of the existence and form of these unique unsaturated normal compression and critical state surfaces. The GCM also provides expressions for the values of v and S _r for any general stress states, in terms of the values of the stresses p ^* and s ^* and the values of the hardening parameters p ^*₀ and s ^*₁ .

The GCM provides consistent representation of transitions between saturated and unsaturated states, including the influence of retention hysteresis and the effect of plastic volumetric strains on retention behaviour. The GCM gives unique expressions to predict saturation and de-saturation conditions (air-exclusion and air-entry points, respectively), in the form of two unique straight lines in the ln s ^*:ln p ^*₀ plane. The saturated normal compression line (NCL) plots as a planar surface in both v:ln p ^*:ln s ^* and S _r:ln p ^*:ln s ^* spaces, and when transitions from unsaturated to saturated conditions occur under isotropic stress states at the intersection of M and WR yield surfaces, the saturation line corresponds to the intersection of unsaturated and saturated isotropic normal compression planar surfaces in both spaces.

The GCM provides consistent modelling of mechanical behaviour across the transitions between saturated and unsaturated conditions, including appropriate representation of the variation of mechanical yield stress. This appropriate variation of mechanical yield stress across transitions between unsaturated and saturated conditions occurring at nonzero values of suction emerges naturally from the GCM, whereas it would be very difficult to achieve in any mechanical model expressed in terms of net stresses and suction.

A straightforward methodology is proposed (and has been demonstrated) for determining the values of all GCM model parameters and initial state from a limited number of suction-controlled triaxial tests. Central to this methodology is plotting the experimental data defining the unsaturated isotropic normal compression planar surfaces in v:ln p ^*:ln s ^* and S _r:ln p ^*:ln s ^* spaces.

GCM simulations of the isotropic loading stages of the experimental tests of Sivakumar [41] on compacted speswhite kaolin demonstrate that the model is able to predict accurately the variations of both v and S _r during isotropic stress paths under saturated and unsaturated conditions. A clear pattern emerges when the experimental results for unsaturated and saturated isotropic normal compression states are plotted against ln p ^*, whereas no such pattern is apparent when the same results are plotted against $\ln \bar{p}$. The GCM represents the clear pattern observed in the v:ln p ^* plane and, as a consequence, also captures the complex variation of the experimental results when re-plotted in the v:$\ln \bar{p}$ plane. This would be extremely difficult to achieve with any constitutive model developed in terms of net stresses and suction, and this provides a strong argument in favour of models, such as the GCM, which employ p ^* as a stress state variable.