1 Introduction

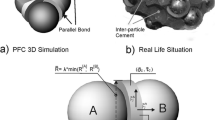
Cemented granular materials (CGMs) are of great importance in engineering construction. CGMs consist of a skeleton of densely packed particles and cohesive materials filling the pores completely or partially [55]. CGMs can be found in different forms and scales such as mortars, concretes, asphalts [27], grouted soils [5], cemented sands, sedimentary rocks and some biomaterials (e.g. wheat endosperm) [1] ranging from meso- to macroscales [25]. Both the contact force field between particles [3] and cohesive materials may affect the stress distribution to a high extent and control overall mechanical behaviour of CGMs. Therefore, in addition that the matrix governs the cohesive force field between particles, its bulk behaviour is a determinative factor in overall behaviour of CGMs; thus, the behaviour of CGMs is more complicated over cohesive granular materials [57]. Numerous methods have been proposed to describe the mechanical behaviour of CGMs such as experimental methods [10, 44, 60], theoretical methods [36, 52] and numerical methods [15]. Topin et al. have recognized four dominant features in mechanism of CGM behaviour, including: (1) cohesion between matrix and particles, (2) the arching effect whereby weekly stressed zones are initiated and propagated through CGM bulk, (3) partially filled pores leading to frictional behaviour of contact zones and (4) particle jamming whereupon the stress concentration and particle crushing may happen. It has been indicated that even a small change in volume of cohesive matrix may strongly affect the strength and stiffness of CGMs [14]. Thus, the complex mechanical behaviour of CGMs has been a great challenge in numerical studies.

Nnumerical methods for simulation of CGMs may be broadly classified into homogenization/continuum methods and discrete methods. Regarding the scale of simulations, Shen et al. [46] have categorized these numerical methods into three major groups, including (1) macroscopic phenomenological models such as modified elastic–plastic models which treat CGMs as a continuous single-phase material, (2) double-phase mixture models and (3) micromechanical-based models in which CGMs are simulated based on integration of microscopic mechanical features of each component.

Many efforts have been ever made in modelling CGMs using macroscopic theoretical constitutive models, homogenization theories and numerical methods based on classical continuum mechanics (CCM), for example, the traditional finite element method (FEM) [9]. Some approaches have been developed to simulate initiation and propagation of cracks and failure processes in homogenized CGMs or continuum cement-based materials like concrete using CCM-based methods such as cohesive zone model (CZM) [13, 21], lattice element method (LEM) [1, 10] and extended finite element method (XFEM) [32, 33]. In CZM, a cohesive zone is presumed in front of crack initiation point. Once the stress level is reached to a threshold, crack initiates and the stress level decreases as the crack propagates and the damage zone grows. CZM and LEM are highly mesh dependent and become less computationally efficient as the number of elements increases. To overcome this drawback, XFEM has been developed [8, 19] in which enrichment functions with additional degrees of freedom are embedded in FEM with nodes or elements to make it capable of modelling initiation and propagation of cracks in a continuum material. However, the selection of the enrichment functions and crack propagation criteria is still an obscure challenge. Moreover, the mechanism of these methods in controlling crack coalescence and branching as well as multiple cracks propagation is still ambiguous [54]. The main problem with continuum-based methods is that once the fracture is initiated, singularities arise near separated parts of solids. Extra efforts are often needed to solve the problem with singularities. On the other hand, the homogenization methods describe a CGM as a single-phase continuum material and approximates macroscopic responses of a CGM by homogenizing the properties of particles and cement in a representative volume element (RVE). The methods cannot be accurate enough to simulate the complex discontinuous nature and highly heterogeneous load distribution within the media [23].

Various numerical studies on CGMs have been carried out using discrete methods. In discreet methods, local microscale phenomena are considered to predict the anisotropic response of CGMs based on the geometries and heterogeneous properties of the individual phases whereby a more accurate predication of damage process in CGMs can be achieved. For example, discrete element method (DEM) [7] is known as one of the commonly used numerical methods for modelling CGMs in the form of rigid particles connected to each other by cement bonds [6, 27, 46, 53, 59]. DEM is relatively simple to use and computationally inexpensive. It is also able to upscale micromechanical phenomena to macroscale simulations by a multi-scale method. For example, the FEMDEM has been proposed to combine the continuum simulation with the discrete modelling, where the FEM solves the boundary value problem of a macroscopic model and DEM is used for microscopic behaviour of the CGM [38, 58].

Two types of bonds can be easily modelled in DEM: parallel bonds for cement bond formed in the physical contact point between two contacting particles and serial bonds in which cement bond is placed in between two separated particles [47]. However, DEM is difficult to model the bulk behaviour of cement that fills in the void space among a cluster of particles. The cement “clogs”, as termed in this paper, play an important role in controlling the mechanical behaviour of the CGM [1]. In addition, damage and failure processes in DEM are simulated by breakage of the bonds using analytical [56] or experimental [26] constitutive models. These constitutive models often require extra parameters to fit to real damage/failure processes. Another limitation of DEM is that it is difficult to model irregular particle shapes, so that simple geometrical shapes are often adopted, e.g. 2D circular/ellipsoidal shapes or 3D spherical/oval shapes. “Clumps” of overlapping spheres have been developed in DEM as a remedy to solve this problem [18]. However, the clumped particles are considered as rigid bodies, and a proper cement bond model for this type of model (especially for modelling “clogs”) is yet to be developed.

There are some non-local continuum-based methods that can provide solutions to simulate the mechanical behaviour and damage/failure process for solid materials in an engineering scale [40, 43, 63]. PD is a meshless non-local integral-based numerical method developed by Silling [50] in which singular partial derivatives do not arise as discontinuities initiate and propagate in continuum solids. Instead, the force–displacement calculations of a material point are integrated over its neighbourhood [49]. Therefore, PD has been a suitable method to model damage/failure processes in continuum solids [12]. It has been shown that PD is able to predict important characteristics of dynamic fracture propagation including fracture branching, fracture path and propagation speed [20]. Also, no external constitutive model is required in PD to locate crack tips and determine crack propagation and direction.

There are many applications of PD among the literature. A comprehensive review of different engineering applications of PD has been collected in [24]. Dihel et al. surveyed experimental applications for validation of the bond-based and the state-based PDs [11]. Many practical uses of PD for the homogeneous and heterogeneous cemented materials have been reported. For example, 2D [22, 23, 48] and 3D [28, 30, 37, 45] models of PD for simulation of the mechanical behaviour and the damage/failure process of cement pastes and concretes with ideally spherical particles have been provided. The results of PD simulations of the three-point load test of notched mortar beams are compared to those of XFEM simulations, showing that PD is reasonably able to simulate the failure process with fewer parameters than XFEM [8]. The bond-based PD [19] and the state-based PD [54] have also been upscaled in a FEM framework to model progressive cracking through cohesive brittle materials. A two-dimensional coupled PD/DEM has been provided in [25] to model the behaviour of granular materials. Some couplings of PD with smoothed particle hydrodynamics (PD-SPH) have been reported among the literature for geomaterials [16, 17, 41].

However, the PD method has limitations to model discrete systems such as densely packed granular materials because inter-particle contact cannot be accurately simulated. As a remedy, some hybrid methods were used to model a single particle crushing using PD and physics engine for inter-particle contact [62]. Recently, a DEM-like contact model has been developed for PD and used in some simple 2D simulation [25].

In this paper, a new PD model with an innovative contact algorithm is developed to simulate cemented granular materials with complex shapes. Development of this peridynamics model makes it able to employ peridynamics as a continuum-based method for the simulation of highly heterogenous materials like CGMs. As shown in Fig. 1, different phenomena in CGMs can be simulated using the model, including the effect of cement bonds surrounding contact points and bulk behaviour of cement clogs within the void space enclosed by multiple particles. In addition, the irregular shapes of the granular particles are simulated accurately and efficiently. The developed model can demonstrate initiation and propagation of cracks, and damage processes of CGMs only based on the material properties of different. The present model can continuously simulate all phases in CGMs without the need to couple with the other homogenization/discrete numerical methods. Also, the effect of pre-existing discontinuities and defects in different phases is considered. The results of the model are compared to laboratorial tests of CGMs with different cement volume fractions.

Fig. 1
figure 1

Different entities in a schematic CGM

Full size image

This article is organized as follows. In Sect. 2, the fundamentals of PD model are described along with the formulation of ordinary state-based PD material model, damage model and time integration scheme. The illustration of a new contact model is provided further in this section. In Sect. 3, the process of experimental tests is illustrated including constructing CGM samples and tests process. Section 4 is dedicated to implementation of the PD simulations to conduct different tests and compare the results to those of experimental.

2 Fundamentals of PD modelling

In this section, details of elastic state-based material model, damage model, the touch-aware contact model and time integration scheme for PD simulations are provided.

A PD solid material is discretized into a set of material points with certain volume and mass so that the total volume of all material points equals to the volume of the solid. Each material point has a neighbourhood of adjacent material points within a radius of “horizon” and vector connecting a material point to a neighbour is called a “bond”. PD has been initially developed as “bond-based PD” in which the bond stretch is linearly proportional to internal force between a material point and its neighbour. The restriction with the bond-based PD is that it leads to a constant Poisson’s ratio of 0.33 in 2D and 0.25 in 3D [12]. Although bond-based PD may be deemed as a sufficient approximation for some brittle materials like some types of ceramics, it is not valid for all kinds of material. To overcome this shortcoming, the “state-based PD” has been developed [51]. In the state-based PD model, the relation between displacement and internal force within material points is defined using “states”. The states are mathematical functions which link deformation of a bond to collective deformation of other bonds within a neighbourhood [42]. The state-based PD is divided into two classes: “ordinary state-based PD” and “non-ordinary state-based PD”. In this research, ordinary state-based PD is used. Note that the ordinary state-based peridynamics is formulated in material (or initial) configuration using the total Lagrangian approach. The non-ordinary state-based PD can be formulated in both material (initial) and current (deformed) configurations [4].

2.1 Ordinary state-based linear elastic material

The constitutive equation of motion for the ordinary state-based PD can be established based on a strain energy density obtained from CCM. In the ordinary state-based PD, the direction of the states is necessarily along the bonds, whereas the non-ordinary state-based PD is independent from CCM, and this curtailment is removed. However, the non-ordinary state-based PD can be computationally expensive. In the state-based generalization of PD theory, force states calculate pairwise force densities between a material point \({\varvec{x}}\) and its neighbours within \(H_{x}\) with horizon \((\delta )\) in initial configuration. The deformation between \({\varvec{x}}\) and its neighbours is also calculated by the deformation states; therefore, the state-based PD material model is defined as a constitutive relationship between the deformation and force states. Figure 2a, b shows a PD domain of a CGM in initial and deformed configurations, respectively. Assume that \(\Omega \in {\mathbb{R}}^{3}\) denotes a CGM domain in a 3D space. Superscriptions I and D demonstrate initial and deformed configurations of \(\Omega\), respectively. \(\Omega\) is a union of individual bodies, \({\Omega }_{i}\), \(i = 1,2, \ldots ,N\) including rock particles and cement matrix. The system is under an external force density \(f^{\mathrm{ext}}\) and displacement boundaries \(\partial {\Omega }^{u}\), which may cause geometrical deformations whereby damage and failure of CGM occur.

Fig. 2
figure 2

Schematics of an ordinary state-based PD domain \((\Omega )\) representing a CGM includes two particles \(\Omega_{1}\) and \(\Omega_{2}\) in frictional contact, and a cohesive body \(\Omega_{3}\) between particles under different types of boundary conditions. a Initial configuration and b deformed configuration

Full size image

In the present PD model, both intra-body force densities denoted as \(f^{\mathrm{int}}\) within rock or cement bodies and inter-body cohesive force densities, \(f^{\mathrm{coh}}\), between rock particles and cement bodies are calculated by PD material model, and inter-particle fictional contact force densities \(f^{\mathrm{cont}}\) are determined by a touch-aware contact model. Let \({\varvec{x}} \in \Omega^{I}\) denote the coordinates of a material point, \(\user2{x^{\prime}} \in \Omega^{I}\) be the coordinates of a neighbour material point in \(H_{x}\) with \(\delta\) in the initial configuration and \({\varvec{y}}\) and \({\varvec{y}}^{\prime} \in \Omega^{D}\) be the coordinates of those material points in the deformed configuration.

The vector connecting material points \({\varvec{x}}\) and \({\varvec{x}}^{\prime}\) is called “bond” and denoted by \({\varvec{\xi}}\). States are mathematical objects mapping \({\varvec{\xi}}\) in \(H_{x}\) to some other quantities, such as vectors and scalars. Assume that \({\varvec{u}}\left( {{\varvec{x}},t} \right)\) is the displacement vector of point \({\varvec{x}}\) at time \(t\). The conservation of the linear momentum [2] is formulated in a total Lagrangian formulation as in Eq. (1):

$$\rho ({\varvec{x}})\ddot{u}({\varvec{x}},t) = f^{{{\text{int}}}} ({\varvec{x}},t) + b({\varvec{x}},t).$$
(1)

where \(\rho \left( {\varvec{x}} \right)\) is the mass density, \(f^{\mathrm{int}} \left( {{\varvec{x}},t} \right)\) is the internal force density field and \(b\left( {{\varvec{x}},t} \right)\) is an external body force field acting on a material point \({\varvec{x}}\) at time \(t\). \(b\left( {{\varvec{x}},t} \right)\) includes all force density fields acting on a material point \({\varvec{x}}\), such as \(f^{\mathrm{ext}}\), \(f^{\mathrm{coh}}\) and \(f^{\mathrm{cont}}\). Different PD material models are defined based on how \(f^{\mathrm{int}} \left( {{\varvec{x}},t} \right)\) is calculated.The ordinary state-based linear elastic PD was introduced in [51] in which the internal force density field (\(f^{\mathrm{int}} \left( {{\varvec{x}},t} \right)\)) and the cohesive force density (\(f^{\mathrm{coh}} \left( {{\varvec{x}},t} \right)\)) may be obtained from Eq. (2).

$$f^{{{\text{int}}}} ({\varvec{x}},t) = h(s,t)\mathop \int \limits_{{H_{x} }} \left\{ {{\varvec{T}}({\varvec{x}},t)\langle {\varvec{\xi}}\rangle - {\varvec{T}}(\user2{x^{\prime}},t)\langle {\varvec{\xi}}\rangle } \right\}{\text{d}}V_{x\prime } .$$
(2)

where \(dV_{x^{\prime}}\) denotes an infinitesimal volume around \(\user2{x^{\prime}}\) \(\in H_{x} ,\) and \(h\left( {s,t} \right)\) is a history-dependent scalar function which controls breakage of a single bond between \({\varvec{x}}\) and \(\user2{x^{\prime}}\) based on a bond stretch parameter \(s\) (see Sect. 2.2). \({\varvec{T}}\left( {{\varvec{x}},t} \right)\langle {\varvec{\xi}}\rangle\) is a vector state which represents the pairwise force density along \({\varvec{\xi}}\) acting on \({\varvec{x}}\). \({\varvec{T}}\left( {{\varvec{x}},t} \right)\langle {\varvec{\xi}}\rangle\) calculates the pairwise force density due to the relative deformation between two adjacent material points \({\varvec{x}}\) and \(\user2{x^{\prime}}\). Therefore, a non-local \(f^{\mathrm{int}} \left( {{\varvec{x}},t} \right)\) can be achieved by an integration over all material points within \(H_{x} .\) Different material models can be obtained based on how \({\varvec{T}}\) is defined and whether \({\varvec{T}}\) is in direction of \({\varvec{\xi}}\) or not. In this paper, the ordinary state-based linear elastic material model is considered to simulate the behaviour of rock particles and cementitious bodies. For an ordinary PD material model, \({\varvec{T}}\) is given by Eq. (3) [34].

$${\varvec{T}}\left( {{\varvec{x}},t} \right)\langle {\varvec{\xi}}\rangle = C\left( {{\varvec{x}},t} \right){\varvec{M}}\langle {\varvec{\xi}}\rangle ,$$
(3)

where \({\varvec{M}}\) is a unit state vector in direction of the position state vector from \({\varvec{x}}{ }\) to \(\user2{x^{\prime}}\), and \(C\left( {{\varvec{x}},t} \right)\) is a scalar coefficient. For a linear elastic material model \(C\left( {{\varvec{x}},t} \right)\) is given by Eq. (4).

$$C({\varvec{x}},t) = \frac{3K\theta }{m}\left( {\omega \langle {\varvec{\xi}}\rangle a\langle {\varvec{\xi}}\rangle } \right) + \frac{15G}{m}\left( {\omega \langle {\varvec{\xi}}\rangle e^{d} \langle {\varvec{\xi}}\rangle } \right).$$
(4)

where \(K\) and G are bulk and shear moduli of material, respectively. \(\theta\) and \(m\) are scalars called “dilation” and “weighted volume”, respectively, and \(\omega \langle {\varvec{\xi}}\rangle\) is a scalar state called “influence function” and defines the degree of interactions of material points. In fact, choice of the influence function controls the PD “surface effect”, meaning that if a material point is consumedly close to the surfaces of domain, its neighbourhood may not be completely spherical. Therefore, the influence of absent neighbours within the horizon must be considered [29]. \(a\langle {\varvec{\xi}}\rangle\) is a scalar state indicating the norm of \({\varvec{\xi}}\) and \(e^{d} \langle {\varvec{\xi}}\rangle\) is deviatoric part of the displacement scalar state \(e\langle {\varvec{\xi}}\rangle\). (For more details, see [34])

Time integration is one of the most principal parts of a numerical simulation. In this study, a central difference explicit time integration scheme has been formulated in PD. In the explicit time integration, the final response of a model is obtained through a sequence of calculations over small time step \((\Delta t)\) and it is suitable for simulations in which inertial effect and time-dependent phenomena are important [31].

2.2 PD damage model

The pairwise force density between \({\varvec{x}}\) and \(\user2{x^{\prime}}\) is denoted as \(f(s)\). The relative bond stretch \(s\) due to \(f(s)\) is defined by Eq. (5) [50].

$$s = \frac{{e\langle {\varvec{\xi}}\rangle }}{{a\langle {\varvec{\xi}}\rangle }}.$$
(5)

In PD formulation, the crack is initiated where the bond stretch exceeds a threshold value \(S_{\mathrm{c}}\); thus, the bond is called “broken”. Moreover, the propagation of the crack is defined as the coalescence of a chain of broken bonds. Therefore, initiation and propagation of cracks and the damage process are inherently defined in PD and no other constitutive relations is required. On the other hand, the relation between two material points is irreversibly terminated once a bond is broken; thus, \(h(s,t)\) in Eq. (2) may be defined according to Eq. (6).

$$h(s,t) = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if}}\; s < S_{\mathrm{c}} \;{\text{and}}\;t_{0} \le t \le t_{1} } \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right.,$$
(6)

where \([t_{0} ,t_{1} ]\) is the time history range. As shown in Eq. (7), assume \(\underline {\xi } = \left| {\varvec{\xi}} \right|\) and the work required to break a bond is \(w\left( \xi \right)\), therefore, according to Fig. 3, the total work \((G_{0} )\) needed to break all the bonds around a material point within a neighbourhood to initiate a unit area of crack surface can be achieved by Eq. (8) [50].

$$w\left( \xi \right) = \mathop \int \limits_{0}^{{S_{\mathrm{c}} }} f(s)\underline {\xi } {\text{d}}s,$$
(7)
$$G_{0} = \mathop \int \limits_{0}^{\delta } \mathop \int \limits_{0}^{2\pi } \mathop \int \limits_{z}^{\delta } \mathop \int \limits_{0}^{{\cos^{ - 1} \left( {{\raise0.7ex\hbox{$z$} \!\mathord{\left/ {\vphantom {z {\underline {\xi } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\underline {\xi } }$}}} \right)}} w\left( \xi \right)\underline {\xi }^{2} \sin \phi {\text{d}}\phi {\text{d}}\xi {\text{d}}\theta {\text{d}}z.$$
(8)
Fig. 3
figure 3

Calculation scheme of PD model for total energy required to break bonds within a horizon

Full size image

Since \(G_{0}\) is a function of \(S_{\mathrm{c}}\), its inverse may yield \(S_{\mathrm{c}}\). Therefore, \(S_{\mathrm{c}}\) is called “critical stretch” can be written in terms of the “energy release rate” \((G_{0} )\). It is the only parameter required to model damage process in PD. A closed-form prediction of \(S_{\mathrm{c}}\) for a 3D state-based PD model is presented in Eq. (9) [54].

$$S_{\mathrm{c}} = \sqrt {\frac{{G_{0} }}{{\left( {3G + \left( {{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}} \right)^{4} \left( {K - \left( {{\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \right)G} \right)} \right)\delta }}} .$$
(9)

As a criterion for demonstrating the local damage ratio of the material points in this article, a damage parameter \(\varphi\) is defined in Eq. (10) which is normalized in the range of [0,1].

$$\varphi (x,t) = \frac{{\mathop \int \nolimits_{{H_{x} }} h(s,t){\text{d}}V_{x\prime } }}{{\mathop \int \nolimits_{{H_{x} }} {\text{d}}V_{x\prime } }}.$$
(10)

Note that the choice of the critical bond stretch may depend on fracture patterns, crack size and crack location or orientation [61]. However, if the horizon (or element size) is fine enough, the critical stretch bond model can still be good for engineering applications.

2.3 The touch-aware non-local contact model

The contact force field plays a key role in simulation of the mechanical behaviour of CGMs. CGMs are known to have a densely packed initial configuration of rock particles with cement filled in between the particles. Therefore, in numerical simulations of CGMs, it is of great important for the contact model to have the capability of calculating the contact force field accurately enough for the densely packed particle system.

Most recently, a touch-aware contact model is developed [35] for PD simulations of contact force field in highly irregularly shaped particles. The advantages of the touch-aware contact model are summarized as follows:

  • It is appropriate for highly irregular, densely packed granular systems.

  • Contact calculation is triggered once two bodies are “in touch”. The contact force calculation is non-local, which is consistent with PD framework.

  • The contact model converges to theoretical solutions efficiently.

  • The contact model is “stiffer” than the conventional PD contact model that is based on the short-range force.

  • It can model frictional contacts with dynamic impact damping.

Figure 4 depicts a schematic of the touch-aware contact model. In the first step, radii of surficial material points of each contacting body are calculated. (Radius of material point \(x_{i}\) is denoted as \(r_{{x_{i} }}\).) Also, the normal contact vectors of surficial material points are determined (\({\mathbb{N}}_{{x_{i} }}\) for material point \(x_{i}\)). In the second step, the touch-aware algorithm looks for a material point like \(x_{i}\) in \({\Omega }_{1}\) called as a “direct contact point” and in touch with another material point \(x_{j}^{*}\) in \({\Omega }_{2}\). The neighbourhood \(H_{{x_{i} }}\) contains materials points (shades of red colours) in \({\Omega }_{1}\) within a radius of δ around \(x_{i}\). We define the contact neighbourhood \(L_{{x_{i} }}\) as the material points \(x_{j}\) (shades of green colours) in \({\Omega }_{2}\) within a contact radius of \(r_{{x_{i} }}^{c}\), as shown in Fig. 4.

Fig. 4
figure 4

Schematic of the touch-aware contact model

Full size image

Define a non-dimensional overlap ratio \(\Delta\) between the pair of material points in touch (\(x_{i}\) and \(x_{j}^{*}\)) (Eq. 11).

$$\Delta = \frac{{r_{{x_{i} }} + r_{{x_{j}^{*} }} - \left| {{\varvec{x}}_{i} - {\varvec{x}}_{j}^{*} } \right|}}{{\left| {{\varvec{x}}_{i} - {\varvec{x}}_{j}^{*} } \right|}}$$
(11)

The normal contact force density on \({\varvec{x}}_{i}\) is calculated by integrating its interaction with all \({\varvec{x}}_{j}\) in its contact neighbour \(L_{{{\varvec{x}}_{i} }}\) (Eq. 12) [35],

$$f_{n}^{{{\text{cont}}}} \left( {{\varvec{x}}_{i} } \right) = \frac{1}{2}\mathop \sum \limits_{j = 1}^{N} \frac{1}{{\left| {{\varvec{\xi}}_{ij} } \right|}}\left( {\frac{18s}{{\pi \delta^{4} }}} \right)\Delta \frac{{{\mathbb{N}}_{{{\varvec{x}}_{i} }} }}{{{\mathbb{N}}_{{{\varvec{x}}_{i} }} }} \forall {\varvec{x}}_{i} \in \Omega_{1} , \;{\varvec{x}}_{j} \in L_{{{\varvec{x}}_{i} }} ,\;j = 1,2,3 \ldots ,N,$$
(12)

where N is the number of material points in direct contact neighbourhood and \({\varvec{\xi}}_{ij}\) is the bond length between points \(x_{i}\) and \(x_{j}\). \(s\) is “contact stiffness” with the unit of force per length, \(\delta\) is the horizon and \(\frac{{{\mathbb{N}}_{{{\varvec{x}}_{i} }} }}{{{\mathbb{N}}_{{{\varvec{x}}_{i} }} }}\) is the unit outer-normal vector at the direct contact point. The above equation shows a non-local feature of the contact algorithm. Another non-local feature of the algorithm is that the contact force is also distributed to all material points \(x_{k}\) within \(H_{{x_{i} }}\), which are called “indirect contact points”, [35], i.e.

$$f_{n}^{{{\text{cont}}}} \left( {{\varvec{x}}_{k} } \right) = \frac{1}{2}\mathop \sum \limits_{j = 1}^{M} \frac{1}{{\left| {{\varvec{\xi}}_{kj} } \right|}}\left( {\frac{18s}{{\pi \delta^{4} }}} \right),\;\Delta \frac{{{\mathbb{N}}_{{{\varvec{x}}_{i} }} }}{{{\mathbb{N}}_{{{\varvec{x}}_{i} }} }} \quad \forall {\varvec{x}}_{k} \in H_{{{\varvec{x}}_{i} }} ,\;{\varvec{x}}_{j} \in (L_{{{\varvec{x}}_{i} }} \cap L_{{{\varvec{x}}_{k} }} ),\;j = 1,2,3 \ldots ,N$$
(13)

where M is the numbers of material points in indirect contact neighbourhood and \({\varvec{\xi}}_{kj}\) is the bond length between points \(x_{k}\) and \(x_{j}\). Note that the summation is over the overlapped region of two contact neighbourhoods around \({\varvec{x}}_{i}\) and \({\varvec{x}}_{k}\), i.e. \((L_{{{\varvec{x}}_{i} }} \cap L_{{{\varvec{x}}_{k} }} )\), which is called “indirect neighbourhood”.

Damping force density can be calculated using Eq. (14).

$$f_{{{\text{damp}}}}^{{{\text{cont}}}} \left( {{\varvec{x}}_{i} } \right) = {\mathfrak{c}}_{i} {\mathbb{v}}_{{{\varvec{x}}_{i} }} ,$$
(14)

where \({\mathfrak{c}}_{i}\) is the damping coefficient and \({\mathbb{v}}_{{{\varvec{x}}_{i} }}\) is the local velocity vector of the material point \({\varvec{x}}_{i}\). The fiction force density for a material point \({\varvec{x}}_{i}\) can be achieved by Coulomb’s law given in Eq. (15).

$$f_{{{\text{fric}}}}^{{{\text{cont}}}} \left( {{\varvec{x}}_{i} } \right) = \mu \left| {f_{n}^{{{\text{cont}}}} \left( {{\varvec{x}}_{i} } \right)} \right|{\mathbb{T}}_{{{\varvec{x}}_{i} }} ,$$
(15)

where \(\mu\) is friction coefficient and \({\mathbb{T}}_{{{\varvec{x}}_{i} }}\) is a unit vector normal to \({\mathbb{N}}_{{{\varvec{x}}_{i} }}\).

Finally, the total contact force density \((f^{{{\text{cont}}}} )\) is included in the body force term \(b\) in Eq. (1) and can be calculated using Eq. (16).

$$f^{{{\text{cont}}}} (x) = f_{n}^{{{\text{cont}}}} (x) + f_{{{\text{damp}}}}^{{{\text{cont}}}} (x) + f_{{{\text{fric}}}}^{{{\text{cont}}}} (x).$$
(16)

where \(f_{n}^{{{\text{cont}}}} (x)\), \(f_{{{\text{damp}}}}^{{{\text{cont}}}} (x)\) and \(f_{{{\text{fric}}}}^{{{\text{cont}}}} (x)\) are the normal contact force density, the damping force density and frictional contact force density, respectively. One can refer to [35] for detailed numerical implementation and validation of the “touch-aware” contact model.

3 Experimental tests on CGM

In this study, a set of CGM samples were prepared using different cementation percentages followed by a series of uniaxial compression tests conducted on these samples. As shown in Fig. 5a, the CGM is comprised of irregular rock particles with a size from 14 to 20 mm, washed and dried to make the initial packing of granular aggregates in a mould with an inner diameter and height of 100 and 200 mm, respectively. The rock particles are crushed granite with Young’s Modulus, Poisson’s ratio, uniaxial compressive strength and mass density of 55 GPa, 0.2, 150 MPa and 2780 kg/m3, respectively. As shown in Fig. 5b, the self-compaction cement was poured into the mould that cement the rock particles into a CGM. Two ends of the mould are kept open to flow the cement slurry from top to bottom, and a screen net and a container is placed beneath the mould to collect overflowed slurry and. After curing for 28 days in the wet room, the sample was ready for the uniaxial compression test, see Fig. 5c.

Fig. 5
figure 5

CGM sample preparation a rock particles, b pouring cement slurry into the sample in a mould, c a CGM sample in a cylindrical shape with a diameter of 100 mm and height of 200 mm

Full size image

In this research, the volume fraction of rock aggregates is in the range of 48 to 52% is obtained for all samples. To quantify the amount of cement used in each sample, the cement volume fractions \((\emptyset )\) are defined as the ratio of the volume of cement to the total volume of the sample. By controlling the viscosity of the cement, 38 samples were prepared with different cement volume fractions (5%, 10%, 15%, 20%, 25%, 30%, 40%, 45% and 50%), and 3 to 6 samples were prepared for each cement percentage. In addition, 4 samples purely from the cement slurry (without rock particles) were prepared to test the mechanical parameters of the cement matrix.

Figure 6 shows images of some prepared samples with different \(\emptyset\). A uniaxial servo control loading machine (MTS) is used to achieve the mechanical behaviour of CGM samples through uniaxial loading tests under a displacement rate control of 0.03 mm/min (see Fig. 7). Two MTS external linear variable differential transducers (LVDTs) with an initial gauge length of 100 mm are attached to lateral surfaces of samples to accurately measure the strain data.

Fig. 6
figure 6

Pictures of samples for experimental tests with different cement ratios \((\emptyset )\) (a)–(d)

Full size image
Fig. 7
figure 7

A picture of an experimental CGM sample under uniaxial loading by MTS machine. The extensometers are connected to the sample to record the strain accurately

Full size image

Two parameters, uniaxial compressional strength (UCS) \((\sigma_{c} )\) and Young’s modulus \((\overline{E})\), were obtained from each uniaxial compression test. \(\sigma_{c}\) is calculated based on the maximum stress the sample can tolerate and \(\overline{E}\) is the linear slope of the stress–strain curve at 50% of \(\sigma_{c}\). The first experimental test series are performed on three pure cement samples to obtain the averaged UCS and Young’s modulus of the cement. The tests reflect a complete brittle behaviour for the pure cement matrix with \(\sigma_{c}\) = 85 MPa and \(\overline{E}\) = 20 GPa can be obtained. The result of experimental tests on some of CGM samples is provided in Fig. 8. Also, plots of UCS and Young’s modulus of CGM samples versus different cement volume fractions \((\emptyset )\) are presented in Figs. 9 and 10, respectively.

Fig. 8
figure 8

Stress–strain plots of experimental tests for CGM samples in different cement volume fractions, \(\emptyset\)

Full size image
Fig. 9
figure 9

Uniaxial compressive strength versus cement volume fraction for experimental tests

Full size image
Fig. 10
figure 10

Young’s modulus versus cement volume fraction for experimental tests

Full size image

As shown in Fig. 9, UCS of experimental samples increases with a downward curvature as \(\emptyset\) increases up to 16.5%. Then, the increase in USC becomes linear to 36.5%. After 36.5% of the cement volume fraction, UCS dramatically increases. Young’s modulus of cement increases with a downward curvature up to 6.5% of cement volume fraction; afterwards, it increases with a uniform linear trend with \(\emptyset\) (see Fig. 10). In the next section, the results of PD simulations are demonstrated and compared to those of the experimental tests.

4 PD sample preparation

In this paper, an open-source PD software “Peridigm” [39] has been used to implement the program codes and conduct the numerical simulations. Peridigm is capable of performing parallel computations on the framework of the message passing interface (MPI) platform on multi-thread central processing units (CPUs). The hardware used in this research consists of a CPU of 20 threads with a calculation frequency of 5.3 GHz and 60 GB of memory.

4.1 Generation of irregular particles

In this section, the details of the numerical simulations of CGMs using the present PD model are provided. In the first step, rock particle geometries are created based on X-ray data points scanned directly from real rock particles (the first step). Then, the geometry of each particle is converted to 3D tetrahedron mesh as shown in Fig. 11a. The material points are placed in the centres of inspheres of tetrahedrons to form a particle, as shown in Fig. 11b.

Fig. 11
figure 11

Geometries of created rock particles with a tetrahedron meshes, b material points

Full size image

The second step of the numerical simulation process is creating densely packed aggregates of rock particles. It is the skeleton of CGM samples and plays a determinative rule in mechanical behaviour of CGMs. For this purpose, an initial cylindrical configuration of 70 rock particles is designed in which the rock particles with irregular shapes (created in the first step) are condensed to obtain a final configuration of densely packed aggregates under an isotropic body force field \(f\) so that \(\left| f \right| = \rho g\), where \(\rho\) is the density of rock particles and \(g\) is the gravitational acceleration. The diameter of the final configuration is 5 cm with a height of approximately 20 cm.

The mechanical properties of rock particles are based on those of Granite in Table 1. The touch-aware contact model with a normal stiffness (s) of 550 MN/m and a friction coefficient \((\mu )\) of 0.5 is used to simulate contact field between the rock particles. A rock volume fraction of 0.52 is achieved after condensation of the particles. Changing \(\mu\) to 0.4 or 0.45 will result in a slightly different rock volume fraction to 0.55 and 0.53, respectively, as shown in Fig. 12a–c. A contact damping ratio of 5% is applied to attenuate the dynamic vibrations and improve the stability of contact interactions. The 3D plots of contact force fields for three densely packed aggregates are illuminated in Fig. 12d–f.

Table 1 Mechanical properties and peridynamics simulation parameters of rock particles
Full size table
Fig. 12
figure 12

Densely packed aggregates of rock particles created using different frictional coefficients, a \(\mu\) = 0.4, b \(\mu\) = 0.45 and c \(\mu\) = 0.5, and their corresponding 3D plots of contact force in N for final condensing configurations (d), (e) and (f)

Full size image

4.2 Determination of critical stretch of the cement phase

Critical stretch is a key parameter to control the damage and failure of the cement phase. To calibrate this parameter, a pure cylindrical specimen of cement with diameter and height of 5 and 10 cm, respectively, is simulated using the present PD model. The properties of the cement phase used in the simulation are obtained directly from experimental tests, as listed in Table 2.

Table 2 Mechanical properties and peridynamics simulation parameters of cement
Full size table

A critical stretch \((S_{\mathrm{c}} )\) of 0.1 mm is determined such that the simulation results are in a good agreement with those of experimental tests in terms of UCS of the pure cement samples. Correspondingly, the energy release rate of the cement phase is determined, \(G_{c}\) = 760 J/m2 (see Eq. 9).

4.3 Cementation schemes

In the third step, cylindrical samples with diameter and height of 5 and 10 cm, respectively, are randomly truncated from the final configuration of condensed packings for cementation and uniaxial testing. Each test sample possesses about 42 rock particles.

Since bonding distribution and its bulk behaviour as well as the presence of discontinuities and defects in the sample are important controlling factors for the behaviour of CGMs, PD samples were created according to the following three different schemes.

  1. 1.

    CGMs with pure bonds

  2. 2.

    CGMs with bonds and clogs

  3. 3.

    CGMs with bonds, clogs and discontinuities

The details of each scheme are described in the following sections.

4.3.1 Scheme 1: CGMs with pure bonds

In scheme 1, cement bonds are generated between two rock particles if their shortest distance is smaller than a threshold value, which is considered to be 2 mm in this study. Since the particles are irregular, theoretically, the bond between them is also of an irregular shape. However, to simplify the modelling, each bond is idealized as a cylinder whose cross-sectional area is the same as the average contact area between particles. Figure 13 shows examples of cement bond objects between contacting particles.

Fig. 13
figure 13

Cement bond objects between two or more rock particles

Full size image

Finally, two circular platens are added to the ends of the samples. As show in Fig. 14, a CGM sample is created as a combination of rock particles and pure cement bonds. A total of 24 CGM samples with the cement volume fractions of 2%, 5%, 10%, 15%, 30% and 50% (4 samples each) are created by this scheme.

Fig. 14
figure 14

a A CGM sample with pure bonds (\(\emptyset = 5\%\)), b rock particles, c cement bonds

Full size image

4.3.2 Scheme 2: CGMs with bonds and clogs

To analyse the effect of bulk behaviour of the cement phase on CGMs, another scheme is created in this section so called “cement bonds and clogs”. The geometry of this scheme is created by assuming an initial volume fraction of perfect cement bonds equal to 2%. The rest of cement phase is dispersedly placed inside CGM samples as “cement clogs” to achieve the intended total cement volume fraction. In fact, connected voids between particles form complicated paths for the cement paste to flow through CGM samples. The bonds between particles are formed when the cement paste is initially flowing around contacting points. Because of constrictions in some paths, they might be blocked, form burgeons of clogs and grow in voids. Therefore, the cement clogs are that part of the cement phase that dispersedly fill voids between rock particles, not necessarily around the local contact points. Attention must be paid that clogs can include bonds. As the cement volume fraction increases, uniformly dispersed clogs in this scheme can grow and stick to each other or join the initial bonds to make them partially thicker or form a unified body or may be stayed separate if they are not close enough which make discontinuous clog bodies. The process of creating initial bonds is similar to Sect. 4.3.1. The geometry of clog objects is irregular shapes inspired by qualitative investigation on experimental samples randomly distributed within CGM samples (see Fig. 15).

Fig. 15
figure 15

An image of PD geometry of a CGM with bonds and clogs

Full size image

After creation of initial bonds around contact points between particles and clog objects, the volume of rock particles is subtracted from them using a Boolean operation. Figure 16 shows different phases of a CGM sample created in this scheme with rock particles, initial bonds and a clog body.

Fig. 16
figure 16

a Perfect clogged CGM sample (\(\phi = 15\%\)) including rock particles (b), perfect cement bonds (c) and a clog body (d)

Full size image

In total, 22 CGM samples with the cement volume fractions of 6.5%, 11.5%, 16.5%, 21.5%, 26.5% and 36.5% are created in this scheme.

4.3.3 Scheme 3: CGMs with bonds, clogs and discontinuities

As the cement volume fraction increases, the number and volume of dispersed clog objects increase and more paths between particles are blocked. Therefore, with the increase in the cement volume fraction, the possibility in forming discontinuities increases. A qualitative investigation on the cross sections of experimental CGM samples has shown that at least one discontinuity is clearly observable in CGM samples in a range of cement volume fraction between 25 and 45% (Fig. 17). Therefore, the effect of discontinuities in CGM samples in this range must be considered.

Fig. 17
figure 17

A clear discontinuity through clogs and defects in bonds (highlighted in red) in CGM samples with \(\emptyset\) = 30%

Full size image

The effect of discontinuities in forming bonds and clogs in CGMs is considered in this scheme. The distribution of burgeons of clogs in this scheme is not uniform. The burgeons of clogs are distributed randomly in some clusters which are deliberately distanced from each other to make pre-existed discontinuities. The following procedure is used to create the CGM samples in this scheme:

  1. I.

    Initial bonds with a cement volume fraction of 2% is created in all contact points between rock particles (see Sect. 4.3.2).

  2. II.

    The remaining part of cement volume fraction of the matrix is placed by adding clog objects dispersedly distributed within distanced clusters to the geometry of CGM samples.

  3. III.

    The bond and clog objects are scaled with a factor.

  4. IV.

    The volume of rock particles is subtracted from bond and clog objects with a boolean operation.

  5. V.

    If the total volume fraction of the cement matrix is obtained, the process is finished; otherwise, stage IV is followed.

The initial bonds and clog objects can make heterogenous bonds and at least one discontinuity (two clusters) is considered through CGM samples in this scheme. Discontinuities of the clog objects satisfy defects in the physics of the cement matrix; however, the CGM samples make a unified geometry with bonds and clogs sticking to rock particles. Figure 18 shows schematics of a CGM with rock particles, defected bonds and discontinuous clogs in this scheme.

Fig. 18
figure 18

a Defect clogged CGM sample (\(\phi = 26.5\%\)) including rock particles (b), defect cement bonds (c) and discontinuous clogs (d)

Full size image

In total, 20 samples are created in this scheme with different cement volume fractions including: 16.5%, 21.5%, 26.5%, 36.5% and 41.5% (4 samples each) while the rock volume fraction is kept constant equals to 50%.

5 PD simulation of cemented granular materials using different cementation schemes

5.1 Simulations of scheme 1

The PD simulations of this scheme are performed using different cement volume fractions of 2%, 5%, 10%, 15%, 30% and 50% while the volume fraction of rock particles is kept as 50%. To account for randomness of the samples, the samples are created for each cement volume fraction (24 samples in total) (see Sect. 4.3.1). In fact, all samples have three phases: rock particles, cement matrix and voids, except that the samples with cement volume fraction of 50% have only two phases (rock particles and cement matrix) because the voids are filled by the cement. The material model of rock and cement phases is modelled by linear elastic ordinary state-based PD.

In scheme 1, it is assumed that the cement body is idealized as cylinders and bond two rock particles in a close distance. The “touch-aware” contact model is used to model frictional contact with damping between the rock particles. The loading platens are modelled as elastic materials much stiffer than both the rock particles and the cement. The mechanical parameters of the simulations are provided in Table 3.

Table 3 Mechanical and operational parameters of PD simulation on CGM samples
Full size table

The simulations are performed in a uniaxial compressional strain-controlled mode with a strain rate of 0.01 s−1.

5.2 Simulations of scheme 2

PD simulations are performed using scheme 2, where cements are assumed to form perfectly distributed cement bonds and randomly generated clogs. Numerical samples were created in this scheme with different cement volume fractions \((\phi )\) including: 6.5%, 11.5%, 16.5%, 21.5%, 26.5% and 36.5% (see Sect. 4.3.2). The volume fraction of rock particles is kept constant to 50% and 3–5 samples are created for each cement volume fraction, which gives 22 samples in total. The material model, contact model and the simulation parameters are the same as Sect. 5.1.

5.3 Simulations of scheme 3

In total, 20 samples are prepared for PD simulations using scheme 3. The cement volume fractions of the samples are 16.5%, 21.5%, 26.5%, 36.5% and 41.5%, respectively. Again, the material model, contact model and the simulation parameters are the same as Sects. 5.1 and 5.2. Figure 19 shows complete stress–strain curves, and Fig. 20 depicts 3D plots of the damage parameter \((\varphi )\) at the failure moment of all samples and surface of fracture for typical samples, respectively.

Fig. 19
figure 19

Stress–strain plots of PD simulation for defect clogged CGM samples in different cement volume fractions, \(\emptyset\)

Full size image
Fig. 20
figure 20

3D damage \((\varphi )\) plots of defect clogged CGM samples for different cement volume fractions \(\phi\)

Full size image

Note that scheme 3 introduced defects into the cement bonds and clogs. Under this scheme, the simulated UCS and Young’s modulus are presented in Figs. 21 and 22, respectively. A good agreement between the PD simulations and experiments can be observed for all cement volume fractions in the range between 16.5 and 41.5%.

Fig. 21
figure 21

Uniaxial compressive strength versus cement volume fraction for defect clogged CGM simulations compared to pure bonded CGM, perfect clogged CGM and experimental results

Full size image
Fig. 22
figure 22

Young’s modulus compressive strength versus cement volume fraction for defect clogged CGM simulations compared to pure bonded CGM, perfect clogged CGM and experimental results

Full size image

6 Discussion

From the results provided in Sects. 4 and 5, it is understood that the skeleton of a CGM consists of packed aggregate of rock particles with irregular shapes and occupies roughly 50% of total volume of a CGM sample. In the PD simulations, adjusting the friction coefficient of the contact between the rock particles can slightly affect this volume fraction of the generated packings. The increase in the friction coefficient between the rock particles leads to the decrease in the rock volume fraction.

PD analyses were carried out based on three different schemes for cement phase distribution. Then, the mechanical behaviour of CGMs was simulated under different cement volume fractions. Scheme 1 assumed that all cement bonds are perfectly formed between two particles wherever they are close enough. As shown in Figs. 21 and 22, a roughly bilinear trend (stages OB and BC) can be seen in both mechanical properties (UCS and Young’s modulus) of CGMs. The simulations show that the mechanical properties of CGMs (UCS and Young’s modulus) are initially controlled by pure perfect cement bonds between the particles up to approximately 2% of the cement volume fraction (OA). The uniaxial compression strength and Young’s modulus of CGM increase most significantly with the cement fraction up to 16.5% (OB). Beyond this volume fraction, cement bonds begin to connect to each other within CGMs. The increase in the cement amount has a reduced effect on the increase in the compressive strength and modulus of the CGMs (BC). Obviously, scheme 1 significantly overestimates the strength and modulus of CGMs when the cement volume fraction is greater than 2%.

In scheme 2, the mechanical behaviour of CGMs has three distinctive stages (AD, DE and EC). For cement ratios less than 11.5% (AD), the clog bodies are small and dispersedly distributed. The increase in the compressive strength and Young’s modulus is much smaller as compared to scheme 1, but the simulations fit better to the experimental results. From cement volume fraction of 11.5% to 26.5% (DE), burgeons of clog continue to grow larger and form connected clogs. During the stage DE, the compressive strength and Young’s modulus increase most significantly with the increase in cement volume fraction. After that (stage EC), the remaining voids are filled up with cement, and the slope of UCS/Young’s modulus change decreases. Note that scheme 3 considerably overestimates the experimental results in the stages DE and EC.

Scheme 3 is similar to scheme 2, but the distribution of the clog burgeons is heterogeneous such that they are randomly distributed in distanced clusters and “discontinuities” pre-existed in CGMs. Attention must be paid that the point D is where the clogs gradually start to connect to each other. For cement volume fraction from 11.5 to 36.5% (DF), the discontinuities partially prevent connecting cement clogs to each other. Therefore, these discontinuities form weak surfaces in which only heterogeneous bonds can make chains of load transfer through CGMs. The slope of the stage DF is similar to that of scheme 2 (AD). As cement volume fraction increases, all discontinuities are gradually closed and stronger chains of load transfer are created through clogs. When it is greater than 36.5% (FC), the last discontinuity (the weak surface of CGM) closes rapidly and significant increases in compressive strength and Young’s modulus can be observed, until the CGM is completely filled with cement (\(\emptyset\) = 50%).

Figure 23 shows the computational time of all simulations (schemes 1, 2 and 3) with different cement volume ratios on a computer with a 20-core CPU of 5.3 GHz. As shown in the figure, the computational time linearly increases with an increase in cement volume ratio up to 20%, due to the increasing number of material points needed for modelling the cement phase. Above 20%, the cement bodies start to merge and connect with each other, reducing the overall complexity of shapes. Therefore, similar amount of material points can be used in simulations for cement ratios of above 20%, and the averaged computational time is about 150 h for each case.

Fig. 23
figure 23

Computational time of the simulations performed using the present PD model for all samples (pure bonded, perfectly clogged and defectively clogged) with different cement volume ratios

Full size image

7 Conclusions

In this paper, a new PD model is developed to investigate the mechanical behaviour of CGMs in terms of two important parameters: Young’s modulus and UCS. Different steps of modelling CGMs consist of condensing the rock particles with irregular shapes, creation of the cement matrix geometry (bonds and clogs), uniaxial loading and failure of CGMS are accurately modelled in comparison with the experimental tests. The experimental CGM samples consist of an initial packings of granite rock particles with a volume fraction of 50% cemented by a self-compacting cement. A series of uniaxial loading tests have been performed on the samples to achieve the stress–strain curves. The PD model with the touch-aware contact algorithm simulates CGMs with different phases (rock, cement and voids) and mechanical phenomena including the bulk behaviour and deformability of rock particles and cement matrix, frictional contact force field between rock particles, cohesive force field between cement and rock particles and damage/failure process of CGMs. The results demonstrate that the mechanical behaviour of CGMs is highly affected by the cement volume fraction. In cement volume fractions less than 2%, the mechanical behaviour of CGMs is mainly controlled by pure bonds. In cement volume fractions from 2 to 12%, their behaviour is governed by clogs. In more than 12% of cement volume fraction, discontinuities gradually become more effective. The research is ongoing on considering the effect of other physical parameters on the mechanical parameters of CGMs.