1 Introduction

Natural soft clays exhibit significant creep under both laboratory and in situ conditions after primary consolidation [2, 3, 7, 9, 10, 15, 17, 19, 27, 29–32, 34]. In early days, this was often called “secondary consolidation.” The term “creep” is preferable because it is referred to the compression of soil skeleton under a constant loading, having nothing to do with consolidation [28]. The creep coefficient, defined as C αe = Δe/Δlogt based on one-dimensional creep testing, is a key parameter for engineering practice and viscoplastic modeling [1, 11, 12, 26, 29, 32, 33]. Thus, it is important to evaluate this coefficient with accuracy.

Many studies on the characteristics of the creep have been carried out through one-dimensional creep tests on both reconstituted and intact natural clay samples. For reconstituted clay, the value of C αe varies with the void ratio. For instance, Yin [27] and Yin et al. [30] formulated a nonlinear expression of C αe function of volumetric strain and time under applied stresses considering the density or void ratio of soils. More recently, Yin et al. [34] proposed in a more precise way a linear decrease in C αe with the void ratio in a double logarithm plane based on results on various reconstituted clays. For intact natural soft clays, the value of C αe depends highly on the destructuration, as demonstrated by Karstunen and Yin [10], Leroueil et al. [15], Mesri and Godlewski [17] and Yin et al. [33], etc. Therefore, C αe is generally not constant but dependent on both the void ratio and the soil structure (or inter-particle bonding and debonding) of soft soils. However, few studies have been devoted to a quantitative description of the nonlinear evolution of C αe due to changes of both soil density and soil structure in natural soft clays. Furthermore, for correlating C αe to clay physical properties (e.g., Atterberg limits), an average value or the value of C αe corresponding to a final high stress level in conventional oedometer tests has usually been adopted. Since C αe is not a constant, it is necessary to seek a reference value of C αe to re-establish the correlation.

In this study, therefore, we focus on the quantitative description of the evolution of C αe with both void ratio and soil structure under the condition of applied stresses exceeding the yield stress. For this purpose, available test results on intact and reconstituted samples of natural soft clays are selected for analyses. We also carry out conventional consolidation tests on reconstituted and intact samples of several clays for expanding our data base. The values of C αe corresponding to liquid and plastic limits (C αeL, C αeP) are then estimated as reference values, based on which C αe could be expressed as a function of one of the reference values C αef (=C αeL or C αeP), the water content (w) and the inter-particle bonding (χ). Furthermore, correlations could be established in order to estimate the value of C αe from Atterberg limits for a given natural soft clay. Then, the proposed function is validated by comparing the estimated and experimental C αe values.

2 Nonlinear creep related to soil density

2.1 Experimental evidence

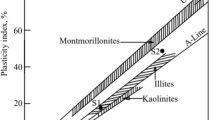
Conventional consolidation tests on various soft clays with different mineral contents and Atterberg limits were selected for this study. In this section, all the selected data are based on reconstituted samples to eliminate the influence of soil structure. Some physical properties of the selected clays are summarized in Table 1. According to the chart shown in Fig. 1, the selected soils consist of low plastic clays, high plastic inorganic clays and high plastic silty clays. Since the void ratio (e) is a physical state of soils representing the soil density and the deformation potential, the C αe values for all the selected clays are individually plotted against the void ratio in a double logarithmic plane, presented in Fig. 2. All the results show that log(C αe) is linearly related to log(e).

Table 1 Summary of creep coefficient of reconstituted clays under normally consolidated state
Full size table
Fig. 1
figure 1

Classification of soils by liquid limit and plasticity index

Full size image
Fig. 2
figure 2

Creep coefficient versus void ratio in double logarithmic scale for different reconstituted clays

Full size image

2.2 Nonlinear creep formulation accounting for void ratio

The consideration of the density and void ratio has been addressed by Yin [27] based on Hong Kong marine clay. Based on the results in Fig. 2, the nonlinear creep formulation based on Finnish clays proposed by Yin et al. [34] can be adopted:

$$ {{C_{{\upalpha{\text{e}}}} } \mathord{\left/ {\vphantom {{C_{{\upalpha{\text{e}}}} } {C_{{\upalpha{\text{ef}}}} }}} \right. \kern-0pt} {C_{{\upalpha{\text{ef}}}} }} = \left({e \mathord{\left/ {\vphantom {e {e_{\text{f}} }}} \right. \kern-0pt} {e_{\text{f}} }}\right)^{m} $$
(1)

where C αef and e f are reference values of C αe and e, respectively (the initial in situ void ratio e 0 was used as e f by Yin et al. [34]) and m is a material constant representing the slope of the log(C αe)–log(e) curve which can be measured in a straightforward way (summarized in Table 1 for all clays). It is worth noting that C αe is conventionally defined as the slope of the secondary compression line with the logarithm of time, which is reasonable for design purpose in civil engineering, but resulting in a negative void ratio during creep under long periods of time, whereas Eq. (1) imposes a value of e converging toward zero but remaining always positive.

The reference point (C αef, e f) can be arbitrary selected. However, it could be of interest to select specific values of the reference void ratio. The void ratio at the liquid or plastic limit (e L or e P) is usually adopted to establish the equations for compressibility [20, 21]. These two values can be easily determined from the liquid or plastic limits w L and w P which are usually available physical properties of clayey soils. Along these lines, two representative points (corresponding to e L and e P) on the log(C αe)–log(e) curve can be alternatively used as reference points. Based on Fig. 2, both C αeL and C αeP corresponding to the void ratios e L and e P can be obtained and Eq. (1) can be rewritten as

$$ C_{{\upalpha{\text{e}}}} = C_{{\upalpha{\text{eL}}}} \left( {{e \mathord{\left/ {\vphantom {e {w_{\text{L}} G_{\text{s}} }}} \right. \kern-0pt} {w_{\text{L}} G_{\text{s}} }}} \right)^{m} \quad {\text{or}}\,C_{{\upalpha{\text{e}}}} = C_{{\upalpha{\text{eP}}}} \left( {{e \mathord{\left/ {\vphantom {e {w_{\text{P}} G_{\text{s}} }}} \right. \kern-0pt} {w_{\text{P}} G_{\text{s}} }}} \right)^{m} $$
(2)

3 Nonlinear creep related to soil structure

3.1 Experimental evidence

During conventional consolidation tests on intact samples of natural soft clays, the shape of the post-yield compression curve is significantly influenced by the debonding process during straining [10, 13, 23]. Figure 3 shows the schematic plot of the compression curves of intact and reconstituted clay samples. For a given inelastic strain level Δe p, the bond degradation results in the current stress \( \sigma_{\text{v}}^{\prime } \) reaching point A instead of point B (assuming no destructuring). Corresponding to stress \( \sigma_{\text{v}}^{\prime } \) at Δe P, we define an intrinsic stress \( \sigma_{\text{vi}}^{\prime } \), which is the stress for a reconstituted sample at the same inelastic strain increment (point C). Based on this plot, a bonding ratio can be defined by \( \chi = {{\sigma_{\text{v}}^{{\prime }} } \mathord{\left/ {\vphantom {{\sigma_{\text{v}}^{{\prime }} } {\sigma_{\text{vi}}^{{\prime }} - 1}}} \right. \kern-0pt} {\sigma_{\text{vi}}^{{\prime }} - 1}} \) with an initial bonding ratio of \( \chi_{0} = {{\sigma_{{{\text{p}}0}}^{{\prime }} } \mathord{\left/ {\vphantom {{\sigma_{{{\text{p}}0}}^{{\prime }} } {\sigma_{{{\text{pi}}0}}^{{\prime }} - 1}}} \right. \kern-0pt} {\sigma_{{{\text{pi}}0}}^{{\prime }} - 1}} \) (similar to Gens and Nova [8]; Yin et al. [33, 34]). When the strain increases, the inter-particle bonds are progressively broken and χ decreases from its initial value χ 0 toward zero, corresponding to a state where all the bonds are completely destroyed, as shown in Fig. 3.

Fig. 3
figure 3

Definition of the amount of inter-particle bonds

Full size image

Adopting this concept, we consider that the difference between the values of C αe at point A and point C is due to the effect of soil structure. Defining the creep coefficients C αe(I) and C αe(R) at points A and C (Fig. 3), the additional creep induced by destructuration (or inter-particle debonding) can be written as:

$$ \Delta C_{{\upalpha{\text{e}}}} = C_{{\upalpha{\text{e}}}} \left( I \right) - C_{{\upalpha{\text{e}}}} \left( R \right) $$
(3)

3.2 Nonlinear creep formulation accounting for soil structure

To investigate the contribution of soil structure on C αe, conventional consolidation tests on both intact and reconstituted clay samples of the same clay are necessary. Table 2 summarizes the available results of 1D creep tests on both intact and reconstituted samples of ten different clays (corresponding to the first ten clays in Table 2, including the tests on Shanghai clay performed in this study). The classification of these clays is shown in Fig. 1.

Table 2 Summary of creep coefficient of intact clays under normally consolidated state
Full size table

Figure 4 presents the plots of C αe(I) with the bonding ratio χ, where C αe(I) in these graphs was directly measured from tests on intact clays. Note that C αe(R) was estimated by Eq. (1) from experimental data on reconstituted clays at the corresponding void ratio (point C in Fig. 3) and served as the reference for the effect of destructuration. It can be seen that C αe(I) decreases linearly with the decreasing of χ in a logarithmic scale. Based on the concept used to define χ (Fig. 3), we can express the contribution of the soil structure to the creep coefficient by the index ρ:

$$ \rho = {{C_{{\upalpha{\text{e}}}} \left( I \right)} \mathord{\left/ {\vphantom {{C_{{\upalpha{\text{e}}}} \left( I \right)} {C_{{\upalpha{\text{e}}}} \left( R \right)}}} \right. \kern-0pt} {C_{{\upalpha{\text{e}}}} \left( R \right)}} - 1\, {\text{or}}\,\rho = {{\Delta C_{{\upalpha{\text{e}}}} } \mathord{\left/ {\vphantom {{\Delta C_{{\upalpha{\text{e}}}} } {C_{{\upalpha{\text{e}}}} \left( R \right)}}} \right. \kern-0pt} {C_{{\upalpha{\text{e}}}} \left( R \right)}} $$
(4)

where ρ is always positive. In order to investigate the relation between ρ and χ, values of ρ for all the selected clays were estimated by Eq. (4) and plotted versus χ in Fig. 5. It can be observed that ρ presents a linear relationship with log(χ), which can be expressed as:

$$ \rho = n\log \left( {{\chi \mathord{\left/ {\vphantom {\chi {\chi_{0} }}} \right. \kern-0pt} {\chi_{0} }}} \right) + \rho_{0} $$
(5)

where n is a material constant representing the slope of the ρ–log(χ) curve, ρ 0 is the initial value of ρ corresponding to χ = χ 0 and ρ decreases from ρ 0 toward zero when all the bonds are completely destroyed.

Fig. 4
figure 4

Creep coefficient of intact and reconstituted clays versus bonding ratio

Full size image
Fig. 5
figure 5

Inter-particle debonding induced creep versus normalized bonding ratio

Full size image

Substituting Eqs. (1) and (5) into Eq. (4), the creep coefficient for intact natural soft clays can be written as:

$$ C_{{\upalpha{\text{e}}}} = \left( {n\log \left( {{\chi \mathord{\left/ {\vphantom {\chi {\chi_{0} }}} \right. \kern-0pt} {\chi_{0} }}} \right) + \rho_{0} + 1} \right)C_{{\upalpha{\text{ef}}}} \left( {{e \mathord{\left/ {\vphantom {e {e_{\text{f}} }}} \right. \kern-0pt} {e_{\text{f}} }}} \right)^{m} $$
(6)

Equation (6) indicates that C αe depends on the material constants C αef, e f, m, χ 0, ρ 0, n and the current state variables χ and e. As described earlier, e L or e P can be used as e f, and the corresponding values C αeL or C αeP obtained from Fig. 2 can be used as C αef. The material constants C αef, e f, m can be determined from tests on reconstituted clay and χ 0, ρ 0, n from tests on both reconstituted and intact clays. Note that all material constants can be determined from conventional oedometer tests in a straightforward way.

The creep behavior is closely connected to the micro-properties of clay, such as the shape of particle, the inter-/intra-aggregate pore size distribution and the double layer, which can be characterized by Atterberg limits [18]. Thus, the correlations between material constants relating to creep (Eq. 6) and Atterberg limits were investigated based on available results, considering that such correlations would be useful for engineering practice.

4 Correlations of nonlinear creep properties with Atterberg Limits

4.1 Correlations of CαeL and CαeP with Atterberg Limits

For correlating C αeL and C αeP with Atterberg limits, the available test results on 15 reconstituted clays (with tests on three clays performed in this study) listed in Table 1 were selected. Figure 6a, b presents the plots of C αeL with Atterberg limits, from which the following relation could be obtained with a correlation coefficient R 2 = 0.9336:

$$ C_{{\upalpha{\text{eL}}}} = 0.0007w_{\text{L}} - 0.0223 $$
(7)
Fig. 6
figure 6

Relationship between reference creep coefficients and Atterberg limits

Full size image

Similarly, Fig. 6c, d shows the correlations for C αeP indicating that the optimized correlation is obtained by using both the liquid limit and the plasticity index with a correlation coefficient R 2 = 0.6913:

$$ C_{{\upalpha{\text{eP}}}} = 0.0013w_{\text{L}} - 0.0013I_{\text{p}} - 0.0209 $$
(8)

From these correlations, it appears that the choice of C αeL as the reference value for C αe in Eqs. (2) and (6) is preferable given the higher correlation coefficient. Thus, the C αeL with w L can be used as reference in Eq. (6), and the Eq. (6) is rewritten as,

$$ C_{{\upalpha{\text{e}}}} = \left( {n\log \left( {{\chi \mathord{\left/ {\vphantom {\chi {\chi_{0} }}} \right. \kern-0pt} {\chi_{0} }}} \right) + \rho_{0} + 1} \right)C_{{\upalpha{\text{eL}}}} \left( {{w \mathord{\left/ {\vphantom {w {w_{\text{L}} }}} \right. \kern-0pt} {w_{\text{L}} }}} \right)^{m} $$
(9)

4.2 Correlation of m with Atterberg Limits

Based on all the estimated values of m shown in Eq. (6) for 15 reconstituted clays, the correlations between m and Atterberg limits were fitted. Figure 7 shows that the optimized correlation is obtained by using both liquid limit and plasticity index with a correlation coefficient R 2 = 0.5217:

$$ m = 0.7872 - 0.0369w_{\text{L}} + 0.0619I_{\text{P}}. $$
(10)
Fig. 7
figure 7

Relationship between m and Atterberg limits

Full size image

4.3 Correlation of n with Atterberg Limits

Figure 8 presents the correlations between the material constant n shown in Eq. (6) and Atterberg limits based on test results on both intact and reconstituted samples of ten clays. It can be observed that the magnitude of n decreases with the increase in the liquid limit or plasticity index. Furthermore, the values of n are shown to relate better with the liquid limit and plasticity index with a correlation coefficient R 2 = 0.6300:

$$ n = 2.4630 - 0.0585w_{\text{L}} + 0.0532I_{\text{P}}. $$
(11)
Fig. 8
figure 8

Relationship between n and Atterberg limits

Full size image

4.4 Correlation of ρ 0 with Atterberg Limits

As mentioned above, ρ 0 is the initial value of ρ corresponding to χ = χ 0 and it represents the secondary compression potential induced by debonding. Consequently, a certain relation between ρ 0 and χ 0 can be observed. Hence, the link between the ratio ρ 0/χ 0 and Atterberg limits was analyzed from the test results on both intact and reconstituted samples of ten clays. Based on the findings, ρ 0/χ 0 can be expressed either by the liquid limit (Fig. 9a), or the plasticity index (Fig. 9b), or also by a unified expression with the liquid limit and the plasticity index (Fig. 9c). We adopted the latter expression with a correlation coefficient R 2 = 0.7641:

$$ {{\rho_{0} } \mathord{\left/ {\vphantom {{\rho_{0} } {\chi_{0} }}} \right. \kern-0pt} {\chi_{0} }} = 2.34\exp \left( { - 0.047w_{\text{L}} } \right) $$
(12)
Fig. 9
figure 9

Relationship between ratio ρ 0/χ 0 and Atterberg limits

Full size image

5 Discussions

5.1 Correlation between I P with w L

A certain relationship between I P and w L is apparent. In the past, several expressions have been proposed such as the ones by Burland [4] with I P = 0.73(w L − 20) and Biarez and Hicher [5] with I P = 0.73(w L − 13). Figure 10 presents the plots of these two parameters for the clays selected in this study together with the two lines representing the above correlations. The differences between these two lines and the experimental points are rather small, and we could consider one or the other correlation for our own materials. In order to remain as close as possible to our set of data, we chose to adopt the following best correlation represented in Fig. 10 by the bold line with a correlation coefficient R 2 = 0.9587:

$$ I_{\text{P}} = 0.8381w_{\text{L}} - 16.438 $$
(13)

Using Eq. (12), the above correlations of parameters with Atterberg limits can be simplified.

Fig. 10
figure 10

Relationship between plasticity index and liquid limit

Full size image

5.2 How to determine nonlinear creep

Over all, if the current water content (w), the bonding ratio (χ) and the liquid limit (w L) of the clayey soil are known, the current C αe can be obtained with the following process:

  1. 1.

    Substituting w L into Eqs. (7), (12) and (13), C αeL, ρ 0/χ 0 and I p are obtained, respectively.

  2. 2.

    With w L and I p, m and n can be obtained by Eqs. (10) and (11), respectively.

  3. 3.

    The initial bonding ratio χ 0 can be taken equal to (S t − 1) according to Karstunen and Yin [10] and Yin et al. [32] with S t the soil sensitivity, and then ρ 0 can be obtained since ρ 0/χ 0 is known from the first step of process.

  4. 4.

    Substituted all above correlated parameters into Eq. (9), C αe is obtained.

Note that w and χ are two state variables representing current soil density and current soil structure, respectively. Thus, Eq. (9) accounts for the soil density and the soil structure during straining with clear physical meaning, and can be of practical use for determining simply the creep potential of a given natural soft clay.

5.3 Validation for reconstituted clays

For reconstituted clays, the structure between particles is eliminated; therefore, χ 0 can be regarded null. Consequently, a reduced form of Eq. (9) for reconstituted clays can be written as:

$$ C_{{\upalpha{\text{e}}}} = \left( {0.0007w_{\text{L}} - 0.0223} \right)\left( {{w \mathord{\left/ {\vphantom {w {w_{\text{L}} }}} \right. \kern-0pt} {w_{\text{L}} }}} \right)^{{0.014978w_{\text{L}} - 0.23031}} $$
(14)

Figure 11 shows the comparison between experimental and predicted results estimated by Eq. (14) for all the selected clays. Despite there are some discrepancies between measured and estimated values, Eq. (14) generally describes the evolution of C αe for reconstituted clays fairly well. We illustrated the influence of w L on C αe in Fig. 12. Because the maximum and minimum values of w L in Table 1 are 90 and 40 %, we plotted the evolution of C αe with water content for two clays having these liquid limits. It can be seen that the clay with a higher w L presents a higher increasing rate and that C αe decreases with the decreasing water content (i.e., decreasing void ratio) for each clay.

Fig. 11
figure 11

Comparison of measured and estimated values of C αe for reconstituted clays

Full size image
Fig. 12
figure 12

Evolution of C αe with water content for liquid limit equal to 40 and 90 %

Full size image

5.4 Validation for intact clays

For the ten intact clays shown in Fig. 4, the predicted values of C αe were estimated by Eq. (9) with the liquid limit w L and the structural parameter χ 0 listed in Table 2. Figure 13 compares experimental and predicted results in a 3D form (C αe–w–χ). It can be concluded that Eq. (9) is able to estimate with good accuracy the evolution of C αe for the majority of the studied clays. For the others, even if differences between measured and estimated values still remain (e.g., Lianyungang clay), the trend is well captured.

Fig. 13
figure 13

Comparison of measured and estimated values of C αe for intact clays

Full size image

Furthermore, the proposed formulation (Eq. 9) was examined on predicting the evolution of void ratio with time during creep. For this, long-term oedometer tests on Vanttila and Wenzhou intact clays, with strong and moderate level of soil structure, were selected. Only parts of curves apparently after consolidation or dissipation of excess pore pressure were plotted for both computed and measured results in Fig. 14. Curves by using constant C αeL were also computed shown by dash lines for comparison. The computed void ratio by Eq. (9) decreases nonlinearly with time in logarithm scale for each loading shown by solid lines, which demonstrates that the proposed formulation can well capture the nonlinear creep degradation.

Fig. 14
figure 14

Comparison of measured and computed void ratio versus time on two intact clays

Full size image

6 Conclusions

The one-dimensional creep characteristics of soft clays have been investigated based on experimental results from oedometer testing. The evolution of C αe for reconstituted and intact clays was studied.

For reconstituted clays, the influence of the soil structure could be eliminated. A nonlinear creep behavior has been observed with C αe decreasing when the soil density increases. Based on these results, a simple nonlinear creep formulation was adopted with an additional parameter of nonlinearity m. For simplification and practical use, C αeL (corresponding to the liquid limit) and C αeP (corresponding to the plastic limit) were suggested as the reference C αe.

The bond degradation process during straining exerts a significant influence on the values of C αe. The significant difference of C αe between intact and reconstituted clays was analyzed. The ratio of C αe between intact clay and the corresponding value for reconstituted clay was related to the bonding ratio with an additional parameter n, leading to a nonlinear creep formulation accounting for soil structure.

The proposed formulation of C αe for intact clays contains five material constants C αeL, C αeP, m, n and ρ 0, which can be determined in a straightforward way from conventional oedometer testing. Furthermore, correlations between these material parameters and Atterberg limits were proposed based on available data. By expressing the material constants as functions of the liquid limit and the plasticity index, we are able to suggest a practical expression of C αe as a function of the current water content w, the bonding ratio and the physical properties of the clay. These correlations allow the determination of the material constants from the sole knowledge of the liquid limit of a given clayey soil. Its capacity of estimating the C αe values of various clays has been demonstrated, and accurate estimations of the one-dimensional creep characteristics of both reconstituted and natural soft clays were obtained. Furthermore, the proposed formulation is also validated by comparing the computed and measured void ratio with time on two intact clays.

This study provides a simple way of estimating the creep coefficient of natural clays, which can be of practical use in geotechnical engineering. Since it is a key parameter for many creep modeling approaches, the creep coefficient can be used as a state variable based on this study and applied to a framework of modern and full-edged constitutive description in future studies, along with the modeling of the consolidation phase.