Introduction

Functionally graded materials (FGMs) are non-homogeneous composites having discrete or continuous variation of material composition involving two or more material systems over a definable geometrical length. This variation in composition along the gradient direction can result in gradually varying physical, mechanical or thermal behavior of such material systems. The principal concept behind the design of FGMs is their ability to utilize multiple functionalities in an integrated material system which can provide a balanced performance in several applications [1, 2]. The progressive spatial variation of material properties in FGMs is their key difference compared with common homogeneous materials or traditional laminated composites.

Depending on the application and fabrication process, the material gradation could be either through thickness or along a direction in the plane of an FGM plate. The elastic properties and the fracture response of FGMs with in-plane material gradation have been studied extensively [3–6]. These studies report that the nature and extent of the elastic modulus variation affects the stress intensity factor significantly. On the other hand, there are only few studies on FGMs with through thickness gradation [7–12]. It was documented that the elastic properties of FGMs substantially control the deformation and fracture response under different loading and temperature conditions during their service. In fact, knowing the through thickness elastic properties of FGMs is essential for understanding the behavior of these materials under different loading conditions.

So far, a large number of studies have been reported focusing on micromechanical approaches to estimate the properties of FGMs [13–17]. For instance, Weissenbeck et al. [13] used a micromechanics approach based on Mori-Tanaka method and proposed a rule-of-mixture model to calculate the material properties of ceramic/metal graded systems. Recently, Yu and Kidane [14] employed a micromechanics modeling procedure to obtain the variation of elastic properties of through thickness graded ceramic/metal FGMs containing various heterogeneities. In their work, the influence of filler geometry and size on the effective elastic properties of through thickness graded materials was presented. Micromechanical approaches have also been used by Gasik [15] and Rahman and Chakraborty [16] to determine the physical and mechanical properties of functionally graded structures. Although these approaches are great tools to estimate the elastic and thermal properties of such material systems, the accuracy of the models is highly dependent on many simplifying assumptions.

On the other hand, indentation technique has been utilized as an experimental methodology to determine the through thickness material properties of FGMs. Researchers have used this technique to determine the nonlinear or elastic–plastic mechanical behavior of FGMs [18–20]. This technique is cumbersome in terms of number of tests and data collection if the thickness of each layer is large, and is practically limited to FGM coatings having smaller thickness. The elastic characterization of bulk graded materials differs from homogeneous materials and conventional composites. For example, homogeneous materials are characterized by a single value of elastic modulus. Though laminated composites have several layers, once the elastic constants of a single lamina are characterized, the overall elastic behavior of the laminate can be arrived at by using appropriate laminate theory. Contrary to this, in a graded laminate, the elastic constants of each layer should be known, or the elastic property profile which provides the variation of the elastic constants along the laminate thickness has to be determined. Though the layers can be individually tested to evaluate their elastic properties, when a large number of layers are involved, this procedure can become inefficient. A quick, simple and efficient method of obtaining the elastic property profile of graded plates will be highly useful to evaluate the material in the development stage itself.

Butcher et al. [21] used ultrasonic pulse echo method to measure the wave speed at different locations along the gradient and from this information generated the elastic modulus profile. The direction of wave propagation was chosen in such a manner that the elastic constants do not change along that direction. Marur and Tippur [22] determined the elastic modulus profile of a continuously graded plate using a novel miniature drop weight test, wherein an instrumented ball was dropped at different locations along the gradient and the elastic modulus was determined from the force-time history.

There are also attempts at determining the property profile of FGMs using inverse techniques [18, 23–29]. Using an inverse analysis and the instrumented indentation technique, Nakamura et al. [18] have measured the elastic property profile of FGM coatings. This approach involves determining the FGM parameters by matching the load-depth data from finite element analysis (FEA) of the indentation test with the experimentally obtained load-depth data. Liu et al. [23] used elastic waves and an inverse procedure to characterize the elastic profile of FGM plates. Their method involves exciting the FGM plate on one surface and measuring the displacement response on the other surface. The forward problem of wave propagation in the FGM plate is solved with assumed elastic profile and this profile is revised until the measured response and the response from forward problem are in close agreement. The error minimization can be performed using gradient search methods, genetic algorithms (GA), neural networks, non-linear least squares method or a combination of either of these [23–26]. Yu and Wu [27] proposed an inverse approach using the guided circumferential dispersion characteristics as the signature along with artificial neural network to measure the material properties of functionally graded pipes. Very complex analytical or computational procedures and/or state of the art equipment are usually required in the studies listed above. Further demonstration of the proposed approach through experimental determination of the elastic profile is not reported in these investigations. On the other hand, the inverse analyses performed based on full-field measurements have successfully been practiced in recent years to identify the deformation of nonhomogeneous materials under rather complex loading conditions [28, 29]. Although these methods seem to offer high levels of accuracy, identification of the material parameters using such methods requires state of the art experimental apparatus as well as precise computational strategies to facilitate the analysis of the experimental data.

The focus of the present work is towards the development of a simple yet sufficiently accurate method to obtain the elastic modulus profile of a through thickness graded FGM. Accordingly, two independent simple experiments, a four-point bend and a tensile test, are carried out and the axial load, bending moment, strain and curvatures are measured. Strain gages are used to measure the strains on the samples surfaces. Using the measured data along with classical laminate theory, the elastic modulus profile of the graded structure through its gradient direction is obtained using a minimization procedure based on GA. To demonstrate the efficacy of the proposed method, the elastic modulus profile of a through-thickness graded Ti/TiB material is evaluated using the proposed method and the results thus obtained are compared with available literature data.

Modified Classical Laminate Theory for FGMs

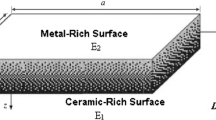
Consider a functionally graded plate in the Cartesian coordinate system, graded in z-direction, as shown in Fig. 1. Classical laminate theory (CLT) [30] was utilized to study the deformation response of the examined FGM. As opposed to laminated composites, the layers of the graded plate in this study are isotropic. Further, since the width of the FGM considered in the present work is much smaller than the length, the plane-stress assumption can be further relaxed and a one-dimensional equivalent of CLT can be utilized [30].

Fig. 1
figure 1

Stress and the resultant force representation

Full size image

The following basic assumptions are considered in the mathematical calculations in the present work:

  • Each layer of the FGM is assumed to be isotropic

  • Each layer is sufficiently thin compared to its lateral dimensions

  • Plane stress condition is dominant

  • Displacements are small compared to the laminate thickness, and are continuous throughout the laminate

  • The bonding between layers is perfect and infinitesimally small and no gaps or flaws exist between layers

  • The magnitudes of the inter-lamina shear stresses are assumed to be much smaller than the axial stress.

The Lamina Strain–Displacement Relationship

Defining the displacement components in x, y and z directions to be u, v and w, respectively, (as shown in Fig. 1) the slopes of a bent plate are given by:

$$ \frac{\partial w}{\partial x}\kern1em \mathrm{in}\ \mathrm{the}x-z\mathrm{plane} $$
(1a)
$$ \frac{\partial w}{\partial y}\kern1em \mathrm{in}\ \mathrm{the}\ \mathrm{y}-\mathrm{z}\ \mathrm{plane} $$
(1b)

The total in-plane displacement at any given point within the plate would be the sum of normal displacement component and the displacement induced by bending. Designating the displacement on the mid-plane of the plate in x and y-directions as u 0 and v 0, respectively, the total displacement components at any given position along z-direction (thickness) can be expressed as:

$$ u={u}_0-z\frac{\partial w}{\partial x},\kern1em v={v}_0-z\frac{\partial w}{\partial y} $$
(2)

Assuming that no strain is applied in the thickness direction and using the small strain definition, the strain components can be written as:

$$ {\varepsilon}_x=\frac{\partial u}{\partial x}=\left(\frac{\partial {u}_0}{\partial x}-z\frac{\partial^2w}{\partial {x}^2}\right) $$
(3a)
$$ {\varepsilon}_y=\frac{\partial v}{\partial y}=\left(\frac{\partial {v}_0}{\partial y}-z\frac{\partial^2w}{\partial {y}^2}\right) $$
(3b)
$$ {\gamma}_{xy}=\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)=\frac{\partial {u}_0}{\partial y}+\frac{\partial {v}_0}{\partial x}-2z\frac{\partial^2w}{\partial x\partial y} $$
(3c)

where ε x , ε y and γ xy are in-plane strain components. At this point, the mid-plane strains, ε 0 i , and curvatures, κ i , (i = x, y, xy) can be defined as:

$$ \begin{array}{ccc}\hfill {\varepsilon}_x^0\equiv \frac{\partial {u}_0}{\partial x}\hfill & \hfill {\varepsilon}_y^0\equiv \frac{\partial {v}_0}{\partial y}\hfill & \hfill {\gamma}_{xy}^0\equiv \frac{\partial {u}_0}{\partial y}+\frac{\partial {v}_0}{\partial x}\hfill \end{array} $$
(4a)
$$ \begin{array}{ccc}\hfill {\kappa}_x\equiv -\frac{\partial^2w}{\partial {x}^2}\hfill & \hfill {\kappa}_y\equiv -\frac{\partial^2w}{\partial {y}^2}\hfill & \hfill {\kappa}_{xy}\equiv -2\frac{\partial^2w}{\partial x\partial y}\hfill \end{array} $$
(4b)

This results in the following matrix form description of strains:

$$ \left[\begin{array}{c}\hfill {\varepsilon}_x\hfill \\ {}\hfill {\varepsilon}_y\hfill \\ {}\hfill {\gamma}_{xy}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\varepsilon}_x^0\hfill \\ {}\hfill {\varepsilon}_y^0\hfill \\ {}\hfill {\gamma}_{xy}^0\hfill \end{array}\right]+z\left[\begin{array}{c}\hfill {\kappa}_x\hfill \\ {}\hfill {\kappa}_y\hfill \\ {}\hfill {\kappa}_{xy}\hfill \end{array}\right] $$
(5)

The Lamina Constitutive Relationship

The stress–strain relation for an isotropic layer under plane-stress condition can be written based on the Voigt convention as:

$$ \left\{\begin{array}{c}\hfill {\sigma}_x\hfill \\ {}\hfill {\sigma}_y\hfill \\ {}\hfill {\tau}_{xy}\hfill \end{array}\right\}=\left[\begin{array}{ccc}\hfill {Q}_{11}\hfill & \hfill {Q}_{11}\hfill & \hfill 0\hfill \\ {}\hfill {Q}_{21}\hfill & \hfill {Q}_{22}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {Q}_{66}\hfill \end{array}\right]\left\{\left[\begin{array}{c}\hfill {\varepsilon}_x^0\hfill \\ {}\hfill {\varepsilon}_y^0\hfill \\ {}\hfill {\gamma}_{xy}^0\hfill \end{array}\right]+z\left[\begin{array}{c}\hfill {\kappa}_x\hfill \\ {}\hfill {\kappa}_y\hfill \\ {}\hfill {\kappa}_{xy}\hfill \end{array}\right]\right\} $$
(6)

where Q ij ’s are the components of the material’s stiffness matrix, and only depend on two independent elastic constants, since the layers are assumed to be isotropic. Q ij ’s are defined for an isotropic layer as:

$$ {Q}_{11}={Q}_{22}=\frac{E}{1-{\upsilon}^2}\kern1em {Q}_{12}={Q}_{21}=\upsilon {Q}_{11}\kern1em {Q}_{66}=\frac{E}{2\left(1+\upsilon \right)} $$
(7)

with E and υ being the elastic modulus and Poisson’s ratio of the layer, respectively.

Since the stress components vary through the thickness of the beam, it will be convenient to define stresses in terms of equivalent forces acting on the middle plane. As illustrated in Fig. 1, the stresses acting on each edge can be integrated to give the resulting forces per unit width applied on the edge as:

$$ \begin{array}{ccc}\hfill {N}_x\equiv {\displaystyle {\int}_{-\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\sigma}_xdz}\hfill & \hfill {N}_y\equiv {\displaystyle {\int}_{-\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\sigma}_ydz}\hfill & \hfill {N}_{xy}\equiv {\displaystyle {\int}_{-\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\tau}_{xy}dz}\hfill \end{array} $$
(8)

where h is the thickness of each layer, and N i denotes the resultant force/unit width applied in i-direction. Similarly, the moments per unit width (M i ) applied on the beam can be expressed as:

$$ \begin{array}{ccc}\hfill {M}_x\equiv {\displaystyle {\int}_{-\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\sigma}_xzdz}\hfill & \hfill {M}_y\equiv {\displaystyle {\int}_{-\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\sigma}_yzdz}\hfill & \hfill {M}_{xy}\equiv {\displaystyle {\int}_{-\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\tau}_{xy}zdz}\hfill \end{array} $$
(9)

The summation of forces and moments over the whole thickness of the FGM plate will result in the following matrix equations:

$$ \left[\begin{array}{c}\hfill {N}_x\hfill \\ {}\hfill {N}_y\hfill \\ {}\hfill {N}_{xy}\hfill \end{array}\right]={\displaystyle \sum_{k=1}^n{\displaystyle {\int}_{h_{k-1}}^{h_k}\left[\begin{array}{ccc}\hfill {Q}_{11}\hfill & \hfill {Q}_{12}\hfill & \hfill 0\hfill \\ {}\hfill {Q}_{21}\hfill & \hfill {Q}_{22}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {Q}_{66}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\varepsilon}_x^0\hfill \\ {}\hfill {\varepsilon}_y^0\hfill \\ {}\hfill {\gamma}_{xy}^0\hfill \end{array}\right\}dz+{\displaystyle {\int}_{h_{k-1}}^{h_k}\left[\begin{array}{ccc}\hfill {Q}_{11}\hfill & \hfill {Q}_{12}\hfill & \hfill 0\hfill \\ {}\hfill {Q}_{21}\hfill & \hfill {Q}_{22}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {Q}_{66}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\kappa}_x\hfill \\ {}\hfill {\kappa}_y\hfill \\ {}\hfill {\kappa}_{xy}\hfill \end{array}\right\}zdz}}} $$
(10a)
$$ \left[\begin{array}{c}\hfill {M}_x\hfill \\ {}\hfill {M}_y\hfill \\ {}\hfill {M}_{xy}\hfill \end{array}\right]={\displaystyle \sum_{k=1}^n{\displaystyle {\int}_{h_{k-1}}^{h_k}\left[\begin{array}{ccc}\hfill {Q}_{11}\hfill & \hfill {Q}_{12}\hfill & \hfill 0\hfill \\ {}\hfill {Q}_{21}\hfill & \hfill {Q}_{22}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {Q}_{66}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\varepsilon}_x^0\hfill \\ {}\hfill {\varepsilon}_y^0\hfill \\ {}\hfill {\gamma}_{xy}^0\hfill \end{array}\right\}zdz+{\displaystyle {\int}_{h_{k-1}}^{h_k}\left[\begin{array}{ccc}\hfill {Q}_{11}\hfill & \hfill {Q}_{12}\hfill & \hfill 0\hfill \\ {}\hfill {Q}_{21}\hfill & \hfill {Q}_{22}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {Q}_{66}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\kappa}_x\hfill \\ {}\hfill {\kappa}_y\hfill \\ {}\hfill {\kappa}_{xy}\hfill \end{array}\right\}{z}^2dz}}} $$
(10b)

With n being the total number of layers. Integrating these equations and combining the resultant matrices into a single one, the following equation is obtained:

$$ \left[\begin{array}{c}\hfill \begin{array}{c}\hfill {N}_x\hfill \\ {}\hfill {N}_y\hfill \\ {}\hfill {N}_{xy}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{c}\hfill {M}_x\hfill \\ {}\hfill {M}_y\hfill \\ {}\hfill {M}_{xy}\hfill \end{array}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill \begin{array}{ccc}\hfill {A}_{11}\hfill & \hfill {A}_{12}\hfill & \hfill 0\hfill \\ {}\hfill {A}_{21}\hfill & \hfill {A}_{22}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {A}_{66}\hfill \end{array}\hfill & \hfill \begin{array}{ccc}\hfill {B}_{11}\hfill & \hfill {B}_{12}\hfill & \hfill 0\hfill \\ {}\hfill {B}_{21}\hfill & \hfill {B}_{22}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {B}_{66}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{ccc}\hfill {B}_{11}\hfill & \hfill {B}_{12}\hfill & \hfill 0\hfill \\ {}\hfill {B}_{21}\hfill & \hfill {B}_{22}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {B}_{66}\hfill \end{array}\hfill & \hfill \begin{array}{ccc}\hfill {D}_{11}\hfill & \hfill {D}_{12}\hfill & \hfill 0\hfill \\ {}\hfill {D}_{21}\hfill & \hfill {D}_{22}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {D}_{66}\hfill \end{array}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \begin{array}{c}\hfill {\varepsilon}_x^0\hfill \\ {}\hfill {\varepsilon}_y^0\hfill \\ {}\hfill {\gamma}_{xy}^0\hfill \end{array}\hfill \\ {}\hfill \begin{array}{c}\hfill {\kappa}_x\hfill \\ {}\hfill {\kappa}_y\hfill \\ {}\hfill {\kappa}_{xy}\hfill \end{array}\hfill \end{array}\right] $$
(11)

where,

$$ {A}_{ij}={\displaystyle \sum_{k=1}^n{\left[{Q}_{ij}\right]}_k\left({h}_k-{h}_{k-1}\right)} $$
(12a)
$$ {B}_{ij}=\frac{1}{2}{\displaystyle \sum_{k=1}^n{\left[{Q}_{ij}\right]}_k\left({h}_k^2-{h}_{k-1}^2\right)} $$
(12b)
$$ {D}_{ij}=\frac{1}{3}{\displaystyle \sum_{k=1}^n{\left[{Q}_{ij}\right]}_k\left({h}_k^3-{h}_{k-1}^3\right)} $$
(12c)

In the above equations, k denotes the layer number and h k denotes the position of k th layer. The load vector on the left side of equation (11) can be determined if the strains and curvature values given on the right side of equation (11) are known, and vice versa. When testing layered beams, it is reasonable to assume that each layer is in a state of one dimensional stress, particularly when the width of each layer is sufficiently small compared to its length. In such conditions, the stress components σ y and τ xy can be assumed to be zero, and equation (11) can be further reduced to the following form:

$$ \left[\begin{array}{c}\hfill {N}_x\hfill \\ {}\hfill {M}_x\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill A\hfill & \hfill B\hfill \\ {}\hfill B\hfill & \hfill D\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\varepsilon}_x^0\hfill \\ {}\hfill {\kappa}_x\hfill \end{array}\right] $$
(13)

with,

$$ A={\displaystyle \sum_{k=1}^n\frac{E_k}{1-{\upsilon}_k^2}\left({h}_k-{h}_{k-1}\right)} $$
(14a)
$$ B=\frac{1}{2}{\displaystyle \sum_{k=1}^n\frac{E_k}{1-{\upsilon}_k^2}\left({h}_k^2-{h}_{k-1}^2\right)} $$
(14b)
$$ D=\frac{1}{3}{\displaystyle \sum_{k=1}^n\frac{E_k}{1-{\upsilon}_k^2}\left({h}_k^3-{h}_{k-1}^3\right)} $$
(14c)

where E k and υ k are the elastic modulus and Poisson’s ratio of layer k and n denotes the total number of layers.

When the applied forces and moments are known and the strain and curvature are measured, the stiffness matrix can be calculated based on an inverse method, from which the elastic constants can be extracted. The ideal procedure would be conducting two independent experiments, a four-point bend test to measure moment and curvature, and a tensile test to measure axial load and strain. In the next section, further explanations are provided on the performed experimental procedure and the inverse calculations used to extract the elastic constants of the examined material.

Experimental Procedure

Material and Specimen Geometry

Although the present method can be applied to general through thickness stepwise graded materials, a seven-layer graded Ti/TiB material system is employed in the present work. The 3.175 mm thick discretely graded plate having 7 layers with composition ranging from pure titanium on one side to 85 % TiB (15 % Ti) on the other is used to demonstrate the technique. The graded plates were manufactured by BAE systems Inc. through a powder metallurgy processing route. The FGM plates were fabricated from Ti and TiB2 powders as 150 × 150 mm size plate form through a hot press sintering process at 1578 K and 13.8 MPa pressure in vacuum conditions. In order to facilitate the densification, as well as to minimize the amount of residual TiB2, a nickel-based powder has been reported as the sintering aid, added to the powder mixture prior to the sintering process [31]. In this manner, a through thickness graded material system with 7 discrete homogenous layers were fabricated. More details on the processing method of the material can be found elsewhere [31, 32].

Since the boundaries of the layers could not be clearly distinguished through microstructural observations, micro-hardness testing was performed along the thickness direction to obtain the thickness of each layer. To do this, the hardness profile across the thickness obtained using a 10 N indentation force was plotted and the boundaries of the layers were identified by tracking the stepwise changes in the hardness value across the thickness. The thickness of each of the 7 layers within the material was obtained using this method and the results were compared to the data provided by the manufacturer.

Rectangular coupons of 100 × 15 × 3.175 (mm3) were prepared for the bending and tensile experiments. The coupons were extracted from the as-manufactured plates using Electron Discharge Machine (EDM) with 0.07 mm diameter wire. To minimize the development of residual stresses during EDM cutting, the specimens were fully immersed in the coolant during the entire wire cutting process [31].

Four-Point Bend Test

A four-point bend test setup, as shown in Fig. 2, made of hardened steel (manufactured by Wyoming Test Fixtures Inc.) affixed into a 5 kN load-cell universal testing machine, was used to apply a pure bending moment (M b ) at the mid-section of the specimen described above. Due to its very brittle nature, the TiB-rich side was chosen to be on the top, on which compressive stress is dominant. In this manner, any possibility of cracking due to the applied tensile stress on the TiB-rich side can be eliminated.

Fig. 2
figure 2

The four-point bending experiment setup along with the specimen shown on the left. A schematic view of the specimen is illustrated on the right

Full size image

Two strain gauges were placed at the center of each side of the specimen to measure the strains along x-direction on each surface. Note that the x-direction denotes the direction along the length of the specimen in this case. Load was applied at a rate of 0.1 mm/min under displacement control and the load data acquisition was synchronized with the output from strain gauges through a DAQ system. The bending moment on the specimen was calculated from the recorded load, facilitating the calculation of the moment-strain curves on the Ti side and TiB-rich sides of the specimen.

Tensile Test

The tensile test was performed on the same specimen used for the bending experiment, in a 220 kN universal tensile machine shown in Fig. 3(a). To prevent any damage caused by the hardened hydraulic grips, 1 mm thick aluminum tabs of 15 × 15 mm2 (width × length) were epoxied at specimen ends on each side of the specimen as shown in Fig. 3(b). The axial stress values in this case were simply calculated by dividing the recorded load by the cross sectional area of the specimen. Attempts were made not to exceed the yield strength of the weaker component of the FGM, i.e. titanium; such that the experiment would remain in the elastic region and to assure the validity of the analyses.

Fig. 3
figure 3

(a) The tensile frame with the specimen mounted on, along with the cameras and lighting system, (b) the tensile specimen showing the aluminum tabs attached to the ends, (c) a close up view of the speckled section with the grey-scale pattern shown in (d)

Full size image

In order to study the deformation of the examined FGM under tension, two different methods were regarded. First, similar to the bending experiment, a single strain gage was attached to the center point at each side of the specimen to measure the strain on two sides from which the curvature can be obtained. The specimen was inserted into the grips, and loaded to about 5000 N in tension at a rate of 0.1 mm/min in displacement control mode. The load and strain measurements were synchronized through a data acquisition system.

Digital image correlation (DIC) was also used during the tensile testing to obtain the strains on each side of the specimen, i.e. Ti side and TiB-rich side. Note that the intention for using full-field DIC observation was to verify whether the strains developed on both sides of the specimen are fairly uniform over the examined region of interest or not. In the case of the graded sample, due to the asymmetry in the property variation along the thickness, one could envisage a coupling of deformation. A tensile load can induce a curvature. This curvature may or may not develop freely, depending on the grip stiffness. Due to this the strains may not be homogeneous along the length of the specimen. To verify this, one has to use full-field methods and DIC is a very well established technique for this purpose. To perform the DIC measurements, the middle section of the specimen was coated with a thin layer of white paint on both sides. A fine black speckle pattern was then applied on top of the white layer using an air brush. Typical speckle pattern applied on the specimen with its corresponding grey-scale intensity can be seen in Fig. 3(c) and (d), respectively. A pair of 5 megapixel Point Grey cameras equipped with 60 mm Nikon lenses was used to capture images of the specimen surfaces during the loading. Full-field images with 2448 × 2048 pixel resolution were taken during the tensile loading at a rate of 1 fps. In this case also, the imaging frequency was synchronized with the load data acquisition to facilitate the calculation of load-strain curves.

Inverse Analysis to Obtain Elastic Properties

Calculation of the Constants A, B and D from Test Data

Unlike homogeneous materials, for the case of a graded laminate, due to asymmetrical variation of the elastic modulus along the thickness, a pure bending moment can result in an in-plane strain at the mid-plane, while a pure in-plane load can result in a curvature. Applying a pure bending moment in the four-point bend test is quite straight forward, as the in-plane load (N b ) can be assumed zero at mid-span, the location at which the strains are recorded. In the tensile test, however, the section of the beam at which the strains are measured will be subjected to both an in-plane load (N t ) and a bending moment (M t ). Due to the asymmetric variation of the elastic modulus, the curvature developed under the tensile load will be partially restrained by the grips, resulting in a moment to be developed within the tensile specimen. Further, any curvature developed during loading in the tensile specimen will induce an eccentricity in the load line at the mid-length of the specimen, resulting in a bending moment (M t ). This moment cannot be measured, however, can be calculated from the test data, as explained later.

The curvature of the beam and the mid-plane strain for both experiments can be calculated as:

$$ \begin{array}{l}{\kappa}_x=\frac{\varepsilon_x^{Ti}-{\varepsilon}_x^{TiB}}{t}\\ {}{\varepsilon}^0=\frac{\varepsilon_x^{Ti}+{\varepsilon}_x^{TiB}}{2}\end{array} $$
(15)

where, κ x represents the curvature, t is the overall thickness of the beam (=3.175 mm), and ε i x denotes the measured in-plane strain in x-direction on each side of the specimen (i = Ti, TiB). It should again be emphasized that the x-direction denotes the length direction in both four-point bend and tensile tests in this work. As explained earlier in Modified Classical Laminate Theory for FGMs section, the relation between the measured strains, curvature, loads and moments can be written for both tensile and four-point bend tests as:

$$ \left\{\begin{array}{c}\hfill {N}_t\hfill \\ {}\hfill {M}_t\hfill \end{array}\right\}=\left[\begin{array}{cc}\hfill {A}_e\hfill & \hfill {B}_e\hfill \\ {}\hfill {B}_e\hfill & \hfill {D}_e\hfill \end{array}\right]{\left\{\begin{array}{c}\hfill {\varepsilon}_x^0\hfill \\ {}\hfill {\kappa}_x\hfill \end{array}\right\}}_{tensile}\kern1em \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{tensile}\ \mathrm{test} $$
(16)
$$ \left\{\begin{array}{c}\hfill 0\hfill \\ {}\hfill {M}_b\hfill \end{array}\right\}=\left[\begin{array}{cc}\hfill {A}_e\hfill & \hfill {B}_e\hfill \\ {}\hfill {B}_e\hfill & \hfill {D}_e\hfill \end{array}\right]{\left\{\begin{array}{c}\hfill {\varepsilon}_x^0\hfill \\ {}\hfill {\kappa}_x\hfill \end{array}\right\}}_{bending}\kern1em \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{fo}\mathrm{ur}-\mathrm{point}\ \mathrm{bend}\ \mathrm{test} $$
(17)

With subscript “e” denoting that the constants A, B and D are determined from the “experiments” in this case.

Having known the values N t , M b , ε 0 x and κ x from both sets of experiments, the unknown parameters A e , B e , D e and M t can be calculated using the following expressions:

$$ {A}_e=\frac{-{\kappa}_x^{bending}\left({N}_t\right)}{\left({\left.{\varepsilon}_x^0\right|}_{bending}\right){\kappa}_x^{tensile}-\left({\left.{\varepsilon}_x^0\right|}_{tensile}\right){\kappa}_x^{bending}} $$
(18)
$$ {B}_e=\frac{N_t\left({\left.{\varepsilon}_x^0\right|}_{bending}\right)}{\left({\left.{\varepsilon}_x^0\right|}_{bending}\right){\kappa}_x^{tensile}-\left({\left.{\varepsilon}_x^0\right|}_{tensile}\right){\kappa}_x^{bending}} $$
(19)
$$ {D}_e=\frac{M_b-{B}_e\left({\left.{\varepsilon}_x^0\right|}_{bending}\right)}{\kappa_x^{bending}} $$
(20)
$$ {M}_t=\frac{\left({\kappa}_x^{tensile}\right)\left({M}_b\right)-\left({N}_t\right)\left({\left.{\varepsilon}_x^0\right|}_{bending}\right)}{\kappa_x^{bending}} $$
(21)

Determination of the Elastic Moduli of the Layers

Using equation (14) and the known stiffness parameters (A e , B e and D e ) obtained from equations (18) to (20), the elastic modulus of each layer (E k ) is determined following an error minimization scheme. The error function is defined here as:

$$ er=\sqrt{{\left(\frac{A}{A_e}-1\right)}^2+{\left(\frac{B}{B_e}-1\right)}^2+{\left(\frac{D}{D_e}-1\right)}^2} $$
(22)

where ‘er’ denotes the dimensionless error magnitude, A e , B e and D e are the experimentally obtained stiffness coefficients, and A, B and D are stiffness coefficients calculated at each iteration during the error minimization. Plugging equation (14) into equation (22), the error function ‘er’ would turn into an explicit function of the layers’ elastic moduli, as:

$$ er=\sqrt{{\left(\frac{{\displaystyle \sum_{k=1}^n\left(\frac{E_k}{1-{\upsilon}_k^2}\right)\left({h}_k-{h}_{k-1}\right)}}{A_e}-1\right)}^2+{\left(\frac{{\displaystyle \sum_{k=1}^n\left(\frac{E_k}{1-{\upsilon}_k^2}\right)\left({h}_k^2-{h}_{k-1}^2\right)}}{2{B}_e}-1\right)}^2+{\left(\frac{{\displaystyle \sum_{k=1}^n\left(\frac{E_k}{1-{\upsilon}_k^2}\right)\left({h}_k^3-{h}_{k-1}^3\right)}}{3{D}_e}-1\right)}^2} $$
(23)

with n denoting the total number of layers in a layered FGM. To solve the minimization problem given by equation (23) and extract the elastic moduli of the layers, an optimization code based on the Genetic Algorithm (GA) optimization method was utilized. The GA optimization procedure used in this work was performed using the MATLAB® GA toolbox. A simple flow chart showing the analysis procedure followed in this work is shown in Fig. 4. Also, the details of the parameters used in the GA are listed in Table 1. The results from 15 independent attempts were averaged and reported as the values of the elastic modulus of each layer of the graded material considered. These values were compared to those reported by the manufacturer as well as the results obtained from a recent micromechanical model [14, 32].

Fig. 4
figure 4

The flow chart showing the steps of the inverse analysis followed in this work

Full size image
Table 1 Parameters used in the GA optimization in this work
Full size table

A GA is basically an optimization method in which the evolutionary principles and chromosal processing in natural genetics are mimicked. Genetic Algorithms have recently found many applications in the field of engineering, mainly due to their computationally efficient nature as well as the reduced running times [33–35]. A GA optimization process begins with generating a random population of the individuals, in this case a total number of n = 7 elastic moduli, corresponding to the actual seven layers within the material. The algorithm systematically analyzes each group of the individuals according to the specifications set by the designer. Each analyzed set of individuals is then assigned a fitness rating, which reflects the designated criterion, in this case the magnitude of the error ‘er’. The fitness ratings obtained for all the random sets are then used to identify which set of individuals have satisfied the acceptance criterion better than the others, thereby enabling the algorithm to eliminate the weaker selections of the individuals. The remaining selections of the better sets are then used to produce the next generation of the population. This process is iterated over many generations of the population to result in the optimized set of individuals.

Note that a solution obtained from GA is not a unique one. Therefore, certain practical guidelines need to be considered to eliminate unacceptable solutions. Owing to the unbound choices existing at the population generation stage, Genetic Algorithms usually take into account specific constraints as for the optimization guidelines. For instance, in the present work, the elastic moduli (population) generated in GA optimization cannot take zero or negative values. Also, the range of the individual elastic moduli has to be bound, e.g. maximum effective elastic modulus present across the thickness may not possess a value greater than 500 GPa. Such constraints are usually specified considering the physical nature of the problem to be handled. Further, the fact that the moduli vary progressively (monotonically) from layer to layer can also be used as additional constraints. In this work, the following constraints were used in the algorithm:

  • The sum of all the elastic moduli is bound with the minimum and maximum values of 560 GPa and 2100 GPa, respectively, i.e. \( 560\le {\displaystyle \sum_{k=1}^7{E}_k}\le 2100 \) (GPa). Note that this criterion does not have a physical meaning. Rather, it was only used as a constraint to limit the lower and upper bound solutions. The lower and upper bound constraints were considered assuming conditions in which all the E i values take 80 GPa (lower limit) and 300 GPa (upper limit), respectively.

  • The start point to generate population was chosen as the condition in which all the layers have an elastic modulus of 80 GPa, i.e. E 1 = E 2 = ⋯ = E 7 = 80 (GPa)

Finally, it must be stated that the GA-based method used in this work was initially tested for accuracy and effectiveness by comparing the elastic profile of a known epoxy/glass bead FGM with the results obtained from the proposed method [36]. Once the agreement between the two sets of results was confirmed (see Elastic Modulus Profile section), the proposed method was utilized to identify the elastic modulus of the Ti/TiB graded material.

Results and Discussion

Determining the Thickness of the Layers

The Vickers hardness profile across the gradient direction in Ti/TiB FGMs has been utilized and demonstrated to be an applicable method in determining the thickness of each layer [37]. It should be noted that the resolution of the micro-hardness measurement is limited by the size of the indentation marks on specimen surface. To overcome this limitation and have a better resolution of the measurements, particularly within Ti-rich layers where the indentation marks would be larger in size due to lower hardness, the testing was conducted by carefully varying the position of indentation along x-direction as shown in Fig. 5. In this case, since the layers’ composition and properties remain the same along x-direction, the resolution of the hardness measurements can be further improved and the thickness of each layer can be captured with better accuracy, particularly in the case of thinner layers. The hardness value increases with increasing the volume fraction of TiB in the layers. The minimum and maximum hardness values of 247 and 1549 kg/mm2 were measured on pure Ti and 85%TiB-15%Ti layers, respectively. The jumps observed in the layer-to-layer hardness value were large enough to facilitate the measurement of the layer thickness within the material. Accordingly, the thickness of each layer was determined and compared to the data reported by the manufacturer [31]. A comparison between two sets of data can be found in Table 2. Note that the thickness values obtained in this work were used in the inverse analysis.

Fig. 5
figure 5

A schematic view of the location on which micro-hardness testing has been performed

Full size image
Table 2 The thickness of the layers in the examined FGM plate
Full size table

Mechanical Test Results

Figure 6(a) demonstrates the variation of in-plane strains on Ti and TiB-rich sides of the specimen as a function of the applied moment. The strain-moment relation is linear, with compressive and tensile strains developed on the TiB-rich and Ti sides of the specimen, respectively. Considering the moment-strain curves shown in Fig. 6(a), it is indicated that the value of the strain on two surfaces are not equal in magnitude, in contrast to the case of homogenous beams subjected to pure bending. The absolute magnitude of the strain developed on the TiB-rich side is about 79 % of the strain developed on Ti-side at any given moment. Accordingly, a perfectly linear response is observed, leading to a linear moment-curvature relation, as shown in Fig. 6(b).

Fig. 6
figure 6

(a) Variation of surface strain on Ti and TiB-rich sides with respect to the applied bending moment and (b) bending moment vs. developed curvature in the four-point bend test

Full size image

For the case of tensile experiments, the axial strain on either side of the specimen was extracted from strain gages. As mentioned earlier, the camera system was also synchronized with the load-cell, assuring that the correct deformation response is captured using DIC. Typical DIC contours showing the axial displacement, v, and axial strain component, ε yy , at a far-field tensile load of 5000 N are shown in Fig. 7. It can be observed from Fig. 7(c) and (d) that the strain is distributed fairly uniform in the areas studied. The grips we have used are sufficiently rigid to prevent the curvature due to asymmetry resulting in a homogeneous strain field. Variation of the axial strains, extracted from strain gages, as a function of the applied tensile load on Ti and TiB-rich sides of the specimen is shown in Fig. 8(a). A slight difference can be witnessed between the magnitude of strains measured on Ti and TiB-rich sides of the specimen. The difference between these strains results in a curvature to be developed during uniaxial tensile test. This curvature is calculated from the strains measured by the strain gauges using equation (15) and plotted as a function of tensile load as shown in Fig. 8(b). A linear curvature-load relation is observed in tensile experiment, similar to that observed in case of the bending test.

Fig. 7
figure 7

The vertical displacment component, v, on (a) Ti side and (b) TiB-rich side and the axial strain component, ε yy , on (c) Ti side and (d) TiB-rich side

Full size image
Fig. 8
figure 8

(a) Variation of surface strain on Ti and TiB-rich sides with respect to the applied axial load and (b) axial load vs. developed curvature in the tensile test

Full size image

Next, based on the results obtained from the tensile and four-point bend experiments, the unknown constants A e , B e and D e were calculated using equations (16) to (20). These constants were calculated using the entire collection of data points acquired during tensile and bending tests, and using the strain gage results. The average value and standard deviation of each constant obtained through such process are shown in Table 3. The standard deviations of <2 % reported for the constants A e , B e and D e confirm the accuracy of the experiments and the data analysis.

Table 3 Average value of stiffness constants calculated based on the experimental data points obtained from tensile and bending experiments
Full size table

The evolution of the bending moment, M t , developed within the specimen during tensile experiment was calculated using equations (16) and (21) and plotted as a function of axial load, N t , as shown in Fig. 9. The bending moment, M t , varies linearly with N t . If the grips are rigid, they will not allow any curvature to develop at the clamped ends and the beam will remain straight. In such a situation, M t will be related to N t as M t  = (B/A) N t . Note that the slope of the curve shown in Fig. 9 is close to B/A ratio. (See Table 3 for values of A and B.)  Accordingly, the strains developed on both surfaces of the specimen will be uniform along the length in the middle region (away from the grips). It can be observed from Fig. 7(c) and (d) that the strain is fairly uniform in the area studied. This along with the fact that the curvature is small indicates that the grips are considerably restraining the curvature of the specimen.

Fig. 9
figure 9

Evolution of the moment developed within the tensile sample with respect to the axial load

Full size image

Elastic Modulus Profile

As described in Inverse Analysis to Obtain Elastic Properties section, the accuracy of the GA-based method used in this work was first validated by testing the proposed method to determine the elastic modulus profile of a seven layer FGM with known elastic profile. The FGM considered here was an epoxy/glass bead graded material made of seven 1.5 mm thick layers of different elastic properties. The elastic properties were varied by changing the glass bead volume fraction progressively in each layer. The elastic properties of the individual layers were first evaluated, and the results were used to compare with that obtained using the method proposed in this work. Details of the manufacturing of the resin/glass bead FGM, as well as the mechanical testing results are beyond the scope of this work and can be found in [36]. A graph showing the through thickness variation of the elastic moduli of the epoxy/glass bead graded specimen is depicted in Fig. 10. A good agreement between two sets of results validates the effectiveness of the proposed GA-based algorithm considered in this work.

Fig. 10
figure 10

Comparison of the elastic modulus profile of a seven layer epoxy/glass bead FGM, obtained using the proposed method with that obtained by measuring the elastic modulus of individual layers

Full size image

The distribution of the effective elastic moduli across the Ti/TiB FGM thickness was found using the code written in the MATLAB® programming platform, as explained in detail in earlier sections. A typical evolution of the population, i.e. a set of seven elastic moduli values corresponding to the actual seven layers in the Ti/TiB FGM, is plotted in Fig. 11 demonstrating a very fast convergence to have taken place in the GA analysis in this work. The elastic modulus of each layer obtained from 15 independent runs of the GA program was averaged and the same is listed in Table 4 for each layer. The elastic moduli obtained using the strain data measured using strain gages in the tensile test are shown in Fig. 12. The method is shown to be able to resolve the monotonic increase in the elastic modulus of the layers with increasing the TiB without such a constraint being imposed on the minimization scheme. To compare with the existing results [14, 32], the elastic modulus of each layer was normalized and plotted as a function of the normalized thickness of the specimen as shown in Fig. 13. The results obtained from the present work are in very good agreement with the effective elastic moduli obtained from a previous micromechanics model [14]. It was also observed that the elastic modulus profile obtained in the present work is closest to that obtained from a modified Mori-Tanaka micromechanical approach in which evenly distributed TiB phase is modeled in the form of platelets with an aspect ratio of 100 in a Ti matrix [14]. It is interesting to note that from a material processing standpoint, the fabrication of Ti-TiB materials using hot press apparatus normally results in the development of TiB platelets with aspect ratios of up to 40 [38, 39].

Fig. 11
figure 11

The evolution of (a) population and (b) ‘er’ function value, with respect to generation. E(i) represents the elastic modulus of the ith layer, with i = 1 denoting the pure Ti layer and i = 7 showing the TiB-rich side

Full size image
Table 4 The GA optimization results from 15 attempts, with their average and standard deviation shown at the bottom
Full size table
Fig. 12
figure 12

The elastic modulus profile of the specimen found from the GA results

Full size image
Fig. 13
figure 13

Distribution of the normalized effective elastic modulus vs. thickness, compared with the results published in the literature. The results of the strain gage measurements have been presented in this figure

Full size image

On the other hand, comparison of the elastic modulus values found from the current method with those determined by testing individual layers presented in Ref. [32] shows a significant difference. The difference is more substantial (>20 %) on the middle layers, from layer #2 to layer #5. The reason behind this discrepancy might be due to the difference in geometry and size of the specimen used in these methods. Slicing each layer of the graded material into thin monolithic sections and individually testing these sections will not take into account the contribution of the interface deformation and complexities present when testing the graded beams.

Conclusions

A simple yet sufficiently accurate method is proposed to obtain the elastic modulus profile of a through-thickness functionally graded material. Two independent experimental evaluations, i.e. tensile and bending tests were performed, followed by an inverse calculation scheme to determine the material’s elastic constants. A minimization algorithm was then utilized to calculate the elastic modulus of each layer within the graded structure. The proposed method was successfully applied to a layered Ti/TiB graded specimen. The experimentally determined elastic modulus profile was compared to the estimates obtained from individual-layer testing, as well as from a micromechanical approach reported in literature. Good agreement between the experimental results with those from the micromechanical approach was observed. It is believed that the simple method proposed here will be highly useful in quick estimation of the elastic modulus profile of graded plates with good accuracy, particularly during their developmental stages.