Introduction

One of the most promising capabilities of additive manufacturing (AM) is the production of novel lightweight structures, which are in high demand across sectors such as automotive, medicine and aerospace. AM enables parts with high geometrical complexity, such as those determined by topology optimisation, to be produced with little or no additional expense over more conventional forms, which is in stark contrast to subtractive manufacturing processes. Indeed, many innovations in AM have come from the use of topology optimisation as a design tool, which is typically used to identify the material layout that maximises specific mechanical properties[1–4].

An alternate and complementary route to designing better parts for AM, i.e. designs that make more efficient use of material,is the replacement of otherwise solid volumes with lattice structures. Lattice designs involving functional grading, variable cell properties and conformity to complex geometries (see Fig. 1) are only realistically manufacturable with AM Such lattice designs have the potential to deliver large reductions in part weight, while offering high levels of stiffness and energy absorption under static and dynamic loading[5–12]. Compared to topology optimisation methods, lattices may also offer more robust solutions to problems which include uncertainty in the loading conditions or have multiple objectives. However, the choice of lattice unit cell design is large and the mechanical properties of different cell types are far from fully understood. There are also features of AM in particular that may influence the design process, such as relatively high surface roughness and the possible requirement for support structures, which depend on the choice of part build orientation. These factors are obstacles in the development of design methods that utilise lattice structures effectively.

Fig. 1
figure 1

Lattice structures in a range of lightweight part designs. (a) shows a cross-section through an AM part with an internal repeating cellular structure[5], (b) shows a tetrahedral lattice conforming to a complex shape (in this case a component for a commercial airliner), and (c) shows a lattice structure in a topology optimised part featuring internal routing channels for structural health monitoring

Full size image

In addition to the choice of cell type, at least two other cell properties are significant in determining its mechanical performance; its relative density (also referred to as the volume fraction) and its size. The first of these factors has received some prior attention[6–9], largely because of the similarity between lattice structures and the more well established foams, while the second has received very little[13].

This work examines the modulus and ultimate tensile strength of latticed parts with body-centred-cubic (BCC) unit cells of varying size and fixed relative density. The parts were produced in Ti-6Al-4V alloy using selective laser melting (SLM), which is an AM process used to produce parts from a feedstock of metal powder.The cell type was chosen principally because it is known to be self-supporting, that is, it does not include overhanging features which would require the addition of supporting structures. In SLM, support structures are manufactured from the same material as the part being manufactured, and they can be difficult to remove in a secondary process. Also, there is strong motivation to characterise the mechanical properties of BCC lattice cells as they have been examined experimentally and theoretically elsewhere[7, 8, 11, 14–16]. Note that ‘BCC’ here refers to a macroscopic 3D structure of the order several mm, and is not being used in the crystallographic sense.

The main aim of this investigation is to uncover how the mechanical properties of lattice structures vary according to the size of the chosen unit cell. We will attempt to explain the origins of these relationships and add our findings to the analytical and semi-empirical models that currently exist. This will aid the development of design methodologies for latticed parts that enable the most appropriate cell type to be chosen for a certain application or set of load conditions. Ultimately this will facilitate lightweight latticed parts with the highest achievable mechanical performance.

Following this general introduction, a short section of this paper introduces the pre-existing models for the cell density and size dependence of the mechanical properties of lattices. We go on to present our experimental methods, including SLM part production and tensile testing, before analysing and discussing the results. In a concluding section we discuss the implications of our findings for the future use of lattices in AM and propose areas for future investigation.

The Gibson-Ashby Model

Gibson and Ashby analysed the mechanical properties of metal and polymer foams by considering them as systems of open or closed regular cells, expanding upon previous work on honeycomb structures[17, 18]. They used analytical methods based on the beam theories of Timoshenko and Goodier[19], and Roark and Young[20] to relate several properties (the modulus and plastic yield strength, amongst others) of a foam under compression or tension to its relative density, ρ ∗. The relationships put forward by Gibson and Ashby were seen to describe the mechanical bahaviour of several foams adequately[17, 21, 22]. The equations have since been applied to latticed structures comprising repeating regular unit cells, an application for which they were essentially devised[6, 23, 24].

Before presenting Gibson and Ashby’s relationships, some properties of a lattice structure must be defined. We define the relative density as

$$ \rho^{*}=\rho_{\textrm{latt.}}/\rho_{\textrm{sol.}}, $$
(1)

where ρ latt. and ρ sol. are the densities of a lattice structure and a fully-dense solid, respectively (both composed of the same material). In this way, ρ ∗, can be seen simply as the fraction of a particular volume taken up by the solid material of the lattice. Similarly, we define

$$\begin{array}{@{}rcl@{}} E^{*}&=E_{\textrm{latt.}}/E_{\textrm{sol.}}, \end{array} $$
(2a)
$$\begin{array}{@{}rcl@{}} \sigma_{U}^{*}&=\sigma_{U~{\textrm{latt.}}}/\sigma_{U~{\textrm{sol.}}}, \end{array} $$
(2b)

where E ∗ and \(\sigma _{U}^{*}\) are the modulus and ultimate tensile strength of a lattice represented as fractions of those of a fully-dense solid of the same material. These will henceforth be referred to as the relative modulus and relative ultimate tensile strength. Gibson and Ashby proposed a semi-empirical scaling relationship for E ∗ as a function of the relative density[17, 18, 25]:

$$ E^{*}=C_{1}\rho^{*m}, $$
(3)

where the exponent m varies depending on the relative contributions of stretching and bending of the struts in the cellular deformation process; it is given as m=2 for open, bending-dominated, cell types, such as the BCC cell studied here, with additional terms being added to equation (3) to account for membrane stresses and gas pressure effects in closed cells. The prefactor C 1,“includes all of the geometric constants of proportionality[17],” and therefore varies according to the specimens being examined.

The issue of ultimate tensile strength is more involved, with a simple relationship of the form of equation (3) not forthcoming. However, for an open-celled lattice under compression, Gibson and Ashby proposed

$$ \sigma_{\text{cr}}^{*} \propto l_{c}^{~(-\frac{3}{m_{w}})}\rho^{*(\frac{3}{2}-\frac{1}{m_{w}})}, $$
(4)

for the crushing strength, \(\sigma _{\text {cr}}^{*}\), as a function of cell width, l c , and relative density. m w is the Weibull modulus, a parameter used to quantify the variance in strength amongst samples of brittle parts. It is related to the distribution of flaws in a material and, in this case, it principally dictates the size dependence of the part strength; the larger the Weibull modulus, the smaller the reduction in strength due to increasing cell size. The physical mechanism behind this is the fact that larger cells are more likely to contain larger pre-existing cracks or pores, which are ultimately responsible for part failure[17].

For an open-celled lattice under tension, Gibson and Ashby similarly proposed

$$ K_{IC}^{*} \propto l_{c}^{~(\frac{1}{2}-\frac{3}{m_{w}})}\rho^{*(\frac{3}{2}-\frac{1}{m_{w}})}, $$
(5)

to describe the fracture toughness, \(K_{IC}^{*}\), again, as a function of cell width and relative density. In this case, m w =6 indicates cell size independence, with the fracture toughness increasing with cell size if m w >6 and decreasing with cell size if m w <6. The possible applicability of these relationships, and the meaning of the Weibull modulus in the context of lattice structures, is explored later in this work.

Cell size Dependence of the Mechanical Properties

The motivation for this work stems from the recognition that Gibson and Ashby’s parameter C 1, introduced in equation (3), must subsume virtually all of the geometrical information about the lattice except for its relative density. The factors thought to determine this parameter are; (i) the choice of unit cell type, of which there are a great many with different potential applications and varying suitability for SLM, and AM in general, (ii) the global shape of the lattice structure, (iii) the type of stress, and (iv) the size of the repeating unit cell. This work focuses on the last of these properties, providing information to better design latticed parts for real applications.

Notably, Yan et al. studied Shoen gyroidal cells, made by SLM from 316 L stainless steel, and observed a reduction in Young’s modulus from ∼ 306 to 241 MPa upon increasing the cell size from 2 to 8 mm[13]. The authors attributed this 21% reduction in Young’s modulus to a decrease in the density of their specimens’ lattice struts, from 99.5 to 90.6%, which accompanied the increase in cell size. Gibson and Ashby’s density relationship (equation 3) seems to support this explanation, as it would provide a Young’s modulus reduction of (0.9952−0.9062)/0.9952×100%=17%, if we make the choice m=2 (i.e. bending dominated deformation). Therefore, if varying density was the cause for Yan et al.’s observed Young’s modulus reduction, it provides evidence that the deformation of their Shoen gyroidal cells was bending dominated, as is suggested in recent theoretical work by Khaderi et al.[26].

With respect to the relative ultimate tensile strength of lattices, a cell size dependence is essentially already predicted (through the closely related properties in equations (4) and (5), though its form has not been explicitly determined. We will attempt to identify this dependence and relate it to existing theory. Any knowledge gleaned regarding the performance of lattices with different sized cells and equivalent density, will be useful in the development of more comprehensive lattice design tools.

Experimental Methods

Specimen Production

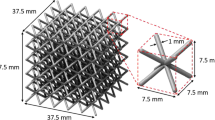
Tensile test specimens with square cross-section were designed according to the ISO standard 6892-1:2009. Specimens with two gauge widths, 5.00 and 7.00 mm, were manufactured. The gauge volumes comprised a repeating BCC unit cell of varying size contained within a ‘net skin’, which is a thin surrounding wall (determined after production to have thickness 0.243±0.007 mm) with periodic holes to allow the egress of the unmelted powder after part production. The net skin was employed so that an extensometer could be fitted to the exterior of the gauge surfaces, allowing more accurate and precise strain measurements than could otherwise be achieved. The BCC unit cell, which in our work had a relative density of 0.36, is illustrated in Fig. 2.

Fig. 2
figure 2

BCC unit cell with a relative density, ρ ∗, of 0.36

Full size image
Table 1 Range of unit cell widths and total number of cells in the gauge volumes of the two types of test specimen
Full size table

The specimen details, that is the range of unit cell sizes for each tensile bar, are provided in Table 1. Figures 3 and 4 are CAD representations of the tensile specimens; the former shows both the 5.00 and 7.00 mm width versions of the specimen, including dimensions, while the latter provides a comparison of a latticed gauge region with and without the net skin, revealing the BCC cells beneath. Several parts with solid gauge volumes were also examined, so that the relative mechanical performance of the latticed specimens could be determined.

Fig. 3
figure 3

CAD representations of the 5.00 mm width (right) and 7.00 mm width (left) tensile specimens, including dimensions

Full size image
Fig. 4
figure 4

CAD representation of the latticed region of the 5.00 mm width specimen with \(1.\dot {66}\) mm unit cells. The region is shown with (left) and without (right) the net skin that was employed so that a surface-mounted extensometer could be used during testing

Full size image

The specimens were manufactured from Ti-6Al-4V using a Renishaw AM250 SLM machine. The laser power, laser scan speed and hatch spacing were 200 W, 600 mms −1 and 150 μm, respectively, and a ‘meander’ scanning strategy was taken, whereby the hatch path of each subsequent layer was rotated by 67∘ from the previous one. This strategy serves to reduce any build plane anisotropy, geometric or mechanical, that might occur if there were no hatch rotation. The feedstock powder was deposited in 50 μm layers prior to each laser scan. The powder particles were spherical (see Fig. 5) and had a Gaussian size distribution with a mean of 32 μm and standard deviation of 13 μm. The test specimens underwent a stress relieving heat treatment (600 ∘C for 3 hours under an Ar-rich atmosphere) before removal from the build plate. Figure 6 shows a selection of the 7.00 mm gauge width specimens prior to testing, including one which is solid and two latticed parts with unit cells of width 3.50 and 7.00 mm.

Fig. 5
figure 5

SEM micrograph of the Ti-6Al-4V feedstock powder used in the production of SLM specimens

Full size image
Fig. 6
figure 6

Photographs of a selection of 7.00 mm gauge parts. From left to right; solid gauge section, 3.50 mm unit cell and 7.00 mm unit cell. The inset shows a close-up of the latticed regions, with the net skin and internal spars visible

Full size image

An important factor relating to the design of the test specimens described here is that of number of cells. As can be seen in figures 4 and 6, the smaller unit cells tessellate more than the larger cells in the gauge volumes of our specimens. This is clearly a consequence of constraining the size of the specimens as opposed, say, to scaling them in relation to the cell size, keeping the number of cells constant in each case. Regarding applicability to actual parts, these designs should provide findings which are more useful because of the constrained specimen size; part dimensions are generally constrained by application and environment, therefore it is more useful to determine how the combination of cell size and cell number affect mechanical properties, even if the effects of these two variables cannot be isolated easily. Section 1 of this work contains a data analysis strategy that recognises and addresses this issue. Table 1 provides the numbers of repeating unit cells contained in the 5 and 7 mm gauge specimens.

Tensile Testing

Moduli, E latt., and ultimate tensile strengths, σ U latt., were recorded for the latticed 5.00 and 7.00 mm test bars. All measurements were made using an Instron-5969 universal testing machine, with the displacement applied at a rate of 0.01 mm s −1. An Instron series 2630 surface-mounted extensometer with 25 mm gauge length was clamped to the center of the latticed section of each test specimen in order to accurately record the strain.

The moduli were determined from the regions up to around 0.5% strain of the experimental stress-strain curves; at approximately this level of strain, the surface-mounted extensometer was removed to ensure it would not be damaged upon part failure. Simultaneously, and continuing above 0.5 %, the strain values were recorded directly from the displacement of the universal testing machine cross heads. This method is sensitive to the deformation of the part and several components of the machine, due to machine compliance.

For this reason, a machine compliance correction was applied by comparing the cross head displacement data with that from the extensometer. This assumes a relationship of the form[27],

$$ \delta_{R} = \delta_{S} + \delta_{C}, $$
(6)

where δ R is the total displacement recorded by the testing machine, δ S is the sample deformation (in this case measured by the surface-mounted extensometer) and δ C is the deformation in the loading system due to the machine compliance. The machine compliance, C m , is given by δ C /F, where F is the applied load. Its values were seen to be consistent across multiple specimens, yielding a mean of 5.9±0.5×10−5 mm N −1.

Importantly, the moduli, which were determined purely from the low strain extensometer data, and ultimate tensile strengths were unaffected by this post-measurement compliance correction. Therefore, even allowing for non-ideal correction of the cross head displacement data, there was no invalidation of the most pertinent information from the tests. Measurements were performed on at least two, but usually three, specimens per design (each combination of cell size and gauge width), with the means and standard errors being used for subsequent analysis.

The moduli of completely solid (non-latticed) test specimens were also recorded. These were 102.3±0.9 and 101±1 GPa for the 5.00 and 7.00 mm bars, respectively, and provide the E sol. of equation (2a). They agree with each other within experimental error and are slightly lower than values typically associated with cast and forged alloys (∼105−116 GPa[28, 29]). The ultimate tensile strength of the solid bars was found to be 1.07±0.01 GPa, slightly higher than expected from cast alloy but lower than has been reported for some Ti-6Al-4V SLM parts[29–31]. This value constitutes σ U sol. of equation (2b).

Results and Discussion

Figure 7 shows the fractured ends of a sample of latticed test specimens. A feature among the majority of the examined latticed bars was that critical fracture occurred across a single horizontal plane; only occasionally were intact lattice nodes (the intersections of eight diagonal struts) observed protruding from fracture surfaces. This suggests that a likely failure mode was the initial fracture of an individual strut followed by others in the same plane which, as each failed, led to a greater load distributed over a smaller cross-sectional area. This is supported by the observation, presented in Fig. 8, of sawtooth features in the stress-strain curves of some specimens.

Fig. 7
figure 7

Photographs of a selection of fractured latticed specimens. (a) and (b) are 7.00 mm bars with 3.50 and 7.00 mm unit cells, respectively, while (c) and (d) are 5.00 mm bars with 2.50 and 5.00 mm unit cells, respectively

Full size image
Fig. 8
figure 8

Stress-strain curves for the 5 mm (above) and 7 mm (below) width latticed tensile specimens with varying cell size. Below ∼ 0.5% strain the data from the surface-mounted extensometer is shown as a thicker black line

Full size image

Experimental stress-strain curves for some 5.00 and 7.00 mm latticed bars are provided in Fig. 8. There are a few features of note; (i) the modulus, taken from the extensometer data below ∼0.5% strain, and ultimate tensile strength of each latticed part decreases with increasing unit cell size, (ii) though we must be careful in extracting absolute values, due to the the machine compliance correction discussed above, there is evidence that increasing unit cell size generally results in lower maximum strain at break (the 7 mm gauge bar with 3.50 mm cells is a clear exception, with a relatively high maximum strain at break), and lastly (iii) the sawtooth features seen for the 7 mm bar with 1 mm cells (figure 8, marked with ‡) are believed to relate to the successive tensile failure of individual lattice struts prior to the ultimate failure of the part; this was evidenced audibly during the testing of all three such specimens, but was absent for other types.

Numerical results from the mechanical testing of all specimens are provided in Table 2, where the relative properties, E ∗ and \(\sigma _{U}^{*}\), are as defined in equations (2a) and (2b). The unit cell volumes, v c , for each specimen type are also included; for BCC cells these are simply the unit cell width cubed. v ∗ is the relative volume, which is defined and discussed in Section 1. The results in Table 2 are discussed in the following sections.

Table 2 Absolute and relative mechanical properties of the latticed specimens for varying unit cell sizes. The relative properties v ∗, E ∗, and \(\sigma _{U}^{*}\)are defined in the text
Full size table

The Modulus

The relative moduli of the 5 and 7 mm gauge bars are plotted in Fig. 9 as a function of cell width. The E ∗ values decrease with increasing cell width, from (19.4±0.5)% to (7.0±0.5)% of the E sol. values obtained from solid bars. The reduction in modulus over the full range of cell size is ∼ 64%. As previously discussed, Yan et al. observed a smaller reduction (21%) in the modulus of their latticed parts with increasing cell size and attributed it to decreasing strut density[13]. X-ray computed tomography (CT) measurements of a sample of our 5 and 7 mm latticed bars put the strut density at (97.6±0.2)%, with little variation between parts and no correlation between density and cell size. This density is not ideal, but the lack of variation in strut density between specimens with different cell sizes implies that our modulus reduction with increasing cell size is not caused by increasing levels of porosity. The second feature of note in Fig. 9 is that the data from both the 5.00 and 7.00 mm test bars appear follow the same distribution, signifying that we may possibly treat them as a single data set for the purposes of data analysis.

Fig. 9
figure 9

Relative modulus, E ∗, of the 5.00 and 7.00 mm latticed test bars as a function of cell width, l c . Weighted least-squares power law fits are shown as dashed, solid and dotted lines. The fitting procedure is described in the text. The inset shows the same data and resulting power law fits plotted with a log-log scale

Full size image

We first hypothesize that there is a power law relating E ∗ and l c , similar to the relationship provided in equation (3) for ρ ∗, i.e.

$$ E^{*} = U_{1}~l_{c}^{~n_{1}}, $$
(7)

where U 1 and n 1 are analagous to Gibson and Ashby’s parameters C 1 and m. The resulting weighted least-squares fit is shown as a dashed line in Fig. 9. The values of U 1 and n 1 were found to be 0.179± 0.009 and −0.56± 0.05, respectively. However, this fit is statistically rather poor, with a \(\bar {\chi ^{2}}\) (reduced- χ 2) value of 2.29, and the fit residual, shown in the upper panel of Fig. 10, shows significant additional structure. Clearly, this simple model is incapable of describing the data set well.

Fig. 10
figure 10

Residuals from the relative modulus fits of Fig. 9.

Full size image

Two variations on this scaling law were trialled; one with a constant to modify the cell width, the other with a constant to modify the relative modulus. The modified power laws are given by \(E^{*} = U_{1}~(l_{c} + \delta _{l_{c}})^{n_{1}}\) and \(E^{*} = U_{1}~l_{c}^{~n_{1}}+\delta _{E^{*}}\), and are shown in Fig. 9 as solid and dotted lines, respectively. The \(\bar {\chi ^{2}}\) values associated with these fits were much improved, with the former providing a value very close to unity. Furthermore, the central panel of Fig. 10 shows far less residual structure for the \(E^{*} = U_{1}~(l_{c} + \delta _{l_{c}})^{n_{1}}\) fit, compared to the the unmodified form. The parameters from this fit were U 1=0.11±0.01, \(\delta _{l_{c}} = -0.8 \pm 0.1~\text {mm}\) and n 1=−0.28±0.07. The determined cell width offset of -0.8 mm could have been indicative of a systematic error in the manufacture of the latticed bars, i.e. the cells widths being consistently too large by 0.8 mm. This issue was subsequently investigated; the cell widths were found to conform well to the designed values as specified in the CAD drawings.

The second modified power law, \(E^{*} = U_{1}~l_{c}^{~n_{1}}+\delta _{E^{*}}\), provided a poorer fit than that described above, with \(\bar {\chi ^{2}} = 1.18\) and more residual structure, but it was still superior to the unmodified form. The fitted parameters are \(U_{1} = 0.12 \pm 0.01\), n 1=−1.3±0.4 and \(\delta _{E^{*}} = 0.06 \pm 0.01\).

Anomalous Behaviour of the Smallest Cells

Furthering the analysis of the modulus data, an alternate interpretation is that data from samples with 1.00 mm cells may be statistical outliers or are described by a different physical model than that which describes the rest of the data set. Evidence to support this hypothesis comes from the fit residuals in Fig. 10, where the 1.00 mm data are almost equally poorly described by all three models trialled so far. There may be a physical cause for this; the cavities, or voids, in the 1.00 mm lattice structures are small enough for the complete removal of Ti-6Al-4V feedstock powder to be problematic. If residual powder remained in some of the internal cavities for the 1.00 mm cells, the mechanical properties of those bars under tension may have been higher, or at least in some way different, than if they had been completely empty.

Another explanation is that the performance of these cells is affected by the presence of loosely bound powder around the lattice struts and nodes. Loosely bound, or partially sintered, powder is a persistent issue in SLM, often increasing the surface roughness and possibly providing regions of high stress concentration, though this is more likely to affect part strength than modulus. Its presence is related to the choice of laser processing parameters and the morphology of the feedstock powder. It has been previously observed attached to the struts of SLM lattice structures [6, 13, 32]. In the case of our latticed structures, loosely bound powder may have a larger effect for smaller cells, where the dimensions of the struts and nodes are smallest. The removal of much of this powder from the exterior of a part can often be achieved with a post-process treatment such as sandblasting. However, this technique is not particularly suitable for lattice structures where most of the interior cells are obscured by those around the outside edges.

A final possible reason for the anomalous behaviour of the smallest cells lies in the fact that their constitutive struts have designed thicknesses which are not significantly greater than the width of the characteristic melt pools formed by the SLM process. These melt pools are around 200 μm for Ti-6Al-4V[33], whereas the strut thicknesses for the 1.00 mm cells are around 300 μm. Further, the microstructure of SLM Ti-6Al-4V is composed of prior β columnar grains with widths of the order 100 μm[33]. The similarity of these length scales means that the smallest struts are likely to have pronounced staircase-shaped profiles, as has been previously reported by Yan et al.[6], and, unlike the thicker struts of the larger cells, may not be sufficiently greater in size than the microscopic features of the material to be reasonably treated by continuum mechanics. Therefore, the anomalous behaviour of the 1.00 mm cells may be due to their struts being close in size to a representative volume element (RVE) for SLM Ti-6Al-4V.

The relative moduli were re-fit with the basic power law, \(E^{*} = U_{1}~l_{c}^{~n_{1}}\), this time excluding those data from the 1.00 mm cells; the result is shown in Fig. 11. The parameters are U 1=0.144±0.002 and n 1=−0.130±0.004. The \(\bar {\chi ^{2}}\) value is extremely low at 0.02, most likely indicating that, with the exclusion of two data points (and the reduction to just three degrees of freedom for the fitting procedure), the fit is over-paramaterised. Nevertheless, it is worth noting that SLM has inherent processing limitations, and these may affect the observed mechanical properties of a part when the feature sizes become relatively small .

Fig. 11
figure 11

5.00 and 7.00 mm bar E ∗ data fit with \(E^{*} = U_{1}~l_{c}^{~n_{1}}\). Data from the 1.00 mm cells are excluded from the fit, as described in the text. The inset shows the same data and power law fit plotted with a log-log scale. The lower panel shows the corresponding fit residual

Full size image

Alternate Analysis

In Fig. 12 we present E ∗ as a function of the relative cell volume, v ∗, which we define as

$$ v^{*} = v_{\mathrm{c}}/v_{\textrm{latt.~env.}}, $$
(8)

where v c is the cell volume (given simply by \(l_{c}^{~3}\)) and v latt. env. is the volume of the latticed environment in which the cell resides. For the 5.00 and 7.00 mm bars, v latt. env. has values of 875 and 2401 mm 3, respectively (i.e. 5×5×35 mm and 7×7×49 mm, where 35 and 49 mm are the lengths of the latticed gauge sections of the bars).

Fig. 12
figure 12

Relative modulus, E ∗, of the 5.00 and 7.00 mm latticed test bars as a function of relative cell volume, v ∗. The inset shows the same data and resulting power law fit plotted with a log-log scale

Full size image

Choosing to work with a relative measure of cell size like v ∗, rather than the absolute values of l c or v c , may provide a way to formulate general descriptions of lattices that are independent of the size of the part and, therefore, the absolute size of the cells it contains. There is precedent for this methodology in the way we work with E ∗, for example, instead of E. This is done so that general rules, such as equations (3), (4) and (5), may be developed that apply to a range of materials, including polymers, ceramics and metals, where the absolute moduli differ greatly. Similarly, ρ ∗ is used instead of ρ because the absolute densities of the materials in question also vary significantly. The main property of interest is how a lattice of a certain material performs compared to a fully dense solid of the same material.

To explore this, an unmodified power law was applied to the E ∗(v ∗) data and it is shown as a solid line in Fig. 12. Weighted least-squares fitting provided the result; E ∗=(0.051±0.004) v ∗(−0.17±0.01) with \(\bar {\chi ^{2}} = 1.68\). The fit is statistically poorer than the previous best, but it has the advantage of describing the E ∗ behaviour equally well over the full range of cell size, including the smallest cells.

We can see from Fig. 12 that two pairs of specimens, both the bars that contain 56 cells and both the bars that contain 7 cells, have performed similarly, with the larger bar having E ∗ values ∼9.5% lower than the smaller bar. In fact, when analysed with this approach, the data from the largest cell specimens agree within experimental error.

If we examine the limiting case in which v ∗ tends to its largest possible value, 1, we find for our fitted function, \(\lim _{v^{*} \to 1}E^{*}(v^{*}) = 0.051 \pm 0.004\). This suggests that a specimen in which the latticed region was composed of a single BCC unit cell, that is v ∗=1, would have a modulus around one twentieth of the value observed for solid material. Such a specimen cannot exist for our test bar geometry with its elongated gauge region. However, it would be beneficial for future investigations, which make use of different test specimen geometries, to also consider this extreme value case.

Ultimate Tensile Strength

The relative ultimate tensile strengths, \(\sigma _{U}^{*}\), of the 5.00 and 7.00 mm latticed bars are shown in Fig. 13. They take values similar to those seen in Fig. 9 for E ∗, decreasing from (17.7±0.2)% to (5.2±0.2)% of the strengths of fully-dense test bars, a reduction of ∼71%. Following the same approach as outlined above, three power laws, two with additional constants for l c and \(\sigma _{U}^{*}\), were trialled; they are shown as dashed, solid and dotted lines in Fig. 13.

Fig. 13
figure 13

Relative ultimate tensile strength, \(\sigma _{U}^{*}\), of the 5.00 and 7.00 mm latticed test bars as a function of cell width, l c . The inset shows the same data and resulting power law fits plotted with a log-log scale

Full size image

Once again, the power law of the form \(\sigma _{U}^{*} = U_{2}~(l_{c} + \varepsilon _{l_{c}})^{n_{2}}\) provided the best fit, with the unmodified power law performing significantly worse. The parameters are U 2=0.7±0.6, \(\varepsilon _{l_{c}} = 2 \pm 1~\text {mm}\) and n 2=−1.2±0.3. The \(\bar {\chi ^{2}}\) values for the three trialled fits are larger than those obtained in the E ∗ analysis, reflecting statistically poorer fits overall; this is due mainly to the smaller fractional errors associated with the σ U measurements. This has also given rise to larger uncertainties in the determined parameters U 2, \(\varepsilon _{l_{c}}\) and n 2. The larger \(\bar {\chi ^{2}}\) values might be indicative that a different, and perhaps more complex, model is required to describe the \(\sigma _{U}^{*}\) data. The possibility of treating and fitting the data from 5 and 7 mm gauge bars separately was explored, but the relatively small number of data points in each case, 4 and 3, respectively, rendered this exercise uninformative. Interestingly, switching the dependent variable to the relative cell volume, v ∗, instead of l c , as implemented previously for the E ∗ data, did not provide an improved fit when using the unmodified power law, \(\sigma _{U}^{*} \propto v^{*n_{2}}\).

The Weibull Modulus

In a final and novel exploration of our data set, we used the determined parameter n 2 from our best fit of the \(\sigma _{U}^{*}\) data to estimate the effective Weibull modulus of our set of latticed parts. We speculate that the cell width dependence for \(\sigma _{U}^{*}\) is likely to be, or be similar to, one of those provided in equations (4) and (5) for related mechanical properties . Thus, our \(\sigma _{U}^{*}\) values would decrease with cell size according to \(l_{c}^{~-\frac {3}{m_{w}}}\) or \(l_{c}^{~(\frac {1}{2}-\frac {3}{m_{w}})}\). The first case yields m w =2.5±0.6, whilst the second provides m w =1.8±0.4. Reasonable sources of comparison for these values are understandably scarce in the literature, owing to the paucity of experimental research on lattice structures produced by SLM. The most meaningful results currently available may be the work of Blazy et al. and Ramamurty et al., who provide values of m w between 8 and 16.7±0.6 for some aluminium foams[34, 35], but since both the material and the manufacturing process in those works are different from our own, direct comparison cannot be made.

The deduction of Weibull moduli for parts in this way is new. In the characterisation of materials, Weibull moduli are generally used to describe the flaw distributions and failure statistics in brittle, but fairly uniform, solids. In contrast, our specimens possess the kind of flaws normally associated with failure analysis (surface roughness, internal pores, etc.) as well as unique features that result from the use of AM, most significantly the complex repeating lattice geometry with its non-uniform stress distribution and incompletely understood deformation mechanisms. Therefore, the comparability of these Weibull moduli with values obtained for more conventional materials is uncertain.

As mentioned in our introductory section, the role of the Weibull modulus is to determine the magnitude of the cell size dependence of the part strength and fracture toughness. Understanding how our values of m w , which have here been determined solely for the BCC lattice with a fixed density, relate to other work on lattices is worthy of further research, as it may be found that different combinations of cell geometries and SLM materials exhibit different size effects, and are therefore better suited to use in parts of different shapes and under different loading conditions.

Conclusions

The main, and novel, finding of this investigation is that there is a significant dependence of the mechanical properties of BCC lattice structures on the size and number of the cells they comprise. This has a major implication for the design of latticed parts; with a fixed relative density, and therefore part mass, large numbers of smaller cells provide superior mechanical properties than small numbers of larger cells.

We have shown that analysing the E ∗ data as a function, not of the absolute cell width, l c , but of the relative cell volume, v ∗, provided a reasonable description across the full range of cell size. An advantage of this analytical method is that it provides a way to generalise the performance of latticed parts of different sizes and number of cells, in much the same way that the well established use of E ∗ and ρ ∗ allows us to directly compare lattices of different materials and volume fractions. If this relationship proves similarly successful in further investigations, it may ultimately be found that the relative modulus of lattices can be described generally by

$$ {E}^{*} = U\rho^{*m}v^{*n}, $$
(9)

where U is dependent only on the choice of unit cell and the global shape of the part. The implication would be that a latticed cube composed of 1000 unit cells would have the same relative modulus regardless of its size. This requires further investigation.

We used the determined l c exponent from the ultimate tensile strength data to estimate an effective Weibull modulus four our lattices, making the assumption that \(\sigma _{U}^{*}\) follows a law similar to those proposed by Gibson and Ashby for crushing strength and fracture toughness. Our determination of Weibull moduli with this approach delivers a new and useful metric for comparing the mechanical performance of different lattice structures.

On the basis of the results presented here, there are several areas which should be investigated further to advance the understanding of SLM lattice structures and improve their applicability to real parts. These include; (i) the possible role of the net skin in determining the mechanical properties of latticed parts (which is expected to decrease in significance with increasing part size), (ii) the physical mechanism for the dependence of E ∗ on v ∗, (iii) the behaviour of E ∗ as v ∗ approaches the value of 1 (i.e. a single unit cell encompassing the volume of the part), and (iv) the effect of cell size on the mechanical properties of lattices with a range of different cell types. Further attention should also be paid to the energy absorption of lattice structures under dynamic loading (i.e. high velocity impact). It would be of great academic and industrial interest to determine how the energy absorption and associated deformation mechanisms relate to the cell design variables (cell type, size and density), so that truly optimised latticed parts, which provide stiffness, strength and energy absorption where required, can be realised.