Mining latent patterns in geoMobile data via EPIC

Abstract

We coin the term geoMobile data to emphasize datasets that exhibit geo-spatial features reflective of human behaviors. We propose and develop an EPIC framework to mine latent patterns from geoMobile data and provide meaningful interpretations: we first ‘E’xtract latent features from high dimensional geoMobile datasets via Laplacian Eigenmaps and perform clustering in this latent feature space; we then use a state-of-the-art visualization technique to ‘P’roject these latent features into 2D space; and finally we obtain meaningful ‘I’nterpretations by ‘C’ulling cluster-specific significant feature-set. We illustrate that the local space contraction property of our approach is most superior than other major dimension reduction techniques. Using diverse real-world geoMobile datasets, we show the efficacy of our framework via three case studies.

1 Introduction

The wide proliferation of various kinds of (physical or virtual) sensors in the physical and/or cyber worlds has enabled us to collect a whole gamut of (spatial-temporal) data, e.g., voice calls between users at various locations in a cellular network, human commuting behaviors across different locations in a transport network such as buses, subways, taxicabs or car sharing services, check-ins and social interactions among users at diverse locations in a location-based online social network such as Foursquare. We use the term geoMobile to refer to such datasets collected from these networks, as they are characterized with two salient features: they are associated with geo-locations (e.g., gathered at cell towers or tagged with location information), and more often they capture user actions on-the-move.

With abundance of diverse geoMobile datasets, mining them is an important activity that has wide applications, from cellular network traffic engineering to urban transportation management, smart city planning, social behavior analysis and cyber-physical world security. For example, one can ask questions such as: can geo-locations and user actions (e.g., making phone calls) at these locations capture and reflect certain underlying community structures? In other words, can one classify regions into various communities based on their associated human-actions at certain geo-locations? More broadly, how user mobility and behavior are associated with geo-locations? Unfortunately, gleaning meaningful and actionable knowledge from geoMobile data are non-trivial. We list several reasons why mining geoMobile datasets is a challenging task. First, there is huge heterogeneity in (user) activities associated with different geo-locations, which leads to very skewed data distributions. This is partly due to the fact that there are often very disparate factors driving user mobility and behavior at various geo-locations; geoMobile data is thus likely to more closely mirror user relations and interactions in the real “physical” world (than mere the “cyber” world). Second, depending upon the spatial and temporal resolutions, geoMobile datasets are often high-dimensional. Underlying patterns, if present, may either be a linear or a non-linear combination of a varying subset of features. Therefore, judicious feature engineering is paramount. However, without prior knowledge of the problem domain coupled with high pattern diversity in geoMobile datasets, feature selection or extraction from high-dimensional data becomes difficult. Third, even once we have appropriate representative (or latent) features and can obtain clusters, it is hard to make sense out of the clusters without the aid of a visualization technique. Lastly, the factors which cause the formation of (latent) clusters in the feature space are not always easily understood. It is important to relate and map a cluster back to its “raw” feature set (rather than the latent feature set) that are critical to its formation. Such information can help to naturally interpret the results.

We combine some of the popular algorithms with state-of-the-art machine learning tools to develop a framework to extract, visualize and interpret latent patterns arising from geoMobile datasets. We address the challenges discussed earlier and summarize our central contributions as follows:

1) :

Instead of directly working on observed features, we take into account the feature distribution of every data point and derive a new (symmetric) similarity matrix. This amounts to transforming the data points into a high-dimensional feature space. We apply the Laplacian Eigenmap (LE) method to extract latent features and “clusters” data points lying in certain lower-dimensional (non-linear) sub-manifolds (see Section 3.1).

2) :

We show that a state of the art visualization technique t-SNE [21] is a density preserving algorithm. This provides a theoretical justification for its success in practice. To get insights about the structure of geoMobile data and visualize clusters in the feature space, we further project latent features into a 2-dimensional space using Lt-SNE – a proposed approach that uses t-SNE in conjunction with LE which is an improvement over standard t-SNE (see Section 3.2). To show the effectiveness of Lt-SNE, we provide justification by studying and comparing its local space contraction property with other prominent dimension reduction techniques (see Section 4.2).

3) :

Taking cue from information theory, we supplement our framework by designing an algorithm to further cull a set of raw (i.e., observable) features that are most significant in contributing to the cluster’s formation (see Section 3.3) so as to obtain meaningful interpretations of extracted latent patterns.

4) :

We evaluate our framework based on the performance of its individual components specifically clustering and visualization component (see Section 4) and show its empirical superiority over other state-of-art baselines.

5) :

Finally to demonstrate the efficacy and generality of ourv proposed framework in real world, we share our experience of analyzing geoMobile datasets under multiple settings using several case studies (see Section 5). We employ two real-world geoMobile datasets: i) a mobile call detail record (CDR) dataset consisting of more than 500 million voice calls and SMS messages between users collected at cell-tower levels spanning a couple of months from a nation-wide cellular service provider in Africa, and ii) a subway transit dataset collected over a week from Shenzhen, China with more than 2.7 million passengers. Despite very different nature of these two datasets, the results look promising.

1.1 Related work

In literature, there exist multiple methods to extract latent patterns from geoMobile-based datasets. One of the classical approach is principal component analysis (PCA). PCA-based methods have been successfully applied to traffic matrix estimation, network tomography and anomaly detection [10, 23, 26] using origin-destination (OD) matrices derived from Internet traffic. As discussed earlier, user actions and behavior are often driven by disparate factors leading to high diversity and skewed data distributions in geoMobile datasets rendering classical linear methods such as PCA and latent semantic indexing (LSI) ineffective. Hristova et al. [6] further provides a detailed analysis of measuring social diversities from mobility datasets and reveals the large diverse nature of such datasets. Another matrix factorization approach is non-negative matrix factorization NMF (e.g., [27]) developed to address the interpretability issue associated with the low-rank matrix approximations. A fundamental premise of NMF is that the entities lies in lower linear subspaces of the original higher-dimensional matrix which may not hold for geoMobile datasets. Fan and Zhang [5, 28] adopt tensor factorization, the generalization of NMF, to study city basic life pattern and analyze urban transportation.

Many other methods such as hidden Markov models (HMMs) and Gaussian mixtures models (GMMs) have also been developed to analyze and predict urban dynamics [2, 7, 24]. Unfortunately, inference in HMMs and GMMs suffer severe performance degradation in the high-dimensional setting due to overfitting and constraints (e.g. covariance matrices should have simple structure, say diagonal). These models have large number of free parameters that lead EM algorithm to converge to poor clustering results [9, 20].

Latent Dirichlet Allocation (LDA) models are also employed for extracting latent patterns for tasks such as identifying regions of different functions in urban areas and urban topic analysis [8, 25]. In general, LDA models have the capability to handle high dimensional data, however choice of hyper-parameters is not apparent [22] and relies upon approximate inference algorithms such as Gibbs sampling for efficiency.

Deep learning frameworks such as discussed in [1, 11] have also been developed to extract latent features and can be seen as a complement to our work. But we go beyond to include visualization and interpretation as an important step for aiding and justifying the data analysis part and provide theoretical and empirical evaluations with respect to other popular techniques.

2 geoMobile datasets & its characteristics

In this paper, we primarily focus on two geoMobile datasets representing different application domains; 1) a mobile call detail record (CDR) dataset collected from a nationwide cellular network; and 2) a subway transit record dataset from a large city in China. We provide the description of the datasets and show the diversity in patterns inherent in them. Note, the nature and user population of both datasets are completely different from each other.

2.1 Dataset 1: Mobile call detail records

Dataset 1 is a call detail record (CDR) dataset that comes from a national cellular service provider of a developing African nation. Every record of this dataset contains information such as <timestamp, source base station, destination base station> associated with a voice call or a SMS message (both of which we will refer to as calls in this paper). The dataset spans over a couple of months. This dataset consists of over 1,000 towers (or base stations) covering the entire country, with over 500 million call records.

We refer to a cellular base station as a tower. When Bob (caller), connected to tower A, makes a call to Alice (callee) who is connected to tower B, tower A is the origin tower, whereas tower B is the destination tower. In other words, this call will be considered as an outgoing call for tower A, and an incoming call for tower B. However, if both Alice and Bob are connected to the same tower C, i.e., both the origin and destination towers are the same, then we refer to such a call as a “local¹” call. Geographic coordinates of all the towers are known a priori.

Terminologies:

We use call direction to define four aggregated metrics associated with every tower i, 1) SELFcalls: the total number of local calls for tower i, 2) INcalls: the total number of incoming calls received by tower i excluding SELF calls, 3) OUTcalls: the total number of outgoing calls made by tower i excluding SELF calls, and, 4) ALLcalls: the total number of calls seen at tower i (IN + OUT + SELF).

Dataset Characteristics:

In Figure 1, we fix the rank of the towers based on the average number of ALL calls seen per hour, and plot their distributions based on the total volume (ALL calls) as well as the call directions, IN, OUT, and SELF calls. We see that the distributions are highly skewed, with call volumes varying significantly among towers. Some cell towers experience significantlly more calls (either ALL, IN, OUT or SELF calls) than others. Due to their larger population size, we would expect that as a whole, towers in urban cities would have higher call volume than the towers located in rural areas. While the capital city of this nation captures more than 25% of the entire call volume, we observe that the towers with the highest ALL calls are not just from the capital city but also from some of the tier-2 cities of the nation. Moreover, we also observe certain towers in the city do not have high ALL call volumes at all. For each individual cell tower (especially those with high call volumes), we also see that there are high variances in terms of calls to or from other cell towers; there are no discernible patterns across cell towers, suggesting there is high diversity among cell towers.

Figure 1

Distribution of ALL, IN, OUT, and SELF calls, with a fixed order of towers (x-axis) ranked by the ALL calls (i.e. total number of calls)

We now investigate the proportions of SELF, IN and OUT calls over ALL calls at the towers. In Figure 2, we fix the rank of towers the same as in Figure 1 and plot the distributions of call proportions – SELF over ALL (% of local calls), IN over ALL (% of incoming calls), and OUT over ALL (% of outgoing calls). We observe that in general SELF over ALL call ratios dominate compared to IN over ALL and OUT over ALL call ratios, implying people tend to make more SELF calls than IN or OUT calls. However, Figures 1 and 2 show no clear linear relationship between call volume distributions and call proportion distributions. To further investigate, we fix the rank of the towers based on SELF over ALL call ratio (decreasing order), and plot all the call ratio distributions (see Figure 3). We observe there is still high variance in the call proportions. For example, the SELF over ALL call proportions vary between 30% to 55%. This implies certain towers tend to make more SELF calls than others.

Figure 2

IN, OUT, and SELF call ratio distributions with a fixed order of towers (x-axis) ranked by the ALL calls (same as in Figure 1)

Figure 3

Plot similar to Figure 2, only difference being, the x-axis is now ranked by SELF over ALL ratio

Diversity in Locality Effects:

For every tower i in this dataset, we find its $\mathbb {N}$ geographically closest (or neighboring) set of towers G_i and compute tower i’s geo-distance defined as: gd_i = ${\sum }_{j \in G_{i}} dist(i,j) \left / |G_{i}|\right .$, where dist(i,j) is the geographic distance in kilometers (KM) between towers i and j. Similarly, we identify another $\mathbb {N}$ set of towers C_i with whom tower i communicates the most (or makes the most numbers of calls to). We then compute tower i’s call-distance defined as: cd_i = ${\sum }_{j \in C_{i}} dist(i,j) \left / |C_{i}|\right .$, where dist(i,j) has the same semantics as before. To compute geographic distance between towers using their geographic coordinates (which is known a priori), we use the Haversine formula [18]. In this paper, value of k is set to be 5. We compute both gd and cd for all the towers, and show the results in Figure 4. We can clearly see that overall there is slight correlation between both gd and cd values of towers. In other words, majority of the localities (or towers) tend to make more calls to towers that are geographically closer to them, there by exhibiting certain “locality” effect. However, as seen in the plot, there is high diversity in such locality effects. While this maybe a side effect to choosing $\mathbb {N}$= 5, our objective was to show the diversity in these relations. All in all, this gives us an intuition of the existence of certain communities of people (i.e. collection of towers) that tend to talk with each other more than others. However, as evident from the plot, geographic distances between such towers vary significantly. Later, we describe an approach (see Section 3) to identify such communities and show the results obtained in the form of a case study (see Section 5.1).

Figure 4

Relation between (geo-distance) and (call-distance) of towers

All of these observations suggest that there are strong dependency relations between call volumes at tower levels, human activities of either “local” and “mobile” users around these towers. However, these relations are highly varied and non-linear, as evidenced by the eigenvalue plot of a call-volume based origin-destination (OD) matrix derived from the CDR dataset shown in Figure 5. We see that eigenvalues decrease slowly, requiring more than 100 eigenvalues to account for 90% of the variance in the OD matrix. This indicates that PCA is ill-suited for extracting patterns inherent in the OD matrix.

Figure 5

Results of PCA from Dataset 1

2.2 Dataset 2: Subway transit data

Our second dataset represents commute patterns in a subway transit system in Shenzhen, China. The dataset contains information such as – (timestamp, smart card ID, direction (entry/exit), station ID), collected for an entire week in March 2014. More than 2.7 million users traveled over this period. Shenzhen Metro has 5 subway lines (see Figure 15) comprising a total of 118 stations.

Data Preprocessing & Categorization:

We first construct trips by using the direction field of the record – ENTRY indicates a user entering the station while EXIT indicates leaving. We match an ENTRY record with an EXIT record for the same user if both the records satisfy the following three conditions, 1) both records should have occurred on the same day, 2) ENTRYtimestamp is earlier than EXITtimestamp, 3) if there are multiple EXIT records, then we consider the one with the earliest timestamp. Matching user-specific ENTRY with EXIT records helped construct trip information. Next, we categorize users as regular or adhoc. A user is labeled as a regular user if they satisfy the following two conditions: 1) seen on all the working days of the week (Mon. to Fri.), 2) take at least 2 trips per day. We consider regular users to be of the working class population who use the subway system for their everyday commute between home and work. Finally, we consider users to be as adhoc if they are seen for not more than a day or if they just had a single trip for the entire week. We assume that the adhoc users are either visitors or users who take random trips. All remaining users were excluded from our study. More than 10% of the users were categorized as regular and ∼80% as adhoc users. For gaining insights into temporal patterns, we create three intervals of 2 hours representing different periods of the day: 1) Morning: 7-9am, 2) Mid-day: 11am-12pm, 3) Evening: 3-5pm. We label records that fell in these intervals and excluded the rest from our analysis.

Dataset Characteristics:

There is high diversity in the traveling patterns across stations; the distributions of number of passengers boarding and alighting from subway trains at each station are also skewed. We use the subway transit dataset to illustrate the temporal variations and latent patterns therein. Figure 6 is a bubble map showing volume of regular users entering and leaving the subway stations at different time intervals of the day. For example, during the morning rush hours, we see a large number of commuters entering at certain stations and exit in and around downtown area. This suggests, such stations with higher volume of entries correspond to residential areas, i.e. people board the train to go for work. An opposite pattern is seen during the evening rush hours. Volume of traffic during mid-day hours is drastically low compared to the rush hours. However, there are certain subway stations that have relatively higher volume of users entering and leaving. Thus, we observe diversity in the trip patterns seen over time between subway stations.

Figure 6

Effect of time-of-day over travel patterns. Bubble size is proportional to the volume of users entering (or exiting) a station

In summary, we observe both datasets contain highly diverse and skewed data distributions, rendering classical linear dimension reduction or clustering techniques ineffective. As characteristics differ depending upon what dataset is being analyzed, it is nontrivial to come up with a formal definition for diversity. Nonetheless, we assume there are latent factors driving human mobility and user behavior across various geo-locations and over time, as suggested by certain “locality” and “time-of-day” effects. For instance, peak usage hours of public transit systems depend on the general working hours associated to that region. In a similar vein, humans are more likely to interact with others (e.g. by making a voice call) who reside within their local community. Extracting meaningful (latent) patterns from such geoMobile datasets requires us to go beyond classical linear methods to effectively account for the inherent high variability and diversity (thus strong non-linearity). In the next section we present such an approach.

3 EPIC framework

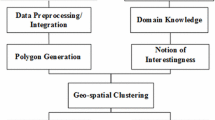
geoMobile datasets (e.g. human mobility data) are rich in both spatial and temporal aspects. The underlying structures of such datasets are complex. Since the data is high-dimensional, extracting features manually is not feasible. Instead, EPIC framework relies on ML-algorithms to judiciously extract relevant features (or latent features) which may be a linear or non-linear combination of a subset of features from the full set of raw features. We favor feature extraction over selection because the latter does not exploit the power of feature combination that could identify non-linear patterns in the data. EPIC derives set(s) of latent features from observable features such as traffic volume density, peak traffic hours etc. However, it is quite likely that these sets of latent features give rise to low-dimensional sub-manifolds forming various kinds of clusters in the data. This results in having each cluster formed by few latent factors which are a (nonlinear) function of the observable features. Based on this intuition, we are interested in an approach that find clusters while accounting for possible latent features in the data. For this purpose, we consider Laplacian Eigenmaps (LE) [3] – a theoretically sound non-linear dimension reduction technique and provide justification about its suitability in our case. As mentioned earlier, standard clustering techniques such as K-means and linear dimension reduction techniques such as PCA or NMF are not appropriate, due to the curse of high dimensions and strong non-linearity, respectively in geoMobile data. Although, other non-linear dimension reduction techniques like Deep Autoencoders, Hessian Locally Linear Embedding, Local Tangent Space Alignment or Kernel PCA can also be employed but we show (theoretically as well empirically) that LE in conjunction with t-SNE technique produces superior visualization maps over these dimension reduction techniques based on interesting local space contraction properties in latent feature space. Figure 7 depicts a schematic overview of our framework.

Figure 7

Overview of EPIC Framework

3.1 Extracting latent features from geoMobile datasets

We propose a simple but effective enhancement of LE. This enhancement comes from carefully accounting for skewed data density distribution while computing the similarity matrix. LE extracts the latent features associated with each data point $\mathbf {x}\in \mathbb {R}^{D}$, where D is a feature dimension, by performing eigenvalue decomposition of graph Laplacian L. We execute the following carefully devised algorithm, so that standard clustering algorithms can be applied on the newly obtained features which are then free from curse of dimensionality and data density skewness.

Handling the Skewness:

The most crucial component for computing L is similarity matrix W. Since the set of features are large, we take the exponential of euclidean distance in feature space to counteract the curse of dimensionality. More precisely, we adopt the following form of Gaussian kernel:

$$ \mathbf{W}_{ij} = \exp{(- {\| \mathbf{x}_{i}-\mathbf{x}_{j}\|^{2}}/{2{\sigma^{2}_{i}}} )} $$

(1)

which is suitable under this condition, though more theoretical motivation can be found in [3]. W_ij can also be seen as a conditional probability p_j|i of picking data point x_j as the neighbor of x_i.

In particular, σ is kept same of each data point but we stress on computing specific σ_i at each data point x_i to handle the skewness in the data density. We choose σ_i based on our belief that the entropy of density distribution p(x_i,σ_i) given as,

$$ p(\mathbf{x}_{i},\sigma_{i}) =-\sum\limits_{j} p_{j|i}\log p_{j|i} $$

(2)

remains constant at each data point and equal to log k. Here k is a user defined parameter which physically represents a smooth measure of effective number of neighbors. We finally perform a binary search over the value of σ_i which gives log k entropy for each data point. Turns out that the similarity matrix is robust for different values of k and its typical value lies in the range of 5 − 50.

Justification:

We adopt LE for two main reasons. First, it can handle non-linearity in the data as shown in [3] and ensures that the new reduced latent features obtained are similar if their respective feature distributions are also similar. This can be confirmed by looking at the LE objective function given as:

$$ \underset{\mathbf{y}}{min} \hspace{0.3em} \frac{1}{2}\sum\limits_{i}\sum\limits_{j} \mathbf{W}_{ij} \| {\mathbf{y}_{i}-\mathbf{y}_{j}} \|^{2} $$

(3)

subjected to scaling constraints, where $\mathbf {y}_{i} \in \mathbb {R}^{d} (d<<D)$ is a new latent feature vector for x_i data point. Secondly, it helps in producing superior visualization maps (see Section 3.2, Section 4.2). LE enforces two similar data points x_i and x_j to have similar latent features according to the weight W_ij which itself depends upon the original feature distribution. For computing L, we adopt a symmetric normalized graph Laplacian proposed in [14]:

$$ \mathbf{L}=\mathfrak{D}^{-1/2}W\mathfrak{D}^{-1/2} $$

(4)

as it is less susceptible to bad clustering when different clusters are connected with varied degree. where $\mathfrak {D}$ is the diagonal degree matrix whose elements are the sum of rows of the similarity matrix. From eigen decomposition of L, d largest eigenvectors are stacked as columns in a Y matrix which is renormalized to yield latent features of points projected on a hypersphere in $\mathbb {R}^{d}$. Graph Laplacian implicitly provides a way to estimate d by examining drop in eigenvalues of L but more approaches can be also found in [12]. For our datasets LE approach was sufficient enough to yield faithful results. We observed there is an eigenvalue drop (see Figure 8) with 15 components pointing to the existence of 15 intrinsic dimensions in OD matrix which earlier PCA could not estimate correctly (see Figure 5). We choose DBSCAN clustering algorithm to be applied on obtained latent features due to its robustness against outliers. Next, we present our powerful Lt-SNE visualization algorithm.

Figure 8

Laplacian Eigenvalue Decomposition

3.2 Lt-SNE visualization algorithm

Density Preserving Maps:

According to Gauss Theorema Egregium [16], manifolds with intrinsic curvature cannot be mapped to the $\mathbb {R}^{2}$ plane (as it has zero Gaussian curvature) without distorting distances. However, no such obstruction exists for density preserving maps (see Moser Theorem [15]). Hence, we seek a method that preserves (probability) density maps rather than distances below intrinsic dimensions for visualization purpose.

Success of t-SNE:

t-SNE [21] is a state-of-art technique for visualizing clusters inherent in the data by mapping latent features to $\mathbb {R}^{2}$ (or $\mathbb {R}^{3}$) space. But its theoretical justification remains somewhat a mystery. Here, we prove that the objective function of t-SNE upper bounds the loss function in kernel density estimation (KDE) (see Proposition 1). This makes t-SNE a density preserving mapping algorithm which provides a theoretical justification for its success as compared to other dimension reduction techniques which tend to preserve (geodesic) distances.

Proposition 1

t-SNE is a density preserving algorithm which upper bounds the estimated kernel density loss function.

Proof

KDE is a non-parametric way to estimate probability density function; it leverages the chosen kernel in the input space for smooth estimation. Given sub-manifold density estimates p(y_i) for data points $\mathbf {y}_{i}\in \mathbb {R}^{d}$ ∀i, we want to find a representation $\mathbf {z}_{i}\in \mathbb {R}^{p}$ ∀i such that the new density estimates q(z_i) agree with the original density estimates. Here K_H, and K_L denote the kernel in higher and lower dimension respectively, where h is the kernel bandwidth, $\mathbf {y}\in \mathbb {R}^{d}$, $\mathbf {z}\in \mathbb {R}^{p}$, p < d, and N is the number of data points. KDE in higher and lower dimensions (assuming bandwidth remains the same) are given by:

$$ \begin{array}{@{}rcl@{}} {p}(\mathbf{y})&=&\frac{1}{N}\sum\limits_{j=1}^{N} \frac{1}{h^{d}} K_{H} \left( \frac{|| (\mathbf{y}-\mathbf{y}_{j} ||_{d}}{h} \right) \\ {q}(\mathbf{z})&=&\frac{1}{N}\sum\limits_{j=1}^{N} \frac{1}{h^{p}} K_{L} \left( \frac{|| \mathbf{z}-\mathbf{z}_{j} ||_{p}}{h} \right) \hspace{0.5em} \text{, s.t.} \int K(u)du =1 \end{array} $$

(5)

The KL divergence loss for KDE can be computed as follows:

$$ \begin{array}{@{}rcl@{}} \mathcal{L} &=& \underset{\mathbf{z}}{min}\hspace{0.2em} KL(p||q) = \underset{\mathbf{z}}{min}\hspace{0.2em} {\sum}_{i=1}^{N}p(\mathbf{y}_{i})\log \frac{p(\mathbf{y}_{i})}{q(\mathbf{z}_{i})} \\ &=& \underset{\mathbf{z}}{min}\hspace{0.2em} \frac{1}{Nh^{d}}\sum\limits_{i =1}^{N} {\Sigma}_{j} K_{H}(\mathbf{y}_{i},\mathbf{y}_{j}) \log \frac{{\sum}_{j} K_{H}(\mathbf{y}_{i},\mathbf{y}_{j})}{{\sum}_{j} K_{L}(\mathbf{z}_{i},\mathbf{z}_{j})} +c_{1} \\ &\leq& \frac{1}{Nh^{d}}\hspace{0.2em} \underbrace{ \underset{\mathbf{z}}{min}\hspace{0.2em} \sum\limits_{i=1}^{N} \sum\limits_{j =1}^{N} K_{H}(\mathbf{y}_{i},\mathbf{y}_{j}) \log \frac{ K_{H}(\mathbf{y}_{i},\mathbf{y}_{j})}{ K_{L}(\mathbf{z}_{i},\mathbf{z}_{j})}}_{\mathcal{J}} +c_{1} \\ & \leq& c_{2} \times \mathcal{J} +c_{1} \end{array} $$

(6)

$\mathcal {J}$ is the objective function of t-SNE (with specific kernels) which upper bounds (with a multiplicative scale and an additive constant) the estimated kernel density estimation loss function. See Appendix for details. □

Superiority of Lt-SNE:

Instead of directly applying t-SNE on raw features, we feed latent features obtained via LE to t-SNE. This results in more superior maps (see Proposition 2, Figure 9 and Section 4.2 for justification) and called as “Lt-SNE”. In Lt-SNE, we employ the same kernel functions as in t-SNE, i.e. normalized gaussian kernel in higher dimensions and heavy tailed kernel (a student t-distribution with one degree of freedom) in lower dimensions as follows.

$$ \begin{array}{@{}rcl@{}} K_{H}(\mathbf{y}_{i},\mathbf{y}_{j})&=&p_{ij} =\frac{\exp{\left( - \frac{\| \mathbf{y}_{i}-\mathbf{y}_{j} \|^{2}}{2{\sigma^{2}_{i}}} \right)}}{{\sum}_{k\neq l}\exp{\left( - \frac{\| \mathbf{y}_{k}-\mathbf{y}_{l} \|^{2}}{2{\sigma^{2}_{k}}} \right)}} \text{ and} \\ K_{L}(\mathbf{z}_{i},\mathbf{z}_{j})&=&q_{ij} =\frac{(1+\| \mathbf{z}_{i}-\mathbf{z}_{j} \|^{2})^{-1}}{{\sum}_{k\neq l}(1+\| \mathbf{z}_{k}-\mathbf{z}_{l} \|^{2})^{-1}} \end{array} $$

(7)

such that K_H(y_i,y_j) and K_L(z_i,z_j) sum to 1. Hence, Lt-SNE has the same final objective function as t-SNE which matches the expressions given in (6):

$$ \mathcal{J} =\underset{\mathbf{z}}{min}\hspace{0.2em} \sum\limits_{i,j=1}^{N}p_{ij}\log \frac{p_{ij}}{q_{ij}} $$

(8)

Figure 9

Lower dimension mapping results on WINE dataset

The above optimization problem is non-convex, but the gradient descent method yields reasonable results. Although it is possible to directly apply t-SNE on the original data matrix, we demonstrate that Lt-SNE produces much better visualization maps in $\mathbb {R}^{2}$ than t-SNE, theoretically in case of finite mixture of nonparametric distributions (Proposition 2) and empirically in comparison with other major dimension reduction techniques (see Section 4.2).

Proposition 2

Assume that the data points are i.i.d. samples generated from a finite mixtureof nonparametric distributions. Let(i,j) be any pair of data points belonging to different distribution. Then the mappingof Lt-SNE yields a larger separation distance as compare to t-SNE in the lowerdimensions (with high probability) i.e.,

$$ \| \mathbf{y}^{\prime}_{i}-\mathbf{y}^{\prime}_{j} \|^{2} \geq a_{1}\| \mathbf{y}_{i}-\mathbf{y}_{j} \|^{2}+a_{2}, $$

where $\mathbf {y}^{\prime }_{i}, \mathbf {y}^{\prime }_{j}$ and y_i,y_j are lower dimension feature vectors of Lt-SNE and t-SNE respectively. a₁,a₂ are positive constants.

Proof

The proof relies on the “Finite-Sample Angular Structure” theorem [19] shown for kernelized spectral clustering. The above proposition shows that if a₁ ≥ 1, which is generally the case, different clusters in Lt-SNE are mapped farther to each other as compared to t-SNE with high probability. See Appendix for details. □

3.3 Culling Cluster-Specific Significant Feature-Set

To help characterize and interpret the relations among different clusters, we define the term significant feature-set of a cluster as a set of observable features that are most critical to the cluster’s formation (as opposed to latent features based on which interpretation is difficult). We take cue from information theory and device an algorithm to fit in the framework of our analysis to cull cluster-specific significant feature-sets for meaningful interpretations.

After applying our extraction and projection steps, suppose we have obtained C clusters from some data matrix, say M, of size N × D. Note that every cell in the data matrix M represents the relation between the data point and the observed feature. We slice the data matrix M horizontally into cluster-specific sub-matrices {m_c}_c∈C, where rows represent only those data points that are part of cluster c, and columns represent the feature set D. We therefore obtain |C| sub-matrices, where every sub-matrix {m_c} is of size n_c × D, where n_c is the number of data points in cluster c ∈ C. Our goal is to inspect each of the sub-matrix m_c individually, and cull a subset of features S_c (or significant set) from the entire observable feature set D, such that the features selected are most critical to cluster c’s existence.

We now explain our approach to cull this cluster-specific significant feature set. For easier readability of equations, we refer sub-matrix m_c as m and its associated notations n_c,S_c as n,S, respectively. N remains unchanged. From some cluster-specific sub-matrix m, we first build a weight vector W defined by:

$$ \mathsf{W} = \left\{x_{i} = \left( \sum\limits_{j} m_{ij} \left/ \sum\limits_{k}\sum\limits_{l} m_{kl}\right.\right) \forall j, k, l \right\}_{i \in D} $$

(9)

Every i^th element in W is an aggregated value that quantifies interactions between the i^th observed feature and all the data points belonging to cluster c. Using W vector, we check if any of its values stand out and are significantly different from others. An easy way to verify this would be to sort vector W, say in decreasing order, and observe the fall in the distribution.

Black curves in Figure 10a and b show the values of weight vectors W for clusters 8 and 18, respectively. These clusters were obtained as part of a case study discussed later in Section 5.1. We observe that cluster 8’s slope drops relatively slower than that of cluster 18. In other words, data points of cluster 8 collectively state that more number of features are vital to its formation than cluster 18. In order to account and quantify these differences, we introduce a notion of relative uncertainty$\widetilde {\mathsf {RU}}(\mathsf {W})$ defined as $\tilde {\mathsf {H}}(\mathsf {W})/\log |\mathsf {W}|$, where $\tilde {\mathsf {H}}(\mathsf {W})$ is the “entropy-like” measure used to quantify the unpredictability of the values in vector W. |W| is the support (or size) of the vector W or the number of observed features. The degree of uniformity (or relative uncertainty) of W is given by:

$$ \widetilde{\mathsf{RU}}(\mathsf{W}) = \frac{\tilde{\mathsf{H}}(\mathsf{W})}{\log |\mathsf{W}|} = \frac{-\sum\limits_{i} w_{i} \log w_{i}}{\log |\mathsf{W}|} $$

(10)

If $\widetilde {\mathsf {RU}}(\mathsf {W})$ is close to 1, it implies the induced distribution is uniform. In other words, nothing is interesting that stand out, hence all the features in W vector have close to similar values. On the other hand if $\widetilde {\mathsf {RU}}(\mathsf {W})$ is less than some threshold, say β, there are high chances of certain distinguishable features. We are interested in the latter case as they are significantly different from others. In order to cull such significant features, we use a second parameter α that acts as a “cut-off” threshold to decide if an element in W is significant. All elements that satisfy the α threshold are removed from W and put in S (i.e. significant feature set). We then perform the second iteration with the new W vector and make parameter αslightly relaxed. We keep repeating the process till the relative uncertainty exceeds β. Once the loop terminates, S contains the significant feature-set of cluster c. For the complete pseudo-code of our approach, see Algorithm 1. β parameter decides the threshold of relative uncertainty. Setting β to lower value would cause the significant sets to be larger compared to setting it to higher values. In general, value of β parameter for our case studies were set between 0.87 and 0.95. Initial value of α depends on the initial distribution of W. Based on our experience, a good starting point would be to set it to min[W]. Line 7 in Algorithm 1 indicates the decreasing factor (or relaxing factor) of α that one may have to tune for subsequent iterations. Value of α and the decreasing factor assert a trade-off between faster run time versus better results. Figure 10a and b illustrate the results of applying our algorithm over sub-matrices of cluster 8 and 18, respectively. The portion to the left of every vertical blue line indicates the number of features that were part of the significant set (for intermediate iterations). The red line however indicates the iteration when our algorithm terminated. It is also evident from our results that the right portion of red line (which were not part of the significant set) are close to being uniform with not just very low weights but are also nearly indistinguishable. Hence, such features are deemed unimportant.

Figure 10

Step-by-step illustration of culling significant feature-set from Clusters 8 & 18 (also discussed in case study 1 Section 5.1 - Dataset 1). |Cluster set x|: number of data points in cluster x; |S_x|: number of features in significant set of cluster x;

4 EPIC framework evaluation

Before we apply EPIC framework to real-world geoMobile datasets, we first briefly evaluate and compare the performance of our framework with other existing methods. Since our framework consists of multiple components such as clustering and visualization, we compare each of these components individually with state-of-the-art baselines. The evaluation is conducted from two perspectives: performance of i) LE+DBSCAN clustering performance in comparison with other major clustering algorithms, and 2) Lt-SNE visualization algorithm based on local space contraction property.

4.1 Clustering performance

Table 1 shows the performance of clustering on case study 1’s data matrix with respect to different algorithms under three clustering evaluation criteria: CalinskiHarabasz, Silhouette, DaviesBouldin – ↑ indicates higher values show better performance, similarly ↓ indicates otherwise (bold text indicates the best performing algorithm for a given evaluation criteria). LE+DBSCAN’s clustering performance dominates on two evaluation criteria and is reasonably good on the other one, showing the efficacy of our clustering approach. Similar results are also hold for dataset 2.

Table 1 Clustering performance evaluation on dataset 1 (see Section 5.1)

One may wonder about the lower performance of LLE+DBSCAN on CalinskiHarabasz in comparison with other DBSCAN-related methods. This results possibly due to the combination of the following two factors. First, it has the lowest contraction ratio compared to other reduction methods as can be observed in Figure 11. Secondly, LLE tends to perform very poorly on non-uniform sample data and might have spread the data points far from each other in a cluster leading to a very low CalinskiHarabasz measure.

Figure 11

Contraction curve of Lt-SNE have highest contraction ratio on two benchmark datasets

4.2 Best local space contraction property

Local Space Contraction Property:

We provide justification for adopting LE approach in conjunction with t-SNE by analyzing the local space contraction effects in the (low dimensional) latent feature space. Building upon the work of [17], we define the contraction ratio as the ratio of distance between two points in the input space and the distance mapped in the low dimensional feature space. Contraction ratio helps illustrate the deformation of the latent feature space in local regions. To measure this isometric property, we compute the average distance ratio of a point x randomly generated on a sphere of radius r centered at a fixed point x₀ in the input space over its corresponding distance in the feature space as a function of r. This function yields a curve called the contraction curve.

Best Results:

We compute the contraction curves on two benchmark datasets: WINE-dataset² and MNIST-dataset³ and compare them (see Figure 11) with other major dimension reduction techniques: Deep-Autoencoder (DE), Local Linear Embedding (LLE), Local Tangent Space Alignment (LTSA), ISOMAP, Hessian LLE (H-LLE). These results also holds for other contraction curves such as Maximum Variance Unfolding (MVU), Kernel PCA and Probabilistic PCA which we do not show here.

The process for generating contraction curves is as follows: x₀ is picked at centroid of a random cluster (using class label information) in the input space in order to study the propagation effects of contraction ratio from the center of a cluster. A random point x is generated at distance r on a sphere centered at x₀ and is included in the dataset. On this appended dataset, we apply dimension reduction techniques. In this process, we first reduce the input dimensions of the data (13 for WINE and 784 for MNIST datasets) to its intrinsic dimensions (3 and 12, respectively). Next, we apply t-SNE to embed the intrinsic data into a two dimensional space. An alternative and less expensive way to compute contraction curves is to implement “out of sample extension” methods [4].

Figure 11 shows the contraction curves for major dimension reduction techniques. For both the datasets, Lt-SNE produces the highest contraction ratio, yielding low-dimensional maps with tighter clusters. Further, the strength of contraction gradually decreases with radius – until the effect vanishes marking the end of cluster radius size. Intuitively, Lt-SNE encourages contraction of neighborhood data points in the map since LE places data points on mutually orthogonal axes which, upon further applying t-SNE, helps produce tight clusters. Thus, Lt-SNE is capable of creating more distinguishable gaps between the clusters and in visualization. The same effect can be observed in the case of Deep-Autoencoder (with a depth of four layers), but with less contraction strength than Lt-SNE. On the other hand, t-SNE in one-shot reduction (i.e. directly reducing from the input dimension to $\mathbb {R}^{2}$) can produce a slightly lower contraction ratio than DE. Interestingly, applying LE in conjunction with DE (LE+DE) significantly boosts up the contraction ratio of DE but still remains lower than the Lt-SNE. This further indicates that the amalgam of LE and t-SNE are well suited to achieve high contraction ratio. Lastly, LLE produces the smallest ratio, suggesting that the resulting mapping contains more loose clusters as compared to others.

Hidden Physics Behind the Dimension Reduction:

A close analogy can be made between the contraction ratio and the strength of an electric field around a charged point. Just like the electric field strength propagates inversely proportional to square of radius, in the vein the strength of contraction ratio decays non-linearly as an inverse function of the radius. However, unlike an electric field where the strength is equal in all directions, in the case of contraction ratio, the strength varies along the tangent space directions of the manifold on which the data is embedded non-linearly. For instance, Figure 9b depicts the contour lines corresponding to the same level of contraction ratios in the low dimensional feature space. As expected, the shape of contour lines are not necessarily spherical but elongated along the dense regions of data points and falls off along the orthogonal direction which corresponds to the drop in the density of data points. These contraction curves reveal the internal feature transformation made by dimension reduction techniques along with their field strength (i.e., contraction ratio) & range (i.e., radius where contraction ratio becomes a constant). Such a comparison intuitively aids in the choice of the best dimension reduction technique in accordance with the application domain.

5 Case studies

We primarily focus on analyzing two geoMobile datasets: i) a mobile call detail record (CDR) dataset collected from a nation-wide cellular network; and ii) a subway transit record dataset from a large city in China. The goal of this section is two-fold: 1) show the efficacy and generality of EPIC framework to wheel out interesting latent patterns from the datasets under multiple settings, 2) show tactical results and provide their interpretations. We share our experience in the form of three case studies.

5.1 Case study 1: Revealing communication patterns

In this case study, we use dataset 1 to extract communication patterns (driven by user actions such as making a voice call) between different origin and destination towers. Earlier in Section 2, we observed a locality effect prevailing in communication patterns between towers in this dataset, suggesting people tend to call others more often who are geographically closer to them. In this case study, we try to find such communication patterns, and to do so, start by representing this geoMobile dataset in the so-called form of origin-destination (or data) matrix. Mobile voice (and SMS) calls between users data in the cellular network as captured at cell tower levels are represented as OD matrices where origins are the cell towers calls originating from, destinations are cell towers these calls terminating at, and the entries in the OD matrix represent the number of calls between an origin-destination pair during some fixed time interval (in our case, average hourly calls). We formulate our problem using an input OD matrix of size N × D, where the set of origins (or rows) and destinations (or columns) correspond to the set of unique towers, i.e. N = D. Each cell value x_ij in the square-OD matrix correspond to the average number of hourly calls made from the origin tower i to the destination tower j. Cell value x_ij will represent the number of local calls for tower i when i = j.

In this data matrix, origins act as data points where as the destination towers act as the feature vector. Therefore, our clustering approach will group origin towers based on their call patters driven by human actions. In other words, two origin towers will be in the same cluster if both their outgoing call distributions to destinations towers are similar. It is important to note that the input data matrix has no information about the geographic coordinates or distances between towers. Results obtained by applying EPIC on this data matrix are shown in Figure 12a. There are a total of 21 well-separated clusters, representing 21 distinct communication patterns in the dataset. Using GPS coordinates, in Figure 12b we overlay the cellular-towers from these 21 clusters over a geographic map of the nation. Except for cluster , all other clusters represent regional communication patterns of varying localities and sizes. Since these communication patterns are driven by human behavior, these distinct patterns capture social interactions in this African nation. We look more closely at the regional patterns in the capital city of the nation (see Figure 12c) as it comprises of over 300 out of the 900 towers of the nation. It is interesting to observe that the city itself is divided into five distinct communication “zones” driven by user interaction (in this case, call or message) and behavior: cluster which is the largest in the city, cluster , cluster , cluster and cluster . Finally, the towers in cluster are sparsely distributed across the nation, most of which have relatively low overall call volumes and many are located along major transportation networks. This suggests that cluster represents call activities of users in transit across the nation. Although this approach is clustering origin towers, the same observations would hold true from the destination towers’ perspective – this is because we observed that our OD data matrix is approximately symmetric.

In the context of this case study, each significant set of a cluster captures a particular kind of human behavior. In other words, each cluster’s significant set are a set of features (or destination towers) that were most critical to that cluster’s formation. Using the algorithm discussed earlier in Section 3.3, we cull the significant sets for each of the 21 clusters, and visualize them in Figure 13 using a Venn diagram. Each circle (labeled using cluster number) in the Venn diagram represents a significant set of the corresponding cluster; size of the circle indicates the size of its significant set. Two circles intersect if their significant sets share common features (or destination towers). Metrics such as “jaccard similarity” can be used to quantify the similarity of human behavior among two intersecting significant sets.

Figure 12

Results showing 21 clusters (or distinct communication patterns) obtained from Dataset 1 (best viewed in color)

Figure 13

Venn diagram of cluster-specific significant sets

From Figure 13 and by further investigating the geographical features of the capital city, we find that cluster 2 (the mainland part of the capital city) not only has the largest significant set, but also intersects with a diverse set of other clusters. This suggests that the capital city is likely a hodgepodge of residents and a mobile population that originally come from other parts of the nation who still maintain strong social, commercial or other interactions with the rest of the nation. A similar (but to a less degree) pattern holds for cluster 1 which represents towers in a second-tier city in the nation. We see strongest similarities in communication patterns between clusters 18 and 19, as well as between clusters 2 and 8, reflecting their highly localized and close-knit communication patterns. Despite its towers distributed across the nation, cluster 21 intersects mostly with clusters 2, 8 and 17 representing towers in either the capital city or its suburbs, implying its communication pattern is due to users from the capital city and its vicinities travel across the nation.

5.2 Case study 2: Temporal communication patterns

In this case study, we use the same dataset as in the previous case study to investigate if different hours of the day across the week have any similarity in their call patterns. For instance, do calling behaviors differ between morning and evening hours? How about weekends? Obtaining such insights would assist cellular operators to profile different hours (and days) based on user demands and usage to deploy, manage energy requirement and provide other personalized and value-added services.

To extract such latent patterns, we treat every data point to represent a day of the week and an hour. Therefore, we have 168 data points x_i for i = 1,2,..,168 (7 days of a week × 24 hours in a day). Every data point is represented by a N-feature vector f_j for j = 1,2,..,N, where N is the number of towers. Each feature in the vector represents a tower and the value represents the non-local calls recorded by that tower, aggregated for the entire data set. In other words, given a data point x_{d=MON,h= 08} (i.e. day=Monday and hour= 08:00 to 09:00 hours), each feature of the data point x_{d=MON,h= 08} would represent the average number of non-local calls recorded by that tower every Monday from 08:00 to 09:00 hours over a period of around 3 months. We now represent our data points and feature vectors as a data matrix X of size 168 × N such that rows represent the data points and columns represent the N towers. Figure 14 shows the results by applying EPIC framework over X. In the $\mathbb {R}^{2}$ map (see Figure 14a), we clearly see two well-separated regions, one that captures data points representing usual sleeping hours (22:00 to 06:00) while the other represents non-sleeping hours. Looking more closely at the non-sleeping region, we observe some interesting patterns. The right half of this region seems to capture data points representing working hours, whereas the left half captures hours when people are at home. A complete list of the intuitively inferred “latent” patterns are listed in Figure 14b. We also see some outliers (anomalies) in the results indicating certain hours in the week have unique patterns. Although we considered hourly intervals for illustrating temporal communication similarities, one could also opt for intervals with smaller/higher temporal granularity. Intuitively, the extracted patterns suggest that the underlying reasoning behind the formation of clusters are related to human behavior, community interactions, social features, geographic features, etc. All in all, we show that EPIC framework is able to find some very interesting patterns in this case study.

Figure 14

Temporal similarities in communication patterns (Dataset 1)

5.3 Case study 3: Temporal variations in human mobility

In the third case study, we use Shenzhen Subway System’s dataset (dataset 2) to gain insights about temporal variations in human mobility. As discussed earlier, we preprocessed the data to extract trip information. We also categorized users (as regular/adhoc) and their trips (as morning/evening/midday).

In order to investigate “if” and “how”EPIC is able to extract temporal variations in human mobility, we apply our framework to multiple data matrices, where each data matrix represents a particular time of the day (morning/evening/midday). We aggregated our processed dataset to obtain the number of trips between every pair of origin-destination subway station. We then build an OD matrix of size N × D, such that every cell in the matrix represents the number of trips from the origin subway station to some destination subway station. As there are 118 unique subway stations in Shenzhen Metro, we have a matrix of size 118 × 118, i.e. N = D = 118.

Labeling the records and users enable us to generate a number of OD matrices. For example, an OD matrix could represent trips made by regular users during morning hours. Note, rather than just looking at similarities between individual origin-destination pairs, our approach groups together origin data points based on the similarity in the distribution of the number of trips with all other destinations. Shenzhen Metro has 5 subway lines (see Figure 15). If we assume that each subway line is independent of each other without the possibility for commuters to transfer from one line to another; applying our framework to such a dataset should ideally extract at least 5 clusters, where each cluster represents a particular subway line. This is because all possible pairs of origin-destination stations (representing a trip) are limited by the set of stations that are part of a particular subway line, owing to our assumption that people cannot transfer to other subway lines. Therefore, the probability of a commuter entering subway line A and exiting at subway line B is 0. Likewise, if the user enters and exits on subway stations that are part of the same subway line A, it is very likely that the probability of such trips will be greater than 0. However this assumption does not hold true for Shenzhen metro, as there are multiple subway stations that act as transfer points between different subway lines. But it is fair to assume that in the interest of reducing travel times, transit operators would design the subway lines so as to minimize transfers.

Figure 15

Shenzhen Metro Subway Station and Line Map

We construct four different OD matrices – M_a, M_b, M_c, and M_d. For instance, OD matrix M_a is built using trip information of regular users observed during the morning rush hours (construction details of other OD matrices is depicted in Table 2).

Table 2 Comparison of results

Figure 16 shows the results rendered by our framework in low-dimensional space, which are then further overlaid over Shenzhen’s geographic map (see Figure 17). The first clear pattern we see is that certain clusters correspond to a particular subway line. For example, all the red-colored clusters represent Subway Line 4 suggesting users traveling on this line have more localized traveling patterns who reach their destination with minimal transfers. Since this line also did not break into multiple clusters, it suggests that the trip volume distribution between any two subway stations are close to similar. A similar observation is observed with the dark blue clusters, which represents Subway Line 5. Therefore, by quick visual inspection of Figures 16 and 17, we are able to find probable patterns, which we list in Table 2. We consider a “pattern” to be a set of clusters, one from every OD-matrix if present. For example, we refer to one of our earlier observation regarding red clusters as “Pattern 4”. Table 2 shows Pattern 4 is observed in all the OD matrices M_a, M_b, M_c, and M_d. From our earlier discussion regarding trip volumes, we observed large number of morning rush hour trips for regular users originate from suburban areas and end near Shenzhen’s central (or downtown) region. Pattern 1 represents such trips for regular commuters (i.e. home → workplace trip). We also observe that the compactness of pattern 1 (green clusters) in M_a and M_b clearly differ. Note, this pattern represents majority of the trips during morning and evening rush hours.

Figure 16

Output for four OD matrices (obtained from Dataset 2) categorized using temporal (morning/evening/mid-day) and user (regular/adhoc) labels. Numbers besides data points represent cluster dentifiers. Gray data points indicate outliers

Figure 17

Results from Figure 16 mapped over Shenzhen’s geographic map (obtained from Dataset 2)

One plausible reason for this diversity in compactness could be that during the morning hours, all the trips end near the downtown area. On the other hand, evening trips appear to be dispersed. This could be due to the fact that while people travel back home, majority of the trips start from the downtown area but end at different regions around Shenzhen. Hence, we see an increased degree of spatial dispersity in the low-dimensional map for M_b in Figure 16b. Patterns seen during mid-day hours and evening hours for regular users seem to be almost the same. Even though the trip volumes during mid-day hours are significantly lesser than the rush hours, our approach is able to obtain the clusters. The interesting part in OD matrices M_b and M_c is that the green cluster contains many subway stations from multiple Subway Lines L1, L2 and L5. This indicates all those subway stations have a higher degree of similarity in the travel patterns, thus suggesting dependency among each other. A possible side effect of such dependencies is increase in line transfers between subway lines. This may be the reason why one of the future plans of Shenzhen metro is to establish a new track connecting Lines L1 with L5 (see Figure 15) [13]. For OD M_d representing adhoc users, we obtained relatively more number of clusters compared to regular users, where certain subway lines are partitioned. One probable reason could be that adhoc users (i.e. visitors, tourists, etc.) tend to take shorter trips within the central region of the city.

EPIC framework yields very interesting results for all the three case studies. Visualizing clusters in a low-dimensional ($\mathbb {R}^{2}$) map and further relating raw features to the cluster’s formation adds different perspectives to interpret the clusters.

6 Conclusion

In this paper, we used the term geoMobile datasets to emphasize data that exhibit geo-spatial and human-behavioral features. To effectively handle high dimensional and skewed feature distributions inherent in geoMobile data, we developed EPIC framework to extract latent structures by combining and improving upon existing non-linear kernel clustering methods. We also uncover a theoretical reason for t-SNE’s success and enhance it further to develop a visualization technique called Lt-SNE. In conjunction, we provide justifications on the effectiveness of our approach by studying & comparing contraction curves with other major dimension reductions techniques. Further, we developed a novel method to characterize the clusters based on raw features to aid in natural interpretation of the latent patterns. The tactical results obtained from our geoMobile datasets are very interesting. In this regards, our work yields an important tool in aiding data scientists to analyze diverse geoMobile datasets and uncover useful actionable knowledge embedded in them.

Appendix

1.1 Proof of Proposition 1

Proof

KDE is a non-parametric way to estimate probability density function; it leverages the chosen kernel in the input space for smooth estimation. Given sub-manifold density estimates p(y_i) for data points $\mathbf {y}_{i}\in \mathbb {R}^{d}$ ∀i, we want to find a representation $\mathbf {z}_{i}\in \mathbb {R}^{p}$ ∀i, p < d, such that the new density estimates q(z_i) agrees with the original density estimates. Here K_H, K_L denote the kernel in higher, lower dimensions, h is the kernel bandwidth and N is the number of data points. KDE’s in higher and lower dimensions (assuming bandwidth h remains the same) are given by:

$$ {p}(\mathbf{y})=\frac{1}{N}\sum\limits_{j=1}^{N} \frac{1}{h^{d}} K_{H} \left( \frac{|| (\mathbf{y}-\mathbf{y}_{j} ||_{d}}{h} \right), {q}(\mathbf{z})=\frac{1}{N}\sum\limits_{j=1}^{N} \frac{1}{h^{p}} K_{L} \left( \frac{|| \mathbf{z}-\mathbf{z}_{j} ||_{p}}{h} \right) $$

$\text {such that} \int K(u)du =1$. The objective function of KL divergence loss for KDE can be computed as follows:

$$ \begin{array}{@{}rcl@{}} \mathcal{L} &=& \underset{\mathbf{z}}{min}\hspace{0.2em} KL(p||q) = \underset{\mathbf{z}}{min}\hspace{0.2em} \sum\limits_{i=1}^{N}p(\mathbf{y}_{i})\log \frac{p(\mathbf{y}_{i})}{q(\mathbf{z}_{i})} \\ &=& \underset{\mathbf{z}}{min}\hspace{0.2em} \frac{1}{Nh^{d}}\sum\limits_{i =1}^{N}{\Sigma}_{j} K_{H}(\mathbf{y}_{i},\mathbf{y}_{j}) \log \frac{{\sum}_{j} K_{H}(\mathbf{y}_{i},\mathbf{y}_{j})}{{\sum}_{j} K_{L}(\mathbf{z}_{i},\mathbf{z}_{j})} +c_{1} \end{array} $$

$$ \begin{array}{@{}rcl@{}} && \text{Using log-sum inequality, we can show that,} \\ &&\leq \frac{1}{Nh^{d}}\hspace{0.2em} \underbrace{ \underset{\mathbf{z}}{min}\hspace{0.2em} \sum\limits_{i=1}^{N} \sum\limits_{j =1}^{N} K_{H}(\mathbf{y}_{i},\mathbf{y}_{j}) \log \frac{ K_{H}(\mathbf{y}_{i},\mathbf{y}_{j})}{ K_{L}(\mathbf{z}_{i},\mathbf{z}_{j})}}_{\mathcal{J}} +c_{1} \\ && \leq c_{2} \times \mathcal{J} +c_{1} \end{array} $$

$\mathcal {J}$ is the objective function of t-SNE (with specific kernels) which upper bounds (with a multiplicative scale and an additive constant) the estimated kernel density estimation loss function. □

1.2 Proof of Proposition 2

Schiebinger et al. [19] studied normalized Laplacian embedding for i.i.d. samples generated from a finite mixture of nonparametric distribution. When the distribution overlap is small and samples are large, then with high probability they showed that the embedded samples forms a orthogonal cone data structure (OCS). Figure 18 shows that (1 − α) fraction of two clusters are accumulated in a cone form of 𝜃 angle around e₁ and e₂ orthogonal axis.

Figure 18

Visualizing (α,𝜃)-OCS [19]

Theorem 1 (Finite-sample angular structure)

There are numbersb,b₀,b₁,b₂,δ,tsatisfying certain conditions such that the embedded dataset$\{\phi (X_{i}),Z_{i}\}^{n}_{i=1}$has(α,𝜃) − OCSwith

$$ |cos\theta|\leq \frac{b_{0} \sqrt{\varphi_{n}(\delta)}}{w_{min}^{3} t - b_{0} \sqrt{\varphi_{n}(\delta)}}, \alpha \leq \frac{b_{1}}{w_{m}in^{1.5}} \varphi_{n}(\delta)+ \psi({2t}) $$

(11)

and holds with probability at least $1-8K^{2}\exp (\frac {b_{2} n \delta ^{4}}{\delta ^{2}+S_{max}(\overline {\mathbb {P}} )+ B(\overline {\mathbb {P}} )} )$.

Proof of Proposition 2:

Our strategy is to exploit the OCS structure of the input data. Let X ∈R^N×D be the normalized data with unit norm, corresponding to p_ij,q_ij as higher, lower dimensional kernel densities and Z₁,Z₂ as normalization constant respectively. Let X^′∈R^N×d,d < D,be the normalized data obtained after LE dimension reduction and have similar corresponding variables $p_{ij}^{\prime },q_{ij}^{\prime },Z_{1}^{\prime },Z_{2}^{\prime }$. Let $\beta \in (0,\frac {\pi }{2})$ and β^′ are angles between input feature vectors < x_i,x_j > and $<\mathbf {x}^{\prime }_{i},\mathbf {x}^{\prime }_{j}>$ respectively. Constant are denoted by $c_{1}, c_{1}^{\prime }, c_{2}, c_{3}, a_{1}, a_{2} \geq 0$. Also σ and σ^′ are the kernel bandwidth of the estimated kernel densities in the X and X^′ input data respectively. Let i^th cluster has N_i samples out of K clusters. For our analysis, we will focus on this i^th cluster.

Since t-SNE preserves kernel density in lower dimensions, we will have p_ij = q_ij and $p_{ij}^{\prime }=q_{ij}^{\prime }$. Some t-SNE related expressions that we will use for the proof are as follows,

$$ \begin{array}{@{}rcl@{}} && p_{ij} =\frac{\exp{\left( - \frac{\| \mathbf{x}_{i}-\mathbf{x}_{j} \|^{2}}{2\sigma^{2}} \right)}}{{\sum}_{k\neq l}\exp{\left( - \frac{\| \mathbf{x}_{k}-\mathbf{x}_{l} \|^{2}}{2\sigma^{2}} \right)}};q_{ij} =\frac{(1+\| \mathbf{y}_{i}-\mathbf{y}_{j} \|^{2})^{-1}}{{\sum}_{k\neq l}(1+\| \mathbf{y}_{k}-\mathbf{y}_{l} \|^{2})^{-1}}\\ && Z_{1}={\sum}_{k\neq l}\exp{\left( - \frac{\| \mathbf{x}_{k}-\mathbf{x}_{l} \|^{2}}{2\sigma^{2}} \right)};Z_{2}={\sum}_{k\neq l}(1+\| \mathbf{y}_{k}-\mathbf{y}_{l} \|^{2})^{-1}\\ \end{array} $$

Similar expressions can be obtained for $p_{ij}^{\prime },q_{ij}^{\prime },Z_{1}^{\prime }$ and $Z_{2}^{\prime }$. From these equations, we can show that,

$$ \frac{(1-\cos\beta)}{{\sigma_{i}^{2}}} =\log\left( \frac{1}{p_{ij}}-2\right) \frac{1}{\log \sum\limits_{{k\neq l; k,l \neq i,j}}\exp{\left( - \frac{\| \mathbf{x}_{k}-\mathbf{x}_{l} \|^{2}}{2\sigma^{2}} \right)}} $$

(12)

$$ \| \mathbf{y}_{i}-\mathbf{y}_{j} \|^{2}=\left( \frac{1}{q_{ij}}-2\right)\frac{1}{\sum\limits_{{k\neq l; k,l \neq i,j}}(1+\| \mathbf{y}_{k}-\mathbf{y}_{l} \|^{2})^{-1}}-1 $$

(13)

$\text {Let,} c_{1} =\sum \limits _{{k\neq l; k,l \neq i,j}}(1+\| \mathbf {y}_{k}-\mathbf {y}_{l} \|^{2})^{-1}$. Now according to Theorem 1, β^′ is bounded in $(\frac {\pi }{2}-2\theta , \frac {\pi }{2}+2\theta )$ with high probability, if (i,j) belongs to different class labels. In general for small 𝜃, we can assume that the different clusters form a separation angle (with respect to origin) such that $\frac {\pi }{2}-2\theta > \beta$ i.e β^′≥ β for all pairs of (i,j). Then according to (12), $p_{ij} \geq p_{ij}^{\prime }$ and therefore $q_{ij} \geq q_{ij}^{\prime }$, if (i,j) belongs to different class labels. Equation (13) further yields,

$$ \log \frac{c_{1}^{\prime}(1+\| \mathbf{y}^{\prime}_{i}-\mathbf{y}^{\prime}_{j} \|^{2})+2}{c_{1}(1+\| \mathbf{y}_{i}-\mathbf{y}_{j} \|^{2})+2} = \log \frac{q_{ij}}{q_{ij}^{\prime}} = \log \frac{p_{ij}}{p_{ij}^{\prime}} \geq 0 $$

This shows that Lt-SNE always provide better mapping than t-SNE for $c_{1}^{\prime } \leq c_{1}$ which is generally the case. For small 𝜃, we expect $p_{kl} > p^{\prime }_{kl}$$(\Rightarrow q_{kl} > q^{\prime }_{kl})$ for (k,l) belonging to different class and $p_{kl} \approx p^{\prime }_{kl}$$(\Rightarrow q_{kl} \approx q^{\prime }_{kl})$ for (k,l) belonging to the same class. This leads to $c_{1}^{\prime } \leq c_{1}$ since q_kl ∝ (1 + ∥y_k −y_l∥²)^− 1. Next, we establish an lower bound on this mapping ratio using this expression,

$$ \log \frac{c_{1}^{\prime}(1+\| \mathbf{y}^{\prime}_{i}-\mathbf{y}^{\prime}_{j} \|^{2})+2}{c_{1}(1+\| \mathbf{y}_{i}-\mathbf{y}_{j} \|^{2})+2} = \frac{1-\cos\beta^{\prime}}{\sigma^{\prime2}}+ \log \frac{Z_{1}^{\prime}}{Z_{1}}+ \frac{\cos \beta -1}{\sigma^{2}} $$

(14)

For fixed β, $(\frac {\cos \beta -1} {\sigma ^{2}}- \log Z_{1})$ term is constant. Now normalization constant $Z_{1}^{\prime }$ is the sum of kernel densities between samples within cluster itself and across other clusters. From Theorem 1, we know that (1 − α) fraction of a cluster belongs to a orthogonal cone structure with $\theta \in (0,\frac {\pi }{4})$ angle with high probability. Ignoring α samples (which add positive values to $Z_{1}^{\prime }$), we can provide a lower bound on $Z_{1}^{\prime }$ with the same probability bound as given in Theorem 1 for 𝜃,α.

$$ \begin{array}{@{}rcl@{}} Z^{\prime}_{1} &\geq& \underbrace{ \sum\limits_{k = 1}^{K} (1-\alpha)^{2} N_{K} (N_{k}-1) e^{-\frac{(1-\cos 2\theta)}{\sigma^{\prime2}}}}_{\text{sum of densities within clusters}}+ \underbrace{ \sum\limits_{k \neq l} (1-\alpha)^{2} N_{k} N_{l} e^{-\frac{(1+\sin 2\theta)}{\sigma^{\prime2}}}}_{\text{sum of densities across clusters}} \\ Z^{\prime}_{1} &\geq& \frac{(1-\alpha)^{2}}{e^{\frac{(1-\cos 2\theta)}{\sigma^{\prime2}}}} \left( \sum\limits_{k = 1}^{K} N_{K} (N_{k}-1) + \sum\limits_{k \neq l} (1-\alpha)^{2} N_{k} N_{l} e^{- \sqrt{2}\cos (\frac{\pi}{4} -2\theta)} \right)\\ \end{array} $$

Finally, we can plug $Z^{\prime }_{1}$ in (14) and putting $\beta ^{\prime }=\frac {\pi }{2}-\theta$ for getting lower bound, we obtain our final expressions.

$$ c_{2} =\frac{\cos \beta -1} {\sigma^{2}}- \log Z_{1} + \log\left( \sum\limits_{k = 1}^{K} N_{K} (N_{k}-1) +\sum\limits_{k \neq l} (1-\alpha)^{2} N_{k} N_{l} e^{- \sqrt{2}}\right) $$

$$ \begin{array}{@{}rcl@{}} \log \frac{c_{1}^{\prime}(1+\| \mathbf{y}^{\prime}_{i}-\mathbf{y}^{\prime}_{j} \|^{2})+2}{c_{1}(1+\| \mathbf{y}_{i}-\mathbf{y}_{j} \|^{2})+2} & \geq& \frac{\sqrt{2}\sin (\frac{\pi}{4} -2\theta)} {\sigma_{\prime}^{2}}+ 2\log(1-\alpha)+c_{2} \\ \implies \| \mathbf{y}^{\prime}_{i}-\mathbf{y}^{\prime}_{j} \|^{2} & \geq& a_{1}\| \mathbf{y}_{i}-\mathbf{y}_{j} \|^{2} +a_{2} \end{array} $$

Here, $c_{3}= \exp (\frac {\sqrt {2}\sin (\frac {\pi }{4} -2\theta )} {\sigma _{\prime }^{2}}+ 2\log (1-\alpha )+c_{2}) \geq 1$, $a_{2}=\frac {c_{3}+c_{3}c_{1}-c_{1}^{\prime }-1}{c_{1}^{\prime }}\geq 0$ and $a_{1}=\frac {c_{3}c_{1}}{c_{1}^{\prime }} \geq 1$, if $c_{1} \geq c_{1}^{\prime }$ which is the case for small 𝜃. This completes the full proof. □