Low-rank dimensionality reduction for multi-modality neurodegenerative disease identification

Abstract

In this paper, we propose a novel dimensionality reduction method of taking the advantages of the variability, sparsity, and low-rankness of neuroimaging data for Alzheimer’s Disease (AD) classification. We first take the variability of neuroimaging data into account by partitioning them into sub-classes by means of clustering, which thus captures the underlying multi-peak distributional characteristics in neuroimaging data. We then iteratively conduct Low-Rank Dimensionality Reduction (LRDR) and orthogonal rotation in a sparse linear regression framework, in order to find the low-dimensional structure of high-dimensional data. Experimental results on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset showed that our proposed model helped enhance the performances of AD classification, outperforming the state-of-the-art methods.

1 Introduction

Alzheimer’s Disease (AD) is an irreversible and progressive brain disorder and typically begins with mild memory loss and later may seriously impair an individual’s ability of daily activities [12, 25, 26, 30, 44]. Due to limited knowledge about the cause of AD, there is no cure for AD and most drugs only help slow down the advance of AD.

As neuroimaging data provide in-vivo information to complement clinical evaluations, computer-aided neuroimaging analysis becomes a powerful tool to help complement the conventional clinical-based assessments and cognitive measurement for AD diagnosis [13]. Computer-aided neuroimaging analysis focuses on conducting AD study with multi-modality neuroimaging data, such as functional imaging data (e.g., Positron Emission Tomography (PET)) and structural imaging data (e.g., Magnetic Resonance Imaging (MRI)), because different types of imaging information could be complementary to investigate a human brain. In computer-aided neuroimaging analysis, neuroimaging data may be extracted with a number of features for characterizing the variability of data. However, both multi-modality data and high-dimensional features easily result in the issue of ‘curse-of-dimensionality’ [32,33,34, 47, 48].

To address this issue, many machine learning techniques (such as feature selection [3, 14, 32, 38, 50] and low-rank regression [5, 36, 37, 49]) have been designed to reduce the feature dimension. Feature selection methods, such as statistical t-test and sparse linear regression [42, 45], find informative feature subsets from original feature set to output interpretable results [7, 41], and thus is preferable in neuroimaging studies [23, 43]. For example, Liu et al. [15] and Zhu et al. [43] showed that feature selection improves the classification accuracy of AD diagnosis, and Chu et al. [2] demonstrated that feature selection does improve the classification accuracy, but depends on the method used. Besides, feature selection has been widely applied in other domains, such as gait analysis [31] and Parkinson’s disease diagnosis [22]. Low-rank regression considers the relations among the response variables to conduct subspace learning under the assumption that the rank of the coefficient matrix in regression is no large than each of its dimension [17], and is very popular in machine learning and statistics but used less in AD study. Furthermore, subspace learning methods have recently presented promising performances in various applications [23]. Hence, it is interesting to integrate them in a unified framework, in which we can complement the limitations of each of them.

In this work, we consider the variability, sparsity, and low-rankness of data into a unified framework by utilizing various relations inherent in data, to seek possible solutions to the problems of multi-modality and high-dimensionality of nueroimaging data, for improving the interpretability and predictability of multi-modality AD classification. We first employ existing clustering methods to divide each class (i.e., each clinical status in this work) into sub-classes to form a multi-output representation of response variables, for reflecting the variability of neuroimaging data. Then we iteratively conduct a Low-Rank Dimensionality Reduction (LRDR) step and an orthogonal rotation step to seek the low-dimensional structure in data. In the LRDR step, low-rank constraints conduct subspace learning to extract low-dimensional latent factors, while a sparsity constraint via an ℓ_2,1-norm regularizer allows to select class-discriminative features, which thus has the effect of feature selection. The orthogonal rotation step considers the relations among modalities such that the multi-modality data, which share the same response variables, are kept consistent in different modalities. Moreover, these two iteration steps adjust each of steps to output representative features in feature selection for improving the interpretability and predictability of AD diagnosis.

Different from the previous study for early AD diagnosis, the contributions of this paper have the following three folds.

First, this paper takes the advantages of the variability, sparsity, and low-rankness of data for AD classification. Second, in this paper, the column-wise low-rank constraints on coefficient matrices extract low-dimensional latent factors from all features for explaining the response variables, while the row-wise sparsity constraints on coefficient matrices impose to select class-discriminative features. This enables us to simultaneously conduct subspace learning and feature selection, and thus making up for the limitations of each dimensionality reduction method. Last but not least, unlike the existing multi-task feature selection methods [29, 40] that select the representative features across tasks, our method considers the complementary information among modalities to separately select representative features of each modality (i.e., MRI and PET), since studies have manifested that MRI features have different informative brain regions with PET features for AD diagnosis [27]. Moreover, our method also considers the relations among modalities in the orthogonal rotation step to lead to a nonlinear dimensionality reduction framework. Such considerations among modalities are naturally designed to exploit the complex system of brain regions.

2 Materials and image preprocessing

We downloaded all neuroimaging data from the ADNI website,¹ where the used structural MR images were obtained from 1.5T scanners and the used PET images used were obtained 30-60 minutes post Fluoro-DeoxyGlucose (FDG) injection. Moreover, these MR images have been finished with the following preprocessing, including quality and automatically corrected, while PET images have been finished with the processes including averaging, spatially aligning, interpolating, intensity normalizing, and smoothing.

In this paper, we use 396 subjects of baseline MRI and 18F-FluoroDeoxyGlucose (18F-FDG) PET, including 93 AD, 202 MCI, and 101 NC subjects. We further partitioned MCI subjects into progressive MCI (pMCI), stable MCI (sMCI), and others. More specifically, 55 pMCI subjects converted from MCI to AD in 24 months, while 63 sMCI subjects did not convert to AD in both 24 months and 36 months² We summarize the demographics of the subjects in Table 1.

Table 1 Demographic and clinical information of the subjects

2.1 Image analysis

We followed the literature [40] to conduct image processing for all MR images and PET images via the following steps:

• using MIPAV software³ to conduct anterior commissure-posterior commissure correction.

• correcting intensity inhomogeneity.

• extracting the brain region on each structural MR image via the robust skull-stripping method.

• conducting manual edition (if needed) and intensity inhomogeneity correction.

• removing cerebellum based on registration.

• correcting intensity inhomogeneity by repeating N3 for three times.

• using FAST algorithm [35] in the FSL package to segment each structural MR image into three different tissues: Gray Matter (GM), White Matter (WM), and CerebroSpinal Fluid (CSF).

• using HAMMER [24] to conduct registration to obtain the Region-Of-Interests (ROIs) based on the Jacob template [11], which dissects a brain into 93 ROIs.

We computed the GM tissue volume in the ROI region by integrating the GM segmentation result of this subject. We further used affine registration to align the PET image to its responding MR T1 image, and then computed the average intensity of each ROI. As a result, we have 93 features for each MRI and 93 features for each PET.

3 Proposed method

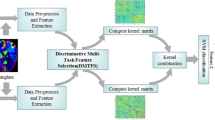
In our framework, we first extract neuroimaging features from MRI images and PET images, and then select informative features by the proposed Orthogonal Low-Rank Dimensionality Reduction (OLRDR), that iteratively conducts a low-rank dimensionality reduction step and an orthogonal rotation step. The selected features are then fed into a Support Vector Machine (SVM), by which we finally identify clinical labels of testing data. Figure 1 shows the schematic diagram of our method.

Figure 1

A framework of our method. LRDR represents the low-rank dimensionality reduction step

3.1 Notations

In this paper, we denote matrices as boldface uppercase letters, vectors as boldface lowercase letters, and scalars as normal italic letters, respectively. For a matrix X = [x_ij], its i-th row and j-th column are denoted as xⁱ and x_j, respectively. Also, we denote the Frobenius norm and the ℓ_2,1-norm of a matrix X as $\|\mathbf {X}\|_{F} = \sqrt {{\sum }_{i}\|\mathbf {x}^{i}\|_{2}^{2}} = \sqrt {{\sum }_{j}\|\mathbf {x}_{j}\|_{2}^{2}}$ and $\|\mathbf {X}\|_{2,1} = {\sum }_{i}\|\mathbf {x}^{i}\|_{2} = {\sum }_{i}{\sqrt {{\sum }_{j} x_{ij}^{2}}}$, respectively. We further denote the transpose operator, the trace operator, the rank, and the inverse, of a matrix X, as X^T, tr(X), rank(X), and X^− 1, respectively.

3.2 Low-rank regression

Let $\mathbf {X} = [\mathbf {x}^{1};...;\mathbf {x}^{n}] = [\mathbf {x}_{1},...,\mathbf {x}_{d}] \in \mathbb {R}^{n \times d}$ and Y = [y¹;...;yⁿ] ∈{0,1}^n×c be, respectively, a feature matrix and the corresponding class label matrix (as known as a response matrix), where n, d, and c denote the numbers of samples (or subjects), feature variables, and response variables, respectively. As for the class label of the i-th sample xⁱ, we use an indicator vector yⁱ = [y_i1,...,y_ij,...,y_ic] ∈{0,1}^c such that when xⁱ belongs to the j-th class, the corresponding j-th element in yⁱ is set to one, i.e.,y_ij = 1, and all the other elements are set to 0.

A linear regression [49] finding the relationship between the response variables in Y and the feature variables in X is formulated as follows:

$$ \mathbf{Y} = \mathbf{X}\mathbf{W} + \mathbf{e}\mathbf{b} $$

(1)

where $\mathbf {W} \in \mathbb {R}^{d \times c}$ is a regression coefficient matrix, $\mathbf {b} \in \mathbb {R}^{1 \times c}$ is a bias term, and $\mathbf {e} \in \mathbb {R}^{n \times 1}$ denotes a column vector with all ones. Then the solution of W for a loss function defined by least square error can be obtained by Ordinary Least Square (OLS) estimation [8, 38] as follows:

$$ {\hat{\mathbf{W}}} = (\mathbf{X}^{T} \mathbf{X})^{-1}\mathbf{X}^{T}(\mathbf{Y} - \mathbf{e}\mathbf{b}). $$

(2)

Note that for multiple response variables, i.e.,c > 1, the k-th column coefficients of W are just the least square estimation in the regression of y_k on x₁,…,x_d, thus (2) is equivalent to conduct the OLS estimation for each response variable separately. In other words, it does not make use of the possible relations among the response variables, thus limiting its modeling power.

One potential approach to circumvent such limitation is to explicitly take into account the possible relations among response variables by imposing a constraint on the rank of W, i.e.,rank(W) ≤ min(d,c), as described in [28]. The motivation using the low-rank constraint is that, in real applications, noises or outliers often increase the rank of a feature matrix, or the features of X are not linearly independent (i.e, X is not of full rank) [16].

Certainly, rank(W) = r, where r ≤ min(d,c), implies rank(XW) ≤ r and the inverse is not necessarily true. With the constraint rank(XW) ≤ r, we know that the rank of the predicted matrix $\hat {\mathbf {Y}}$ (i.e.,$\hat {\mathbf {Y}} = \mathbf {X}\mathbf {W}$) of the response variables Y is also less than r. We can interpret this as follows: there are less than r columns of Y (corresponding to less than r response variables) such that each of c columns of Y is actually a linear combination of those r columns, i.e., there are only r effectively independent response variables. Such a low-rank constraint obviously considers the relations among response variables.

The low-rank constraint on W also implies that the coefficient matrix can be expressed as the product of two lower rank matrices [14, 37], i.e.,

$$ \mathbf{W} = \mathbf{BA}^{T} $$

(3)

where $\mathbf {B} \in \mathbb {R}^{d \times r}$ and $\mathbf {A} \in \mathbb {R}^{c \times r}$. For a fixed r, by replacing W with BA^T in (1), a low-rank regression can be formulated as:

$$ \min \limits_{\mathbf{A}, \mathbf{B}, \mathbf{b}} \|\mathbf{Y} - \mathbf{X}\mathbf{BA}^{T} - \mathbf{e}\mathbf{b}\|_{F}^{2} $$

(4)

Note that XB transforms the feature matrix into an r-dimensional space, spanned by r latent factors, and when r is smaller than d, it has the effect of reducing dimensionality. That is, r latent factors estimated from d features of X are sufficient to explain the response variables. In this regard, the low-rank constraint on the coefficient matrix can be considered as conducting subspace learning on X. Furthermore, the low-rank constraint also seeks the interaction between Y and X because it enables to use r latent response variables to linearly explain the original c response variables while the value of r depends on the rank of XW. Hence, the low-rank constraint could improve prediction accuracy by conducting subspace learning on X, considering the relations in the columns of Y, and seeking the interaction between Y and X.

3.3 OLRDR on multi-modality data

Multi-modality data (e.g., MRI and PET) have been shown to provide complementary information to each other, thus helping enhance the performance of AD diagnosis [43, 46, 47]. Denoting the feature matrices of MRI and PET as $\mathbf {X}_{1} \in \mathbb {R}^{n \times d}$ and $\mathbf {X}_{2} \in \mathbb {R}^{n \times d}$, respectively, we define the objective function of low-rank multi-modality regression⁴ as follows:

$$\begin{array}{@{}rcl@{}} \begin{array}{l} \min \limits_{{\mathbf{A}_{1},\mathbf{A}_{2}}, \mathbf{B}_{1}, \mathbf{B}_{2}, \mathbf{b}_{1}, \mathbf{b}_{2}} \|\mathbf{Y} - \mathbf{X}_{1}\mathbf{B}_{1}\mathbf{A}_{1}^{T} - \mathbf{e}\mathbf{b}_{1}\|_{F}^{2} \\ + \|\mathbf{Y} - \mathbf{X}_{2}\mathbf{B}_{2}\mathbf{A}_{2}^{T} - \mathbf{e}\mathbf{b}_{2}\|_{F}^{2} \end{array} \end{array} $$

(5)

where $\mathbf {B}_{i} \in \mathbb {R}^{d \times r}$, $\mathbf {A}_{i} \in \mathbb {R}^{c \times r}$, and b_i$\in \mathbb {R}^{1 \times c}$, i = 1,2. Although the low-rank regression allows r latent factors of X_iB_i (i = 1,2) to directly represent the response variables, such r latent factors were basically obtained from d-dimensional features. When there are a large number of features from neuroimaging data, some of them may not be useful in prediction. The un-useful features may affect the extraction of r latent factors of X_i and also the interpretation of Y. Thus, it is helpful to perform feature selection on the low-rank multi-modality regression to exclude the redundant features. In this way, conducting feature selection on X_i can be regarded as conducting subspace learning and explaining response variables using ‘clean’ data. To this end, we employ two ℓ_2,1-norm regularizers, one for each modality, and additional orthogonal constraints to encourage the latent factors unrelated as follows:

$$\begin{array}{@{}rcl@{}} \begin{array}{l} \min \limits_{\mathbf{A}_{1},\mathbf{A}_{2}, \mathbf{B}_{1}, \mathbf{B}_{2}, \mathbf{b}_{1}, \mathbf{b}_{2}} \|\mathbf{Y} - \mathbf{X}_{1}\mathbf{B}_{1}\mathbf{A}_{1}^{T} - \mathbf{e}\mathbf{b}_{1}\|_{F}^{2} \\ + \alpha \|\mathbf{B}_{1}\|_{2,1} + \|\mathbf{Y} - \mathbf{X}_{2}\mathbf{B}_{2}\mathbf{A}_{2}^{T} - \mathbf{e}\mathbf{b}_{2}\|_{F}^{2}\\ + \beta \|\mathbf{B}_{2}\|_{2,1}, \mathrm{s.t.}, \mathbf{A}_{1}^{T}\mathbf{A}_{1} = \mathbf{I}_{r}, \mathbf{A}_{2}^{T}\mathbf{A}_{2} = \mathbf{I}_{r}. \end{array} \end{array} $$

(6)

where $\mathbf {I}_{r} \in \mathbb {R}^{r \times r}$ and α and β are the tuning parameters. The ℓ_2,1-norm regularizers on B_i penalize coefficients of B_i in a row-wise manner for joint selection or un-selection of the features in predicting the response variables.

It is worth noting that the column-wise low-rank constraints and the row-wise ℓ_2,1-norm regularizers on B_i have the effects of conducting subspace learning and feature selection on X_i, respectively. That is, the low-rank constraints obtain r latent factors and the ℓ_2,1-norm regularizers remove redundant features, both from d features of X_i. In this work, we propose to consider both low-rankness and sparsity in regression to conduct a low-rank dimensionality reduction (LRDR), with the goal of selecting informative features by considering the relations between the neuroimaging features and the response variables via ℓ_2,1-norm regularizers and utilizing the relations among response variables via low-rank constraints. Moreover, motivated from the previous studies that the presentation of informative brain regions in MRI for AD diagnosis are different from those in PET [15, 34], we consider the difference between modalities by applying ℓ_2,1-norm regularizers on B_i for each modality separately with the assumption that MRI and PET may select different brain regions for AD diagnosis.

We also take advantage of the relations among modalities by replacing two orthogonal variables (i.e.,A₁ and A₂) in (6) with an orthogonal variable A as follows:

$$\begin{array}{@{}rcl@{}} \begin{array}{l} \min \limits_{\mathbf{A}, \mathbf{B}_{1}, \mathbf{B}_{2}, \mathbf{b}_{1}, \mathbf{b}_{2}} \|\mathbf{Y} - \mathbf{X}_{1}\mathbf{B}_{1}\mathbf{A}^{T} - \mathbf{e}\mathbf{b}_{1}\|_{F}^{2}\\ + \alpha \|\mathbf{B}_{1}\|_{2,1} + \|\mathbf{Y} - \mathbf{X}_{2}\mathbf{B}_{2}\mathbf{A}^{T} - \mathbf{e}\mathbf{b}_{2}\|_{F}^{2}\\ + \beta \|\mathbf{B}_{2}\|_{2,1}, \mathrm{s.t.}, \mathbf{A}^{T}\mathbf{A} = \mathbf{I}_{r}. \end{array} \end{array} $$

(7)

where B₁ and B₂, respectively, are the subspace matrices of MRI and PET, and A is the shared regression parameter matrix of two modalities. The reason of such replacement is that A connects two modalities. Specifically, MRI and PET have different low-level representations (i.e.,X₁ and X₂) but share the same high-level representation Y, thus it should have relation between each of the feature matrices and the response matrix. Once conducting dimensionality reduction on X₁ and X₂, the new low-dimensional representations (i.e.,X₁B₁ and X₂B₂) could change the distribution of original low-level representations, so a rotation (or transformation) A^T should be used to transfer them into the original label space spanned by the high-level representation Y. In other words, Y should take a rotation (i.e.,A) for seamlessly connecting these two new spaces. Such an orthogonal rotation step naturally makes up for the disadvantage resulted by the LRDR step, and explores the relation among modalities.

3.4 OLRDR on multi-output multi-modality data

In neuroimaging study, one often conducts a binary classification, such as AD vs. NC, MCI vs. NC, and progressive MCI (pMCI) vs. stable MCI (sMCI), for AD diagnosis. In this way, the dimensions c of Y is low, e.g.,c = 2, for binary classification with 0-1 encoding, so the value of r may be very small according to the constraint, i.e.,r ≤ min(d,c). Thus (6) makes little improvement. We, therefore, extend the abstract low-dimensional representation of Y in the conventional AD study to a concrete multi-output representation by exploiting the clustering methods, based on the inter-subject variability (or subject variability) of neuroimaging data [20, 39].

In imaging analysis, a low-level representation X and a high-level representation Y characterize, respectively, the concreteness and abstractness of imaging data. The high-level representation can be characterized with more details since the inter-subject variability indicates that neuroimaging data may have multiple peaks in distribution [20]. In AD study, the high-level representation of MCI can be further categorized into sub-classes, such as pMCI and sMCI. In this way, the complicated distribution of a class with multiple peaks can be modeled with multiple simple distributions, one for each sub-class. By following the previous work in [39], we propose to divide each class, i.e., each high-level representation (e.g., either AD or NC in the classification of AD vs. NC) into sub-classes via a clustering method (e.g., hierarchical clustering [9] in this paper) and each of the resulting clusters is regarded as a sub-class.

Specifically, given the response matrix $\mathbf {Y} \in \mathbb {R}^{n \times c}$, we separately cluster the subjects in each i-th original class to form its corresponding sub-classes by denoting the m_i extended sub-classes of the i-th original class as $[\mathbf {Y}_{{\sum }_{j = 1}^{i-1} m_{j} + 1}, ..., \mathbf {Y}_{{\sum }_{j = 1}^{i-1} m_{j} + m_{i}}]$ and each row has only one ‘1’, which means that each subject in m_i sub-classes only belongs to one sub-class. The new response matrix $\hat {\mathbf {Y}}$ (i.e.,$\hat {\mathbf {Y}} = [\mathbf {Y}_{1}, \mathbf {Y}_{2}, ..., \mathbf {Y}_{c}, \mathbf {Y}_{c + 1}, ..., \mathbf {Y}_{c + m_{1}}, ...,$$\mathbf {Y}_{c + {\sum }_{j = 1}^{c-1} m_{j} + 1},$$...., \mathbf {Y}_{c + {\sum }_{j = 1}^{c-1} m_{j} + m_{c}}] \in \{0,1\}^{n \times m}$, where $m = c + {\sum }_{i = 1}^{c} m_{i}$ includes two parts, i.e., original labels copied in the first c columns and the extended labels produced by a clustering method in the remaining (m − c) columns. By rearranging $\hat {\mathbf {Y}}$ as $\hat {\mathbf {Y}} = [\hat {\mathbf {Y}}_{1}, ...,\hat {\mathbf {Y}}_{m}]$, our final objective function can be written as follows:

$$\begin{array}{@{}rcl@{}} \begin{array}{l} \min \limits_{\hat{\mathbf{A}}, \hat{\mathbf{B}}_{1}, \hat{\mathbf{B}}_{2}, \hat{\mathbf{b}}_{1}, \hat{\mathbf{b}}_{2}} \|\hat{\mathbf{Y}} - \mathbf{X}_{1}\hat{\mathbf{B}}_{1}\hat{\mathbf{A}}^{T} - \mathbf{e}\hat{\mathbf{b}}_{1}\|_{F}^{2} \\ + \alpha \|\hat{\mathbf{B}}_{1}\|_{2,1} + \|\hat{\mathbf{Y}} - \mathbf{X}_{2}\hat{\mathbf{B}}_{2}\hat{\mathbf{A}}^{T} - \mathbf{e}\hat{\mathbf{b}}_{2}\|_{F}^{2}\\ + \beta \|\hat{\mathbf{B}}_{2}\|_{2,1}, \mathrm{s.t.}, \hat{\mathbf{A}}^{T}\hat{\mathbf{A}} = \mathbf{I}_{r} \end{array} \end{array} $$

(8)

where $\hat {\mathbf {Y}} \in \mathbb {R}^{n \times m}$, $\hat {\mathbf {B}}_{1}, \hat {\mathbf {B}}_{2}$$\in \mathbb {R}^{d \times r}$, $\hat {\mathbf {A}} \in \mathbb {R}^{m \times r}$ and $\hat {\mathbf {b}}_{1}, \hat {\mathbf {b}}_{2}$$\in \mathbb {R}^{1 \times m}$.

After optimizing (8) by Algorithm 1, we have different zero row vectors in both $\hat {\mathbf {B}}_{1}$ and $\hat {\mathbf {B}}_{2}$, so we can discard the irrelevant or noisy components, i.e., the features whose regression coefficient vectors are zero in the rows on $\hat {\mathbf {B}}_{1}$ and $\hat {\mathbf {B}}_{2}$. Given representative features from MRI and PET, we concatenate the reduced features and then use them to build binary classifiers with SVM.

3.5 Optimization

This section describes the optimization process to find optimal parameters of $\hat {\mathbf {A}}$, $\hat {\mathbf {b}}_{1}$, $\hat {\mathbf {b}}_{2}$, $\hat {\mathbf {B}}_{1}$ and $\hat {\mathbf {B}}_{2}$. Specifically, we iteratively conduct the following two steps until satisfying predefined conditions: (i) Update $\hat {\mathbf {A}}$ with fixed $\hat {\mathbf {b}}_{1}$, $\hat {\mathbf {b}}_{2}$, $\hat {\mathbf {B}}_{1}$ and $\hat {\mathbf {B}}_{2}$, i.e., the orthogonal rotation step. (ii) Update $\hat {\mathbf {b}}_{1}$, $\hat {\mathbf {b}}_{2}$, $\hat {\mathbf {B}}_{1}$ and $\hat {\mathbf {B}}_{2}$ with fixed $\hat {\mathbf {A}}$, i.e., the LRDR step.

3.5.1 Update $\hat {\mathbf {A}}$ with fixed $\hat {\mathbf {b}}_{1}$, $\hat {\mathbf {b}}_{2}$, $\hat {\mathbf {B}}_{1}$ and $\hat {\mathbf {B}}_{2}$.

For fixed $\hat {\mathbf {b}}_{1}$, $\hat {\mathbf {b}}_{2}$, $\hat {\mathbf {B}}_{1}$ and $\hat {\mathbf {B}}_{2}$, the optimization problem in (8) reduces to

$$\begin{array}{@{}rcl@{}} \begin{array}{l} \min \limits_{\hat{\mathbf{A}}} \|\hat{\mathbf{Y}} - \mathbf{X}_{1}\hat{\mathbf{B}}_{1}\hat{\mathbf{A}}^{T} - \mathbf{e}\hat{\mathbf{b}}_{1}\|_{F}^{2} \\ + \|\hat{\mathbf{Y}} - \mathbf{X}_{2}\hat{\mathbf{B}}_{2}\hat{\mathbf{A}}^{T} - \mathbf{e}\hat{\mathbf{b}}_{2}\|_{F}^{2}, \mathrm{s.t.}, \hat{\mathbf{A}}^{T}\hat{\mathbf{A}} = \mathbf{I}_{r}. \end{array} \end{array} $$

(9)

After simple mathematical manipulation, (9) becomes:

$$ \min \limits_{\hat{\mathbf{A}}} \|\tilde{\mathbf{Y}} - \tilde{\mathbf{X}}\hat{\mathbf{A}}^{T}\|_{F}^{2} , \mathrm{s.t.}, \hat{\mathbf{A}}^{T}\hat{\mathbf{A}} = \mathbf{I}_{r}, $$

(10)

where $\tilde {\mathbf {Y}} = [\hat {\mathbf {Y}}- \mathbf {e}\hat {\mathbf {b}}_{1}; \hat {\mathbf {Y}}- \mathbf {e}\hat {\mathbf {b}}_{2}] \in \mathbb {R}^{2n \times m}$ and $\tilde {\mathbf {X}} = [\mathbf {X}_{1}\hat {\mathbf {B}}_{1}; \mathbf {X}_{2}\hat {\mathbf {B}}_{2}] \in \mathbb {R}^{2n \times r}$. Equation (10) is actually an orthogonal Procrustes problem [6]. The optimal solution of $\hat {\mathbf {A}}$ is UV^T, where $\mathbf {U} \in \mathbb {R}^{m \times r}$ and $\mathbf {V} \in \mathbb {R}^{r \times r}$ are obtained from the singular value decomposition of $\tilde {\mathbf {Y}}^{T}\tilde {\mathbf {X}} = \mathbf {UDV}^{T}$, and $\mathbf {D} \in \mathbb {R}^{r \times r}$ is a diagonal matrix.

3.5.2 Update $\hat {\mathbf {b}}_{1}$, $\hat {\mathbf {b}}_{2}$, $\hat {\mathbf {B}}_{1}$ and $\hat {\mathbf {B}}_{2}$ with fixed $\hat {\mathbf {A}}$.

For fixed $\hat {\mathbf {A}}$, the optimization problem in (8) reduces to

$$\begin{array}{@{}rcl@{}} \begin{array}{l} \min \limits_{\hat{\mathbf{B}}_{1}, \hat{\mathbf{B}}_{2}, \hat{\mathbf{b}}_{1}, \hat{\mathbf{b}}_{2}} \|\hat{\mathbf{Y}} - \mathbf{X}_{1}\hat{\mathbf{B}}_{1}\hat{\mathbf{A}}^{T} - \mathbf{e}\hat{\mathbf{b}}_{1}\|_{F}^{2} + \alpha \|\hat{\mathbf{B}}_{1}\|_{2,1} \\ + \|\hat{\mathbf{Y}} - \mathbf{X}_{2}\hat{\mathbf{B}}_{2}\hat{\mathbf{A}}^{T} - \mathbf{e}\hat{\mathbf{b}}_{2}\|_{F}^{2} + \beta \|\hat{\mathbf{B}}_{2}\|_{2,1}, \end{array} \end{array} $$

(11)

By setting the derivative of (11) w.r.t.$\hat {\mathbf {b}}_{1}$ to zero, we have:

$$ 2\mathbf{e}^{T}\mathbf{X}_{1}\hat{\mathbf{B}}_{1}\hat{\mathbf{A}}^{T} + 2\mathbf{e}^{T}\mathbf{e}\hat{\mathbf{b}}_{1} - 2\mathbf{e}^{T}\hat{\mathbf{Y}} = 0 $$

(12)

After simple mathematical manipulation, we have:

$$ \hat{\mathbf{b}}_{1} = \frac{1}{n}\mathbf{e}^{T}\hat{\mathbf{Y}} - \frac{1}{n}\mathbf{e}^{T}\mathbf{X}_{1}\hat{\mathbf{B}}_{1}\hat{\mathbf{A}}^{T} $$

(13)

Similarly, by setting the derivative of (11) w.r.t.$\hat {\mathbf {b}}_{2}$ to zero, we obtain optimal $\hat {\mathbf {b}}_{2}$ as:

$$ \hat{\mathbf{b}}_{2} = \frac{1}{n}\mathbf{e}^{T}\hat{\mathbf{Y}} - \frac{1}{n}\mathbf{e}^{T}\mathbf{X}_{2}\hat{\mathbf{B}}_{2}\hat{\mathbf{A}}^{T} $$

(14)

Substituting (13) and (14) into (11) and letting $\mathbf {H} = \mathbf {I}_{n} - \frac {1}{n}\mathbf {e}\mathbf {e}^{T} \in \mathbb {R}^{n \times n}$, where $\mathbf {I}_{n} \in \mathbb {R}^{n \times n}$ is an identity matrix, we have:

$$\begin{array}{@{}rcl@{}} \begin{array}{l} \min \limits_{\hat{\mathbf{B}}_{1},\hat{\mathbf{B}}_{2}} \|\mathbf{H}\hat{\mathbf{Y}} - \mathbf{H}\mathbf{X}_{1}\hat{\mathbf{B}}_{1}\hat{\mathbf{A}}^{T}\|_{F}^{2} + \alpha \|\hat{\mathbf{B}}_{1}\|_{2,1} \\ + \|\mathbf{H}\hat{\mathbf{Y}} - \mathbf{H}\mathbf{X}_{2}\hat{\mathbf{B}}_{2}\hat{\mathbf{A}}^{T}\|_{F}^{2} + \beta \|\hat{\mathbf{B}}_{2}\|_{2,1}, \end{array} \end{array} $$

(15)

As $\hat {\mathbf {A}}$ has orthogonal columns, there is a matrix $\hat {\mathbf {A}}^{\perp }$ with orthogonal columns such that $(\hat {\mathbf {A}}, \hat {\mathbf {A}}^{\perp })$ is an orthogonal matrix. Thus, we have

$$\begin{array}{@{}rcl@{}} &&\|\mathbf{H}\hat{\mathbf{Y}} - \mathbf{H} \mathbf{X}_{1}\hat{\mathbf{B}}_{1}\hat{\mathbf{A}}^{T}\|_{F}^{2} + \|\mathbf{H}\hat{\mathbf{Y}} - \mathbf{H}\mathbf{X}_{2}\hat{\mathbf{B}}_{2}\hat{\mathbf{A}}^{T} \|_{F}^{2} \\ &&= \|(\mathbf{H}\hat{\mathbf{Y}} - \mathbf{H}\mathbf{X}_{1}\hat{\mathbf{B}}_{1}\hat{\mathbf{A}}^{T})(\hat{\mathbf{A}}, \hat{\mathbf{A}}^{\perp})\|_{F}^{2} \\ &&\quad+ \|(\mathbf{H}\hat{\mathbf{Y}} - \mathbf{H}\mathbf{X}_{2}\hat{\mathbf{B}}_{2}\hat{\mathbf{A}}^{T})(\hat{\mathbf{A}}, \hat{\mathbf{A}}^{\perp})\|_{F}^{2} \\ &&= \|\mathbf{H}\hat{\mathbf{Y}}\hat{\mathbf{A}} - \mathbf{H}\mathbf{X}_{1}\hat{\mathbf{B}}_{1}\|_{F}^{2} + \|\mathbf{H}\hat{\mathbf{Y}} \hat{\mathbf{A}}^{\perp}\|_{F}^{2} \\ &&\quad+ \|\mathbf{H}\hat{\mathbf{Y}}\hat{\mathbf{A}} - \mathbf{H}\mathbf{X}_{2}\hat{\mathbf{B}}_{2}\|_{F}^{2} + \|\mathbf{H}\hat{\mathbf{Y}}\hat{\mathbf{A}}^{\perp}\|_{F}^{2} \end{array} $$

(16)

Both the second term and the fourth term in (16) do not involve $\hat {\mathbf {B}}_{1}$ and $\hat {\mathbf {B}}_{2}$. Therefore, for fixed $\hat {\mathbf {A}}$, $\hat {\mathbf {b}}_{1}$ and $\hat {\mathbf {b}}_{2}$, the objective function in (15) reduces to

$$\begin{array}{@{}rcl@{}} \begin{array}{c} \min \limits_{\hat{\mathbf{B}}_{1}, \hat{\mathbf{B}}_{2}} \|\mathbf{H}\hat{\mathbf{Y}}\hat{\mathbf{A}} - \mathbf{H}\mathbf{X}_{1}\hat{\mathbf{B}}_{1}\|_{F}^{2} + \alpha \|\hat{\mathbf{B}}_{1}\|_{2,1}\\ + \|\mathbf{H}\hat{\mathbf{Y}}\hat{\mathbf{A}} - \mathbf{H}\mathbf{X}_{2}\hat{\mathbf{B}}_{2}\|_{F}^{2} + \beta \|\hat{\mathbf{B}}_{2}\|_{2,1}. \end{array} \end{array} $$

(17)

In this work, we used the framework of iteratively reweighted least square [10] to optimize (17), which is thus equivalent to

$$\begin{array}{@{}rcl@{}} \begin{array}{c} \min \limits_{\hat{\mathbf{B}}_{1}, \hat{\mathbf{B}}_{2}} \|\mathbf{H}\hat{\mathbf{Y}}\hat{\mathbf{A}} - \mathbf{H}\mathbf{X}_{1}\hat{\mathbf{B}}_{1}\|_{F}^{2} + \alpha tr(\hat{\mathbf{B}}_{1}^{T}\mathbf{P}\hat{\mathbf{B}}_{1})\\ + \|\mathbf{H}\hat{\mathbf{Y}}\hat{\mathbf{A}} - \mathbf{H}\mathbf{X}_{2}\hat{\mathbf{B}}_{2}\|_{F}^{2} + \beta tr(\hat{\mathbf{B}}_{2}^{T}\mathbf{Q}\hat{\mathbf{B}}_{2}), \end{array} \end{array} $$

(18)

where $\mathbf {P} \in \mathbb {R}^{d \times d}$ and $\mathbf {Q} \in \mathbb {R}^{d \times d}$, respectively, are the diagonal matrices with ${p}_{jj} = \frac {1}{2\|\hat {\mathbf {B}}_{1}^{j}\|_{2}^{2}}$ and ${q}_{jj} = \frac {1}{2\|\hat {\mathbf {B}}_{2}^{j}\|_{2}^{2}}, j = 1,...,d$. By setting (18) w.r.t.$\hat {\mathbf {B}}_{1}$ to zero, we obtain:

$$\begin{array}{@{}rcl@{}} \begin{array}{l} \hat{\mathbf{B}}_{1} = (\mathbf{X}_{1}^{T}\mathbf{HX}_{1} + \alpha \mathbf{P})^{-1}\mathbf{X}_{1}^{T}\mathbf{H}\hat{\mathbf{Y}}\hat{\mathbf{A}}. \end{array} \end{array} $$

(19)

Similarly, by setting the derivative of (18) w.r.t.$\hat {\mathbf {B}}_{2}$ to zero, we have:

$$ \hat{\mathbf{B}}_{2} = (\mathbf{X}_{2}^{T}\mathbf{HX}_{2} + {\beta} \mathbf{Q})^{-1}\mathbf{X}_{2}^{T}\mathbf{H}\hat{\mathbf{Y}}\hat{\mathbf{A}} $$

(20)

We summarize the pseudo code of solving (8) in Algorithm 1. It can be proved that the objective function value in (8) monotonically decreases in each iteration using Algorithm 1 according to literature [10]. In Algorithm 1, the LRDR step and the orthogonal rotation step adjust each other to help find optimal parameters $\hat {\mathbf {b}}_{1}$, $\hat {\mathbf {b}}_{2}$, $\hat {\mathbf {B}}_{1}$, $\hat {\mathbf {B}}_{2}$, and $\hat {\mathbf {A}}$, thus ensuring the output of class-discriminative features.

4 Experimental results

We conducted various experiments on the ADNI dataset to compare our method with the state-of-the-art methods.

4.1 Competing methods

In order to validate the effectiveness of the proposed method, we compared with the following methods: 1) Original features based method (‘Original’) conducts classification on the concatenation of MRI data and PET data with all features, i.e., without feature selection.

2) The feature selection methods on single-modality data include MRI-based Feature Selection (MRIFS) and PET-based Feature Selection (PETFS), where MRIFS and PETFS, respectively, conduct feature selection via Inter-Modality-based Feature Selection (IDFS) [15] with only MRI data and PET data.

3) The state-of-the-art feature selection methods include Multi-Modal Multi-Task (M3T) [34], IDFS [15], and Sparse Joint Classification and Regression (SJCR) [29]. M3T includes two steps: (1) using multi-task feature selection to determine a common subset for multiple response variables (or multiple tasks) from each modality, and (2) using a multi-kernel decision fusion to integrate the selected features from all modalities for prediction. IDFS conducts feature selection by simultaneously imposing the preservation of the inter-modality relationship (i.e., preserving the relative distance between the feature vectors extracted from different modalities of the same subject) on multi-modality data, and also enforcing the sparseness of selected features from each modality. SJCR uses a logistic loss function and a least square loss function simultaneously along with an ℓ_2,1-norm regularizer for multi-task feature selection.

The methods (e.g., M3T, IDFS, and SJCR) embedded their feature selection models into a multi-task learning framework and selected the same features for both MRI and PET. Both M3T and SJCR do not consider the relations among tasks, while IDFS considers the preservation of relative distance between features.

(4) Baseline: (6) that considers the subclass issue is used to test the effectiveness of the assumption of (8), i.e., different modalities share the same high-level representation.

4.2 ADNI study

4.2.1 Experimental setup

We considered three binary classification tasks (including AD vs. NC, MCI vs. NC, and pMCI vs. sMCI) on two-modality data (i.e., MRI and PET) to evaluate the performance of all competing methods, in terms of the metrics of classification accuracy, sensitivity, specificity, and Area Under a receiver operating characteristic Curve (AUC).

We used a 10-fold cross-validation method to compare all methods. Specifically, we first randomly partitioned the whole dataset into 10 subsets. We then selected one subset for testing and used the remaining 9 subsets for training. We repeated the whole process 10 times to avoid the possible bias during dataset partitioning for cross-validation. The final result reported in Tables 2, 3, 4 and 5 was computed by averaging results from all ten experiments.

Table 2 Classification performance of all methods for AD vs. NC

Table 3 Classification performance of all methods for MCI vs. NC

Table 4 Classification performance of all methods for pMCI vs. sMCI

Table 5 Classification performance of all methods for AD vs. MCI

For the model selection, we set α ∈{10^− 5,...,10⁵}, β ∈{10^− 3,...,10³}, the number of sub-classes for each response variable ∈{5,8,10,12}, and r ∈{10%,30%,50%, 70%,90%} of the number of full-rank⁵ in (8) and C ∈{2^− 5,...,2⁵} in SVM with a linear kernel by a 5-fold inner cross-validation, where the training data are further partitioned into five parts to select the best combination of parameters with the highest classification accuracy, to be used in testing.. For fair comparison, we also conducted 5-fold inner cross-validation to conduct model selection for each competing method. Specifically, for MRIFS, PETFS, and IDFS, we followed the literature [15] to set the values in the ranges of λ₁ ∈{10^− 3,10^− 2...,10³} and λ₂ ∈{10^− 4,10^− 2...,10¹}. For SJCR and M3T, we optimized their sparsity parameters by cross-validating the value in the ranges of {10^− 5,10^− 3...,10⁵} (as in [29]) and {10^− 5,...,10²}, respectively, to obtain their best performance.

4.3 Classification results

We summarized the performances of all methods on four binary classification tasks in Tables 2–5.⁶ The proposed method outperformed all the competing methods in all classification tasks. For example, for four binary classification tasks, our method improved, on average, the classification accuracy by 4.9% (vs. Baseline), 5.4% (vs. IDFS), 6.9% (vs. M3T), 7.2% (vs. PETFS), 8.0% (vs. MRIFS), and 9.9% (vs. Original), respectively. Meanwhile, compared to all the competing feature selection methods, our method achieved the maximal and minimal improvements by 8.3% (vs. PETFS) and 4.8% (vs. Baseline) on AD vs. NC, 8.8% (vs. SJCR) and 5.0% (vs. Baseline) on MCI vs. NC, 7.4% (vs. PETFS) and 4.9% (vs. Baseline) on pMCI vs. sMCI, and 9.6% (vs. MRIFS) and 4.0% (vs. Baseline) on AD vs. MCI, respectively. The reason may be that, the proposed method considered the following constraints for conducting feature selection: 1) all kinds of relations inherent in data; 2) iteratively conducting the procedures of low-rank dimensionality reduction and orthogonal rotation; and 3) selecting different features from different modalities.

It is noteworthy that all methods achieved the highest classification performance on AD vs. NC. For example, the average classification accuracy of all methods was 85.7% (AD vs. NC), 67.4% (MCI vs. NC), 66.4% (pMCI vs. sMCI), and 72.7% (AD vs. MCI), respectively. Another observation is the low sensitivity (or specificity) for the classification of MCI vs. NC (or pMCI vs. sMCI). A possible reason for these two observations is that the difference between AD and NC is relatively prominent while there is no substantial difference between MCI and NC (or between pMCI and sMCI). Furthermore, our proposed method outperformed Baseline on all the datasets, which supports our assumption “different modalities share the same high-level representation”.

4.4 Most discriminative brain regions

We investigated the brain regions as potential biomarkers for AD diagnosis based on the selected frequency of the brain regions by the proposed method. We listed the frequency (defined as the probability of a feature appeared in the 100 experiments - ten times of ten-fold cross-validation) of each feature in our 10 repeated 10-fold cross-validation experiments in Figure 2 and also visualized the top selected brain regions in Figure 3. In the classification task of MCI vs. NC, our method selected regions of uncus right, hippocampal formation right, uncus left, middle temporal gyrus left, hippocampal formation left, amygdala left, middle temporal gyrus right, and amygdala right as top selected ones, which have also been pointed out in the previous work [34] and have been shown to be highly related to AD or related dementia (e.g., MCI) in clinical diagnosis [1, 4, 18]. Hence, brain regions selected by our method could be further incorporated for future clinical analysis.

Figure 2

Frequency of the selected ROIs of MRI (upper row) and PET (down row) by the proposed method on four binary classification tasks, where horizontal axis represents the number of ROIs and vertical axis represents the frequency (ranging from 0 to 100) in ten cross-validation experiments. Frenquency₁ = 11 in the first sub-figure (i.e., the top left sub-figure) means that the first ROI was selected 11 times over 100 repeats by the proposed method

Figure 3

Top selected regions of the proposed method on three binary classification tasks

Besides, we had some interesting observations: 1) In the process of feature selection, our method selected less number of MRI features than PET features in our experiments. For example, our method selected, on average, 16.3/40.3, 16.6/40.8, 13.3/32.6, and 32.1/31.6, respectively, of MRI/PET features on the classification tasks of AD vs. NC, MCI vs. NC, pMCI vs. sMCI, and AD vs. MCI. This observation manifested that MRI and PET could provide complementary information to each other to enhance the classification performance of multi-modality data for AD classification. 2) Different classification tasks have selected different brain regions from each modality.

4.5 Discussion

In this section, we investigate three aspects of the proposed method, i.e., the effect of different number of ranks (i.e.,r) in (8), and the effect of different number of sub-classes for each original class in Section 3.4.

Figures 4 and 5 visualize, respectively, the change of classification accuracies according to different values of a rank, i.e.,r ∈{10%,30%,50%,70%,90%,100%} of the number of the full rank and different number of clusters or sub-classes (i.e., {1, 2, 3, 4, 5}) in each class. From Figure 4, we observe that the performance with low-rank constraint in most of cases outperformed the performance of the cases with full-rank. This manifested that it is reasonable to analyze neuroimaging data with a low-rank constraint in AD study. The reason is that, the low-rank constraints, conducting subspace learning, help find the low-dimensional structure of high-dimensional neuroimaging data via considering the relations among response variables.

Figure 4

Classification accuracy of our method with different number of ranks of coefficient matrix in the case of the fixed number of subclasses (i.e., 6) for each response variable on four different classification tasks

Figure 5

Classification accuracy of the proposed method with different numbers of clusters in the case of the fixed number of ranks (i.e.,r = 5) on four different classification tasks

Figure 5 explains that different numbers of sub-classes for each original class outputted different results, and the case, in which the response variables are partitioned into 6 sub-classes, achieved the best classification performance on all three classification tasks in our experiments. Besides, we found that the results of using one cluster 1) were worse than the results of using more than one clusters, which indicates the variability of real datasets; and 2) were better than the results of all the competing methods, which shows the effectiveness of our proposed OLRDR on multi-modality data, i.e., Section 3.3. By combing these two observations together, we conclude that the variability assumption (i.e., Section 3.4) does work.

5 Conclusion

In this paper, we focused on taking advantages of different aspects of data such as variability, sparsity, and low-rankness with multiple modalities for AD classification. Specifically, we first extended conventional label representation (e.g., 0-1 encoding) to a multi-output representation, and then iteratively conducted a low-rank dimensionality reduction step and an orthogonal rotation step to select representative features, by taking advantages of all kinds of relations inherent in the neuroimaging data. The experimental results on the ADNI dataset with MRI and PET verified the efficacy of the proposed method over the state-of-the-art methods in terms of classification performance on three binary classification tasks.

According to Section 4.3, the classification performance on both MCI vs. NC and pMCI vs. sMCI are lower than the performance of AD vs. NC. This may result from the subtle changes between two clinical statuses. In our future work, we will focus on selecting representative features via transfer learning methods (e.g., [21]) to further improve the classification performance of AD-to-MCI classification, such as MCI vs. NC and pMCI vs. sMCI. For example, we could use the information of the classification AD vs. NC to help enhance classification performance of the classification pMCI vs. sMCI according to the conclusion in [19], which demonstrated that the features selected by the classification AD vs. NC can be regarded as representative features of the classification pMCI vs. sMCI.