1 Introduction

Regression is one of the most widely popular statistical tools for analyzing multifactor data. It provides a conceptual process for estimating the relationship amongst continuous entities and also suitable for analyzing functional dependencies [59]. Regression analysis is well known theoretically due to its elegant underlying mathematics [29]. Regression is primarily used as a tool for prediction, forecasting and casual inference [31] and has been applied in many fields including software engineering, physical and chemical sciences, biology for nutrient and sediment, weather forecasting, credit scoring among others[31].

Currently, there are two categories of regression schemes: single regression model and ensemble regression model [16]. The former can further be split into two main subcategories, namely, non-kernel and kernel techniques. Some typical methods in this subcategory are Linear Regression (LR), Ridge Regression (RR), Lasso Regression, ElasticNet Regression, etc. For example, Shah et al. [42] proposed a novel image set classification technique based on the linear regression model. Fan et al. [8] also presented a ridge regression to estimate the variations in the quantity and distribution of land surface temperature in response to various land cover patterns. Stransky et al. [44] proposed a novel elastic net regression model for pharmacogenomics agreement between two cancer cell line datasets.

Compared with the non-kernel regression technique, the kernel regression methods have a higher performance since the Reproducing Kernel Hilbert Space (RKHS) is introduced, thus the non-linear relationship among data samples can be characterized better. Typical instances of such kernel-based methods are the Kernel Ridge Regression (KRR)[32] and Support Vector Regression (SVR) [1]. Unfortunately, regression performance varied dramatically with the selection of both kernel functions and their parameters. Additionally, it is also hard to get suitable Kernel functions and parameters which are selected manually in practice.

Ensemble regression (ER) models combine individual regressors together to improve the accuracy and stability of an individual model. Random Forest (RF) [45, 54], Gradient Boosting [53, 57] and Tree Regression [37, 40] amongst other techniques fall under such category.All of them are based on tree structure technique that combines several decision trees to produce better predictive performance than utilizing a single decision tree. The main principle behind the ensemble model is that, a group of weak learners can work together to form a strong learner [5].

Based on the aforementioned challenges, a novel Co-Regularized Kernel Ensemble Regression (CoKER) is proposed, whereby we combine kernel regression and ensemble models together. Different from the previously proposed methods of multiple kernel learning (MKL) in the field of dimension reduction [23, 56], classification [12, 33] and label propagation [13, 34]. The proposed CoKER optimizes each base kernel regressor in a separate RKHS and then co-regularizes them into one regression model in multiple RKHS. Therefore, overcomes the difficulty in selection of kernel function and parameters which resides in single kernel methods whiles existing multiple kernel learning methods combine several kernel RKHS spaces into one unified space.

The main contributions of this paper are as follows:

  1. 1.

    We propose a novel kernel ensemble regression method that takes advantage of both single kernel regression method and ensemble regression method, which can accomplish multi-kernel selection and parameter-decision automatically in an ensemble way.

  2. 2.

    The proposed method can combine multiple kernel regressors into a unified ensemble regression framework and the weight of each kernel regressor in this ensemble method is co-regularized by minimizing total loss of ensembles in Reproducing Kernel Hilbert Spaces. This gives an advantage of one kernel regressor having more accurate fitting precession on data and can, therefore, obtain bigger weight which leads to a better overall ensemble performance.

  3. 3.

    The experimental results on several UCI datasets for regression and classification, compared with several single models and other ensemble models such as Gradient Boosting(GB), Tree Regression(TR), Support Vector Regression(SVR), Ridge Regression(RR) and Random Forest(RF), illustrate that the proposed method achieves best performances among the comparative methods.

The rest of the paper is organized as follows: Section 2 introduces some related works with respect to the topic under discussion. Section 3 presents the proposed method. Experimental results are presented in section 4. Finally, Section 5 concludes the paper.

2 Related work

In this Section, we present an overview of some empirical studies on regression methods. Regression methods could be classified into two categories, the single regression model and ensemble regression model. Besides, some multiple kernel learning methods are introduced as well.

2.1 Single regression model

Ridge Regression (RR) is a technique that can fit data well when they have near-linear relationships among the independent data variables. Li et al. [22] proposed an RR-ELM algorithm to improve the stability and generalization of the extreme learning machine (ELM). The experimental results showed that the RR-ELM can reduce the adverse effects that are caused by the perturbation or multicollinearity in linear models. Lasso regression, similar to ridge regression has also become a widely used alternative method to ordinary least squares method for parameter estimation in regression problems. Its popularity is in part due to a key feature that it can make shrinkage of the vector of regression coefficients towards zero to obtain a sparse solution. Some applications of this method can be found in the literature [17, 27]. Lu et al. [27] proposed a lasso regression model to identify miRNA-mRNA targeting relationships. Homrighausen et al. [17] used Lasso regression for high-dimensional risk estimation problem.

Meanwhile, ElasticNet regression is the combination of Lasso and ridge regression techniques. This implies that elastic net also enjoys the computational advantages of lasso regression. Lenters et al. [21] used the penalized elastic net to assess a mixture of environmental contaminants and this model proves useful for similar environmental epidemiology analyses of multiple exposures. Chen et al. [4] proposed a model to analyze the uncertainty level of voltage with the elastic net. Experiments showed that the proposed linear analysis model with the elastic net can precisely describe the mapping relations among deviations of random numbers.

Furthermore, the kernel-based regression (KR) methods [31] are extensively studied due to their capacity of characterizing the data in Reproducing Kernel Hilbert Space (RKHS) [41, 43]. By using RKHS, many techniques can be extended into such kernel methods, for example, kernel ridge regression (KRR) [32] is an instance of a natural extension of ridge regression. Exterkate et at. [7] proposed a kernel ridge regression as a framework for estimating non-linear predictive relations in a data-rich environment. Liu et al. [25], applied regularized kernel regression (KLR) for Web image annotation. Their experimental results showed that regularized kernel regression (KLR) provides a smooth loss function.

Similarly, the kernel technique can be applied to other classical methods such as Support Vector Machines (SVM). Support Vector Regression methods [38, 50] are the natural extension of SVM. Drucker et al. [6] proposed an SVR method to pursue the best trade-off between empirical errors of models and their complexities. Qiu et al. [35] also investigated multiple learning SVR methods. The experimental results revealed that it can reduce a much complex dataset into a simpler one and increase the adaptability of SVR, especially for a complex dataset.

2.2 Ensemble regression model

Ensemble regression (ER) can combine individual regressors together and keep their performance better as compared to the single regression model. Tree regression method is used to predict the numerical outcomes of the dependent variables. It is also known as an m5p algorithm, which is an implementation of Quin-lan’s M5 algorithm [36]. Rathore et al. [37] presented a decision tree regression-based approach for the number of faults prediction in a given software module.

Furthermore, Gradient Boosting Decision Trees (GBDT) [58] is an addictive ensemble regression model in decision trees. Wang et al. [53] proposed a new fusion method based on the LR algorithm and GBDT algorithm for mobile recommendation system. Their method is observed to achieve a good F1 score in a mobile recommendation scenario.

Among ensemble regression methods, random forest (RF) method is a useful machine learning technique which can be applied in both regression and classification problems [3]. Hasan et al. [14] applied random forest for intrusion detection problems. The research indicated that random forest takes less time to train its classifier than SVM and also achieves more accurate results than SVM classifier. Wu et al. [54] used random forest regression approach to analyze the weekly analysis of influenza-like illness rate using one year period of factors. Experimental results showed that regression errors decreased from 5.04% to 4.35% in mean absolute percentage error (MAPE) and 2.85E-04 to 1.97E-04 in mean square error (MSE) for prediction of weekly ILI rate.

2.3 Multiple kernel learning

Multiple Kernel Learning (MKL) plays an important role in tackling many learning tasks in non-linear cases [18, 26]. The choice of kernels is a crucial issue for kernel-based algorithms. Many efforts have been devoted to yield an optimal kernel for specific applications. Szafranski et al. [46] developed the composite kernel learning (CKL) approach with group Lasso. Tang et al. [47] proposed a new multi-kernel for the classification task. It provides an alternative optimization algorithm as the efficient solution for multiple kernel learning.

Besides the above discussions, some new classification, regression and multiple feature techniques appear in the latest advancement in deep learning [20, 39]. Many deep models have been proposed for large-scale image and video annotation [24, 51]. Johnson et al. [19] found a neighborhood of images which are non-parametrical according to the image metadata and combined the visual features of each image and its neighborhoods. Gao et al. [11] proposed an optimal graph from multiple cues (i.e., partial labels and multiple features) to embed the relationships among data points more precisely. Wang et al. [52] proposed an end-to-end pipeline named Two-Stream3DconvNetFusion, which can recognize human actions in videos of arbitrary size and length using multiple features. Gao et al. [10] on the other hand, designed some effective learning schemes for high-dimensional data. Where they covered feature transformation, feature selection and feature encoding to curb the consequences of the curse of dimensionality.

3 The proposed method

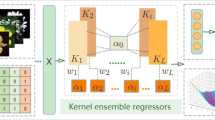
In this section, co-regularized kernel ensemble regression (Coker) scheme is presented. In the scheme, multiple kernel regressors are absorbed into a unified ensemble regression framework simultaneously and co-regularized by minimizing total loss of ensembles in reproducing kernel Hilbert space. In this way, one kernel regressor with more accurate fitting precession on data can obtain bigger weight, which leads to a better overall ensemble performance.

3.1 RKHS and representer theorem

The use of geometric intuitions to extend an established framework for functional learning has been on the rise. A number of popular algorithms such as SVM, ridge regression, splines and radial basis functions, may be broadly interpreted as regularized algorithms with different empirical cost functions and complexity measures in an appropriately chosen Reproducing Kernel Hilbert Space (RKHS) [15, 48, 49] to address the poor generalization properties of existing nonlinear regression techniques. Some suitable functions can be regarded as kernels:

  • The Polynomial kernel

    $$\begin{array}{@{}rcl@{}} k(x_{i},x_{j})=(a{x_{i}^{T}}x_{j}+b)^{c} \end{array} $$
    (1)

  • The RBF kernel(Radial Basis Function)

    $$\begin{array}{@{}rcl@{}} k(x_{i},x_{j})=exp(-\frac{\|x_{i}-x_{j}\|}{\mu}) \end{array} $$
    (2)

  • The Gaussian kernel

    $$\begin{array}{@{}rcl@{}} k(x_{i},x_{j})=exp(-\frac{\|x_{i}-x_{j}\|^{2}}{2\sigma^{2}}) \end{array} $$
    (3)

where \(a,b,c,\mu ,\sigma \in R\). For a Mercer Kernel \(K:x \times x \in R\), there is an associated RKHS \({H_{k}}\) of the function \(x \to R\) with the corresponding norm \({\left \| {\left . {} \right \|} \right ._{k}}\). Meanwhile, \(\textbf {K}\) denotes a Gram matrix which is obtained according to samples. It is a symmetric and semi-positive definite matrix, which can be shown as follows:

$$\begin{array}{@{}rcl@{}} \textbf{K} =\left( \begin{array}{cccc} k(x_{1},x_{1}) & k(x_{1},x_{2}) & {\cdots} & k(x_{1},x_{N}) \\ k(x_{2},x_{1}) & k(x_{2},x_{2}) & {\cdots} & k(x_{2},x_{N}) \\ {\vdots} & {\vdots} & {\ddots} & \vdots\\ k(x_{N},x_{1}) & k(x_{N},x_{2}) & {\cdots} & k(x_{N},x_{N})\\ \end{array} \right) \end{array} $$
(4)

Given a set of labeled examples \(({x_{i}},{y_{i}}),i = 1,2,3,...,N\) the standard framework estimates an unknown function by minimizing

$$\begin{array}{@{}rcl@{}} {f^{*}} = \arg \min \frac{1}{1}\sum\limits_{i = 1}^{N} {v({x_{i}},{y_{i}},f)} + \gamma \left\| f \right\|_{k}^{2} \end{array} $$
(5)

Where v is some loss function, such as squared loss \({({y_{i}} - f({x_{i}}))^{2}}\) for RLS or hinge loss function max \(\left [ {0,1 - {y_{i}}f\left ({{x_{i}}} \right )} \right ]\) for SVM. Penalizing the RKHS norm imposes smoothness conditions on possible solutions. \(\gamma \|f\|_{k}^{2}\) is regarded as smoothness conditions on possible solutions in the RKHS and the gamma is a parameter to trade off the balance. The classical representation theorem states that the solution to minimization problems exists in \({H_{k}}\) and can be written as

$$\begin{array}{@{}rcl@{}} {f^{*}}(x) = \sum\limits_{i = 1}^{N} {{\alpha_{i}}} k({x_{i}},x) \end{array} $$
(6)

Therefore, the problem is reduced to optimizing over the finite dimensional space or coefficients \({\alpha _{1}}\), which is the algorithmic basis for SVM, regularized least squares and other regression methods.

3.2 Co-regularized kernel ensemble regression

The proposed method can combine multiple kernel regressors into a unified ensemble regression framework and the weight of each kernel regressor in this ensemble method is co-regularized by minimizing total loss of ensembles in Reproducing Kernel Hilbert Spaces. This gives an advantage of one kernel regressor having more accurate fitting precession on data and can, therefore, obtain bigger weight which leads to a better overall ensemble performance.

Firstly, different kernels are obtained according to samples. Suppose a regression problem has a training set X with regression result \((X = \{ ({x_{1}},{y_{1}}),...,\\({x_{N}},{y_{N}})\} )\) and a testing set \({X_{t}}\) without regression result \(({X_{t}}{{ = \{ (}}{x_{1}},...,{x_{{N_{t}}}})\} )\) where \({x_{n}}({x_{n}} \in {R^{d}},n = 1,...,N)\) expresses a training sample, \(y_{n}\) is the true regression result of \({x_{n}}\), and \({{x_{m}}({x_{m}} \in {R^{d}},m = 1,...,{N_{t}})}\) expresses a testing sample. \({N}\) is the number of training samples and \({N_{t}}\) is the number of testing samples. The base kernel regression model is

$$\begin{array}{@{}rcl@{}} {\left\| {K\alpha + b - y} \right\|^{2}} + \lambda {\alpha^{T}}K\alpha \end{array} $$
(7)

where \({K}\) denotes a kernel matrix which can be obtained according to samples, \({\alpha }\) is a column vector related to the weight of every sample, \({b}\) expresses bias term for the specific \({K}\).Our approach aims to obtain the optimal co-regularized weight vector of base regressors. The term \({\left \| {K\alpha + b - y} \right \|^{2}}\) is the square loss for determining the performance of the base kernel regression model.

Unfortunately, since regression performance varies dramatically with the selection of both kernel functions and their parameters, it is also hard to obtain suitable Kernel functions and parameters which are commonly selected manually in practice. To overcome this problem, our proposed method can combine multiple kernel regressors into a unified ensemble regression framework without considering the selection of both kernel functions and their parameters in individual kernel regressors. L different kernels are used in our framework and a new co-regularized kernel ensemble regression model is proposed:

$$\begin{array}{@{}rcl@{}} \mathop {\arg \min }\limits_{w,{\alpha_{i}}} \frac{1}{2}\sum\limits_{i = 1}^{L} {{W_{i}}({{\left\| {{K_{i}}{\alpha_{i}} + {b_{i}} - y} \right\|}^{2}} + \lambda {\alpha_{i}}^{T}{K_{i}}} {\alpha_{i}}) \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} s.t. \quad {1^{T}}W = 1 \end{array} $$
(9)

Where \({L}\) is the number of kernels. Assuming that the number of training samples is \({N}\), and the number of testing samples is \({N_{t}}\) and \({W = {[{W_{1}},...,{W_{L}}]^{T}}}\) denotes a weight vector of individual kernel regression model. \({K_{i}}\) represents the different kernel matrix. \({K_{i}}\) is the i-th base Gram matrix and the dimension of \({K_{i}}\) is \({N \times N}\) for training dataset, \({{N_{t}} \times N}\) for testing dataset. \({\alpha _{i}}\) denotes a column vector related to the weight of every sample for each \({K_{i}}\). The dimension of \({\alpha _{i}}\) is \({N \times 1}\) for training dataset, \({{N_{t}} \times 1}\) for testing dataset. \({b_{i}}\) is the bias item for a specific \({K_{i}}\). \({b_{i}}\) is a column vector that has the same dimension as samples, and each value in the vector is equal to a specific \({K_{i}}\). \({y}\) denotes the true output and its dimension is the same as samples. \({\lambda }\) is the constriction parameter that smoothens the model.

We take the derivative of formula (7) with respect to \({\alpha _{i}}\) and obtain the following formula.

$$\begin{array}{@{}rcl@{}} {\alpha_{i}} = {({K_{i}} + \lambda I)^{- 1}}y \end{array} $$
(10)

where \({I}\) is an identity matrix which has the same dimension as training \({K_{i}}\).

According to Formula (10), we can get

$$\begin{array}{@{}rcl@{}} {b_{i}} = \frac{1}{N}(\sum\limits_{t = 1}^{N} {{y_{t}} - \sum\limits_{j = 1}^{N} {{K_{i}}({x_{j}},{x_{t}}){\alpha_{i,j}})} } \end{array} $$
(11)

We considered \({W_{i}}\) to be \({{W_{i}}^{T}}\) (r represents the control parameter for the weights of multiple features) because linear programming attains its optimum solution at the extreme ends, i.e either \({{W_{i}} = 0}\) or \({{W_{i}} = 1}\). That means there will only be one kernel selected contrary to our objective of exploring the rich complementation of multiple kernels. When \({r = 1}\), it is only one kernel that will be selected in the optimal result, which is undesirable, but if \({r>1}\) the outcome is based on multi-kernel balancing. \({r}\) is a man-made value to obtain appropriate \({w}\). We can further derive that

$$\begin{array}{@{}rcl@{}} {W_{i}} = \frac{{{{(\frac{1}{{{\zeta_{i}}}})}^{r - 1}}}}{{\sum\limits_{i = 1}^{L} {{{(\frac{1}{{{\zeta_{i}}}})}^{r - 1}}} }} \end{array} $$
(12)

Where \({{\zeta _{i}} = {\left \| {{K_{i}}{\alpha _{i}} + {b_{i}} - y} \right \|^{2}} + \lambda {\alpha _{i}}^{T}{K_{i}}{\alpha _{i}}}\) denotes the loss of each kernel. From this equation, we can see that the more the loss of a kernel, the lesser the weight of that kernel. In this way, we obtain an ensemble regression model by combining the various base kernels linearly. This becomes our final model and can be determined by using Formula (13)

$$\begin{array}{@{}rcl@{}} f({x_{t}}) = \sum\limits_{i = 1}^{L} {{W_{i}}(\sum\limits_{j = 1}^{N} {{K_{i}}} } ({x_{j}},{x_{t}}){\alpha_{i,j}} + {b_{i}}) \end{array} $$
(13)

4 Experimental results

In this section, all the experimental results under different settings are presented. For a fair comparison, each dataset is randomly split into 2/3 (training data) and 1/3 (testing data) and the regularization parameter is obtained by cross-validation method. In our experiments, five comparative methods (Gradient boosting, Tree Regression, Support Vector Regression, Ridge Regression and Random Forest) are selected as base models. Mean Square Error (MSE) and Mean Absolute Error (MAE) are selected as the criteria [2].

$$\begin{array}{@{}rcl@{}} MAE = \frac{1}{{{N_{t}}}}\sum\limits_{i = 1}^{{N_{t}}} {\left| {f({x_{i}}) - {y_{i}}} \right|} \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} MSE = \frac{1}{{{N_{t}}}}\sum\limits_{i = 1}^{{N_{t}}} {{{(f({x_{i}}) - {y_{i}})}^{2}}} \end{array} $$
(15)

In the proposed method, we demonstrate how to combine the base kernel model of the ensemble. A single polynomial kernel model in (1) is applied as the basic model of the ensemble for different datasets.

There are three parameters (a,b and c) in this type of model and the different values of the parameters show different effects on the experimental results. Generally, we set a ∈{1 ∗ 1e − 6,1 ∗ 1e − 5,⋯ ,1000}, \(b\in \{1*1e-6,1*1e-5, \cdots , 1000\}\) and \(c\in \{1,2,3,4,5\}\). For each dataset, we select the optimal parameters (a,b and c) and base kernels are obtained by 10-fold cross validation in experiments. The parameter L in (8) denotes the number of base polynomial kernel models. The generalization ability of an ensemble regressor will be good if there are enough base models. However, excessive base models may consist of many worse base models and result in low classification accuracy. Therefore, we take \(L\in \{10,20,50,100,150\}\). In our experiments, we select 20 combinations among three parameters (a,b and c).

And the parameter in (8) is the parameter that smoothens the base regressor. The parameter r in (12) is the control parameter for the weights of multiple base models. In our experiments, we select values for \(\lambda \) and r as 0.1 and 2, respectively.

4.1 Dataset description

We selected nine benchmark publicly available datasets for the evaluation of the performance of our algorithm. These datasets are from the UCI database repository, a detailed summary is presented in Table 1 [55].

Table 1 Descriptions of UCI dataset
Full size table

4.2 Experimental settings

We compared the effectiveness and robustness of the proposed novel Kernel Ensemble Regression with the conventional multi-kernel features. We as well showed the performance of some single and ensemble regression preserving methods: Ridge Regression, Random Forest and Support Vector Regression among others but with careful tuning of the parameters we applied them to all our datasets.

4.3 Performance evaluations and comparisons

Here, we discuss the general performance of the proposed co-regularized kernel ensemble regression algorithm and all the comparative methods.

Table 2 presents the mean MSE comparisons among our method, single models and ensemble models. From the results, CoKER produces a smaller Mean Square Error (MSE) of 3.599 on Abalone dataset as compared with the other comparative methods while tree regression performing poorly with values of 4.491. On RedWine dataset, all the methods perform very well with CokER still giving us the best MSE of about 0.15% over the other methods. SVR performs quite poorly as compared to the other methods with regards to WhiteWine dataset and our proposed CoKER still maintaining its best results of 0.491. Furthermore, we observed that the proposed CoKER performed better than the other methods with a result of 38.552 for Housing dataset, with a 3.51% result better than the other methods. Ridge regression has the worst performance for this dataset. For the Concrete dataset a wide margin exists between our method result and the others. CoKER leads with a value of 56.0335 which is 3.42% better. It is then followed by ridge regression, while tree regression comes in with the least performance. The Bodyfat dataset result changed the trend. Here, the proposed method slightly lags behind gradient boosting method which comes on top with a value of 2.904. CoKER yielded a value of 3.765. Tree regression method has the worst performance of 6.4709 for this dataset. With the exception of the Bodyfat dataset, CoKER continues to perform better than other methods when applied to the remaining datasets. With Mg dataset, we get the best performance with a value of 0.013. Compared with the second best performing method, Random forest provides a result of 0.014, giving a difference of 0.0093. Tree regression has the worst performance for this dataset. CoKER obtains the best result of 24.404 for the Mpg dataset. 1.06% better than the next best result of 26.004 from ridge regression. Finally, with a value of 0.022,CoKER leads the others on the Space dataset. It is followed by the random forest method by a margin of 0.0005. The SVR method generates a result of 0.0392 which makes it the worst performer for the Space dataset.

Table 2 The average of MSE comparison of ours, single models and ensemble models
Full size table

From the experiments of Table 2, it demonstrates that for MSE values, the propose CoKER method outperforms the comparative single and ensemble models.

Figure 1 gives a different view of MSE comparisons among the propose CoKER, single models and ensemble methods on UCI regression datasets and Figure 1a illustrates MSE comparison when applied to the abalone dataset, our method shows the lowest median of 3.599. The model with the next best median is the random forest. In Figure 1b, the box plot indicates that for the RedWine dataset, CoKER again performs better than the other methods with a value of 0.410. Gradient boosting is the second best performer while SVR has the worst lower bound performance. The trend continues in all the box plots displayed, with CoKER performing better with lower median values the other single and ensemble methods. It can be seen in Figure 1a and c that, most of the plots have flat shape, which means the smaller the regression variance, the more stable the method and the lower the median of the method in the figure, the better the regression result of the method. This because most of the variance is very small,i.e., \(10^{-4}\) and we did not show them in our tables. Here, CoKER again performed better than the rest of the methods.

Figure 1
figure 1

Box Plot of the respective datasets for MSE: a Abalone b Redwine c Mg d space

Full size image

From the above discussion, we can conclude that the propose CoKER outperforms the comparative methods.

Table 3 presents the mean MAE comparisons among the propose CoKER, single models and ensemble models. From the results, it can be seen that, when applied to the Abalone dataset, the CoKER attains the optimal result of 0.1245. Gradient boosting lags slightly behind by 0.01% with a value of 0.134. Random forest yields the worst result with a value of 4.002. Applied to RedWine dataset, CoKER leads with a value of 0.051 closely followed by gradient boosting with a margin of 0.009. Random forest, ridge regression, tree regression, and SVR follow in that order with SVR having a value of 0.517. When applied to WhiteWine, CoKER performs better than other methods by 1.17%. Random forest yields the next best result with a value of 0.107, with ridge regression being the worst performer. With the housing dataset, CoKER again yields the best result. The margin between our method (1.627) and the worst ridge regression (10.273) is 8.6 while the second best performer is 1.940. Concrete dataset results also indicate a wide margin between the results. CoKER provides the best result with a value of 0.134 which is 35% better than the others. With the Bodyfat dataset, Random forestpr provides the best performance with a value of -3.649 followed by gradient boosting. CoKER, when applied to Mg turns out to be the best performer with a value of 7.0000e-04 and gradient boosting being the worst performer with a value of 0.001. With the Mpg dataset, CoKER leads with a value of 1.792 and is followed by ridge regression which has a value of 2.572. SVR has the worst performance for this dataset. The Space dataset had our method performing better than the others by 1.3%. Gradient boosting lags behind CoKER with a value of 0.0284 and is followed by ridge regression. SVR has the worst performance with a result of 0.0542.

Table 3 The average of the MAE comparison of ours, single model and ensemble models
Full size table

It could be seen from the results in Table 3 that the propose CoKER has better MAE values compared with the prior studies on the various datasets. From the experimental results, it could be realized that, the propose CoKER outperforms the prior approaches in all experiments.

Figure 2 also gives a different view of MAE comparisons among the propose CoKER, single models and ensemble methods. From Figure 2a we can see that, has a better MAE value for the Abalone dataset, with the upper bound value of 0.1245. In 2b, CoKER again outperforms the other methods. It is closely followed by gradient boosting with an upper bound value of 0.1345. In Figure 2c, for the RedWine dataset we find a wide margin between tree regression and SVR. Both had the worst lower bound performances. Again CoKER yields better results and is followed by gradient boosting. For the WhiteWine dataset, Figure 2d shows that CoKER retains the best result with an upper bound value of 0.102. Gradient boosting follows closely behind with a value of 0.1042. A difference of 0.003. From Figure 2, most of the plots have flat shape, which means the smaller the regression variance, the more stable the method. And the lower the median of the method in the figure, the better the regression result of the method. This because most of the variance is very small, i.e., \(10^{-4}\) and we did not show them in our tables.

Figure 2
figure 2

Box Plot of the respective datasets for MAE: a Abalone b Mpg c Redwine d WhiteWine

Full size image

From the above discussion, we can conclude that, the proposed CoKER demonstrates more effectiveness and superiority than the prior studies in regression accuracy.

4.4 Classification

Although all the models discussed in the previous section are intended for regression tasks, we will also use them for classification to further verify the stability of our model.

4.5 Data description

We selected five benchmark publicly available datasets for the evaluation of the performance of our algorithm, which are Diabetes, German, Liver-disorders (LD), Abalone, and Dexter. A summary is presented in Table 4.

Table 4 Descriptions of UCI classification dataset
Full size table

Table 5 did not present the variance of the experiment because they were very small, of about \(10^{-4}\). which means the smaller the variance, the more stable the method and the lower the median of the method in the table, the better the classification result of the method.

Table 5 The comparison of classification mean accuracies of CoKer comparative methods
Full size table

Figure 3 presents a comparison of the mean classification accuracies of all the methods across the five datasets. From the figure we can see that, the propose CoKER obtains the highest accuracy of 81.86% on the diabetes dataset, followed closely by Ridge Classification method with an accuracy of 81.66%. Random Forest, Tree Classification and Gradient boosting methods followed suit in that order with the LibSvm method being the worst in classification performance of about 67.58%.

Figure 3
figure 3

Comparison of the mean classification accuracies of the various datasets across the five comparative methods

Full size image

On the German dataset, all the methods show similar performance maintaining their positions as in the Diabetes dataset. But while all the methods saw a reduction in classification performance moving from Diabetes dataset to German dataset, LibSvm rather experience an increase. Also CoKER and Ridge classification method obtain a slight reduction in classification performance of less than 2%. Whilst Random Forest, Gradient boosting and Tree Classification methods all experience a great reduction of at least 5%.

Moving on to Abalone Dataset from Diabetes dataset, similar situations transpire amongst all the methods just as in German dataset. Only LibSvm method saw an increase in classification accuracy of more than 12%. On the other hand, CoKER, Random Forest, Ridge Classification and Tree Classification experience a slight decrease with Gradient boosting being the worst of more than 3% reduction.

Dexter dataset got all the methods performing below 70% accuracy, with CoKER leading with an accuracy of 68.83% which is a reduction of about 13% from the diabetes dataset. Random Forest, Ridge Classification and Tree Classification all experience a reduction of close to 13%. Gradient boosting obtains the greatest reduction of about 14% with LibSvm being the least reduced of about 2%.

Finally, on the LD dataset, CoKER obtains the highest accuracy together with two other methods: Ridge Classification and LibSvm. Interestingly, LibSvm which has been the worst performing in all the datasets became one of the best in LD dataset. Also Random Forest which has been performing well in classification in other datasets got the worst classification performance of 31.30%. Tree Classification on the other hand obtains 61.35% of classification accuracy being the second followed by Gradient Boosting with an accuracy of 60.78%.

Generally, CoKER obtains the highest classification accuracy across all the datasets, with the best coming from Diabetes, Abalone and German datasets in that order, followed by Dexter and lastly LD dataset which did not perform so well. It demonstrates a clear distinction between CoKER and the comparative methods on classification datasets as shown in Figure 3. Hence, we can conclude that our propose CoKER obtains a better classification performance according to all the experimental results of classification performance.

4.5.1 Digits recognition

In this section we discuss the classification performance of the propose CoKER in recognition of handwritten digits using MNIST dataset. It contains 10,000 handwritten digit images for classifier testing. We compared CokER with five different methods namely Weighted Classier Ensemble method based on Quadratic Forms (QFWEC) [28], Ridge regression (RR), Random Forest (RF), Simple Vote Rule (SVRule) [30] and Adaboost (AB) [9].

Figure 4 shows the classification accuracy of the propose CoKER and the comparative methods on the MNIST dataset. The proposed method outperforms the rest of the comparative methods. More significantly, AB achieves the lowest classification accuracy performance than the rest of the comparative methods which also perform a poorly as compared to the propose CoKER.

Figure 4
figure 4

Box plot of the mean classification accuracies of MNIST dataset across the five comparative methods

Full size image

5 Conclusion

In this paper, we investigated the problem of how to combine a set of kernel regressors into a unified ensemble regression framework. The framework can simultaneously co-regularize multiple kernel regressors by minimizing total loss of ensembles in Reproducing Kernel Hilbert Space. In this way, one kernel regressor with more accurate fitting precession on data, can obtain bigger weight, which leads to a better overall ensemble performance. Experimental results on several UCI datasets for regression and classification, compared with several single models and ensemble models such as Gradient Boosting (GB), Tree Regression (TR), Support Vector Regression (SVR), Ridge Regression (RR) and Random Forest (RF), illustrate that, the proposed method achieves best performances among the comparative methods.