1 Introduction

Non-orthogonal multiple access (NOMA) is urgently required to be used in order to remove the orthogonality requirement in frequency, time, and code resources by overlapping signals partially with an acceptable degree of interference [1]. This is due to the constantly growing demands for massive connectivity, low latency, and high spectral efficiency. From the perspective of enhancing the multiplexing advantage by leveraging various domains, NOMA has recently been subdivided into power-domain NOMA and code-domain NOMA. The fundamental idea behind power-domain NOMA is to allow signals from several users to share the same resource block (frequency, time, or code) while occupying it at various power levels. NOMA, in particular, employs superposition coding (SC) at the transmitting end to transmit the superimposed massage in the exact same resource, as well as successive interference cancellation (SIC) at the receiving end to separate the superimposed massage of the user with poor channel conditions before decoding its own massage with relatively better channel conditions [2]. NOMA can enable enormous connections, achieve improved spectral efficiency [3, 4], and enhance user fairness [5,6,7,8]. The ergodic secrecy rate in cooperative NOMA systems is a measure of the average secure communication rate attained by users in the network over an extended period of time. In such systems, several users share the same frequency and time resources. The transmission of cooperative NOMA focuses on collaboration between users to strengthen the security and dependability of the connection [9,10,11,12]. Cooperative NOMA may be categorized into two types, specifically based on the network components: relay-aided and user-aided cooperative NOMA. In user-aided cooperative NOMA, users who benefit from better channel conditions serve as a relay to improve the performance of weaker user. In [13, 14], the performance of cooperative NOMA in terms of outage probability and throughput is analyzed and showed the outage performance of user-aided cooperative NOMA is superior to the non-cooperative NOMA cell-centre users can act as relays in both full-duplex (FD) and half-duplex (HD) modes to produce diversity gain, which improves cell-edge user performance in a cellular NOMA network [15,16,17,18]. The NOMA approach has received a lot of attention in an effort to boost spectral efficiency [19,20,21]. The traditional orthogonal multiple access (OMA) approaches assign orthogonal resources only to one user. As a result, OMA does not provide the requisite spectral efficiency to meet 5G specifications. Because NOMA serves numerous customers with the same resource block, it effectively utilizes the spectrum and offers greater connection than traditional OMA systems. The NOMA shares a single frequency channel with several users rather than dividing the available bandwidth across users like the OMA does [3, 22]. As a consequence, the throughput of system increases since each user may transmit data using the whole spectrum [23]. There are two basic approaches used in NOMA: superposition coding and SIC. The key factor of NOMA is its ability to simultaneously send information to many users from the same signal by using superposition coding. At the transmitter, a power allocation coefficient is assigned to each user on the basis of channel quality, and after that, the transmitter superimposes the information signals [24,25,26]. At the receiver, each message is arranged in accordance with the channel strength, and the weaker message is first decoded and subtracted from the incoming superimposed message. In order to extract the desired message, the user must repeat this step repeatedly until it gets its own message by performing SIC [27].

1.1 Related Work

In [28], strictly positive secrecy capacity (SPSC) and secrecy outage probability (SOP) of cooperative NOMA system with two users and multiple DF relays in the presence of an eavesdropper are analyzed over Rayleigh fading channel and results show that SPSC can be maximized or SOP can be minimized by optimizing the power allocation of NOMA users. In [29], SOP of cooperative NOMA system with two NOMA users and multiple DF relays in presence of multiple eavesdroppers is analyzed over Nakagami-m fading. In [30], the SOP of a cooperative NOMA system with two users and one untrusted user is analyzed over Rician fading, in which the near user acts as a relay and performs the SIC. In [31], the SOP of a cooperative NOMA system with two users, multiple DF relays and multiple base stations is studied in the presence of an untrusted user using relay selection technique over Nakagami-m fading. In [32], the SPSC and SOP of a cooperative NOMA system with two users, one DF relay, one eavesdropper, and all the end users have direct link, are studied over Rayleigh fading. Ergodic secrecy analysis is impotent factor for designing and optimizing the wireless network. It assists in evaluating resource allocation schemes to maximize collective secrecy rate by taking the dynamic nature of wireless channels and possible eavesdroppers into consideration. In [33], ergodic secrecy sum rate (ESSR) of cooperative NOMA system with two users, one passive eavesdropper, and one DF is analyzed over Rayleigh fading for downlink communication. Simulation results show that ESSR degrades as the eavesdropper comes closer to either of the users. In [34], the ESSR of a cooperative NOMA system with two users and one untrusted amplify-and-forward (AF) relay is analyzed over Rayleigh fading channels for both uplink and downlink communication. In [35], the ergodic secrecy rate (ESR) of a cooperative NOMA system with one user, one DF relay and one eavesdropper is analyzed over Rayleigh fading channel for downlink communication. In [36], the ESR of cooperative NOMA system with three users and one of the three user acting as DF relay is analyzed over the Rayleigh fading channel for downlink communication.

1.2 Motivation

The following observations have been made on the basis of the above literature survey:

  • The cooperative NOMA increases spectral efficiency by allowing several users to utilize the same time and frequency resources concurrently. As a result, it addresses to the growing demand for data and multimedia services while using the limited spectrum resources more effectively.

  • Cooperative NOMA also increases system capacity, which is necessary to handle the expanding number of connected devices and applications in modern wireless networks. This is accomplished by allowing several users to access the network at once.

  • The main aim of ergodic secrecy analysis is to improve the security and privacy of wireless communications by creating methods that can shield confidential information from eavesdropping, which is crucial in today's digital age. Also, it measures the fastest rate at which information may be sent securely while being intercepted.

It can also be observed from the above literature survey that the secrecy performance analysis of a cooperative NOMA network in terms of ESC has not been addressed with two NOMA users and an AF relay in the presence of an eavesdropper. Motivated by the above observations, in this paper, we propose and analyze the secrecy performance of a downlink cooperative NOMA system with an untrusted user.

1.3 Contribution

To the best of our knowledge, no analysis of ESC for proposed NOMA-based systems with untrusted user has been performed yet. The main contributions of this paper are given below:

  • We propose a cooperative NOMA system for downlink communication that consists of an untrusted user, a DF relay, and two mobile users with different channel conditions.

  • We derive the closed-form expressions of lower bound ESC for the proposed cooperative system model and analyze the performance in terms of power allocation coefficient, variance between relay and eavesdropper, variance between relay and mobile user, and the average signal-to-noise ratio (SNR) of the eavesdropper link. The proposed method, in particular, defines a positive lower limit of ESC, showing that complete secrecy may be assured.

  • To validate the theoretical analysis, Monte Carlo simulations are used, and the advantage of the proposed cooperative NOMA technique with an untrusted user over the OMA scheme is also shown.

The remaining sections of the paper are structured as follows: Sect. 2 presents the system model and the secure transmission scheme assisted by AF. The ESC of proposed system model is analyzed in Sect. 3. Section 4 evaluates the numerical results. Lastly, Sect. 5 concludes the paper.

2 System Model

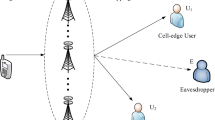
We consider a cooperative NOMA based wireless network that consists of a satellite (X) as the source, an amplify and forward relay (AFR) that works in half-duplex mode, two mobile users (MU2 as a strong mobile user and MU1 as a weak mobile user), and an eavesdropper (E), as shown in Fig. 1. It is assumed that there are no direct links between X and both users and also between X and E. The E, X, and both users consist of a single antenna, whereas the relay consists of both transmitting and receiving antennas. The only link between the AFR and the E is considered as an illegal link which is an unauthorized pathway that may be utilized for a variety of illegal activities and threaten legitimate communication systems. We also assume that all the channels suffer from independent Rayleigh fading distribution. The channel coefficients for X-to-AFR, AFR-to-MU1, AFR-to-MU2 and AFR-to-E link are denoted as \(h_{X,AFR}\), \(h_{{AFR,MU_{1} }}\), and \(h_{{AFR,MU_{2} }}\) and \(h_{AFR,E}\) respectively.

Fig. 1
figure 1

Satellite-based NOMA relaying network with two mobile users and one eavesdropper

Full size image

The X transmits the superposition of two different information, \(x_{{s_{1} }}\) and \(x_{{s_{2} }}\), to the AFR in the first time slot (FTSL) which is defined as follows:

$$y_{X} = a_{{s_{1} }} x_{{s_{1} }} \sqrt {W_{st} } + a_{{s_{2} }} x_{{s_{2} }} \sqrt {W_{st} }$$
(1)

where \(x_{{s_{i} }}\) denotes the data symbol of ith mobile user with normalized power \(E\left[ {\left| {x_{{s_{i} }} } \right|^{2} } \right] = 1\), \(W_{st}\) is the total transmit power of X, and \(a_{{s_{i} }}\) is the power allocation coefficient of ith mobile user. To fulfill the quality of service requirement of weak user, we consider the power allocation coefficient of weak user is greater than power allocation coefficient of strong user \((a_{{s_{1} }} > a_{{s_{2} }} )\) that satisfy the condition \(a_{{s_{1} }}^{2} + a_{{s_{2} }}^{2} = 1\).

The received signals at the AFR in the FTSL from X (\(y_{X}^{AFR} )\) can be expressed as

$$y_{X}^{AFR} = h_{X,AFR} \left( {a_{{s_{1} }} x_{{s_{1} }} \sqrt {W_{st} } + a_{{s_{2} }} x_{{s_{2} }} \sqrt {W_{st} } } \right) + n_{X}^{AFR}$$
(2)

where \(n_{X}^{AFR}\) represents the additive white Gaussian noise (AWGN) with \(N_{MU}\) variance and zero mean.

Using (2), the received SINR at AFR to get the information \(x_{{s_{1} }}\) (\(\gamma_{X,AFR}^{{s_{1} }} )\) can be defined as

$$\gamma_{X,AFR}^{{s_{1} }} = \frac{{\left| {h_{{{\text{X}},{\text{AFR}}}} } \right|^{2} a_{{s_{1} }}^{2} }}{{\begin{array}{*{20}c} {\left| {h_{{{\text{X}},{\text{AFR}}}} } \right|^{2} a_{{s_{2} }}^{2} + \frac{1}{{\rho_{s} }} } \\ \\ \end{array} }}$$
(3)

where \(\rho_{s} = \frac{{W_{st} }}{{N_{MU} }}\)

Similarly, the received SINR at AFR to get the information \(x_{{s_{2} }}\) (\(\gamma_{X,AFR}^{{s_{2} }} )\) can be defined as

$$\gamma_{X,AFR}^{{s_{2} }} = \frac{{\left| {h_{{{\text{X}},{\text{AFR}}}} } \right|^{2} a_{{s_{2} }}^{2} }}{{\begin{array}{*{20}c} {\left| {h_{{{\text{X}},{\text{AFR}}}} } \right|^{2} a_{{s_{1} }}^{2} + \frac{1}{{\rho_{s} }} } \\ \\ \end{array} }}$$
(4)

In the second time slot (STSL), AFR amplifies the received signal and forward it to the mobile users. Now, the received message signal at mobile users can be expressed as

$$y_{{MU_{i} }}^{AFR} = \beta y_{X}^{AFR} h_{{AFR,MU_{i} }} + n_{{MU_{i} }}^{AFR}$$
(5)

where \(MU_{i}\) represents the ith mobile user, \(h_{{AFR,MU_{i} }}\) is the channel gain between the AFR and ith mobile user,\(n_{{MU_{i} }}^{AFR}\) represents the AWGN with \(N_{MU}\) variance and zero mean between the AFR and ith mobile user and, \(\beta\) shows the gain of AFR and it can be defined as

$$\beta = \sqrt {\frac{1}{{\left| {h_{X,AFR} } \right|^{2} + \frac{1}{{\rho_{s} }}}}}$$
(6)

Substituting \(y_{X}^{AFR}\) from (2) in to (5), we obtain

$$y_{{MU_{i} }}^{AFR} = \beta \left[ {h_{X,AFR} \left( {a_{{s_{1} }} x_{{s_{1} }} \sqrt {W_{st} } + a_{{s_{2} }} x_{{s_{2} }} \sqrt {W_{st} } } \right) + n_{X}^{AFR} } \right]h_{{AFR,MU_{i} }} + n_{{MU_{i} }}^{AFR}$$
(7)

So, the signals received (\(y_{{MU_{1} }}^{AFR} and y_{{\begin{array}{*{20}c} {MU_{2} } \\ \\ \end{array} }}^{AFR} )\) at both mobile users can be represented as

$$y_{{MU_{1} }}^{AFR} = \left( {\beta h_{X,AFR} a_{{s_{1} }} x_{{s_{1} }} \sqrt {W_{st} } h_{{AFR,MU_{1} }} + \beta h_{X,AFR} a_{{s_{2} }} x_{{s_{2} }} \sqrt {W_{st} } h_{{AFR,MU_{1} }} } \right) + \beta n_{X}^{AFR} h_{{AFR,MU_{1} }} + n_{{MU_{1} }}^{AFR}$$
(8)
$$y_{{MU_{2} }}^{AFR} = \left( {\beta h_{X,AFR} a_{{s_{1} }} x_{{s_{1} }} \sqrt {W_{st} } h_{{AFR,MU_{2} }} + \beta h_{X,AFR} a_{{s_{2} }} x_{{s_{2} }} \sqrt {W_{st} } h_{{AFR,MU_{2} }} } \right) + \beta n_{X}^{AFR} h_{{AFR,MU_{2} }} + n_{{MU_{2} }}^{AFR}$$
(9)

In the STSL, E also gets the same message signal as both mobile user (MU) gets. The signal received at the E can be defined as

$$y_{E}^{AFR} = \beta y_{X}^{AFR} h_{AFR,E} + n_{E}^{AFR}$$
(10)

where \(n_{E}^{AFR}\) show the AWGN with \(N_{E}\) variance and zero mean. Now (10) can be modified using (2) as

$$y_{E}^{AFR} = \left( {\beta h_{X,AFR} a_{{s_{1} }} x_{{s_{1} }} \sqrt {W_{st} } h_{AFR,E} + \beta h_{XAFR} a_{{s_{2} }} x_{{s_{2} }} \sqrt {W_{st} } h_{AFR,E} } \right) + \beta n_{X}^{AFR} h_{AFR,E} + n_{E}^{AFR}$$
(11)

Furthermore, SINR of weak mobile user (\(\gamma_{{AFR,MU_{1} }}^{ } )\) using (8) can be defined as

$$\gamma_{{AFR,MU_{1} }}^{ } = \frac{{\beta^{2} \left| {h_{X,AFR} } \right|^{2} a_{{s_{1} }}^{2} W_{st} \left| {h_{{AFR,MU_{1} }} } \right|^{2} }}{{\beta^{2} \left| {h_{X,AFR} } \right|^{2} a_{{s_{2} }}^{2} W_{st} \left| {h_{{AFR,MU_{1} }} } \right|^{2} + \beta^{2} N_{MU} \left| {h_{{AFR,MU_{1} }} } \right|^{2} + N_{MU} }}$$
(12)

Further (12) can be modified as

$$\gamma_{{AFR,MU_{1} }}^{ } = \frac{{\left| {h_{X,AFR} } \right|^{2} a_{{s_{1} }}^{2} \left| {h_{{AFR,MU_{1} }} } \right|^{2} }}{{\left| {h_{X,AFR} } \right|^{2} a_{{s_{2} }}^{2} \left| {h_{{AFR,MU_{1} }} } \right|^{2} + \left( {\frac{1}{{\rho_{s} }}} \right)\left| {h_{{AFR,MU_{1} }} } \right|^{2} + \frac{{\left| {h_{X,AFR} } \right|^{2} }}{{\rho_{s} }} + \frac{1}{{\rho_{s}^{2} }}}}$$
(13)

The strong mobile first decodes the information of the weak user and then subtracts this information to get its own information by performing perfect SIC. So, the SINR of a strong mobile user (\(\gamma_{{AFR,MU_{2} }}^{ }\)) using (9) and similar to [37] can be defined as

$$\gamma_{{AFR,MU_{2} }}^{ } = \frac{{\rho_{s} \left| {h_{X,AFR} } \right|^{2} a_{{s_{2} }}^{2} \left| {h_{{AFR,MU_{2} }} } \right|^{2} }}{{\begin{array}{*{20}c} {\left| {h_{{AFR,MU_{2} }} } \right|^{2} + \left| {h_{X,AFR} } \right|^{2} + \frac{1}{{\rho_{S} }}} \\ \\ \end{array} }}$$
(14)

Similarly, the SINR at eavesdropper using (11) can be defined as

$$\gamma_{{AFR,E_{i} }}^{ } = \frac{{\rho_{s} \rho_{E} \left| {h_{X,AFR} } \right|^{2} a_{{s_{i} }}^{2} \left| {h_{AFR,E} } \right|^{2} }}{{\begin{array}{*{20}c} {\rho_{E} \left| {h_{AFR,E} } \right|^{2} + \rho_{s} \left| {h_{X,AFR} } \right|^{2} + 1} \\ { } \\ \end{array} }}$$
(15)

where \(\rho_{E}\) shows average SINR of eavesdropper link and it is defined as \(\rho_{E} = \frac{{W_{st} }}{{N_{E} }}\). \(\gamma_{{AFR,E_{i} }}^{ }\) shows the SINR of ith mobile user at the eavesdropper.

Now considering the case of high SINR similar to [37], (13), (14) and (15) can be modified as

$$\gamma_{{AFR,MU_{1} }}^{ } = \frac{{a_{{s_{1} }}^{2} }}{{a_{{s_{2} }}^{2} }}$$
(16)
$$\gamma_{{AFR,MU_{2} }}^{ } = \frac{{\rho_{s}^{2} \left| {h_{X,AFR} } \right|^{2} a_{{s_{2} }}^{2} \left| {h_{{AFR,MU_{2} }} } \right|^{2} }}{{\begin{array}{*{20}c} {\rho_{s} \left| {h_{{AFR,MU_{2} }} } \right|^{2} + \rho_{s} \left| {h_{X,AFR} } \right|^{2} } \\ \\ \end{array} }}$$
(17)
$$\gamma_{{AFR,E_{i} }}^{ } = \frac{{\rho_{s} \rho_{E} \left| {h_{X,AFR} } \right|^{2} a_{{s_{i} }}^{2} \left| {h_{AFR,E} } \right|^{2} }}{{\begin{array}{*{20}c} {\rho_{E} \left| {h_{AFR,E} } \right|^{2} + \rho_{S} \left| {h_{X,AFR} } \right|^{2} } \\ { } \\ \end{array} }}$$
(18)

3 Secrecy Analysis

In this section, we derive the analytical expression of ergodic secrecy capacity (ESC) for proposed cooperative NOMA system with an untrusted user. The maximum achievable data rate for sending secret data over a wireless communication channel while ensuring its secrecy from eavesdroppers is known as ESC. ESC is calculated as the average rate of secure communication accomplished over time, taking into consideration the worst-case scenario with regard to the eavesdropper's channel circumstances. It's simply the average rate at which confidential data may be transferred securely.

The achievable rate of strong mobile user using AFR [38] can be defined by

$$C_{{x_{{s_{2} }} }} = min \left\{ {\frac{1}{2}\log_{2} \left( {1 + \gamma_{X,AFR}^{{s_{2} }} } \right),\frac{1}{2}\log_{2} \left( {1 + \gamma_{{AFR,MU_{2} }}^{ } } \right)} \right\}$$
(19)

Now considering the case of high SINR and using (4) and (17), (19) can be modified as

$$C_{{x_{{s_{2} }} }} = \frac{1}{2}\log_{2} \left( {1 + \gamma_{{AFR,MU_{2} }}^{ } } \right)$$
(20)

Similarly, the achievable rate of weak mobile user can be defined by

$$C_{{x_{{s_{1} }} }} = min \left\{ {\frac{1}{2}\log_{2} \left( {1 + \gamma_{X,AFR}^{{s_{1} }} } \right),\frac{1}{2}\log_{2} \left( {1 + \gamma_{{AFR,MU_{1} }}^{ } } \right)} \right\}$$
(21)

Further, considering the case of high SINR and using (3) and (16), (21) can be modified as

$$C_{{x_{{s_{1} }} }} = \frac{1}{2}log_{2} \left( {1 + \gamma_{X,AFR}^{{s_{1} }} { }} \right)$$
(22)

Similarly, the achievable rate of \(x_{{s_{1} }}\) and \(x_{{s_{2} }}\) at eavesdropper can be defined as

$$C_{{Ex_{{s_{1} }} }} = \frac{1}{2}\left[ {log_{2} \left\{ {1 + \gamma_{{AFR,E_{1} }}^{ } { }} \right\}} \right]$$
(23)
$$C_{{Ex_{{s_{2} }} }} = \frac{1}{2}\left[ {log_{2} \left\{ {1 + \gamma_{{AFR,E_{2} }}^{ } { }} \right\}} \right]$$
(24)

Since eavesdropper only wiretaps the massage from the AFR, the ESC of the cooperative NOMA system can be represented as

$$C_{SC} = \left\{ {C_{{x_{{s_{1} }} }} - C_{{Ex_{{s_{1} }} }} } \right\}^{ + } + \left\{ {C_{{x_{{s_{2} }} }} - C_{{Ex_{{s_{2} }} }} } \right\}^{ + }$$
(25)

where \(\left\{ {\text{X}} \right\}^{ + } = \max { }\left\{ {0,{\text{X}}} \right\}^{ + }\)

Now, the lower bound of ESC of proposed system can be defined by using Jensen’s inequality [39], which is written as

$${\mathbb{E}}[C_{SC} ] \ge { }C_{SC,lb}$$
(26)

Now, using (25) and (26) the lower bound of ESC can be defined as

$$C_{SC,lb} \triangleq \left\{ {{\mathbb{E}}\left[ {C_{{x_{{s_{1} }} }} } \right] - {\mathbb{E}}\left[ {C_{{Ex_{{s_{1} }} }} } \right]} \right\}^{ + } + { }\left\{ {{\mathbb{E}}\left[ {C_{{x_{{s_{2} }} }} } \right] - {\mathbb{E}}\left[ {C_{{Ex_{{s_{2} }} }} } \right]} \right\}^{ + }$$
(27)

Now, \({\mathbb{E}}[C_{{x_{{s_{1} }} }} ]{ }\) can be obtained using (23) as

$${\mathbb{E}}\left[ {C_{{x_{{s_{1} }} }} } \right] = {\text{\rm E}}_{{\gamma_{X,AFR}^{{s_{1} }} }} \left[ {log_{2} \left\{ {1 + z_{1} } \right\}} \right]$$
(28)
$${\mathbb{E}}[C_{{x_{{s_{1} }} }} ] = \mathop \int \limits_{0}^{\infty } {\text{f}}_{{\gamma_{X,AFR}^{{s_{1} }} }} \left( {z_{1} } \right)\log \left( {1 + z_{1} { }} \right){\text{d}}z_{1}$$
(29)
$${\mathbb{E}}[C_{{x_{{s_{1} }} }} ] = \frac{1}{2\ln 2}\mathop \int \limits_{0}^{\infty } \frac{{1 - {\text{F}}_{{\gamma_{X,AFR}^{{s_{1} }} }} \left( {z_{1} } \right)}}{{1 + z_{1} }}{\text{d}}z_{1}$$
(30)

Now \({\text{F}}_{{\gamma_{X,AFR}^{{s_{1} }} }} \left( {z_{1} } \right)\) can be simplified as

$$F_{{\gamma_{X,AFR}^{{s_{1} }} }} \left( {z_{1} } \right) = {\text{Pr}}\left( {\gamma_{X,AFR}^{{s_{1} }} < z_{1} } \right)$$
(31)

After substituting the value of \(\gamma_{X,AFR}^{{s_{1} }}\) from (3) and using the CDF of the Rayleigh fading distribution, Eq. (31) can be modified as

$$F_{{\gamma_{X,AFR}^{{s_{1} }} }} \left( {z_{1} } \right) = 1 - e^{{ - \left( {\mathbf{\mathcal{P}}} \right)\frac{{z_{1} }}{{N_{MU} }}}}$$
(32)

where \({\mathcal{P}} = \frac{1}{{\rho_{s} \left( {a_{{s_{1} }}^{2} - z_{1} a_{{s_{2} }}^{2} } \right)}}\)

Now substituting (32) in to (30), we obtain

$${\mathbb{E}}\left[ {C_{{x_{{s_{1} }} }} } \right] = \frac{1}{2\ln 2}\mathop \int \limits_{0}^{{\frac{{a_{{s_{1} }}^{2} }}{{a_{{s_{2} }}^{2} }}}} \frac{{e^{{ - \left( {\mathbf{\mathcal{P}}} \right)\frac{{z_{1} }}{{N_{MU} }}}} }}{{1 + z_{1} }}{\text{d}}z_{1}$$
(33)

Using Gauss–Chebyshev integral [40], (33) can be modified as

$${\mathbb{E}}\left[ {C_{{x_{{s_{1} }} }} } \right] = \frac{\pi }{2N}\mathop \sum \limits_{n = 1}^{N} \frac{{a_{{s_{1} }}^{2} \sqrt {1 - z_{n}^{2} } }}{{2\ln 2\left( {1 + z_{n} } \right)a_{{s_{2} }}^{2} }}e^{{ - \left( {\mathbf{\mathcal{P}}} \right)\frac{{z_{n} }}{{N_{MU} }}}}$$
(34)

where \(N\) represents the Gauss–Chebyshev quadrature approximation and \(z_{n} = \cos \left[ {\frac{2n\pi - \pi }{{2N}}} \right]\)

Using (18), \({\mathbb{E}}[C_{{x_{{s_{2} }} }} ]\) of strong mobile user (MU2) can be defined as

$${\mathbb{E}}\left[ {C_{{x_{{s_{2} }} }} } \right] = \frac{1}{2}\mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \log \left( {\frac{{1 + a_{{s_{2} }}^{2} u_{2} }}{{1 + \frac{{u_{2} }}{{u_{1} }}}}} \right){\text{f}}_{{U_{2} }} \left( {u_{2} } \right) \times {\text{f}}_{{U_{1} }} \left( {u_{1} } \right){\text{d}}u_{2} {\text{d}}u_{1}$$
(35)

where \(u_{2} = \rho_{s} \left| {h_{{AFR,MU_{2} }} } \right|^{2}\) and \(u_{1} = \rho_{s} \left| {h_{X,AFR} } \right|^{2}\)

$${\mathbb{E}}\left[ {C_{{x_{{s_{2} }} }} } \right] = \frac{1}{2}\mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \log \left( {\frac{{1 + a_{{s_{2} }}^{2} u_{2} }}{{1 + \frac{{u_{2} }}{{u_{1} }}}}} \right){\text{f}}_{{U_{2} }} \left( {u_{2} } \right) \times {\text{f}}_{{U_{1} }} \left( {u_{1} } \right){\text{d}}u_{2} {\text{d}}u_{1}$$
(36)
$${\mathbb{E}}\left[ {C_{{x_{{s_{2} }} }} } \right] = \frac{1}{{2\rho_{s} N_{MU} \rho_{s} N_{MU} }}\mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \left( {\log \left( {1 + a_{{s_{2} }}^{2} u_{2} } \right) - \log (1 + \frac{{u_{2} }}{{u_{1} }})} \right) \times {\text{e}}^{{ - \frac{{u_{2} }}{{\rho_{s} N_{MU} }}}} {\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{2} {\text{d}}u_{1}$$
(37)
$${\mathbb{E}}\left[ {C_{{x_{{s_{2} }} }} } \right] = \frac{1}{{2\rho_{s} N_{MU} \rho_{s} N_{MU} }}\left[ {\mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \log \left( {1 + a_{{s_{2} }}^{2} u_{2} } \right){\text{e}}^{{ - \frac{{u_{2} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{2} {\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{1} - \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \log \left( {1 + \frac{{u_{2} }}{{u_{1} }}} \right) \times {\text{e}}^{{ - \frac{{u_{2} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{2} {\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{1} } \right]$$
(38)

As \(\mathop \int \limits_{0}^{\infty } e^{ - \delta x} \ln \left( {1 + \varphi x} \right)dx = - \frac{1}{\delta }e^{{\frac{\delta }{\varphi }}} E_{i} \left( { - \frac{\delta }{\varphi }} \right)\) [37], (38) can be modified as

$$\begin{aligned} {\mathbb{E}}\left[ {C_{{x_{{s_{2} }} }} } \right] & = \frac{1}{{2\rho_{s} N_{MU} \rho_{s} N_{MU} }} \times \left[ {\mathop \int \limits_{0}^{\infty } - \rho_{s} N_{MU} e^{{\frac{1}{{a_{{s_{2} }}^{2} \rho_{s} N_{MU} }}}} E_{i} \left( { - \frac{1}{{a_{{s_{2} }}^{2} \rho_{s} N_{MU} }}} \right){\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{1} } \right. \\ & \quad \left. { - \mathop \int \limits_{0}^{\infty } - \rho_{s} N_{MU} e^{{\frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} E_{i} \left( { - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}} \right){\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{1} } \right] \\ \end{aligned}$$
(39)
$$\begin{aligned} {\mathbb{E}}\left[ {C_{{x_{{s_{2} }} }} } \right] & = \frac{1}{{2\rho_{s} N_{MU} \rho_{s} N_{MU} }} \times \left[ {\mathop \int \limits_{0}^{\infty } - \rho_{s} N_{MU} e^{{\frac{1}{{a_{{s_{2} }}^{2} \rho_{s} N_{MU} }}}} E_{i} \left( { - \frac{1}{{a_{{s_{2} }}^{2} \rho_{s} N_{MU} }}} \right){\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{1} } \right. \\ & \quad \left. { - \mathop \int \limits_{0}^{\infty } - \rho_{s} N_{MU} E_{i} \left( { - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}} \right){\text{d}}u_{1} } \right] \\ \end{aligned}$$
(40)

After applying Gauss–chebyshev integral [40], (40) can be modified as

$${\mathbb{E}}\left[ {C_{{x_{{s_{2} }} }} } \right]{ } \approx \frac{{{\uppi }^{2} }}{{2N\rho_{s} N_{MU} }}\left[ { - \rho_{s} N_{MU} e^{{\frac{1}{{a_{{s_{2} }}^{2} \rho_{s} N_{MU} }}}} E_{i} \left( { - \frac{1}{{a_{{s_{2} }}^{2} \rho_{s} N_{MU} }}} \right) + \mathop \sum \limits_{n = 1}^{N} \sqrt {1 - z_{n}^{2} } E_{i} \left( { - \frac{{\tan \theta_{n} }}{{\rho_{s} N_{MU} }}} \right)\sec^{2} \theta_{n} } \right]$$
(41)

where \(\theta_{n} = \frac{\pi }{4}\left( {z_{n} + 1} \right)\).

Similarly the ESC of \(x_{{s_{1} }}\) at eavesdropper can be defined as,

$${\mathbb{E}}\left[ {C_{{Ex_{{s_{1} }} }} } \right] = \frac{1}{2}\mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \log \left( {\frac{{1 + a_{{s_{1} }}^{2} u_{3} }}{{1 + \frac{{u_{3} }}{{u_{1} }}}}} \right) \times {\text{f}}_{{U_{3} }} \left( {u_{3} } \right){\text{f}}_{{U_{1} }} \left( {u_{1} } \right){\text{d}}u_{3} {\text{d}}u_{1}$$
(42)

where \(u_{3} = \rho_{E} \left| {h_{{AFR,E_{1} }} } \right|^{2}\) and \(u_{1} =\) \(\rho_{s} \left| {h_{X,AFR} } \right|^{2}\)

$${\mathbb{E}}\left[ {C_{{Ex_{{s_{1} }} }} } \right] = \frac{1}{{2\rho_{s} N_{MU} \rho_{E} N_{E} }} \times \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \log \left( {\frac{{1 + a_{{s_{1} }}^{2} u_{3} }}{{1 + \frac{{u_{3} }}{{u_{1} }}}}} \right) \times {\text{e}}^{{ - \frac{{u_{3} }}{{\rho_{s} N_{MU} }}}} {\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{3} {\text{d}}u_{1}$$
(43)
$${\mathbb{E}}\left[ {C_{{Ex_{{s_{1} }} }} } \right]{ = } \frac{1}{{2\rho_{s} N_{MU} \rho_{E} N_{E} }}\mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \left( {\log \left( {1 + a_{{s_{1} }}^{2} u_{3} } \right) - \log \left( {1 + \frac{{u_{3} }}{{u_{1} }}} \right)} \right) \times {\text{e}}^{{ - \frac{{u_{3} }}{{\rho_{E} N_{E} }}}} {\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{3} {\text{d}}u_{1}$$
(44)
$${\mathbb{E}}\left[ {C_{{Ex_{{s_{1} }} }} } \right]{ } = \frac{1}{{2\rho_{s} N_{MU} \rho_{E} N_{E} }}\left[ {\mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \log \left( {1 + a_{{s_{1} }}^{2} u_{3} } \right){\text{e}}^{{ - \frac{{u_{3} }}{{\rho_{E} N_{E} }}}} {\text{d}}u_{3} {\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{1} - \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \log \left( {1 + \frac{{u_{3} }}{{u_{1} }}} \right) \times {\text{e}}^{{ - \frac{{u_{3} }}{{\rho_{E} N_{E} }}}} {\text{d}}u_{3} {\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{1} } \right]$$
(45)

Now (45) can be modified using approximation provided in [41] as,

$${\mathbb{E}}\left[ {C_{{Ex_{{s_{1} }} }} } \right]{ } = \frac{1}{{2\rho_{s} N_{MU} \rho_{E} N_{E} }}\left[ {\mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \log \left( {1 + a_{{s_{1} }}^{2} u_{3} } \right){\text{e}}^{{ - \frac{{u_{3} }}{{\rho_{E} N_{E} }}}} {\text{d}}u_{3} {\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{1} - \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \log \left( {1 + \frac{{u_{3} }}{{u_{1} }}} \right) \times {\text{e}}^{{ - \frac{{u_{3} }}{{\rho_{E} N_{E} }}}} {\text{d}}u_{3} {\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{1} } \right]$$
(46)
$${\mathbb{E}}\left[ {C_{{Ex_{{s_{1} }} }} } \right] = \frac{1}{{2\rho_{s} N_{MU} \rho_{E} N_{E} }} \times { }\left[ {\mathop \int \limits_{0}^{\infty } - \rho_{s} N_{MU} e^{{\frac{1}{{a_{{s_{1} }}^{2} \rho_{E} N_{E} }}}} E_{i} \left( { - \frac{1}{{a_{{s_{1} }}^{2} \rho_{E} N_{E} }}} \right){\text{e}}^{{ - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} {\text{d}}u_{1} - \mathop \int \limits_{0}^{\infty } - \rho_{E} N_{E} e^{{\frac{{u_{1} }}{{\rho_{E} N_{E} }} - \frac{{u_{1} }}{{\rho_{s} N_{MU} }}}} E_{i} \left( { - \frac{{u_{1} }}{{\rho_{E} N_{E} }}} \right){\text{d}}u_{1} } \right]$$
(47)

After further calculation, (47) can be modified as

$${\mathbb{E}}\left[ {C_{{Ex_{{s_{1} }} }} } \right]{ } \approx \frac{{{\uppi }^{2} }}{{2N\rho_{s} N_{MU} }}\left[ { - \rho_{s} N_{MU} e^{{\frac{1}{{a_{{s_{1} }}^{2} \rho_{E} N_{E} }}}} E_{i} \left( { - \frac{1}{{a_{{s_{1} }}^{2} \rho_{E} N_{E} }}} \right) + \mathop \sum \limits_{n = 1}^{N} \sqrt {1 - z_{n}^{2} } e^{{\frac{{\tan \theta_{n} }}{{\rho_{E} N_{E} }} - \frac{{\tan \theta_{n} }}{{\rho_{s} N_{MU} }}}} E_{i} \left( { - \frac{{\tan \theta_{n} }}{{\rho_{E} N_{E} }}} \right)\sec^{2} \theta_{n} } \right]$$
(48)

Similarly, the ESC of \(x_{{s_{2} }}\) at eavesdropper can be defined as

$${\mathbb{E}}\left[ {C_{{Ex_{{s_{2} }} }} } \right]{ } \approx \frac{{{\uppi }^{2} }}{{2N\rho_{s} N_{MU} }}\left[ { - \rho_{s} N_{MU} e^{{\frac{1}{{a_{{s_{2} }}^{2} \rho_{E} N_{E} }}}} E_{i} \left( { - \frac{1}{{a_{{s_{2} }}^{2} \rho_{E} N_{E} }}} \right) + \mathop \sum \limits_{n = 1}^{N} \sqrt {1 - z_{n}^{2} } e^{{\frac{{\tan \theta_{n} }}{{\rho_{E} N_{E} }} - \frac{{\tan \theta_{n} }}{{\rho_{s} N_{MU} }}}} E_{i} \left( { - \frac{{\tan \theta_{n} }}{{\rho_{E} N_{E} }}} \right)\sec^{2} \theta_{n} } \right]$$
(49)

Now after substituting the value of \({\mathbb{E}}\left[ {C_{{x_{{s_{1} }} }} } \right],{\mathbb{E}}\left[ {C_{{x_{{s_{2} }} }} } \right],{\mathbb{E}}\left[ {C_{{Ex_{{s_{1} }} }} } \right]{ }\) and \({\mathbb{E}}\left[ {C_{{Ex_{{s_{2} }} }} } \right]\) from (34), (41), (48) and (49) respectively in to (27), we obtain

$$\begin{aligned} C_{ESC} & \triangleq \left\{ {\frac{\pi }{2N}\mathop \sum \limits_{n = 1}^{N} \frac{{a_{{s_{1} }}^{2} \sqrt {1 - z_{n}^{2} } }}{{2\ln 2\left( {1 + z_{n} } \right)a_{{s_{2} }}^{2} }}e^{{ - \left( {\frac{1}{{\rho_{s} \left( {a_{{s_{1} }}^{2} - z_{{\text{n}}} a_{{s_{2} }}^{2} } \right)}}} \right)\frac{{z_{n} }}{{N_{MU} }}}} } \right. \\ & \quad - \frac{{{\uppi }^{2} }}{{2N\rho_{s} N_{MU} }}\left[ { - \rho_{s} N_{MU} e^{{\frac{1}{{a_{{s_{1} }}^{2} \rho_{E} N_{E} }}}} E_{i} \left( { - \frac{1}{{a_{{s_{1} }}^{2} \rho_{E} N_{E} }}} \right)} \right. \\ & \quad \left. {\left. { + \mathop \sum \limits_{n = 1}^{N} \sqrt {1 - z_{n}^{2} } e^{{\frac{{\tan \theta_{n} }}{{\rho_{E} N_{E} }} - \frac{{\tan \theta_{n} }}{{\rho_{s} N_{MU} }}}} E_{i} \left( { - \frac{{\tan \theta_{n} }}{{\rho_{E} N_{E} }}} \right)\sec^{2} \theta_{n} } \right]} \right\}^{ + } \\ & \quad + \left\{ {\frac{{{\uppi }^{2} }}{{2N\rho_{s} N_{MU} }}\left[ { - \rho_{s} N_{MU} e^{{\frac{1}{{a_{{s_{2} }}^{2} \rho_{s} N_{MU} }}}} E_{i} \left( { - \frac{1}{{a_{{s_{2} }}^{2} \rho_{s} N_{MU} }}} \right)} \right.} \right. \\ & \quad \left. { + \mathop \sum \limits_{n = 1}^{N} \sqrt {1 - z_{n}^{2} } E_{i} \left( { - \frac{{\tan \theta_{n} }}{{\rho_{s} N_{MU} }}} \right)\sec^{2} \theta_{n} } \right] \\ & \quad - \frac{{{\uppi }^{2} }}{{2N\rho_{s} N_{MU} }}\left[ { - \rho_{s} N_{MU} e^{{\frac{1}{{a_{{s_{2} }}^{2} \rho_{E} N_{E} }}}} E_{i} \left( { - \frac{1}{{a_{{s_{2} }}^{2} \rho_{E} N_{E} }}} \right)} \right. \\ & \quad \left. {\left. { + \mathop \sum \limits_{n = 1}^{N} \sqrt {1 - z_{n}^{2} } e^{{\frac{{\tan \theta_{n} }}{{\rho_{E} N_{E} }} - \frac{{\tan \theta_{n} }}{{\rho_{s} N_{MU} }}}} E_{i} \left( { - \frac{{\tan \theta_{n} }}{{\rho_{E} N_{E} }}} \right)\sec^{2} \theta_{n} } \right]} \right\} \\ \end{aligned}$$
(50)

4 Results and Discussion

In this section, we analyze the performance of proposed system from the derived expression of ESC. We use the Monte carlo simulation (MC) to verify the results obtained from the Analytical simulation (AS). The values of parameters taken in simulation are shown in Table 1.

Table 1 Simulation parameters for ESC
Full size table

Figure 2 shows the plots of ESC vs. average SNR of legal link with parameters \({\text{N}}_{{{\text{MU}}}} = 1\), \({\text{N}}_{{\text{E}}} = 1\), \({\uprho }_{{\text{E}}}\) = 1, \({\text{a}}_{{{\text{s}}_{1} }}\) = 0.4, 0.5 and 0.6. The plots show that ESC increases significantly with the average SNR of legal link at lower values of average SNR, i.e., up to 10 dB, and after that, it becomes almost constant with respect to the average SNR of legal link. Further, ESC increases with increasing the value of \({\text{a}}_{{{\text{s}}_{1} }} { }\) at fixed values of \({\text{N}}_{{{\text{MU}}}}\), \({\text{N}}_{{\text{E}}}\), and \({\uprho }_{{\text{E}}}\). This result shows that there is a boost to ESC when more power allocation factor is given to weak mobile user.

Fig. 2
figure 2

ESC versus average SNR of legal link at different values of \(a_{{s_{1} }}\)

Full size image

Figure 3 shows the plots of ESC versus average SNR of the legal link with parameters \({\text{N}}_{{\text{E}}} = 1\), \({\uprho }_{{\text{E}}}\) = 1, \({\text{a}}_{{{\text{s}}_{1} }}\) = 0.4, and \({\text{N}}_{{{\text{MU}}}} = 1\), 2 and 4. The plots show that as the value of \({\text{N}}_{{{\text{MU}}}}\) increases at fixed values of \({\text{a}}_{{{\text{s}}_{1} }}\), \({\text{N}}_{{\text{E}}}\) and \({\uprho }_{{\text{E}}}\), ESC increases. So, a higher value of variance between the relay and user increases the system performance in terms of ESC.

Fig. 3
figure 3

ESC versus average SNR of legal link with different values of the variance (\(N_{MU}\)) of legal link

Full size image

Figure 4 shows the plots of ESC vs. average SNR of legal link with parameters \({\text{N}}_{{{\text{MU}}}} = 1\), \({\uprho }_{{\text{E}}} = 1\), \({\text{a}}_{{{\text{s}}_{1} }} = 0.4\), and \({\text{N}}_{{\text{E}}} = 1\), 2 and 4. The plots show that as the value of \({\text{N}}_{{\text{E}}}\) increases at fixed values of \({\text{a}}_{{{\text{s}}_{1} }}\), \({\text{N}}_{{\text{E}}}\) and \({\uprho }_{{\text{E}}}\), ESC decreases. So, higher value of variance of eavesdropper link decreases the system performance in term of ESC.

Fig. 4
figure 4

ESC versus average SNR of legal link with different values of the variance (\(N_{E}\)) of illegal link

Full size image

Figure 5 shows the plots of ESC vs. average SNR of legal link with parameters \({\text{N}}_{{{\text{MU}}}} = 1\), \({\text{a}}_{{{\text{s}}_{1} }}\) = 0.4, and \({\uprho }_{{\text{E}}}\) = 1, 4 and 8. The plots show that as the value of \({\uprho }_{{\text{E}}}\) increases at fixed values of \({\text{a}}_{{{\text{s}}_{1} }}\), \({\text{N}}_{{\text{E}}}\) and \({\text{N}}_{{{\text{MU}}}}\) ESC decreases. So, as the value of average SNR of the eavesdropper link increase the performance of system decreases in term of ESC.

Fig. 5
figure 5

ESC versus average SNR of legal link with different values of average SNR of the eavesdropper

Full size image

To provide a comparative analysis of the proposed cooperative NOMA system, a cooperative OMA system is considered in the simulation. Figure 6 shows the plots of ESC versus average SNR of legal link and results that cooperative NOMA system outperforms the cooperative OMA system in terms of ESC.

Fig. 6
figure 6

ESC versus average SNR of legal link of both NOMA and OMA system

Full size image

5 Conclusion

In this paper, we propose a cooperative NOMA model with an untrusted user. We derive the lower bound of ergodic secrecy capacity of the proposed cooperative NOMA system. Simulation results demonstrate that proposed NOMA system outperforms the conventional cooperative OMA system in terms of secrecy performance. The analysis of proposed system model may be help in current wireless networks to avoid the leakage of confidential data by untrusted users with strong eavesdropping capabilities, which receives a lot of interest from both academics and industry. In the future, multi-relay scenarios may be used for proposed system model in which the best relay need to be chosen to transfer the message signal and the other relays may be used to provide interference to the untrusted user.