Keywords

1 Introduction

Since the available frequency band of mobile communication is mainly below 3 GHz, 5G networks need to meet the requirements of low latency and massive connections under limited spectrum resources. Non-orthogonal multiple access (NOAM) is a important technology to solve the shortage of spectrum resources. Its basic principle is that the transmitter adopts power domain superposition coding, actively introducing interference information, and the receiver adopts successive interference cancellation (SIC) to realize correct demodulation [1].

Due to shadow fading and path loss, the communication reliability of users far from the transmitter is poor. Relay cooperative NOMA network can improve the communication quality of far users. According to the NOMA superposition coding principle, strong user know the signal information of weak users and act as a Decode-and-Forward (DF) relay to assist in forwarding the signal information of weak users [2]. Under the statistical channel state information (CSI), the authors analyzed a communication system in which a single relay forwards the signals of multiple edge users over Nakagami-m fading channels, and the differences between DF relay and amplify-and-forward (AF) relay in improving communication performance was compared in [3]. In addition, device-to-device (D2D) technology allows two adjacent user equipment to communicate directly by reusing the spectrum resources of the cellular network, thereby reducing communication delay and improve spectrum utilization. So D2D relay cooperative communication based on NOMA has attracted extensive research scholars’ attention. For D2D cooperative NOMA network, a power allocation strategy based on signal-to-noise ratio (SNR) was proposed in [4] to achieve the maximum capacity. Moreover, two different SIC decoding schemes were proposed in [5], namely the single signal decoding scheme and the maximum ratio combining (MRC) decoding scheme, respectively, and the authors compared and analyzed the influence of different decoding schemes on communication performance. In order to avoid the loss of communication performance caused by SIC error decoding, according to the decoding of D2D relay, three different relay forwarding strategies were studied in [6].

Due to the openness of RF signals, sensitive information with high security requirements is easily attacked by eavesdroppers during transmission. Therefore, the security of NOMA network must be considered. Relay cooperation can not only improve the communication reliability of cell-edge users, but also help legitimate nodes improve the physical layer security of the system. Physical layer security technology is based on Shannon theory. Its main idea is to protect the physical layer by using the inherent random characteristics of wireless channel [7]. At present, many researches on physical layer security are relay selection, cooperative beamforming, cooperative interference and so on. According to the different understanding of the eavesdropping channel, the corresponding relay selection strategy was proposed to combat the malicious eavesdropping of adaptive eavesdroppers in [8]. Considering the problem of energy limitation in communication, a AF relay collected energy from part of artificial interference signals, and forwarded the remaining artificial interference signals to eavesdroppers, so as to protect the legitimate signals [9]. In [10], the multi-antenna relay beamforming technology was used to design artificial interference signals to interfere with eavesdroppers without affecting the communication of legitimate users.

At present, there is little research on D2D cooperative NOMA scheme in the intelligent eavesdropping scenario. Furthermore, each user has different requirements for information security service experience. For example, sensitive information such as bank information and personal privacy information has high security requirements, but ordinary data information has low security requirements. So this paper proposes a multi-user cooperative NOMA scheme by using the differences of users’ security service requirements, in order to further improve physical layer security, a user selection strategy was studied. We derive the expression on the ergodic secrecy sum capacity lower bound of the proposed scheme, and compare the performance differences between the scheme and single user cooperative NOMA scheme.

2 System Model

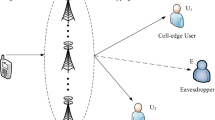
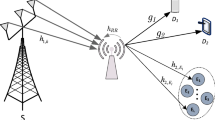
Figure 1 shows the system model of the proposed scheme, where a source node denoted S, a number N of DF relay user nodes denoted \({\text{R}}_k \left( {k = 1,2, \ldots ,N} \right)\), two destination nodes denoted \({\text{D}}_{1}\) and \({\text{D}}_2\), and a eavesdropping node denoted E are considered. All nodes work in half-duplex mode, equipped with a single antenna. Moreover, E is equipped with a directional antenna. We assume that all channels are independent quasi-static Rayleigh fading channels. Denote \(h_{{\text{S1}}}\), \(h_{{\text{SR}}_k }\), \(h_{{\text{R}}_k {\text{E}}}\), \(h_{{\text{R}}_k {2}}\), \(h_{{\text{E1}}}\), \(h_{{\text{ER}}_k }\) as the channel coefficients of links \({\text{S - D}}_1\), \({\text{S - R}}_k\), \({\text{R}}_k {\text{ - E}}\), \({\text{R}}_k {\text{ - D}}_2\), \({\text{E - D}}_1\), \({\text{E - R}}_k\) respectively. According to [11], \(h_{{\text{R}}_k {\text{E}}} = h_{{\text{ER}}_k }\). Due to path loss and shadow fading, the links \({\text{S - D}}_2\) and \({\text{S - E}}\) are not available. \(h_{{\text{S1}}}\), \(h_{{\text{SR}}_k }\), \(h_{{\text{R}}_k {\text{E}}}\), \(h_{{\text{R}}_k {2}}\), \(h_{{\text{E1}}}\), \(h_{{\text{ER}}_k }\) are independent complex Gaussian random variables with mean denoted as \(\lambda_{{\text{S1}}}\), \(\lambda_{{\text{SR}}_k }\), \(\lambda_{{\text{R}}_k {\text{E}}}\), \(\lambda_{{\text{R}}_k 2}\), \(\lambda_{{\text{E1}}}\), \(\lambda_{{\text{R}}_k {\text{E}}}\). Each node knows the CSI between itself and other nodes, and the CSI of the eavesdropping channel can be obtained by the method mentioned in [12]. Here E is an intelligent eavesdropper, which means that if E detects the signal transmitted by \({\text{R}}_k\), E will work in eavesdropping mode and directed eavesdropping \({\text{R}}_k\), otherwise it will switch to interference mode.

Fig.1
figure 1

System model

Full size image

2.1 Design of Transmission Scheme

The entire transmission process comprises two phases. In the first phase, the source node S broadcasts the superimposed signal \(\sqrt {a_1 P_{\text{S}} } x_1 + \sqrt {a_2 P_{\text{S}} } x_2\), where \(P_{\text{S}}\) is the transmit power of S, \(x_i\) represents the intended message for \({\text{D}}_i\), \(i \in \left\{ {1,2} \right\}\). According to NOMA principles, the power allocation coefficient \(a_1 < a_2\) and \(a_1 + a_2 = 1\). At the same time, the eavesdropper E executes interference mode and transmits interference signals \(\sqrt {P_{\text{J}} } x_{\text{J}}\) to legitimate nodes. The signal received at \({\text{D}}_1\) and R are given by

$$y_1 = h_{{\text{S1}}} \left( {\sqrt {a_1 P_{\text{S}} } x_1 + \sqrt {a_2 P_{\text{S}} } x_2 } \right) + h_{{\text{E1}}} \sqrt {P_{\text{J}} } x_{\text{J}} + n_1$$
(1)
$$y_{\text{R}_k} = h_{{\text{SR}}_k } \left( {\sqrt {a_1 P_{\text{S}} } x_1 + \sqrt {a_2 P_{\text{S}} } x_2 } \right) + h_{{\text{ER}}_k } \sqrt {P_{\text{J}} } x_{\text{J}} + n_{{\text{R}}_k }$$
(2)

where \(n_1 \sim CN\left( {0,\sigma_1 } \right)\) and \(n_{{\text{R}}_k } \sim CN\left( {0,\sigma_{{\text{R}}_k } } \right)\) represent the additive white Gaussian noise AWGN at \({\text{D}}_1\) and \({\text{R}}_k\) respectively. To abide with the principle of SIC, \({\text{D}}_1\) first decodes and removes the symbol \(x_2\) by treating the symbol \(x_1\) as noise, and then will decode symbol \(x_1\). The received signal-to-interference-plus-noise ratio (SINR) for \(x_1\) and \(x_2\) at \({\text{D}}_1\) are given by

$$\gamma_{{1} \to x_2 } = \frac{{\left| {h_{{\text{S1}}} } \right|^2 a_2 P_{\text{S}} }}{{\left| {h_{{\text{S1}}} } \right|^2 a_1 P_{\text{S}} + \left| {h_{{\text{E1}}} } \right|^2 P_{\text{J}} + \sigma_1^2 }}$$
(3)
$$\gamma_{{1} \to x_1 } = \frac{{\left| {h_{{\text{S1}}} } \right|^2 a_1 P_{\text{S}} }}{{\left| {h_{{\text{E1}}} } \right|^2 P_{\text{J}} + \sigma_1^2 }}$$
(4)

Similarly, the received SINR for \(x_2\) at \({\text{R}}_k\) is expressed as

$$\gamma_{{\text{R}}_k \to x_2 } = \frac{{\left| {h_{{\text{SR}}_k } } \right|^2 a_2 P_{\text{S}} }}{{\left| {h_{{\text{SR}}_k } } \right|^2 a_1 P_{\text{S}} + \left| {h_{{\text{ER}}_k } } \right|^2 P_{\text{J}} + \sigma_{{\text{R}}_k }^2 }}$$
(5)

In the second phase, in order to alleviate the communication congestion and reduce the SINR of the eavesdropper, \({\text{R}}_k\) forwards the new superimposed signal \(\sqrt {a_1 P_{\text{R}} } x_{\text{R}} + \sqrt {a_2 P_{\text{R}} } x_2\) with the transmit power \(P_{\text{R}}\). \(x_{\text{R}}\) is the normal data signal intended for \({\text{D}}_2\). Assuming that in the entire time slot, E can detect the signal forwarded by R, so it works in eavesdropping mode. The signal received at \({\text{D}}_2\) and E are given by

$$y_2 = h_{{\text{R}}_k {2}} \left( {\sqrt {a_1 P_{\text{R}} } x_{\text{R}} + \sqrt {a_2 P_{\text{R}} } x_2 } \right) + n_2$$
(6)
$$y_{\text{E}} = h_{{\text{R}}_k {\text{E}}} \left( {\sqrt {a_1 P_{\text{R}} } x_{\text{R}} + \sqrt {a_2 P_{\text{R}} } x_2 } \right) + n_{\text{E}}$$
(7)

where \(n_2 \sim CN\left( {0,\sigma_2 } \right)\) and \(n_{\text{E}} \sim CN\left( {0,\sigma_{\text{E}} } \right)\) represent the AWGN at \({\text{D}}_2\) and E respectively. The received SINR for \(x_2\) and \(x_{\text{R}}\) can be obtained as

$$\gamma_{2 \to x_2 } = \frac{{\left| {h_{{\text{R}}_k 2} } \right|^2 a_2 P_{\text{R}} }}{{\left| {h_{{\text{R}}_k 2} } \right|^2 a_1 P_{\text{R}} + \sigma_2^2 }}$$
(8)
$$\gamma_{2 \to x_{\text{R}} } = \frac{{\left| {h_{{\text{R}}_k 2} } \right|^2 a_1 P_{\text{R}} }}{\sigma_2^2 }$$
(9)

Since E only decodes sensitive signals \(x_2\) that have eavesdropping value, the received SINR at E is given by

$$\gamma_{{\text{E}} \to x_2 } = \frac{{\left| {h_{{\text{R}}_k {\text{E}}} } \right|^2 a_2 P_{\text{R}} }}{{\left| {h_{{\text{R}}_k {\text{E}}} } \right|^2 a_1 P_{\text{R}} + \sigma_{\text{E}}^2 }}$$
(10)

In order to reduce the eavesdropping quality of E, we propose a relay selection strategy that minimizes the channel gain of eavesdropping, and the mathematical expression is as follows

$${\text{R}}_b = \arg \mathop {\min }\limits_{k = 1,2, \ldots ,N} \left| {h_{{\text{R}}_K {\text{E}}} } \right|^2$$
(11)

3 Analysis of Ergodic Secrecy Sum Capacity

Here we use ergodic secrecy sum capacity (ESSC) as the performance indicator to evaluate the effectiveness of the proposed scheme. For the convenience of writing, let \(\sigma_i^2 = \sigma^2\), for \(i \in \left\{ {1,2,{\text{R}}_b ,{\text{E}}} \right\}\), \(\gamma_{\text{S}} = \frac{{P_{\text{S}} }}{\sigma^2 }\), \(\gamma_{\text{J}} = \frac{{P_{\text{J}} }}{\sigma^2 }\), \(\gamma_{\text{R}} = \frac{{P_{\text{R}} }}{\sigma^2 }\), \(\beta_\varphi \triangleq \left| {h_\varphi } \right|^2\), for \(\varphi \in \left\{ {{\text{S1,SR}}_b ,{\text{R}}_b {\text{E}},{\text{R}}_b {\text{2,E1,ER}}_b } \right\}\).

3.1 Ergodic Secrecy Capacity of \({\varvec{x}}_{\bf{1}}\)

Ergodic secrecy capacity (ESC) of \(x_1\) is defined as \(\overline{C}_{{\text{ESC}}}^{x_1 } \triangleq {\mathbb{E}}\left[ {\left\{ {C_1^{x_1 } - C_{\text{E}}^{x_1 } } \right\}^+ } \right]\), where \(C_1^{x_1 }\) and \(C_{\text{E}}^{x_1 }\) is the achievable maximum instantaneous rate of \(x_1\) at \({\text{D}}_1\) and E respectively. According to Jensen’s inequality, the definition of the ESC lower bound of \(x_1\) can be expressed as

$$\overline{C}_{\text{ESC,lb}}^{x_1 } \triangleq \left\{ {{\mathbb{E}}\left[ {C_1^{x_1 } } \right] - {\mathbb{E}}\left[ {C_{\text{E}}^{x_1 } } \right]} \right\}^+ = \left\{ {\overline{C}_1^{x_1 } - \overline{C}_{\text{E}}^{x_1 } } \right\}^+$$
(12)

Let \(Q_1 = \gamma_{1 \to x_1 }\), the complementary cumulative distribution function (CCDF) of \(Q_1\) is written as

$$\overline{F}_{Q_1 } \left( {q_1 } \right) = \Pr \left( {\frac{{\beta_{{\text{S1}}} a_1 P_{\text{S}} }}{{\beta_{{\text{E1}}} P_{\text{J}} + \sigma^2 }} > q_1 } \right) = \frac{{\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} }}{{\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} + \lambda_{{\text{E1}}} \gamma_{\text{J}} q_1 }}{\text{e}}^{ - \frac{q_1 }{{\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} }}}$$
(13)

Using the equation in [5]

$$\int\limits_0^\infty {\log \left( {1 + x} \right)} f_X \left( x \right)dx = \frac{1}{\ln 2}\int\limits_0^\infty {\frac{1 - F\left( x \right)}{{1 + x}}} dx$$
(14)

and [13, Eq. (25.4)], we can finally obtain

$$\approx \frac{{{\uppi }^2 }}{8L_1 \ln 2}\sum_{i = 1}^{L_1 } {\frac{{\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} \sqrt {1 - \alpha_i } \sec^2 \theta_i }}{{\left( {\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} + \lambda_{{\text{E1}}} \gamma_{\text{J}} \tan \theta_i } \right)\left( {1 + \tan \theta_i } \right)}}} {\text{e}}^{ - \frac{\tan \theta_i }{{\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} }}}$$
(15)

where \(\alpha_i = \cos \frac{{\left( {2i - 1} \right)\pi }}{2L_1 }\), \(\theta_i = \frac{\pi }{4}\alpha_i + \frac{\pi }{4}\), \(L_1\) denotes the number of the Gauss–Chebyshev quadrature approximation. Due to path loss and shadows, the eavesdropper E cannot eavesdrop on the superimposed signal broadcasted by S, thus \(\overline{C}_{\text{E}}^{x_1 } = 0\)。Substituting \(\overline{C}_{\text{E}}^{x_1 } = 0\) and (15) into (12), the expression of the ESC lower bound of \(x_1\) can be obtained as

$$\overline{C}_{\text{ESC,lb}}^{x_1 } \approx \left\{ {\frac{{{\uppi }^2 }}{8L_1 \ln 2}\sum_{i = 1}^{L_1 } {\frac{{\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} \sqrt {1 - \theta_i } \sec^2 \theta_i }}{{\left( {\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} + \lambda_{{\text{E1}}} \gamma_{\text{J}} \tan \theta_i } \right)\left( {1 + \tan \theta_i } \right)}}} {\text{e}}^{ - \frac{\tan \theta_i }{{\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} }}} } \right\}^+$$
(16)

3.2 Ergodic Secrecy Capacity of \({\varvec{x}}_{\bf{2}}\)

Similar to \(x_1\), using Jensen’s inequality, the definition of the ESC lower bound of \(x_2\) can be expressed as

$$\overline{C}_{\text{ESC,lb}}^{x_2 } \triangleq \left\{ {{\mathbb{E}}\left[ {C_2^{x_2 } } \right] - {\mathbb{E}}\left[ {C_{\text{E}}^{x_2 } } \right]} \right\}^+ = \left\{ {\overline{C}_2^{x_2 } - \overline{C}_{\text{E}}^{x_2 } } \right\}^+$$
(17)

where \(C_2^{x_2 }\) and \(C_{\text{E}}^{x_2 }\) is the achievable maximum instantaneous rate of \(x_2\) at \({\text{D}}_1\) and E. Let \(T_1 = \min \left\{ {\gamma_{1 \to x_2 } ,\gamma_{{\text{R}}_k \to x_2 } ,\gamma_{2 \to x_2 } } \right\}\), \(T_2 = \gamma_{{\text{E}} \to x_2 }\), \(V_1 = \beta_{{\text{R}}_b {\text{E}}}\), where \(T_1\) is the effective received SNR for \(x_2\). Due to \(\left| {h_{{\text{R}}_{1} {\text{E}}} } \right|^2 ,\left| {h_{{\text{R}}_2 {\text{E}}} } \right|^2 , \ldots ,\left| {h_{{\text{R}}_N {\text{E}}} } \right|^2\) are an independent and identically distributed random variable, the probability density function (PDF) of \(V_1\) is \(f_{V_1 } \left( {v_1 } \right) = \frac{N}{{\lambda_{{\text{RE}}} }}{\text{e}}^{ - \frac{N}{{\lambda_{{\text{RE}}} }}v_1 }\). The achievable ESC of \(x_2\) at \({\text{D}}_2\) and E can be written as

$$\overline{C}_2^{x_2 } = \frac{1}{2}\int\limits_0^\infty {\log \left( {1 + t_1 } \right)} f_{T_1 } \left( {t_1 } \right)dt_1 = \frac{1}{2\ln 2}\int\limits_0^\infty {\frac{{1 - F_{T_1 } \left( {t_1 } \right)}}{1 + t_1 }} dt_1$$
(18)
$$\overline{C}_{\text{E}}^{x_2 } = \frac{1}{2}\int\limits_0^\infty {\log \left( {1 + t_2 } \right)} f_{T_2 } \left( {t_2 } \right)dt_2 = \frac{1}{2\ln 2}\int\limits_0^\infty {\frac{{1 - F_{T_2 } \left( {t_2 } \right)}}{1 + t_2 }} dt_2$$
(19)

In order to obtain the expression of \(C_2^{x_2 }\) and \(C_{\text{E}}^{x_2 }\), we derive the CCDF of \(T_1\) and \(T_2\) as follows:

$$\begin{aligned} \overline{F}_{T_1 } \left( {t_1 } \right) & = \Pr \left( {\min \left\{ {\gamma_{1 \to x_2 } ,\gamma_{{\text{R}}_k \to x_2 } ,\gamma_{2 \to x_2 } } \right\} > t_1 } \right) \\ & = \frac{N}{{\lambda_{{\text{E1}}} \lambda_{{\text{ER}}_b } }}{\text{e}}^{ - \left( {\frac{1}{{\lambda_{{\text{S}}1} \gamma_{\text{S}} }} + \frac{1}{{\lambda_{{\text{SR}}} \gamma_{\text{S}} }} + \frac{1}{{\lambda_{{\text{R2}}} \gamma_{\text{R}} }}} \right)\frac{t_1 }{{\left( {a_2 - a_1 t_1 } \right)}}} \\ & \quad \int\limits_0^\infty {{\text{e}}^{ - u\left( {\frac{{\gamma_{\text{J}} t_1 }}{{\lambda_{{\text{S1}}} \left( {a_2 - a_1 t_1 } \right)\gamma_{\text{S}} }} + \frac{1}{{\lambda_{{\text{E1}}} }} + \frac{{\gamma_{\text{J}} t_1 }}{{\lambda_{{\text{SR}}} \left( {a_2 - a_1 t_1 } \right)\gamma_{\text{S}} }} + \frac{N}{{\lambda_{{\text{ER}}_b } }}} \right)} } {\text{d}}u \\ & = \frac{{\lambda_{{\text{S}}1} \lambda_{{\text{SR}}} \gamma_{\text{S}}^2 N\left( {a_2 - a_1 t_1 } \right)^2 {\text{e}}^{ - \left( {\frac{1}{{\lambda_{{\text{S}}1} \gamma_{\text{S}} }} + \frac{1}{{\lambda_{{\text{SR}}} \gamma_{\text{S}} }} + \frac{1}{{\lambda_{{\text{R2}}} \gamma_{\text{R}} }}} \right)\frac{t_1 }{{\left( {a_2 - a_1 t_1 } \right)}}} }}{{\left[ {\lambda_{{\text{S}}1} \gamma_{\text{S}} \left( {a_2 - a_1 t_1 } \right) + \lambda_{{\text{E}}1} \gamma_{\text{J}} t_1 } \right]\left[ {\lambda_{{\text{SR}}} \gamma_{\text{S}} N\left( {a_2 - a_1 t_1 } \right) + \lambda_{{\text{ER}}} \gamma_{\text{J}} t_1 } \right]}} \\ \end{aligned}$$
(20)
$$\overline{F}_{T_2 } \left( {t_2 } \right) = \Pr \left( {\gamma_{{\text{E}} \to x_2 } > t_2 } \right){\text{ = Pr}}\left( {\frac{{\beta_{{\text{R}}_k {\text{E}}} a_2 P_{\text{R}} }}{{\beta_{{\text{R}}_k {\text{E}}} a_1 P_{\text{R}} + \sigma_{\text{E}}^2 }} > t_2 } \right){\text{ = e}}^{ - \frac{Nt_2 }{{\lambda_{{\text{RE}}} \gamma_{\text{R}} \left( {a_2 - a_1 t_2 } \right)}}}$$
(21)

Substituting (20) into (18), the achievable ESC of \(x_2\) at \({\text{D}}_2\) is given by

$$\overline{C}_2^{x_2 } = \frac{{\uppi }}{2L_2 \ln 2}\sum_{i = 1}^{L_2 } {\frac{{\lambda_{{\text{S1}}} \lambda_{{\text{SR}}} \gamma_{\text{S}}^2 a_1^2 a_2 N\left( {1 - x_i } \right)^2 \sqrt {1 - y_i^2 } \times {\text{e}}^{ - \left( {\frac{1}{{\lambda_{{\text{S}}1} \gamma_{\text{S}} }} + \frac{1}{{\lambda_{{\text{SR}}} \gamma_{\text{S}} }} + \frac{1}{{\lambda_{{\text{R2}}} \gamma_{\text{R}} }}} \right)\frac{{\left( {1 + x_i } \right)}}{{a_1 \left( {1 - x_i } \right)}}} }}{{A\left( {x_i } \right)}}}$$
(22)

where \(L_2\) denotes the number of the Gauss–Chebyshev quadrature approximation, \(y_i = \cos \frac{{\left( {2i - 1} \right)\pi }}{2L_2 }\), \(x_i = y_i\), and

$$\begin{aligned} A\left( {x_i } \right) & = \left( {2a_1 + a_2 \left( {1 + x_i } \right)} \right)\left( {\lambda_{{\text{S}}1} \gamma_{\text{S}} a_1 \left( {1 - x_i } \right) + \lambda_{{\text{E}}1} \gamma_{\text{J}} \left( {1 + x_i } \right)} \right) \\ & \quad \times \left( {\lambda_{{\text{SR}}} \gamma_{\text{S}} Na_1 \left( {1 - x_i } \right) + \lambda_{{\text{ER}}} \gamma_{\text{J}} \left( {1 + x_i } \right)} \right) \\ \end{aligned}$$
(23)

Using (19), (21) and [14, Eq. (3.352.2)], the achievable ESC of \(x_2\) at E is given by

$$\overline{C}_{\text{E}}^{x_2 } = \frac{1}{2\ln 2}\left[ {{\text{e}}^{\frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} a_1 }}} {\text{Ei}}\left( { - \frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} a_1 }}} \right) - {\text{e}}^{\frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} }}} {\text{Ei}}\left( { - \frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} }}} \right)} \right]$$
(24)

where \({\text{Ei}}\left( \cdot \right)\) is exponential integral function. Therefore, the expression of the ESC lower bound of \(x_2\) can be finally obtained as

$$\overline{C}_{\text{ESC,lb}}^{x_2 } \approx \frac{1}{2\ln 2}\left\{ \begin{gathered} \frac{{\uppi }}{L_2 }\sum_{i = 1}^{L_2 } {\frac{{\lambda_{{\text{S1}}} \lambda_{{\text{SR}}} \gamma_{\text{S}}^2 a_1^2 a_2 N\left( {1 - x_i } \right)^2 \sqrt {1 - y_i^2 } \times {\text{e}}^{ - \left( {\frac{1}{{\lambda_{{\text{S}}1} \gamma_{\text{S}} }} + \frac{1}{{\lambda_{{\text{SR}}} \gamma_{\text{S}} }} + \frac{1}{{\lambda_{{\text{R2}}} \gamma_{\text{R}} }}} \right)\frac{{\left( {1 + x_i } \right)}}{{a_1 \left( {1 - x_i } \right)}}} }}{{A\left( {x_i } \right)}}} \hfill \\ - \left[ {{\text{e}}^{\frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} a_1 }}} {\text{Ei}}\left( { - \frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} a_1 }}} \right) - {\text{e}}^{\frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} }}} {\text{Ei}}\left( { - \frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} }}} \right)} \right] \hfill \\ \end{gathered} \right\}^+$$
(25)

3.3 Ergodic Secrecy Capacity of \({\varvec{x}}_{\bf{R}}\) and ESSC of System

Since \(x_{\text{R}}\) is a ordinary data signal, and E only intercepts valuable and sensitive signals, the ergodic secrecy capacity of \(x_{\text{R}}\) is its ergodic capacity. Let \(V_2 = \gamma_{2 \to x_{\text{R}} }\), CCDF of \(V_2\) is as follows

$$\overline{F}_{V_2 } \left( {v_2 } \right) = \Pr \left( {\frac{{\left| {h_{{\text{R}}_k 2} } \right|^2 a_1 P_{\text{R}} }}{\sigma_2^2 } > v_2 } \right) = {\text{e}}^{ - \frac{v_2 }{{\lambda_{{\text{R2}}} \gamma_{\text{R}} a_1 }}}$$
(26)

According to [14, Eq. (3.352.4)], the ergodic secrecy capacity of \(x_{\text{R}}\) can be written as

$$\begin{aligned} \overline{C}_{{\text{ESC}}}^{x_{\text{R}} } & = \frac{1}{2}\int\limits_0^\infty {\log \left( {1 + v_1 } \right)} f_{V_1 } \left( {v_1 } \right)dv_1 = \frac{1}{2\ln 2}\int\limits_0^\infty {\frac{{1 - F_{v_1 } \left( {v_1 } \right)}}{1 + v_1 }} dv_1 \\ & = - \frac{1}{2\ln 2}{\text{e}}^{\frac{1}{{\lambda_{{\text{R2}}} \gamma_{\text{R}} a_1 }}} {\text{Ei}}\left( { - \frac{1}{{\lambda_{{\text{R2}}} \gamma_{\text{R}} a_1 }}} \right) \\ \end{aligned}$$
(27)

So the ESSC of system is approximated as

$$\begin{aligned} \overline{C}_{\text{ESSC,lb}} & = \overline{C}_{\text{ESC,lb}}^{x_{\text{R}} } + \overline{C}_{\text{ESC,lb}}^{x_1 } + \overline{C}_{\text{ESC,lb}}^{x_2 } \approx - \frac{1}{2\ln 2}{\text{e}}^{\frac{1}{{\lambda_{{\text{R2}}} \gamma_{\text{R}} a_1 }}} {\text{Ei}}\left( { - \frac{1}{{\lambda_{{\text{R2}}} \gamma_{\text{R}} a_1 }}} \right) \\ & \quad { + }\left\{ {\frac{{{\uppi }^2 }}{8L_1 \ln 2}\sum_{i = 1}^{L_1 } {\frac{{\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} \sqrt {1 - \theta_i } \sec^2 \theta_i }}{{\left( {\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} + \lambda_{{\text{E1}}} \gamma_{\text{J}} \tan \theta_i } \right)\left( {1 + \tan \theta_i } \right)}}} {\text{e}}^{ - \frac{\tan \theta_i }{{\lambda_{{\text{S1}}} a_1 \gamma_{\text{S}} }}} } \right\}^+ \\ & \quad { + }\frac{1}{2\ln 2}\left\{ \begin{gathered} \frac{{\uppi }}{L_2 }\sum_{i = 1}^{L_2 } {\frac{{\lambda_{{\text{S1}}} \lambda_{{\text{SR}}} \gamma_{\text{S}}^2 a_1^2 a_2 N\left( {1 - x_i } \right)^2 \sqrt {1 - y_i^2 } \times {\text{e}}^{ - \left( {\frac{1}{{\lambda_{{\text{S}}1} \gamma_{\text{S}} }} + \frac{1}{{\lambda_{{\text{SR}}} \gamma_{\text{S}} }} + \frac{1}{{\lambda_{{\text{R2}}} \gamma_{\text{R}} }}} \right)\frac{{\left( {1 + x_i } \right)}}{{a_1 \left( {1 - x_i } \right)}}} }}{{A\left( {x_i } \right)}}} \hfill \\ - \left[ {{\text{e}}^{\frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} a_1 }}} {\text{Ei}}\left( { - \frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} a_1 }}} \right) - {\text{e}}^{\frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} }}} {\text{Ei}}\left( { - \frac{N}{{\lambda_{{\text{RE}}} \gamma_{\text{R}} }}} \right)} \right] \hfill \\ \end{gathered} \right\}^+ \\ \end{aligned}$$
(28)

4 Numerical Analysis

In this section, we will evaluate the performance of our proposed D2D-NOMA system in terms of ESSC under the user selection scheme through simulation. The relevant parameter settings in the simulation are as follows: \(L_1 = L_2 = 100\), legal channel parameters \(\lambda_{{\text{S1}}} = \lambda_{{\text{SR}}} = 1\), \(\lambda_{{\text{R2}}} = 2\), in order to avoid being discovered, the eavesdropper is far away from the legal nodes, so \(\lambda_{{\text{RE}}} = \lambda_{{\text{E1}}} = 0.1\). If there is no special instructions, we set \(\gamma_{\text{S}} = \gamma_{\text{R}} = 30\,{\text{dB}}\), \(a_1 = 0.2\), \(a_2 = 0.8\) and \(N = 10\). Similarly, due to the need for concealment, \(\gamma_{\text{J}} = 5\,{\text{dB}}\). The number of Monte Carlo simulations is 1,000,000.

For comparison, we consider the following benchmark schemes in the simulation.

  1. (1)

    Benchmark scheme 1 is a multi-relay user cooperative NOMA scheme, in which the number of relay users is \(N = 10\). In the first time slot, S broadcast superimposed signal \(\sqrt {a_1 P_{\text{S}} } x_1 + \sqrt {a_2 P_{\text{S}} } x_2\), at the same time the eavesdropper transmits interference signals \(\sqrt {P_{\text{J}} } x_{\text{J}}\). In the second time slot, the selected relay forward the signal \(x_2\) with the transmit power \(P_{\text{R}}\), and E switches to eavesdropping mode.

  2. (2)

    Benchmark scheme 2 is a single-relay user cooperative NOMA scheme, in which the number of relay users is \(N = 1\). In first time slot, S broadcast superimposed signal \(\sqrt {a_1 P_{\text{S}} } x_1 + \sqrt {a_2 P_{\text{S}} } x_2\), and the eavesdropper transmits interference signals \(\sqrt {P_{\text{J}} } x_{\text{J}}\). In the second time slot, relay user forwards signal \(\sqrt {a_1 P_{\text{R}} } x_{\text{R}} + \sqrt {a_2 P_{\text{J}} } x_2\), and E switches to eavesdropping mode.

Figure 2 shows the relationship between the number of relay users and the system ESSC under different power allocation factors. As shown in Fig. 1, as the number of relay users increases, the ESSC of the system increases monotonically, and compared to \(a_1 = 0.4\), the number of relay users has a greater impact on the system ESSC when \(a_1 = 0.2\). It can also be observed from the figure, secrecy performance of the system when \(a_1 = 0.4\) is better than that of the system when \(a_1 = 0.2\). This is because there is more power allocated to \(x_1\) and \(x_{\text{R}}\) when \(a_1 = 0.4\), which is beneficial for \({\text{D}}_1\) to resist the interference attack of E, furthermore the eavesdropper does not eavesdrop on the ordinary data signals \(x_{\text{R}}\).

Fig. 2
figure 2

The effect of \(N\) on system ESSC with different power allocation factors

Full size image

Figure 3 simulates the influence of the eavesdropper’s transmitted SINR on the system ESSC. The simulation shows that the security performance of the proposed scheme is better than that of Benchmark scheme 1 and Benchmark scheme 2, and the performance gap between the proposed scheme and Benchmark scheme 1 is more obvious. It implies that it is of great significance to design a secure communication scheme based on the differences in user experience requirements for information security services. In addition, it can also be observed that the ESSC of the proposed scheme and Benchmark scheme 2 tend to a positive definite value in the high SIR, this is because the transmission of \(x_{\text{R}}\) occurs in the second time slot, so it will not be affected by the interference of E. By comparing the curves of Monte Carlo simulation and theoretical analysis, it can be found that the two basically overlap, reflecting the accuracy of the numerical calculation.

Fig. 3
figure 3

The effect of \(\gamma_{\text{J}}\) on system ESSC with different transmission schemes

Full size image

5 Conclusions

This paper combines user selection technology with D2D technology to design a NOMA communication scheme against intelligent eavesdropping, and derives the expression of the ESSC lower bound of the proposed scheme. Theoretical derivation and simulation show that the proposed scheme is better than the two Benchmark schemes. The communication system can take advantage of the differences in information security service experience requirements of each user to alleviate communication congestion and improve the overall security performance. In addition, by increasing the number of relay users, the security of information transmission can be further ensured.