1 Introduction

The use of an unmanned aerial vehicle (UAV) as a flying base station (BS) shows a great potential for providing emergency connectivity support in natural disaster situations, as well as for civilian applications [1,2,3]. In recent years, manufacturing of energy-efficient, low-cost, and small-size UAVs has commenced plenty of new applications in upcoming wireless networks [1, 4]. In addition, UAV-assisted communication has an obvious advantage over a terrestrial network in providing a line of sight (LoS) transmission condition, thanks to the UAV’s ability to reach higher altitudes and adjustable trajectory. As a result, it can mitigate the effect of terrestrial blockage caused by buildings, trees, and other infrastructure [1, 3, 5].

In general, UAV-enabled communications can be categorized into three application scenarios [1, 6]:

  1. (i)

    UAV-assisted ubiquitous coverage: In this type of networks, UAVs are used for providing coverage along with the existing cellular networks.

  2. (ii)

    Cooperative relaying: In this category, the UAVs are mainly employed to provide a reliable network among users when the direct communication between user pairs is not good enough or in the absence of a terrestrial network.

  3. (iii)

    UAV-aided data collection and information dissemination: It is another application category, in which UAVs are deployed for collecting data, e.g., from the Internet of Things (IoT) devices that are small and have limited battery life. This type of data collection can prolong the operating life of such a network by reducing overall power transmission from these nodes.

Despite these numerous potential applications, there are many challenges that need to be addressed for realizing UAV-assisted communication. For instance, the durability of the UAV-assisted network is limited by frequent power shortages due to its size and weight constraints. In order to prolong communication through such an UAV-assisted network, it requires an onboard power source with its mechanical and communication modules. To address this issue, simultaneous wireless information and power transfer (SWIPT) has been introduced that can make communication networks self-sufficient and reliant [7, 8]. Conventional sources of energy harvesting (EH) rely on their environment and surroundings, and therefore, they may fail to provide a perpetual energy supply. In contrast, the use of radio-frequency (RF) signals for providing power and carrying the information can be accomplished through the SWIPT technique. The relay reduces the overall power consumption of the network by utilizing the harvested energy for signal transmission in the next hop. In general, two SWIPT receiver architectures, namely power splitting (PS) and time switching (TS), are commonly used in the literature. Several research works [7, 9] have adopted these receiver architectures to investigate system performance.

1.1 Related Works

Plenty of works [10,11,12,13,14,15,16,17,18] have considered UAV-enabled communications for different application scenarios. Specifically, the authors in [10] have studied UAV-assisted one-way relaying (OWR) and performed optimization of the trajectory of moving UAV. Further, UAV heading angle control has been considered in [11] to optimize the performance of the link between UAV-based relay and ground node. In [12], the optimal UAV relay placement and performance analysis have been conducted for decode-and-forward (DF) and amplify-and-forward (AF) operations. In [13], multiple UAVs with AF and DF operations have been investigated for multi-hop single links and multiple dual-hop links in terms of outage probability (OP) and bit error rate (BER). Furthermore, SWIPT has been studied for UAV-assisted OWR with a mobile node and hovering UAV in [14]. In [15], the throughput maximization for SWIPT-enabled UAV-assisted cooperative communication based on DF and AF protocols has been done with power profile and power splitting ratio profile. Efficient deployment of UAV networks to collect data from IoT devices has been discussed in [16]. In [17], the authors have investigated UAV as a flying BS in coexistence with the underlay device-to-device (D2D) communications. In [18], the authors have performed joint optimization for power and trajectory for a UAV-relaying network.

A hybrid decode-amplify-forward operation has been considered in [19] for relay assistance to reduce overall power usage. Further, the authors in [20] have analyzed the secrecy OP with imperfect CSI for a multi-antenna relay system with a non-linear EH architecture. In [21, 22], the authors have emphasized modeling LoS/non-LoS channels and path-loss for the uplink and downlink of UAV-based networks in diverse propagation scenarios. Specifically, the authors in [23] have adopted probabilistic path-loss modeling in deriving the analytical expressions. In [24], the authors have formulated the PDF expressions for the Nakagami-N-gamma model considering composite fading channels. In contrast, an accurate alternate for the Rayleigh log-normal shadowed model in terms of Rayleigh-gamma distribution has been provided in [25]. Furthermore, the authors in [26] have obtained expressions for the fade duration of the signal envelope and the average level crossing rate under Nakagami-m fading and log-normal shadowing. Similarly, the statistical characterization of the wireless channel with log-normal shadowing has been done in [27]. In [28], authors have considered a heterogeneous network and investigated the system performance in terms of OP over composite fading channels.

In [29], the authors have derived expressions for the OP and bit error rate for a SWIPT-based UAV-assisted IoT system considering PS and TS architectures separately over the Nakagami-m fading channels. Further, the authors in [30] have introduced a unified energy management framework assuming wireless power transfer, SWIPT, and self-interference cancellation in UAV-based relay communication with full-duplex transmission mode. Similarly, a full-duplex UAV-assisted SWIPT-enabled network has been studied in [31], where the authors have formulated an optimization problem to minimize the system’s OP over Nakagami-m fading. Likewise, the authors in [32] have derived closed-form expressions for the OP and system throughput over the Weibull fading channel for SWIPT-based half/full duplex UAV networks. Recently, the authors in [33] have exploited the concept of non-orthogonal multiple access (NOMA) in SWIPT-based UAV networks and derived OP and throughput expressions for two RF-EH protocols, namely, TS and PS. In practice, UAVs may suffer from severe path-loss and diverse channel conditions that can be characterized by probabilistic path-loss and channel models. However, these works [29,30,31,32,33], as shown in Table 1, have not taken shadowing, probabilistic path-loss and channel modeling into account for investigating the performance of the systems.

Table 1 Comparison of the current work with the most recent literature
Full size table

To the best of the authors’ knowledge, no work has considered the effect of shadowing and probabilistic path-loss and channel modeling for hybrid TS-PS based UAV cooperative networks.

Fig. 1
figure 1

SWIPT-enabled UAV-assisted communications

Full size image

1.2 Contributions

Motivated by the above-mentioned works and highlighted research gap, this paper considers a hybrid TS-PS SWIPT architecture for UAV-based relay system where one-way communication is realized in three phases with the help of the DF protocol. The UAV is assumed to perform relay transmission using the harvested RF energy, and the onboard battery is used for flying and maneuvering. To study performance of such a dual-hop UAV-assisted network, expressions of OP, system throughput, and energy efficiency are derived over mixed LoS/NLoS shadowed fading channels. The main contributions of this paper are summarized as follows:

  • A linear EH model is adopted for enabling RF energy harvesting at UAV and the DF operation is considered to provide relay assistance. Closed-form expressions for the probability density functions (PDFs) of composite channels are derived for log-normal shadowing using the Gauss–Hermite quadrature. The accuracy of the obtained PDFs for shadowed Nakagami-m, shadowed Rayleigh, shadowed Rayleigh-shadowed Rayleigh, shadowed Rayleigh-shadow Nakagami, and shadowed Nakagami-shadowed Nakagami channels is demonstrated.

  • Closed-form expressions of OP, system throughput, and energy efficiency considering the probability of LoS/NLoS mixed channels are derived for shadowed and un-shadowed channels.

  • Extensive numerical and simulation results are provided to offer key insights into the system behavior.

Notations: \(Pr [\cdot ]\), \(f_{Z}(\cdot )\), and \(F_{Z}(\cdot )\) represent the probability, PDF and the cumulative distribution function (CDF) of a random variable Z, respectively. The upper incomplete, the lower incomplete, and the complete gamma functions are denoted, respectively, as \(\Gamma [\cdot ,\cdot ]\), \(\Upsilon [\cdot ,\cdot ]\), and \(\Gamma [\cdot ]\), [34, eq. (8.350)]. \({\mathcal {K}}_{v}(\cdot )\) is used to denote vth order modified Bessel function of the second kind [34, eq. (8.432.1)].

2 System Model

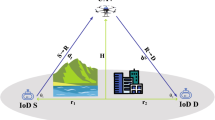
The UAV-assisted relay network considered in this paper is illustrated in Fig. 1, where the UAV relay cooperates the wireless information transfer between the BS and the remote mobile user. All nodes are assumed to be equipped with a single antenna and communication is carried out in the half-duplex mode. The DF strategy is utilized at the UAV for performing relay assistance. The UAV hovers at a certain altitude, with height \(H_\textsf{U}\). The ground distances from the BS to UAV and UAV to the mobile user are \(R_{1}\) and \(R_{2}\), respectively. The elevation angles between UAV to BS and UAV to the mobile user are \(\theta _\textsf{T}\) and \(\theta _\textsf{R}\), respectively. The direct link between the BS and the mobile user is assumed to be missing due to blockage. The UAV relay is considered an energy-constrained node. Thus, it harvests energy from the received RF signals and then applies DF operation to broadcast the information. Here, the energy consumed for information processing is assumed to be negligible compared to the energy requirement for information forwarding. All channel coefficients are assumed to be independent and quasi-static for one block duration. The receiver noise is modeled as a complex Gaussian random variable with zero mean and variance \(\sigma ^{2}\). The probability of LoS-based path-loss is considered as given in [23]. Log-normal shadowing is adopted for channel modeling throughout this work.

In practice, the path-loss depends on the frequency, distance, and gain of the antenna at the sending and receiving nodes. In this work, a practical model for path-loss between ground nodes and UAV is considered, in which the average path-loss (\(\mu _\textsf{T}\)) can be expressed as [21, 23]

$$\begin{aligned} \mu _\textsf{T}={\mathcal {P}}_\textsf{LoS}(\theta )\times \mu _\textsf{LoS}+{\mathcal {P}}_\textsf{NLoS}(\theta )\times \mu _\textsf{NLoS}, \end{aligned}$$
(1)

where the probability of LoS can be given as

$$\begin{aligned} {\mathcal {P}}_\textsf{LoS}(\theta )=\frac{1}{1+a e^{-b(\theta -a)}}. \end{aligned}$$
(2)

Here, a and b are constants related to the propagation environment and \(\theta\) is angle, expressed in degree, between the UAV and ground nodes. Now, the expressions of \(\mu _\textsf{LoS}\) and \(\mu _\textsf{NLoS}\) can be given as

$$\begin{aligned} \mu _\textsf{LoS}&=20\log _{10}d\!+\!20\log _{10}f\!+\!20\log _{10}\left( \frac{4\pi }{c}\right) \!+\!\eta _\textsf{LoS}, \end{aligned}$$
(3)
$$\begin{aligned} \mu _\textsf{NLoS}&=20\log _{10}d\!+\!20\log _{10}f\!+\!20\log _{10}\left( \frac{4\pi }{c} \right) \!+\!\eta _\textsf{NLoS}, \end{aligned}$$
(4)

where d is the distance between the UAV and ground nodes, f is the operating frequency, c is the speed of light, \(\eta _\textsf{LoS}\) and \(\eta _\textsf{NLoS}\) are propagation constants for a particular communication scenario at a fixed frequency.

Fig. 2
figure 2

Frame structure of one block

Full size image

The transmission block structure for the considered system is shown in Fig. 2. Here, one block duration is divided into three phases to enable hybrid SWIPT and one-way information transmission. In the first phase, the BS transmits RF signals to the UAV for a duration of \(\alpha T\), where \(0\le \alpha <1\) is the time allocation ratio and T is the duration of the entire block. Now, considering a linear EH model for harvesting energy. The received energy is given by \({\mathcal {E}}_\textsf{TS} = \eta \alpha T P_{T}\mid \!\! h_\textsf{T,U}\!\!\mid ^{2}\) where \(P_\textsf{T}\) is the transmit power at the BS and \(h_\textsf{T,U}\) is the channel coefficient between the BS and the UAV. In the second phase, the BS transmits the information signal to the UAV for a duration of \(\lambda (1-\alpha ) T\), where \(\lambda (1-\alpha )\) is the time allocation ratio with \(0<\lambda <1\). In the second phase, the received signal is given as \(y_\textsf{T,U}=\sqrt{P_\textsf{T}} h_\textsf{T,U}x_\textsf{T}+n_\textsf{U}\). Further, \(x_\textsf{T}\) represents unit energy symbol transmitted from the BS and \(n_\textsf{U}\in {{\mathcal {C}}}{{\mathcal {N}}}(0,\sigma ^{2})\) is additive white Gaussian noise (AWGN) at the UAV.

At the UAV, the signal power is split into two portions, \(\beta\) and \((1-\beta )\), where \(\beta\) is the power allocation factor. Here, \(\beta\) portion is used for harvesting energy and \((1-\beta )\) portion for information decoding. The harvested energy is given as \({\mathcal {E}}_\textsf{PS}=\eta \beta \lambda (1-\alpha ) TP_{T} \mid \!\! h_\textsf{T,U}\!\!\mid ^{2}\). Now, the total harvested energy can be expressed as \({\mathcal {E}}_{T}= \eta (\alpha +\beta \lambda (1-\alpha )) T P_{T}\mid \!\! h_\textsf{T,U}\!\!\mid ^{2}\). The transmit power at the UAV can be given as

$$\begin{aligned} P_\textsf{U}=\frac{\eta (\alpha +\beta \lambda (1-\alpha )) P_{T} \mid \!\! h_\textsf{T,U}\!\!\mid ^{2}}{(1-\alpha )(1-\lambda )}. \end{aligned}$$
(5)

The received signal-to-noise ratio (SNR) at the UAV can be expressed as

$$\begin{aligned} \Lambda _\textsf{T,U}=\frac{(1-\beta )P_\textsf{T} \mid \!\! h_\textsf{T,U}\!\!\mid ^2}{\sigma ^2}. \end{aligned}$$
(6)

It then follows that the achievable rate at the UAV is given as \({\mathcal {R}}_\textsf{T,U}=\lambda (1-\alpha ) \log _{2}(1+\Lambda _\textsf{T,U}).\)

In the third phase, the UAV uses the harvested energy for forwarding the received signal to a mobile user in the remaining block duration of \((1-\lambda )(1-\alpha )T\). The received signal at the mobile user is given as \(y_\textsf{U,R}=\sqrt{P_\textsf{U}} h_\textsf{U,R} x_\textsf{T}+ n_\textsf{R}\), where \(n_\textsf{R}\in {{\mathcal {C}}}{{\mathcal {N}}}(0,\sigma ^{2})\) is AWGN at the mobile user. The expression of the instantaneous SNR at the mobile user is given as

$$\begin{aligned} \Lambda _\textsf{U,R}=\frac{\eta (\alpha +\beta \lambda (1-\alpha )) P_{T}\mid \!\! h_\textsf{T,U} \!\! \mid ^{2} \mid \!\! h_\textsf{U,R}\!\!\mid ^2}{(1-\lambda )(1-\alpha )\sigma ^2}. \end{aligned}$$
(7)

Based on (7), the instantaneous rate can be expressed as \({\mathcal {R}}_\textsf{U,R}=(1-\alpha )(1-\lambda )\log _{2}(1+\Lambda _\textsf{U,R})\).

3 Performance Analysis

In this section, accurate expressions of OP, system throughput, and energy efficiency are derived for the considered dual-hop UAV-assisted network.

3.1 Outage Probability

An outage event occurs if the instantaneous rate at the UAV or the mobile user falls below a predefined target rate. Thereby, the OP can be mathematically formulated as [30]

$$\begin{aligned} {\mathcal {P}}_\textrm{out}=1-\left( 1-Pr [{\mathcal {R}}_\textsf{T,U}< r_\textrm{th}]\right) \left( 1-Pr [{\mathcal {R}}_\textsf{U,R}<r_\textrm{th}]\right) . \end{aligned}$$
(8)

By incorporating the probabilities of LoS and NLoS components in the first hop and considering \({\mathcal {P}}_\textsf{T,U}=Pr [{\mathcal {R}}_\textsf{T,U}<r_\textrm{th}]\), one can have

$$\begin{aligned} {\mathcal {P}}_\textsf{T,U}={\mathcal {P}}_\textsf{LoS}(\theta _\textsf{T})Pr [{\mathcal {R}}^{ {(SN) }}_\textsf{T,U}<r_\textrm{th}]+{\mathcal {P}}_\textsf{NLoS}(\theta _\textsf{T})Pr [{\mathcal {R}}^{ {(SR) }}_\textsf{T,U}<r_\textrm{th}], \end{aligned}$$
(9)

where \({\mathcal {R}}^{ {(SN) }}_\textsf{T,U}\) and \({\mathcal {R}}^{ {(SR) }}_\textsf{T,U}\) are the instantaneous rates at the UAV in the first phase when \(h_\textsf{T,U}\) follows shadowed Nakagami-m and shadowed Rayleigh fading, respectively. Similarly, the other probability term in (8), i.e., \({\mathcal {P}}_\textsf{U,R}=Pr [{\mathcal {R}}_\textsf{U,R}<r_\textrm{th}]\), can be formulated as

$$\begin{aligned} {\mathcal {P}}_\textsf{U,R}&={\mathcal {P}}_\textsf{LoS}(\theta _\textsf{T})\left( {\mathcal {P}}_\textsf{LoS}(\theta _\textsf{R})\,Pr \left[ {\mathcal {R}}^{ {(SN,SN) }}_\textsf{U,R}<r_\textrm{th}\right] \right. \nonumber \\&\quad \left. +\,{\mathcal {P}}_\textsf{NLoS}(\theta _\textsf{R})\,Pr \left[ {\mathcal {R}}^{(SN,SR )}_\textsf{U,R}<r_\textrm{th}\right] \right) \nonumber \\&\quad +\,{\mathcal {P}}_\textsf{NLoS}(\theta _\textsf{T})\left( {\mathcal {P}}_\textsf{LoS}(\theta _\textsf{R})\,Pr \left[ {\mathcal {R}}^{ {(SR,SN) }}_\textsf{U,R}<r_\textrm{th}\right] \right. \nonumber \\&\quad \left. +\,{\mathcal {P}}_\textsf{NLoS}(\theta _\textsf{R})\,Pr \left[ {\mathcal {R}}^{ {(SR,SR) }}_\textsf{U,R}<r_\textrm{th}\right] \right) , \end{aligned}$$
(10)

where \({\mathcal {R}}^{ {(SN,SN) }}_\textsf{U,R}\) and \({\mathcal {R}}^{ {(SR,SR) }}_\textsf{U,R}\) denote the instantaneous rates at the mobile user in the second phase when both uplink and downlink follow shadowed Nakagami-m and shadowed Rayleigh. Moreover, \({\mathcal {R}}^{(SR,SN )}_\textsf{U,R}\) and \({\mathcal {R}}^{ {(SN,SR) }}_\textsf{U,R}\) correspond to the case when uplink and downlink follow shadowed Rayleigh-shadowed Nakagami-m and vice-versa.

To obtain the complete OP expression, one can invoke (9) and (10) in (8). The final OP expression is a generalized form whereby on changing the LoS probability, the framework can represent both terrestrial and aerial communication scenarios. For instance, when \({\mathcal {P}}_\textsf{LoS}(\theta )=0\), the system will transform to a terrestrial network with shadowed Rayleigh channel characterization. When \({\mathcal {P}}_\textsf{LoS}(\theta )=1\), the system is valid for the aerial network at a high altitude and the channel between nodes can be modeled as shadowed Nakagami-m. Further, by changing the values of \(\delta _{i}\), the system can handle shadowed and un-shadowed cases.

Now, different probability terms of (9) and (10) are evaluated and the related results are stated in the following Lemmas. First, one can represent \(Pr [{\mathcal {R}}^{ {(SR) }}_\textsf{T,U}<r_\textrm{th}]=Pr [\Lambda ^{ {(SR) }}_\textsf{T,U}<\bar{\gamma }_\textsf{U}]=F_{\Lambda ^{ {(SR) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})\), where \(\bar{\gamma }_\textsf{U}=2^{r_\textrm{th}/\lambda (1-\alpha )}-1\) is the target SNR at the UAV. An accurate expression of the required CDF \(F_{\Lambda ^{ {(SR) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})\) is given in the following Lemma.

Lemma 1

The expression of \(F_{\Lambda ^{ {(SR) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})\) can be shown to be

$$\begin{aligned} F_{\Lambda ^{ {(SR) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})&=Pr [{\mathcal {R}}^{ {(SR) }}_\textsf{T,U}<r_\textrm{th}]\nonumber \\& =\frac{1}{\sqrt{\pi }}\sum _{n=1}^{N}w_n\left( 1-e^{-\frac{\bar{\gamma }_\textsf{U}\sigma ^{2}}{\left( (1-\beta )P_\textsf{T}\right) 10^{\frac{\sqrt{2}\delta _{1} t_n+\mu _{1}}{10}}}}\right) . \end{aligned}$$
(11)

where N represents sample points, \([t_{n}]_{n=1}^N\) give the roots of the Hermite polynomial, and \(w_{n}\) gives the weights of Gauss–Hermite quadrature. Moreover, \(\mu _{1}\) and \(\delta _{1}\), respectively, represent the mean path-loss and standard deviation for shadowing of the first hop in dB.

Proof

The CDF \(F_{\Lambda ^{ {(SR) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})\) can be expressed as

$$\begin{aligned} F_{\Lambda ^{ {(SR) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})&=Pr \left[ \frac{(1-\beta )P_\textsf{T} \mid \!\! h^{ {(SR) }}_\textsf{T,U}\!\!\mid ^2}{\sigma ^2 }<\bar{\gamma }_\textsf{U}\right] \nonumber \\&=Pr \left[ \mid \!\! h^{ {(SR) }}_\textsf{T,U}\!\!\mid ^2<\frac{\bar{\gamma }_\textsf{U}\sigma ^2 }{(1-\beta )P_\textsf{T}}\right] \nonumber \\&=F_{\mid h^{ {(SR) }}_\textsf{T,U}\!\mid ^2}\left( \frac{\bar{\gamma }_\textsf{U}\sigma ^2 }{(1-\beta )P_\textsf{T}}\right) . \end{aligned}$$
(12)

Further, (12) can be expressed in an integral form as

$$\begin{aligned} F_{\Lambda ^{ {(SR) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})&=\int ^{\frac{\bar{\gamma }_\textsf{U}\sigma ^2 }{(1-\beta )P_\textsf{T}}}_{0}f_{\mid h^{ {(SR) }}_\textsf{T,U}\mid ^2}(x)dx. \end{aligned}$$
(13)

By incorporating the PDF expression from (A4) derived in Appendix A and performing integration, one can obtain the desired expression as in Lemma 1. \(\square\)

The other probability term of (9) corresponding to the shadowed Nakagami-m channel can be written as \(Pr [{\mathcal {R}}^{ {(SN) }}_\textsf{T,U}<r_\textrm{th}]=Pr [\Lambda ^{ {(SN) }}_\textsf{T,U}<\bar{\gamma }_\textsf{U}]=F_{\Lambda ^{ {(SN) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})\). Following the similar approach used to obtain (11), the resulting CDF \(F_{\Lambda ^{ {(SN) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})\) is stated in the following Lemma.

Lemma 2

The expression of \(F_{\Lambda ^{ {(SN) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})\) is

$$\begin{aligned} F_{\Lambda ^{ {(SN) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})&= \frac{1}{\sqrt{\pi }}\sum _{n=1}^{N}\frac{w_n}{\Gamma [m_{1}]}\Upsilon \left( m_{1},\frac{m_{1}\frac{\bar{\gamma }_\textsf{U}\sigma ^2 }{(1-\beta )P_\textsf{T}}}{10^{\frac{\sqrt{2}\delta _{1}t_n+\mu _{1}}{10}}} \right) . \end{aligned}$$
(14)

Proof

The CDF \(F_{\Lambda ^{ {(SN) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})\) can be formulated as

$$\begin{aligned} F_{\Lambda ^{ {(SN) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})&=Pr \left[ \frac{(1-\beta )P_\textsf{T} \mid \! h^{ {(SN) }}_\textsf{T,U}\!\mid ^2}{\sigma ^2 }<\bar{\gamma }_\textsf{U}\right] \nonumber \\&=Pr \left[ \mid \! h^{ {(SN) }}_\textsf{T,U}\!\mid ^2<\frac{\bar{\gamma }_\textsf{U}\sigma ^2 }{(1-\beta )P_\textsf{T}}\right] \nonumber \\&=F_{\mid h^{ {(SN) }}_\textsf{T,U}\mid ^2}\left( \frac{\bar{\gamma }_\textsf{U}\sigma ^2 }{(1-\beta )P_\textsf{T}}\right) . \end{aligned}$$
(15)

Now, (15) can be expressed in an integral form as

$$\begin{aligned} F_{\Lambda ^{ {(SN) }}_\textsf{T,U}}(\bar{\gamma }_\textsf{U})&=\int ^{\frac{\bar{\gamma }_\textsf{U}\sigma ^2 }{(1-\beta )P_\textsf{T}}}_{0}f_{\mid h^{ {(SN) }}_\textsf{T,U}\mid ^2}(x)dx. \end{aligned}$$
(16)

On inserting the PDF from (B7), derived in Appendix B, and solving the integral, one can obtain the desired expression as in Lemma 2. \(\square\)

Now, for evaluating (10), one of the involved probability terms can be expressed as \(Pr \left[ {\mathcal {R}}^{ {(SR,SR) }}_\textsf{U,R}<r_\textrm{th}\right] =Pr \left[ \Lambda ^{ {(SR,SR) }}_\textsf{U,R}<\bar{\gamma }_\textsf{R}\right] =F_{\Lambda ^{ {(SR,SR) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})\), where \(\bar{\gamma }_\textsf{R}=2^{r_\textrm{th}/(1-\lambda )(1-\alpha )}-1\) is the target SNR at the mobile user, which is derived as in the next Lemma.

Lemma 3

The expression of \(F_{\Lambda ^{ {(SR,SR) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})\) is

$$\begin{aligned} F_{\Lambda ^{ {(SR,SR) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})&=\frac{1}{\pi }\sum _{n=1}^{N}\sum _{p=1}^{P}w_p w_n\left( 1-\frac{2}{10^{\frac{\sqrt{2}\delta _{1} t_n+\mu _{1}+\sqrt{2}\delta _{2} t_p+\mu _{2}}{20}}}\right. \nonumber \\&\quad \times \left( \frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_{T}}\right) ^{\frac{1}{2}}\nonumber \\&\quad \left. \times \,{\mathcal {K}}_1\left( 2\sqrt{\frac{\left( \frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T}}\right) }{10^{\frac{\sqrt{2}\delta _{1} t_n+\mu _{1}+\sqrt{2}\delta _{2} t_p+\mu _{2}}{10}}}}\right) \right) , \end{aligned}$$
(17)

where \(\mu _{2}\) and \(\delta _{2}\) represent the mean path-loss and standard deviation for shadowing of the second hop in dB.

Proof

The CDF can be first written as

$$\begin{aligned} F_{\Lambda ^{ {(SR,SR) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})&=Pr \left[ \frac{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T} \mid \! h^{ {(SR) }}_\textsf{T,U}\!\mid ^2 \mid \! h^{ {(SR) }}_\textsf{U,R}\!\mid ^2}{(1-\alpha )(1-\lambda )\sigma ^2}<\bar{\gamma }_\textsf{R}\right] \nonumber \\&=Pr \left[ \mid \! h^{ {(SR) }}_\textsf{T,U}\!\mid ^2 \mid \! h^{ {(SR) }}_\textsf{U,R}\!\mid ^2<\frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T}}\right] \nonumber \\&=F_{\mid h^{ {(SR) }}_\textsf{T,U}\mid ^2\mid h^{ {(SR) }}_\textsf{U,R}\mid ^2}\left( \frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T}}\right) , \end{aligned}$$
(18)

where \(\mid \!\! h^{(SR) }_\textsf{T,U}\!\!\mid ^2\) and \(\mid \!\!h^{{(SR) }}_\textsf{U,R}\!\!\mid ^2\) are distributed as shadowed Rayleigh. Further, (18) can be represented in an integral form as

$$\begin{aligned} F_{\Lambda ^{ {(SR,SR) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})&=\int ^{\frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T}}}_{0}f_{\mid h^{ {(SR) }}_\textsf{T,U}\mid ^2\mid h^{ {(SR) }}_\textsf{U,R}\mid ^2}(z)\,dz. \end{aligned}$$
(19)

On invoking the PDF from (C11), derived in Appendix C, and solving the integral, one can obtain the final expression as stated in Lemma 3. \(\square\)

Further, another term of (10) can be expressed as \(Pr \left[ {\mathcal {R}}^{ {(SN,SR) }}_\textsf{U,R}<r_\textrm{th}\right] =Pr \left[ \Lambda ^{ {(SN,SR) }}_\textsf{U,R}<\bar{\gamma }_\textsf{R}\right] =F_{\Lambda ^{ {(SN,SR) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})\) which can be derived as in the following Lemma.

Lemma 4

The expression of \(F_{\Lambda ^{ {(SN,SR) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})\) is

$$\begin{aligned} F_{\Lambda ^{ {(SN,SR) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})&=\frac{1}{\pi }\sum _{n=1}^{N}\sum _{p=1}^{P}w_{n}w_{p} \left( 1-\left( \frac{m_{1}}{10^{\frac{\sqrt{2}\delta _{1} t_n+\mu _{1}}{10}}} \right) ^{m_{1}}\right. \nonumber \\&\quad \times \frac{2}{\Gamma [m_{1}]} \left( \frac{\left( \frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T}}\right) 10^{\frac{\sqrt{2}\delta _{1} t_n+\mu _{1}}{10}}}{m_{1}10^{\frac{\sqrt{2}\delta _{2} t_p+\mu _{2}}{10}}} \right) ^{\frac{m_{1}}{2}}\nonumber \\&\left. \quad \times \, {\mathcal {K}}_{m_{1}}\left( 2\sqrt{\frac{\left( \frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T}}\right) m_{1}}{10^{\frac{\sqrt{2}(\delta _{1} t_n+\delta _{2} t_p)+\mu _{1}+\mu _{2}}{10}}}} \right) \right) . \end{aligned}$$
(20)

Proof

Following the similar approach as in (18), \(F_{\Lambda ^{ {(SN,SR) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})\) is given as

$$\begin{aligned} F_{\Lambda ^{ {(SN,SR) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})&=F_{\mid h^{ {(SN) }}_\textsf{T,U}\mid ^2\mid h^{ {(SR) }}_\textsf{U,R}\mid ^2}\left( \frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T}}\right) \nonumber \\&=\int ^{\frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T}}}_{0}f_{\mid h^{ {(SN) }}_\textsf{T,U}\mid ^2\mid h^{ {(SR) }}_\textsf{U,R}\mid ^2}(z)\,dz. \end{aligned}$$
(21)

Inserting the PDF expression from (D14) in (21) and solving the integral, one can obtain the final expression as stated in Lemma 4. \(\square\)

Lastly, \(Pr \left[ {\mathcal {R}}^{ {(SN,SN) }}_\textsf{U,R}<r_\textrm{th}\right] =Pr \left[ \Lambda ^{ {(SN,SN) }}_\textsf{U,R}<\bar{\gamma }_\textsf{R}\right] =F_{\Lambda ^{ {(SN,SN) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})\) which is obtained as in the following Lemma.

Lemma 5

The expression of \(F_{\Lambda ^{ {(SN,SN) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})\) is

$$\begin{aligned} F_{\Lambda ^{ {(SN,SN) }}_\textsf{U,R}}(\bar{\gamma }_\textsf{R})&=\frac{1}{\pi }\frac{1}{\Gamma [m_{1}]\Gamma [m_{2}]}\sum _{n=1}^{N}\sum _{p=1}^{P}w_{n}w_{p}\nonumber \\&\quad \times \left( \Gamma [m_1]\Gamma [m_2] -\sum _{s=0}^{m_{2}-1}\Gamma [m_2]\frac{2}{\Gamma (s+1)}\right. \nonumber \\&\quad \times \left( \frac{m_{2} \left( \frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T}}\right) 10^{\frac{\sqrt{2}\delta _{1} t_{n}+\mu _{1}}{10}}}{m_{1} 10^{\frac{\sqrt{2}\delta _{2} t_{p}+\mu _{2}}{10}}} \right) ^{\frac{m_{1}-s}{2}}\nonumber \\&\quad \times \left( \frac{m_{1}}{10^{\frac{\sqrt{2}\delta _{1}t_{n}+\mu _{1}}{10}}} \right) ^{m_{1}} \left( \frac{m_{2}\left( \frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T}}\right) }{10^{\frac{\sqrt{2}\delta _{2}t_{p}+\mu _{2}}{10}}} \right) ^{s}\nonumber \\&\quad \left. \times \, {\mathcal {K}}_{m_{1}-s}\left( 2\sqrt{\frac{\left( \frac{\bar{\gamma }_\textsf{R}(1-\alpha )(1-\lambda )\sigma ^2}{\eta (\alpha +\beta \lambda (1-\alpha )) P_\textsf{T}}\right) m_{1}m_{2}}{10^{\frac{\sqrt{2}\delta _{2} t_{p}+\mu _{2}+\sqrt{2}\delta _{1} t_n+\mu _{1}}{10}}}} \right) \right) . \end{aligned}$$
(22)

Proof

Performing the change of variables in (E19), derived in Appendix E, one can obtain the final expression as stated in Lemma 5. \(\square\)

3.2 System Throughput

For a delay-limited transmission, the system throughput can be calculated as the average target rate that can be attained successfully when the system operates over the fading channels. Here, the data rate is assumed to be equal to the target transmission data rate \(r_\textrm{th}\), in bps/Hz. Therefore, the throughput can be formulated as

$$\begin{aligned} \!\!{\mathcal {T}}_\textsf{S}\!=\!\min \left\{ \lambda (1\!-\!\alpha ) (1\!-\!{\mathcal {P}}_\textsf{T,U})r_\textrm{th},(1\!-\!\alpha )(1\!-\!\lambda )(1\!-\!{\mathcal {P}}_\textsf{U,R})r_\textrm{th}\right\} , \end{aligned}$$
(23)

where \({\mathcal {P}}_\textsf{T,U}\) and \({\mathcal {P}}_\textsf{U,R}\) are derived in (9) and (10), respectively.

3.3 Energy Efficiency

It is always beneficial to maintain a higher system throughput while minimizing the energy consumption, contributing to environment-friendly transmission. Thus, energy efficiency has become an essential parameter in designing and investigating the system performance for communication systems. For the considered system, the energy efficiency is defined as

$$\begin{aligned} \!\!\eta _\textsf{EE}\!=\!\frac{\min \left\{ \lambda (1\!-\!\alpha ) (1\!-\!{\mathcal {P}}_\textsf{T,U})r_\textrm{th}, (1\!-\!\alpha )(1\!-\!\lambda )(1\!-\!{\mathcal {P}}_\textsf{U,R})r_\textrm{th}\right\} }{(\alpha +(1-\alpha )\lambda ) P_\textsf{T}}. \end{aligned}$$
(24)

4 Numerical and Simulation Results

In this section, numerical and simulation results are provided to draw insightful observations with respect to the system, channel, and environmental parameters on the OP, system throughput, and energy efficiency. All numerical and simulation results are obtained by setting the noise variance \(\sigma ^{2}=-104\) dBm, and the carrier frequency as 700 MHz. The path-loss model used in this section is similar to that of [21, 23]. Throughout this section, the parameters \(N=15\) and \(P=15\) are set for the Gauss–Hermite quadrature approximations. The values of fading severity parameters are considered as \(m_{1}=m_{2}=4\), unless specified otherwise. The standard deviation for shadowing is expressed as \(\delta _{i}=c_{i}e^{(-d_{i}\theta _{l})}\) where \(i\in \{1,2\}\) and \(l\in \{\textsf {T,R}\}\). Herein, the standard deviation for shadowing and probability of LoS are calculated using (2) and Table 2.

Table 2 Environment parameters for different scenarios [21, 23]
Full size table
Fig. 3
figure 3

OP versus \(P_\textsf{T}\) curves for different values of \(r_\textrm{th}\)

Full size image

The curves in Fig. 3 are obtained by setting the parameters as \(\alpha =0.1\), \(\beta =0.5\), \(\lambda =0.5\), \(\eta =0.6\), \(H_\textsf{U}=20\) m and \(R_{1}=R_{2}=20\) m. This figure plots the OP versus transmit power curves for different values of \(r_{th }\). In Fig. 3, one can observe that as the transmit power increases, the system experiences better outage performance. This performance behavior is reasonable as the transmit power increases, the instantaneous SNR for both links improves. As a result, the system enjoys better OP performance. It can also be seen that for a higher value of \(r_{th }\), the OP increases. This is because, with the higher value of \(r_\textrm{th}\), the system requires higher transmit power to achieve the target SNR so that the instantaneous rate becomes higher than \(r_{th }\) for having a successful transmission. All the analytical curves in this figure are in perfect agreement with the simulation, thus confirming the accuracy of the derived analytical results.

Fig. 4
figure 4

OP versus \(P_\textsf{T}\) curves for different values of \(R_{1}\) and \(R_{2}\)

Full size image

The curves in Fig. 4 are obtained by setting the parameters as \(\alpha =0.1\), \(\beta =0.5\), \(\lambda =0.5\), \(\eta =0.6\), \(H_\textsf{U}=20\) m, and \(r_{th }=1\) bps/Hz. In Fig. 4, OP versus transmit power curves are plotted for different values of distance between the BS and the remote mobile user. This figure shows that the OP decreases with an increase in the transmit power for different distances between the nodes. This phenomenon can be explained in the same way as done for Fig. 3. Here, the symmetric positioning of the relay is considered, i.e., \(R_{1}=R_{2}\) and as the value of \(R_{1}\) or \(R_{2}\) increases, the outage performance degrades. This is because as the distance increases, the LoS probability decreases under a fixed height of the UAV. Therefore, the overall path-loss increases as a result of a larger distance. Moreover, as the LoS probability decreases, the channel fading characterization weights shift from shadowed Nakagami-m to shadowed Rayleigh. All these factors contribute to the increase of the OP.

Fig. 5
figure 5

OP versus \(P_\textsf{T}\) curves for different UAV altitudes

Full size image

Figure 5 shows the OP versus transmit power curves for different UAV heights in a suburban environment with the parameters set as \(\alpha =0.1\), \(\lambda =0.5\), \(\beta =0.5\), \(\eta =0.6\), \(R_{1}=R_{2}=20\) m, and \(r_\textrm{th}=1\) bps/Hz. It can be noted from this figure that with the increase in the transmit power, the OP decreases for a particular operational height of the UAV. One can also observe that as the operational height increases from 5 to 10 m, the outage performance becomes better, and when increasing the height further from 10 to 25 m, the OP performance degrades. The reason behind this behavior can be explained as follows. With \(H_\textsf{U}=5\) m, the system possesses a low LoS probability that makes the overall path-loss and shadowing high. But, as the height increases to \(H_\textsf{U}=10\) m, the system LoS probability improves, which reduces the overall path-loss and shadowing. Thus, the OP performance improves. Nevertheless, when the height is further increased to \(H_\textsf{U}=25\) m, the LoS probability only improves marginally as it is already high for the case when \(H_\textsf{U}=10\) m. But with the further increase in UAV height, the resulting path-loss becomes dominating, and therefore, the system outage performance degrades.

Fig. 6
figure 6

OP versus \(P_\textsf{T}\) curves for different EH receiver architectures

Full size image

Various works have highlighted the effects of both PS and TS based RF energy harvesting receivers on the system performance. In order to provide a comparative performance evaluation, Fig. 6 demonstrates the OP versus transmit power curves for different SWIPT receiver architectures where the parameters are set as \(\eta =0.6\), \(H_\textsf{U}=20\) m, \(R_{1}=R_{2}=20\) m, and \(r_\textrm{th}=1\) bps/Hz. For converting the considered model into PS-based SWIPT, the TS parameter \(\alpha =0\) and \(\beta =0.5\), \(\lambda =0.5\). Similarly, for converting the derived expressions for TS-based SWIPT, the PS parameter \(\beta =0\) and \(\alpha =\lambda =0.5\). For the hybrid TS-PS model, the parameters are set as \(\alpha =0.1\), \(\beta =0.5\) and \(\lambda =0.5\). For the considered set of parameters, the hybrid TS-PS model outperforms other models in terms of OP performance. This is because there is an increase in total harvested power in the hybrid case at the UAV. As a result, the overall instantaneous SNR at the mobile user increases in the third phase, which improves the OP performance.

Fig. 7
figure 7

OP versus \(P_\textsf{T}\) curves for different environmental conditions

Full size image

Figure 7 demonstrates the OP versus transmit power curves for various urban environmental deployment scenarios where the parameters are set as \(\alpha =0.1\), \(\beta =0.5\), \(\lambda =0.5\), \(\eta =0.6\), \(H_\textsf{U}=10\) m, \(R_{1}=R_{2}=20\) m, and \(r_\textrm{th}=1\) bps/Hz. From Fig. 7, one can see that the OP performance gets better with the increase in transmit power for any environmental conditions. It can also be observed in Fig. 7 that the OP becomes higher as the communication environment changes from suburban to a dense urban. This system performance behavior can be understood by considering the LoS probability in different environmental conditions for the same value of the angle between UAV and ground nodes. The LoS probability decreases when changing from a suburban to a dense urban environment, hence increasing the path-loss and shadowing between the nodes. Moreover, a decrease in \({\mathcal {P}}_\textsf{LoS}(\theta )\) makes fading more severe, and thus the OP increases.

Fig. 8
figure 8

OP versus \(P_\textsf{T}\) curves for different environmental conditions with shadowed/un-shadowed channels

Full size image

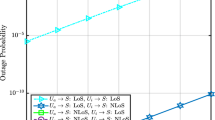
Figure 8 depicts the OP versus transmit power curves for the shadowed and un-shadowed channels in different environmental conditions. For numerical investigations in Fig. 8, the parameters are given as \(\alpha =0\), \(\lambda =0.5\), \(\beta =0.5\), \(\eta =0.6\), \(H_\textsf{U}=10\) m, \(R_{1}=R_{2}=20\) m and \(r_\textrm{th}=1\) bps/Hz. From Fig. 8, it can be seen that as the transmit power increases, the OP performance improves, and the system has better OP performance in the un-shadowed scenario. In the case of a suburban environment, the curve for un-shadowed scenario is almost similar to that of the shadowed case since with given distance and height set up, the system already enjoys the high LoS probability, and shadowing standard deviation is equal to 0.002 dBm from Table 2, which should not impact the system performance significantly. For other environments, the improvement of OP in the un-shadowed scenario is due to the fact that the system does not have a high LoS probability. Thus the impact of shadowing is visible in the plots because of the high shadowing standard deviation.

Fig. 9
figure 9

OP versus \(P_\textsf{T}\) curves for different fading scenarios and environmental conditions

Full size image

Figure 9 shows the OP versus transmit power curves for the different values of fading severity parameters in suburban and dense urban scenarios. Herein, the parameters are set as \(\alpha =0.1\), \(\lambda =0.5\), \(\beta =0.5\), \(\eta =0.6\), \(H_\textsf{U}=10\), \(R_{1}=R_{2}=10\) m, and \(r_\textrm{th}=1\) bps/Hz. From this figure, it can be observed that by increasing the values of \(m_{1}=m_{2}\) from 2 to 4, the system becomes more reliable for information transmission. This is because the system with \(m_{1}=m_{2}=4\) has better instantaneous SNR at the same transmit power than the system with \(m_{1}=m_{2}=2\), hence enjoying a better OP performance.

Fig. 10
figure 10

OP versus \(\lambda\) curves for different values of \(\alpha\)

Full size image

Figure 10 plots the OP versus \(\lambda\) curves for different values of \(\alpha\). For obtaining the plots in Fig. 10, the other parameters are set as \(\eta =0.6\), \(P_\textsf{T}=30\) dBm, \(H_\textsf{U}=20\) m, \(R_{1}=R_{2}=20\) m, and \(r_\textrm{th}=1\) bps/Hz. From this figure, it can be noticed that with the increase in \(\lambda\), first, the OP decreases up to a certain value of \(\lambda\). After that, the OP starts increasing with the increase in \(\lambda\). This characteristic can be explained as follows. When \(\lambda\) initially increases, the amount of harvested energy also increases at the UAV, which results in an improvement in the instantaneous SNR for the downlink transmission. However, when further increasing \(\lambda\), the \(1-\lambda\) factor decreases, and thus the instantaneous rate decreases at the mobile user, and consequently, the outage performance degrades. From this figure, one can also observe that as \(\alpha\) increases, the system initially enjoys a better OP performance, and if it continues increasing, the OP performance starts degrading. This happens because, initially, the system harvests more energy due to the higher splitting factor. Thus, it has higher SNR at the destination node, compensating the effect of lesser rates in the next phases. When \(\alpha\) is set beyond a certain value, the overall time duration for the next phase decreases, which results in decreasing the overall rate of transmission at UAV and reception at the mobile user. From the figure, it can be seen that when \(\alpha\) is changed from 0.05 to 0.5, the OP performance improves. However, when \(\alpha\) varies from 0.5 to 0.6, the OP performance degrades.

Fig. 11
figure 11

System throughput versus transmit power curves for different target rates

Full size image

Figure 11 shows the relationship between the system throughput and transmit power for different values of \(r_\textrm{th}\). Here, the parameters are set as \(\eta =0.6\), \(\alpha =0.1\), \(\lambda =0.5\), \(\beta =0.5\), \(H_\textsf{U}=20\) m, \(R_{1}=20\) m, \(R_{2}=20\) m. From this figure, one can infer that as the transmit power increases for any specific \(r_\textrm{th}\) value, the system throughput first starts increasing, and then after a certain power level, it gets saturated at a maximum attainable throughput with that target rate. This is because as the transmit power increases, the instantaneous SNR increases, which decreases the OP. One can also see that for lower transmit power values, the system attains better throughput with lower values of \(r_\textrm{th}\). On the contrary, for higher values of transmit power, the higher \(r_\textrm{th}\) values provide better throughput. Initially, at a lower power level, the instantaneous SNR is the same for all the cases. Still, as the threshold rate increases, the OP increases significantly, and thus the overall throughput decreases. However, when the power level is higher than a particular value, the increase in OP becomes negligible as compared to more dominating factor, i.e., \(r_\textrm{th}\), that can also be verified from (23).

Fig. 12
figure 12

System throughput versus \(r_\textrm{th}\) and \(\lambda\)

Full size image

For obtaining Fig. 12, the parameter values are set as \(\eta =0.6\), \(\beta =0.5\), \(P_\textsf{T}=30\) dBm, \(\alpha =0.1\), \(H_\textsf{U}=20\) m, \(R_{1}=20\) m, \(R_{2}=20\) m. This figure shows a 3D plot to highlight the relationship between the system throughput, \(r_\textrm{th}\), and \(\lambda\). From this figure, one can observe that as the value of \(r_\textrm{th}\) increases, the system throughput increases for a given set of parameters. Further, one can also see that as \(\lambda\) increases, initially, the throughput increases and at \(\lambda =0.4\), the system throughput attains the peak value, and after that it starts decreasing. Thus it can be inferred from this figure that with this set up, the threshold value will attain the peak value when \(\lambda =0.4\).

Fig. 13
figure 13

Energy efficiency versus transmit power curves for different values of target rates

Full size image

For the results in Fig. 13, the parameters are set as \(\eta =0.6\), \(\alpha =0.1\), \(\lambda =0.5\) \(\beta =0.5\), \(H_\textsf{U}=20\) m, \(R_{1}=20\) m, \(R_{2}=20\) m. This figure shows the relationship between the energy efficiency and transmit power for different values of \(r_\textrm{th}\). One can infer from Fig. 13 that when the transmit power increases, initially, the energy efficiency also increases due to the increase in the throughput. But as the transmit power increases further when the throughput is in the saturation region, the energy efficiency starts decreasing. Note that as \(r_\textrm{th}\) increases, the peak of energy efficiency shifts toward a higher transmit power region and likewise the lower value of \(r_\textrm{th}\) exhibits a higher peak energy efficiency in lower power region.

Fig. 14
figure 14

Energy efficiency versus \(r_\textrm{th}\) and \(\lambda\)

Full size image

Finally, the results in Fig. 14 are obtained with the parameters set as \(\eta =0.6\), \(\alpha =0.1\), \(\beta =0.5\), \(P_\textsf{T}=30\) dBm, \(H_\textsf{U}=20\) m, \(R_{1}=20\) m, \(R_{2}=20\) m. This figure highlights the relationship between the energy efficiency, \(r_\textrm{th}\), and \(\lambda\). From this figure, one can see that as the value of \(r_\textrm{th}\) increases, initially, the energy efficiency increases and then at some value of \(r_\textrm{th}\), it reaches a peak value. Then it starts decreasing with increasing \(r_\textrm{th}\). It is also observed that as \(\lambda\) increases, the energy efficiency first increases and starts decreasing after a certain value of \(\lambda\).

5 Conclusion

This paper has examined the performance of a UAV-assisted hybrid SWIPT-enabled DF relayed communication system where a UAV provides relay assistance to a remote mobile user under mixed LoS/NLoS channels. For the considered system, closed-form expressions for the OP, system throughput, and energy efficiency have been derived with composite channel modeling, including the LoS probability-based path-loss and log-normal shadowing. From the numerical results, it has been observed that for a particular distance between ground nodes, there exists an optimal height of the UAV for which the system exhibits the best OP performance. The optimal height of the UAV depends on various parameters like time switching factor, power allocation factor, target rate, and transmit power. In addition, the effects of various system and environmental parameters on the OP, throughput, and energy efficiency have been thoroughly studied over mixed LoS/NLoS channels. Numerical and simulation results have verified the accuracy of all the derived analytical expressions. This work can be extended with the consideration of a full-duplex mode of transmission. As a sequence, the system decoder at the UAV will need more complex functionality to mitigate the effect of self-interference. Nevertheless, by incorporating a high-quality self-interference cancellation along with optimal setting of system parameters, the overall OP of the system may decrease, which further improves energy efficiency and throughput performance.