1 Introduction

Unmanned aerial vehicles (UAVs) [1, 2] are flying devices without a human pilot onboard and is a type of the unmanned vehicle developed for rescues and military applications [3]. In areas where communication infrastructure is destroyed or the radio frequency (RF) signal transmission can not reach the desired destination, thus existing methods are limited by space and environment. To overcome these challenges, the UAVs are employed as BSs/APs/relays to aid the wireless communications of ground nodes due to their mobility, 3D coverage, and agility [4].

Currently, NOMA is recognized as a potential candidate and considered by many researchers for the fifth generation (5G) network and beyond in the last decade [5,6,7,8]. Compared to conventional OMA, NOMA shows advantages such as low latency, high spectral efficiency, high energy efficiency, and user fairness [9,10,11]. The critical concept of NOMA is to serve multiple users on the same frequency resource. In NOMA, with the assistance of superposition coding (SC) and successive interference cancellation (SIC) mechanism [12], the signals of users are combined at the transmitter and decoded at the receiver, sequentially.

NOMA-based UAV communication was studied by several researchers [13, 14]. In [14], a UAV-enabled downlink NOMA system was investigated. This system consisted of two ground users, and one flying base station acted UAV. The outage probability for both ground users was derived. The outage performance for NOMA was better than that for OMA. In [15], a wireless system with distributed ground terminals and a flying base station acted UAV was studied. The throughput gains for the case of a mobile UAV base station were superior to the case of a static UAV base station in delay-tolerant applications. In [16], a UAV aided NOMA network consisted of BS, UAV, and ground users in which the BS and UAV cooperated with each other to communicate with these ground users. The sum-rate was optimized between the NOMA precoding and trajectory.

Although the UAVs have demonstrated their benefits in rescue, civil and military applications, they are still limited by a power supply. Solving energy harvesting issues in the UAVs paves the way for the development of UAV based 5G networks. In [17], an account of the applicability of NOMA for UAV-aided communication systems was studied. The relationship between altitude and energy efficiency of a UAV was considered. Two cases inspired the solution to the optimization problem, namely altitude fixed NOMA and altitude optimized NOMA, which were exploited to boost the spectral efficiency and energy efficiency. In [18], the authors proposed a UAV enabled wireless power transfer architecture to enhance the energy transfer efficiency. In [19], the throughput maximization problem of UAV-based cooperative communication systems for both decode-and-forward (DF) and amplify-and-forward (AF) protocols were investigated. In these systems, the UAV acted as a mobile relay. The transmission capacity of the UAV depended on the energy harvesting from the source.

In this paper, we proposed a system model along with two simultaneous energy harvesting and information processing protocols based on PSR and TSR for UAV-assisted cooperative relaying SWIPT NOMA. The best UAV selection is solved by repeat algorithms. Closed-form expressions of the performance metric are derived.

The main contribution of our work in this paper is summarized as follows:

  • We propose a system model along with two energy harvesting protocols based on PSR and TSR, namely BS-based PSR and BS-based TSR, for a cooperative relaying SWIPT NOMA system. This model consists of one BS and k types of UAVs and two users’ devices. In addition, we also compare the performance in terms of outage probability and throughput between two these protocols.

  • We propose an algorithm to achieve the best UAV for information processing.

  • Closed-form expressions of outage probability and throughput are derived for our system model in cases of perfect and imperfect SIC.

  • The simulation results show that the outage performance, as well as the throughput for BS-based PSR are enhanced over that for BS-based TSR.

2 System Model

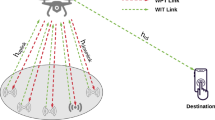
The system model under investigation consists of k types of UAVs, where \(k=1, 2, ..., K\), and two users’ devices, i.e., \(D_{1}\) and \(D_{2}\), as shown in Fig. 1. One BS acts as a source unit in the system. Let \(d_{k}\) denote the distance between UAV\(_k\) and BS. It is assumed that all UAV\(_k\) are connected to BS via wireless connections with perfect synchronous signals.

In a wireless environment, downlink channel from the BS to UAV\(_k\) is assumed to be the flat fading channel \(g_{k}\) and \({n_{k}}\) is the additive white Gaussian noise (AWGN) at UAV\(_k\) with zero mean and variance of \(\sigma _{k}^2\).

Fig. 1
figure 1

A general system model

Full size image

Their expectations are \(E\left[ {{{\left| {{g_k}} \right| }^2}} \right] \, = \,d_k^{{\nu _k}}\) and \(E\left[ {{{\left| {{n_{k}}} \right| }^2}} \right] \, = \,\sigma _k^2\), where \(v_{k}\) is the path-loss of the channel model.

Assuming that UAVs operate within the coverage of the BS. The transmitted signal from the BS to UAV\(_k\) is \(x_{k}\), and its expectation is \(E\left[ {{{\left| {{x_k}} \right| }^2}} \right] = 1.\)

The BS transmits the signal to users using multiple UAVs. The UAV\(_k\) is equipped with a single antenna and operates in half-duplex (HD) communication mode.

In our work, we consider the case of the best UAV selection among UAVs. Moreover, all UAVs are provided via wireless energy from the BS along with conventional batteries. The channel from the BS to UAV\(_{k}\) and from UAV\(_{k}\) to users is the flat Rayleigh block fading.

As shown in Fig. 1, \({g_{k}} \sim CN\left( {0,{\Omega _{k}}} \right)\) is the channel coefficient of the BS and UAV\(_{k}\). \({\mathrm{{n}}_{k}},{\mathrm{{n}}_{Di}} \sim CN\left( {0,1} \right)\) are the AWGNs at UAV\(_{k}\) and \(D_{i}\), respectively. \({h_i} \sim CN\left( {0,{\Omega _{Di}}} \right)\) is the channel coefficient of the UAV\(_{k}\) and \(D_{i}\), with \(i \in \left\{ {1,2} \right\}\). Because the shadowing impact and path-loss of \({h_2}\) are less than that of \({h_1}\), the relation between \({\Omega _{D1}}\) and \({\Omega _{D2}}\) satifies \({\Omega _{D1}} < {\Omega _{D2}}\).

2.1 Energy Harvesting at \(UAV_{k}\)

At \(UAV_{k}\), we consider two energy harvesting mechanisms including BS-based PSR and BS-based TSR at \(D_{1}\)

2.1.1 BS-Based PSR Protocol of Energy Harvesting at UAV\(_{k}\)

Fig. 2
figure 2

BS-based PSR protocol of Energy harvesting system

Full size image

Figure 2 describes the communication block diagram using BS-based PSR protocol for harvesting energy at UAV\(_{k}\) in the time block of T. It is assumed that the BS transmits the information to UAV\(_{k}\) in the half-block of T while the information is transmitted from UAV\(_{k}\) to users in the remaining time of T.

The decoded signal at the BS is given by

$$\begin{aligned} {X_{BS}} = (\sqrt{{{\Theta _1}}{P_{BS}}} {x_1} + \sqrt{{\Theta _2}{P_{BS}}} {x_2}) \end{aligned}$$
(1)

Applying the signal superposition coding at the BS, the observed signal at UAV\(_{k}\) is given by

$$\begin{aligned} {y_{UAV}} = \sqrt{{P_{\mathrm{{BS}}}}} {g_k}\left( {\sqrt{{\Theta _1}} {x_1} + \sqrt{{\Theta _2}} {x_2}} \right) + {\mathrm{{n}}_k}\,, \end{aligned}$$
(2)

where \(P_{BS}\) denotes the transmit power at the BS.

By employing BS-based PSR protocol, UAV\(_{k}\) divides the received energy into: i) harvested energy, and ii) energy for processing the information. Let \(0< \beta < 1\) denote the power ratio. The harvested energy at UAV\(_{k}\) can be given by

$$\begin{aligned} E_H^{PSR} = \sum \limits _{k = 1}^K {{\beta _{k,}}{\eta _{k,}}{\rho _{k}}{{\left| {{g_k}} \right| }^2}\left( {T/2} \right) }\,, \end{aligned}$$
(3)

where \({\rho _{k}} \buildrel \Delta \over = {P_{k}}/{\mathrm{{w}}_{k}}\) represents the transmit signal-to-noise ratio (SNR) and \({\beta _{k}}\) is the power splitting ratio at the \(UAV_{k}\) , \(0<{\beta _{k}}<1\).

Then, the power of UAV\(_{k}\) for BS-based PSR protocol can be determined from (3) as follows

$$\begin{aligned} P_{UAV}^{PSR} = \frac{{E_H^{PSR}}}{{\left( {T/2} \right) }} = \frac{{{\beta _{k}}{\eta _{k}}{\rho _{k}}{{\left| {{g_{k}}} \right| }^2}\left( {T/2} \right) }}{{\left( {T/2} \right) }} = {\beta _{k}}{\eta _{k}}{\rho _{k}}{\left| {{g_{k}}} \right| ^2}\,, \end{aligned}$$
(4)

It is assumed that \({\beta _{k}}\) values at UAV\(_{k}\), as well as \({\eta _{k}}\) at UAVs, are equal. Where \({\eta _{k}}\) is the energy conversion efficiency at the UAV\(_{k}\) and \(0<{\eta _{k}}\le 1\). For simplicity, \(0<\eta \le 1\) is named the energy harvesting efficiency. \(\eta \,\) depends on the energy conversion process from RF signal to direct current in the receiver at UAV\(_{k}\).

2.1.2 BS-Based TSR Protocol of Energy Harvesting at UAV\(_{k}\)

Fig. 3
figure 3

BS-based TSR protocol of Energy harvesting system

Full size image

Figure 3 illustrates the BS-based TSR protocol of the energy harvesting (EH) system. In this figure, T is the time block where the information is transmitted from BS to UAV\(_{k}\), and \(0\!<\!\alpha \!<\!1\) is the time block fraction where UAV\(_{k}\) harvests the energy from BS. The first time block of T, i.e., \(\alpha T\), is utilized for EH while the remaining time block, i.e., \(\left( {1 - \alpha } \right) T\), is utilized for forwarding the information. In the \(\left( {1 - \alpha } \right) T\), the half of this, i.e., \(\left( {1 - \alpha } \right) T/2\), is dedicated to transmitting data from BS to UAV\(_{k}\) and the remaining \(\left( {1 - \alpha }\right) T/2\) is for forwarding data from UAV\(_{k}\) to user k. The harvested energy at UAV\(_{k}\) is given by

$$\begin{aligned} \mathrm{{E}}_H^{TSR} = \sum \limits _{k = 1}^K {\alpha {\eta _{k,}}{\rho _{k,}}{{\left| {{\mathrm{{g}}_\mathrm{{k}}}} \right| }^2}T} \end{aligned}$$
(5)

Therefore, the power of UAV\(_{k}\) for BS-based TSR protocol can be determined from (5) as follows

$$\begin{aligned} P_{UAV}^{TSR} = \frac{{E_H^{T\mathrm{{SR}}}}}{{\left( {1 - \alpha } \right) \left( {T/2} \right) }} = \frac{{2\alpha {\eta _k}{\rho _k}{{\left| {{g_k}} \right| }^2}}}{{1 - \alpha }} \end{aligned}$$
(6)

It is noted that both BS-based PSR and BS-based TSR protocols are considered in this work, where the UAV\(_{k}\) selection is based on instantaneously technical specifications of the channel relating to the first hopping step. The BS continuously observes the quality of the connection between its own and UAV\(_{k}\) under the local feedback signals. From these signals, the best link between the BS and UAV\(_{k}\) is selected for data transmission. By grouping UAV\(_{k}\) multi-relays, the UAV with the best conditions is selected. This strategy is expressed by

$$\begin{aligned} k^* = \arg \underbrace{\max }_{k = 1,2, \ldots ,K}{\left| {{g_{k}}} \right| ^2} \end{aligned}$$
(7)

We assume that the harvested energy is consumed by UAV\(_{k}\) to forward the signal to \(D_{1}\) and \(D_{2}\). The power for the transmitting-receiving circuit of UAV\(_{k}\) is negligible over the power for transmitting signal.

We can briefly describe the operation of the system as follows. Each communication block occupies two-time slots. All blocks are normalized to the unit. In the first time slot, the BS transmits the superimposed signal, i.e., \(\sqrt{{{\Theta _1}}} {x_1} + \sqrt{{{\Theta _2}}} {x_2}\) , where \(x_{i}\) and \(\Theta _{i}\) denote the signal and power allocation coefficients of \(D_{i}\), respectively. The expression of \(({\Theta _1} + {\Theta _2})\) satisfies 1. Without loss of generality, we assume \({{\Theta _2}}\ge {{\Theta _1}}\).

In downlink power domain NOMA, SIC and superimposed coding are two key mechanisms utilized to decode the received signals at receivers and to code the transmitted signals at transmitters, respectively. Thus, the SIC process is only considered at UAVs to achieve the best data forwarding, as well as \(D_{1}\) and \(D_{2}\), are allocated a higher power in our work. For instance, at UAV\(_{k}\), the best UAV first decodes symbol \(x_{2}\) by treating symbol \(x_{1}\) as noise and then performs the SIC process to achieve signal \(x_{1}\). Therefore, the signal to interference plus noise ratio (SINR) for symbol \(x_{2}\) and signal to noise ratio (SNR) for symbol \(x_{1}\) are respectively given by

$$\begin{aligned}&{\gamma _{2,UA{V_k}}} = \frac{{{\Theta _2}{P_{BS}}{{\left| {{g_k}} \right| }^2}}}{{{\Theta _1}{P_{BS}}{{\left| {{g_k}} \right| }^2} + 1}} \end{aligned}$$
(8)
$$\begin{aligned}&{\gamma _{1,UA{V_k}}} = {\Theta _1}{P_{BS}}{\left| {{g_k}} \right| ^2} \end{aligned}$$
(9)

It is noted from Fig. 1 that UAV\(_{k}\) processes signals \(x_{1}\) and \(x_{2}\) during the first time slot, then the selected UAV sends the signal \(\sqrt{P_{UAV}^X} \left( {\sqrt{{\Theta _1}} {x_1} + \sqrt{{\Theta _2}} {x_2}} \right)\) to two users \(D_{1}\) and \(D_{2}\) during the second time slot, where \(X \in (PSR, TSR)\).

Thus, the received signal at \(D_{1}\) combined by \(x_{1}\), \(x_{2}\) and noise is given by

$$\begin{aligned} {y_{Di}} = \sqrt{P_{UAV}^X} {h_i}\left( {\sqrt{{\Theta _1}} {x_1} + \sqrt{{\Theta _2}} {x_2}} \right) + {\mathrm{{n}}_{Di}}\,, \end{aligned}$$
(10)

where \(h_{i}\) is the channel gain between the selected UAV and \(D_{i}\).

From (10), the SINR at \(D_{2}\) is determined by applying SIC, i.e., \(D_{2}\) decodes \(x_{2}\) while treating \(x_{1}\) as noise, as follows:

$$\begin{aligned} {\gamma _{2,{D_2}}} = \frac{{{\Theta _2}P_{UAV}^X{{\left| {{h_2}} \right| }^2}}}{{{\Theta _1}P_{UAV}^X{{\left| {{h_2}} \right| }^2} + 1}} \end{aligned}$$
(11)

Similarly, since both \(x_{1}\) and \(x_{2}\) are in \(D_{1}\), it is necessary for SIC to decode its own symbol \(x_{1}\). To perform SIC, \(D_{1}\) decodes symbol \(x_{2}\) by treating symbol \(x_{1}\) as a noise according to their priority power level and cancels \(x_{1}\) using SIC to obtain symbol \(x_{1}\). Therefore, the SINR for \(x_{2}\) at \(D_{1}\) is given by

$$\begin{aligned} {\gamma _{2,{D_1}}} = \frac{{{\Theta _2}{P_{UAV}^X}{{\left| {{h_1}} \right| }^2}}}{{{\Theta _1}{P_{UAV}^X}{{\left| {{h_1}} \right| }^2} + 1}} \end{aligned}$$
(12)

The SNR for \(x_{1}\) at \(D_{1}\) decoded by its own \(D_{1}\) is given by

$$\begin{aligned} {\gamma _{1,{D_1}}} = {\Theta _1}{P_{UAV}^X}{\left| {{h_1}} \right| ^2} \end{aligned}$$
(13)

3 Performance Analysis

3.1 Outage Behaviour at UAVs

3.1.1 The Exact Outage Behaviour of \(x_{1}\) at UAV\(_{k}\)

The outage probability \(P_{{x_1}}^{UA{V_k}}\) at UAV is the probability where UAV cannot decode completely since the SINR/SNR of \(x_{2}\) is below the threshold \({\gamma _{th2}}\) and the SINR of \(x_{1}\) is below the threshold \({\gamma _{th1}}\), with \({\gamma _{th1}} = {2^{\frac{{2{R_{1}}}}{{1 - \alpha }}}} - 1\), where \({R_1}\) is the target data rate of \(D_{1}\). From (8) and (9), the expression of \(P_{{x_1}}^{UA{V_k}}\) is given by

$$\begin{aligned} \begin{array}{l} \begin{array}{l} P_{{x_1}}^{UA{V_k}} = \Pr \left\{ {{\gamma _{2,UA{V_k}}}< {\gamma _{th2}},{\gamma _{1,UA{V_k}}} < {\gamma _{th1}}} \right\} \\ \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,= 1 - \sum \limits _{k = 1}^K {{{\left( { - 1} \right) }^{k - 1}}\left( {\begin{array}{*{20}{l}} K\\ k \end{array}} \right) \exp \left( { - \frac{{k\varsigma }}{{{\Omega _2}}}} \right) } \end{array} \end{array} \end{aligned}$$
(14)

Proof see “Appendix 1”.

3.1.2 The Exact Outage Behaviour of \(x_{2}\) at \(UAV_{k}\)

Similar to Sect. 3.1.1, the outage probability \(P_{{x_2}}^{UA{V_k}}\) at UAV is defined as the probability at which the UAV can not successfully decode \(x_{2}\) due to the SINR/SNR values below the threshold \({\gamma _{th2}}\). From (8), we can express the \(P_{{x_2}}^{UA{V_k}}\) by

$$\begin{aligned} \begin{array}{l} \begin{array}{l} P_{{x_2}}^{UA{V_k}} = \Pr \left\{ {{\gamma _{2,UA{V_k}}} < {\gamma _{th2}}} \right\} \\ \\ \quad \,\,\,\,\,\,\,\,\,\,\,= 1 - \Pr \left\{ {\frac{{{\psi _I}{\Theta _2}{P_{BS}}{{\left| {{g_k}} \right| }^2}}}{{{\psi _I}{\Theta _1}{P_{BS}}{{\left| {{g_k}} \right| }^2} + 1}} > {\gamma _{th2}}} \right\} \end{array}, \end{array} \end{aligned}$$
(15)

where \({\psi _I} = 1 - \beta\) and \({\psi _I} = \frac{{1 - \alpha }}{2}\) are the information processing coefficients for BS-based PSR and BS-based TSR protocols, respectively. \({\gamma _{th2}} = {2^{\frac{{2{R_{2}}}}{{1 - \alpha }}}} - 1\) and \({R_{2}}\) is the target data rate of \(D_{2}\). Given \({\left| {{g_{k}}} \right| ^2} = A\), \({\left| {{h_1}} \right| ^2} = B\) and \({\left| {{h_2}} \right| ^2} = C\) are the channel gains of the BS-the best UAV and the best UAV-\(D_{1}\) and \(D_{2}\) links, respectively. It is assumed that all channel gains are modelized independently. Random variables are Rayleigh distribution. Thus, \({\left| {{g_{k}}} \right| ^2}\), \({\left| {{h_1}} \right| ^2}\) and \({\left| {{h_2}} \right| ^2}\) have exponential distributions as follows

$$\begin{aligned}&{f_X}\left( x \right) =\sum \nolimits _{k = 1}^K {{{\left( { - 1} \right) }^{k - 1}}\left( \begin{array}{l} K\\ k \end{array} \right) \frac{k}{{{\Omega _1}}}\exp \left( { - \frac{{kx}}{{{\Omega _1}}}} \right) } \end{aligned}$$
(16)
$$\begin{aligned}&{f_B}\left( b \right) =\frac{1}{{{\Omega _2}}}\exp \left( { - \frac{y}{{{\Omega _2}}}} \right) ,{F_B}\left( b \right) =1 - \exp \left( { - \frac{b}{{{\Omega _2}}}} \right) , \end{aligned}$$
(17)

where f and F are cumulative density function and probability density function, respectively. \({\Omega _1}=E\left\{ {{{\left| {{g_{k}}} \right| }^2}} \right\} ,{\Omega _2}=E\left\{ {{{\left| {{h_1}} \right| }^2}} \right\}\) and \({\Omega _3}=E\left\{ {{{\left| {{h_2}} \right| }^2}} \right\}\) are coefficients of the random variables.

Then, the expression of \(P_{{x_2}}^{UA{V_k}}\) can be rewritten by

$$\begin{aligned} \begin{array}{l} P_{{x_2}}^{UA{V_k}}\!=\!1\!-\!\Pr \left\{ {{\psi _I}{\Theta _2}{P_{BS}}A\!>\!{\psi _I}{\gamma _{th2}}{\Theta _1}{P_{BS}}A\!+\!{\gamma _{th2}}} \right\} \quad \quad \quad \quad \quad \quad \quad \quad {} {} {} {} {} {} {} {} \\ \\ \quad \quad \quad =\!1\!-\!\Pr \left\{ {A\left( {{\psi _I}{\Theta _2}{P_{BS}}\!-\!{\psi _I}{\gamma _{th2}}{\Theta _1}{P_{BS}}} \right) \!>\!{\gamma _{th2}}}\right\} \quad \quad {} {}\\ \\ \quad \quad \quad =\!1\!-\!\Pr \left\{ {A\!>\!\frac{{{\gamma _{th2}}}}{{{\psi _I}{P_{BS}}\left( {{\Theta _2}\!-\!{\gamma _{th2}}{\Theta _2}}\right) }}}\right\} \\ \\ \quad \quad \quad =\!1\!-\!{F_A}\left( {\frac{{{\gamma _{th2}}}}{{{\psi _I}{P_{BS}}\left( {{\Theta _2}\!-\!{\gamma _{th2}}{\Theta _1}} \right) }}} \right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ =\!1\!-\!\sum \limits _{k = 1}^K {{{\left( { - 1} \right) }^{k - 1}}\left( {\begin{array}{*{20}{l}} K\\ k \end{array}}\right) \exp \left( {\!-\!\frac{{k{\gamma _{th2}}}}{{{\Omega _2}{\psi _I}{P_{BS}}\left( {{\Theta _2}\!-\!{\gamma _{th2}}{\Theta _1}}\right) }}}\right) } \end{array} \end{aligned}$$
(18)

3.2 The Exact Outage Behaviour at the User

3.2.1 The Exact Outage Behaviour of \(x_{1}\) at \(D_{1}\)

The SIC process can occur incompletely SIC. Thus, in this section, two cases of perfect and imperfect SIC are considered at both \({k^*}\) and \(D_{1}\)

  1. (a)

    For perfect SIC From Fig. 1, it is seen that the SIC is performed at \(D_{1}\) to remove signal \(x_{2}\) before detecting its own signal. In the case of perfect SIC at \(D_{1}\), the \(P_{{x_1}}^{OP}\) is defined as the best UAV or \(D_{1}\) can not successfully decode signal \(x_{1}\) due to the SNR below the threshold value. Then, \(P_{{x_1}}^{OP}\) is given by

    $$\begin{aligned} P_{{x_1}}^{OP} &= \Pr \left( {\min \left( {{\gamma _{1,UAV_{k}}},{\gamma _{1,D_1}}} \right) \le {\gamma _{th1}}} \right) \\ &= 1 - \Pr \left( {{\Theta _1}P_{BS}{{\left| {{g_k}} \right| }^2}> {\gamma _{th1}},{\Theta _1}P_{UAV}^X{{\left| {{h_1}} \right| }^2} > {\gamma _{th1}}} \right) \end{aligned}$$
    (19)

    First, let us consider the outage probability for BS-based PSR protocol as follows: By substituting \(P_{UAV}^{PSR}\) from (4) into (19), the outage probability of the signal \(x_{1}\) is given by

    $$\begin{aligned} \begin{array}{l} P_{{x_1}}^{OP} = 1 - \Pr \left( {{{\left| {{g_{k}}} \right| }^2}> \frac{{{\gamma _{th1}}}}{{{\Theta _1}{P_{BS}}}},{{\left| {{h_1}} \right| }^2}> \frac{{{\gamma _{th1}}}}{{{\Theta _1}\beta \eta {P_{BS}}{{\left| {{g_{k}}} \right| }^2}}}} \right) \\ \quad \quad \,= 1 - \Pr \left( {A> \frac{{{\gamma _{th1}}}}{{{\Theta _1}{P_{BS}}}},C > \frac{{{\gamma _{th1}}}}{{A{\Theta _1}\beta \eta {P_{BS}}}}} \right) \end{array} \end{aligned}$$
    (20)

    This outage probability can be expressed as follows

    $$\begin{aligned} P_{{x_1}}^{OP} = 1 - \int _u^\infty {\left[ {1 - {F_C}\left( {\frac{v}{a}} \right) } \right] {f_A}\left( a \right) da}\,, \end{aligned}$$
    (21)

    where \(u = \frac{{{\gamma _{th1}}}}{{{\Theta _1}{P_{BS}}}}\) and \(v = \frac{{{\gamma _{th1}}}}{{{\Theta _1}\beta \eta {P_{BS}}}}\) are for the BS-based PSR protocol, \(v = \frac{{{\gamma _{th1}}\left( {1 - \alpha } \right) }}{{2{\Theta _1}\alpha \eta {P_{BS}}}}\) is for the BS-based TSR protocol. Applying Taylor series expansion as well as substituting CDF and PDF functions of A and C into (21), we can obtain the expanded \(P_{{x_1}}^{OP}\) expression as follows (see Eq. (22) at the top of the next page)

    $$\begin{aligned} \begin{array}{l} P_{{x_1}}^{OP} = 1 - \sum \limits _{k = 1}^K {{{\left( { - 1} \right) }^{k - 1}}\left( \begin{array}{l} K\\ \\ k \end{array} \right) \frac{k}{{{\Omega _2}}}} \int _u^\infty {\exp \left( { -\frac{v}{{{\Omega _3}x}}} \right) \exp \left( { - \frac{{ka}}{{{\Omega _2}}}} \right) da} \\ \\ \quad \,\,\,\,\,\,\,\,= 1 - \sum \limits _{k = 1}^K {{{\left( { - 1} \right) }^{k - 1}}\left( \begin{array}{l} K\\ k \end{array} \right) \frac{k}{{{\Omega _2}}}} \sum \limits _{n = 1}^{{K_t}} {\frac{{{{\left( { - 1} \right) }^n}}}{{n!}}{{\left( {\frac{v}{{{\Omega _3}}}} \right) }^n}} {\left( {\frac{1}{u}} \right) ^{n - 1}}{E_n}\left( {\frac{{ku}}{{{\Omega _2}}}} \right) \end{array} \end{aligned}$$
    (22)
  2. b)

    For imperfect SIC In this case, signal \(x_{2}\) does not appear at \(D_{1}\) and becomes interference. The SINR of symbol \(x_{1}\) at \({k^ *}\) and \(D_{1}\) is correspondingly given by

    $$\begin{aligned}&{\gamma _{1,UA{V_k}}} = \frac{{{\Theta _1}{P_{BS}}{{\left| {{g_k}} \right| }^2}}}{{{\Theta _2}{\rho _2}{P_{BS}}{{\left| {{g_k}} \right| }^2} + 1}} \end{aligned}$$
    (23)
    $$\begin{aligned}&{\gamma _{1,D1}} = \frac{{{\Theta _1}P_{UAV}^X{{\left| {{h_1}} \right| }^2}}}{{{\Theta _2}{\rho _1}P_{UAV}^X{{\left| {{h_1}} \right| }^2} + 1}}\,, \end{aligned}$$
    (24)

    where \(0 < {\rho _j} \le 1\) , \(j \in \left\{ {1,2,...,{N_k}} \right\}\), represents the remaining noise level due to imperfect SIC at \(k^*\) and \(D_{1}\). In particular, \({\rho _j} = 1\) and \({\rho _j} = 0\) relate to the cases without SIC and perfect SIC, respectively. From (23) and (24), the outage probability of \(x_{1}\) for imperfect SIC is given by (see Eq. (25) at the top of the next page)

    $$\begin{aligned} \begin{array}{l} P_{{x_1},{D_1}}^{I\_SIC} = \Pr \left[ {\min \left( {{\gamma _{1,UA{V_k}}},{\gamma _{1,D1}}} \right) \le {\gamma _{th1}}} \right] = 1 - \Pr \left[ {A \ge \frac{{{\gamma _{th1}}}}{{{P_{BS}}\left( {{\Theta _1} - {\gamma _{th1}}{\Theta _2}{\rho _2}} \right) }},C \ge \frac{{{\gamma _{th1}}}}{{A{\psi _E}{P_{BS}}\left( {{\Theta _1} - {\gamma _{th1}}{\Theta _2}{\rho _1}} \right) }}} \right] \end{array} \end{aligned}$$
    (25)

    Proof see “Appendix 2” Solving (25), we can obtain

    $$\begin{aligned} P_{{x_1},{D_1}}^{I\_SIC} = 1 - \int _w^\infty {\left[ {1 - {F_C}\left( {\frac{s}{a}} \right) } \right] {f_A}\left( a \right) da}, \end{aligned}$$
    (26)

    where \(w = \frac{{{\gamma _{th1}}}}{{{P_{BS}}\left( {{\Theta _1} - {\gamma _{th1}}{\Theta _2}{\rho _2}} \right) }}\), \(s = \frac{{{\gamma _{th1}}}}{{{\psi _E}{P_{BS}}\left( {{\Theta _1} - {\gamma _{th1}}{\Theta _2}{\rho _1}} \right) }}\) Then, by some calculation processes, the \(P_{{x_1},{D_1}}^{I\_SIC}\) can be rewritten by (see Eq. (27) in the next page)

    $$\begin{aligned} \begin{array}{l} P_{{x_1},{D_1}}^{I\_SIC} = 1 - \sum \limits _{k = 1}^K {{{\left( { - 1} \right) }^{k - 1}}\left( \begin{array}{l} K\\ k \end{array} \right) \frac{k}{{{\Omega _2}}}\int _w^\infty {\exp \left( { - \frac{s}{{{\Omega _3}a}}} \right) \exp \left( { - \frac{{ka}}{{{\Omega _2}}}} \right) da} } \\ \\ \quad \quad \quad \,\,= 1 - \sum \limits _{k = 1}^K {{{\left( { - 1} \right) }^{k - 1}}\left( \begin{array}{l} K\\ k \end{array} \right) \frac{k}{{{\Omega _2}}}\sum \limits _{n = 0}^{{K_t}} {\frac{{{{\left( { - 1} \right) }^n}}}{{n!}}{{\left( {\frac{d}{{{\Omega _3}}}} \right) }^n}{{\left( {\frac{1}{w}} \right) }^{k - 1}}{E_n}\left( {\frac{{kw}}{{{\Omega _2}}}} \right) } } \end{array} \end{aligned}$$
    (27)

3.2.2 The Exact Outage Behaviour of \(x_{2}\) at \(D_{2}\)

We define that \(P_{{x_2}}^{OP}\) as an event that transfers the best UAV or \(D_{1}\) or \(D_{2}\) can not successfully decode \(x_{2}\) because the SINR/SNR is below threshold value \({\gamma _{th2}}\).

From (8), (11) and (12), the \(P_{{x_2}}^{OP}\) is given by (see Eq. (28) in the next page).

$$\begin{aligned} \begin{array}{l} P_{{x_2}}^{OP} = \Pr \left\{ {{\gamma _{2,UA{V_k}}}< {\gamma _{th2}}\,\,\mathrm{{ or }}\,\,{\gamma _{2,D2}}< {\gamma _{th2}}\,\,\mathrm{{ or }}\,\,{\gamma _{2,D1}} < {\gamma _{th2}}} \right\} \\ \\ \quad \quad \,\,= 1 - \Pr \left\{ {\frac{{{\Theta _2}{P_{BS}}{{\left| {{g_{k}}}\right| }^2}}}{{{\Theta _1}{P_{BS}}{{\left| {{g_{k}}} \right| }^2} + 1}}> {\gamma _{th2}},\frac{{{\Theta _2}{P_{UAV}^X}{{\left| {{h_2}} \right| }^2}}}{{{\Theta _1}{P_{UAV}^X}{{\left| {{h_2}} \right| }^2} + 1}}>{\gamma _{th2}},\frac{{{\Theta _2}{P_{UAV}^X}{{\left| {{h_1}}\right| }^2}}}{{{\Theta _1}{P_{UAV}^X}{{\left| {{h_1}} \right| }^2} + 1}} > {\gamma _{th2}}} \right\} \end{array} \end{aligned}$$
(28)

Eq. (28) can be rewritten by (see Eq. (29) in the next page)

$$\begin{aligned} \begin{array}{l} P_{{x_2}}^{OP} = 1 - \Pr \left\{ \begin{array}{l} {\Theta _2}{P_{BS}}{\left| {{g_{k}}} \right| ^2}> {\gamma _{th2}}\left( {{\Theta _1}{P_{BS}}{{\left| {{g_{k}}} \right| }^2} + 1} \right) ,\frac{{{\Theta _2}{\psi _E}{P_{BS}}{{\left| {{g_{k}}} \right| }^2}{{\left| {{h_2}}\right| }^2}}}{{{\Theta _1}{\psi _E}{P_{BS}}{{\left| {{g_{k}}} \right| }^2}{{\left| {{h_2}} \right| }^2} + 1}}> {\gamma _{th2}},\\ \frac{{{\Theta _2}{\psi _E}{P_{BS}}{{\left| {{g_{k}}} \right| }^2}{{\left| {{h_1}}\right| }^2}}}{{{\Theta _1}{\psi _E}{P_{BS}}{{\left| {{g_{k}}} \right| }^2}{{\left| {{h_1}} \right| }^2} + 1}}> {\gamma _{th2}} \end{array} \right\} \\ \\ \quad \quad \,\,= 1 - \Pr \left\{ \begin{array}{l} A> \frac{{{\gamma _{th2}}}}{{{P_{BS}}\left( {{\Theta _2} - {\gamma _{th2}}{\Theta _1}} \right) }}, AB> \frac{{{\gamma _{th2}}}}{{{P_{BS}}{\psi _E}\left( {{\Theta _2} - {\gamma _{th2}}{\Theta _1}} \right) }}, AC > \frac{{{\gamma _{th2}}}}{{{P_{BS}}{\psi _E}\left( {{\Theta _2} - {\gamma _{th2}}{\Theta _1}} \right) }}\,, \end{array} \right\} \end{array} \end{aligned}$$
(29)

where \({\psi _E} = \beta \eta\) and \({\psi _E} = \frac{{2\alpha \eta }}{{1 - \alpha }}\) represent EH for BS-based PSR and BS-based TSR protocols, respectively.

Proof see “Appendix 3”.

It can be seen from (29) that the outage probability always satisfies \({\gamma _{th2}} > \frac{{{\Theta _2}}}{{{\Theta _1}}}\).

Therefore, we need to allocate more power for symbol \(x_{1}\) to satisfy \({\Theta _2} > {\Theta _1}{\gamma _{th2}}\). Thus, (29) can be expressed by (see Eq. (30) in the next page)

$$\begin{aligned} \begin{array}{l} P_{{x_2}}^{OP} = 1 - \int _{{t_1}}^\infty {\Pr \left\{ {B> \frac{{{t_1}}}{a}, C > \frac{{{t_1}}}{a}} \right\} {f_A}\left( a \right) da} = 1 - \int _{{t_2}}^\infty {\int _{\frac{{{t_1}}}{a}}^\infty {\Pr \left\{ {1 - {F_B}\left( {\frac{{{t_1}}}{a}} \right) } \right\} {f_C}\left( c \right) {f_A}\left( a \right) dadc} }\,, \end{array} \end{aligned}$$
(30)

where \({t_2} = \frac{{{\gamma _{th2}}}}{{{P_{BS}}\left( {{\Theta _2} - {\gamma _{th2}}{\Theta _1}} \right) }}\) and \({t_1} = \frac{{{\gamma _{th2}}}}{{{P_{BS}}{\psi _E}\left( {{\Theta _2} - {\gamma _{th2}}{\Theta _1}} \right) }}\)

From (30) and the transformations, the expression can be obtained by (see Eq. (31))

$$\begin{aligned} \begin{array}{l} P_{{x_2}}^{OP} = 1 - \int _{{t_2}}^\infty {\int _{\frac{{{t_1}}}{a}}^\infty {\Pr \left\{ {1 - {F_B}\left( {\frac{{{t_1}}}{a}} \right) } \right\} {f_C}\left( c \right) {f_A}\left( a \right) dadc} } \\ \\ \quad \quad \,\,= 1 - \sum \limits _{k = 1}^K {{{\left( { - 1} \right) }^{k - 1}}\left( \begin{array}{l} K\\ k \end{array} \right) \frac{k}{{{\Omega _2}}}} \underbrace{\int _{{t_2}}^\infty {\exp \left( { - \frac{\tau }{a} - \frac{{ka}}{{{\Omega _2}}}} \right) da} }_\chi \,, \end{array} \end{aligned}$$
(31)

Proof see “Appendix 4”.

where \(\tau = \frac{{{t_1}}}{{{\Omega _3}}} + \frac{{{t_1}}}{{{\Omega _1}}}\). Since it is highly complex to calculate a closed-form expression, thus an approximate calculation method, namely Taylor series expansion, is utilized as the following expression

$$\begin{aligned} \exp \left( { - \frac{u}{a}} \right) = \sum \nolimits _{n = 0}^{{K_t}} {\frac{{{{\left( { - 1} \right) }^k}}}{{k!}}{{\left( {\frac{u}{a}} \right) }^k}}\,, \end{aligned}$$
(32)

where \({K_t} \in \left\{ {1, \ldots ,\infty } \right\}\).

Then, we obtain the following expression

$$\begin{aligned} \begin{array}{c} \,\,\,\,\chi = \sum \limits _{n = 0}^{{K_t}} {\frac{{{{\left( { - 1} \right) }^k}}}{{k!}}} \int _{{t_2}}^\infty {{{\left( {\frac{\tau }{a}} \right) }^k}\exp \left( { -\frac{{ka}}{{{\Omega _2}}}} \right) da} \\ \\ \,\,\,\,= \sum \limits _{n = 0}^{{K_t}} {\frac{{{{\left( { - 1} \right) }^k}{\tau ^n}}}{{n!}}} {\left( {\frac{1}{{{t_2}}}} \right) ^{n - 1}}{E_n}\left( {\frac{{k{t_2}}}{{{\Omega _2}}}} \right) \,, \end{array} \end{aligned}$$
(33)

where \({E_n}\left( .\right)\) is an exponential integral function.

Substituting (33) into (31), the \(P_{{x_2}}^{OP}\) is given by (see Eq. (34) at the top of the next page)

$$\begin{aligned} \begin{array}{l} P_{{x_2}}^{OP} = 1 - \sum \limits _{k = 0}^K {\sum \limits _{n = 0}^{{K_t}} {\frac{{{{\left( { - 1} \right) }^k}{{\left( { - 1} \right) }^n}{\beta ^n}}}{{n!}}} \left( \begin{array}{l} K\\ k \end{array} \right) \frac{k}{{{\Omega _2}}}{{\left( {\frac{1}{{{t_2}}}} \right) }^{n - 1}}} {E_n}\left( {\frac{{k{t_2}}}{{{\Omega _2}}}} \right) \end{array} \end{aligned}$$
(34)

4 Throughput

4.1 Throughput at UAV

The throughput at \(UAV_{k}\) is given by

$$\begin{aligned} {\tau _{UA{V_k}}} = \left( {1 - P_{{x_1}}^{UA{V_k}}} \right) {R_{1,k}} + \left( {1 - P_{{x_2}}^{UA{V_k}}} \right) {R_{2,k}}\,, \end{aligned}$$
(35)

Where \(P_{{x_1}}^{UA{V_k}}\) and \(P_{{x_2}}^{UA{V_k}}\) are determined from (14) and (18), respectively. \({R_{1,k}}\) and \({R_{2,k}}\) are the rates to decode signal \(x_{1}\) and \(x_{2}\) at UAV\(_{k}\), respectively.

4.2 Throughput at the User

For perfect SIC at the user, the throughput at user \(D_{k}\) is given by

$$\begin{aligned} \tau _{{D_k}}^{error} = \left( {1 - P_{{x_1}}^{OP}} \right) {R_{1,k}} + \left( {1 - P_{{x_2}}^{OP}} \right) {R_{2,k}} \end{aligned}$$
(36)

For imperfect SIC at the user, the throughput at user \(D_{k}\) is given by

$$\begin{aligned} \tau _{{D_k}}^{ISIC} = \left( {1 - P_{{x_1},{D_1}}^{I\_SIC}} \right) {R_{1,k}} + \left( {1 - P_{{x_2 }}^{OP}} \right) {R_{2,k}} \end{aligned}$$
(37)

5 Simulation Results

In this section, we provide several results to illustrate the effects of the number of relays, channel increasing level (distance or path-loss), and imperfect SIC for the RF energy harvesting efficiency of NOMA systems. The parameters of the system are set as follows. Because \(D_{1}\) is closer to the relaying node than \(D_{2}\), power allocation coefficients are \(\Theta _1=0.2\) and \(\Theta _2=0.8\) for \(D_{1}\) and \(D_{2}\), respectively. Bit rates are set \(R_{1}=1\) (bpcu) and \(R_{2}=0.5\) (bpcu) for \(D_{1}\) and \(D_{2}\), respectively.

The energy harvesting fraction in the BS-based TSR protocol is \(\alpha =0.3\). The channel gains are \({\Omega _1}={\Omega _3}=1\) and \({\Omega _2}=2\) and the energy conversion factor is \(\eta =1\).

Fig. 4
figure 4

The outage probability for decoding the signal \(x_{1}\) with perfect SIC and varried UAV number

Full size image
Fig. 5
figure 5

The outage probability for decoding the signal \(x_{1}\) with imperfect SIC and varried UAV number

Full size image

Figures 4 and 5 show the comparison of the outage probability \(x_{1}\) at \(D_{1}\) and the average SNR in cases of perfect and imperfect SIC and varied UAV numbers. The power allocation coefficients for decoding \(x_{1}\) and \(x_{2}\) are \(\Theta _1=0.25\), \(\Theta _2=0.75\), respectively. It can be observed from these figures that the outage probability decreases significantly as the UAV number increases from 1 to 3 for perfect and imperfect SIC. Besides, the outage probability for perfect SIC is considerably lower than that for imperfect SIC. It proves that the efficiency of the system with perfect SIC is over the desired threshold level. In addition, the outage probability for BS-based PSR is also lower than that for BS-based TSR.

Fig. 6
figure 6

The outage probability for decoding the signal \(x_{2}\) at UAV\(_{k}\) versus varried UAV number

Full size image
Fig. 7
figure 7

The outage probability for decoding the signal \(x_{2}\) at UAV\(_{k}\) versus varried UAV number

Full size image
Fig. 8
figure 8

The outage probability for decoding the signal \(x_{1}\) at UAV\(_{k}\) versus varried UAV number

Full size image
Fig. 9
figure 9

The outage probability for decoding the signal \(x_{1}\) at UAV\(_{k}\) versus varried UAV number

Full size image

Figures 6, 7, 8, 9 describe the outage probabilities for decoding the signals \(x_{2}\) and \(x_{1}\) at the UAV, respectively. It is observed for both figures that the outage probability is low more and more as the number of UAVs increases from 1 to 3. It is proved that when the number of UAVs increases, the system is stable. Besides, the BS-based PSR has a lower outage probability than the BS-based TSR.

Fig. 10
figure 10

The probability for decoding the signal \(x_{2}\) at \(D_{2}\) with the varied UAV number

Full size image
Fig. 11
figure 11

The probability for decoding the signal \(x_{2}\) at \(D_{2}\) with the varied UAV number

Full size image

Figures 10 and 11 plot the outage probability for decoding \(x_{2}\) at \(D_{2}\) with the varied UAV number. In this figure, we use two PSR and TSR protocols corresponding with the varied UAV number. As shown in Figs. 10, 11, the outage probability is lower as the UAV number increases from 1 to 3. Furthermore, the outage probability for BS-based PSR is lower than that for BS-based TSR. The reason is that the best UAV is chosen to provide the best channel from the source to relay so that a better decoding efficiency and a higher energy harvesting efficiency from the source in the first phase can be achieved. We can see that the simulation results match the analytic results.

Fig. 12
figure 12

The throughput of users in cases of perfect and imperfect SIC for BS-based PSR and BS-based TSR protocols

Full size image
Fig. 13
figure 13

The throughput of users in cases of perfect and imperfect SIC for BS-based PSR and BS-based TSR protocols

Full size image

Figures 12 well as figure 13 plot the common throughput for two cases at UAV\(_{k}\), and at two users \(D_{1}\) and \(D_{2}\). The BS-based PSR achieves the highest throughput at UAV\(_{k}\) as compared to the throughput at the users. The throughput threshold value is 1.5. The throughput at UAV\(_{k}\) for BS-based PSR protocol is higher than that for BS-based TSR. On the contrary, the throughput at the users for BS-based PSR is lower than that for BS-based TSR. Furthermore, from Fig. 13, we can also see that the throughput at the users in cases of perfect SIC is much better than the throughput at the users in cases of imperfect SIC.

Fig. 14
figure 14

Comparison of outage probability between this work and [20]

Full size image

Figure 14 describes the comparison in terms of outage probability for User1-exact of NOMA scheme between our work and the work of [20]. The figure shows that the protocols for our work obtain a lower outage probability than that for the work of [20] in the SNR region of from 0 to 8 dB. In contrast, the protocols for our work obtain a slightly higher outage probability than that for the work of [20] in the SNR region of from 0 to 8 dB. It can be concluded that the higher the target rate, the higher the dropped data. This can be explained that the quality of propagation path of the NOMA downlink cooperative dual-hop relay system in [20] is better than our system model with UAVs in cooperative relaying networks in the SNR region of from 0 to 8 dB. In general, the work in [20] achieves slightly better performance than in our work when SNR increases (SNR > 8 dB).

6 Conclusion

Two BS-based PSR and BS-based TSR protocols for the NOMA system have been presented in this paper. The closed-form expressions of the outage probability and throughput for UAVs and users were derived. Particularly, the outage probabilities at cooperative relaying user’s device, i.e., \(D_{1}\), were also derived in closed-form expressions for perfect and imperfect SIC. The simulation results show that the outage probability and throughput for BS-based PSR protocol were superior to that for BS-based TSR protocol. The analytic results matched the simulation results. For future work, we can develop the system using multiple antennas at two users \(D_{1}\) and \(D_{2}\) to enhance the performance of the system.