Partial Relay Selection in Energy Harvesting Based NOMA Network with Imperfect CSI

Abstract

In this paper, we analyse the performance of partial relay selection (PRS) for non orthogonal multiple access (NOMA) dual hop relay assisted network, where a source (S) node transmits two signals to respective two destinations $(D_1,D_2)$ with help of relays. All the relays are powered by harvested energy from RF signal of source. The performance of network is analysed for both signals $S_1$ and $S_2$. The availability of channel state information (CSI) knowledge effects the outage probabilities of both the symbols. We derive closed form expressions of outage probability for both the symbols. Further, we use monte carlo simulation to evaluate ergodic capacity and throughput. The impact of power allocation between both the signals on outage probability is also depicted and a feasible region of power allocation factor between symbols is obtained where NOMA is fairly working.

1 Introduction

Non-orthogonal multiple access (NOMA) is an emerging radio access technology to increase the spectral efficiency in 5G wireless communication networks. NOMA exploits the power domain to allow multiple access while other orthogonal multiple access (OMA) technologies like time division multiple access (TDMA), frequency division multiple access (FDMA) and code division multiple access (CDMA) exploit time, frequency and code division to allow multiple access [1]. In [2], the authors have given insight to the NOMA technology in MIMO environment and NOMA technology in cognitive radio environment in context of LTE and 5G wireless network. In [3], the authors have analysed the achievable rate in cooperative relaying based NOMA. In [4], a comparison of NOMA and OMA is carried out, and it is found that NOMA outperforms OMA in terms of coding gain. In [5, 6] the authors have analysed the system performance of a relaying network with NOMA technology, considering diversity technology like MRC of relaying path and direct path between source and destination. In [7], the authors have evaluated performance of a cooperative full duplex amplify-forward (AF) relaying system with NOMA radio access technology.

To resolve the power supply problem for energy constrained node, RF energy harvesting is a emerging technology to power up wireless communication device in 5G network [8, 9]. The combination of cognitive radio technology and RF energy harvesting technology boosts the proposed wireless network in terms of spectral efficiency and renewable power utilization. The authors in [8], evaluated throughput performance in energy harvesting network considering both the AF and DF relaying system. Several power allocation strategies are discussed in [9] to distribute energy among relays in energy constrained cooperative network. The interferer RF signals are utilized to harvest energy along with the desired RF signal in [10].

Several schemes for relay selection have been reported in RF energy harvesting based OMA network. In [11], the authors have analyzed performance of energy harvesting based on dual hop relay network, where the relay having highest energy is being selected in the time switching based energy harvesting network. In [12], the authors analysed performance of PSR based on energy harvesting considering dual hop network, in PRS and ORS (optimal relay selection) schemes. In [13], the authors investigate outage probability of dual hop relaying time switching relaying (TSR) based energy harvesting network, where best relay has been selected based on highest end to end signal to interference noise (SINR) in CRN network. In [14], the authors have investigated outage probability of an energy harvesting based dual hop relaying system where the best relay has been selected having maximum end to end SINR and MRC diversity techniques is also considered with relay link and direct link between source and destination.

In [15], a two stage relay selection strategy is proposed and evaluated for a cooperative NOMA network. In [16, 17] performance of the partial relay selection (PRS) scheme is investigated for an AF relaying network under NOMA technology and in [17] a closed form expression for outage probability has been derived. In [18], the authors have analyse the performance of energy harvesting based NOMA network with PRS scheme following TSR protocol, whereas, power splitting relaying protocol for simultaneous wireless information and power transfer has been followed in PRS based NOMA network [19]. In [20], the performance of PRS based NOMA network is analysed considering both linear and non-linear model of energy harvesting.

In [21], the authors have proposed NOMA based model in CRN environment, where two messages are transmitted to a primary user by a secondary user (SU) selected from a group of SUs. In [22], the authors have considered mth order NOMA in CRN and evaluated performance under several power allocation schemes. Recently, PRS scheme in multi-user NOMA network has been reported [23, 24]. The pairwise error probability of NOMA network under cognitive scenario is analysed via simulation and theoretical analysis [23]. All the above mentioned literature deal with half duplex mode of operation. In [24], the authors have analysed NOMA network under CRN environment employing PRS scheme in half duplex as well as full duplex mode of operation. With little advancement, a PRS is utilized in NOMA network where near user act as a relay and participates in selection procedure if near user successfully decodes signals for both users, otherwise only dedicated relays participate for selection to assist both users [25].

Due to the randomness of fading channels and channel estimation error, it is difficult to acquire the perfect information about channel condition. Most recently, several papers considering imperfect CSI have been reported in NOMA based network to make the analysis more realistic. In [26], the imperfect CSI is considered between secondary source and primary receiver to estimate maximum allowable transmit power based on the limitation of received interference power at primary receiver below a threshold. In [27], the authors have considered imperfect CSI to compute the accumulated interferences at primary receiver in a multihop secondary network. In [28], the authors have analysed the impact of imperfect CSI on the performance of MIMO based energy harvesting network. An outage performance is analysed in an underlay NOMA cognitive radio network assuming imperfect CSI between source-to-primary receiver and relay-to-primary receiver [29].

1.1 Contributions of the Paper

NOMA is an emerging technology for multiple access to boost the spectrum utilization and reduces spectrum scarcity problem. Inspired by the advantage of the technology, we are investigating the performance of a NOMA based relay selective network considering imperfect CSI. Imperfection in CSI is not considered in selection of relay in NOMA based transmission in existing literature, to the best of our knowledge. Hence, it is important to analyze the performance of energy harvesting relay selective network utilizing NOMA considering an imperfect CSI, which is more realistic.

In summary, the major contributions of this paper are as bellow:

• We consider NOMA access technology in dual hop network to increase the spectrum efficiency of the network.

• We derive closed form expressions of outage probabilities for both the symbols in order to assess the performance of PRS scheme using NOMA considering an imperfect CSI.

• We analyse the outage and throughput for NOMA based transmission in relay assisted network and indicate the impact of several network parameters.

• We find a feasible region for power allocation factor $(\frac{a_1}{a_2})$ for fairness of NOMA schemes.

• We also analyse the impact of channel correlation co-factor.

1.2 Organization of the Paper

The rest of the paper is organized as follows: Sect. 2 depicts system model and time frame structure. A brief discussions of the performance analyses are given in Sect. 3. In Sect. 4, the results and discussion are described. Finally, Sect. 5 concludes the paper.

2 System Model

Fig. 1

System model for a NOMA network

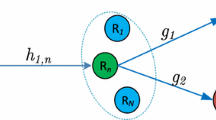
As shown in Fig. 1, we considered a dual hop cooperative network consisting of one source (S), two destinations $(D_1, D_2)$ and $N_r$ number of relays $(R_i)$, where $i \in \{1,N_r\}$. The source transmits a superimposed signal to the selected relay and the relay forwards the same to $SD_1$ and $SD_2$. We assume that all the relays are powered by harvesting energy extracted from RF signal of S. All the relays, S, $D_1$ and $D_2$ are equipped with a single antenna. We also assume that there is no direct path between source and destinations due to deep faded channel.

The channel co-efficient between S and ith relay $(R_i)$ is denoted as $h_{SR_i}$, $i \in \{1, N_r\}$ which is a Complex Normal random variable i.e. $h_{SR_i} \sim \mathcal {CN}(0,\lambda _{SR})$. Accordingly, the channel gain $(|h_{SR_i}|^2)$ is following an exponential distribution. The channel co-efficient between ith relay to $D_1$ and $D_2$ are given by $h_{{R_i}{D_1}}$ and $h_{{R_i}{D_2}}$, which follows Complex Normal random variable i.e. $h_{R_iD_1} \sim \mathcal {CN}(0,\lambda _{RD_1})$ and $h_{R_iD_2} \sim \mathcal {CN}(0,\lambda _{RD_2})$. Correspondingly the channel gain are denoted by $|h_{{R_i}{D_1}}|^2$ and $|h_{{R_i}{D_2}}|^2$ which follows exponential distribution.

The probability density function (PDF) of channel gains are given as

$$\begin{aligned}&{f_{{{\left| {{h_{{S}R_i}}} \right| }^2}}}\left( x \right) = \frac{1}{{{\lambda _{{S}R}}}}{e^{ - \frac{x}{{{\lambda _{{S}R}}}}}} \qquad \forall i \in [1, N_r] \end{aligned}$$

(1)

$$\begin{aligned}&{f_{{{\left| {{h_{R{D_1}}}} \right| }^2}}}\left( y \right) = \frac{1}{{{\lambda _{R{D_1}}}}}{e^{ - \frac{y}{{{\lambda _{R{D_1}}}}}}} \end{aligned}$$

(2)

$$\begin{aligned}&{f_{{{\left| {{h_{R{D_2}}}} \right| }^2}}}\left( y \right) = \frac{1}{{{\lambda _{R{D_2}}}}}{e^{ - \frac{y}{{{\lambda _{R{D_2}}}}}}} \end{aligned}$$

(3)

Here, the relay which is having the strongest channel gain between the source and the relays is selected. The relay selection depends on the CSI of source to relays. But in practice, it is difficult to acquire the information about perfect CSI due to several reasons such as channel estimation error, mobility of user, feedback error, delay. The error between estimated channel and actual channel leads to inaccurate analysis. Hence, it is important to consider imperfect CSI. Let us assume $\rho$ is the correction co-efficient between $h_{SR_{i}}$ and $\widehat{h}_{SR_{i}}$. The relation between $h_{SR_{i}}$ and $\widehat{h}_{SR_{i}}$ is expressed as follows [28],

$$\begin{aligned} \widehat{h}_{SR_{i}} = \rho h_{SR_{i}} + \sqrt{1 - {\rho ^2}} \varepsilon \end{aligned}$$

(4)

where $\varepsilon$ is a circular symmetric complex Gaussian (CSCG) random variable with mean zero and variance $\lambda _{SR}$ i.e., $\varepsilon \sim \mathcal {CN}(0, \lambda _{SR})$ and $\rho \in$ [0, 1].

Fig. 2

Time frame for a NOMA network at relay

As shown in Fig. 2, simultaneous wireless information and power transfer (SWIPT) concept has been used for data transmission in this relaying system. The S node transmits signal to a group of relays and all the relays harvest energy from the radio frequency signal of S node during $\alpha T$ time. The remaining $(1-\alpha ) T$ time is equally used as $\frac{(1-\alpha ) T}{2}$ time for receiving information from S node and $\frac{(1-\alpha ) T}{2}$ time for transmission of information to destination nodes.

3 Performance Analysis

In the system model, the source transmits $( \sqrt{a_1 P_S} S_1+ \sqrt{a_2 P_S} S_2)$ to the group of relays during first phase of time slot where $S_1$, $S_2$ are information symbols, $P_S$ is the transmit power of source, $a_1$, $a_2$ are power allocation co-efficients, $a_1+a_2=1$, $a_1> a_2$ and let $\theta =\frac{a_1}{a_2}$.

The received signal at the ith relays during first phase is given by,

$$\begin{aligned} y_{R_i}=(\sqrt{a_1 P_S} S_1+ \sqrt{a_2 P_S} S_2) \widehat{h}_{SR_{i}}+n_{R_i} \end{aligned}$$

(5)

where, $n_{SR_i}$ is received AWGN noise with zero mean and $N_0$ variance at ith relay.

The relay decodes the symbol $S_1$ by treating the symbol by $S_2$ as noise and cancels it using a successive interference noise cancellation (SIC) to extract $S_2$ symbol from (5). Thus the received SINRs for symbol $S_1$ and $S_2$ at ith relay are expressed as

$$\begin{aligned} \gamma _{R_i}^I= & {} \frac{ a_1 P_S |\widehat{h}_{SR_{i}}|^2}{a_2 P_S |\widehat{h}_{SR_{i}}|^2+N_0} \nonumber \\ \gamma _{R_i}^{II}= & {} \frac{a_2 P_S |\widehat{h}_{SR_{i}}|^2}{N_0} \end{aligned}$$

(6)

As shown in Fig. 2, the received signal at ith relay is first sent to the energy harvesting circuit for a duration of $\alpha T$ time and rest $(1-\alpha )\frac{T}{2}$ time is utilized for receiving information and $(1-\alpha )\frac{T}{2}$ for transmitting information following a TSR scheme of energy harvesting [8]. The harvested energy extracted from RF signal during $\alpha T$ is given by,

$$\begin{aligned} E_i=\eta P_S |\widehat{h}_{SR_{i}}|^2 \frac{\alpha T}{2} \end{aligned}$$

(7)

Correspondingly, transmit power of ith relay, based on harvested energy is given by,

$$\begin{aligned} P_{R_i}=\eta P_S |\widehat{h}_{SR_{i}}|^2 \frac{2\alpha }{1-\alpha }=\alpha ^{'} P_S |\widehat{h}_{SR_{i}}|^2 \end{aligned}$$

(8)

where, $\alpha ^{'}=\eta \frac{2\alpha }{1-\alpha }$.

We assume that the selected relay is able to decode faithfully and SIC is also perfect. In the second phase of time, the selected relay sends the decoded message to the destination. Hence the received signal at the destination $D_1$ and $D_2$ are given by,

$$\begin{aligned} y_{D_1}= & {} \sqrt{P_{R_i}} h_{R_i D_1} (\sqrt{a_1} S_1+ \sqrt{a_2}S_2)+n_{D_1}\nonumber \\ y_{D_2}= & {} \sqrt{P_{R_i}} h_{R_i D_2} (\sqrt{a_1} S_1+ \sqrt{a_2}S_2)+n_{D_2} \end{aligned}$$

(9)

where, $P_{R_i}$ is the transmit power of ith relay, $n_{D_j}$ is AWGN with zero mean and $N_0$ variance, received at jth destination, $h_{R_i D_j}$ is the channel co-efficient between ith relay and jth destination where $j={1,2}$.

The $D_1$ decodes the symbol $S_1$ received from selected relays $(R_{i^*})$ considering $S_2$ as noise. So, the SINR at $D_1$ is given by,

$$\begin{aligned} \gamma ^I_{D_1}=\frac{a_1 P_{R_{i^*}} |h_{R_{i^*}D_1}|^2}{a_2P_{R_{i^*}}|h_{R_{i^*}D_1}|^2+N_0 } \end{aligned}$$

(10)

To obtain $S_2$ symbol at $D_2$ using SIC method, $D_2$ needs to decode the symbol $S_1$ first. Hence, the SINR for $S_1$ at $D_2$ is given by,

$$\begin{aligned} \gamma ^I_{D_2}=\frac{a_1 P_{R_{i^*}}|h_{R_{i^*}D_2}|^2}{a_2 P_{R_{i^*}}|h_{R_iD_2}|^2+N_0} \end{aligned}$$

(11)

After cancelling $S_1$ symbol using SIC method, $D_2$ decodes desire signal at $S_2$. The SINR for $S_2$ at $D_2$ is given by

$$\begin{aligned} \gamma ^{II}_{D_2}=a_2 P_{R_{i^*}}|h_{R_{i^*}D_2}|^2 \end{aligned}$$

(12)

In this case, the symbol $S_1$ is faithfully decoded and completely removed before decoding $S_2$ at $D_2$.

3.1 Partial Relay Selection

In this scheme, the relay having the strongest channel gain between source to relay is chosen out of all channels from the group of all available relays. The selected selected is given as,

$$\begin{aligned} i^{*}= arg \mathop {\max }\limits _{i \in \{ 1,2,\ldots ,N_r\} } {\widehat{h}_{SR_{i}}} \end{aligned}$$

(13)

Hence, the channel gain between source and selected relay is given by,

$$\begin{aligned} \widehat{h}_{SR_{i^{*}}}= \mathop {\max }\limits _{i \in \{ 1,2,\ldots ,N_r\} } {\widehat{h}_{SR_{i}}} \end{aligned}$$

(14)

The PDF expression of ${h_{SR_{i^{*}}}}$ following (14) is given as [28],

$$\begin{aligned} {f_{{{\left| {{h_{SR_{i^{*}}}}} \right| }^2}}}\left( x \right)= & {} {N_r}{\left[ {{F_{{{\left| {{h_{{S}R_i}}} \right| }^2}}}\left( x \right) } \right] ^{{N_r} - 1}}{f_{{{\left| {{h_{{S}R_i}}} \right| }^2}}}\left( x \right) \nonumber \\= & {} \sum \limits _{n = 1}^{{N_r}} {\left( {_{\; n}^{{N_r}}} \right) } {\left( { - 1} \right) ^{n-1}}\frac{{n}}{{{\lambda _{{S}R}}}}{e^{ - \frac{{nx}}{{{\lambda _{{S}R}}}}}} \end{aligned}$$

(15)

The joint PDF of two correlated fading channel is given by [28]

$$\begin{aligned} {f_{{{\left| {{{\widehat{h}}_{{S}R_{i}}}} \right| }^2},{{\left| {{h_{{S}R_{i}}}} \right| }^2}}}\left( {x,y} \right) = \frac{1}{{\left( {1 - {\rho ^2}} \right) \lambda _{{S}R}^2}}{e^{ - \frac{{x + y}}{{\left( {1 - {\rho ^2}} \right) \lambda _{{S}R}^{}}}}}{I_0}\left( {\frac{{2\rho \sqrt{xy} }}{{\left( {1 - {\rho ^2}} \right) \lambda _{{S}R}^{}}}} \right) \end{aligned}$$

(16)

The conditional probability of correlated fading channels is given by,

$$\begin{aligned} {f_{{{\left| {{{\widehat{h}}_{{S}R_{i}}}} \right| }^2}{{\left| {{h_{{S}R_i}}} \right| }^2}}}\left( {x|y} \right) = \frac{{{f_{{{\left| {{{\hat{h}}_{{S}R_i}}} \right| }^2}{{\left| {{h_{{S}R_i}}} \right| }^2}}}\left( {x,y} \right) }}{{{f_{{{\left| {{h_{{S}R_i}}} \right| }^2}}}\left( y \right) }} \end{aligned}$$

(17)

The PDF of $| \widehat{h}_{SR_{i^{*}}}|^2$ is expressed by marginal distribution and is given as

$$\begin{aligned} {f_{{{\left| {{{\hat{h}}_{{S}R_{i^{*}}}}} \right| }^2}}}\left( x \right) = \int \limits _0^\infty {{f_{{{\left| {{{\hat{h}}_{{S}R_i}}} \right| }^2}{{\left| {{h_{{S}R_i}}} \right| }^2}}}\left( {x|y} \right) } {f_{{{\left| {{h_{{S}R_{i^{*}}}}} \right| }^2}}}\left( y \right) dy \end{aligned}$$

(18)

Putting (1), (15), (16), (17) in (18), we get

$$\begin{aligned} {f_{{{\left| {{{\widehat{h}}_{{S}R_{i^{*}}}}} \right| }^2}}}\left( x \right)= & {} \int \limits _0^\infty {\frac{1}{{\left( {1 - {\rho ^2}} \right) \lambda _{{S}R}^2}}{e^{ - \frac{{x + y}}{{\left( {1 - {\rho ^2}} \right) \lambda _{{S}R}^{}}}}}{I_0}\left( {\frac{{2\rho \sqrt{xy} }}{{\left( {1 - {\rho ^2}} \right) \lambda _{{S}R}^{}}}} \right) }\sum \limits _{n = 1}^{{N_r}} {\left( {_{\;n}^{{N_r}}} \right) } {\left( { - 1} \right) ^{n-1}}\frac{{n}}{{{\lambda _{{S}R}}}}{e^{ - \frac{{ny}}{{{\lambda _{{S}R}}}}}}dy\nonumber \\= & {} \sum \limits _{n = 1}^{{N_r} } {\left( {_{ \;n}^{{N_r} }} \right) } \frac{{{{\left( { - 1} \right) }^{n-1}}n}}{{{\lambda _{{S}R}}\left[ {1 + (n+1)\left( {1 - {\rho ^2}} \right) } \right] }}{e^{ - \frac{{nx}}{{{\lambda _{{S}R}}\left[ {1 + (n-1)\left( {1 - {\rho ^2}} \right) } \right] }}}} \end{aligned}$$

(19)

where, $I_0(x)$ is modified Bessel function of first kind of zeroth order, $\rho$ is the correlation coefficient and $\int \limits _0^\infty {{e^{ - \alpha x}}{I_0}\left( {2\sqrt{\beta x} } \right) dx = \frac{1}{\alpha }} {e^{\frac{\beta }{\alpha }}}$, [30, §6.614.3].

Outage probability of $S_1$: An outage occurs for $S_1$ when the end to end SINR from source node to first destination node is below a predefined threshold. The outage expression for $S_1$ is given by [18], as

$$\begin{aligned} \mathcal {O}^I_{PRS }=F_{e2e}^I(\gamma _{th})=\mathcal {P}_r \{ min(\gamma ^I_{R_{i^*}}, \gamma ^I_{D_1}, \gamma ^I_{D_2} ) < \gamma _{th}\} \end{aligned}$$

(20)

Proposition 1

The closed form expression for outage probability for symbol $S_1$ in PRS scheme

$$\begin{aligned} \begin{aligned} \mathcal {O}^I_{PRS }&= 1 - \sum \limits _{n = 1}^{{N_r}} {\left( {_{\,n}^{{N_r}}} \right) \frac{{{{\left( { - 1} \right) }^n}n}}{{{\lambda _{{S}R}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}\\&\quad \underbrace{\int \limits _\phi ^\infty {{e^{ - \left( {\frac{\phi }{{{\alpha ^{'}}{\lambda _{R{D_1}}}}} + \frac{\phi }{{{\alpha ^{'}}{\lambda _{R{D_2}}}}}} \right) \frac{1}{u} - \frac{{nu}}{{{\lambda _{S{R}}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}}} du}_{{A_1}} \end{aligned} \end{aligned}$$

(21)

where, $b_1=\left( {\frac{1 }{{{\lambda _{R{D_1}}}}} + \frac{1}{{{\lambda _{R{D_2}}}}}} \right) \frac{\phi }{\alpha ^{'}}$, $C={\frac{{n}}{{{\lambda _{S{R_i}}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}$, $A_1= \frac{{{e^{ - {a_1}C}}}}{C} - {b_1}\varGamma \left( {0,{a_1}C} \right) + \sum \nolimits _{k = 0}^\infty {\frac{{{{\left( { - 1} \right) }^k}{b_1}^k}}{{k!}}} \left[ {{e^{ - {a_1}C}}\sum \nolimits _{l = 1}^{k - 1} {\frac{{\left( {l - 1} \right) !{{\left( { - C} \right) }^{k - l - 1}}}}{{\left( {k - 1} \right) !{a_1}^l}}} - \frac{{{{\left( { - C} \right) }^{k - 1}}}}{{\left( {k - 1} \right) !}}{E_i}\left( { - {a_1}C} \right) } \right]$.

Proof

Please refer to Appendix 1. $\square$

Outage probability of $S_2$: Similarly, an outage occurs for $S_2$ when the end to end SINR for $S_1$ from source to first destination or the end to end SINR for $S_2$ from source to second destination is below a predefined threshold. The outage probability for $S_2$ is given by,

$$\begin{aligned} \begin{aligned} \mathcal {O}^{II}_{PRS}&=\mathcal {P}_r [ min(\gamma ^{I}_{e2e},\gamma ^{II}_{e2e} )< \gamma _{th}]\\&=\mathcal {P}_r \left[ min\{ min(\gamma ^I_{R_{i^*}}, \gamma ^I_{D_1}, \gamma ^I_{D_2} ), min(\gamma ^{II}_{R_{i^*}}, \gamma ^{II}_{D_2} )\} < \gamma _{th}\right] \\&=1-\left[ {1 - {F_{\gamma _{e2e}^I}}\left( {{\gamma _{th}}} \right) } \right] \left[ {1 - {F_{\gamma _{e2e}^{II}}}\left( {{\gamma _{th}}} \right) } \right] \end{aligned} \end{aligned}$$

(22)

Proposition 2

The closed form expression for outage probability for symbol $S_2$ in PRS scheme

$$\begin{aligned} \mathcal {O}^{II}_{PRS }= & {} 1-\left[ {1 -\mathcal {O}^I_{PRS } } \right] \left[ {1 - {F_{\gamma _{e2e}^{II}}}\left( {{\gamma _{th}}} \right) } \right] \end{aligned}$$

(23)

$$\begin{aligned}&{{F_{\gamma _{e2e}^{II}}}\left( {{\gamma _{th}}} \right) }= 1 - \sum \limits _{n = 1}^{{N_r}} {\left( {_{\,n}^{{N_r}}} \right) \frac{{{{\left( { - 1} \right) }^n}n}}{{{\lambda _{{S}R}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}\nonumber \\&\underbrace{\int \limits _\psi ^\infty {{e^{ - { \frac{\psi }{{{\alpha ^{'}}{\lambda _{R{D_2}}}u}}} - \frac{{nu}}{{{\lambda _{S{R_i}}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}}} du}_{{A_2}} \end{aligned}$$

(24)

where, $b_2=\frac{\psi }{\alpha ^{'}\lambda _{R{D_2}}}$ $C={\frac{{n}}{{{\lambda _{S{R_i}}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}$, $A_2= \frac{{{e^{ - {a_2}C}}}}{C} - {b_2}\varGamma \left( {0,{a_2}C} \right) + \sum \nolimits _{k = 0}^\infty {\frac{{{{\left( { - 1} \right) }^k}{b_2}^k}}{{k!}}} \left[ {{e^{ - {a_2}C}}\sum \nolimits _{l = 1}^{k - 1} {\frac{{\left( {l - 1} \right) !{{\left( { - C} \right) }^{k - l - 1}}}}{{\left( {k - 1} \right) !{a_2}^l}}} - \frac{{{{\left( { - C} \right) }^{k - 1}}}}{{\left( {k - 1} \right) !}}{E_i}\left( { - {a_2}C} \right) } \right]$.

Proof

Please refer to Appendix 2. $\square$

Let us assume that the ergodic capacity of source to ith relay link for $S_1$ symbol is $C^I_{SR_i}$ and the ergodic capacity of ith relay to destination links for $S_1$ symbol, $C^{I}_{R_iD_1}$ and $C^{I}_{R_iD_2}$. Similarly the ergodic capacity of source to ith relay link for $S_2$ symbol is $C^{II}_{SR_i}$ and the capacity of ith relay to destination link for $S_2$ symbol is $C^{II}_{R_iD_2}$. Using the SINR expressions of (6), (10), (11), and (12),

$$\begin{aligned} \begin{aligned} C^I_{SR_i}&=\mathbb {E}\{log_2(1+\gamma ^I_{R_i})\}, \\ C^I_{R_iD_1}&=\mathbb {E}\{log_2(1+\gamma ^I_{D_1})\}, \\ C^I_{R_iD_2}&=\mathbb {E}\{log_2(1+\gamma ^I_{D_2})\} \end{aligned} \end{aligned}$$

(25)

And,

$$\begin{aligned} \begin{aligned} C^{II}_{SR_i}&=\mathbb {E}\{log_2(1+\gamma ^{II}_{R_i})\},\\ C^{II}_{R_iD_2}&=\mathbb {E}\{log_2(1+\gamma ^{II}_{D_2})\} \end{aligned} \end{aligned}$$

(26)

The ergodic capacity for $S_1$ and $S_2$ are given by [8]

$$\begin{aligned} \begin{aligned} C^I&=min\{C^I_{SR_i},C^I_{R_iD_1},C^I_{R_iD_2}\},\\ C^{II}&= min\{C^{II}_{SR_i},C^{II}_{R_iD_2}\} \end{aligned} \end{aligned}$$

(27)

For our model, effective communication time is $\frac{(1-\alpha )T}{2}$ for source to destination transmission. Hence, the throughput for $S_1$ and $S_2$ are given as

$$\begin{aligned} \tau ^{I}=\frac{(1-\alpha )T/2}{T}C^I , \quad \tau ^{II}=\frac{(1-\alpha )T/2}{T}C^{II}. \end{aligned}$$

(28)

4 Results and Discussion

In this section, several simulation results on the performance of partial relay selection based energy harvesting network with NOMA access technology are presented following our formulation developed above. A Monte Carlo simulation is carried out to analyse the performance of the considered energy harvesting based NOMA network. The considered system parameters are as follow $\alpha =0.3$, $\lambda _{SR_i}=\lambda _{{R_i}{D_1}}=\lambda _{{R_i}{D_2}}=1$, $\eta =0.8$ and $P_S=20$ dBW.

Fig. 3

Outage probability with respect to power allocation factor

The Fig. 3 shows outage probabilities with respect to power allocation factor $(\theta =\frac{a_1}{a_2})$ for different values target SINR $(\gamma _{th})$. We observe that the outage probability dramatically decreases from value 1 with the value of $\theta$. For lower value of $\theta$, the value of $a_1$ is less than value of $a_2$. Due to lower value of $a_1$, signal strength of the desired signal may be less than the interference signal, causing high outage. However, at high value of $(\frac{a_1}{a_2})$, SINR may be higher, causing outage probability to decrease. It is observe that for higher value of target SINR, the outage probability curve is shifted to the right. It is observed that the outage improves for more number relays. We found a feasible region for a specific value of number of relays and target SINR for fairness of NOMA scheme. An increase in target SNR threshold for outage, requires an increase in power allocation factor so as to achieve a region for successful operation of NOMA.

Fig. 4

Outage probability with respect to target SINR

Figure 4 shows the outage probabilities with respect to the target SINR threshold $(\gamma _{th})$ for both the symbols with different number of relays. With the increase of $\gamma _{th}$, the outage for both $S_1$ and $S_2$ increases rapidly. In the lower SINR region, the outage probability for $S_1$ and $S_2$ significantly differ from each other and for higher SINR region the outage probability for both the symbols are close to each others. The system performance is improved for both the symbols as the number of relay is increased. The outage probability for $N_r=3$ and $N_r=5$ are compared. Approximate closed form expression is following same nature of the curve.

Fig. 5

Outage probability with respect to $\gamma$th

Figure 5 shows the outage probabilities for $S_1$ and $S_2$ with respect to target SINR with different values of $\rho$. It is observed that our theoretical results agree well with our simulation results. The outage probabilities for both symbols increase with the target SINR as explained in Fig. 4. Here, outage probabilities for both the symbols are shown assuming perfect CSI $(\rho =1)$ and imperfect CSI $(\rho =0.8)$. When an imperfect CSI is considered, the source node does not have actual knowledge about channel condition between the source and the relay. In presence of imperfect CSI, the channel gain between the source node and the selected relay as obtained on basis of maximizing channel gain, may not have the maximum channel gain in reality. This type of incorrectness may occur due to random variation of fading channel and channel estimation error. Due to the inaccurate selection of relay, lowered value of $\rho$ which indicates higher level of imperfection, gives higher outage probability.

Fig. 6

Throughput of secondary network with respect to energy harvesting time

Figure 6, shows the throughput of secondary network with respect to energy harvesting time $(\alpha )$ for different number of relays and for different power allocation coefficient factor. As the value of $\alpha$ increases, the throughput of the secondary system increases first for lower value of $\alpha$ as harvested energy increases with harvesting duration. For a certain value of $\alpha$, throughput attain a maximum value. Beyond the point, the throughput reduces for further increased value of $\alpha$. It is observed that the nature of the throughput curve is concave, due to the fact that with increased value of $\alpha$, the harvested energy and transmit power of relay increases which leads to higher SINR at destination and improve thereby tends to improve throughput. On the other side, the time fraction part reduces as $\alpha$ increases, which tends to reduce throughput. The throughput is improved for higher number of relays for both the symbols.

5 Conclusion

In this paper, we have analysed the impact of RF energy harvesting technology in NOMA based relay network. The PRS scheme is used to improve the system performance of NOMA based network. The system performance of the network is studied in terms of throughput and outage. We also find a feasible region of the values of power allocation factor where NOMA can be used successfully. The closed form expression for outage probabilities are derived for both the symbols considering the practical aspect of imperfect CSI in relay selection. It is observed that the perfect knowledge about the channel condition always improves the performance. The closed form expressions for outage probabilities for symbols are presented to verify our analysis.

Appendices

Appendix 1: Proof of Proposition I in (21)

To calculate $\mathcal {O}^I_{PRS}$, we need to derive pdf of U and cdf of V, W.

From (19), we can rewrite the CDF of $|\widehat{h}_{SR_{i^{*}}}|^2$, assuming $|\widehat{h}_{SR_{i^{*}}}|^2=U$,

$$\begin{aligned} {f_{{{\left| {{{\widehat{h}}_{{S}R_{i^{*}}}}} \right| }^2}}}\left( x \right) = \sum \limits _{n = 1}^{{N_r} } {\left( {_{ \;n}^{{N_r} }} \right) } \frac{{{{\left( { - 1} \right) }^{n-1}}n}}{{{\lambda _{{S}R}}\left[ {1 + (n+1)\left( {1 - {\rho ^2}} \right) } \right] }}{e^{ - \frac{{nx}}{{{\lambda _{{S}R}}\left[ {1 + (n-1)\left( {1 - {\rho ^2}} \right) } \right] }}}} \end{aligned}$$

(29)

From (2), we can rewrite the cdf of $|h_{RD_1}|^2$, assuming $|h_{RD_1}|^2=V$,

$$\begin{aligned} F_V(v)=1- {e^{ - \frac{v}{{{\lambda _{R{D_1}}}}}}} \end{aligned}$$

(30)

From (3), we can rewrite the cdf of $|h_{RD_2}|^2=W$, assuming $|h_{RD_2}|^2=W$,

$$\begin{aligned} F_W(w)=1- {e^{ - \frac{w}{{{\lambda _{R{D_2}}}}}}} \end{aligned}$$

(31)

From (20), $\mathcal {O}^I_{PRS}$ is given by,

$$\begin{aligned} \begin{aligned} \mathcal {O}^I_{PRS}&={F_{\gamma _{e2e}^I}}\left( {{\gamma _{th}}} \right) =\mathcal {P}_r \{ min(\gamma ^I_{R_{i^*}}, \gamma ^I_{D_1}, \gamma ^I_{D_2} )< \gamma _{th}\}\\&= {P_r}\left\{ {\min \left( {\frac{ a_1 P_S |\widehat{h}_{SR_{i^{*}}}|^2}{a_2 P_S |\widehat{h}_{SR_{i^{*}}}|^2+N_0},\frac{a_1 P_{R_{i^*}} |h_{R_{i^*}D_1}|^2}{a_2P_{R_{i^*}}|h_{R_{i^*}D_1}|^2+N_0 },\frac{a_1 P_{R_{i^*}}|h_{R_{i^*}D_2}|^2}{a_2 P_{R_{i^*}}|h_{R_iD_2}|^2+N_0}} \right)< {\gamma _{th}}} \right\} \\&= {P_r}\left\{ {\min \left( {\frac{ a_1 P_S |\widehat{h}_{SR_{i^{*}}}|^2}{a_2 P_S |\widehat{h}_{SR_{i^{*}}}|^2+N_0},\frac{a_1 \alpha ^{'} P_S |\widehat{h}_{SR_{i^{*}}}|^2 |h_{R_{i^*}D_1}|^2}{a_2\alpha ^{'} P_S |\widehat{h}_{SR_{i^{*}}}|^2|h_{R_{i^*}D_1}|^2+N_0 },\frac{a_1 \alpha ^{'} P_S |\widehat{h}_{SR_{i^{*}}}|^2|h_{R_{i^*}D_2}|^2}{a_2 \alpha ^{'} P_S |\widehat{h}_{SR_{i^{*}}}|^2|h_{R_iD_2}|^2+N_0}} \right) < {\gamma _{th}}} \right\} \\&= 1 - {P_r}\left\{ {\min \left( {\frac{{{a_1}P_S U}}{{{a_2}P_S U + {N_0}}} \ge {\gamma _{th}},\frac{{{a_1}\alpha ^{'} P_S U V}}{{{a_2}\alpha ^{'} P_S U V + {N_0}}} \ge {\gamma _{th}},\frac{{{a_1}\alpha ^{'} P_S U W}}{{{a_2}\alpha ^{'} P_S U W + {N_0}}} \ge {\gamma _{th}}} \right) } \right\} \\&= 1 - \int \limits _{\frac{{{\gamma _{th}}{N_0}}}{{P_S({a_1} - {a_2}{\gamma _{th}})}}}^\infty {\left\{ {1 - {F_V}\left( {\frac{{{\gamma _{th}}{N_0}}}{{\alpha ^{'} P_S u ({a_1} - {a_2}{\gamma _{th}})}}} \right) } \right\} } \left\{ {1 - {F_W}\left( {\frac{{{\gamma _{th}}{N_0}}}{{\alpha ^{'} P_S u({a_1} - {a_2}{\gamma _{th}}})}} \right) } \right\} {f_U}\left( u \right) du\\&= 1 - \int \limits _{\phi }^\infty {\left\{ {1 - {F_V}\left( {\frac{\phi }{{\alpha ^{'}u }}} \right) } \right\} } \left\{ {1 - {F_W}\left( {\frac{{{\phi }}}{{\alpha ^{'} u}}} \right) } \right\} {f_U}\left( u \right) du\\&= 1 - \int \limits _\phi ^\infty {{e^{ - \frac{{\phi }}{{{\alpha ^{'}u}{\lambda _{R{D_1}}}}}\frac{{\phi }}{{{\alpha ^{'}u}{\lambda _{R{D_2}}}}}}}} \sum \limits _{n = 1}^{{N_r}} {\left( {_{\,n}^{{N_r}}} \right) \frac{{{{\left( { - 1} \right) }^{n-1}}n}}{{{\lambda _{{S}R}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}{e^{ - \frac{{nu}}{{{\lambda _{S{R}}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}}} du\\&= 1 - \sum \limits _{n = 1}^{{N_r}} {\left( {_{\,n}^{{N_r}}} \right) \frac{{{{\left( { - 1} \right) }^n}n}}{{{\lambda _{{S}R}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}} \underbrace{\int \limits _\phi ^\infty {{e^{ - \left( {\frac{\phi }{{{\alpha ^{'}}{\lambda _{R{D_1}}}}} + \frac{\phi }{{{\alpha ^{'}}{\lambda _{R{D_2}}}}}} \right) \frac{1}{u} - \frac{{nu}}{{{\lambda _{S{R}}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}}} du}_{{A_1}} \end{aligned} \end{aligned}$$

(32)

where, $A_1=\int \limits _\phi ^\infty {{e^{ - \frac{{{b_1}}}{u} - Cu}}} du$ (for details please see Appendix 3), $b_1=\left( {\frac{1 }{{{\lambda _{R{D_1}}}}} + \frac{1}{{{\lambda _{R{D_2}}}}}} \right) \frac{\phi }{\alpha ^{'}}$, $C={\frac{{n}}{{{\lambda _{S{R}}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}$.

Appendix 2: Proof of Proposition II in (23)

From (22), $\mathcal {O}^{II}_{PRS}$ is given by,

$$\begin{aligned} \begin{aligned} {F_{\gamma _{e2e}^{II}}}\left( {{\gamma _{th}}} \right)&=\mathcal {P}_r \{ min(\gamma ^{II}_{R_{i^*}}, \gamma ^{II}_{D_2} )< \gamma _{th}\}\\&= {P_r}\left\{ {\min \left( {\frac{a_2 P_S |\widehat{h}_{SR_{i^{*}}}|^2}{N_0},\frac{a_2P_{R_{i^*}}|h_{R_{i^*}D_2}|^2}{N_0 }} \right)< {\gamma _{th}}} \right\} \\&= {P_r}\left\{ {\min \left( {\frac{a_2 P_S |\widehat{h}_{SR_{i^{*}}}|^2}{N_0},\frac{a_2 \alpha ^{'} P_S |\widehat{h}_{SR_{i^{*}}}|^2|h_{R_iD_2}|^2}{N_0}} \right) < {\gamma _{th}}} \right\} \\&= 1 - {P_r}\left\{ {\min \left( {\frac{{{a_2}P_S U}}{{ {N_0}}} \ge {\gamma _{th}}, \frac{{{a_2}\alpha ^{'} P_S U W}}{{{N_0}}} \ge {\gamma _{th}}} \right) } \right\} \\&= 1 - \int \limits _{\frac{{{\gamma _{th}}{N_0}}}{{P_S a_2}}}^\infty \left\{ {1 - {F_W}\left( {\frac{{{\gamma _{th}}{N_0}}}{{\alpha ^{'} P_S {a_2} u}}} \right) } \right\} {f_U}\left( u \right) du\\&= 1 - \int \limits _\psi ^\infty {{e^{ - \frac{{\psi }}{{{\alpha ^{'}u}{\lambda _{R{D_2}}}}}}}} \sum \limits _{n = 1}^{{N_r}} {\left( {_{\,n}^{{N_r}}} \right) \frac{{{{\left( { - 1} \right) }^n}n}}{{{\lambda _{{S_i}R}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}{e^{ - \frac{{nu}}{{{\lambda _{S{R}}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}}} du\\&= 1 - \sum \limits _{n = 1}^{{N_r}} {\left( {_{\,n}^{{N_r}}} \right) \frac{{{{\left( { - 1} \right) }^n}n}}{{{\lambda _{{S}R}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}} \underbrace{\int \limits _\psi ^\infty {{e^{ - { \frac{\psi }{{{\alpha ^{'}}{\lambda _{R{D_2}}}u}}} - \frac{{nu}}{{{\lambda _{S{R_i}}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}}} du}_{{A_2}} \end{aligned} \end{aligned}$$

(33)

where, $\psi ={\frac{{{\gamma _{th}}{N_0}}}{{P_S a_2}}}$ $A_2=\int \limits _\psi ^\infty {{e^{ - \frac{{{b_2}}}{u} - Cu}}} du$ (for details please see Appendix 3), $b_2=\frac{\psi }{\alpha ^{'}\lambda _{R{D_2}}}$, $C={\frac{{n}}{{{\lambda _{S{R}}}\left[ {1 + \left( {n - 1} \right) \left( {1 - {\rho ^2}} \right) } \right] }}}$.

Appendix 3

In order to derive (32) and (33), let us consider $A_j$, where $j=1,2$

$$\begin{aligned} \begin{aligned} {A_j}&= \int \limits _{{a_j}}^\infty {{e^{ - \frac{{{b_j}}}{u} - Cu}}du} \qquad \forall j \in [1, 2]\\&=\int \limits _{{a_j}}^\infty {{e^{ - Cu}}\sum \limits _{k = 0}^\infty {\frac{{{{\left( { - 1} \right) }^k}{b_j}^k}}{{k!{u^k}}}} du} \\&= \sum \limits _{k = 0}^\infty {\frac{{{{\left( { - 1} \right) }^k}{b_j}^k}}{{k!}}} \int \limits _{{a_j}}^\infty {\frac{{{e^{ - Cu}}}}{{{u^k}}}du} \\&= \int \limits _{{a_j}}^\infty {{e^{ - Cu}}du} + {b_j}\int \limits _{{a_j}}^\infty {\frac{{{e^{ - Cu}}}}{u}du} + \sum \limits _{k = 2}^\infty {\frac{{{{\left( { - 1} \right) }^k}{b_j}^k}}{{k!}}} \int \limits _{{a_j}}^\infty {\frac{{{e^{ - Cu}}}}{{{u^k}}}du} \\&= \frac{{{e^{ - {a_j}C}}}}{C} - {b_j}\varGamma \left( {0,{a_j}C} \right) + \sum \limits _{k = 0}^\infty {\frac{{{{\left( { - 1} \right) }^k}{b_j}^k}}{{k!}}} \left[ {{e^{ - {a_j}C}}\sum \limits _{l = 1}^{k - 1} {\frac{{\left( {l - 1} \right) !{{\left( { - C} \right) }^{k - l - 1}}}}{{\left( {k - 1} \right) !{a_j}^l}}} - \frac{{{{\left( { - C} \right) }^{k - 1}}}}{{\left( {k - 1} \right) !}}{E_i}\left( { - {a_j}C} \right) } \right] \end{aligned} \end{aligned}$$

(34)

where, ${e^{ - u\mu }}\sum \nolimits _{k = 1}^{n - 1} {\frac{{\left( {k - 1} \right) !{{\left( { - \mu } \right) }^{n - k - 1}}}}{{\left( {n - 1} \right) !{{\left( {u + \beta } \right) }^k}}}} - \frac{{{{\left( { - \mu } \right) }^{k - 1}}}}{{\left( {n - 1} \right) !}}{e^{\beta \mu }}Ei\left[ { - \left( {u + \beta } \right) \mu } \right] ,\;n \ge 2$ [30, §3.353.1].