1 Introduction

Filter bank multicarrier (FBMC) system based on offset quadrature amplitude modulation (OQAM) has been considered as a promising technique for replacing OFDM in future wireless communication systems [1,2,3]. Due to the associated sharp pulse shaping filters, FBMC/OQAM systems efficiently address the problem of power radiated outside the nominal frequency band, which makes these systems attractive for many applications of future mobile broadband systems [4, 5]. Moreover, since FBMC/OQAM requires no cyclic prefix (CP), it has the benefit of high spectral efficiency. In view of successful merger of multiple-input multiple-output (MIMO) with OFDM [6, 7], FBMC/OQAM has been combined with MIMO to enhance the system capacity and/or to increase the diversity gain on time-variant and frequency-selective channels [8, 9].

The channel knowledge at the receiver is mandatory to have reliable data detection in the coherent wireless communication systems, hence channel needs to be estimated accurately. All the nice features of FBMC/OQAM demand orthogonality to hold in the real field only [10]. Consequently, a particular problem of intrinsic interference needs to be solved, which makes channel estimation challenging in FBMC/OQAM. Moreover, while addressing channel estimation in FBMC/OQAM, it is not always possible to import existing schemes from OFDM domain directly. However, despite of the barrier of intrinsic interference, there has been a significant progress in the field of channel estimation for FBMC/OQAM systems, e.g., the authors in [11] have proposed two methods for channel frequency response (CFR) estimation by assuming that the symbol time is much longer than the maximum channel delay spread. The first method uses a pair of real pilots (POP), while the second method is based on the interference approximation method (IAM)Footnote 1. Other variants of the IAM-based CFR estimation in single-input single-output (SISO)-FBMC/OQAM systems are given in [12,13,14,15,16]. A preamble-based time domain channel estimation in FBMC/OQAM systems without any constraint on symbol time, is presented in [17,18,19], where channel is estimated with optimized preambles (optimize with respect to mean square error) using a Gauss-Markov estimator.

Coming to the channel estimation in MIMO-FBMC/OQAM systems, the authors in [20] have extended the idea of IAM-based CFR estimation in MIMO-FBMC/OQAM systems. An IAM-based CFR estimation for MIMO-FBMC/OQAM systems using scattered pilots is presented in [21]. Another variant of the IAM-based channel estimation for MIMO-FBMC/OQAM systems with overhead reduced preambles, has been discussed in [22]. Moreover, a review on the IAM-based CFR estimation for SISO as well as MIMO-FBMC/OQAM systems is given in [23]. In fact, like SISO-FBMC/OQAM systems, most of the channel estimation techniques for MIMO-FBMC/OQAM systems are also based on the IAM model. However, when the maximum channel delay spread is not sufficiently smaller than the symbol time, the IAM based CFR estimation suffers from severe performance degradation. The author in [24] investigates least squares (LS) time domain channel estimation in MIMO-FBMC/OQAM systems which does not require symbol time to be sufficiently longer than than the channel delay spread. However, the work in [24] neither derives the Cramer–Rao lower bound (CRLB) for the estimator proposed therein nor shows its achievability. In this paper, we derive a general time domain channel estimation model for MIMO-FBMC/OQAM systems. Unlike the IAM model, the derived model does not require symbol time to be sufficiently longer than the maximum channel delay spread. To estimate the channel in MIMO-FBMC/OQAM systems based on the time domain model, the key contributions of this paper are as follows. (1) The minimum mean square error (MMSE) and weighted least square (WLS) estimators are proposed; (2) we derive the Cramer–Rao lower bound (CRLB) for the proposed estimators; and (3) it is demonstrated via numerically evaluated results that the proposed estimators not only achieve their respective CRLB bounds, but also significantly outperform the existing IAM and time domain LS estimator.

The remainder of this paper is organized as follows. Next Section discusses MIMO-FBMC/OQAM system model. We revisit the framework of the conventional IAM channel estimation for MIMO-FBMC/OQAM systems in Sect. 3. In Sect. 4, we present the time domain model and proposed estimators (WLS and MMSE) for MIMO-FBMC/OQAM systems. Section 5 presents the simulation results and Sect. 6 concludes the paper.

Notation: The upper bold face and lower bold face letters denote the matrices and vectors, respectively. \(j \triangleq \sqrt{-1}\), \({\mathfrak{R}}\{\cdot \}\) and \({\mathfrak {I}}\{\cdot \}\) represent real and imaginary parts, respectively. The superscripts \((\cdot )^{*}\), \((\cdot )^{T}\) and \((\cdot )^{H}\) represent complex conjugate, transpose and Hermitian operators. The operations \(E[\cdot ]\), \(\text {Var}[\cdot ]\) and \(\text {Cov}[\cdot ]\) denote the expectation, variance and covariance. The, \(\text {Tr}(\cdot )\) and \(x[k]*y[k]\) represent trace and convolution of x[k] with y[k]. \(\vert \vert \varvec{\varDelta } \vert \vert _{F}\) denotes the frobenius norm of the matrix \(\varvec{\varDelta }\) and \(\varvec{I}_{N}\) represents an \(N\times N\) identity matrix. Further, \(\vert \varvec{C} \vert\) denotes the determinant of matrix \(\varvec{C}\) and \({\mathbb {Z}}\) represents the set of integers. Furthermore, \(\text {diag}\left[ \gamma _{0}\ \gamma _{1}\cdots \ \gamma _{L_{h}-1}\right]\) represents \(L_{h}\times L_{h}\) diagonal matrix with diagonal entries \(\left[ \gamma _{0}\ \gamma _{1}\cdots \ \gamma _{L_{h}-1}\right]\) and \(\varvec{0}_{L}\) denotes a zero matrix of size \(L\times L\). Finally, the upper bold face letter with a dot on the top e.g. \({\dot{\varvec{C}}}\), represents a block matrix.

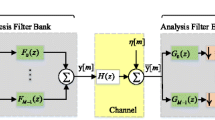
2 MIMO-FBMC/OQAM System Model

The discrete-time equivalent baseband signal for MIMO-FBMC/OQAM system at the t-th transmit antenna is written as [10]

$$\begin{aligned} s^{t}[k]=\sum _{m=0}^{N-1} \sum _{n\in {\mathbb {Z}}}^{}d^{t}_{m,n}\chi _{m,n}[k],\ \ \text {for}\ 1\le t\le N_{t}, \end{aligned}$$
(1)

where k is the sample index, \(d^{t}_{m,n}\) represents real valued OQAM symbol for the t-th transmit antenna at sub-carrier and symbol time indices m and n, receptively, N is the (even) number of sub-carriers and \(N_{t}\) represents the number of transmit antennas. The basis function

$$\begin{aligned} \chi _{m,n}[k]= & {} p[k-n M]e^{j\dfrac{2\pi }{N}mk}e^{j\phi _{m,n}}, \end{aligned}$$
(2)

where \(M=N/2\) and p[k] is a discrete-time symmetrical real valued pulse of length \(N_{p}\) which is generally different from the rectangular pulse. The phase factor \(\phi _{m,n}\) is defined as modulo \(\pi\), e.g., \(\phi _{m,n}= (\pi /2)(m+n)-\pi mn\) [25]. The real valued OQAM symbols (each of duration T / 2) \(d^{t}_{m,n}\) are drawn by extracting the real and imaginary parts of the complex QAM symbol with an offset of T / 2, where T is the QAM symbol duration. Further, the OQAM symbols \(d^{t}_{m,n}\) are assumed to be spatially and temporally independent and identically distributed (i.i.d.) with power \(\sigma ^{2}_{d}\) such that \(E \left[ d^{t}_{m,n}\left( d^{t}_{m,n}\right) ^{*}\right] =\sigma ^{2}_{d}\). In order to recover the symbols \(d^{t}_{m,n}\), \(\chi _{m,n}[k]\) are the basis functions satisfying the following orthogonality condition in the real field [10]

$$\begin{aligned} {\mathfrak {R}}\left\{ \sum _{k=-\infty }^{+\infty }\chi _{m,n}[k]\chi _{{\bar{m}},{\bar{n}}}^{*}[k] \right\} =\delta _{m,\bar{m}}\delta _{n,\bar{n}}, \end{aligned}$$
(3)

where \(\delta _{m,n}\) denotes the Kronecker delta. For ease of mathematical analysis, we define

$$\begin{aligned} \xi ^{\bar{m},\bar{n}}_{m,n}=\sum _{k=-\infty }^{+\infty }\chi _{m,n}[k]\chi _{\bar{m},\bar{n}}^{*}[k]= \left\{ \begin{array}{@{}ll@{}} 1, &{} \text {if}\ (m,n)=(\bar{m},\bar{n}) \\ \text {Imaginary}, &{}\text {if}\ (m,n)\ne (\bar{m},\bar{n}). \end{array}\right. \end{aligned}$$
(4)

The difference between OFDM and FBMC/OQAM lies in the choice of the prototype pulse p[k]. In classical OFDM, p[k] is the rectangular pulse of duration T, whereas in FBMC/OQAM, the duration of the pulse p[k] is greater than T (usually, an integer multiple of T). Hence, unlike OFDM, the successive data symbols in FBMC/OQAM overlap in the time domain. The increased duration of the pulse p[k] in FBMC/OQAM allows each sub-carrier to be shaped by a well frequency–time (FT) localized prototype filter, which is different from the traditional rectangular pulse in classical OFDM with its Sinc-shaped spectrum. Moreover, good frequency–time localization of the prototype pulse in FBMC/OQAM allows for removing the cyclic prefix typically applied in classical OFDM in order to combat the inter-symbol interference (ISI) problem. Note that these features come with following major changes: (1) The QAM symbol of duration T in OFDM is replaced by the real OQAM symbol of duration T / 2 in FBMC/OQAM; and (2) unlike OFDM, orthogonality in FBMC/OQAM holds in the real field only as shown in (3).

The signal received at the r-th receive antenna is given as

$$\begin{aligned} y^{r}[k]=\sum _{t=1}^{N_{t}} \left( s^{t}[k]*h^{r,t}[k]\right) + \eta ^{r}[k],\ \text {for}\ 1\le r\le N_{r}, \end{aligned}$$
(5)

where \(N_{r}\) denotes the number of receive antennas, \(h^{r,t}[k]\) is an \(L_{h}\) tap multipath fading channel between t-th transmit and r-th receive antenna and the term \(\eta ^{r}[k]\) is temporally and spatially white noise at the r-th receive antenna, and is distributed as \({\mathcal {C}}\mathcal {N}(0,\sigma ^{2})\).

At the receiver, the demodulated signal at the r-th receive antenna at the sub-carrier index \(\bar{m}\) and symbol time index \(\bar{n}\) is obtained as [10]

$$\begin{aligned} y^{r}_{\bar{m},\bar{n}}=\sum _{k=-\infty }^{+\infty } y^{r}[k] \chi _{\bar{m},\bar{n}}^{*}[k]. \end{aligned}$$
(6)

Substituting (1), (2) and (5) in (6), \(y^{r}_{\bar{m},\bar{n}}\) is written as

$$\begin{aligned} y^{r}_{\bar{m},\bar{n}}= & {} \sum _{t=1}^{N_{t}} \sum _{m=0}^{N-1} \sum _{n\in {\mathbb {Z}}}^{} d^{t}_{m,n} \sum _{l=0}^{L_{h}-1}h^{r,t}[l]e^{-j\dfrac{2\pi }{N}ml}\sum _{k}^{} p[k-l-nM]p[k-\bar{n}M] \nonumber \\&e^{j(\phi _{m,n}-\phi _{\bar{m},\bar{n}})}e^{j\dfrac{2\pi }{N}(m-\bar{m})k}+\eta ^{r}_{\bar{m},\bar{n}}, \end{aligned}$$
(7)

where

$$\begin{aligned} \eta ^{r}_{\bar{m},\bar{n}}= \sum _{k=-\infty }^{+\infty }\eta ^{r}[k]\ \chi _{\bar{m},\bar{n}}^{*}[k] \end{aligned}$$
(8)

is the demodulated noise at the r-th receive antenna.

3 Frequency Domain Channel Estimation Model

In this section, we revisit the conventional IAM-based CFR estimation for MIMO-FBMC/OQAM systems. The IAM model is based on the assumption that the symbol time is sufficiently longer than the maximum channel delay spread. Since, the IAM model estimates the CFR, it is a frequency domain channel estimation method.

Under the assumption that the symbol time is sufficiently longer than the maximum channel delay spread, the prototype pulse p[k] has low variations in time over the channel length and the following condition holds approximately true [11] i.e.

$$\begin{aligned} p[k-l-nM]\approx p[k-nM]\ \ \text {for} \ \ l\in [0,\, L_{h}]. \end{aligned}$$
(9)

However, when the above condition does not hold, the frequency domain method suffers from severe performance degradation. Substituting (9) in (7), we get

$$\begin{aligned} y^{r}_{\bar{m},\bar{n}}\approx \sum _{t=1}^{N_{t}}\sum _{m=0}^{N-1} \sum _{n\in {\mathbb {Z}}}^{}d^{t}_{m,n} H^{r,t}_{m}\xi ^{\bar{m},\bar{n}}_{m,n}+\eta ^{r}_{\bar{m},\bar{n}}, \end{aligned}$$
(10)

where

$$\begin{aligned} H^{r,t}_{m}=\sum _{l=0}^{L_{h}-1}h^{r,t}[l]e^{-j\dfrac{2\pi }{N}ml} \end{aligned}$$
(11)

is the CFR of the channel from t-th transmit to the r-th receive antenna at m-th sub-carrier. In this paper, the CFR \(H^{r,t}_{m}\) is assumed to be time invariant over a frame. Solving (10), we get

$$\begin{aligned} y^{r}_{\bar{m},\bar{n}}= \sum _{t=1}^{N_{t}}H^{r,t}_{\bar{m}} \left( d^{t}_{\bar{m},\bar{n}}+\underbrace{\sum _{\begin{array}{c} m\ne \bar{m} \\ n\ne \bar{n} \end{array}}^{} d^{t}_{m,n} \dfrac{H^{r,t}_{m}}{H^{r,t}_{\bar{m}}}\xi ^{\bar{m}, \bar{n}}_{m,n}}_{\text {Interference}}\right) +\eta ^{r}_{\bar{m}\bar{n}}. \end{aligned}$$
(12)

Assuming that the prototype filter is well FT localized. Then, the interference due to the FT points outside the neighborhood \(\Omega _{\bar{m},\bar{n}}\)\((\text {excluding}\ (\bar{m},\bar{n}))\) of FT point \((\bar{m},\bar{n})\), is negligibleFootnote 2 [11]. In addition, if the CFR is constant over the neighborhood \(\Omega _{\bar{m},\bar{n}}\) of the FT point \((\bar{m},\bar{n})\), (12) is simplified as [20, 23]

$$\begin{aligned} y^{r}_{\bar{m},\bar{n}}\approx \sum _{t=1}^{N_{t}} H^{r,t}_{\bar{m}}\ c^{t}_{\bar{m},\bar{n}}+\eta ^{r}_{\bar{m},\bar{n}}, \end{aligned}$$
(13)

where \(c^{t}_{\bar{m},\bar{n}} = d^{t}_{\bar{m},\bar{n}}+I^{t}_{\bar{m},\bar{n}}\) is the virtual symbolFootnote 3 at frequency–time point \((\bar{m},\bar{n})\) with imaginary intrinsic interference

$$\begin{aligned} I^{t}_{\bar{m},\bar{n}} = \sum _{\begin{array}{c} (m,n)\in \Omega _{\bar{m},\bar{n}} \end{array}} d^{t}_{m,n}\xi ^{\bar{m},\bar{n}}_{m,n}. \end{aligned}$$
(14)

Since \(E\left[ d^{t}_{m,n}\left( d^{t}_{m,n}\right) ^{*}\right] =\sigma ^{2}_{d}\), from [11], we have \(E\left[ c^{t}_{m,n}\left( c^{t}_{m,n}\right) ^{*}\right] \approx 2\sigma ^{2}_{d}\). For convenience, (13) can be written in the vector form as

$$\begin{aligned} \varvec{y}_{\bar{m},\bar{n}}\approx \varvec{H}_{\bar{m}}\varvec{c}_{\bar{m},\bar{n}}+ \varvec{\eta }_{\bar{m},\bar{n}}, \end{aligned}$$
(15)

where \(\varvec{y}_{\bar{m},\bar{n}}=[y^{1}_{\bar{m},\bar{n}}\ y^{2}_{\bar{m},\bar{n}} \ \ldots \ y^{N_{r}}_{\bar{m},\bar{n}}]^{T}\) is \(N_{r}\times 1\) vector of received symbols at frequency–time index \((\bar{m},\bar{n})\), \(\varvec{\eta }_{\bar{m},\bar{n}}=[\eta ^{1}_{\bar{m},\bar{n}}\ \eta ^{2}_{\bar{m},\bar{n}}\ \ldots \)\(\eta ^{N_{r}}_{\bar{m},\bar{n}}]^{T}\) is the corresponding noise vector such that \(E[\varvec{\eta }_{\bar{m},\bar{n}}\varvec{\eta }_{\bar{m},\bar{n}}^{H}]=\sigma ^{2}_{\eta }\varvec{I}_{N_{r}}\), \(\varvec{c}_{\bar{m},\bar{n}}=[c^{1}_{\bar{m},\bar{n}}\ c^{2}_{\bar{m},\bar{n}} \ \ldots \ c^{N_{t}}_{\bar{m},\bar{n}}]^{T}\) is \(N_{t}\times 1\) vector of virtual symbols such that \(E[\varvec{c}_{\bar{m},\bar{n}}\varvec{c}_{\bar{m},\bar{n}}^{H}]=2\sigma ^{2}_{d}\varvec{I}_{N_{t}}\) and \(\varvec{H}_{\bar{m}}\) is an \(N_{r}\times N_{t}\) CFR matrix which is given as

$$\begin{aligned} \varvec{H}_{\bar{m}}= \begin{bmatrix} H^{1,1}_{\bar{m}}&H^{1,2}_{\bar{m}}&\dots&H^{1,N_{t}}_{\bar{m}} \\\\ H^{2,1}_{\bar{m}}&H^{2,2}_{\bar{m}}&\dots&H^{2,N_{t}}_{\bar{m}} \\ \vdots&\vdots&\ddots&\vdots \\ H^{N_{r},1}_{\bar{m}}&H^{N_{r},2}_{\bar{m}}&\dots&H^{N_{r},N_{t}}_{\bar{m}} \end{bmatrix}. \end{aligned}$$
(16)

For \(0\le \bar{m}\le N-1\), we write the \(N_{r}\times NN_{t}\) MIMO-CFR matrix as

$$\begin{aligned} \varvec{H} = \left[ \varvec{H}_{0}, \varvec{H}_{1},\ldots , \varvec{H}_{N-1}\right] . \end{aligned}$$
(17)

From (15), it is clear that the IAM model requires atleast \(N_{t}\) nonzero preamble symbols to estimate the CFR matrix at each sub-carrier. Figure 1 shows the frame structure for preamble-based MIMO-FBMC/OQAM system [20, 23]. As explained in the previous section that the adjacent FBMC/OQAM symbols overlap in the time domain, z zero symbols have been insertedFootnote 4 between adjacent preamble symbols to reduce ISI as shown in Fig. 1. Note that in view of inter-frame time gaps commonly used in wireless communication, the insertion of zero symbols at the beginning of the frame is in general unnecessary [23]. It is obvious that z should be as small as possible to have batter spectral efficiency. It is shown in the Sect. 5 that \(z=1\) is sufficient to ignore the ISI among the preamble symbols. With \(z=1\), the MIMO-FBMC/OQAM systems requires an overhead (nonzero preambles plus zeros) of atleast \(2N_{t}\) OQAM symbols for estimating channel at each sub-carrier. This is equivalent to \(N_{t}\) complex QAM symbols. On the other side, MIMO–OFDM requires atleast \(N_{t}\) QAM symbols for estimating channel on each sub-carrier [26]. Thus, the overhead requirement for channel estimation for MIMO-FBMC/OQAM is same as that of MIMO–OFDM.

The \(N_{t}\) nonzero preambles are located at the \(q(1+z)\) locations on the symbol time axis with \(0\le q\le N_{t}-1\). Using this preamble structure, it is shown in the “Appendix” that the interference can be calculated the at the nonzero preamble locations as

$$\begin{aligned} I^{t}_{\bar{m},q(1+z)} =\displaystyle \sum _{m=0,\, \begin{array}{c} m\ne \bar{m} \end{array}}^{N-1} d^{t}_{m,q(1+z)}\xi ^{\bar{m},0}_{m,0}. \end{aligned}$$
(18)

Now, by writing (15) at nonzero preamble locations, we get

$$\begin{aligned} \varvec{Y}_{\bar{m}}\approx \varvec{H}_{\bar{m}}\varvec{C}_{\bar{m}}+ \varvec{\eta }_{\bar{m}}, \end{aligned}$$
(19)

where \(\varvec{Y}_{\bar{m}}=[\varvec{y}_{\bar{m},0}\ \varvec{y}_{\bar{m},(1+z)}\cdots \varvec{y}_{\bar{m},(N_{t}-1)(1+z)}]\) and \(\varvec{\eta }_{\bar{m}}=[\varvec{\eta }_{{\bar{m}},0}\ \varvec{\eta }_{{\bar{m}},(1+z)}\cdots \varvec{\eta }_{{\bar{m}},(N_{t}-1)(1+z)}]\) are \(N_{r}\times N_{t}\) matrices of received preamble and noise, respectively, and \(\varvec{C}_{\bar{m}}=[\varvec{c}_{{\bar{m}},0} \ \varvec{c}_{{\bar{m}},(1+z)}\cdots \varvec{c}_{{\bar{m}},(N_{t}-1)(1+z)}]\) is an \(N_{t}\times N_{t}\) matrix of virtual preamble symbols. From (19), the LS estimate of CFR matrix using IAM model is obtained as

$$\begin{aligned} {\hat{\varvec{H}}}_{\bar{m}}=\varvec{Y}_{\bar{m}}\varvec{C}_{\bar{m}}^{\dagger }=\varvec{H}_{\bar{m}}+\varvec{\eta }_{\bar{m}}\varvec{C}_{\bar{m}}^{\dagger }, \end{aligned}$$
(20)

where \(\varvec{C}_{\bar{m}}^{\dagger }=\varvec{C}_{\bar{m}}^{H} \left( \varvec{C}_{\bar{m}}\varvec{C}_{\bar{m}}^{H}\right) ^{-1}\) denotes the Moore–Penrose pseudo-inverse of \(\varvec{C}_{\bar{m}}\). The IAM-based LS estimate of the channel matrix at all the sub-carriers is obtained as

$$\begin{aligned} \widehat{\varvec{H}}_{LS}=\left[ \widehat{\varvec{H}}_{0},\widehat{\varvec{H}}_{1},\ldots ,\widehat{\varvec{H}}_{N-1}\right] . \end{aligned}$$
(21)
Fig. 1
figure 1

Frame structure for the t-th transmit antenna. Here, , ◯ and \(\bigotimes\) represent the preamble, zero and data symbols, respectively. The overhead inside the dotted line box is required for the IAM model, where the preamble structure inside first solid line box is repeated atleast \(N_{t}\) times. However, the overhead inside first solid line box is sufficient for the time domain model

Full size image

3.1 The CRLB of the IAM-Based LS Estimator

From (20), the error matrix at the \(\bar{m}-\text{th}\) sub-carrier for the LS estimator is given as

$$\begin{aligned} \varvec{\varDelta }_{\bar{m}}=\widehat{\varvec{H}}_{\bar{m}}-\varvec{H}_{\bar{m}}=\varvec{\eta }_{\bar{m}}\varvec{C}^{\dagger }_{\bar{m}}. \end{aligned}$$
(22)

Since, \(E[\varvec{\varDelta }_{\bar{m}}]=\varvec{0}\), the covariance matrix of the error is calculated as

$$\begin{aligned} E\left[ \varvec{\varDelta }_{\bar{m}}\varvec{\varDelta }_{\bar{m}}^{H}\right] =E\left[ \varvec{\eta }_{\bar{m}}\varvec{C}^{\dagger }_{\bar{m}}\left( \varvec{\eta }_{\bar{m}}\varvec{C}^{\dagger }_{\bar{m}}\right) ^{H}\right] =\dfrac{\text {Tr} \left[ \varvec{C}^{\dagger }_{\bar{m}}{\varvec{C}^{\dagger }_{\bar{m}}}^{H}\right] }{N_{t}}E\left[ \varvec{\eta }_{\bar{m}}\varvec{\eta }_{\bar{m}}^{H}\right] . \end{aligned}$$
(23)

Since \(\text {Tr}\left[ \varvec{C}^{\dagger }_{\bar{m}}\left( \varvec{C}^{\dagger }_{\bar{m}}\right) ^{H}\right] =N_{t}/\left( 2\sigma ^{2}_{d}N_{t}\right)\) and \(E\left[ \varvec{\eta }_{\bar{m}}\varvec{\eta }^{H}_{\bar{m}}\right] =N_{t}\sigma ^{2}_{\eta }\varvec{I}_{N_{r}}\), the error covariance matrix is written as

$$\begin{aligned} E\left[ \varvec{\varDelta }_{\bar{m}}\varvec{\varDelta }_{\bar{m}}^{H}\right] =\dfrac{\sigma ^{2}_{\eta }}{2\sigma ^{2}_{d}}\varvec{I}_{N_{r}}. \end{aligned}$$
(24)

Given the estimation error matrix \(\varvec{\varDelta }_{\bar{m}}\), it is reasonable to consider the mean of the squared Frobenius norm of error matrix as a performance measure. Thus, the CRLB of the LS estimator can be obtained as,

$$\begin{aligned} E\left\{ \left\| \widehat{\varvec{H}}_{\bar{m}}-\varvec{H}_{\bar{m}}\right\| ^{2}_{F} \right\} =\text {Tr}\left( E\left[ \varvec{\varDelta }_{\bar{m}}\varvec{\varDelta }_{\bar{m}}^{H}\right] \right) =\dfrac{\sigma ^{2}_{\eta }}{2\sigma ^{2}_{d}}N_{r}. \end{aligned}$$

The CRLB for the LS estimator in (21), can now be written as

$$\begin{aligned} \text {CRLB}_{LS}=\sum _{\bar{m}=0}^{N-1}E\left[ \left\| \widehat{\varvec{H}}_{\bar{m}}-\varvec{H}_{\bar{m}}\right\| ^{2}_{F} \right] =\dfrac{\sigma ^{2}_{\eta }NN_{r}}{2\sigma ^{2}_{d}}. \end{aligned}$$
(25)

Although, the IAM-based LS channel estimator for FBMC/OQAM systems have been investigated a lot, but any of the works neither derives the CRLB for the LS estimator nor shows its achievability.

4 Time Domain Channel Estimation Model

In this section, we derive a general time domain channel estimation model for MIMO-FBMC/OQAM systems. Unlike the frequency domain model, this model does not impose any constraints on the length of the symbol time. In short, it need not to hold (9) or it does not require channel to be frequency flat.

The preamble symbols \(\lbrace d^{t}_{m,0}\rbrace ^{N-1}_{m=0}\) of the frame are sufficient to estimate the channel using this model. In order to reduce the ISI between this preamble and adjacent data symbols to an acceptable level, z zero symbols have been inserted as shown in Fig. 1. Therefore, from (7), the received preamble at the r-th receive antenna at frequency–time index (\(\bar{m},0\)) is obtained as

$$\begin{aligned} y^{r}_{\bar{m},0} = \sum _{t=1}^{N_{t}} \sum _{l=0}^{L_{h}-1}h^{r,t}[l]D^{t}_{\bar{m},l}+\eta ^{r}_{\bar{m},0}, \end{aligned}$$
(26)

where \(0\le \bar{m}\le N-1\) and \(D^{t}_{\bar{m},l}\) is given as

$$\begin{aligned} D^{t}_{\bar{m},l}= \sum _{m=0}^{N-1} d^{t}_{m,0}e^{j(\phi _{m,0}-\phi _{\bar{m},0})}e^{-j\dfrac{2\pi }{N}ml}\sum _{k=l}^{N_{p}-1} p[k]p[k-l]e^{j\dfrac{2\pi }{N}(m-\bar{m})k}. \end{aligned}$$
(27)

For the analytical convenience, (26) can be written in the vector form as

$$\begin{aligned} \varvec{y}^{r}_{0} = \sum _{t=1}^{N_{t}} \varvec{D}^{t} \varvec{h}^{r,t}+\varvec{\eta }^{r}_{0}, \end{aligned}$$
(28)

where \(\varvec{y}^{r}_{0}=[y^{r}_{0,0}\ \ y^{r}_{1,0}\cdots y^{r}_{N-1,0}]^{T}\) is \(N\times 1\) vector of received preambles at the r-th receive antenna, \({\boldsymbol\eta }^{r}_{0}=[\eta ^{r}_{0,0}\ \ \eta ^{r}_{1,0}\cdots \eta ^{r}_{N-1,0}]^{T}\) is the corresponding \(N\times 1\) noise vector and \(\varvec{h}^{r,t}=[h^{r,t}[0]\ \ h^{r,t}[1]\)\(\cdots h^{r,t}[L_{h}-1]]^{T}\) is the \(L_{h}\times 1\) CIR vector between t-th transmit and r-th receive antennas. The \(N\times L_{h}\) matrix \(\varvec{D}^{t}\) for the t-th transmit antenna is calculated at the receiver using the preamble \(\lbrace d^{t}_{m,0}\rbrace ^{N-1}_{m=0}\) and pulse shaping filter, and its element for \(\bar{m}\)-th row and l-th column is given by \(D^{t}_{\bar{m},l}\). Rewriting (28) as

$$\begin{aligned} \varvec{y}^{r}_{0}= & {} \underbrace{ \begin{bmatrix} \varvec{D}^{1}&\varvec{D}^{2}&\cdots \varvec{D}^{N_{t}} \end{bmatrix}}_{{{\dot{\mathcal {\varvec{D}}}}}} \underbrace{\left[ \begin{array}{c} \varvec{h}^{r,1} \\ \varvec{h}^{r,2}\\ \vdots \\ \varvec{h}^{r,N_{t}} \end{array} \right] }_{\varvec{h}^{r}}+\ \varvec{\eta }^{r}_{0}, \end{aligned}$$
(29)

where \({{\dot{\mathcal {\varvec{D}}}}}\) is a block matrix of size \(N\times N_{t}L_{h}\) and \(\varvec{h}^{r}\) is \(N_{t}L_{h}\times 1\) channel vector consisting of channels from all the transmit antennas to the r-th receive antenna. Next, by concatenating the vectors \(\varvec{y}^{r}_{0}\) for \(1\le r\le N_{r}\), the time domain channel estimation model is given as

$$\begin{aligned}&\underbrace{\left[ \begin{array}{c} \varvec{y}^{1}_{0}\\ \\ \varvec{y}^{2}_{0}\\ \vdots \\ \varvec{y}^{N_{r}}_{0} \end{array} \right] }_{\varvec{y}_{0}}= \underbrace{ \begin{bmatrix} {{\dot{\varvec{\mathcal {D}}}}}&\varvec{0}&\cdots&\varvec{0} \\ \\ \varvec{0}&{{\dot{\varvec{\mathcal {D}}}}}&\cdots&\varvec{0} \\ \vdots&\vdots&\ddots&\vdots \\ \varvec{0}&\varvec{0}&\cdots&{{\dot{\varvec{\mathcal {D}}}}} \end{bmatrix} }_{{\dot{\varvec{\varGamma }}}} \underbrace{\left[ \begin{array}{c} \varvec{h}^{1} \\ \\ \varvec{h}^{2}\\ \vdots \\ \varvec{h}^{N_{r}} \end{array} \right] }_{\varvec{h}}+ \underbrace{\left[ \begin{array}{c} \varvec{\eta }^{1}_{0} \\ \\ \varvec{\eta }^{2}_{0}\\ \vdots \\ \varvec{\eta }^{N_{r}}_{0} \end{array} \right] }_{\varvec{\eta }_{0}} \end{aligned}$$
(30)
$$\begin{aligned}&\varvec{y}_{0}={\dot{\varvec{\varGamma }}} \varvec{h}+\varvec{\eta }_{0}, \end{aligned}$$
(31)

where \(\varvec{y}_{0}\) is \(NN_{r}\times 1\) vectors of received preambles, \(\varvec{\eta }_{0}\) is \(NN_{r}\times 1\) noise vector, \(\varvec{h}\) is \(N_{t}N_{r}L_{h}\times 1\) CIR vector, \({\dot{\varvec{\varGamma }}}\) is an \(NN_{r}\times N_{t}N_{r}L_{h}\) matrix determined by the preamble \(\lbrace d^{t}_{m,0}\rbrace ^{N-1}_{m=0}\) and pulse shaping filter, and ‘\(\varvec{0}\)’ is an \(N\times N_{t}L_{h}\) zero matrix.

Since, the orthogonality condition in FBMC/OQAM holds only in the real field, the noise across the sub-carriers at the r-th receive antenna in (29), is correlated [14]. The expectation of noise \(\eta ^{r}_{\bar{m},0}\) is

$$\begin{aligned} E\left[ \eta ^{r}_{\bar{m},0}\right] = E \left[ \sum _{k=-\infty }^{+\infty }\eta ^{r}[k]\chi _{\bar{m},0}^{*}[k]\right] =0. \end{aligned}$$
(32)

Since \(E\left[ \eta ^{r}_{\bar{m},0}\right] =0\), the variance of \(\eta ^{r}_{\bar{m},0}\) is

$$\begin{aligned} \text {Var}\left[ \eta ^{r}_{\bar{m},0}\right] = E \left[ \eta ^{r}_{\bar{m},0}\eta ^{r*}_{\bar{m},0}\right] =\sigma ^{2}\xi ^{\bar{m},0}_{\bar{m},0}=\sigma ^{2}. \end{aligned}$$
(33)

Thus, \(\eta ^{r}_{\bar{m},0}\backsim \mathcal {CN}(0,\sigma ^{2})\). The covariance between \(\eta ^{r}_{\bar{m}_{1},0}\) and \(\eta ^{r}_{\bar{m}_{2},0}\) for \(0\le \bar{m}_{1},\bar{m}_{2}\le N-1\) is given as

$$\begin{aligned} \text {Cov}\left[ \eta ^{r}_{\bar{m}_{1},0},\eta ^{r*}_{\bar{m}_{2},0}\right] = E \left[ \eta ^{r}_{\bar{m}_{1},0}\eta ^{r*}_{\bar{m}_{2},0}\right] =\sigma ^{2}\xi ^{\bar{m}_{1},0}_{\bar{m}_{2},0}. \end{aligned}$$
(34)

Therefore, the noise vector \(\varvec{\eta }^{r}_{0}\backsim \mathcal {CN}(\varvec{0},\varvec{R}_{\varvec{\eta }^{r}_{0}\varvec{\eta }^{r}_{0}})\), where \(\varvec{R}_{\varvec{\eta }^{r}_{0}\varvec{\eta }^{r}_{0}}= E[\varvec{\eta }^{r}_{0}\varvec{{\eta }^{r}}^{H}_{0}]\) is the \(N\times N\) noise covariance matrix whose element for \(\bar{m}_{1}\)-th row and \(\bar{m}_{2}\)-th column is given by \(\sigma ^{2}\xi ^{\bar{m}_{1},0}_{\bar{m}_{2},0}\). Since, the noise \(\eta ^{r}[k]\) is spatially white, \(NN_{r}\times NN_{r}\) covariance matrix \({\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}= E[\varvec{\eta }_{0}\varvec{\eta }^{H}_{0}]\) of the noise vector \(\varvec{\eta }_{0}\) is obtained as

$$\begin{aligned} {\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}= \begin{bmatrix} \varvec{R}_{\varvec{\eta }^{1}_{0}\varvec{\eta }^{1}_{0}}&\varvec{0}_{N}&\dots&\varvec{0}_{N}\\ \varvec{0}_{N}&\varvec{R}_{\varvec{\eta }^{2}_{0}\varvec{\eta }^{2}_{0}}&\dots&\varvec{0}_{N} \\ \vdots&\vdots&\ddots&\vdots \\ \varvec{0}_{N}&\varvec{0}_{N}&\dots&\varvec{R}_{\varvec{\eta }^{N_{r}}_{0}\varvec{\eta }^{N_{r}}_{0}} \end{bmatrix}. \end{aligned}$$
(35)

Based on the time domain model in (31), we now propose the WLS and MMSE estimators to estimate the channel vector \(\varvec{h}\).

4.1 WLS Estimator

If we ignore the noise correlations, from (31), the classical LS estimation of \(\varvec{h}\) is given as

$$\begin{aligned} \hat{\varvec{h}}_{LS} = ({\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{\varGamma }}})^{-1}{\dot{\varvec{\varGamma }}}^{H} \varvec{y}_{0}. \end{aligned}$$
(36)

However, since, the noise vector \(\varvec{\eta }_{0}\) is correlated, the LS is not the optimal estimate of \(\varvec{h}\). In order to get the optimal estimate of \(\varvec{h}\), we derive the WLS estimator as

$$\begin{aligned} \min _{\varvec{h}}\left[ \left( \varvec{y}_{0}-{\dot{\varvec{\varGamma }}}\varvec{h}\right) ^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}\left( \varvec{y}_{0}-{\dot{\varvec{\varGamma }}}\varvec{h}\right) \right] , \end{aligned}$$
(37)

where \({\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}\) is the weighting matrix. The solution of (37) leads to the WLS estimate of \(\varvec{h}\) which is given as

$$\begin{aligned} \hat{\varvec{h}}_{WLS}= & {} \left( {\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}}\right) ^{-1}{\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}\varvec{y}_{0}. \end{aligned}$$
(38)

Here the matrix \({\dot{\varvec{\varGamma }}}\) is tall i.e \(NN_{r}\ge N_{t}N_{r}L_{h}\) or \(N\ge N_{t}L_{h}\). Therefore, we can deploy at most \(\lfloor N/N_{t}L_{h}\rfloor\) number of transmit antennas.

Since, the matrices \({\dot{\varvec{\varGamma }}}\) and \({\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}\) are block diagonal, the matrix \(\left( {\dot{\varvec{\varGamma }}}^{H} {\dot{\varvec{R}}}_{{\varvec{\eta }} _{0}{\varvec{\eta }}_{0}}^{-1} {\dot{\varvec{\varGamma }}}\right) ^{-1}{\dot{\varvec{\varGamma }}}^{H} {\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}\) of size \(N_{r}N_{t}L_{h}\times N_{r}N\) is also a block diagonal matrix with \(N_{r}\) diagonal matrices each of size \(N_{t}L_{h}\times N\). With the knowledge of the matrices \({\dot{\varvec{\varGamma }}}\) and \({\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}\), the block diagonal matrix \(\left( {\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}}\right) ^{-1}{\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}\) can be precomputed at the receiver. Therefore, the complexity of the WLS estimator for estimating all \(N_{t}N_{r}\) channels is \(N_{r}{\mathcal {O}}(NN_{t}L_{h})\).

4.1.1 The CRLB

In this subsection, we derive the CRLB for the WLS estimator given by (38) with the assumption that there is no ISI between the preamble symbols \(\lbrace d^{t}_{m,0}\rbrace ^{N-1}_{m=0}\) and the adjacent data symbols.

The log-likelihood function of the model in (31) is written as

$$\begin{aligned} \text {ln} f (\varvec{y}_{0};\,\varvec{h})=-\dfrac{N}{2} \text {ln}(2\pi ) - \dfrac{1}{2}\text {ln}\vert {\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}\vert -\left( \varvec{y}_{0}-{\dot{\varvec{\varGamma }}}\varvec{h}\right) ^{H} {\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}\left( \varvec{y}_{0}-{\dot{\varvec{\varGamma }}}\varvec{h}\right) . \end{aligned}$$
(39)

Taking the derivative of (39) with respect to \(\varvec{h}^{*}\)

$$\begin{aligned} \dfrac{\partial \ \text {ln}\ f\left( \varvec{y}_{0};\varvec{h}\right) }{\partial \varvec{h}^{*}}= & {} {\dot{\varvec{\varGamma }}}^{H} {\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}\varvec{y}_{0}-{\dot{\varvec{\varGamma }}}^{H} {\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}}\varvec{h} \nonumber \\= & {} {\dot{\varvec{\varGamma }}}^{H} {\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}} \left[ ({\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}})^{-1}{\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}\varvec{y}_{0}-\varvec{h}\right] . \end{aligned}$$
(40)

Substituting (38) in (40), we get

$$\begin{aligned} \dfrac{\partial \ \text {ln}\ f\left( \varvec{y}_{0};\,\varvec{h}\right) }{\partial \varvec{h}^{*}}=\varvec{I}(\varvec{h})\left[ \hat{\varvec{h}}_{WLS}-\varvec{h}\right] , \end{aligned}$$
(41)

where \(\varvec{I}(\varvec{h})={\dot{\varvec{\varGamma }}}^{H} {\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}}\) is an \(N_{t}L_{h}\times N_{t}L_{h}\) Fisher information matrix. Since, the equality condition is satisfied in (41), \(\hat{\varvec{h}}_{WLS}\) is an efficient and minimum variance unbiased (MVU) estimator of \(\varvec{h}\) [27]. Therefore, the CRLB for the WLS estimator is calculated as

$$\begin{aligned} \text {CRLB}\left( \varvec{h}_{WLS}\right) = \text {Tr}\left[ {[\varvec{I}(\varvec{h})]}^{-1}\right] =\text {Tr} \left[ \left( {\dot{\varvec{\varGamma }}}^{H} {\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}} \right) ^{-1}\right] . \end{aligned}$$
(42)

4.2 MMSE Estimator

In this paper, all the \(N_{t}N_{r}\) channels are assumed to be zero mean i.i.d. complex Gaussian with exponential power delay profile given as

$$\begin{aligned} \gamma _{l} = \dfrac{e^{-l/2}}{ \sum \nolimits _{l=0}^{L_{h}-1}e^{-l/2}}, \ \ \ \text {for} \ \ \ 0\le l\le L_{h}-1. \end{aligned}$$
(43)

The \(L_{h}\times L_{h}\) channel covariance matrix \(\varvec{R}_{\varvec{h}^{r,t}\varvec{h}^{r,t}} = E[\varvec{h}^{r,t}{\varvec{h}^{r,t}}^{H}]=\text {diag}\left[ \gamma _{0}\ \gamma _{1}\cdots \gamma _{L_{h}-1}\right]\). Next, \(N_{t}L_{h}\times N_{t}L_{h}\) covariance matrix of the channel vector \(\varvec{h}^{r}\) in (29) is

$$\begin{aligned} {\dot{\varvec{R}}}_{\varvec{h}^{r}\varvec{h}^{r}}= \begin{bmatrix} \varvec{R}_{\varvec{h}^{r,1}\varvec{h}^{r,1}}&\varvec{0}_{L_{h}}&\dots&\varvec{0}_{L_{h}} \\ \varvec{0}_{L_{h}}&\varvec{R}_{\varvec{h}^{r,2}\varvec{h}^{r,2}}&\dots&\varvec{0}_{L_{h}} \\ \vdots&\vdots&\ddots&\vdots \\ \varvec{0}_{L_{h}}&\varvec{0}_{L_{h}}&\dots&\varvec{R}_{\varvec{h}^{r,N_{t}}\varvec{h}^{r,N_{t}}} \end{bmatrix}. \end{aligned}$$
(44)

Further, using (44), \(N_{t}N{r}L_{h}\times N_{t}N_{r}L_{h}\) covariance matrix of the channel vector \(\varvec{h}\) in (31) is obtained as

$$\begin{aligned} {\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}= \begin{bmatrix} {\dot{\varvec{R}}}_{\varvec{h}^{1}\varvec{h}^{1}}&\varvec{0}_{N_{t}L_{h}}&\dots&\varvec{0}_{N_{t}L_{h}} \\ \varvec{0}_{N_{t}L_{h}}&{\dot{\varvec{R}}}_{\varvec{h}^{2}\varvec{h}^{2}}&\dots&\varvec{0}_{N_{t}L_{h}} \\ \vdots&\vdots&\ddots&\vdots \\ \varvec{0}_{N_{t}L_{h}}&\varvec{0}_{N_{t}L_{h}}&\dots&{\dot{\varvec{R}}}_{\varvec{h}^{N_{r}}\varvec{h}^{N_{r}}} \end{bmatrix}. \end{aligned}$$
(45)

Since, the mean (\(E[\varvec{h}]=\varvec{0}\)) and covariance of the channel vector \(\varvec{h}\) are available a priori, we can perform the MMSE estimation of the channel \(\varvec{h}\) which is given by the conditional mean \(E[\varvec{h}\vert \varvec{y}_{0}]\). For the linear model in (31), \(E[\varvec{h}\vert \varvec{y}_{0}]\) is determined as [27]

$$\begin{aligned} E[\varvec{h}\vert \varvec{y}_{0}]= E[\varvec{h}]+\varvec{R}_{\varvec{h}\varvec{y}_{0}}\varvec{R}_{\varvec{y}_{0}\varvec{y}_{0}}^{-1} \left( \varvec{y}_{0}- E[\varvec{y}_{0}]\right) . \end{aligned}$$
(46)

Since, \(E[\varvec{h}]=\varvec{0}\), from (31), \(E[\varvec{y}_{0}]=\varvec{0}\). Therefore,

$$\begin{aligned} \varvec{R}_{\varvec{y}_{0}\varvec{y}_{0}}= E\left[ \varvec{y}_{0}{\varvec{y}_{0}}^{H}\right] ={\dot{\varvec{\varGamma }}}{\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}{\dot{\varvec{\varGamma }}}^{H}+{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}} \end{aligned}$$
(47)
$$\begin{aligned} \varvec{R}_{\varvec{h}\varvec{y}_{0}}= E\left[ \varvec{h}{\varvec{y}_{0}}^{H}\right] ={\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}{\dot{\varvec{\varGamma }}}^{H}. \end{aligned}$$
(48)

Substituting \(\varvec{R}_{\varvec{y}_{0}\varvec{y}_{0}}\) and \(\varvec{R}_{\varvec{h}\varvec{y}_{0}}\) in (46), the MMSE estimate of \(\varvec{h}\) is obtained as

$$\begin{aligned} {\hat{\varvec{h}}}_{MMSE}= & {} {\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}{\dot{\varvec{\varGamma }}}^{H} \left( {\dot{\varvec{\varGamma }}}{\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}{\dot{\varvec{\varGamma }}}^{H}+{\dot{\varvec{R}}} _{\varvec{\eta }_{0}\varvec{\eta }_{0}}\right) ^{-1}\varvec{y}_{0} \nonumber \\= & {} \left( {\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}^{-1}+{\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}}\right) ^{-1}{\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}\varvec{y}_{0}. \end{aligned}$$
(49)

Since, the matrices \({\dot{\varvec{\varGamma }}}\), \({\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}\) and \({\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}\) are block diagonal, the matrix \(\left( {\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}^{-1} +{\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0} \varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}}\right) ^{-1}{\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}\) of size \(N_{r}N_{t}L_{h}\times N_{r}N\) is also a block diagonal matrix with \(N_{r}\) diagonal matrices each of size \(N_{t}L_{h}\times N\). With the knowledge of the matrices \({\dot{\varvec{\varGamma }}}\), \({\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}\) and \({\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}\), the block diagonal matrix \(\left( {\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}^{-1}+{\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}}\right) ^{-1}{\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}\) can be precomputed at the receiver. Therefore, the complexity of the MMSE estimator for estimating all \(N_{t}N_{r}\) channels is \(N_{r}{\mathcal {O}}(NN_{t}L_{h})\). Since, \(\varvec{y}_{0}\) and \(\varvec{h}\) are jointly Gaussian, it is worthwhile to mention that the MMSE estimator is identical to the linear MMSE.

4.2.1 The BCRLB

In this subsection, we derive the BCRLB for the MMSE estimator given by (49) with the assumption of no ISI between preamble symbols \(\lbrace d_{m,0}\rbrace ^{N-1}_{m=0}\) and adjacent data symbols.

Since, the estimation error \(\left( \varvec{h}-\hat{\varvec{h}}\right)\) is a function of two jointly Gaussian random variables \(\varvec{y}_{0}\) and \(\varvec{h}\), the covariance matrix \(\varvec{B}_{\hat{\varvec{h}}_{MMSE}}\) of error is given as [27]

$$\begin{aligned} \varvec{B}_{\hat{\varvec{h}}_{MMSE}}={\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}-\varvec{R}_{\varvec{h}\varvec{y}_{0}}\varvec{R}_{\varvec{y}_{0}\varvec{y}_{0}}^{-1}\varvec{R}_{\varvec{y}_{0}\varvec{h}}. \end{aligned}$$
(50)

Substituting (47) and (48), (50) is written as

$$\begin{aligned} \varvec{B}_{\hat{\varvec{h}}_{MMSE}}= {\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}-{\dot{\varvec{R}}}_{\varvec{h}\varvec{h}} {\dot{\varvec{\varGamma }}}^{H}\left( {\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}+{\dot{\varvec{\varGamma }}}{\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}{\dot{\varvec{\varGamma }}}^{H}\right) ^{-1}{\dot{\varvec{\varGamma }}}{\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}. \end{aligned}$$
(51)

The above equation can be further simplified as

$$\begin{aligned} \varvec{B}_{\hat{\varvec{h}}_{MMSE}}=\left( {\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}^{-1}+{\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}}\right) ^{-1}. \end{aligned}$$
(52)

For the MMSE estimator, the variance of the error is the performance measure. Thus, the BCRLB for this estimator is given as

$$\begin{aligned} \text {BCRLB}(\varvec{h}_{MMSE}) = \text {Tr}\left[ \left( {\dot{\varvec{R}}}_{\varvec{h}\varvec{h}}^{-1}+{\dot{\varvec{\varGamma }}}^{H}{\dot{\varvec{R}}}_{\varvec{\eta }_{0}\varvec{\eta }_{0}}^{-1}{\dot{\varvec{\varGamma }}}\right) ^{-1}\right] . \end{aligned}$$
(53)

5 Numerical Results and Discussion

We now numerically evaluate the performance of the proposed estimators with the following system settings. (1) A \(2\times 2\) (\(N_{t}=N_{r}=2\)) MIMO-FBMC/OQAM system has been employed, where the real OQAM training and data symbols are drawn by extracting the real and imaginary parts of the 4-QAM symbols. The offset between the real and imaginary parts of the QAM symbols is T / 2; (2) all the \(N_{t}N_{r}\) channels are assumed to be zero mean i.i.d. complex Gaussian with length \(L_{h}=20\) and exponential power delay profile as given in (43); (3) the discrete time prototype filters of length \(N_{p} = 4N\) (\(N=128\)) are obtained by truncating to the interval \([-2T, \ 2T]\) and sampling at a rate of N / T; and (4) the root raised cosine (RRC) [28] with unity roll-off factor and the family of Extended Gaussian function (EGF) prototype filters are used for the simulations.

The EGF function is obtained from the Gaussian function \(g_{\alpha }(x) = (2\alpha )^{1/4}\)\(e^{-\pi \alpha x^{2}},\)\(\alpha >0\), as [29]

$$\begin{aligned} p_{\alpha ,\nu _{0},\tau _{0}}(x)= & {} \dfrac{1}{2}\sum _{k=0}^{\infty }a_{k,\alpha ,\nu _{0}} \left[ g_{\alpha }\left( x+\dfrac{k}{\nu _{0}}\right) g_{\alpha }\left( x-\dfrac{k}{\nu _{0}} \right) \right] \nonumber \\&\times \sum _{l=0}^{\infty }a_{l,1/\alpha ,\nu _{0}}\text {cos}\left( 2\pi l\dfrac{x}{\tau _{0}}\right), \end{aligned}$$
(54)

where \(\nu _{0}\tau _{0}=1/2\) and \(\alpha\) has to be approximately within the range \([1/4,\ 4]\) to get the best time–frequency localization measures [30]. The real coefficients \(a_{k,\alpha ,\nu _{0}}\) are calculated through the rules given in [30, 31]. The IOTA filter, which is perfectly isotropic in time–frequency plane, is a special case of EGF function with \(\alpha =1,\ \nu _{0} = \tau _{0} = 1/\sqrt{2}\). Moreover, along with IOTA filter, two more variants of the EGF function, EGF1 \(\left( p_{3/2,1/\sqrt{2},1/\sqrt{2}}(x)\right)\) and EGF2 \(\left( p_{1/2,1/\sqrt{2},1/\sqrt{2}}(x)\right)\) have also been used for the simulations.

Fig. 2
figure 2

Performance comparison of the WLS and LS estimators with EGF1 prototype filter, \(N_{t}=N_{r}=2, N=128.\)

Full size image
Fig. 3
figure 3

Performance comparison of the WLS and IAM estimators with IOTA prototype filter, \(N_{t}=N_{r}=2, N=128.\)

Full size image

Figure 2 shows the normalized mean square error (NMSE), \(E\left( \vert \vert \hat{\varvec{h}}-\varvec{h}\vert \vert ^{2}/\vert \vert \varvec{h} \vert \vert ^{2}\right)\) comparison of the LS and WLS estimator. As shown, the WLS estimator has considerable performance gain over the LS estimator, because the former does not ignore the noise correlation across different sub-carriers. Hence, it is not advisable to ignore the noise correlations while estimating the channel for MIMO-FBMC/OQAM systems.

Figure 3 shows NMSE comparison of the WLS and IAM channel estimators, where IOTA prototype filter has been used with \(z=1,2,3\). Unlike the IAM estimator, the WLS estimator does not require symbol time to be much greater than the maximum channel delay spread. Therefore, it significantly outperforms the IAM estimator. For the WLS estimator with \(z=1\), the performance floor appears at high SNR due to the ISI of the preamble \(\lbrace d^{t}_{m,0}\rbrace ^{N-1}_{m=0}\) with adjacent data symbols. The IAM estimator with \(z=1\) exhibits NMSE floors at high SNR due to the ISI among the preamble symbols and the ISI between the preamble symbols \(\lbrace d^{t}_{m,(1+z)}\rbrace ^{N-1}_{m=0}\) and adjacent data symbols. The effect of ISI reduces significantly as z increases, and both the estimators report performance gain. In fact, the proposed WLS estimator achieves CRLB with \(z=3\). However, the IAM estimator does not achieve CRLB with \(z=3\) at high SNR, because the assumption of a locally flat CFR in the neighborhood of FT point (\(\bar{m},\bar{n}\)) is not valid with \(N = 128\). Hence there is a residual intrinsic interference (real part of the interference in (12)) which is masked by the noise at low SNR and shows up in the weak noise regime.

Fig. 4
figure 4

Performance comparison of the MMSE and WLS estimators with IOTA prototype filter, \(N_{t}=N_{r}=2, N=128.\)

Full size image
Fig. 5
figure 5

Performance comparison of the MMSE and WLS estimators with different prototype filters at \(z=1\), \(N_{t}=N_{r}=2, N=128.\)

Full size image

Figure 4 shows the NMSE comparison of the proposed estimators (WLS and MMSE). The prior knowledge of the channel mean and covariance matrix is indeed the reason for the better performance of the MMSE estimator. As z increases, the ISI between the preamble \(\lbrace d^{t}_{m,0}\rbrace ^{N-1}_{m=0}\) and adjacent data symbols reduces. Therefore, for both the estimators, it is observed that the NMSE performance improves as z increases. The CRLB bound for both the estimators is derived with the assumption that there is no ISI between the preamble \(\lbrace d^{t}_{m,0}\rbrace ^{N-1}_{m=0}\) and adjacent data symbols. Hence, both the estimators achieve their respective bounds with \(z=3\) (when the ISI with the preamble symbols \(\lbrace d^{t}_{m,0}\rbrace ^{N-1}_{m=0}\) is negligible.). Since, the MMSE estimator approaches the WLS estimator at high SNR, the NMSE gap with a given z reduces with SNR.

Fig. 6
figure 6

Comparision of BER performances with estimated channel and IOTA prototype filter, \(N_{t}=N_{r}=2, N=128.\)

Full size image

Figure 5 displays NMSE of the proposed MMSE and WLS estimators with different prototype filters with \(z=1\). Since in FBMC/OQAM systems, the successive symbols overlap in time, it is obvious that the prototype filter which concentrates more in time domain will result in lesser ISI with the preamble symbols \(\lbrace d^{t}_{m,0}\rbrace ^{N-1}_{m=0}\). Among the prototype filters EGF1, EGF2, IOTA and RRC, EGF1 concentrates most in the time domain, and is followed by the prototype filters IOTA, RRC and EGF2, respectively. Therefore, for both the estimators, the prototype filter EGF1 performs best, and its performance is followed by the prototype filters IOTA, RRC and EGF2, respectively.

Figure 6 shows the bit error rate (BER) versus SNR per bit [32, 33] plot for the MIMO-FBMC/OQAM system with the maximum ratio combining (MRC). The BER of MIMO-FBMC/OQAM system with perfect channel state information (CSI) is also shown for the reference. As shown, the proposed WLS and MMSE estimators perform significantly better than the IAM estimator because, unlike the later, these estimators do not require symbol time to be sufficiently greater than the maximum channel delay spread. Due to the a priori knowledge of the channel mean and covariance, the MMSE estimator performs better than the WLS estimator.

As observe in Figs. 3 and 4 that NMSE performance of the estimators improves as z increases. However, Fig. 6 shows that this performance improvement with z, does not transform to BER improvement. Therefore, it is advisable to use \(z=1\) to reduce ISI among the preamble symbols.

6 Conclusions

A general time domain channel estimation model for MIMO-FBMC/OQAM systems has been derived. The minimum mean square error (MMSE) and weighted least square (WLS) time domain channel estimators have been investigated. As compared to the frequency domain interference approximation method (IAM)-based channel estimator, the designed time domain estimators do not require symbol time to be sufficiently greater than the maximum channel delay spread, and their preamble requirement does not increase with the number of transmit antennas. Numerical results showed that the proposed time domain channel estimators significantly outperform the existing IAM estimator and achieve their respective bounds. The complexity of the proposed MMSE and WLS estimators is same and varies linearly with the number of receive antennas. Since the proposed MMSE and WLS estimators do not require channel to be frequency flat, MIMO-FBMC/OQAM systems based on the time domain model can be operated with fewer number of sub-carriers (minimum \(N_{t}L_{h}\) for the WLS estimator) than those using the IAM estimator. Therefore, to achieve the same performance, the computational complexity of the proposed MMSE and WLS estimators can be less than the IAM estimator.