A Low Pilot-Overhead Preamble for Channel Estimation with IAM Method in FBMC/OQAM Systems

Abstract

For the channel estimation, a large pilot overhead is required due to the imaginary interference in filter-bank multicarrier employing offset quadrature amplitude modulation (FBMC/OQAM) systems. In this paper, we address the pilot reduction and present a short preamble for the classical interference approximation method (IAM). Compared with the conventional preamble consisting of 3 columns symbols, the pilot overhead is equivalent to 2 column symbols in the proposed preamble. It is proven that there exists no performance loss in the proposed preamble at a significantly reduced pilot overhead. To verify the proposed preamble, numerical simulations are carried out with respect to bit error ratio and mean square error.

1 Introduction

As an emerging multicarrier modulation, filter-bank multicarrier employing offset quadrature amplitude modulation (FBMC/OQAM) was firstly proposed in [1]. Owing to the very low spectral sidelobe property, the FBMC/OQAM system exhibits the high-frequency spectrum utilization and has the good ability of asynchronous transmission, attracting much attention [2,3,4] as a promising technique for future communications. Nevertheless, since the orthogonality condition always is satisfied in real-valued field [4], there exists the imaginary interference among transmitted symbols of FBMC/OQAM. As a result, compared with classical orthogonal frequency division multiplexing (OFDM), it is more complex for the channel estimation and requires further investigation in the FBMC/OQAM system.

In [5], the interference approximation method (IAM) was presented to achieve channel estimation of FBMC/OQAM systems. Afterward, the other versions of this method were proposed, i.e., IAM-C [6] and IAM-I [7], in which imaginary-valued pilots are employed to enhance the pseudo-pilot power. However, the conventional pilot preamble for IAM requires 3 column real-valued symbols, i.e., 1 column pilot symbols for the channel estimation and 2 column zero symbols for reducing the interference to pilot symbols. It should be noted that the symbol interval of FBMC/OQAM is only half of that in OFDM systems; hence, the pilot-overhead preamble for IAM is 50% larger than that of OFDM systems [5]. To achieve the goal of the pilot-overhead reduction, pairs of real pilots (POP) method was proposed [5], which only requires 2 columns real-valued pilots. However, the conclusion has existed in [5], i.e., the POP will suffers from the performance loss compared with the IAM due to the poor ability to deal with the channel noise.

In this paper, we devote to reducing the pilot overhead of channel estimation by proposing a short preamble for IAM, which only consists of 2 columns pilots. It is demonstrated that there exists no performance loss in the proposed preamble, at a significantly reduced pilot overhead. Simulations have been done to evaluate the proposed preamble and for comparison, the performance of the POP method has been also given. As a remark, the proposed scheme of this paper can be also applied in the other versions of the IAM method, for instance, and IAM-C [6] and IAM-I [7].

2 Channel Estimation in FBMC/OQAM

In [5], the IAM method has been proposed based on the following model [5]

$$\begin{aligned} \hat{a}_{m,n}\approx H_{m,n}(a_{m,n}+a^{(*)}_{m,n})+\eta _{m,n}, \end{aligned}$$

(1)

where ${a}_{m,n}$ is the transmitted symbol and $\hat{a}_{m,n}$ is the demodulation in FBMC/OQAM. $H_{m,n}$ is the channel frequency response of m-th subcarrier. $a^{(*)}_{m,n}$ stands for the imaginary interference in FBMC/OQAM, i.e.,

$$\begin{aligned} a^{(*)}_{m,n}=\sum _{\varOmega }a_{m,n}\zeta _{m+p,n+q}^{m,n}, \end{aligned}$$

(2)

with $\varOmega = \{(p,q)\mid |p|,|q|\le 1$ and $(p,q)\ne (0,0)\}$. $\zeta _{m+p,n+q}^{m,n}$ could be written

$$\begin{aligned} \zeta _{m+p,n+q}^{m,n}=\zeta _{p,q}^{0,0}= \sum _{l=-\infty }^{\infty }{g[l]g[l+q\frac{M}{2}]e^{\frac{j2 \pi pl}{M}}e^{\frac{j\pi (p+q)}{2}}}, \end{aligned}$$

(3)

where g[l] is the pulse shaping filter of FBMC/OQAM. Note that $\zeta _{m+p,n+q}^{m,n}=1$ for $(p,q)=(0,0)$. Otherwise, $\zeta _{m+p,n+q}^{m,n}$ is imaginary-valued. Furthermore, it is worthwhile to note that for $|p|>1$ or $|q|>1$, $\zeta _{m+p,n+q}^{m,n}$ is close to zero [5]. $\eta _{m,n}$ could be written as

$$\begin{aligned} {\eta _{m,n}=\sum _{l=-\infty }^{\infty }\eta [l] g[l-n \frac{M}{2}]e^{-\frac{j2 \pi ml}{M}}e^{-\frac{j\pi (m+n)}{2}}}, \end{aligned}$$

(4)

where $\eta [l]$ is the additive white Gaussian noise with variance $\sigma ^2$ [8]. Then, the IAM channel estimation is written as [5]

$$\begin{aligned} \hat{H}_{m,n}&=\frac{\hat{a}_{m,n}}{a_{m,n}+a^{(*)}_{m,n}}=H_{m,n}+\frac{\eta _{m,n}}{a_{m,n}+a^{(*)}_{m,n}}, \end{aligned}$$

(5)

where $\hat{H}_{m,n}$ is the estimate of $H_{m,n}$.

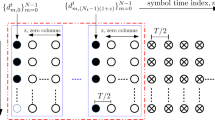
Figure 1a shows the conventional preamble structure, consisting of three columns of pilots, i.e., $a_{m,0}=a_{m,2}=0$ with $m=0,1, \cdots , M-1$, $a_{4l,1}=a_{4l+1,1}=1$ and $a_{4l+2,1}=a_{4l+3,1}=-1$ with $l=0,1, \cdots , \frac{M}{4}-1$. Note that the symbol interval of FBMC/OQAM is half of that in OFDM systems; hence, the pilot overhead of preamble is larger than OFDM.

Fig. 1

Conventional preamble and the proposed preamble in FBMC/OQAM

3 A Novel Preamble with Low Pilot Overhead

In the following, we propose a novel preamble based on IAM, which only consists of 2 columns of pilots. Compared to the conventional scheme in Fig. 1a, the proposed structure reduces 1/3 pilot overhead at a negligible price of channel estimation performance.

3.1 Preamble Structure of the Proposed Scheme

Figure 1b depicts the proposed preamble structure, where $a_{m,1},~m=0,1,\cdots ,M-1$, are pilot symbols. Specifically, $a_{4l,1}=a_{4l+1,1}=1$ and $a_{4l+2,1}=a_{4l+3,1}=-1$ with $l=0,1, \cdots , \frac{M}{4}-1$, which are same as that in Fig. 1a. Differently, 1/3 pilot overhead is saved to transmit additional data symbols (ADS), i.e., $\mathbf {U}=[u_{0},x_{1},\cdots ,u_{M-1}]^{T}$ with $u_{2m}=a_{2m,2}$ and $u_{2m+1}=a_{2m+1,0}$. Since pilot interference is caused by ADS , compensating pilot symbols (CPS) are required and designed to eliminate the interference, i.e., $\mathbf {V}=[v_{0},v_{1},\cdots ,v_{M-1}]^{T}$ with $v_{2m}=a_{2m,0}$ and $v_{2m+1}=a_{2m+1,2}$. Therefore, the total pilot overheads are 2 columns of symbols. To ensure no extra pilot power loss, the power of CPS is from ADS. Since the CPS is designed based on the ADS at the transmitter, the CPS can be used for the channel equalization of the ADS. As a result, the ADS has the similar ability to fight against the noise compared with data symbols as we can see below.

According to (1) and (2), $\boldsymbol{\varPhi }{} \mathbf{U} \mathbf{X}$ and $\boldsymbol{ \varOmega }{} \mathbf{H} \mathbf{V}$ are the interferences to pilots from the ADS and CPS, respectively. To eliminate the interference to pilots, $\boldsymbol{ \varOmega }$ is designed according to the following equation

$$\begin{aligned} \boldsymbol{\varPhi }{} \mathbf{H} \mathbf{U} \;+ \;\boldsymbol{ \varOmega }{} \mathbf{H} \mathbf{V} \;=\; \mathbf{0} , \end{aligned}$$

(6)

where

$$\begin{aligned} \boldsymbol{\varPhi }&= \left( \begin{array}{ccccc} \zeta _{0,2}^{0,1} &{}\zeta _{1,0}^{0,1} &{} \zeta ^{0,1}_{2,2} &{}\cdots &{} \zeta _{M-1,0}^{0,1} \\ \zeta _{0,2}^{1,1} &{}\zeta _{1,0}^{1,1} &{}\zeta _{2,2}^{1,1} &{}\cdots &{} \zeta _{M-1,0}^{1,1} \\ \zeta _{0,2}^{2,1} &{}\zeta _{1,0}^{2,1} &{}\zeta _{2,2}^{2,1} &{}\cdots &{} \zeta _{M-1,0}^{2,1} \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ \zeta _{0,2}^{M-1,1} &{} \zeta _{1,0}^{M-1,1} &{} \zeta ^{M-1,1}_{2,2} &{} \cdots &{}\zeta _{M-1,0}^{M-1,1} \\ \end{array} \right) ,\end{aligned}$$

(7)

$$\begin{aligned} \boldsymbol{\varOmega }&= \left( \begin{array}{ccccc} \zeta _{0,0}^{0,1} &{}\zeta _{1,2}^{0,1} &{} \zeta _{0,2}^{0,1} &{}\cdots &{} \zeta _{M-1,2}^{0,1} \\ \zeta _{0,0}^{1,1} &{}\zeta _{1,2}^{1,1} &{}\zeta _{2,0}^{1,1} &{}\cdots &{} \zeta _{M-1,2}^{1,1} \\ \zeta _{0,0}^{2,1} &{}\zeta _{1,2}^{2,1} &{}\zeta _{2,0}^{2,1} &{}\cdots &{} \zeta _{M-1,2}^{2,1} \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ \zeta _{0,0}^{M-1,1} &{} \zeta _{1,2}^{M-1,1} &{} \zeta _{2,0}^{M-1,1} &{} \cdots &{} \zeta _{M-1,2}^{M-1,1} \\ \end{array} \right) ,\end{aligned}$$

(8)

$$\begin{aligned} \mathbf{H }&= \left( \begin{array}{cccc} H_{0} &{} &{} &{} \\ &{} H_{1} &{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} H_{M-1} \\ \end{array} \right) , \end{aligned}$$

(9)

and $H_{m}=H_{m,0}$. Note that the matrices $\boldsymbol{\varPhi }$ and $\boldsymbol{ \varOmega }$ are known at the receiver, and it is proven that $\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }$ is a unitary matrix, where ${(\cdot )}^{-1}$ is the inverse matrix of a matrix.

Then, the CPS can be obtained according to (6)

$$\begin{aligned} \mathbf{V} =-\mathbf{H} ^{-1}\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }{} \mathbf{H} {} \mathbf{U} . \end{aligned}$$

(10)

However, H is not available for the transmitter, thus, (10) cannot be used for the design of the CPS directly.

Define $\mathbf{C} =\mathbf{H} ^{-1}{} \mathbf{B} ^{-1}{} \mathbf{A} {} \mathbf{H}$, and it could be written as

$$\begin{aligned} \mathbf{C} = \left( \begin{array}{cccc} \frac{H_{0}}{H_{0}}\beta _{00} &{}\frac{H_{0}}{H_{1}}\beta _{01} &{}\cdots &{}\frac{H_{0}}{H_{M-1}}\beta _{0(M-1)} \\ \frac{H_{1}}{H_{0}}\beta _{10} &{}\frac{H_{1}}{H_{1}}\beta _{11} &{}\cdots &{}\frac{H_{1}}{H_{M-1}}\beta _{1(M-1)} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \frac{H_{M-1}}{H_{0}}\beta _{(M-1)1} &{}\frac{H_{M-1}}{H_{1}}\beta _{(M-1)2} &{}\cdots &{}\frac{H_{M-1}}{H_{M-1}}\beta _{(M-1)(M-1)} \\ \end{array} \right) . \end{aligned}$$

(11)

where $\beta _{mn}$ is the (m, n)-th entry of $\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }$. Note that only few entries in each row of $\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }$ can be considered nonzero. Taking the IOTA filter as example, it can be obtained as

$$\begin{aligned} {\left\{ \begin{array}{ll} \sum \limits _{n=0}^{M-1}|\beta _{mn}|^2=1,\\ \\ \sum \limits _{n}|\beta _{mn}|^2\approx 0.9991,~~|m-n|\le 3,~ |m-n|\ge M-3. \end{array}\right. } \end{aligned}$$

(12)

Thus, we can approximately consider that $\beta _{mn}\approx 0$ for $M-3>|m-n|>3$. Obviously, $C_{mn}=\frac{H_{m}}{H_{n}}\beta _{mn}\approx 0$ for $M-3>|m-n|>3$. In addition, the subcarrier spacing of multi-carrier systems is very small compared with the coherence bandwidth. Therefore, for several adjacent subcarriers, their channel frequency responses could be assumed to be constant [5]. Then, we can assume $\frac{H_{m}}{H_{n}}\approx 1$ for $|m-n|\le 3$ or $|m-n|\ge M-3$. Therefore, we can conclude that $C_{mn}\approx \beta _{mn}$ and (13) could be applied to design the CPS,

$$\begin{aligned} \mathbf{V} =-\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }{} \mathbf{U} . \end{aligned}$$

(13)

3.2 Channel Equalization of ADS

In this subsection, it is proven that the CPS can be used for the channel equalization of the ADS. As a result, the ADS has the similar ability to fight against the noise compared with data symbols as we can see below.

From (1), the demodulation of $\hat{\mathbf{V }}$ and $\hat{\mathbf{U }}$ is obtained as

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{\mathbf{U }} &{} = \mathbf{H} \left( \mathbf{U} +\mathbf{U} ^{(*)}\right) +\boldsymbol{\eta }^{u}, \\ \hat{\mathbf{V }} &{} = \mathbf{H} \left( \mathbf{V} +\mathbf{V} ^{(*)}\right) +\boldsymbol{\eta }^{v}, \end{array}\right. } \end{aligned}$$

(14)

where $\mathbf{U} ^{(*)}$ and $\mathbf{V} ^{(*)}$ are the imaginary interference, respectively, i.e., $\mathbf {U}^{(*)}=[u_{0}^{(*)},u_{1}^{(*)}$

$,\cdots ,u_{M-1}^{(*)}]^{\text {T}}$, in which $u_{2k}^{(*)}=a_{2k,2}^{(*)}$ and $u_{2k+1}^{(*)}=a_{2k+1,0}^{(*)}$, $\mathbf {V}^{(*)}=[v_{0}^{(*)},v_{1}^{(*)},\cdots ,v_{M-1}^{(*)}]^{\text {T}}$, in which $v_{2k}^{(*)}=a_{2k,0}^{(*)}$ and $v_{2k+1}^{(*)}=a_{2k+1,2}^{(*)}$. $\boldsymbol{\eta }^{u}=[\eta _{0}^{u},\eta _{1}^{u},\eta ^{u}_{3}, \cdots ,\eta _{M-1}^{u}]^{\text {T}}$ with $\eta _{2i}^{u}=\eta _{2i,2}$ and $\eta _{2i+1}^{u}=\eta _{2i+1,0}$. $\boldsymbol{\eta }^{v}=[\eta _{0}^{v},\eta _{1}^{v},\eta _{2}^{v}, \cdots ,\eta _{M-1}^{v}]^{T}$ with $\eta _{2i}^{v}=\eta _{2i,0}$ and $\eta _{2i+1}^{v}=\eta _{2i+1,1}$.

As shown in (13), there is a linear relationship between $\mathbf{U}$ and $\mathbf{V}$, i.e.,

$$\begin{aligned} \mathbf{U }= \left( -\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }\right) ^{-1}{} \mathbf{V} . \end{aligned}$$

(15)

Let $\tilde{\mathbf{U }}= \left( -\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }\right) ^{-1}\hat{\mathbf{V }}$ and it can be written as

$$\begin{aligned} \tilde{\mathbf{U }}&= \left( -\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }\right) ^{-1}{} \mathbf{H} \left( \mathbf{V} +\mathbf{V} ^{(*)}\right) +\left( -\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }\right) ^{-1}\boldsymbol{\eta }^{v}\nonumber \\&=\left( -\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }\right) ^{-1}{} \mathbf{H} \left( \mathbf{V} +\mathbf{V} ^{(*)}\right) +\tilde{{\boldsymbol{\eta }}}. \end{aligned}$$

(16)

After channel equalization and taking real parts, we have $\mathfrak {R}(\mathbf{H} ^{-1}\tilde{\mathbf{U }})\approx$

$\left( -\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }\right) ^{-1}{} \mathbf{V} =\mathbf{U} =\mathfrak {R}(\mathbf{H} ^{-1}\hat{\mathbf{U }})$ when there is no channel noise. Thus, if the noise $\tilde{{\boldsymbol{\eta }}}$ and $\boldsymbol{\eta }^{u}$ are Gaussian and independent identical distributed, we can use the $\frac{1}{2}\hat{\mathbf{U }}+\frac{1}{2}\tilde{\mathbf{U }}$ as the input of channel equalizer instead of $\hat{\mathbf{U }}$. In this way, the variance of $(\frac{1}{2}\tilde{{\boldsymbol{\eta }}}+\frac{1}{2}\boldsymbol{\eta }^{u})$ is half of that of $\boldsymbol{\eta }^{u}$. In the following, it will be proven that the noise $\tilde{{\boldsymbol{\eta }}}$ and $\boldsymbol{\eta }^{u}$ are identical independent and Gaussian distributed.

According to the definition of $\eta [k]$, it is easily observed that $\eta _{m,n}$ satisfies Gaussian distribution as well, and the variance and covariance can be obtained as (17) and (18), respectively.

$$\begin{aligned} \text {Var}\left[ \eta _{m,n}\right]&=\text {E}\left[ \left( {\sum _{l=-\infty }^{+\infty }\eta [l]g[l-\frac{nM}{2}]e^{-\frac{j2 \pi ml}{M}}e^{-\frac{j(m+n)\pi }{2}}}\right) \right. \nonumber \\&~~~~~\left. \left( {\sum _{l=-\infty }^{+\infty }\eta ^{*}[l]g[l-\frac{nM}{2}]e^{\frac{j2 \pi ml}{M}}e^{\frac{j(m+n)\pi }{2}}}\right) \right] \nonumber \\&={\sigma ^{2}\sum _{l=-\infty }^{\infty }g[l-\frac{nM}{2}]g[l-\frac{nM}{2}]}={\sigma ^{2}}. \end{aligned}$$

(17)

$$\begin{aligned} \text {Cov}\left[ \eta _{m_{1},n_{1}},\eta _{m_{2},n_{2}}\right]&=\text {E}\left[ \left( {\sum _{l=-\infty }^{+\infty }\eta [l]g[l-\frac{n_{1}M}{2}]e^{-\frac{j2 \pi m_{1}l}{M}}e^{-\frac{j(m_{1}+n_{1})\pi }{2}}}\right) \right. \nonumber \\&~~~~~~ \left. \left( {\sum _{l=-\infty }^{+\infty }\eta ^{*}[l]g[l-\frac{n_{2}M}{2}]e^{\frac{j2 \pi m_{2}l}{M}}e^{\frac{j(m_{2}+n_{2})\pi }{2}}}\right) \right] \nonumber \\&={\sigma ^{2}\zeta _{m_{1},n_{1}}^{m_{2},n_{2}}}={\sigma ^{2}\zeta _{m_{1}-m_{2},n_{1}-n_{2}}^{0,0}}. \end{aligned}$$

(18)

Let $e_{mn}$ stands for the element of $\left( -\boldsymbol{\varOmega }^{-1}\boldsymbol{\varPhi }\right) ^{-1}$ at position (m, n). Note that $e_{m(m-1)}=e_{m(m+1)}$. The m-th entries’ covariance of the $\boldsymbol{\eta }^{u}$ and $\tilde{{\boldsymbol{\eta }}}$ could be expressed as

$$\begin{aligned} \text {Cov}\left[ \eta _{m}^{u},\sum _{n=1}^{M-1}e_{m,n}\eta _{n}^{v}\right] =\text {Cov}\left[ \eta _{m}^{u},e_{m,m-1}\eta _{m-1}^{v}+e_{m,m+1}\eta _{m+1}^{v}\right] =0. \end{aligned}$$

(19)

Obviously, the m-th entries of $\boldsymbol{\eta }^{u}$ and $\tilde{{\boldsymbol{\eta }}}$ are independent identically distributed. Thus, according to the maximum likelihood criterion, $\frac{1}{2}\hat{\mathbf{U }}+\frac{1}{2}\tilde{\mathbf{U }}$ could replace $\hat{\mathbf{U }}$ as the input of the equalizer. Compared with $\hat{\mathbf{U }}$, the noise power of $\frac{1}{2}\hat{\mathbf{U }}+\frac{1}{2}\tilde{\mathbf{U }}$ reduces in half, which means that the ADS has similar capability to fight against the noise compared with the data symbols.

4 Simulation Results

In simulations, the following parameters are considered.

• Subcarrier number: 2048

• Sampling rate (MHz): 9.14

• Path number: 6

• Delay of path ( $\mu s$): −3, 0, 2, 4, 7, 11

• Power delay profile (dB): −6.0, 0.0, −7.0, −22.0, −16.0, −20.0

• Modulation: 4QAM

• Channel coding: Convolutional coding [5].

For comparison, this section also gives the performance of pairs of pilots (POP) [5], consisting of two columns of pilots.

Fig. 2

MSE of the proposed scheme

Fig. 3

BER of the proposed scheme

Figure 2 depicts MSE of the proposed preamble in the IAM method. It can be easily seen that the IAM outperforms the POP greatly. Besides, by the IAM method, the proposed preamble achieves similar MSE compared to the conventional preamble. Note that, only two column pilots are needed in the proposed preamble, while the conventional preamble requires three columns of pilots. Therefore, better spectral efficiency can be achieved by our proposed preamble and channel estimation approach.

Figure 3 depticts BER of the proposed preamble in the IAM method. From simulation results, the IAM outperforms the POP greatly, which is accordance to Fig. 2. Besides, the IAM method with the proposed preamble achieves similar BER compared to the conventional preamble, demonstrating the effectiveness of our proposed scheme.

5 Conclusions

In this paper, a novel preamble with low pilot overhead was proposed for FBMC/OQAM. Compared to the conventional preamble consisting of 3 columns symbols, only 2 columns pilot are needed in our scheme. It was proven that, at a significantly reduced pilot overhead, the proposed preamble could exhibit the same performance compared to the conventional preamble. Therefore, by our proposed preamble and channel estimation approach, better spectral efficiency can be achieved in the FBMC/OQAM system.