Cross-Layer Based Asymmetric Resource Allocation in Relay-Aided Cognitive Radio Networks

Abstract

Cross-layer based asymmetric resource allocation in relay-aided cognitive radio networks (CRN) is proposed in this paper. Existing cross-layer schemes on relay-aided CRN are based on symmetric resource allocation (RA) where the transmission duration is assumed to be symmetric between secondary base station (BS) to relay station (RS) and RS to mobile station (MS) links. This may not be realistic and hence our proposed model considers asymmetric resource allocation (ARA) in which the transmission durations are asymmetric. Very little work has been done in ARA for relay-aided networks and most of them considered only power allocation. The queue stability and quality of service (QOS) requirements are other considerations that have a significant impact on RA and hence are considered in this work. The QOS requirements can be brought in terms of the maximum delay threshold and the minimum throughput requirements. The interference threshold is evaluated from the QOS of the primary radio network. Based on the queue state information, channel state information and QOS, resources are allocated to the secondary radio network. Our proposed ARA differs from existing ARA schemes in terms of additionally considering the subcarrier pairing for resource allocation. This work evolves an optimal cross-layer based ARA considering the above mentioned factors into account. The proposed ARA includes subcarrier allocation, subcarrier pairing and power allocation. Simulation results show that the proposed ARA scheme increases the system throughput and serves the edge users satisfactorily.

1 Introduction

The emerging trends in wireless networks have led to the scarcity of resources such as spectrum and power. Cognitive radio network (CRN) is a promising solution to overcome the problem of spectrum scarcity [1]. In the meantime cooperative relay networks (RN) enhance the base station (BS) coverage and the system capacity in wireless communication networks [2]. Relay station (RS) in cooperative relay network can be broadly classified as Amplify and Forward (AF) and Decode and Forward (DF) [3]. Therefore Relay-Aided Cognitive Radio network is proposed as a solution to satisfy the user demands in a resource limited communication system [4]. But to utilize resources of the system effectively, a cross-layer based RA is needed [5]. Cross-layer design based adaptive resource allocation algorithms have been suggested to optimize the system performance and guarantee QOS with the help of channel and system state information in conventional wireless networks [6, 7]. To the best of our knowledge, cross-layer based ARA for relay-aided CRN has not yet been analyzed.

A cross layer based transmission technique was suggested in [8] to guarantee the QOS requirements including delay, bit error rate and overflow. Queue stability was considered in RA where the queue and channel state information are utilized to allocate the resources [9]. These two crosslayer approaches were designed for direct link scenarios. An optimal crosslayer scheme was suggested for RN to guarantee the QOS and queue stability in [5]. In this scheme, however relay selection, SA and SP were ignored. In [4], the PA is proposed for relay aided CRN, but did not consider the power limitation. Maximum power constraint is considered in [10]. Relay selection and PA is achieved for cooperative cognitive radio system in [11]. Solution of relay selection and RA is suggested for Two-Way DF-AF CRN in [12]. In all these above mentioned works subcarrier pairing (SP) in CRN is ignored. SP along with PA is considered in [13] for CRN. SP plays a vital role in RA for CRN. It was first suggested in [14]. SP for AF and DF is proposed in [15]. The joint optimization of SP, subcarrier-pair to relay assignment, and power allocation was proposed in [16]. In [17], joint optimization inclusive of the destination combining has been discussed. For multi-relay network, a PA and SP based algorithm is proposed in [18]. Genetic algorithm based SP was proposed in [19]. All the above mentioned works assume symmetric RA where transmit durations of BS to RS and RS to MS are assumed to be equal. Asymmetric transmit durations is discussed in [20], but they did not consider the RA. An optimum asymmetric resource allocation was proposed for OFDM based RN in [21,22,23]. In [22], ARA was designed for multidestination RS where as in [23], it was designed for multi-relay systems. An ARA was suggested for collaborative RN with imperfect channel state information (CSI) in [24]. These proposed ARA schemes do not consider the queue stability and QOS guarantees.

In this paper we propose a cross-layer based asymmetric resource allocation in relay-aided cognitive radio networks (CARAC) for multidestination relay systems. The objective of the paper is to design a generalized model for DF or AF relay aided CRN which increases the utility of the system subject to queue stability and QOS guarantee. Satisfaction of maximum delay threshold and minimum throughput requirement are considered as QOS guarantees. The proposed scheme is analyzed in a cellular testbed and the simulation results show that the proposed scheme improves the performance of the system.

The major contributions of this paper can be listed as follows:

• 1. The proposed model has been designed to improve the CRN performance with the guarantee of queue stability and QOS, where as in the existing asymmetric RA schemes these two issues have been ignored.

• 2. The interference threshold is formulated from the QOS parameters of the PRN.

• 3. DF and AF relay networks are considered in our proposed model and their performances are compared.

• 4. SP in ARA is proposed in this paper which was ignored in the previous existing works.

• 5. Simulation results are verified in a cellular testbed. Cellular network parameters such as Blocking ratio and QOS assurance [25] are also compared.

2 System Model

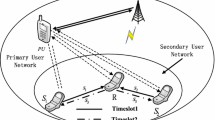
This paper investigates the solution of RA problem in relay-aided cognitive radio networks. As shown in Fig. 1, the proposed system model contains a cognitive BS, $N_R$ number of RSs and MS in the SRN. The CSI is assumed to be available at the MS and is then fed back to the BS. Based on the CSI, QSI and QOS, secondary BS allocate the resources in the system. In this system total bandwidth $(B_w)$ is divided into N independent subchannels. The bandwidth of each subchannel is $B=B_w/N$. Let $h_{BR,i}$ be the ith ($i \in \{1\ldots ,N\}$) BS to RS subchannel gain and $h_{RM,j}$ be the jth ($j \in \{1\ldots ,N\}$) RS to MS subchannel gain, respectively in the secondary system.¹ Rayleigh fading is assumed. Similarly $l_{BR}$ and $l_{RM}$ are path loss components of BS to RS and RS to MS channels, respectively. Let $l_{BP}$ and $l_{RP}$ be the path loss component of the secondary BS to primary source and secondary RS to primary source links with the fading channel coefficients of $h_{BP,i}$ and $h_{RP,j}$ over the subchannels i and j, respectively. Let $P_{BR,i}$ and $P_{RM,j}$ be the transmit power of first and second hop over the subchannel i and j, respectively. Additive white Gaussian noise (AWGN) is assumed at both RS and MS and has the power spectral density of $N_0.$ Let $n_{BR}$ and $n_{RM}$ be the noise components of first and second hop with noise variances $\sigma _{BR}^2$ and $\sigma _{RM}^2,$ respectively. $T_1$ and $T_2$ are transmit durations of the first and second hops which are assumed to be asymmetric i.e $(T_1\ne T_2).$

Fig. 1

System model

To facilitate the readability of the paper, the most significant notations are summarized in Table 1.

Table 1 Summary of most significant notations

2.1 DF Relay Model

Let X be the source transmitted symbol,² then considering the above defined model the received symbol at RS over the subchannel i, is

$$Z = \sqrt{P_{BR,i}l_{BR}}h_{BR,i}X + n_{BR}$$

(1)

After the successful decoding at RS, RS will re-encode the symbol as W and the received symbol at MS over the subchannel j is,

$$Y = \sqrt{P_{RM,j}l_{RM}}h_{RM,j}W + n_{RM}$$

(2)

The SNR of first and second hop with subchannel i and j can be written as,

$$\gamma _{DL,i,1}= \frac{P_{BR,i}l_{BR}|h_{BR,i}|^2}{\sigma _{BR}^2}$$

(3)

$$\gamma _{DL,j,2}= \frac{P_{RM,j}l_{RM}|h_{RM,j}|^2}{\sigma _{RM}^2}$$

(4)

2.2 AF Relay Model

For AF relaying, the received symbol at relay can be written as,

$$Z = \sqrt{P_{BR,i}l_{BR}}h_{BR,i}X + n_{BR}$$

(5)

Received symbol is amplified by a gain factor G in AF relay and the received symbol at MS is,

$$\begin{aligned}Y &= \sqrt{P_{RM,j}P_{BR,i}Gl_{BR}l_{RM}}h_{RM,j}h_{BR,i}X \\&\quad +\sqrt{P_{RM,j,m}l_{RM}G}h_{RM,j}n_{BR} + n_{RM} \end{aligned}$$

(6)

To reduce the impact of noise enhancement, the amplification factor G should be [26]

$$G= \frac{1}{\sigma _{BR}^2+P_{BR,i}|h_{BR,i}|^2l_{BR}}$$

(7)

For simplicity, (6) can be modified as,

$$Y = \tilde{h}X + \tilde{n}+ n_{RM}$$

(8)

where

$$\begin{aligned} \tilde{h} & = \sqrt{P_{RM,j,m}P_{BR,i}Gl_{BR}l_{RM}}h_{RM,j}h_{BR,i}\\ \tilde{n} & = \sqrt{P_{RM,j,m}l_{RM}G}h_{RM,j}n_{BR} \end{aligned}$$

$\tilde{n}$ represents enhanced noise and is modeled as AWGN with zero mean and variance of $\sigma _{\tilde{n}}^2$. For convenience, we represent $|h_{BR,i}|^2l_{BR}$ and $|h_{RM,j}|^2l_{RM}$ as $h_{ri}$ and $h_{rj}$ for rth relay, then the SNR of first and second hop with subchannel i and j in AF relaying can be written as,

$$\gamma _{DL,i,1}= \frac{P_{BR,i}h_{ri}}{\sigma _{BR}^2}$$

(9)

$$\gamma _{DL,j,2}= \frac{P_{BR,i}P_{RM,j}Gh_{ri}h_{rj}}{\sigma _{\tilde{n}}^2+ \sigma _{RM}^2}$$

(10)

2.3 Rate Power Function

Let ${\varGamma }$ be the SNR gap which is defined as a ratio of ideal SNR over a practical SNR. It is a measure of how well the practical system compares to an ideal modulation system and its value depends on the selected Modulation and Coding Scheme (MCS) [5]. The rate power function for SRN corresponding to mth user at first and second hop is written as [21],

$$R_{DL,1}= \sum _{i=1}^N{B\frac{T_1}{T}\log \left( 1+w_{m}\frac{\gamma _{DL,i,1}}{{\varGamma }}\right) }$$

(11)

$$R_{DL,2}= \sum _{j=1}^N{B\frac{T_2}{T}\log \left( 1+w_{m}\frac{\gamma _{DL,j,2}}{{\varGamma }}\right) }$$

(12)

where

$$T=T_1+T_2$$

$w_{m}\in \{0,1\}$ is the channel access parameter for mth MS.

Let us define,

$$\begin{aligned} \xi _{ij,m} &= {} {\left\{ \begin{array}{ll} 1, &{\text{if the subcarrier pair }}(i,j) {\text{ is allotted to MS}}\\ 0, &{\text{otherwise}} \end{array}\right. }\\ \zeta _r & = {} {\left\{ \begin{array}{ll} 1, &{\text{if the relay selection is successful}}\\ 0, &{\text{otherwise}} \end{array}\right. } \end{aligned}$$

$w_{m}$ can then be expressed as,

$$w_{m}= \xi _{ij,m}\zeta _r$$

(13)

The net-throughput can be expressed as,

$$R_{S,DL}=min(R_{DL,1},R_{DL,2})$$

(14)

Let $h_{p,k}$ be the channel gain of the link between PRN source with transmit power of $P_{p,k}$ and its user over the subchannel k and $\sigma _p^2$ is the noise variance of the link, then the downlink capacity of the primary network can be written as,

$$R_{P,DL}=B\sum _{k=1}^{N}\log \left( 1+w_{p,k}\frac{P_{p,k}|h_{p,k}|^2}{{\varGamma }_p(\sigma _{p}^2+I_{k})}\right)$$

(15)

where $I_{k}$ is the interference power over subchannel k.

$$\begin{aligned} I_{k} &= {} {\left\{ \begin{array}{ll} P_{BR,k}|h_{BP,k}|^2, &{} \hbox {if } 1{\rm{st}}\hbox { hop of SRN}\\ P_{RM,k}|h_{RP,k}|^2, &{} \hbox {if}2{\rm{nd}}\hbox { hop of SRN} \end{array}\right. } \end{aligned}$$

(16)

${\varGamma }_p$ is the SNR gap of PRN and $w_{p,k}$ is the access parameter for subchannel k.

$$\begin{aligned} w_{p,k} & = {\left\{ \begin{array}{ll} 1, &{} \hbox {if} \hbox { subcarrier }k\hbox { is selected}\\ 0, &{} \hbox {otherwise} \end{array}\right. } \end{aligned}$$

(17)

2.4 Queue Dynamics

Packets are endogenously generated at higher layers. Let Q[t] be the queue size and a[t] be the arrival rate over the time slot t, respectively. Then, the queue dynamics is represented as follows,³

$$Q[t+1]=Q[t] + \max \left( \widehat{L}a[t] - R_{S,DL}[t],0\right)$$

(18)

where

$$\widehat{L}=\frac{1}{1-\beta }\min (L_1,L_2).$$

(19)

Parameter $\beta$ is the overhead coefficient which considers the packet length variation in the lower layers due to encapsulation and it is bounded as $0 \le \beta < 1$. $L_1$ and $L_2$ are the packet lengths of the first and second hops, respectively.

For a stable queue the following condition has to be satisfied [27].

$$\widehat{L}\bar{a}\le R_{S,DL}$$

(20)

where $\bar{a}$ is the mean arrival rate.

2.5 QOS Requirements

The QOS requirements considered in this paper are maximum delay threshold $D_{th}$ and mean arrival rate threshold $a_{th}$. From little’s formula [28] we can express the maximum delay constraint for SRN as follows,

$$\frac{\widehat{L}}{R_{S,DL}-\widehat{L}\bar{a}} \le D_{th}$$

(21)

From (20) and (21), constraint for queue stability and maximum delay threshold can be formulated as follows,

$$\widehat{L}\bar{a}-R_{S,DL}+\widehat{L}R_D \le 0$$

(22)

where

$$R_D=\frac{1}{D_{th}}$$

Based on their individual QOS each user has a mean arrival rate requirement. To achieve the mean arrival rate requirement the following condition has to be satisfied.

$$a_{th} \le \bar{a}$$

(23)

If the queue stability constraint (22) is achieved, then the mean arrival rate ($\bar{a}$) in the queue can be referred as the system throughput.

2.6 QOS Assurance

QOS assurance decides how many edge users can be served by the BS region. It is defined as follows [25],

$$QOS\,Assurance=\sum _{u \in {\mathbf{I}}_{\mathbf{t}}}\sum _{v\in {\mathbf{S}}}\sum _{t\in {\mathbf{T}}} A(t)r_{uv}$$

(24)

where

$$\begin{aligned} {\mathbf{I}}_{\mathbf{t}}& = {\text{Set\,of\,successful\,calls}}\\ {\mathbf{S}}& = {\text{Available\,set\, of\, cellular\, regions}}\\ {\mathbf{T}}& = {\text{Set\, of\, time\, slots}}\\ A(t)& = {\text{Traffic\, in\, Erlangs\, over\, the\, time\, t}}\\ r_{uv}& = {\left\{\begin{array}{l}{\hbox{Distance between the MS }}\\{\hbox{with successful call }}u \\{\hbox{and BS in region }}v\\ \end{array}\right. } \end{aligned}$$

3 Problem Formulation

The cross-layer based optimal ARA is the solution to constrained utility maximization problem. The objective of this paper is to maximize the utility of the arrival rate with the guarantee of queue stability and QOS. To maximize the utility while satisfying the stability condition in (22), the sum rates at first and second hop must be equal. This constraint can be expressed as follows,

$$\sum _{j=1}^{N}R_{DL,j,2} - \sum _{i=1}^{N}R_{DL,i,1} = 0$$

(25)

If $P_T$ is the maximum power threshold, then the power constraint can be expressed as,

$$\sum _{i=1}^{N}P_{BR,i} + \sum _{j=1}^{N}P_{RM,j}\le {} P_{T}$$

(26)

The interference constraint of the system can be expressed as,

$$\sum _{i=1}^{N}P_{BR,i}|h_{BP,i}|^2\le {} I_{th}$$

(27)

$$\sum _{j=1}^{N}P_{RM,j}|h_{RP,j}|^2\le {} I_{th}$$

(28)

From (14) and (26), it is clear that the hop with poor channel gain will decide the net-throughput.

The utility maximization can be expressed as follows,

$$\arg \max _{\bar{a}, P_{BR,i}, P_{RM,j}} U(\bar{a})$$

(29)

subject to,

(26), (27), (28), (25), (22), (23) and

$$M_{cs}\in {\varPi }$$

where $M_{cs}$ is the MCS and ${\varPi }$ is a set containing all possible MCSs of the system.

3.1 Interference Threshold Selection

Similar to SRN, let $a_{th,p}$ be the mean arrival rate threshold and $D_{th,p}$ be the maximum delay threshold for PRN, respectively. Then, in PRN the following condition has to be satisfied.

$$\widehat{L}(a_{th,p}+R_{D,p}) \le B\sum _{k=1}^{N}\log \left( 1+w_{p,k}\frac{P_{p,k}|h_{p,k}|^2}{{\varGamma }_p(\sigma _{p}^2+I_{k})}\right)$$

(30)

where

$$R_{D,p}=\frac{1}{D_{th,p}}$$

and $w_{p,k}$ is as defined by Eq. (17).

Lets define the number of allocated subcarriers $\widetilde{N}=\sum _{k=1}^{N}w_{p,k}$, then from (30),

$$\begin{aligned} \log \left( 1+\frac{P_{p,k}|h_{p,k}|^2}{{\varGamma }_p(\sigma _{p}^2+I_{th,k})}\right) =\frac{\widehat{L}(a_{th,p}+R_{D,p})}{\widetilde{N}B} \end{aligned}$$

(31)

where, $I_{th,k}$ is the interference threshold for kth subchannel.

We assume that PRN uses water filling algorithm [29] for power allocation, hence

$$\begin{aligned} P_{p,k}=\left[ \frac{1}{\lambda _o}-\frac{{\varGamma }_p(\sigma _{p}^2+I_{th,k})}{|h_{p,k}|^2}\right] ^+ \end{aligned}$$

(32)

where, $\lambda _o$ is a Lagrangian multiplier and optimal value of $\lambda _o$ can be found by using water-filling algorithm. Let,

$$\begin{aligned} \nu =\frac{\widehat{L}(a_{th,p}+R_{D,p})}{\widetilde{N}B} \end{aligned}$$

(33)

Substituting (32) and (33) into (31), we can write

$$\begin{aligned} I_{th,k}=\frac{|h_{p,k}|^2}{\lambda _o2^{\nu }} - \sigma _{p}^2 \end{aligned}$$

(34)

The total threshold over all subcarriers can be written as,

$$\begin{aligned} I_{th}=\sum _{k=1}^N I_{th,k} \end{aligned}$$

(35)

The interference threshold plays a vital role in the RA of SRN, upto a certain stable value and beyond that $I_{th}$ has no impact on RA of SRN. We call this stable value as stable threshold point ($I_{th,s}$). This stable threshold point is achieved when the interference threshold constraints (27) and (28) are satisfied. From (26), it is obvious that $I_{th,s} \le P_T$. We call the ratio of total power to $I_{th,s}$ as interference stability ratio ($S_{I}$) and expressed it from (27), (28) and (26) as,

$$\begin{aligned} S_{I}=\frac{(\sum _{i=1}^{N}P_{BR,i}^*+\sum _{j=1}^{N}P_{RM,j}^*)}{\max \left( \sum _{i=1}^{N}P_{BR,i}^*|h_{BP,i}|^2,\, \sum _{j=1}^{N}P_{RM,j}^* |h_{RP,j}|^2\right) } \end{aligned}$$

(36)

4 Cross-Layer Based Cognitive Asymmetric Resource Allocation

By following the approaches in [9] or [30], the problem defined by (29) can be transformed into a convex problem. This problem can be solved by dual decomposition method. The optimal solution is derived as the function of the dual variables. The optimal dual variables are estimated in every time slot. Let $\varvec{\lambda }=\{ \lambda _1, \lambda _2^a,\lambda _2^b, \lambda _3, \lambda _4\}$ and $\varvec{\mu}=\{\mu\}$ denote the Lagrange multipliers of the constraints in (26), (27), (28), (25), (22) and (23) respectively.

The Lagrangian of (29) is expressed in (37), where ${\mathbf{P}} =\{P_{BR,i},P_{RM,j}\}$ is the set of transmit power allocation and ${\mathbf{w}} =\{w_m\}$ is the set of channel access coefficient.

$$\begin{aligned} L({\mathbf{P}},{\varvec{w}},\varvec{\lambda },\varvec{\mu })& = U(\bar{a}_m)-\lambda _1\left[ \sum _{i=1}^{N}P_{BR,i} + \sum _{j=1}^{N}P_{RM,j} - P_{T}\right] \\&\quad -\,\lambda _2^a\left[ \sum _{i=1}^{N}P_{BR,i}|h_{BP,i}|^2- I_{th}\right] \\&\quad -\, \lambda _2^b\left[ \sum _{j=1}^{N}P_{RM,j} |h_{RP,j}|^2 - I_{th}\right] -\mu \left[ \sum _{j=1}^{N}R_{DL,j,2} - \sum _{i=1}^{N}R_{DL,i,1}\right] \\&\quad -\,\lambda _3\left[ \widehat{L}\bar{a}-R_{S,DL}+\widehat{L}R_D \right] -\lambda _4\left[ a_{th} - \bar{a}\right] \end{aligned}$$

(37)

The dual problem can be written as,

$$g(\varvec{\lambda },\varvec{\mu })=\max {L({\mathbf{P}},{\varvec{w}},\varvec{\lambda},\varvec{\mu})}$$

(38)

 subject to

$$\begin{aligned} M_{cs}\in {\varPi }\end{aligned}$$

5 Solution of Optimal Dual Variables

To solve the dual problem (38), we have to divide the dual problem into sub-problems. Since the dual problem is always convex [31], the sub-problems can be solved by using Karush−Kuhn−Tucker (KKT) conditions.

$$\begin{aligned} g(\varvec{\lambda },\varvec{\mu })& = \max \left( U(\bar{a}_m)-(\lambda _3 - \lambda _4)\bar{a}_m-\left[ \sum _{i=1}^{N}\alpha _{i}^a P_{BR,i}+\sum _{j=1}^{N}\alpha _{j}^b P_{RM,j}\right] \right) \\&\quad +\,\max \left( -\mu \left[ \sum _{j=1}^{N}R_{DL,j,2} - \sum _{i=1}^{N}R_{DL,i,1}\right] +\lambda _3R_{S,DL}\right) +\kappa \end{aligned}$$

(39)

where

$$\begin{aligned} \alpha _{i}^a & = \lambda _1+\lambda _2^a |h_{BP,i}|^2\\ \alpha _{j}^b & = \lambda _1+\lambda _2^b |h_{RP,j}|^2\\ \kappa & = \lambda _1P_T+(\lambda _2^a+\lambda _2^b)I_{th}-\lambda _3R_D-\lambda _4a_{th} \end{aligned}$$

The dual problem (38) can be modified as shown in (39).

5.1 Sub-problem 1: Optimal Transmit Time

The optimal transmit time sub-problem can be deduced from (39). Let $r_1=\sum _{i=1}^N\log \left( 1+\frac{\gamma _{DL,i,1}}{{\varGamma }}\right)$ and $r_2=\sum _{j=1}^N\log \left( 1+\frac{\gamma _{DL,j,2}}{{\varGamma }}\right)$. From (39), the sub-problem can be written as,

$$\begin{aligned} T_1^*=\arg \max _{T_1} F_1(\varvec{\lambda },\varvec{\mu }) \end{aligned}$$

(40)

Such that

$$\begin{aligned} T & = T_1+T_2 \\ \frac{T_1}{T_2} & = \frac{r_2}{r_1} \end{aligned}$$

where

$$\begin{aligned} F_1(\varvec{\lambda },\varvec{\mu })=(\lambda _3-\mu )\sum _{j=1}^{N}R_{DL,j,2} - \sum _{i=1}^{N}R_{DL,i,1} \end{aligned}$$

(41)

To solve (40), we have to partially differentiate the Eq. (41) with respect to T1.

$$\begin{aligned} \frac{\partial }{\partial T_1}\left( F_1(\varvec{\lambda },\varvec{\mu })\right) =0 \end{aligned}$$

(42)

The solution of (42) can be expressed as,

$$\begin{aligned} T_1^*=\frac{\mu T}{\lambda _3} \end{aligned}$$

(43)

From (43), we can derive the optimal $T_2$ as,

$$\begin{aligned} T_2^*=\frac{(\lambda _3-\mu ) T}{\lambda _3} \end{aligned}$$

(44)

5.2 Sub-problem 2: Optimal CBS Transmit Power

From (39), the sub-problem for optimal first hop transmit power can be written as,

$$\begin{aligned} P_{BR,i}^*=\arg \max _{P_{BR,i}} F_2(\varvec{\lambda },\varvec{\mu }) \end{aligned}$$

(45)

Such that

$$\begin{aligned} P_{BR,i}\ge 0 \end{aligned}$$

where

$$F_2(\varvec{\lambda },\varvec{\mu })=(\lambda _3+\mu ) \sum _{i=1}^{N}R_{DL,i,1}-\sum _{i=1}^{N}\alpha _{j}^b P_{BR,i}$$

(46)

$$\frac{\partial }{\partial P_{BR,i}}\left( F_2(\varvec{\lambda },\varvec{\mu })\right) =0$$

(47)

Let $e_1=\log \left( 1+\frac{\gamma _{DL,i,1}}{{\varGamma }}\right)$, then the solution of Eq. (47) can be expressed as,⁴

$$\dot{e_1}=\frac{\alpha _{i}^a\lambda _3}{\mu (\lambda _3+\mu )}$$

(48)

DF relay (48) can be solved as,⁵

$$P_{BR,i}^*=\left[ \frac{\mu (\lambda _3+\mu )}{\alpha _{i}^a\lambda _3}- \frac{{\varGamma }\sigma _{BR}^2}{l_{BR}|h_{BR,i}|^2}\right] ^+$$

(49)

Similarly AF relay (48) can be solved as,

$$P_{BR,i}^*=\left[ \frac{\mu (\lambda _3+\mu )}{\alpha _{i}^a\lambda _3}- \frac{{\varGamma }\sigma _{BR}^2}{h_{ri}}\right] ^+$$

(50)

5.3 Sub-problem 3: Optimal RS Transmit Power

For optimal second hop transmit power,

$$P_{RM,j}^*=\arg \max _{P_{RM,j}} F_3(\varvec{\lambda },\varvec{\mu })$$

(51)

Such that

$$P_{RM,j} \ge 0$$

where

$$F_3(\varvec{\lambda },\varvec{\mu })=(\lambda _3-\mu ) \sum _{j=1}^{N}R_{DL,j,2}-\sum _{j=1}^{N}\alpha _{j}^b P_{RM,j}$$

(52)

$$\frac{\partial }{\partial P_{RM,j}}\left( F_3(\varvec{\lambda },\varvec{\mu })\right) =0$$

(53)

Let $e_2=\log \left( 1+\frac{\gamma _{DL,j,2}}{{\varGamma }}\right)$, then the solution of Eq. (53) can be expressed as,

$$\dot{e_2}=\frac{\alpha _{j}^b\lambda _3}{(\lambda _3-\mu )^2}$$

(54)

DF relay, the Eq. (54) can be expressed as,

$$\begin{aligned} P_{RM,j}^*=\left[ \frac{(\lambda _3-\mu )^2}{\alpha _{j}^b\lambda _3}-\frac{{\varGamma }\sigma _{RM}^2}{l_{RM}|h_{RM,j}|^2}\right] ^+ \end{aligned}$$

(55)

Similarly AF relay, (54) can be solved as,

$$\begin{aligned} P_{RM,j}^*=\left[ \frac{(\lambda _3-\mu )^2}{\alpha _{j}^b\lambda _3}-\frac{{\varGamma }(\sigma _{\tilde{n}}^2+ \sigma _{RM}^2)}{P_{BR,i}Gh_{ri}h_{rj}}\right] ^+ \end{aligned}$$

(56)

5.4 Sub-problem 4: Optimal Arrival Rate

For optimal arrival rate,

$$\bar{a}_m^*=\arg \max _{\bar{a}_m} F_4(\varvec{\lambda },\varvec{\mu })$$

(57)

where

$$F_4(\varvec{\lambda },\varvec{\mu })=U(\bar{a}_m)-(\lambda _3 - \lambda _4)\bar{a}_m$$

(58)

$$\frac{\partial }{\partial \bar{a}_m}\left( F_4(\varvec{\lambda },\varvec{\mu })\right) =0$$

(59)

Solving (59) gives,

$$\bar{a}_m^*=\dot{U}^{-1}(\lambda _3 - \lambda _4)$$

(60)

6 Cross-Layer Based Cognitive ARA

6.1 Cross-Layer Based Cognitive Relay selection (CCRS)

When the path gain ($l_{bm}$) between BS and MS is less than the threshold ($l_{th}$), then the MS has to look for an optimal RS for the indirect link.

$$\begin{aligned} r=\arg \max _r \left( \min \left( \sum _{i=1}^{N}\log \left( \frac{\mu (\lambda _3+\mu )}{\alpha _{i}^a\lambda _3} h_{ri}\right) ,\sum _{j=1}^{N}\log \left( \frac{(\lambda _3-\mu )^2}{\alpha _{j}^b\lambda _3} h_{rj}\right) \right) \right) \end{aligned}$$

(61)

An optimal relay which maximizes the throughput function of (14) can be obtained and this can be expressed with respect to the dual variables is shown in Eq. (61). If the path gain of the selected RS to MS link ($l_{RM}$) is less than $l_{th}$, then the MS is blocked as explained in Algorithm 4. The complexity of the CCRS algorithm is $O(NN_R)$.

6.2 Cross-Layer Based Cognitive Subcarrier Allocation (CCSA)

In SA the optimal subcarriers are allocated to the system which maximize the dual function of (39). From (39), we can derive the following rule for SA,

$$i = \arg \max _i (\lambda _3+\mu )\log \left( \frac{\mu (\lambda _3+\mu )}{\alpha _{i}^a\lambda _3} h_{ri}\right)$$

(62)

$$j = \arg \max _j (\lambda _3-\mu )\log \left( \frac{(\lambda _3-\mu )^2}{\alpha _{j}^b\lambda _3} h_{rj}\right)$$

(63)

Algorithm for SA is exlained in Algorithm 2. The complexity of the CCSA algorithm is O(N).

6.3 Cross-Layer Based Cognitive Subcarrier Pairing (CCSP)

The objective of the SP is to choose the subcarrier pairs in the system which maximize the dual function (39). The profit value of each subcarrier pair from (39) is estimated and optimal pair which maximizes the sum-profit of the system will be evaluated. Let $D_{i,j}$ be the profit function of the subcarrier pair i and j, then the SP problem can be written as,

$$\begin{aligned}&{\varDelta }_{i,j}^*=\{i,j\}=\arg \max _{i,j} \sum _{i=1}^N \sum _{j=1}^N \xi _{ij,m}D_{i,j}(\varvec{\lambda },\varvec{\mu }) \\&{\text{Such\,that}} \\&\quad \sum _{i=1}^N\xi _{ij,m}=1, \forall j \\&\quad \sum _{j=1}^N\xi _{ij,m}=1, \forall i \end{aligned}$$

(64)

The profit function can be derived as,

$$\begin{aligned} D_{i,j}(\varvec{\lambda },\varvec{\mu }) =B\log \left( \left( \frac{\mu (\lambda _3+\mu )}{\alpha _{i}^a\lambda _3}\right) ^{(\lambda _3-\mu )}\left( \frac{(\lambda _3-\mu )^2}{\alpha _{j}^b\lambda _3} \right) ^{\mu }\right) -\upsilon _{i,j} \end{aligned}$$

(65)

where

$$\upsilon _{i,j}=(\lambda _3-\mu )+\frac{2\mu ^2}{\lambda _3}+\left( \frac{\alpha _{i}^a}{h_{ri}}+\frac{\alpha _{j}^b}{h_{rj}}\right)$$

(66)

We can define the NXN profit matrix for N subcarriers as,

$$D(\varvec{\lambda },\varvec{\mu }) =\left( \begin{array}{ccccc} D_{1,1} &{} D_{1,2} &{} \ldots &{} \ldots &{} D_{1,N} \\ D_{2,1} &{} D_{2,2} &{} \ldots &{} \ldots &{} D_{2,N} \\ \ldots &{} \ldots &{} \ldots &{} \ldots &{} \ldots \\ D_{N-1,1} &{} \ldots &{} \ldots &{} D_{N-1,N-1} &{} D_{N-1,N} \\ D_{N,1}&{} \ldots &{} \ldots &{} D_{N,N-1} &{} D_{N,N} \\ \end{array} \right)$$

(67)

The SP problem (64) is equivalent to a transportation problem and it can be solved by using the Hungarian algorithm [32] with a complexity of $O(N^3)$. The whole SP algorithm is described in Algorithm 3.

6.4 Cross-Layer Based Cognitive Power Allocation (CCPA)

The solution of primal power variables with respect to the dual variables is expressed in Sects. 5.2 and 5.3.

$$\lambda _1(n+1) = \left[ \lambda _1(n)-\delta \left( \sum _{i=1}^{N}P_{BR,i} + \sum _{j=1}^{N}P_{RM,j} - P_{T}\right) \right] ^+$$

(68)

$$\lambda _2^a(n+1) = \left[ \lambda _2^a(n)-\delta \left( \sum _{i=1}^{N}P_{BR,i}|h_{BP,i}|^2- I_{th}\right) \right] ^+$$

(69)

$$\lambda _2^b(n+1) = \left[ \lambda _2^b(n)-\delta \left( \sum _{j=1}^{N}P_{RM,j} |h_{RP,j}|^2 - I_{th}\right) \right] ^+$$

(70)

$$\lambda _3(n+1) = \left[ \lambda _3(n)-\delta \left( \widehat{L}\bar{a}-R_{S,DL}+\widehat{L}R_D\right) \right] ^+$$

(71)

$$\lambda _4(n+1) = \left[ \lambda _3(n)-\delta \left( a_{th} - \bar{a}\right) \right] ^+$$

(72)

$$\mu (n+1)= \left[ \mu (n)-\delta \left( \sum _{j=1}^{N}R_{DL,j,2} - \sum _{i=1}^{N}R_{DL,i,1}\right) \right] ^+$$

(73)

The optimal dual variables $\varvec{\lambda }$ and $\varvec{\mu }$ are obtained by subgradient method as expressed in (68)–(73).

Channel state information set $h_m$ contains all the channel coefficients of first and second hops respectively for user m. Similarly, QOS set $q_{s,m}$ contains all $R_{th}$ and $D_{th}$ information. Channel information ($h_m$), QOS information ($q_{s,m}$) and Queue state information (Q[t]) are all required as input parameters for Algorithm 4. The complexity of the CCPA algorithm is O(N).

7 Joint Relay Selection, SA, SP and PA

We have discussed about the relay selection, subcarrier allocation, subcarrier pairing and power allocation in the previous subsections. To achieve the optimal cross-layer based Cognitive Asymmetric Resource Allocation, a combined approach is needed. The flow chart of the entire algorithm is shown in Fig. 2

Fig. 2

Flow chart for joint optimization

8 Performance Evaluation

A single BS with three sectors is considered for the simulation testbed. The channel is modeled using Rayleigh distribution. Different path loss models are implemented in first and second hop links. The path loss (PL) component for first hop can be defined as $l_{BR}=\frac{1}{A_1d^{\tau _1}}$. Similarly for second hop $l_{RM}=\frac{1}{A_2d^{\tau _2}}$. For first hop we apply Type-D (Roof-to-Roof) PL model with PL coefficient $A_1=2.05f_c^{2.6} \times 10^{-26}$, where $f_c=5$ GHz [33] and PL exponent $\tau _1=4.5$ [34]. Applying the Type-E (Roof-to-Ground) PL model in the second hop, we have the PL coefficient as $A_2=38.4\,{\text {dB}}$ and PL exponent as $\tau _2=3.5$ [34]. The total bandwidth $B=5$ MHz and the total number of the subcarriers $N=256$.

Figure 3 shows the impact of mean arrival rate threshold ($a_{th,p}$) on interference threshold ($I_{th}$) with different maximum delay thresholds ($D_{th,p}$) in PRN. If the PRN has high QOS requirement i.e high throughput ($a_{th,p}$) and low delay ($D_{th,p}$), then the interference threshold ($I_{th}$) will be low. The low $I_{th}$ will restrict the RA in SRN. $D_{th,p}$ has an impact on $I_{th}$ only when it is lower. In Fig. 3, $D_{th,p}$ at its higher values like 15 and 20 ms has negligible impact on $I_{th}$. In SRN, the value of $I_{th}$ which is selected based on QOS of PRN plays an important role in RA upto a stable threshold point ($I_{th,s}$). Beyond that it has no effect on RA since the interference constraints of (27) and (28) are satisfied without sacrificing PRN QOS. It is shown in Fig. 4 that this stable threshold point ($I_{th,s}$) is achieved at 27 dBm in our scenario.

Fig. 3

Impact of mean arrival rate requirement on interference threshold ($I_{th}$) with different maximum delay thresholds in PRN

Fig. 4

Impact of interference threshold on mean arrival rate with different maximum delay thresholds ($D_{th}$) in SRN where $P_T=30\,{\text {dBm}}$

Figure 5 shows the impact of interference threshold ($I_{th}$) on mean arrival rate with different maximum power thresholds ($P_T$). From this figure we can say that if $I_{th} \le I_{th,s}$, then the performance of the RA or $a_{th}$ is completely dependent on $I_{th}$ regardless of the maximum $P_T$ because the interference constraints of (27) and (28) restrict the transmit power of the BS and RS. From Fig. 5 we can estimate the interference stability ratio ($S_I$) as 3 dB. From Eq. (36), we can say that the value of $S_I$ is a function of the channel gains of the system.

Fig. 5

Impact of the interference threshold on mean arrival rate with different maximum power thresholds

Figure 6 shows the impact of normalized distance from BS to RS on system bandwidth efficiency with different $P_{T}$, where $I_{th}=26\,{\text {dBm}}$ i.e $a_{th,p}=2100\,packets/sec$ and $D_{th,p}=10\,{\text {ms}}$. The normalized distance from relay can be defined as $\frac{d_{br}}{d_{bm}}$. The interference stability ratio ($S_I$) has been found to be 3 dB from Fig. 5. Hence we can deduce that $I_{th,s}=29\,{\text {dBm}}$ for $P_T=32\,{\text {dBm}}$. From Fig. 6 we can observe that the throughput performance of the system with $P_T=27\,{\text {dBm}}$ and $P_T=22\,{\text {dBm}}$ is poor compared to the system with $P_T=32\,{\text {dBm}}$ because of the possibility for maximum transmit power allocation. The performance of the system with $I_{th} \ge I_{th,s}$ with lower maximum power threshold i.e $P_T=27\,{\text {dBm}}$ and $P_T=22\,{\text {dBm}}$ is smoother than the system which has $I_{th}<I_{th,s}$ with higher $P_T$ i.e $P_T=32\,{\text {dBm}}$ because the only power limitation is maximum power threshold and interference power limitation has no impact on the performance. Hence at minimum $P_T$ levels the relay position has very less impact on the system throughput.

Fig. 6

Impact of normalized distance from BS to RS on system bandwidth efficiency with different $P_{T}$

From Figs. 6 and 7, we can observe that the best system bandwidth efficiency can be achieved at the optimal normalized distance of $d_r=0.7$. This is because of different PL values for the first and second hops. In most of the existing works the same PL were chosen and because of that, the maximum throughput was shown to be achieved at the normalized distance of 0.5. However, this may not happen in practical scenarios. This observation is important for RS placement in BS cell. DF relaying provides better performance when RS is closer to the BS because the second hop data rate capacity dominates the net-throughput in (14). From Fig. 7 we can estimate that DF offers 46% throughput improvement with $P_T=30\,{\text {dBm}}$ and $d_r=0.4$. AF suffers from noise enhancement in second hop. However, after a normalized distance of $d_r=0.7$ DF performance is similar to the AF except for increased processing delay. This observation proves that AF is better choice to provide service to the edge users than DF.

Fig. 7

Impact of normalized distance from BS to RS on mean arrival rate with AF and DF relaying

The impact of normalized distance from BS to RS on mean arrival rate $(\bar{a})$ with SP and without SP is analyzed in Fig. 8. From Fig. 8 we can observe that the system throughput is improved with SP even though the system is in an interference dominated region ($P_T=32\,{\text{dBm}}$) i.e $I_{th} \le I_{th,s}$. We can also observe that the throughput improvement of system which is working in the stable region i.e $I_{th} \ge I_{th,s}$ ($P_T=25\,{\text {dBm}}$) is lower than the system which is working in interference dominated region $I_{th} \le I_{th,s}$ ($P_T=32\,{\text{dBm}}$) because SP algorithm allocate the optimum subcarrier pair which maximize the profit function. The reason for this observation is that in the interference dominated region the transmit power is restricted by the interference constraint rather than the maximum power threshold, and the transmit power is dependent on the channel gains of the first and second hops, where as in the stable region the transmit power is restricted by the maximum power threshold. Figrue 9 compares the system throughput for the systems with SA and SP. From Fig. 9 it is proven that SA and SP improve the system throughput significantly.

Fig. 8

Impact of normalized distance from BS to RS on mean arrival rate with SP and without SP

Fig. 9

Impact of normalized distance from BS to RS on mean arrival rate with SA and SP

The impact of the distance between BS and MS ($d_{bm}$) on system throughput is observed in Fig. 10. This observation helps us to fix the BS cell radius to satisfy the user throughput requirement. Figrue 11 shows the impact of normalized distance from BS to RS on normalized transmit duration with different $d_{bm}$. It is shown that the transmit duration of first and second hop is equal at $d_r=0.63$ which corresponds to symmetric transmission. However, maximum throughput is achieved at $d_r=0.7$ as shown in Fig. 11 which corresponds to asymmetric transmission. Impact of normalized distance from BS to RS on utility with different $d_{bm}$ is analyzed in Fig. 12. We can see the utility is maximum for the edge users. Variation of Queue size (Q[t]) over different time slots is depicted in Fig. 13. The Queue size is stabilized as the mean packet arrival rate is always maintained equal to or less than the mean packet departure rate.

Fig. 10

Impact of normalized distance from BS to RS on mean arrival rate with different $d_{bm}$ where $P_T=38\,{\text {dBm}}$

Fig. 11

Impact of normalized distance from BS to RS on normalized transmit duration with different $d_{bm}$

Fig. 12

Impact of normalized distance from BS to RS on utility with different $d_{bm}$

Fig. 13

Variation of queue size over different time slots

The proposed BS is implemented in a simulation testbed with single BS as shown in Fig. 14. Call blocking ratio and QOS assurance for SRN were analyzed in this model. The impact of minimum threshold requirement on blocking ratio with different $I_{th}$ is analyzed in Fig. 15. A system with high interference threshold provides a lower blocking ratio because of the interference constraint. From Fig. 15, we can estimate that system with $I_{th}=26\,{\text{dBm}}$ provides 24% lower blocking ratio as compared to the system with $I_{th}=22\,{\text{dBm}}$ at $a_{th}=50k$ packets/sec.

Fig. 14

Simulation testbed model for single BS

Fig. 15

Impact of minimum threshold requirement on blocking ratio with different $I_{th}$

The proposed system is compared with existing symmetric RA system [13] in Figs. 16 and 17. From Fig. 16, we can see that the proposed system provides minimum blocking ratio compared to the existing system i.e 27% lower blocking ratio at $a_{th}=50k$ packets/s. Similar performance is observed in Fig. 17 for QOS assurance because from Fig. 12 we can observe that the proposed system provides maximum utility for edge users. QOS assurance tells us how many edge users are served in the cellular system. From Fig. 17, we can observe that the proposed system provides better edge user performance i.e 2% higher value than the existing system at $a_{th}=50k$ packets/s.

Fig. 16

Impact of minimum threshold requirement on blocking ratio with proposed ARA and existing system

Fig. 17

Impact of minimum threshold requirement on QOS assurance with proposed ARA and existing system

9 Conclusion

In this paper we investigated the cross-layer based asymmetric resource allocation in relay-aided cognitive radio networks. The resource allocation problem has been solved by addressing four sub-problems namely relay selection, subcarrier allocation, subcarrier pairing and power allocation. Joint optimization procedure has been developed and performance of the proposed system has been analyzed. Simulation results show that the proposed system provides better performance to edge users compared to the symmetric resource allocation.