1 Introduction

Along with the rapid development of wireless communication networks, the growing of wireless services and related demands for frequency have caused the spectrum allocation table to become more exhausted in recent years. However, actual spectrum utilization measurements indicate that most licensed spectrum is often underutilized with large spectrum holes at different places or at different times [1]. Fortunately, cognitive radio (CR) has been pursued as a promising, feasible and cost-effective technology due to its capability of improving the utilization of idle spectrum [2]. The underlying core idea behind CR is that it allows non-licensed user, referred to as secondary user (SU), to utilize a licensed band under the condition of protecting the quality of service of the primary user (PU).

To improve spectral efficiency further, another spectrally efficient technique called analogue network coding (ANC) which uses an amplify-and-forward (AF) relay protocol was introduced in [3]. Specially, for a more efficient use of power resources, a large number of power allocation schemes have also been proposed for the two-way AF relaying networks in CR [4–7]. In [4, 5], the power allocation scheme is proposed by concentrating on the sum rate maximization issue for two-way relay system in CR. Instead of not involving in the interference to SU and the relay from the PU, the authors in [6, 7] take the interference to each other into account and propose a power allocation scheme subject to the available transmit power and interference power threshold (IPT) constraints of PU in CR.

However, most of existing studies about cognitive two-way relay networks are limited to the idealistic assumption that the system operates in the symmetric traffic mode. Considering the practical situations, the traffic loads of the uplink and the downlink have been changing to be asymmetric to support new multimedia communication services. Therefore, it makes more sense to investigate the impact of traffic asymmetry in practical system. The authors in [8, 9] study the system performance of ANC with asymmetric traffic requirements and propose power allocation and relay selection methods which can achieve significant performance gains in terms of outage probability. In [10], the authors analyze the outage performance and propose a fairness-aware power allocation scheme for asymmetric two-way AF relaying network. However, to the best of our knowledge, in the presence of traffic asymmetry, power allocation scheme for cognitive two-way AF relay network, which takes the outage performance as an objective function, have not been reported yet.

Motivated by aforementioned considerations, we focus on the secondary communication assisted by a relay in CR. The main contribution of this paper is to propose a power allocation strategy for the cognitive two-way AF relay networks with asymmetric traffic requirements. The proposed power allocation scheme is obtained by minimizing the weaker link’s individual outage probability under the sum-power and the IPT of PU constraints. Particularly, the interference to each other between PU and SU nodes and the relay, which has a great influence on system performance, is involved. Importantly, a closed-form solution for the optimum power allocation scheme is derived by using KKT conditions for each case. Simulation results show that the proposed power allocation scheme outperforms the traditional scheme in terms of outage performance no matter with or without IPT. Moreover, the proposed scheme can help maintain the system balance for asymmetric traffic requirements and is more suitable for cognitive two-way AF relay networks.

The rest of the paper is organized as follows. In Sect. 2, we describe the system and the channel model. In addition to that, we analyze the outage probability of the end nodes. In Sect. 3, we give the formulation of optimization problem and study the power allocation scheme in different cases. Numerical results and conclusion are presented in Sects. 4 and  5, respectively.

2 System Model

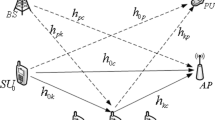
As shown in the Fig. 1, we consider a CR network which is constructed by a base station, a primary user, and a pair of SUs (\({S_1}\) and \({S_2}\) ) communicating with each other via a cognitive relay node. It is assumed that all nodes are synchronized, employ single antenna and operate in a half-duplex way. The SU network’s nodes share the spectrum with the PU and the instantaneous channel state information is available at the transmitter. In this paper, we focus on the SU communication between \({S_1}\) and \({S_2}\) assisted by a relay which applies AF relaying protocol to perform network coding operations. The diagram of SU communication is also shown in Fig. 1 in detail. The transmissions are subject to additive noise and frequency-flat Rayleigh fading with a path loss exponent of \(\alpha > 0\). \({d_i}\) and \({h_{ir}}\sim \mathcal {N}(0,\;d_i^{ - \alpha })\) donate the distance and the channel gain between the source node \({S_i}\) and relay R respectively, where \(i \in \left\{ {1,\;2} \right\} \). The additive white Gaussian noise (AWGN) at node \(S_1, S_2\) and R are donated by \(n_1, n_2\) and \(n_r\), respectively, and are modeled as independent and identically distributed (i.i.d.) \(n_i\sim \mathcal {N}(0,\sigma _{{n_i}}^2)\). The transmit power at the node \(S_1, S_2\) and R are expressed by \(P_1, P_2\) and \(P_r\). In CR network, the SU nodes share the spectrum with the PU. As a result, the PU would cause a certain level of interference to the SU, which can be presented as \({u_i}\sim \mathcal {N}(0,\;\sigma _{{u_i}}^2)\), where \(i = 1,2,r\).

Fig. 1
figure 1

ANC based SU communication in CR network

Full size image

During the first timeslot, both nodes \({S_1}\) and \({S_2}\) transmit unit-power signal \({s_1}\) and \({s_2}\) to the other, and the relay node R receives the signals. Thus, the signal received by the relay can be written as

$$\begin{aligned} {y_r} = \sqrt{{P_1}} {h_1}{s_1} + \sqrt{{P_2}} {h_2}{s_2} + {n_r} + {u_r} \end{aligned}$$
(1)

In the second timeslot, the relay broadcasts the combined signal \({y_r}\) after multiplying with an amplifying gain \(G = \sqrt{{P_r}/({P_1}{{\left| {{h_{1r}}} \right| }^2} + {P_2}{{\left| {{h_{2r}}} \right| }^2} + \sigma _{{n_r}}^2 + \sigma _{{u_r}}^2)}\). Therefore, the received signals at \({S_1}\) and \({S_2}\) via relay can be written as

$$\begin{aligned} {y_1} &= {} G\sqrt{{P_1}} {h_{1r}}{h_{1r}}{s_1} + G\sqrt{{P_2}} {h_{1r}}{h_{2r}}{s_2}\nonumber \\&+ G{h_{1r}}({n_r} + {u_r}) + {u_1} + {n_1} \end{aligned}$$
(2)
$$\begin{aligned} {y_2} &= {} G\sqrt{{P_1}} {h_{2r}}{h_{1r}}{s_1} + G\sqrt{{P_2}} {h_{2r}}{h_{2r}}{s_2}\nonumber \\&+ G{h_{2r}}({n_r} + {u_r}) + {u_2} + {n_2} \end{aligned}$$
(3)

Note that the first term in (2) and the second term in (3) represent self-interference which are just their own transmitted symbols received from the relay. It is assumed that both nodes have the knowledge of amplification factor of the relay and their own transmitted symbols. Therefore, the self-interference can be removed from the received signals. Thus, the signal to interference plus noise ratio (SINR) at node \({S_1}\) and \({S_2}\) can be obtained as

$$\begin{aligned} {\gamma _1} &= {} \frac{{{P_r}{P_2}{{\left| {{h_1}} \right| }^2}{{\left| {{h_2}} \right| }^2}}}{{\left( {{P_r}{\varphi _r} + {P_1}{\varphi _1}} \right) {{\left| {{h_1}} \right| }^2} + {\varphi _1}{P_2}{{\left| {{h_2}} \right| }^2} + {\varphi _1}{\varphi _r}}} \end{aligned}$$
(4)
$$\begin{aligned} {\gamma _2} &= {} \frac{{{P_r}{P_1}{{\left| {{h_1}} \right| }^2}{{\left| {{h_2}} \right| }^2}}}{{\left( {{P_r}{\varphi _r} + {P_2}{\varphi _2}} \right) {{\left| {{h_2}} \right| }^2} + {P_1}{\varphi _2}{{\left| {{h_1}} \right| }^2} + {\varphi _2}{\varphi _r}}} \end{aligned}$$
(5)

where \({\varphi _r} = \sigma _{{n_r}}^2 + \sigma _{{u_r}}^2\), \({\varphi _1} = \sigma _{{n_1}}^2 + \sigma _{{u_1}}^2\) and \({\varphi _2} = \sigma _{{n_2}}^2 + \sigma _{{u_2}}^2\).

The outage probability has been widely used as a performance measure in evaluating wireless systems. Therefore, to proceed, we rewrite the Eq. (4) as

$$\begin{aligned} {\gamma _1} = \frac{{\frac{{{P_r}{P_2}{{\left| {{h_{1r}}} \right| }^2}{{\left| {{h_{2r}}} \right| }^2}}}{{{\varphi _r}{\varphi _1}}}}}{{\frac{{{P_r}{{\left| {{h_{1r}}} \right| }^2}}}{{{\varphi _1}}} + \frac{{{P_1}{{\left| {{h_{1r}}} \right| }^2} + {P_2}{{\left| {{h_{2r}}} \right| }^2}}}{{{\varphi _r}}} + 1}} = \frac{{\frac{{{P_r}}}{{{\varphi _1}}}}}{{\frac{{{P_r}}}{{{\varphi _1}}} + \frac{{{P_1}}}{{{\varphi _r}}}}} \cdot \frac{{{X_1}{X_2}}}{{{X_1} + {X_2} + 1}} \end{aligned}$$
(6)

where we define \({X_1} = (\frac{{{P_r}}}{{{\varphi _1}}} + \frac{{{P_1}}}{{{\varphi _r}}}){\left| {{h_{1r}}} \right| ^2}\) and \({X_2} = \frac{{{P_2}}}{{{\varphi _r}}}{\left| {{h_{2r}}} \right| ^2}\).

The instantaneous rate \({R_1}\) for flow \(2 \rightarrow 1\) can be given as \({R_1} = \frac{1}{2}\log _2(1 + {\gamma _1})\). And the probability that the instantaneous rate \({R_1}\) is less than the data rate requirement \({R_{th1}}\) has been given in [7] as

$$\begin{aligned} {P_{out,1}} &= {} \Pr \{ {R_1} \le {R_{th1}}\}= \Pr \{ {\gamma _1} \le {\gamma _{th1}}\}\nonumber \\ &= {} 1 - 2{e^{ - ({\beta _1} + {\beta _2}){\lambda _1}{\gamma _{th1}}}}\sqrt{{\beta _1}{\beta _2}{\lambda _1}{\gamma _{th1}}({\lambda _1}{\gamma _{th1}} + 1)} \nonumber \\&\quad \times {K_1}(2\sqrt{{\beta _1}{\beta _2}{\lambda _1}{\gamma _{th1}}({\lambda _1}{\gamma _{th1}} + 1)} ) \end{aligned}$$
(7)

where \({\gamma _{th1}} = {2^{2{R_{th1}}}} - 1, {\lambda _1} = \frac{{{P_1}{\varphi _1} + {P_r}{\varphi _r}}}{{{P_r}{\varphi _r}}}, {\beta _1} = {d_1^\alpha }/{\left( \frac{{{P_r}}}{{{\varphi _1}}} + \frac{{{P_1}}}{{{\varphi _r}}}\right) }, {\beta _2} = {{\varphi _2}d_2^\alpha } /{{P_2}}\) and \({K_1}( \cdot )\) is the first-order modified Bessel function [11].

Then, the outage probability of node \(S_2\) can be obtained in a similar way. For better insights, the expression of the individual outage probability can be represent in simple closed-form expression by using a high SNR approximation. Therefore, making use of the approximations \({K_1}(x) \approx 1/x\) and \({e^{ - x}} \approx 1 - x\) for \(x \rightarrow 0\), closed-form expressions of (6) have been derived in [7], which can be given by

$$\begin{aligned}&{P_{out,1}} \approx \left( {\frac{{\left( {{P_r}{\varphi _r} + {P_1}{\varphi _1}} \right) d_2^\alpha }}{{{P_r}{P_2}}} + \frac{{d_1^\alpha {\varphi _1}}}{{{P_r}}}} \right) {\gamma _{th1}} \end{aligned}$$
(8)
$$\begin{aligned}&{P_{out,2}} \approx \left( {\frac{{\left( {{P_r}{\varphi _r} + {P_2}{\varphi _2}} \right) d_1^\alpha }}{{{P_r}{P_1}}} + \frac{{d_2^\alpha {\varphi _2}}}{{{P_r}}}} \right) {\gamma _{th2}} \end{aligned}$$
(9)

On the other hand, the SU also have interference to the PU while they are transmitting signals during the first timeslot. The interferences caused by \(S_1\) and \(S_2\) denoted \(I_1\) and \(I_2\), respectively, are given by

$$\begin{aligned} {I_1} = {P_1}{\left| {{h_{1p}}} \right| ^2}\quad and \quad {I_2} = {P_2}{\left| {h{}_{2p}} \right| ^2} \end{aligned}$$
(10)

where \( h_{1p}\) and \( h_{2p}\) represent the channel gain to the PU from \(S_1\) and \(S_2\), respectively. In the second timeslot, the interference to the PU, which is caused by the relay, can be given as

$$\begin{aligned} {I_r} = {P_r}{\left| {{h_{rp}}} \right| ^2} \end{aligned}$$
(11)

where \( h_{rp}\) represent the channel gain to the PU from the relay.

3 Optimal Power Allocation Scheme

In this section, we turn to allocate the total available power among the SU nodes and the relay. The outage probability of SU communication is selected as our objective function subject to total power consumed constraint, \(P_t,\) and the IPT constraint of the PU. Then, the optimization problem to minimize the maximum of individual outage probability problem can be formulated as

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{{P_r},{P_1},{P_2}} \max \left\{ {{P_{out,1}},{P_{out,2}}} \right\} \\ s.t.\left\{ \begin{array}{l} 0 < {P_r},{P_1},{P_2} \le {P_{\max }}\\ {P_r} + {P_1} + {P_2} \le {P_t}\\ {I_1} + {I_2} \le {P_I}\\ {I_r} \le {P_I} \end{array} \right. \end{array} \end{aligned}$$
(12)

where \({P_{out,1}}\) and \({P_{out,2}}\) are expressed in (8) and (9). Clearly, as \({P_{out,1}}\) and \({P_{out,2}}\) are outage probability functions, they are convex (when drawn in a linear scale) [12]. Therefore, the problem formulated in (12) is a convex problem, which means that it must have a unique optimal solution. Also, it is noted that the equality \({P_{out,1}} = {P_{out,2}} = {P_{out}}\) holds at the optimum. Then the optimization problem can be reformulated as

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{{P_r},{P_1},{P_2}} {P_{out}}\\ s.t.\left\{ \begin{array}{l} 0 < {P_r},{P_1},{P_2} \le {P_{\max }}\\ {P_{out,1}} = {P_{out,2}}\\ {P_r} + {P_1} + {P_2} \le {P_t}\\ {P_1}{\left| {{h_{1p}}} \right| ^2} + {P_2}{\left| {h{}_{2p}} \right| ^2} \le {P_I}\\ {P_r}{\left| {{h_{rp}}} \right| ^2} \le {P_I} \end{array} \right. \end{array} \end{aligned}$$
(13)

Obviously, the problem formulated in (13) is also a convex problem and we can use Karush-Kuhn-Tucker (KKT) conditions to solve it.

As the objective function of (13) is monotonically decreasing function of the transmit power of the relay, \(P_r\), it is obvious that the relay is limited firstly with the increasing of total power. Thus, we consider all the cases which are possible in this kind of CR network and derive the closed-form solution of each case. Then, we can determine the optimal scheme.

3.1 Case I: Interference Doesn’t Exceed IPT Values

When the total power is below a certain level, the interference of \(S_1, S_2\) and R to PU doesn’t exceed IPT levels of PU. Therefore, we exclude IPT constraints to obtain the optimal power allocation and all nodes include \(S_1, S_2\) and R take full advantage of the total power. Thus, the optimal solution is given as

$$\begin{aligned} P_r^*= & {} \frac{{{\eta _3} + {\varphi _1}{d_1}{\eta _0}\gamma _{th1}^2 + {\varphi _2}{d_2}{\eta _1}\gamma _{th2}^2 + {\gamma _{th1}}{\gamma _{th2}}({\eta _4} + {\eta _5})}}{{\eta _0^2\gamma _{th1}^2 + \eta _1^2\gamma _{th2}^2 + 2{\gamma _{th1}}{\gamma _{th2}}({\eta _4} + {\eta _6})}}\nonumber \\ P_2^*= & {} \frac{{{\eta _7} - \sqrt{\eta _7^2 - 4({d_1} - {d_2}){\eta _2}{\eta _8}} }}{{2({d_2} - {d_1}){\eta _2}}},P_1^* = {P_t} - P_2^* - P_r^* \end{aligned}$$
(14)

where \({\eta _0} = {\varphi _1}{d_1} - {\varphi _r}{d_2}, {\eta _1} = {\varphi _2}{d_2} - {\varphi _r}{d_1}, {\eta _3}\mathrm{{ = }}\sqrt{({\eta _0}{\gamma _{th1}} + {\eta _1}{\gamma _{th2}})({\gamma _{th1}} + {\gamma _{th2}}){d_1}{d_2}{\varphi _r}{\eta _2}}, {\eta _2} = {\varphi _1}{\gamma _{th1}} + {\varphi _2}{\gamma _{th2}}, {\eta _4} = {\varphi _r}({\varphi _1}d_1^2 + {\varphi _2}d_2^2), {\eta _5} = {d_1}{d_2}({\varphi _1}{\varphi _2} - {\varphi _r}{\varphi _1} - {\varphi _r}{\varphi _2}), {\eta _6} = {d_1}{d_2}(\varphi _r^2 + {\varphi _1}{\varphi _2} - 2{\varphi _r}{\varphi _1} - 2{\varphi _r}{\varphi _2}), {\eta _7} = ({d_2}{\eta _2} - {\varphi _1}{\gamma _{th1}}({d_1} - {d_2})){P_t} + ({\varphi _r}({d_2}{\gamma _{th1}} + {d_1}{\gamma _{th2}}) + {\varphi _1}{\gamma _{th1}}({d_1} - {d_2}) - {d_2}{\eta _2}){P_r^*}, {\eta _8} = {d_2}{\gamma _{th1}}({P_t} - P_r^*)({\varphi _1}{P_t} + {\varphi _r}{P_r^*} - {\varphi _1}{P_r^*}).\)

3.2 Case II: Relay Node Power is Limited with the Limit of Total Power.

With the increasing of total power, transmit power of the relay node R is limited firstly with the PU experiencing the maximum possible interference level and the optimal value is given by \(P_r^* = \min \left( {{{{P_I}} /{{{\left| {{h_{rp}}} \right| }^2},{P_{\max }}}}} \right) \). Also, the SU nodes make full use of the total power. With the KKT conditions, the optimal solution can be given as follows.

$$\begin{aligned} P_r^* &= {} \min \left( {{{{P_I}}/{{{\left| {{h_{rp}}} \right| }^2},{P_{\max }}}}} \right) \nonumber \\ P_2^* &= {} \min \left( {\frac{{{\eta _7} - \sqrt{\eta _7^2 - 4({d_1} - {d_2}){\eta _2}{\eta _8}} }}{{2({d_2} - {d_1}){\eta _2}}},{P_{\max }}} \right) \nonumber \\ P_1^*&= \min \left( {{P_t} - P_2^* - P_r^*,{P_{\max }}} \right) \end{aligned}$$
(15)

3.3 Case III: All Nodes is Limited Due to IPT of PU

With the increasing of the total power, both the SUs and the relay transmit power are limited due to the highest interference to PU. In this case, the outage probability is limited to a certain level, which means that there is no point of increasing the total power. Then, the optimal solution can be obtained as

$$\begin{aligned} P_r^ * &= {} \min \left( {{{{P_I}} /{{{\left| {{h_{rp}}} \right| }^2},{P_{\max }}}}} \right) \nonumber \\ P_2^ * &= {} \min \left( {\frac{{{k_4} - \sqrt{k_4^2 - 4{k_1}{k_3}{k_5}} }}{{2{k_1}{k_3}}},{P_{\max }}} \right) \nonumber \\ P_1^ * &= {} \min \left( {{{({P_I} - {{\left| {{h_{2p}}} \right| }^2}P_2^ * )} /{{{\left| {{h_{1p}}} \right| }^2}}},{P_{\max }}} \right) \end{aligned}$$
(16)

where \({k_1} = {\varphi _1}{\gamma _{th1}}{\left| {{h_{2p}}} \right| ^2} + {\varphi _2}{\gamma _{th2}}{\left| {{h_{1p}}} \right| ^2}, {k_2} = {d_2}{\gamma _{th1}}{\left| {{h_{2p}}} \right| ^2} + {d_1}{\gamma _{th2}}{\left| {{h_{1p}}} \right| ^2}, {k_3} = {d_1}{\left| {{h_{1p}}} \right| ^2} - {d_2}{\left| {{h_{2p}}} \right| ^2}, {k_4} = P_r^ * {\varphi _r}{\left| {{h_{1p}}} \right| ^2}{k_2} + ({d_2}{k_1} - {\varphi _1}{\gamma _{th1}}{k_3}), {k_5} = {d_2}{\gamma _{th1}}{P_I}(P_r^ * {\varphi _r}{\left| {{h_{1p}}} \right| ^2} - {\varphi _1}{P_I})\).

3.4 Case IV: Relay Node Power is Limited Due to IPT of PU

When transmit power of the relay node is limited with the PU experiencing the maximum possible interference level. In this situation, if the interference to the PU from SU nodes is below the IPT level of PU, its analysis is shown as the Case II. And if not, it is just the same as the Case III.

According to aforementioned analysis and calculation, we do not know which case matches the circumstance in the practical application at first.However, the key steps in determining the OPA scheme can be expressed as follows,

Step 1:

Calculate the local optimal solutions of the different situations above.

Step 2:

Examine the solutions in step 1 whether they satisfy the other constraints or not. If not, remove it out.

Step 3:

Make comparisons of the outage probability of different cases reserved in step 2 and choose the minimum one as the globally optimal solution, which is determined as the OPA scheme.

4 Numerical Results

In this section, some simulation results are provided to evaluate our analytical results of the proposed scheme compared with equal power allocation (EPA) scheme. Outage probabilities for these two schemes are plotted with the total power and the location of the relay R by assuming certain parameters. It is assumed that the path loss exponent \(\alpha = 3\) and that all nodes are located in a straight line with \({d_1} + {d_2} = 1\) and the relay located between the two end nodes.

Fig. 2
figure 2

Comparison between the proposed scheme and EPA scheme in terms of outage performance

Full size image

The outage performance based on secondary communication of the proposed scheme and EPA scheme is illustrated in Fig. 2. Without loss of generality, simulation parameters are set as follows: \({\gamma _{th1}} = 1, {\gamma _{th2}} = 1.5, d_1=0.6, {\varphi _1} = 0.2, {\varphi _2} = 0.3, {\varphi _r} = 0.5, {h_{1p}} = 0.2, {h_{2p}} = 0.3, {h_{rp}} = 0.5\) and \({P_{max}} = 20\). In the EPA case, powers are equally divided between the end and the relay node. As observed, outage probability reduces with the total power in each case and the proposed scheme achieves a gain of 4 dB over the EPA scheme. Particularly, it can be observed that the outage probability converges to a certain level due to the IPT constraint introduced into the optimization scheme, even though the total power is sufficient. In this situation, the SU communication reaches its minimum outage probability while the PU experiencing the highest interference from the secondary transmission. Therefore, there is a limit in the outage probability that the SU transmission can achieve just as Case III analyzes and that reduces with the increasing of the IPT level of PU.

Fig. 3
figure 3

System outage probability against \(d_1\) under the proposed scheme and EPA scheme

Full size image

Figure 3 compares the overall system outage probability versus relay location under the different power allocation scheme with different sets of traffic requirements \({{\{ }}{R_{th1}},{R_{th2}}{{\} }}\): (1)\({{\{ }}0.5,0.5{{\} }}\), (2)\({{\{ }}1,0.5{{\} }}\), (3)\({{\{ }}0.5,1{{\} }}\) with \({P_I} = 10\) and \(P_t=5, 15\) and 25 dB, respectively. Here it can be observed that the proposed scheme have a better performance than the EPA scheme for symmetric or asymmetric traffic mode, which is more remarkable when the relay is located to either end node. Therefore, the proposed scheme can help maintain the system balance for asymmetric traffic requirements. Moreover, regardless of asymmetric or symmetric traffic, the proposed power allocation scheme is more suitable for cognitive two-way AF relay networks.

5 Conclusions

Under the total power constraint and the IPT constraints to the PU, we have proposed a power allocation scheme by minimizing the weaker link’s individual outage probability for cognitive two-way relay networks. The closed-form solution is derived for each case by using KKT conditions. Numerical Results show that the proposed scheme outperforms the EPA scheme under different traffic requirements.Moreover, the proposed scheme can help maintain the system balance for asymmetric traffic requirements and is more suitable for cognitive two-way AF relay networks. As a future work, we will consider the outage probability for the nodes that have imperfect CSI and extend the system to multi-node scenarios.