1 Introduction

The mixed dual-hop amplify-and-forward (AF) relaying system, composed of the radio frequency (RF) and free space optical (FSO) links, was recently proposed in [1,2,3]. This mixed relay configuration was inspired by the concept of multiplexing, i.e. it makes possible multiplexing several RF users into a single FSO link. According to [2], a connectivity gap between a backbone network and last-mile access network can be resolved by using a high-speed FSO link for the last-mile. A subcarrier intensity modulation scheme (SIM) [4,5,6] is employed to convert the RF signal from the first hop to the optical signal for re-transmission, while it was assumed that there is no interference between the RF and the FSO hops, since they operate on completely different sets of frequencies. The FSO link in the second hop will cover the last mile and ensure no existence of fibre optics between the buildings, which provides similar bandwidth in saving economic resources [1,2,3]. Furthermore, the outage performance of the mixed dual-hop RF/FSO relay system with Rayleigh RF link and the Gamma–Gamma FSO link was studied in [1]. Besides outage probability, the error and capacity performance of a similar configuration, which takes the pointing errors at FSO link into account, were investigated in [2]. Under assumption that RF and FSO links are, respectively, subjected to Rayleigh fading and recently proposed M-distributed turbulence with pointing errors, closed form expression for the outage probability was derived in [3].

Inspired by these three works, in this paper, we study the RF/FSO relaying channel, where the RF link is assumed to follow the more general Nakagami-m fading model [7]. Beside the Gamma–Gamma atmospheric turbulence [8,9,10,11], we consider that the intensity fluctuations of the optical signal at the destination are also caused by pointing errors [12,13,14,15], which occur as the consequence of building sway due to thermal expansions, weak earthquakes and strong wind. We present novel accurate closed-form expressions for the outage probability for the practical case when RF link is corrupted by N multiple co-channel interferences (CCIs) and the additive white Gaussian noise (AWGN) at the relay. The analysis of CCIs influence on system performance is important, since CCIs occur as a result of the frequency re-using in RF systems or can be caused by cross-polarization discrimination [16, 17]. The general results are simplified in the case when the RF link is noise-limited (NL). As a special case, the system with the negligible pointing errors is also considered, and the outage probability expressions are reduced. For the special case of Rayleigh fading channels (fading severity parameter equal to one), the novel closed-form expression for the outage probability is reduced to the corresponding result reported in [1]. All analytical results are validated by Monte Carlo simulations.

The paper is organized as follows. Model of the system is described in Sect. 2, while closed-form expressions for the outage probability are derived in Sect. 3. Section 4 presents numerical and simulation results with appropriate comments, while some concluding remarks are given in Sect. 5.

2 System and Channel Model

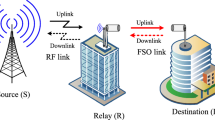
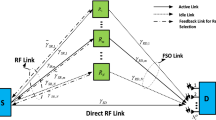
Figure 1 presents the mixed dual-hop relay system in the presence of CCIs and AWGN at the relay node R. The model of independent identically distributed (i.i.d.) CCIs is used, because it corresponds to the two limiting cases of the system performance. The worst case is when the interferers are located near the cell edges closest to the observed user cell, and the best case is when they are located near the farthest edges [16, 17]. The source node S communicates with the node R via the RF link, while the relay node R is connected with the destination node D via the FSO link. The electrical signal at the node R is converted to the optical one by SIM scheme.

The received signal at the relay is corrupted by N multiple CCIs, \(\left\{ {{r_i}} \right\} _{i = 1}^N\) , each with an average power of \(P_i\). After removing the dc bias and an optical-to-electrical conversion, the received signal at the node D has the form

$$\begin{aligned} {r_D} = {I_{RD}}G\eta \left( {{h_{SR}}r + \sum \limits _{i = 1}^N {{h_i}} {r_i} + {n_{SR}}} \right) + {n_{RD}}, \end{aligned}$$
(1)

where r is the RF signal transmitted from the node S with an average power \(P_s\), \(h_{SR}\) is the desired signal fading amplitude over RF link, \(h_i\) is the i-th CCI fading amplitude, \(I_{RD}\) is the intensity of an optical signal at the node D, G is the relay gain, and \(\eta\) is an optical-to-electrical conversion constant. The level of the AWGN with zero mean and variance \(\sigma_{SR}^2\) over RF link is denoted by \(n_{SR}\), while the AWGN with zero mean and variance \(\sigma_{RD}^2\) over the FSO link is denoted by \(n_{RD}\). The thermal, background and dark current noise are all additive and independent [8, 18], so total noise of FSO hop is modelled as the AWGN which comprises all mentioned components.

Fig. 1
figure 1

System model of a mixed RF/FSO dual hop transmission system

Full size image

Since the first RF hop is under the influence of Nakagami-m fading, the instantaneous signal-to-noise ratio (SNR) over the RF hop, \({\gamma _1} = h_{SR}^2{P_S}/\sigma _{SR}^2\), follows the Gamma distribution with probability density function (PDF) given by [7, Eq. (2.21)]

$$\begin{aligned} {f_\gamma }_1({\gamma _1}) = \frac{{m_1^{{m_1}}}}{{\Gamma \left( {{m_1}} \right) \mu _1^{{m_1}}}}\gamma _1^{{m_1} - 1}{e^{ - \frac{{{m_1}{\gamma _1}}}{{{\mu _1}}}}}, \end{aligned}$$
(2)

where \(m_1\) denotes the fading severity parameter, \(\mu _1\) = \(\mathrm{E}\left[ {{{h_{SR}^2{P_s}} \Big / {\sigma _{SR}^2}}} \right]\) is the average SNR over the RF hop, and \(\mathrm{E}\left[ \cdot \right]\) denotes expectation. Since the interfering signals experience i.i.d. Nakagami-m fading, the total instantaneous interference-to-noise ratio (INR), \({\gamma _I} = \sum \nolimits _{i = 1}^N {h_i^2} P_i/\sigma _{SR}^2\), follows also the Gamma distribution with parameters \(Nm_I\) and \(N\mu _I\), where \(m_I\) is the CCI fading severity parameter and \(\mu _I=\mathrm{E}\left[ {{{h_i^2{P_i}} \Big / {\sigma _{SR}^2}}} \right]\) is the average INR per a CCI.

The relay gain can be defined similarly as in [19, 20] by

$$\begin{aligned} {G^2} = \frac{{{P_t}}}{{\mathrm{E}\left[ {h_{SR}^2} \right] {P_s} + \sum \nolimits _{i = 1}^N {\mathrm{E}\left[ {{h_i}^2} \right] {P_i}} + \sigma _{SR}^2}} = \frac{{{P_t}}}{{\sigma _{SR}^2{C_1}}}, \end{aligned}$$
(3)

where \(P_t\) is the relay output signal power. The parameter \({C_1}\) = \({{{P_t}} \Big / {\left( {\sigma _{SR}^2{G^2}} \right) }}\) can be found as

$$\begin{aligned} {C_1} = {\mu _1} + {\mu _I}N + 1. \end{aligned}$$
(4)

Beside the Gamma–Gamma atmospheric turbulence, the second FSO hop is under the influence of pointing errors, so the intensity of an optical signal \(I_{RD}\) is described by the combined model with the PDF [14, Eq. (12)]

$$\begin{aligned} {f_{I_{RD}}}(I_{RD}) = \frac{{{\xi ^2}\alpha \beta }}{{{A_0}{h_l}\Gamma (\alpha )\Gamma (\beta )}} G_{1,3}^{3,0}\left( {\frac{{\alpha \beta }}{{{A_0}{h_l}}}I_{RD}\left| {\begin{array}{c} {{\xi ^2}}\\ {\begin{array}{ccc} {{\xi ^2} - 1,}&{}{\alpha - 1,}&{}{\beta - 1} \end{array}} \end{array}} \right. } \right) , \end{aligned}$$
(5)

where \(G_{p,q}^{m,n}\left( \cdot \right)\) denotes Meijer’s G function defined by [21, Eq. (9.301)], \(\alpha\) and \(\beta\) are atmospheric turbulence parameters, \(h_{l}\) is the attenuation due to atmospheric path loss and \(\xi\) and \(A_{0}\) represent the parameters determined by pointing errors.

The parameters \(\alpha\) and \(\beta\) represent the effective number of the small-scale and large scale cells. If the plane wave propagation and zero inner scale are assumed, the parameters \(\alpha\) and \(\beta\) can be directly related with turbulence strength of FSO link as [8, p. 139, Eqs. (3.127), (3.128), 9, p. 511, Eq. (68)]

$$\begin{aligned} \alpha= & {} {\left( {\exp \left[ {\frac{{0.49\sigma _R^2}}{{{{\left( {1 + 1.11\sigma _R^{12/5}} \right) }^{7/6}}}}} \right] - 1} \right) ^{ - 1}},\nonumber \\ \beta= & {} {\left( {\exp \left[ {\frac{{0.51\sigma _R^2}}{{{{\left( {1 + 0.69\sigma _R^{12/5}} \right) }^{5/6}}}}} \right] - 1} \right) ^{ - 1}}, \end{aligned}$$
(6)

where \({\sigma _R^2}\) is the Rytov variance, defined as

$$\begin{aligned} \sigma _R^2 = 1.23C_n^2{k^{7/6}}{L^{11/6}}, \end{aligned}$$
(7)

with the wave-number \(k=2\pi /\lambda\), the wavelength \(\lambda\), the propagation distance L, and the refractive index \(C_n^2\), which typically varies from \(10^{-17}\) m\(^{-2/3}\) to \(10^{-13}\) m\(^{-2/3}\) for weak to strong turbulence conditions, respectively.

The atmospheric conditions also have impact on the atmospheric path loss \(h_{l}\), which is described by the exponential Beers-Lambert law as [12]

$$\begin{aligned} {h_l} = \exp \left( { - \sigma L} \right) , \end{aligned}$$
(8)

where \(\sigma\) denotes the atmospheric attenuation coefficient.

The pointing errors parameter \(\xi\) is defined as the ratio between the equivalent beam radius at the receiver, \(w_{L_{eq}}\), and the pointing error (jitter) standard deviation, \(\sigma _s\), at the receiver [12]

$$\begin{aligned} \xi = \frac{{{w_{L_{eq}}}}}{{2{\sigma _s}}}. \end{aligned}$$
(9)

The equivalent beam radius at the receiver is dependent on the beam waist (radius calculated at \(e^{-2}\)) of a Gaussian beam propagation at distance L, \(w_{L}\), and the radius of a circular detector aperture, a, as

$$\begin{aligned} {w_{L_{eq}}^{2}} = \frac{{w_L^2\sqrt{\pi }{\mathrm{erf}}\left( v \right) }}{{2v\exp \left( { - {v^2}} \right) }},~~~~v = \frac{{\sqrt{\pi }a}}{{\sqrt{2} {w_L}}}. \end{aligned}$$
(10)

The parameter \(A_{0}\) denotes the fraction of the collected power at \(L = 0\), defined as

$$\begin{aligned} {A_0} = {\left[ {{\mathrm{erf}} \left( v \right) } \right] ^2}, \end{aligned}$$
(11)

where erf(.) is the error function [21, Eq. (8.250.1)].

The optical beam waist at the receiver, \(w_{L}\), can be related to optical beam waist at the output of transmitting laser, \(w_{0}\), and radius of curvature, \(F_{0}\), by [13]

$$\begin{aligned} {w_L} = {w_0}\sqrt{\left( {{\varTheta _o} + {\varLambda _o}} \right) \left( {1 + 1.63\sigma _R^{12/5}{\varLambda _1}} \right) } , \end{aligned}$$
(12)

where

$$\begin{aligned} {\varTheta _o} = 1 - \frac{L}{{{F_0}}},~~{\varLambda _o} = \frac{{2L}}{{kw_0^2}}\hbox { and } {\varLambda _1} = \frac{{{\varLambda _o}}}{{\varTheta _o^2 + \varLambda _o^2}}. \end{aligned}$$
(13)

Using (5), after some mathematical calculation and standard technique of transforming random variables, the PDF of the instantaneous SNR over the FSO hop, \({\gamma _2} = {{{\eta ^2}I_{RD}^2P_t^2} \Big / {\sigma _{RD}^2}}\), is derived as

$$\begin{aligned} {f_{{\gamma _2}}}({\gamma _2}) = \frac{{{\xi ^2}}}{{2\varGamma (\alpha )\varGamma (\beta ){\gamma _2}}} G_{1,3}^{3,0}\!\left( \!{\alpha \beta \varepsilon \sqrt{\frac{{{\gamma _2}}}{{{\mu _2}}}} \left| {\begin{array}{c} {{\xi ^2} + 1}\\ {\begin{array}{ccc} {{\xi ^2},}&{}{\alpha ,}&{}\beta \end{array}} \end{array}}\right. } \right) , \end{aligned}$$
(14)

where \(\varepsilon = {{{\xi ^2}} \Big / {\left( {{\xi ^2} + 1} \right) }}\) and \({\mu _2} = {{{\eta ^2}P_t^2\mathrm{E}^{2}\left[ {I_{RD}} \right] } \Big / {\sigma _{RD}^2}}\) represents the average electrical SNR over the FSO link, with \(\mathrm{E}^{2}\left[ {I_{RD}} \right] = {\varepsilon ^2}A_0^2h_l^2\).

The greater misalignment between transmitter and receiver corresponds to less value of \(\xi\), i.e. to greater values of \(\sigma _s\) and/or less value of \(w_0\). Hence, when \(\xi \rightarrow \infty\), it can be assumed that the intensity fluctuations of the received optical signal originate only from Gamma–Gamma atmospheric turbulence.

The overall signal-to-interference plus noise ratio (SINR) at the destination is given by

$$\begin{aligned} \gamma = \frac{{{\eta ^2}I_{RD}^2{G^2}h_{SR}^2{P_s}}}{{{\eta ^2}I_{RD}^2{G^2}\sum \limits _{i = 1}^N {{h_i}^2} {P_i} + {\eta ^2}I_{RD}^2{G^2}\sigma _{SR}^2 + \sigma _{RD}^2}} = \frac{{{\gamma _1}{\gamma _2}}}{{{\gamma _2}{\gamma _I} + {\gamma _2} + {C_1}}}. \end{aligned}$$
(15)

In the case where the RF subsystem is NL, according to [1, Eq. (6)], the overall SNR at the destination can be expressed as

$$\begin{aligned} {\gamma _{NL}} = \frac{{{\eta ^2}I_{RD}^2{G^2}h_{SR}^2{P_s}}}{{{\eta ^2}I_{RD}^2{G^2}\sigma _{SR}^2 + \sigma _{RD}^2}} = \frac{{{\gamma _1}{\gamma _2}}}{{{\gamma _2} + {C_2}}}, \end{aligned}$$
(16)

where parameter \(C_2\) is constant determined by the relay gain. When NL system is under investigation, the gain is defined as [20, Eq. (6)]

$$\begin{aligned} G_{NL}^2 = \frac{{{P_t}}}{{\mathrm{E}\left[ {h_{SR}^2} \right] {P_s} + \sigma _{SR}^2}} = \frac{{{P_t}}}{{\sigma _{SR}^2{C_2}}}, \end{aligned}$$
(17)

so the parameter \(C_2\) is found as

$$\begin{aligned} {C_2} = {\mu _1} + 1. \end{aligned}$$
(18)

3 Outage Probability Analysis

The outage probability is the probability that the instantaneous end-to-end SINR, \(\gamma\), falls below a predetermined protection ratio, \(\gamma_{th}\) [7]. For the system under the investigation, it can be written as

$$\begin{aligned} {P_{out}}= & {} \Pr \left[ {\frac{{{\gamma _1}{\gamma _2}}}{{{\gamma _2}{\gamma _I} + {\gamma _2} + {C_1}}}< {\gamma _{th}}} \right] \nonumber \\= & {} \,\int \limits _0^\infty {\int \limits _0^\infty {\Pr \left[ {{\gamma _1} < {\gamma _{th}} \left( {{\gamma _I} + 1 + \frac{{{C_1}}}{{{\gamma _2}}}} \right) } \right] } } {f_\gamma }_2({\gamma _2}){f_\gamma }_I({\gamma _I})d{\gamma _2}d{\gamma _I}. \end{aligned}$$
(19)

where Pr[.] denotes probability.

Using the cumulative distribution function (CDF) of the Gamma distribution [7, Table (9.5)], and applying [21, Eq. (1.111), 22, Eq.  (06.06.06.0005.01)], after some mathematical manipulations (19) can be re-written as

$$\begin{aligned} {P_{out}}= & {} 1 - \sum \limits _{k = 0}^{{m_1} - 1} {\sum \limits _{i = 0}^k {k \atopwithdelims ()i} {{\left( {\frac{{{m_I}}}{{{\mu _I}}}} \right) }^{{m_I}N}}\!{{\left( {\frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}} \right) }^{k}}} \frac{{{\xi ^2}{C_1}^i}}{{k!2\Gamma (\alpha )\Gamma (\beta )\Gamma \left( {{m_I}N} \right) }}{e^{ - \frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}}}\nonumber \\&\times \int \limits _0^\infty \! \! \! {\int \limits _0^\infty {{\gamma _2}^{ - i - 1}{e^{ - \frac{{{m_1}{\gamma _{th}}C{}_1}}{{{\mu _1}{\gamma _2}}}}}}} G_{1,3}^{3,0}\left( {\alpha \beta \varepsilon \sqrt{\frac{{{\gamma _2}}}{{{\mu _2}}}} \left| {\begin{array}{c} {{\xi ^2} + 1}\nonumber \\ {\begin{array}{ccc} {{\xi ^2},}&{}{\alpha ,}&{}\beta \end{array}} \end{array}} \right. } \right) \nonumber \\&\times {{\gamma _I}^{{m_I}N - 1}{e^{ - {\gamma _I}\left( {\frac{{{m_1}}}{{{\mu _1}}}{\gamma _{th}} + \frac{{{m_I}}}{{{\mu _I}}}} \right) }}{{\left( {{\gamma _I} + 1} \right) }^{k - i}}} d{\gamma _2}d{\gamma _I}. \end{aligned}$$
(20)

After applying the procedure described in Appendix A, the outage probability when relay suffers from the multiple CCIs and AWGN is derived in the closed-form given by

$$\begin{aligned} {P_{out}}= & {} 1 - \frac{{{2^{\alpha + \beta - 3}}{\xi ^2}}}{{\pi \Gamma (\alpha )\Gamma (\beta )}}{\left( {\frac{{{m_I}}}{{{\mu _I}}}} \right) ^{{m_I}N}}{e^{ - \frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}}}\sum \limits _{k = 0}^{{m_1} - 1} {\sum \limits _{i = 0}^k {k \atopwithdelims ()i} \frac{1}{{k!}}} {\left( {\frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}} \right) ^{k - i}}\nonumber \\&\times {\rm{U}}\left( \! \! {{m_I}N,k \! - \!i \!+ \!{m_I}N + 1;\frac{{{m_I}}}{{{\mu _I}}} \! + \! \frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}} \! \right) \!G_{1,6}^{6,0} \!\left( \! {\frac{{{\alpha ^2}{\beta ^2}{\varepsilon ^2}{m_1}{\gamma _{th}}{C_1}}}{{16{\mu _1}{\mu _2}}}\left| \! {\begin{array}{c} {\begin{array}{c} {\frac{{{\xi ^2} + 2}}{2}} \end{array}}\\ {{\kappa _1}} \end{array}} \right. } \! \! \right) \! \!, \end{aligned}$$
(21)

where \({\rm{U}}\left( \cdot \right)\) is the confluent hypergeometric function defined by [21, Eq. (9.211.4)] and

$$\begin{aligned} {\kappa _1} = \begin{array}{cccccc} {\frac{{{\xi ^2}}}{2},}&{\frac{\alpha }{2},}&{\frac{{\alpha + 1}}{2},}&{\frac{\beta }{2},}&{\frac{{\beta + 1}}{2},}&i \end{array}. \end{aligned}$$
(22)

If the pointing errors effect is negligible small, i.e. the intensity fluctuations of the optical signal at the node D are caused only by the Gamma–Gamma atmospheric turbulence, the instantaneous SNR over the FSO link, \(\gamma _2\), has the PDF given by [1, Eq. (8)]. The outage probability of the system when pointing errors are neglected, can be derived by substituting [1, Eq. (8)] instead (14) into (19) by following similar derivation as in Appendix A. Another method implies considering \(\xi \rightarrow \infty\) in (21) [3], which is presented in Appendix  B. The outage probability of the system without pointing errors is derived as

$$\begin{aligned} {P_{out,GG}}= & {} \mathop {\lim }\limits _{\xi \rightarrow \infty } {P_{out}} = 1 - \frac{{{2^{\alpha + \beta - 2}}}}{{\pi \Gamma \left( \alpha \right) \Gamma \left( \beta \right) }}{\left( {\frac{{{m_I}}}{{{\mu _I}}}} \right) ^{{m_I}N}}{e^{ - \frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}}}\nonumber \\&\times \sum \limits _{k = 0}^{{m_1} - 1} {\sum \limits _{i = 0}^k {k \atopwithdelims ()i} \frac{1}{{k!}}} {\left( {\frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}} \right) ^{k - i}}\nonumber \\&\times {\rm{U}}\left( {{m_I}N,k - i + {m_I}N + 1;\frac{{{m_I}}}{{{\mu _I}}} + \frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}} \right) \!G_{0,5}^{5,0}\left( \! {\frac{{{\alpha ^2}{\beta ^2}{m_1}{\gamma _{th}}{C_1}}}{{16{\mu _1}{\mu _2}}}\left| {\begin{array}{c} - \\ {{\kappa _2}} \end{array}} \right. }\! \right) \!, \end{aligned}$$
(23)

with

$$\begin{aligned} {\kappa _2}\begin{array}{ccccc} { = \frac{\alpha }{2},}&{\frac{{\alpha + 1}}{2},}&{\frac{\beta }{2},}&{\frac{{\beta + 1}}{2},}&i \end{array}. \end{aligned}$$
(24)

The outage probability of the relaying system with the NL RF link can be found as [1, Eq. (9)]

$$\begin{aligned} P_{out}^{NL} = \int \limits _0^\infty {\Pr \left[ {{\gamma _1} < \frac{{{\gamma _{th}}\left( {{\gamma _2} + {C_2}} \right) }}{{{\gamma _2}}}} \right] {f_{{\gamma _2}}}\left( {{\gamma _2}} \right) d{\gamma _2}} , \end{aligned}$$
(25)

or by setting \(N=0\) into (21). After applying [22, Eq. (07.33.03.0013.01)] in (21), the outage probability is expressed as

$$\begin{aligned} P_{out}^{NL}= & {} 1 - \frac{{{2^{\alpha + \beta - 3}}{\xi ^2}{e^{ - \frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}}}}}{{\pi \Gamma (\alpha )\Gamma (\beta )}}\sum \limits _{k = 0}^{{m_1} - 1} {\sum \limits _{i = 0}^k {k \atopwithdelims ()i} \frac{1}{{k!}}} {\left( {\frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}} \right) ^{k - i}}\nonumber \\&\times G_{1,6}^{6,0}\left( {\frac{{{\alpha ^2}{\beta ^2}{\varepsilon ^2}{m_1}{\gamma _{th}}{C_2}}}{{16{\mu _1}{\mu _2}}}\left| \!\! {\begin{array}{c} {\begin{array}{c} {\frac{{{\xi ^2} + 2}}{2}} \end{array}}\\ {{\kappa _1}} \end{array}}\! \right. }\! \!\right) \!, \end{aligned}$$
(26)

where parameter \(C_2\) is given by (18) and \(\kappa _1\) is defied by (22).

For the system without pointing errors, the outage probability expression is derived by considering \(\xi \rightarrow \infty\) in (26) and using similar approach as in Appendix B:

$$\begin{aligned} P_{out,GG}^{NL}= & {} 1 - \frac{{{2^{\alpha + \beta - 2}}{e^{ - \frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}}}}}{{\pi \Gamma \left( \alpha \right) \Gamma \left( \beta \right) }}\sum \limits _{k = 0}^{{m_1} - 1} {\sum \limits _{i = 0}^k {k \atopwithdelims ()i} \frac{1}{{k!}}} {\left( {\frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}} \right) ^{k - i}}\nonumber \\&\times G_{0,5}^{5,0}\left( {\frac{{{\alpha ^2}{\beta ^2}{m_1}{\gamma _{th}}{C_2}}}{{16{\mu _1}{\mu _2}}}\left| {\begin{array}{c} - \\ {{\kappa _2}} \end{array}} \right. } \right) . \end{aligned}$$
(27)

If the RF link follows Rayleigh distribution (which is the special case of Nakagami-m distribution when \(m_1=1\)), then the observed relaying channel comes to that from [1]. It is verified that substituting \(m_1=1\) in (27) and applying [22, Eq.  (07.34.16.0001.01)] leads to [1, Eq. (15)].

4 Numerical Results

Novel outage probability expressions in (21), (23), (26) and (27) are given in terms of Meijer’s G functions that are built in software package Mathematica 10 and can be efficiently numerically evaluated. Using [22, Eq.  (07.34.26.0004.01)], Meijer’s G function can be presented in terms of more familiar generalized hypergeometric functions denoted by \({}_p{F_q}\left( {{a _1},{a _2}, \ldots , {a _p};{b _1},{b _2}, \ldots , {b _q};z} \right)\) [21, Eq. (9.100\(^{7}\))]. After some mathematical manipulations (21), (23), (26) and (27) can be presented in the equivalent forms in terms of the generalized hypergemetric functions that are not presented here because of the space limitations. In that case, \({a _1},{a _2}, \ldots , {a _p},{b _1},{b _2}, \ldots , {b _q}\), should be \(\ne - n,\mathrm{{ }}\left( {n = 0, 1, 2, \ldots } \right)\) since the generalized hypergeometric function has poles in these points. However, this is not inconvenience in practice because parameters \(\alpha , \beta\) and \(\xi\) previously defined are not integers with high probability. In the case that any \({a _i}\) or \({b _j}\) \((i = 1, 2, \ldots ,p;j = 1, 2, \ldots q)\) is negative integer, the numerical value of generalized hypergeometric function could be evaluated for \({a _i} + \varepsilon\) and \({b _j} + \varepsilon\), where \(\varepsilon = {10^{ - 4}}\), instead of \({a _i}\) and \({b _j}\), respectively. In contrast to this, even when \(\alpha ,\beta\) and \(\xi\) are integers, numerical values of outage probability can be evaluated in software package Mathematica 10 using derived Eqs. (21), (23), (26) and (27) containing Meijer’s G functions, since this software package has very efficient algorithms for numerical evaluation of Meijer’s G functions allowing symbolic evaluation of [21, Eq. (9.301)] including necessary reduction of expressions in numerator and denominator. Numerical results are validated by Monte Carlo simulations performed using software package Matlab 2013.

Fig. 2
figure 2

Outage probability versus average electrical SNR over FSO link when relay suffers from noise for different values of jitter standard deviation

Full size image

The results were obtained for the turbulence parameters \(\alpha\) and \(\beta\) defined by (6) and (7), which are dependent on several physical parameters, such as: refractive index \(C_n^2\), the wavelength \(\lambda = 1550\) nm and the propagation distance \(L= 1000\) m. The refractive index determines the turbulence strength in the following way: \(C_n^2 = 6\times 10^{-15}\) m\(^{-2/3}\) for weak , \(C_n^2 = 2\times 10^{-14}\) m\(^{-2/3}\) for moderate and \(C_n^2~=~5\times 10^{-14}\) m\(^{-2/3}\) for strong turbulence conditions [23]. It should be noted that pointing errors parameter, \(\xi\), is dependent on jitter standard deviation, \(\sigma _s\), the radius of a circular detector aperture, \(a= 5\) cm, radius of curvature, \(F_{0}= -10\) m, as well as other parameters such as \(C_n^2\), \(\lambda\), L and the optical beam waist at the output of transmitting laser, \(w_0\).

Figure 2 presents the outage probability dependence on the average electrical SNR over the FSO link for different values of \(\mu _1\) and the jitter standard deviation \(\sigma _s\) in the case when the relay is corrupted only by noise. As expected, outage probability has lower values for greater values of \(\mu _1\). The greater values of parameter \(\sigma _s\) (corresponding to lower values of parameter \(\xi\), see Eq. (9), and greater misalignment between transmitter and the receiver) are manifested in the degradation of the system performance. In the range of low and moderate values of \(\mu _2\), the outage probability decreases, but for great values of \(\mu _2\), outage tends to a constant value. This outage floor cannot be decreased by further increasing average electrical SNR over the FSO link, but only by increasing the average SNR over RF link. The value of \(\mu _2\), when the outage floor appears, decreases with \(\mu _1\) and/or \(\sigma _s\) decreasing. In addition, the case when the pointing errors effect is negligible and the intensity fluctuations are caused only by the Gamma–Gamma turbulence is observed. One can notice overlapping of the curves corresponding to \(\sigma _s=10\) cm (\(\sigma _s/a=2\)) and those when there is no misalignment fading.

Figure 3 plots the outage probability versus the average SNRs over both hops for different values of outage threshold and fading severity in NL system. As expected, outage probability decreases with decreasing \(\gamma _{th}\). In addition, with increasing the parameter \(m_1\), corresponding to decreasing fading severity, system has better outage performance. The worst performance exists for \(m_1~=~1\), which corresponds to Rayleigh fading. The effect of fading severity on the outage performance is more pronounced when outage threshold is lower. For example, for \(\mu _1=\mu _2 = 20\) dB, by changing \(m_1\) from 1 to 4, the outage probability decreases about 6.42 and 22.54 times in the case when \(\gamma _{th}\) is 0 and −10 dB, respectively. It is noticed that the outage floor does not appear in this case, since the outage probability dependence is presented in the function of the average SNR over both hops \((\mu _1=\mu _2)\), so both average SNRs increase simultaneously.

Fig. 3
figure 3

Outage probability versus average SNR over both hops when relay suffers from noise for different values of fading severity

Full size image

The effect of the number of interferers for different values of the average INR is presented in Fig. 4. The increasing of N reflects in worse system performance. The outage floor exists, and it takes different values for various number of CCIs. Also, the average INR effect on the outage floor is noticed. The influence of the number of interferers is more expressed while the average INR is greater. With decreasing the value of \(\mu _I\), the number of CCIs will be of a less importance on system performance. Further decreasing of \(\mu _I\), for example \(\mu _I=\mu _1-40\) dB, leads to the same system performance for any number of CCIs. The curve corresponding to this situation overlaps with one for the case of NL system (the results for this case are left out in Fig. 4. in order to avoid overcrowding of the curves). So, when the power of the CCI is reducing, the CCIs will have no influence on the system performance, because the effect of the noise is dominant.

Fig. 4
figure 4

Outage probability versus average SNR over RF link when relay suffers from multiple CCIs and noise

Full size image
Fig. 5
figure 5

Outage probability versus average electrical SNR over FSO link when relay suffers from multiple CCIs and noise in different turbulence conditions

Full size image

Figure 5 shows the influence of the number of CCIs on the outage performance in different turbulence conditions. As it is expected, system has better performance in weaker turbulence conditions and when number of CCIs is lower. Furthermore, the effect of the number of CCIs is more dominant in weak turbulence conditions, compared to the moderate and strong conditions. The existence of outage floor is also noted in this figure, appearing first in weak turbulence conditions.

The outage probability dependence on the average SNR over FSO hop for different values of the optical beam waist at the laser output, in weak and strong turbulence conditions, is presented in Fig. 6. The greater value of \(w_0\) reflects in greater value of \(\xi\), which corresponds to the case of non-pointing errors system. The overlapping of the curves for the system with \(w_0 =13\) cm and for the system under the influence of only Gamma–Gamma turbulence (Eq. 23), is noticed. With further increase of the optical beam waist, the outage probability performance remains closely the same. Also, the effect of different value of \(w_0\) is more dominant in weak turbulence conditions compared to strong. When FSO link is affected by strong turbulence, the intensity fluctuations of the received signal are primarily caused by turbulence, so the pointing errors effect is of a less importance on system performance.

Fig. 6
figure 6

Outage probability versus average electrical SNR over FSO link when relay suffers from multiple CCIs and noise for different values of the optical beam waist at the laser output

Full size image

It can be noted that there is an agreement between analytical and simulation results presented in all figures.

5 Conclusion

In this paper, a dual-hop semi-blind AF mixed RF/FSO relaying channel has been analysed. Assuming the presence of both multiple CCIs and noise at the relay, the accurate closed-form expressions for the outage probability have been derived for Nakagami-m fading environment over RF link and the Gamma–Gamma turbulence with pointing errors over FSO link. The outage probability expression for the system with noise-limited \(S-R\) link has been also derived, which can be simplified to the particular case of Rayleigh fading environment already reported. All numerical results have been verified by Monte Carlo simulations. The obtained formulae can be applied for estimating the outage probability dependence on the simultaneous effects of the fading severity, outage threshold, average SNRs of the both hops and average INR, as well as optical turbulence strength and pointing errors parameters. The numerical results have shown that there is an outage probability floor in the observed system. This irreducible outage probability is important system parameter and can be efficiently computed by the expressions derived here. The results have shown that effect of N is stronger in the regime of higher values of INR and weaker turbulence over FSO hop. In addition, the effects of photodetector displacement standard deviation could be strong for selected values of parameters.

6 Appendix A

The double integral in (20) consists of two independent integrals, i.e. \(I~=~I_1~\times ~I_2\), where the first one, given by

$$\begin{aligned} {I_1} = \int \limits _0^\infty \!\!{{\gamma _2}^{ - i - 1}} {e^{ - \frac{{{m_1}{\gamma _{th}}{C_1}}}{{{\mu _1}{\gamma _2}}}}} G_{1,3}^{3,0}\left( {\alpha \beta \varepsilon \sqrt{\frac{{{\gamma _2}}}{{{\mu _2}}}} \left| {\begin{array}{c} {{\xi ^2} + 1}\\ {\begin{array}{ccc} {{\xi ^2},}&{}{\alpha ,}&{}\beta \end{array}} \end{array}}\right. } \right) d{\gamma _2} \end{aligned}$$
(28)

can be solved as follows. The exponential function is expressed in terms of Meijer’s G function by [22, Eq.  (01.03.26.0004.01)], and afterwards transformed using [22, Eq.  (07.34.16.0002.01)] as

$$\begin{aligned} {e^{ - \frac{{{m_1}{\gamma _{th}}{C_1}}}{{{\mu _1}{\gamma _2}}}}} \!= \!G_{0,1}^{1,0}\left( \!{\frac{{{m_1}{\gamma _{th}}{C_1}}}{{{\mu _1}{\gamma _2}}}\left| {\begin{array}{c} - \\ 0 \end{array}} \right. }\!\! \right) \! = \!G_{1,0}^{0,1}\left( \! {\frac{{{\mu _1}{\gamma _2}}}{{{m_1}{\gamma _{th}}{C_1}}}\left| {\begin{array}{c} 1\\ - \end{array}} \right. }\!\! \right) \!\!. \end{aligned}$$
(29)

Using [22, Eq. (07.34.21.0013.01)] the integral \(I_1\) can be expressed in the form

$$\begin{aligned} {I_1} = \frac{{{2^{\alpha + \beta - 2}}}}{\pi }{\left( {\frac{{{\mu _1}}}{{{m_1}{\gamma _{th}}{C_1}}}} \right) ^i} G_{2,7}^{7,0}\left( {\frac{{{\alpha ^2}{\beta ^2}{\varepsilon ^2}{m_1}{\gamma _{th}}{C_1}}}{{16{\mu _1}{\mu _2}}}\left| {\begin{array}{c} {\begin{array}{cc} {\frac{{{\xi ^2} + 1}}{2},}&{}{\frac{{{\xi ^2} + 2}}{2}} \end{array}}\\ {{\kappa _3}} \end{array}} \right. } \right) , \end{aligned}$$
(30)

where

$$\begin{aligned} {\kappa _3} = \begin{array}{ccccccc} {\frac{{{\xi ^2}}}{2},}&{\frac{{{\xi ^2} + 1}}{2},}&{\frac{\alpha }{2},}&{\frac{{\alpha + 1}}{2},}&{\frac{\beta }{2},}&{\frac{{\beta + 1}}{2},}&i \end{array}. \end{aligned}$$
(31)

The Meijer’s G function in (30) can be re-written in a simpler form using following transformations. First, the permutations of the Meijer’s G parameters are performed using [22, Eqs. (07.34.04.0003.01), (07.34.04.0004.01)]. Thereafter, the Meijer’s G function is simplified by [22, Eq. (07.34.03.0002.01)], so the integral \(I_1\) is given in the form

$$\begin{aligned} {I_1} = \frac{{{2^{\alpha + \beta - 2}}}}{\pi }{\left( {\frac{{{\mu _1}}}{{{m_1}{\gamma _{th}}{C_1}}}} \!\!\right) ^i} G_{1,6}^{6,0}\left( {\frac{{{\alpha ^2}{\beta ^2}{\varepsilon ^2}{m_1}{\gamma _{th}}{C_1}}}{{16{\mu _1}{\mu _2}}}\left| {\begin{array}{c} {\begin{array}{c} {\frac{{{\xi ^2} + 2}}{2}} \end{array}}\\ {{\kappa _1}} \end{array}} \right. }\right) , \end{aligned}$$
(32)

where \(\kappa _1\) is previously defined by (22).

Using [21, Eq. (9.211.4)], the second integral \(I_2\) is directly solved in the closed form

$$\begin{aligned} {I_2}= & {} \int _0^\infty {{\gamma _I}^{{m_I}N - 1}{{\left( {{\gamma _I} + 1} \right) }^{k - i}}{e^{ - {\gamma _I}\left( {\frac{{{m_1}}}{{{\mu _1}}}{\gamma _{th}} + \frac{{{m_I}}}{{{\mu _I}}}} \right) }}d{\gamma _I}} \nonumber \\= & {} \Gamma \left( {{m_I}N} \right) {\rm{U}}\left( \!\!{{m_I}N,k - i + {m_I}N + 1;\frac{{{m_I}}}{{{\mu _I}}} + \frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}}\!\! \right) . \end{aligned}$$
(33)

Combining previously derived expressions for \(I_1\) and \(I_2\) with (20) leads to (21).

7 Appendix B

In order to obtain the outage probability expression of the system without pointing errors effect, it is necessary to take a limit of derived Eq. (21) for \(\xi \rightarrow \infty\). After applying [22, Eqs. (07.34.25.0007.01), (07.34.25.0006.01)], the outage probability of the system when intensity fluctuations are caused only by the Gamma–Gamma turbulence can be found as

$$\begin{aligned} {P_{out,GG}}= & {} \mathop {\lim }\limits _{\xi \rightarrow \infty } {P_{out}} = 1 - \frac{{{2^{\alpha + \beta - 3}}{\xi ^2}}}{{\pi \Gamma (\alpha )\Gamma (\beta )}}{\left( {\frac{{{m_I}}}{{{\mu _I}}}} \right) ^{{m_I}N}}{e^{ - \frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}}}\nonumber \\&\times \sum \limits _{k = 0}^{{m_1} - 1} {\sum \limits _{i = 0}^k {k \atopwithdelims ()i} \frac{1}{{k!}}} {\left( {\frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}} \right) ^{k - i}} {\rm{U}}\left( {{m_I}N,k - i + {m_I}N + 1;\frac{{{m_I}}}{{{\mu _I}}} + \frac{{{m_1}{\gamma _{th}}}}{{{\mu _1}}}} \right) \nonumber \\&\times \mathop {\lim }\limits _{\xi \rightarrow \infty } {\xi ^2}\frac{{\Gamma \left( {\frac{{{\xi ^2}}}{2}} \right) }}{{\Gamma \left( {\frac{{{\xi ^2} + 2}}{2}} \right) }}G_{0,5}^{5,0}\left( \!\!{\frac{{{\alpha ^2}{\beta ^2}{\varepsilon ^2}{m_1}{\gamma _{th}}{C_1}\left( {{\xi ^2} + 2} \right) }}{{16{\mu _1}{\mu _2}{\xi ^2}}}\left| \!\! {\begin{array}{c} - \\ {{\kappa _2}} \end{array}} \right. }\!\! \right) . \end{aligned}$$
(34)

where \(\kappa _2\) is previously defined by (24). After applying [22, Eq. (06.05.16.0002.01)] and considering \(\mathop {\lim }\limits _{\xi \rightarrow \infty } \left( {1 + 2/{\xi ^2}} \right) = 1\) and \(\mathop {\lim }\limits _{\xi \rightarrow \infty } {\varepsilon }^2 =\mathop {\lim }\limits _{\xi \rightarrow \infty } \left( {1 + 1/{\xi ^2}} \right) ^2 =1\), the outage probability for the system with the Gamma–Gamma distributed atmospheric turbulence over FSO link is derived in the form of (23).