1 Introduction

Nowadays, the increase in the need of high data rate, low cost and improved data security has led to the employment of free space optics (FSO) systems as an alternative promising technology to radio-frequency (RF) systems for point-to-point communication (Varotsos et al. 2018). This is a result of FSO advantages which include higher bandwidth, unlicensed spectrum, immunity to RF interferences and high security (Anees et al. 2015). Also, FSO systems are suitable for a wide range of applications, such as enterprise/building connectivity, the back-haul of cellular systems, redundant backup links and disaster recovery (Kong et al. 2015). In spite of these great benefits, the systems suffer from atmospheric turbulence induced fading which arise as a result of inhomogeneities in temperature and pressure along the propagation channel. This leads to random temporal and spatial irradiance fluctuation in the optical beam at the receiver (Niu et al. 2012). There are different statistical models proposed to emulate the effect of atmospheric turbulence. The most commonly accepted models are the log-normal turbulence model which describe irradiance fluctuations in weak turbulence conditions, K-distributed turbulence model for irradiance fluctuations in strong turbulence conditions, and Gamma–Gamma turbulence model which provides a description of much wider irradiance fluctuation ranges across the weak to strong turbulence regimes (Niu et al. 2012). Recently, a unified statistical model for atmospheric turbulence called M-distribution was developed in Jurado-Navas et al. (2011) which is suitable for all homogeneous and isotropic turbulence conditions. It is a versatile model that includes all the aforementioned distributions as special cases (Varotsos et al. 2017).

Another major impairment suffer by the FSO system is the pointing error which occurs a result of the building sway that arise due to thermal expansion, dynamic wind load and weak earthquakes (Odeyemi et al. 2017a; Farid and Hranilovic 2007; Sandalidis et al. 2009; Song et al. 2013). This causes vibration in the optical beam and leads to misalignment between the transmitter and the receiver. Therefore, to have a perfect line-of-sight between the transmitter and the receiver, there is need to increase the beamwidth and power. A wide beamwidth however, requires higher SNR at the cost of system complexity while a narrow one may lead to link outage failure (Sandalidis et al. 2009). Pointing error has two components, the boresight and the Jitter. The boresight can be described as the fixed displacement between beam center and center of the detector. The jitter, on the other hand, is the random offset of the beam center at detector plane, which is mainly caused by building sway and building vibration (AlQuwaiee et al. 2016; Yang et al. 2014). Several statistical models have been proposed to illustrate the effect of pointing error on the FSO systems (Farid and Hranilovic 2007; Yang et al. 2014; Boluda-Ruiz et al. 2016; Gappmair et al. 2011). Pointing error model was first developed in Farid and Hranilovic (2007) where the radical displacement at the receiver follows Rayleigh distribution. The effect of beamwidth, detector size and zero boresight for independent identical Gaussian distribution for the elevation and horizontal displacement are considered in the work. This model is further extended in Gappmair et al. (2011) for different jitter values and the radical displacement at the receiver follows Hoyt distribution. Moreover, a pointing error model with non-zero boresight at the receiver is presented in Yang et al. (2014) where the radical displacement at the receiver is modeled by lognormal-Rician distribution. A more realistic and versatile pointing model is developed in Boluda-Ruiz et al. (2016) where the effect of different jitter values for the elevation and horizontal displacement and non-zero boresight are assumed. The radical displacement at the receiver follows Beckmann distribution.

To overcome the shortcomings mentioned above, mixed RF/FSO relay technology has been considered as a prominent solution; whereby the source node transmits RF signal to the destination through a single or multiple relay units that converts and amplifies the RF signal to optical signal. The deployment of this technology in FSO systems broadens the coverage area, enhances the performance of the system, and mitigates against the channel impairments (Anees et al. 2014). This hybrid system can be classified as decode-and-forward (DF) and amplify-and-forward (AF) of relaying system (Odeyemi et al. 2017b). In this paper, AF relaying protocol is considered for the proposed system where the received signal is simply amplified and forwarded to the destination without any decoding process. The amplification process can be classified as fixed gain relaying and variable gain relaying. Mixed RF/FSO system has been investigated in many studies under a single relay system between the RF link and FSO link. The outage probability performance of a dual-hop mixed RF/FSO system in which the RF and FSO links are respectively follows Rayleigh fading and Gamma–Gamma distributions is presented in Lee et al. (2011). In Anees et al. (2015) and Anees and Bhatnagar (2015a), the performance analysis of DF and AF based mixed RF/FSO systems are respectively investigated as the FSO link subjected to Gamma–Gamma induced-fading with pointing errors. Error and capacity performance of an asymmetric RF/FSO system was presented in Anees and Bhatnagar (2015b) and the RF link and FSO link were respectively subjected to Nakagami-m and Gamma–Gamma distributions. Also, in Anees and Bhatnagar (2015c), the performance of different adaptive transmission polices was studied for the mixed RF/FSP system. The performance of mixed RF/FSO dual-hop system under different detection techniques and relaying protocols has been investigated in Zedini et al. (2015, 2016). Furthermore, mixed RF/FSO system performance has also been analyzed in Soleimani-Nasab and Uysal (2016), Yang et al. (2017), Zhang et al. (2015) and Samimi and Uysal (2013) where a unified channel distributions are considered for either RF link, FSO link or both. The detailed overview on the mixed RF/FSO systems with a single relay node is presented in Soleimani-Nasab and Uysal (2016) in terms of channel distribution, relaying protocol and detection technique.

The use of multiple relays scheme can be considered to further improve the performance of mixed RF/FSO system with a single relay unit. Multiple relay system thus needs high transmitting power, equally divided power in all relays and strict synchronization at the receiver (Sharma et al. 2017a). Based on this, relay selection technique has been proposed as an efficient solution to mitigate these limitations by selecting the best relays for data transmission. The research work on relay selection has been studied in Sharma et al. (2017b) where the relays employed DF protocol under different selection schemes with the RF link and FSO link respectively subjected to generalized η-μ and Gamma–Gamma distributions. The AF-based system of this work is extended in Sharma et al. (2017a) under the same channel conditions. However, perfect CSI is assumed on RF link of these works and it is impossible to practically have perfect CSI without estimation errors due to rapid channel fluctuation (Lei et al. 2018). As a result of this, a single relay mixed RF/FSO system with outdated CSI has been evaluated in Varshney and Puri (2017) where the performance of a mixed RF/FSO system with a moving source user-equipment unit is studied under different detection schemes. Also, the performance of multiusers mixed RF/FSO system with transmits opportunistic scheduling and outdated CSI of the RF link under a single AF relay unit is investigated in Salhab et al. (2016). At times, in relay selection schemes, the best relay might be unavailable to transmit the source signal to the relay and this may adversely affect the system performance (Soysa et al. 2011). To overcome this issue, partial relay selection (PRS) which selects a relay in accordance to single-hop outdated channel state information can be employed (Petkovic et al. 2015; Suraweera et al. 2010). Based on this, PRS can reduce the system complexity (Krikidis et al. 2008) and avoid the network feedback delays with power waste, contrary to the best and opportunistic relay selection (Petkovic et al. 2016). In this case, the performance of a variable AF relay mixed RF/FSO system with outdated CSI under PRS is presented in Petkovic et al. (2016) where the RF link of the system is subjected to Rayleigh fading and the FSO link followed Gamma–Gamma distribution. The same work is further studied in Petkovic et al. (2015) for a fixed gain AF mixed RF/FSO system under the same channel condition.

Recently, different diversity techniques have been considered to boost the performance of wireless communication systems. This is due to its ability to offers multiple transmission and/or reception path of the same signal (Ansari et al. 2013). Selection combining technique is the simplest technique among the diversity schemes where only one branch with highest SNR is processed (Odeyemi and Owolawi 2019). In Anees et al. (2015) a DF-based mixed RF/FSO system with direct link under different detection techniques is presented; where the RF links and FSO links are respectively subjected to Nakagami-m and Gamma–Gamma distributions with pointing error. The performance of this dual branch cooperative system is evaluated by selection combining diversity scheme. Also, the AF-based type of this work under heterodyne detection is investigated in Zedini et al. (2014) but selection combining and maximum ratio combining is considered for the dual branch performance of the system.

Generally, in all the aforementioned related studies on mixed RF/FSO systems, zero boresight displacement pointing error is assumed for the FSO link. Therefore, by our findings, the research studies on the PSR-based mixed RF/FSO system with direct link over a generalized M-distribution and non-zero boresight pointing have not been yet investigated. Motivated by this, the performance of a PRS-based AF mixed RF/FSO system with a direct RF link and outdated CSI is presented in this paper. The RF links are subjected to Rayleigh distributions while the FSO link experiences M-distribution with generalized non-zero boresight displacement pointing errors. Selection combining diversity with heterodyne detection is considered to evaluate the concerned system performance. The CDF of the end-to-end signal-to-noise under the influence of with/or without a direct link are derived. Through this, the closed-form expressions for the system outage probability and average bit error rate (ABER) are obtained for the concerned system.

The remainder of the paper is structured as follows. In Section II, the system and channel models are presented. The statistical equivalent end-to-end SNR under the influence of with/or without a direct link are presented in Section III. In Section IV, we derive the analytical expressions of the outage probability and ABER for the system under studied. Numerical results and discussions are provided in Section V and finally, concluding remarks are given in Section VI.

2 System and channel models

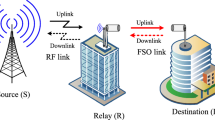
A mixed RF/FSO partial relay selection AF system with direct RF link is illustrated in Fig. 1. The system consists of the source (S), destination (D), and \(N \ge 1\) relay nodes (R). It is assumed that the S-to-R and S-to-D RF links are subjected to Rayleigh distributions while the R-to-D FSO link experiences M-distribution with generalized non-zero boresight pointing errors. The source has one transmit antenna to broadcast signal to the relay nodes and destination via the S-to-R and S-to-D RF links respectively. The relay nodes consist of one receive and transmit aperture while the destination is equipped with \(N_{r}^{D} \ge 1\) receive apertures. Data transmission between the S and D occurs in two phases and Time Division Multiple Access is assumed for transmission so as to prevent inter-signal interference. During the first phase, the source employs a local feedback from the relay nodes to monitor the instantaneous CSI of the S-to-R link through which the best mth relay \(R_{m}\) is selected. Based on this, the PRS scheme considered for the system uses the outdated CSI since the actual S-to-R link CSI is not identical with the CSI employed in selecting the best relay \(R_{m}\). Hence, there is random correlation with correlated coefficient \(\rho\) between the S-to-R SNR \(\gamma_{SR,m}\) and SNR \(\tilde{\gamma }_{SR,m}\) for the PRS. Therefore, the received signal at the receiving nodes \(j \in \left\{ {R_{m} ,D} \right\}\) can be expressed as:

$$y_{Sj} \left( t \right) = h_{Sj} x\left( t \right) + n_{Sj} \left( t \right)$$
(1)

where x represents the data transmitted from the S, \(n_{sj}\) denotes the complex-valued additive white Gaussian noise (AWGN) with zero-mean and variance \(\sigma_{Sj}^{2}\) and \(h_{Sj}\) denotes the Rayleigh distributed channel gain.

Fig. 1
figure 1

A mixed RF/FSO dual-hop system model with a direct RF link

Full size image

During the second phase, after channel estimation, the best selected relay \(R_{m}\) amplifies the received RF signal and converts the signal to optical signal using subcarrier intensity modulation (SIM) scheme before it is being re-transmitted to destination. The received signal at the destination can be expressed as:

$$y_{RD} (t) = \eta I\hat{x}(t) + n_{RD} (t)$$
(2)

where \(\hat{x}(t)\) is the estimate of x in selected relay, \(\eta\) is the optical-to-electrical conversion coefficient, \(n_{R,D} (t)\) denotes the zero-mean AWGN noise with variance, \(\sigma_{R,D}^{2}\) and I is the normalized received irradiance of the optical beam.

Finally, selection combining with heterodyne detection is assumed for the signal reception at the destination. Thus, the selection combining output for the system without a direct link can be defined as (Soliman 2015):

$$\gamma_{SC} = max\left( {\gamma_{RD,1} , \gamma_{RD,2} \ldots \gamma_{{RD,N_{r}^{D} }} } \right)$$
(3)

where \(\gamma_{{RD,N_{r}^{D} }}\) is the instantaneous SNR of the R-to-D received by the \(N_{r}^{D}\) th receive aperture.

Under the influence of a direct link, the selection combing output for the system can be expressed as (Anees et al. 2015; Ansari et al. 2013):

$$\gamma_{SC} = max(\gamma_{SD} ,\gamma_{SRD} )$$
(4)

where \(\gamma_{SD}\) is the instantaneous SNR of S-to-D link, \(\gamma_{SRD}\) is the end-to-end SNR of the system.

2.1 RF link

In this paper, the RF transmission links for both S-to-R and S-to-D links are characterized by the Rayleigh fading and the PDF for the distribution can be expressed as (Kong et al. 2015):

$$f_{Sj} (\gamma_{Sj} ) = \frac{1}{{\bar{\gamma }_{j} }}exp\left( { - \frac{{\gamma_{Sj} }}{{\bar{\gamma }_{j} }}} \right)$$
(5)

where \(\bar{\gamma }_{j}\) is the average SNR.

The CDF for the both links can be obtained from (5) as:

$$F_{Sj} \left( {\gamma_{Si} } \right) = 1 - exp\left( { - \frac{{\gamma_{Sj} }}{{\bar{\gamma }_{Sj} }}} \right)$$
(6)

Moreover, the PDF for the S-to-R link under the partial relay selection mixed RF/FSO system can be expressed as (Petkovic et al. 2015):

$$f_{{\gamma_{SR,m} }} \left( \gamma \right) = m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)\frac{{( - 1)^{p} }}{{((N - m + p)(1 - \rho ) + 1)\bar{\gamma }_{R} }}exp\left( { - \frac{(N - m + p + 1)\gamma }{{((N - m + p)(1 - \rho ) + 1)\bar{\gamma }_{R} }}} \right)$$
(7)

where \(\bar{\gamma }_{R}\) is the average SNR on the S-to-R link and \(\rho\) is the channel correlation coefficient.

2.2 FSO link

As mentioned earlier, the R-to-D FSO link suffered from both atmospheric turbulence and pointing error impairments. Thus, the channel gain for this link can be expressed as \(I = I_{a} I_{p}\) where the \(I_{a}\) and \(I_{p}\) are respectively denoted as atmospheric turbulence and pointing error fading coefficients.

2.2.1 Atmospheric turbulence induced fading

In this paper, the atmospheric turbulence experience on R-to-D link is modeled by generalized M-distribution and the PDF can be expressed as (Kong et al. 2015; Odeyemi and Owolawi 2019; Ansari et al. 2016):

$$f_{I} (I_{a}) = \varLambda \mathop \sum \limits_{q = 1}^{\beta} I_{a}^{{\frac{\alpha + k}{4} - 1}} K_{\alpha - q} \left({2\sqrt {\frac{\alpha \beta}{{\psi \beta + {\acute{\Omega}}}}I_{a}}} \right)$$
(8)

where \(K_{v} (.)\) is the modified Bessel function of the second kind with order \(v = \alpha - q\), \(\alpha\) represents the positive effective number of large scale cells of the scattering process, \(\beta\) is a natural number that denotes the amount of turbulence-induced fading and other parameters given in (8) can be defined as (Jurado-Navas et al. 2011):

$$\left\{ {\begin{array}{*{20}l} {\varLambda = \frac{{2\alpha^{\alpha /2} }}{{\psi^{1 + \alpha /2} \Gamma \left( \alpha \right)}}\left( {\frac{\psi \beta }{\psi \beta + {\acute{\Omega }}}} \right)^{{\frac{\alpha }{2} + \beta }} } \hfill \\ {a_{q} = \left( {\begin{array}{*{20}c} {\beta - 1} \\ {q - 1} \\ \end{array} } \right)\frac{{\left( {\psi \beta + {\acute{\Omega }}} \right)^{1 - q/2} }}{{\left( {q - 1} \right)!}}\left( {\frac{{\acute{\Omega }}}{\psi }} \right)^{q - 1} \left( {\frac{\alpha }{\beta }} \right)^{q/2} } \hfill \\ \end{array} } \right.$$
(9)

where \(\Gamma (.)\) is the gamma function, \(\psi = 2b_{o} (1 - \delta )\) is the average power of the classic scattering component and \(\delta (0 \le \delta \le 1)\) represents the ratio of the power of the scattering component coupled with LOS to that of all scattering components, \({\acute{\Omega}} = \Omega + 2b_{o} \delta + 2\sqrt {2b_{o} \rho \Omega} \cos \left({\phi_{A} - \phi_{B}} \right)\) denotes the average optical power of the coherent contributions and it involves both the LOS component and the scattering component coupled with it, where \(\Omega\) is the average power of the LOS term, \(2b_{o}\) denotes the total average power of the scattering components, and \(\phi_{A} - \phi_{B}\) are respectively, the deterministic phase of the LOS component and the scattering component coupled with it.

2.2.2 Pointing error with non-zero boresight

Generalized Pointing error fading model is employed in this paper, where the impact of beam width, detector size, different jitters for the elevation and the horizontal displacement; and the impact of nonzero boresight error are all considered. Approximately, the attenuation due to geometric spread and pointing errors can be obtained as it is defined in Farid and Hranilovic (2007) and Boluda-Ruiz et al. (2016) by:

$$I_{p} (r,Z) \approx A_{o} exp\left( { - \frac{{2r^{2} }}{{w_{z,eq}^{2} }}} \right),\quad r \ge 0$$
(10)

where \(r\) is the radical displacement at the receiver plane, \(w_{z, eq}\) represents the equivalent beam radius at the receiver given through \(w_{z,eq}^{2} = \sqrt \pi erf(v)W_{z}^{2} /2vexp( - v^{2} )\), \({\text{erf}}(.)\) is the error function, \(v = \sqrt \pi a/\sqrt 2 w_{z}\), \(w_{z}\) is the Gaussian beam radius on the receiver plane, a is the receiver aperture radius and \(A_{o} = \left[ {{\text{erf}}\left( v \right)} \right]^{2}\) is the fraction of the collected power at the center of the receiver for \(r = 0\).

At the receiver plane, the radical displacement can be expressed as \(r^{2} = r_{x}^{2} + r_{y}^{2}\) with \(r_{x}\) and \(r_{y}\) denote the horizontal and elevation displacement respectively. It is commonly thus assumed that both the displacement are modeled as independent Gaussian random variables with different jitters \((\sigma_{x} ,\sigma_{y} )\); and different boresight errors in each axis of the receiver plane, that is, \(r_{x} \sim N\left( {\sigma_{x} ,\mu_{x} } \right)\), \(r_{y} \sim N\left( {\sigma_{y} ,\mu_{y} } \right)\). Therefore, the radical displacement r at the receiver plane is distributed in accordance to Beckmann distribution given as (Varotsos et al. 2017; Boluda-Ruiz et al. 2016):

$$f_{r} \left( r \right) = \frac{r}{{2\pi \sigma_{x} \sigma_{y} }}\mathop \int \limits_{0}^{2\pi } exp\left\{ { - \frac{{(rcos\theta - \mu_{x} )^{2} }}{{2\sigma_{x}^{2} }} - \frac{{(rsin\theta - \mu_{y} )^{2} }}{{2\sigma_{y}^{2} }}} \right\}d\theta$$
(11)

where \(\theta\) is the transmit divergence angle that describe the increase in beam radius with the distance from the transmitter.

Following the analysis demonstrated in Boluda-Ruiz et al. (2016), the Beckmann distribution in (11) for the radical displacement can accurately be approximated through the modified Rayleigh distribution as:

$$f_{r} \left( r \right) = \frac{r}{{\sigma_{mod}^{2} }}exp\left( { - \frac{{r^{2} }}{{2\sigma_{mod}^{2} }}} \right), \quad r \ge 0$$
(12)

where

$$\sigma_{mod}^{2} = \left( {\frac{{3\mu_{x}^{2} \sigma_{x}^{4} + 3\mu_{y}^{2} \sigma_{y}^{4} + \sigma_{x}^{6} + \sigma_{y}^{6} }}{2}} \right)^{1/3}$$
(13)

The PDF for the irradiance dependent on the pointing error effect is approximated as:

$$f_{{I_{p} }} (I_{p} ) = \frac{{\xi_{mod}^{2} }}{{(A_{mod} )^{{\xi_{mod}^{2} }} }}I_{p}^{{\xi_{mod}^{2} - 1}} , \quad 0 \le I_{p} \le A_{mod}$$
(14)

where \(\xi_{mod} = w_{z, eq} /2\sigma_{mod}\) and the expression for the parameter \(A_{mod}\) is obtained as (Boluda-Ruiz et al. 2018):

$$A_{mod} = A_{o} exp\left( {\frac{1}{{\xi_{mod}^{2} }} - \frac{1}{{2\xi_{x}^{2} }} - \frac{1}{{2\xi_{y}^{2} }} - \frac{{\mu_{x}^{2} }}{{2\xi_{x}^{2} \sigma_{x}^{2} }} - \frac{{\mu_{y}^{2} }}{{2\xi_{y}^{2} \sigma_{y}^{2} }}} \right)$$
(15)

where \(\xi_{x} = w_{z, eq} /2\sigma_{x}\) and \(\xi_{y} = w_{z, eq} /2\sigma_{y}\).

2.2.3 Composite channel model with generalized pointing error

By following the analytical expression derived in Varotsos et al. (2017) and Boluda-Ruiz et al. (2016), the PDF closed-form expression for the combined effect of the atmospheric turbulence and generalized pointing error can be obtained as:

$$f_{I} \left(I \right) = \frac{{\xi_{mod}^{2} \varLambda}}{2I}\mathop \sum \limits_{q = 1}^{\beta} b_{q} G_{1,3}^{3,0} \left({\frac{\alpha \beta}{{\left({\psi \beta + {\acute{\Omega}}} \right)A_{mod}}}I\left| {\begin{array}{*{20}c} {\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2},\alpha,q} \\ \end{array}} \right.} \right)$$
(16)

where

$$b_{q} = a_{p} \left({\alpha \beta/\psi \beta + {\acute{\Omega}}} \right)^{- \alpha + q/2}$$

Since we are considering heterodyne detection at the destination of the concerned system, the instantaneous SNR for the FSO link can be defined as \(\gamma_{2} = \bar{\gamma }_{2} I\) and \(I = A_{mod} \xi_{mod}^{2} \left({\psi + {\acute{\Omega}}} \right)\gamma/\bar{\gamma}_{2} \left({\xi_{mod}^{2} + 1} \right)\) (Ansari et al. 2016). By variable transformation, the resulting SNR PDF from (16) can be obtained as:

$$f_{{\gamma_{2} ,m}} \left( {\gamma_{2} } \right) = \frac{{\xi_{mod}^{2} \varLambda }}{2}\mathop \sum \limits_{q = 1}^{\beta } \gamma_{2}^{ - 1} b_{q} G_{1,3}^{3,0} \left( {\frac{{B_{q} }}{{A_{mod} \bar{\gamma }_{2} }}\gamma_{2} \left| {\begin{array}{*{20}c} {\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q} \\ \end{array} } \right.} \right)$$
(17)

where \(\bar{\gamma }_{2}\) is the average received SNR at the destination and \(B_{q} = \alpha \beta \xi_{mod}^{2} (\psi + {\acute{\Omega}})/[(\xi_{mod}^{2} + 1)(\psi \beta + {\acute{\Omega}})]\).

3 Statistical characteristics

In this paper, the fixed relay AF protocol is considered for the concerned system where the relay nodes do not have knowledge about the CSI of the S-to-R link. The received signal is only amplify by the relay fixed gain and re-transmits it to the destination. Hence, the equivalent end-to-end SNR \(\gamma_{eq}\) at the destination can be expressed as (Kong et al. 2015; Odeyemi et al. 2017b):

$$\gamma_{eq,m} = \frac{{\gamma_{SR,m} \gamma_{RD,m} }}{{\gamma_{RD,m} + C}}$$
(18)

where the constant \(C\) can be obtained as (Petkovic et al. 2015; Soysa et al. 2012):

$$\begin{aligned} C & = 1 + \mathop \int \limits_{0}^{\infty } \gamma f_{{\gamma_{SR,m} }} (\gamma )d\gamma \\ & \triangleq 1 + m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)\frac{{( - 1)^{p} ((N - m + p)(1 - \rho ) + 1)\bar{\gamma }_{R} }}{{(N - m + p)^{2} }} \\ \end{aligned}$$
(19)

The CDF for the equivalent end-to-end SNR at the destination can be expressed as (Zedini et al. 2015):

$$\begin{aligned} F_{{\gamma_{eq,m} }} \left( \gamma \right) & = Pr\left[ {\frac{{\gamma_{SR,m} \gamma_{RD,m} }}{{\gamma_{RD,m} + C}} < \gamma } \right] \\ & \triangleq \mathop \int \limits_{0}^{\infty } Pr\left[ {\frac{{\gamma_{SR,m} \gamma_{RD,m} }}{{\gamma_{RD,m} + C}} < \gamma \left| {\gamma_{RD,m} } \right.} \right]f_{RD} (\gamma_{RD,m} )d\gamma_{RD,m} \\ \end{aligned}$$
(20)

3.1 Mixed RF/FSO system without a direct RF link

In order to determine the equivalent CDF without the influence of the direct RF link, (7) and (17) are substituted into (20), then, CDF for the equivalent end-to-end SNR can be obtained as:

$$F_{{\gamma_{eq,m} }} \left( \gamma \right) = 1 - \frac{{\xi_{mod}^{2} \varLambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{((N - m + p) + 1)}exp\left( { - \frac{(N - m + p + 1)\gamma }{{((N - m + p)(1 - \rho ) + 1)\bar{\gamma }_{R} }}} \right)\varXi$$
(21)

where the integral \(\varXi\) can be expressed as:

$$\varXi = \mathop \int \limits_{0}^{\infty } \gamma_{RD}^{ - 1} exp - \left( {\frac{(N - m + p + 1)C\gamma }{{((N - m + p)(1 - \rho ) + 1)\bar{\gamma }_{R} \gamma_{RD,m} }}} \right) G_{1,3}^{3,0} \left( {\frac{{B_{q} }}{{A_{mod} \bar{\gamma }_{2} }}\gamma_{RD,m} \left| {\begin{array}{*{20}c} {\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q} \\ \end{array} } \right.} \right)d\gamma_{RD,m}$$
(22)

By converting the exponential function to Meijer-G function using the identity defined in Adamchik and Marichev (1990, Eq. (11)), then (21) can be solved with the integral identity defined in Gradshteyn and Ryzhik (2014, Eq. (7.813(1))) as:

$$\varXi = G_{1,4}^{4,0} \left( {\frac{{B_{q} (N - m + p + 1)\gamma C}}{{A_{mod} ((N - m + p)(1 - \rho ) + 1)\bar{\gamma }_{R} \bar{\gamma }_{D} }}\left| {\begin{array}{*{20}c} {\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q,0} \\ \end{array} } \right.} \right)$$
(23)

Then, substitute (23) into (21), the equivalent CDF for the system can be expressed as:

$$F_{{\gamma_{eq,m} }} \left( \gamma \right) = 1 - \frac{{\xi_{mod}^{2} \varLambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{((N - m + p) + 1)}exp\left( { - \frac{(N - m + p + 1)\gamma }{{((N - m + p)(1 - \rho ) + 1)\bar{\gamma }_{R} }}} \right)G_{1,4}^{4,0} \left( {\frac{{B_{q} (N - m + p + 1)\gamma C}}{{A_{mod} ((N - m + p)(1 - \rho ) + 1)\bar{\gamma }_{R} \bar{\gamma }_{D} }}\left| {\begin{array}{*{20}l} {\xi_{mod}^{2} + 1} \hfill \\ {\xi_{mod}^{2} ,\alpha ,q,0} \hfill \\ \end{array} } \right.} \right)$$
(24)

Hence, the CDF for the selection combining at the destination can be defined as (Soliman 2015):

$$F_{SC} (\gamma ) = \mathop \prod \limits_{k = 1}^{{N_{r}^{D} }} \left[ {F_{{\gamma_{{\gamma_{eq,m} }} }} (\gamma_{SC} )} \right]$$
(25)

3.2 Mixed RF/FSO system with a direct RF link

From (6), the CDF for the S-to-D link can be expressed as:

$$F_{SD} \left( {\gamma_{SD} } \right) = 1 - exp\left( { - \frac{{\gamma_{SD} }}{{\bar{\gamma }_{SD} }}} \right)$$
(26)

where \(\bar{\gamma }_{SD} = \bar{\gamma }_{SR}\).

Thus, the CDF for the equivalent SNR at the destination can be expressed as (Anees et al. 2015; Ansari et al. 2013):

$$F_{{\gamma_{{\gamma_{eq,m} }} }} (\gamma ) = F_{SRD} (\gamma )F_{SD} (\gamma )$$
(27)

By putting (24) and (26) into (27), the equivalent CDF under the influence of the direct RF link can be expressed as:

$$F_{{\gamma_{{\gamma_{eq,m} }} }} \left( \gamma \right) = \left( {1 - exp\left( { - \frac{\gamma }{{\bar{\gamma }_{SD} }}} \right)} \right) - \left( {1 - exp\left( { - \frac{\gamma }{{\bar{\gamma }_{SD} }}} \right)} \right)\frac{{\xi_{mod}^{2} \varLambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{((N - m + p) + 1)}exp\left( { - \frac{(N - m + p + 1)\gamma }{{((N - m + p)(1 - \rho ) + 1)\bar{\gamma }_{R} }}} \right)G_{1,4}^{4,0} \left( {\frac{{B_{q} (N - m + p + 1)\gamma C}}{{A_{mod} ((N - m + p)(1 - \rho ) + 1)\bar{\gamma }_{R} \bar{\gamma }_{D} }}\left| {\begin{array}{*{20}c} {\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q,0} \\ \end{array} } \right.} \right)$$
(28)

4 Performance analysis

In this section, a CDF-based method was employed to analyze the expressions for the outage probability and average bit error rate performance metrics.

4.1 Outage probability

Outage probability is a key performance metric of a wireless communication system which measures the probability that the end-to-end SNR \(\gamma_{eq}\) falls below a predetermined SNR threshold value \(\gamma_{th}\). Thus, the outage probability for the concerned system can be expressed as (Zedini et al. 2014):

$$P_{out} \left( {\gamma_{th} } \right) = F_{SC} \left( {\gamma_{th} } \right)$$
(29)

4.1.1 Mixed RF/FSO system without a direct RF link

The outage probability for the concerned system without the influence of the direct link can be obtained by putting (24) and (25) into (29) as:

$$P_{out} (\gamma_{th} ) = \left[ {1 - \frac{{\xi_{mod}^{2} \varLambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}exp\left( { - \frac{{(N - m + p + 1)\gamma_{th} }}{{\left( {(N - m + p)(1 - \rho ) + 1} \right)\bar{\gamma }_{R} }}} \right)G_{1,4}^{4,0} \left( {\frac{{B_{q} (N - m + p + 1)C\gamma_{th} }}{{A_{mod} \left( {(N - m + p)(1 - \rho ) + 1} \right)\bar{\gamma }_{R} \bar{\gamma }_{D} }}\left| {\begin{array}{*{20}c} {\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q,0} \\ \end{array} } \right.} \right)} \right]^{{N_{r}^{D} }}$$
(30)

It can be deduced that the derived exact closed-form expression for the outage probability offers limited physical insight about the concerned system. Thus, it is meaningful to provide an asymptotical outage probability through which the system diversity order,\(G_{d}\), can be obtained. At high SNR, the average SNR for the FSO link is assumed to tend to infinity, \(\bar{\gamma }_{D} \to \infty\), then outage probability in the asymptotic regime for the concerned system without direct link can be obtained by applying the identity defined in Gradshteyn and Ryzhik (2014, Eq. (9.303)) to (30) as:

$$P_{out}^{\infty } (\gamma_{th} ) \approx \left[ {1 - \frac{{\xi_{mod}^{2} \varLambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}exp\left( { - \frac{{(N - m + p + 1)\gamma_{th} }}{{\left( {(N - m + p)(1 - \rho ) + 1} \right)\bar{\gamma }_{R} }}} \right)\Omega_{1} } \right]^{{N_{r}^{D} }}$$
(31)

where

$$\Omega_{1} = \mathop \sum \limits_{v = 1}^{4} \left( {\frac{{B_{q} (N - m + p + 1)C\gamma_{th} }}{{A_{\bmod } \left( {(N - m + p)(1 - \rho ) + 1} \right)\bar{\gamma }_{R} \bar{\gamma }_{D} }}} \right)^{{k_{2,v} }} \frac{{\mathop \prod \nolimits_{{\begin{array}{*{20}c} {u = 1,} \\ {u \ne v} \\ \end{array} }}^{4} \Gamma (k_{2,u} - k_{2,v} )}}{{\mathop \prod \nolimits_{u = 1}^{1} \Gamma (k_{1,u} - k_{2,v} )}}$$
(32)

where \(k_{x,y}\) defined as the yth term of \(k_{x}\) with \(k_{1} = \xi_{mod}^{2} + 1\) and \(k_{2} = \xi_{mod}^{2} ,\alpha ,q,0\).

4.1.2 Mixed RF/FSO system with a direct RF link

Similarly, the outage probability under the influence of the direct link can be derived by substituting (28) and (25) into (29) as follows:

$$P_{out} (\gamma_{th} ) = \left[ {\left( {1 - exp\left( { - \frac{{\gamma_{th} }}{{\bar{\gamma }_{SD} }}} \right)} \right) - \left( {1 - exp\left( { - \frac{{\gamma_{th} }}{{\bar{\gamma }_{SD} }}} \right)} \right)\frac{{\xi_{mod}^{2} \varLambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}exp\left( { - \frac{{(N - m + p + 1)\gamma_{th} }}{{\left( {(N - m + p)(1 - \rho ) + 1} \right)\bar{\gamma }_{R} }}} \right)G_{1,4}^{4,0} \left( {\frac{{B_{q} (N - m + p + 1)C\gamma_{th} }}{{A_{mod} \left( {(N - m + p)(1 - \rho ) + 1} \right)\bar{\gamma }_{R} \bar{\gamma }_{D} }}\left| {\begin{array}{*{20}c} {\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q,0} \\ \end{array} } \right.} \right)} \right]^{{N_{r}^{D} }}$$
(33)

Moreover, at high SNR, the asymptotic outage probability for the system with direct link defined in (33) can be expressed as:

$$P_{out}^{\infty } (\gamma_{th} ) \approx \left[ {\left( {1 - exp\left( { - \frac{{\gamma_{th} }}{{\bar{\gamma }_{SD} }}} \right)} \right) - \left( {1 - exp\left( { - \frac{{\gamma_{th} }}{{\bar{\gamma }_{SD} }}} \right)} \right)\frac{{\xi_{mod}^{2}\Lambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}exp\left( { - \frac{{(N - m + p + 1)\gamma_{th} }}{{\left( {(N - m + p)(1 - \rho ) + 1} \right)\bar{\gamma }_{R} }}} \right)\Omega _{1} } \right]^{{N_{r}^{D} }}$$
(34)

It is clearly deduced that the asymptotic expressions for outage probability given in (31), and (34) respectively for the concerned system under with/or without direct link are dominated by \(\hbox{min} \left\{ {\xi_{mod}^{2} ,\alpha ,q,0} \right\}\). Thus, by utilizing Bhatnagar (2013), Bhatnagar and Ghassemlooy (2016) and Wang and Giannakis (2003), the diversity order, \(G_{d}\), for the system is obtained as \(G_{d} = N_{r}^{D} \hbox{min} \left\{ {\xi_{mod}^{2} ,\alpha ,q,0} \right\}\) and this shows that \(G_{d} = 0\). This indicates an error floor which implies that the outage probability results will saturate at high FSO link average SNRs and the increase in SNRs will not improve the system performance.

4.2 Average BER

The performance of the concerned system is also characterized by average BER. Therefore, the average BER can be expressed in terms of CDF as (Chatzidiamantis et al. 2011; Trinh et al. 2017):

$$P_{SC} = \frac{A}{{\sqrt {2\pi } }}\mathop \int \limits_{0}^{\infty } \exp \left( { - \frac{{x^{2} }}{2}} \right)F_{SC} \left( {\frac{{x^{2} }}{{2B^{2} }}} \right)dx$$
(35)

where \(F_{SC} \left( . \right)\) is the CDF of \(\gamma\) defined in (25).

4.2.1 Mixed RF/FSO system without a direct RF link

By substituting (24) and (25) into (35), the average BER for the concerned system without direct link can be expressed as:

$$P_{SC} = \frac{A}{{\sqrt {2\pi}}}\mathop \prod \limits_{n = 1}^{{N_{r}^{D}}} \mathop \int \limits_{0}^{\infty} exp\left({- \frac{{x^{2}}}{2}} \right)dx - \frac{A}{{\sqrt {2\pi}}}\mathop \prod \limits_{n = 1}^{{N_{r}^{D}}} \mathop \int \limits_{0}^{\infty} exp\left({- \frac{{x^{2}}}{2}} \right)\frac{{\xi_{mod}^{2}\Lambda}}{2}m\left({\begin{array}{*{20}c} N \\ m \\ \end{array}} \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta} \left({\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array}} \right)b_{q} \frac{{(- 1)^{m}}}{{\left({(N - m + p) + 1} \right)}}exp\left({- \frac{\epsilon}{{2B^{2} \bar{\gamma}_{R}}}x^{2}} \right)G_{1,4}^{4,0} \left({\frac{{B_{q} \epsilon C}}{{A_{mod} \bar{\gamma}_{R} \bar{\gamma}_{D}}}x^{2} \left| {\begin{array}{*{20}c} {\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2},\alpha,q,0} \\ \end{array}} \right.} \right)dx$$
(36)

where

$$\epsilon = \frac{N - m + p + 1}{{\left({(N - m + p)(1 - \rho) + 1} \right)}}$$

Thus, to solve (36), the ABER for the system can be summarized as:

$$P_{SC} \triangleq \mathop \prod \limits_{k = 1}^{{N_{r}^{D} }} {\beth }_{1} + {\beth }_{2}$$
(37)

where

$${\beth }_{1} = \frac{A}{{\sqrt {2\pi } }}\mathop \int \limits_{0}^{\infty } exp\left( { - \frac{{x^{2} }}{2}} \right)dx$$
(38)

By using the integral identity define in Gradshteyn and Ryzhik (2014, Eq. (3.326(2))), the integral in (38) can be solved as:

$${\beth }_{1} = \frac{A}{{2\sqrt {2\pi } }}\left[ {\frac{{\Gamma \left( {0.5} \right)}}{{\sqrt {0.5} }}} \right]$$
(39)

To determine the \({\beth }_{2}\), we let \(x^{2} = \tau\), \(\frac{d\tau }{dx} = 2x \triangleq 2\sqrt \tau\)

$${\beth}_{2} = \frac{{A\xi_{mod}^{2} \Lambda}}{{4\sqrt {2\pi}}}m\left({\begin{array}{*{20}c} N \\ m \\ \end{array}} \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta} \left({\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array}} \right)b_{q} \frac{{(- 1)^{p}}}{{\left({(N - m + p) + 1} \right)}}\mathop \int \limits_{0}^{\infty} exp\left({- \left({\frac{1}{2} + \frac{\epsilon}{{2B^{2} \bar{\gamma}_{R}}}} \right)\tau} \right)G_{1,4}^{4,0} \left({\frac{{B_{q} \epsilon C}}{{2B^{2} A_{mod} \bar{\gamma}_{R} \bar{\gamma}_{D}}}\tau \left| {\begin{array}{*{20}c} {\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2},\alpha,q,0} \\ \end{array}} \right.} \right)d\tau$$
(40)

By utilizing the integral identity define in Gradshteyn and Ryzhik (2014, Eq. (7.813(1))), the integral in (40) can be solved as:

$${\beth }_{2} = \frac{{A\xi_{mod}^{2} \Lambda }}{{4\sqrt {2\pi } }}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}\left( {\frac{1}{2} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)^{ - 1/2} G_{2,4}^{4,1} \left( {\frac{{B_{q} \epsilon C}}{{2B^{2} A_{mod} \bar{\gamma }_{R} \bar{\gamma }_{D} \left( {\frac{1}{2} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)}}\left| {\begin{array}{*{20}c} {\frac{1}{2},\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q,0} \\ \end{array} } \right.} \right)$$
(41)

Hence, the average BER for the concerned system without direct link can be finally obtained by substituting (39) and (40) into (35) as:

$$P_{SC} = \frac{A}{{2\sqrt {2\pi } }}\left[ {\frac{{\Gamma \left( {0.5} \right)}}{{\sqrt {0.5} }} - \frac{{\xi_{mod}^{2} \Lambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}\left( {\frac{1}{2} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)^{ - 1/2} G_{2,4}^{4,1} \left( {\frac{{B_{q} \epsilon C}}{{2B^{2} A_{mod} \bar{\gamma }_{R} \bar{\gamma }_{D} \left( {\frac{1}{2} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)}}\left| {\begin{array}{*{20}c} {\frac{1}{2},\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q,0} \\ \end{array} } \right.} \right)} \right]^{{N_{r}^{D} }}$$
(42)

Following the same approach as it is in the case of outage probability, at high SNR, the asymptotic ABER for the system without direct link can be expressed as:

$$P_{SC}^{\infty } = \frac{A}{{2\sqrt {2\pi } }}\left[ {\frac{{\Gamma \left( {0.5} \right)}}{{\sqrt {0.5} }} - \frac{{\xi_{mod}^{2} \Lambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}\left( {\frac{1}{2} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)^{ - 1/2} \Omega_{2} } \right]^{{N_{r}^{D} }}$$
(43)

where

$$\Omega_{2} = \mathop \sum \limits_{v = 1}^{4} \left( {\frac{{B_{q} \epsilon C}}{{2B^{2} A_{mod} \bar{\gamma }_{R} \bar{\gamma }_{D} \left( {\frac{1}{2} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)}}} \right)^{{k_{2,v} }} \frac{{\mathop \prod \nolimits_{{\begin{array}{*{20}c} {u = 1,} \\ {u \ne v} \\ \end{array} }}^{4} \Gamma (k_{2,u} - k_{2,v} )\Gamma (1 + k_{2,v} - k_{3,1} )}}{{\mathop \prod \nolimits_{u = 2}^{2} \Gamma (k_{3,u} - k_{2,v} )}}$$
(44)

where \(k_{3} = \frac{1}{2},\;\xi_{mod}^{2} + 1\).

4.2.2 Mixed RF/FSO system with a direct RF link

Following the same approach as it is in the case of without direct link, the average BER for the concerned system under the influence of direct link can be obtained by substituting (25) and (28) into (35) and it is simply summarized as follows:

$$P_{SC} = \mathop \prod \limits_{k = 1}^{{N_{r}^{D} }} \left( {{\beth }_{1} - {\beth }_{2} - {\beth }_{3} + {\beth }_{4} } \right)$$
(45)

Then,

$$\begin{aligned} {\beth }_{3} & = \frac{A}{{\sqrt {2\pi } }}\mathop \int \limits_{0}^{\infty } exp\left( { - \frac{{x^{2} }}{2}} \right)exp\left( { - \frac{{x^{2} }}{{2B^{2} \bar{\gamma }_{SD} }}} \right)dx \\ & \triangleq \frac{A}{{\sqrt {2\pi } }}\mathop \int \limits_{0}^{\infty } exp\left( { - \left( {\frac{1}{2} + \frac{1}{{2B^{2} \bar{\gamma }_{SD} }}} \right)x^{2} } \right)dx \\ \end{aligned}$$
(46)

By applying the integral identity defined in Gradshteyn and Ryzhik (2014, Eq. (3.326(2))), \({\beth }_{3}\) can be expressed as:

$${\beth }_{3} = \frac{A}{{2\sqrt {2\pi } }}\left[ {\frac{{\Gamma \left( {0.5} \right)}}{{\left( {\frac{1}{2} + \frac{1}{{2B^{2} \bar{\gamma }_{SD} }}} \right)^{1/2} }}} \right]$$
(47)

Also,

$${\beth }_{4} = \frac{{A\xi_{mod}^{2} \Lambda }}{{4\sqrt {2\pi } }}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}\mathop \int \limits_{0}^{\infty } exp\left( { - \left( {\frac{1}{2} + \frac{1}{{2B^{2} \bar{\gamma }_{SD} }} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)\tau } \right)G_{1,4}^{4,0} \left( {\frac{{B_{q} \epsilon C}}{{2B^{2} A_{mod} \bar{\gamma }_{R} \bar{\gamma }_{D} }}\tau \left| {\begin{array}{*{20}c} {\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q,0} \\ \end{array} } \right.} \right)d\tau$$
(48)

By utilizing the integral identity in Gradshteyn and Ryzhik (2014, Eq. (7.813(1))), the \({\beth }_{4}\) can be solved as:

$${\beth }_{4} = \frac{{A\xi_{mod}^{2} \Lambda }}{{4\sqrt {2\pi } }}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}\left( {\frac{1}{2} + \frac{1}{{2B^{2} \bar{\gamma }_{SD} }} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)^{ - 1/2} G_{2,4}^{4,1} \left( {\frac{{B_{q} \epsilon C}}{{2B^{2} A_{mod} \bar{\gamma }_{R} \bar{\gamma }_{D} \left( {\frac{1}{2} + \frac{1}{{2B^{2} \bar{\gamma }_{SD} }} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)}}\left| {\begin{array}{*{20}c} {\frac{1}{2},\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q,0} \\ \end{array} } \right.} \right)$$
(49)

Hence, the average BER for the concerned system under the influence of direct link can finally be obtained by putting \({\beth }_{1}\),\({\beth }_{2}\),\({\beth }_{3}\) and \({\beth }_{4}\) into (45) as:

$$\begin{aligned} P_{SC} & = \frac{A}{{2\sqrt {2\pi } }} \left[ {\left[ {\frac{{\Gamma \left( {0.5} \right)}}{{\sqrt {0.5} }}} \right] - \left[ {\frac{{\Gamma \left( {0.5} \right)}}{{\left( {\frac{1}{2} + \frac{1}{{2B^{2} \bar{\gamma }_{SD} }}} \right)^{{\frac{1}{2}}} }}} \right]} \right. - \left[ {\frac{{\xi_{mod}^{2} \Lambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}} \right. \\ &\quad \left. { \times \left( {\frac{1}{2} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)^{ - 1/2} G_{2,4}^{4,1} \left( {\frac{{B_{q} \epsilon C}}{{2B^{2} A_{mod} \bar{\gamma }_{R} \bar{\gamma }_{D} \left( {\frac{1}{2} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)}}\left| {\begin{array}{*{20}c} {\frac{1}{2},\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q,0} \\ \end{array} } \right.} \right)} \right] \\ &\quad - \left[ {\frac{{\xi_{mod}^{2} \Lambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}\left( {\frac{1}{2} + \frac{1}{{2B^{2} \bar{\gamma }_{SD} }} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)^{ - 1/2} } \right. \\ &\quad \left. { \times \,G_{2,4}^{4,1} \left. {\left( {\frac{{B_{q} \epsilon C}}{{2B^{2} A_{mod} \bar{\gamma }_{R} \bar{\gamma }_{D} \left( {\frac{1}{2} + \frac{1}{{2B^{2} \bar{\gamma }_{SD} }} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)}}\left| {\begin{array}{*{20}c} {\frac{1}{2},\xi_{mod}^{2} + 1} \\ {\xi_{mod}^{2} ,\alpha ,q,0} \\ \end{array} } \right.} \right)} \right]} \right]^{{N_{r}^{D} }} \\ \end{aligned}$$
(50)

At high SNR, the asymptotic ABER for the system with direct link can be expressed as:

$$P_{SC}^{\infty } \approx \frac{A}{{2\sqrt {2\pi } }} \left[ {\left[ {\frac{{\Gamma \left( {0.5} \right)}}{{\sqrt {0.5} }}} \right] - \left[ {\frac{{\Gamma \left( {0.5} \right)}}{{\left( {\frac{1}{2} + \frac{1}{{2B^{2} \bar{\gamma }_{SD} }}} \right)^{{\frac{1}{2}}} }}} \right]} \right. - \left[ {\frac{{\xi_{mod}^{2} \Lambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}\left( {\frac{1}{2} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)^{ - 1/2} \Omega_{2} } \right] - \left[ {\left. {\frac{{\xi_{mod}^{2} \Lambda }}{2}m\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)\mathop \sum \limits_{p = 0}^{m - 1} \mathop \sum \limits_{q = 1}^{\beta } \left( {\begin{array}{*{20}c} {m - 1} \\ p \\ \end{array} } \right)b_{q} \frac{{( - 1)^{p} }}{{\left( {(N - m + p) + 1} \right)}}\left( {\frac{1}{2} + \frac{1}{{2B^{2} \bar{\gamma }_{SD} }} + \frac{\epsilon }{{2B^{2} \bar{\gamma }_{R} }}} \right)^{ - 1/2} \Omega_{2} } \right]} \right]^{{N_{r}^{D} }}$$
(51)

5 Numerical results and discussion

In this section, the numerical results of outage probability and average BER for the concerned system with/or without a direct link are presented using the derived closed-form expressions in (30), (31), (39) and (45) respectively. The accuracy of derived mathematical expressions and results is validated through the Monte Carlo simulations. Based on Trinh et al. (2017), the -distributed atmospheric turbulence conditions for the weak, moderate and strong level on the R-to-D FSO link are respectively given as:\(\alpha = 8.0, \beta = 4\), \(\alpha = 4.2, \beta = 3\) and. \(\alpha = 2.296, \beta = 2\). Additionally, other parameters for the M-channel include\(= 0.596\) \(\Omega = 1.3265\), \(b_{o} = 0.1079\), \(\phi_{1} - \phi_{2} = \pi /2\). It can be noted that when \(\delta = 0\),\({\acute{\Omega}} = 0\) and when \(\delta = 0\), \({\acute{\Omega}} = 1\) are respectively correspond to special cases of K-distribution and Gamma–Gamma distribution. Regarding the influence of pointing error on the system performance, two pointing errors scenarios are considered and this include, zero boresight and non-zero boresight. We thus assumed that \(\left( {w_{z} /a,\mu_{x} /a,\mu_{y} /a,\sigma_{x} /a,\sigma_{x} /a} \right) = \left( {5, 0, 0, 2, 1} \right)\) for the case of zero boresight pointing error with different jitters values while \(\left( {w_{z} /a,\mu_{x} /a,\mu_{y} /a,\sigma_{x} /a,\sigma_{x} /a} \right) = \left( {5, 2, 4, 2, 1} \right)\) is also assumed for the case of non-zero boresight pointing error (Boluda-Ruiz et al. 2016). Unless otherwise specified, the following parameter are set for the simulations; \(\rho = 0.8\), \(N = 3\), \(m = 3\), \(\bar{\gamma }_{R} = \bar{\gamma }_{D}\) and \(N_{r}^{D} = 3.\)

In Fig. 2, the outage probability performance of the concerned system under various turbulence conditions is presented. The comparison between the system with/or without direct link under the influence of NZ pointing error illustrated in Fig. 2a. The result show that the increase in turbulence from weak to strong level significantly degrades the system performance and the system with a direct RF link offers a better outage performance. Also, Fig. 2b demonstrated the comparison between the outage probability performance of the system with a direct link under ZB and NB pointing errors. Under the same turbulence condition, it can be inferred from the result that the system performance deteriorates greatly under the NB pointing error than ZB pointing error.

Fig. 2
figure 2

Outage performance of the system under various turbulence conditions when \(\gamma_{th} = 3\;{\text{dB}}\), \(\bar{\gamma }_{SD} = 5\;{\text{dB}}\) a comparison between the system with and without direct link under the influence of NZ pointing error b performance of the system with a direct link under ZB and NB pointing errors

Full size image

Impact of the correlation on the outage probability performance of the system with/or without a direct link under the ZB and NB pointing errors at strong turbulence condition is illustrated in Fig. 3. It can be deduced that as the channel correction increases the more the system performance becomes better under both the pointing error scenario. This is because the higher correlation coefficient signifies that accurate channel estimate is achieved for the relay selection. In all cases, however, the system with a direct link offers a better performance than the one without direct link.

Fig. 3
figure 3

Impact of the correlation on the system with/or without a direct link outage probability performance under the ZB and NB pointing errors when \(\gamma_{th} = 3\;{\text{dB}}\),\(\bar{\gamma }_{SD} = 5\;{\text{dB}}\), \(\bar{\gamma }_{SD} = 10\;{\text{dB}}\) at strong turbulence condition

Full size image

Outage performance of the system with/or without direct link for different threshold SNR values under NB pointing error and strong turbulence is demonstrated in Fig. 4. It can be inferred that as the threshold SNR increases the more the system outage probability performance becomes worsen. The results show that a direct link system yields better outage performance in all cases than the system without direct link.

Fig. 4
figure 4

Outage performance of the system with and without direct link for different threshold SNR values under NB pointing error and strong turbulence when \(\bar{\gamma }_{SD} = 5\;{\text{dB}}\)

Full size image

In Fig. 5, the impact of relay selection on the outage performance of the system with and without a direct link under ZB pointing error and strong turbulence is presented. It can be deduced from the results that the system achieve better outage performance under the best relay selection compared with the worst relay selection. Expectedly, the system with direct link offers a better performance than the system without a direct link. It can also be depicted that the increase in the average SNR over the FSO link yields no improvement in the system performance. This indicates that the diversity order for the concerned system is zero and it proves the accuracy of the exact closed-form expression for the outage probability at high SNR.

Fig. 5
figure 5

Impact of relay selection on the outage performance of the system with and without a direct link when \(\gamma_{th} = 3\;{\text{dB}}\), \(\bar{\gamma }_{SD} = 5\;{\text{dB}}\), \(\bar{\gamma }_{SD} = 10\;{\text{dB}}\), \(N = 4\) under ZB pointing error and strong turbulence

Full size image

The ABER performance of the system under various turbulence conditions is presented in Fig. 6. Figure 6a gives the comparison between the system with and without direct link under the influence of NZ pointing error. From the results, it can be seen that the increase in turbulence severely degrade the system ABER performance for the two system scenarios and the system with direct link offers better performance. Moreover, the performance of the system with a direct link under ZB and NB pointing errors is presented in Fig. 6b. It can be inferred that both turbulence and the pointing error effects severely degrade the system error rate. Thus, the system error rate become more worsens under the NB than ZB displacement pointing error.

Fig. 6
figure 6

ABER performance of the system under various turbulence conditions when \(\bar{\gamma }_{SD} = 3\;{\text{dB}}\) a comparison between the system with and without direct link under the influence of NZ pointing error b performance of the system with a direct link under ZB and NB pointing errors

Full size image

The impact of the correlation on the system ABER performance with/or without a direct link under the ZB and NB pointing errors at strong turbulence condition is demonstrated in Fig. 7. The increase in correlation significantly improves the system error rate and the system with a direct link outperforms the one without the direct link.

Fig. 7
figure 7

Impact of the correlation on the system ABER performance with/or without a direct link under the ZB and NB pointing errors when \(\bar{\gamma }_{SD} = 2\;{\text{dB}}\), \(\bar{\gamma }_{1} = 5\;{\text{dB}}\) at strong turbulence condition

Full size image

In Fig. 8, the impact of receive aperture \(N_{r}^{D}\) on the system ABER with a direct link under the ZB and NB pointing errors at strong turbulence condition is presented. As expected, the increase in the number of receive apertures at the destination offers the system better performance. It can also be deduced from the results that the system has better performance under the ZB than the NB boresight pointing errors.

Fig. 8
figure 8

Impact of receive aperture \(N_{r}^{D}\) on the system ABER with a direct link under the ZB and NB pointing errors when \(\bar{\gamma }_{SD} = 2\;{\text{dB}}\), \(\bar{\gamma }_{1} = 10\;{\text{dB}}\) at strong turbulence condition

Full size image

The ABER performance of the system with/or without a direct link for different values of jitter under the ZB and NB at strong turbulence is depicted in Fig. 9. It can be seen from the result that the increase in jitter values for the horizontal and elevation displacement significantly deteriorate the system error rate for the concerned system. In all cases, the system with a direct link has better performance than the one without direct link.

Fig. 9
figure 9

ABER performance of the system with/or without a direct link for different values of jitter under the ZB and NB at strong turbulence when \(\bar{\gamma }_{SD} = 2\;{\text{dB}}\)

Full size image

Also, the ABER performance of the system with a direct link for different values of channel parameter \(\delta\) under the ZB and NB pointing errors at strong turbulence are demonstrated in Fig. 10. It can be observed that the system error performance becomes better with the increase in the value of \(\delta\). This is due to the fact that the channel turbulence intensity reduces as the parameter \(\delta\) increases. The results also indicate that the system perform better under the ZB pointing error than the NB pointing error condition.

Fig. 10
figure 10

ABER performance of the system with a direct link for different values of channel parameter \(\delta\) under the ZB and NB pointing errors at strong turbulence when \(\bar{\gamma }_{SD} = 2\;{\text{dB}}\)

Full size image

6 Conclusion

In this paper, we analyzed the performance of a PRS-based AF mixed RF/FSO system with a direct link and outdated CSI under the generalized pointing errors. We assumed that the FSO link is subjected to M-distribution while the RF links within the system undergo Rayleigh fading distribution. The analytical expressions for the CDF end-to-end SNR are derived for the system with/or without a direct link. Based on the CDF approach, the outage probability and ABER system performance are then presented. The influence of pointing error under the ZB and NB displacement are investigated. The impact of turbulence, outdated CSI and relay selection are also evaluated. The results show that the system with a direct link offers better performance than the one without direct link. Finally, the Monte-Carlo simulations prove that the derived expressions are accurate.