Secrecy performance analysis of amplify-and-forward cooperative network with relay selection in the presence of multiple eavesdroppers

Abstract

The use of wireless transmission networks in various environments has become widespread. One of the main challenges in wireless networks is that the wireless transmission is highly vulnerable to eavesdropping attacks. In this paper, an amplify-and-forward cooperative relaying wireless system with relay selection is considered to improve the physical layer (PHY) security of the wireless system in the presence of multiple eavesdroppers, under two cases, namely, perfect channel state information (CSI) and outdated CSI cases. To evaluate the PHY security of the system, we derive closed-form expressions for the PHY security performance metrics, including the probability of non-zero secrecy capacity, the average secrecy capacity, and the secrecy outage probability. Then using those expressions, we obtain several numerical results under system parameters. The results show that relay selection provides significant improvement in the PHY security of the system. Moreover, it is observed that, when the CSI used to select the best relay is outdated, the PHY secrecy performance is relatively inferior compared to that of the perfect CSI case. Finally, the obtained mathematical expressions are also validated using Monte-Carlo simulation.

1 Introduction

Wireless networking has become an essential part of our daily life and is widely used in different applications. One of the major challenges of wireless networks is that the transmission between legitimate users can easily be overheard by eavesdroppers due to the broadcast nature of the wireless communication and is highly vulnerable to eavesdropping attacks. In order to increase the security of signal transmission, existing communication systems typically use encryption techniques to prevent eavesdropping attacks on transferring data between legitimate users. However, encryption protocols face several challenges due to the rapid growth of computing systems.

Recently, physical layer (PHY) security methods have been considered as an efficient way to overcome the problems caused by eavesdropping attacks. These methods are usually considered as the alternative and complement methods to create security in wireless communications using the physical properties of the wireless channel. The basis of the physical layer security scheme is the information theoretic approach, which is based on Shannon complete security concepts [1]. The concept of physical layer security was first proposed by Wyner with examining the memoryless wiretap channels [2]. In the considered system, two legitimate users communicate with each other via a main channel, in the presence of an eavesdropper that has access to the reduced version of the channel authorized for the legitimate receivers. Then, the memoryless wiretap channel model proposed by Wyner were extended to the Gaussian wiretap channel and the secrecy capacity concept was introduced [3]. The secrecy capacity is defined as the difference between main channel capacity and wiretap channel capacity. Accordingly, secure communication is not possible unless the signal-to-noise ratio (SNR) of the main channel is higher than that of the wiretap channel. To improve the secrecy capacity of the system, it is desirable to introduce a technique which causes an increase in the capacity of the main channel, and/or a decrease in the channel capacity of wiretap channel. To this end, several theoretical and practical research works have been reported for improving the physical layer security of digital communication systems, in which some effective approaches have been proposed such as modulation, channel coding and diversity methods, cooperative relaying, space-time coding, and multiple-input multiple-output (MIMO) methods [4,5,6,7,8,9,10,11,12,13,14,15,16]. In several research works, the PHY security performances of a direct communication system have been evaluated, in which a source transmits information to the destination while single or multiple eavesdroppers were able to receive the information [17, 18]. On the other hand, it has been shown that cooperative networks with AF relay selection have better system performances than direct communication networks (non-cooperative communications) and the average SNR gain is increased with the number of available relays [19, 20]. Therefore, the concept of relay selection in AF relaying systems can also improve the PHY secrecy performance of the system. It was shown that the security in multicasting through generalized fading channels can be improved with the best relay selection [21].

The performances of cooperative communications with opportunistic relaying have been examined with a perfect channel state information (CSI) in [22] and [23]. However, in time-variable environments, the CSI used for the relay selection, at the moment of selection may be different from the CSI at the moment of signal transmission. Therefore, relay selection based on the outdated CSI can yield a decrease in the performance of opportunistic relay selection [10, 24,25,26]. For example, in [26], authors have analyzed the Shannon capacity of the opportunistic relaying technique in amplify-and-forward cooperative systems over Rayleigh fading channels under outdated channel information. They have evaluated the effects of outdated channel information on the channel capacity and the outage performance. In [9], the secrecy performance has been evaluated for a cooperative transmission in a dual-hop MIMO relay system using a combined transmit antenna selection (TAS) and maximum ratio combining (MRC) scheme, denoted TAS/MRC scheme, over the Nakagami-m fading channels. The secrecy performance of the TAS/MRC scheme is then evaluated and the impacts of outdated CSI have been studied using the numerical results obtained from closed-form expressions of exact ergodic secrecy rate and exact secrecy outage probability. In [27], the impact of imperfect CSI on the PHY secrecy performance of a space time block coded MIMO system is evaluated over Rician fading wiretap channel, showing the advantages of using MIMO system, with respect to the PHY security.

In this paper, we analyze and evaluate the PHY secrecy performance of a cooperative network with multiple AF relays, in which to improve the physical layer security, an opportunistic relay selection is employed in the presence of multiple eavesdroppers. The main contributions of this paper are summarized as follows: (1) We obtain mathematical expressions for three important PHY security performance criteria: the probability of non-zero secrecy capacity, the secrecy outage probability, and the average secrecy capacity of the system. (2) Using the obtained expressions, we evaluate the secrecy performance of signal transmissions in the AF cooperative network. (3) We evaluate and analyze the physical layer security of AF cooperative relaying systems with relay selection under outdated CSI in the presence of multiple eavesdroppers. We also examine the effects of outdated channel information for relay selection using mathematical expressions, obtained for the probability of non-zero secrecy capacity, the secrecy outage probability, and the average secrecy capacity of the system. The validity of the obtained mathematical expressions are also verified using Monte-Carlo simulation.

The rest of this paper is organized as follows: Section 2 presents the system model and the assumptions. In Sect.  3, the PHY secrecy performance analyses of the system are presented and closed-form expressions are derived for the probability of non-zero secrecy capacity, the secrecy outage probability, and the average secrecy capacity of the system, where the analysis of the system under outdated CSI is given in Sect.  4. In Sect. 5, several numerical evaluation results which are verified by computer simulations are presented and discussed. Finally, concluding remarks are given in Sect. 6.

2 System model

Fig. 1

System model

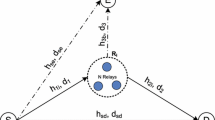
We consider a cooperative communication system over Rayleigh fading channel shown in Fig. 1. The source (S) communicates with the desired receiver (D) through N AF relays $\mathrm {R}_{1},\mathrm {R}_{2},\cdots ,\mathrm {R}_{\mathrm {N}}$, in the presence of multiple eavesdroppers $\mathrm {E}_{1},\mathrm {E}_{2},\cdots ,\mathrm {E}_{\mathrm {K}}$. The main channel consists of $\mathrm {S} \rightarrow \mathrm {D}$ link and $\mathrm {S}\rightarrow \mathrm {R}_{\mathrm {n}} \rightarrow \mathrm {D}$ links ($n=1,\cdots ,N$), and the wiretap channel consists of $\mathrm {S} \rightarrow \mathrm {E}_{\mathrm {k}}$ links ($k=1,\cdots ,K$), and $\mathrm {R}_{\mathrm {n}} \rightarrow \mathrm {E}_{\mathrm {k}}$ links. In the first time-slot, the received signals for $\mathrm {S} \rightarrow \mathrm {D}$ link in terminal $\mathrm {D}$, $\mathrm {S} \rightarrow \mathrm {R}_{\mathrm {n}}$ link in $\mathrm {R}_{\mathrm {n}}$ and $\mathrm {S} \rightarrow \mathrm {E}_{\mathrm {k}}$ link in $\mathrm {E}_{\mathrm {k}}$ can be respectively written as:

$$\begin{aligned} y_{SD}= & {} \frac{1}{\sqrt{d_{SD}^{\alpha }}}\sqrt{P_s}h_{SD}s+n_{SD} \end{aligned}$$

(1)

$$\begin{aligned} y_{SR_n}= & {} \frac{1}{\sqrt{d_{SR_n}^{\alpha }}}\sqrt{P_s}h_{SR_n}s+n_{SR_n} \end{aligned}$$

(2)

$$\begin{aligned} y_{SE_k}= & {} \frac{1}{\sqrt{d_{SE_k}^{\alpha }}}\sqrt{P_s}h_{SE_k}s+n_{SE_k} \end{aligned}$$

(3)

where $P_s$ denotes the source transmit power, $\alpha$ is the path loss exponent. $d_{SD}$, $d_{SR_n}$, and $d_{SE_k}$ are the distances of $\mathrm {S}$ from $\mathrm {D}$, from n-th relay ($\mathrm {R}_{\mathrm {n}}$) and from k-th eavesdropper ($\mathrm {E}_{\mathrm {k}}$), respectively, $h_{SD}$, $h_{SR_n}$ and $h_{SE_k}$ are the fading coefficients of $\mathrm {S}\rightarrow \mathrm {D}$, $\mathrm {S}\rightarrow \mathrm {R}_{\mathrm {n}}$ and $\mathrm {S}\rightarrow \mathrm {E}_{\mathrm {k}}$ links, respectively, and s is the normalized information signal in $\mathrm {S}$ terminal with $\mathcal {E}[|s|^2]=1$, where $\mathcal {E}(\cdot )$ is the expectation operation. The parameters $n_{SD}$, $n_{SR_n}$ and $n_{SE_k}$ are zero mean additive white Gaussian noises (AWGN) in $\mathrm {D}$ terminal with variance $\sigma _{SD}^2$, in relay $\mathrm {R}_{\mathrm {n}}$ with variance $\sigma _{SR_n}^2$, and in $\mathrm {E}_{\mathrm {k}}$ with variance $\sigma _{SE_k}^2$, respectively. From (1), (2) and (3), the channels’ SNRs can respectively be written as

$$\begin{aligned} \gamma _{SD}= & {} \frac{P_s|h_{SD}|^2}{d_{SD}^{\alpha }\sigma _{SD}^2} \end{aligned}$$

(4)

$$\begin{aligned} \gamma _{SR_n}= & {} \frac{P_s|h_{SR_n}|^2}{d_{SR_n}^{\alpha }\sigma _{SR_n}^2} \end{aligned}$$

(5)

$$\begin{aligned} \gamma _{SE_k}= & {} \frac{P_s|h_{SE_k}|^2}{d_{SE_k}^{\alpha }\sigma _{SE_k}^2}. \end{aligned}$$

(6)

In the second time-slot, the received signal for $\mathrm {R}_{\mathrm {n}}\rightarrow \mathrm {D}$ and $\mathrm {R}_{\mathrm {n}}\rightarrow \mathrm {E}_{\mathrm {k}}$ links are given by

$$\begin{aligned} y_{R_nD}=G_n\frac{1}{\sqrt{d_{R_nD}^{\alpha }}}h_{R_nD}y_{SR_n}+n_{R_nD} \end{aligned}$$

(7)

and

$$\begin{aligned} y_{R_nE_k}=G_n\frac{1}{\sqrt{d_{R_nE_k}^{\alpha }}}h_{R_nE_k}y_{SR_n}+n_{R_nE_k}. \end{aligned}$$

(8)

where $G_n$ is n-th relay amplification coefficient that is equal to $G_n=\sqrt{\frac{P_s}{\frac{P_s}{d_{SR_n}^{\alpha }}|h_{SR_n}|^2+\sigma _{SR_n}^2}}$ and $d_{R_nD}$ and $d_{R_nE_k}$ are the distances of $\mathrm {R}_{\mathrm {n}}$ from $\mathrm {D}$ and $\mathrm {E}_{\mathrm {k}}$, respectively. The parameters $h_{R_nD}$ and $h_{R_nE_k}$ parameters are the fading coefficients of $\mathrm {R}_{\mathrm {n}}\rightarrow \mathrm {D}$ and $\mathrm {R}_{\mathrm {n}}\rightarrow \mathrm {E}_{{\mathrm {k}}}$, respectively, and the parameters $n_{R_nD}$ and $n_{R_nE_k}$ parameters are zero mean additive white Gaussian noise (AWGN) in $\mathrm {D}$ terminal with variance $\sigma _{R_nD}^2$, in $\mathrm {R}_{\mathrm {n}}$ with variance $\sigma _{SR_n}^2$ and in $\mathrm {E}_{\mathrm {k}}$ with variance $\sigma _{R_nE_k}^2$, respectively. The SNRs of the channels can be respectively expressed as:

$$\begin{aligned} \gamma _{R_nD}= & {} \frac{P_s|h_{R_nD}|^2}{d_{R_nD}^\alpha \sigma _{R_nD}^2} \end{aligned}$$

(9)

$$\begin{aligned} \gamma _{R_nE_k}= & {} \frac{P_s|h_{R_nE_k}|^2}{d_{R_nE_k}^\alpha \sigma _{R_nE_k}^2}. \end{aligned}$$

(10)

The relay selection algorithm selects the best relay (b) such that

$$\begin{aligned} b={\mathop {\hbox {argmax}}\limits _{n \in \mathcal {R}}} \{\gamma _{SR_nD}\} \end{aligned}$$

(11)

where $\mathcal {R}=\{1,2, \cdots ,N\}$ and $\gamma _{SR_nD}$ is the SNR of $\mathrm {S}\rightarrow \mathrm {R}_{\mathrm {n}} \rightarrow \mathrm {D}$ channel. The SNR $\gamma _{SR_nD}$ can be written as [19, 20]:

$$\begin{aligned} \gamma _{SR_nD}=\frac{\gamma _{SR_n}\gamma _{R_nD}}{1+\gamma _{SR_n}+\gamma _{R_nD}}. \end{aligned}$$

(12)

For the sake of simplicity, we consider an upper bound for the equivalent SNR as the approximate SNR that is given by [19]

$$\begin{aligned} \gamma _{SR_nD}=\min (\gamma _{SR_n},\gamma _{R_nD}) \ge \frac{\gamma _{SR_n}\gamma _{R_nD}}{1+\gamma _{SR_n}+\gamma _{R_nD}}. \end{aligned}$$

(13)

This approximation has been widely used in the literature and has shown to be tight enough especially at medium to high SNR values  [19, 28, 29]. Moreover, in Sect.  4, simulation results have been provided to show the validity of the use this approximation in this work.

Therefor, the SNR of the best relay link $\mathrm {S}\rightarrow \mathrm {R}_{\mathrm {b}}\rightarrow \mathrm {D}$ can be expressed as:

$$\begin{aligned} \gamma _{SR_bD}&=\max \limits _{n \in \mathcal {R}}\{\gamma _n\} \nonumber \\&=\max \limits _{n \in \mathcal {R}}\{\min (\gamma _{SR_n},\gamma _{R_nD})\}. \end{aligned}$$

(14)

Since the main channel consists of $\mathrm {S \rightarrow D}$ and $\mathrm {S} \rightarrow \mathrm {R}_{\mathrm {n}} \rightarrow \mathrm {D}$ links, then, due to the maximum ratio combining (MRC) used at terminal $\mathrm {D}$, the main channel’s SNR can be written as:

$$\begin{aligned} \gamma _M&=\gamma _{SD}+\gamma _{SR_bD} \nonumber \\&=\gamma _{SD}+\max \limits _{n \in \mathcal {R}}\{\min (\gamma _{SR_n},\gamma _{R_nD})\}. \end{aligned}$$

(15)

Since eavesdroppers do not know the channel information of $\mathrm {S} \rightarrow \mathrm {R}_{\mathrm {n}}$, then the wiretap channel consists of $\mathrm {S} \rightarrow \mathrm {E}_{\mathrm {k}}$ and $\mathrm {R}_{\mathrm {n}} \rightarrow \mathrm {E}_{\mathrm {k}}$ links. Therefor, using MRC at k-th eavesdropper receiver, the SNR of k-th wiretap channel can be written as

$$\begin{aligned} \gamma _{W_k}=\gamma _{SE_k}+\gamma _{R_nE_k}. \end{aligned}$$

(16)

In addition, the SNR of the wiretap channel for multiple eavesdroppers can be obtained from [18]:

$$\begin{aligned} \gamma _W=\max \limits _{k \in \{1, \dots , K\}} \{\gamma _{W_k}\}. \end{aligned}$$

(17)

In the following, we express the probability density function (PDF) and cumulative distribution function (CDF) for the main channel’s SNR as well as for the wiretap channel’s SNR, which enable us to obtain and derive closed-form expressions for the probability of non-zero secrecy capacity, the outage probability and the average secrecy capacity of the considered system.

As shown in [19], the PDF and CDF of the main channel’s SNR are respectively given by:

$$\begin{aligned} f_{\gamma _M}(x)&=\sum _{n=1}^{N}\displaystyle {N\atopwithdelims ()n}\frac{n(-1)^{n-1}}{\overline{\gamma }_C -n\overline{\gamma }_{SD}}\nonumber \\&\quad \times \left[ \exp \left( -\frac{nx}{\overline{\gamma }_C}\right) -\exp \left( -\frac{x}{\overline{\gamma }_{SD}}\right) \right] \end{aligned}$$

(18)

and

$$\begin{aligned} F_{\gamma _M}(x)&=1+\sum _{n=1}^{N}\displaystyle {N\atopwithdelims ()n} \frac{n(-1)^{n-1}}{\overline{\gamma }_C-n\overline{\gamma }_{SD}}\nonumber \\&\quad \times \left[ \overline{\gamma }_{SD}\exp \left( -\frac{x}{\overline{\gamma }_{SD}}\right) -\frac{\overline{\gamma }_C}{n}\exp \left( -\frac{nx}{\overline{\gamma }_C}\right) \right] \end{aligned}$$

(19)

where $\overline{\gamma }_{SR_n}=\overline{\gamma }_{R_nD}=\overline{\gamma }$ and $\overline{\gamma }_C=\frac{\overline{\gamma }_{SR_n}\overline{\gamma }_{R_nD}}{\overline{\gamma }_{SR_n}+\overline{\gamma }_{R_nD}}$.

On the other hand, similarly to the approach in [30], we can express the CDF and PDF for the k-th eavesdropper as:

$$\begin{aligned} F_{\gamma _{W_k}}(y)&=1-\frac{\overline{\gamma }_{RE}}{\overline{\gamma }_{RE}-\overline{\gamma }_{SE}} \exp \left( -\frac{y}{\overline{\gamma }_{RE}}\right) +\frac{\overline{\gamma }_{SE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\exp \left( -\frac{y}{\overline{\gamma }_{SE}}\right) \end{aligned}$$

(20)

and

$$\begin{aligned} f_{\gamma _{W_k}}(y)=\frac{1}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\left[ \exp \left( -\frac{y}{\overline{\gamma }_{RE}}\right) -\exp \left( -\frac{y}{\overline{\gamma }_{SE}}\right) \right] \end{aligned}$$

(21)

where $\overline{\gamma }_{SE_k}=\overline{\gamma }_{SE}$ and $\overline{\gamma }_{R_nE_k}=\overline{\gamma }_{RE}$.

According to (17), the wiretap channel’s SNR is given by $\gamma _W=\max \limits _{k \in \{1, \dots , K\}} \{\gamma _{W_k}\}$. Therefore, using the order statistic theory [31], the CDF of $\gamma _W$ can be obtained from $F_{\gamma _{W}}(y)=[F_{\gamma _{W_k}}(y)]^K$, and using (20), we obtain:

$$\begin{aligned} F_{\gamma _W}(y)&=\left[ 1+\frac{\overline{\gamma }_{SE}}{\overline{\gamma }_{RE}-\overline{\gamma }_{SE}} \exp \left( -\frac{y}{\overline{\gamma }_{SE}}\right) -\frac{\overline{\gamma }_{RE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\exp \left( -\frac{y}{\overline{\gamma }_{RE}}\right) \right] ^K. \end{aligned}$$

(22)

Employing the binomial expansions that are $(1+x)^K=\sum _{i=0}^{K}\displaystyle {K\atopwithdelims ()i} x^i$, and $(1-x)^K=\sum _{i=0}^{K}\displaystyle {K\atopwithdelims ()i} (-1)^i\, x^i$, the expression in (23) can be written as:

$$\begin{aligned} F_{\gamma _W}(y)&=\sum _{i=0}^{K}\displaystyle {K\atopwithdelims ()i}\sum _{j=0}^{i} \displaystyle {i\atopwithdelims ()j} \left( \frac{\overline{\gamma }_{SE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^{i-j} \nonumber \\&\quad \times \left( \frac{\overline{\gamma }_{RE}}{\overline{\gamma }_{RE}-\overline{\gamma }_{SE}}\right) ^j(-1)^j \exp \left[ -\left( \frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}\right) y\right] . \end{aligned}$$

(23)

Using the fact that $f_{\gamma _W}(y)=\frac{d}{dy}F_{\gamma _W}(y)$, by obtaining the derivative of (23), the probability density function of the wiretap channel’s SNR can be expressed as

$$\begin{aligned} f_{\gamma _W}(y)&=\sum _{i=0}^{K}\displaystyle {K\atopwithdelims ()i} \sum _{j=0}^{i}\displaystyle {i\atopwithdelims ()j} \left( \frac{\overline{\gamma }_{SE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^{i-j} \left( \frac{\overline{\gamma }_{RE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^j\nonumber \\&\quad \times (-1)^{j+1} \left( \frac{i-j}{\overline{\gamma }_{SE}} +\frac{j}{\overline{\gamma }_{RE}}\right) \exp \left[ -\left( \frac{i-j}{\overline{\gamma }_{SE}} +\frac{j}{\overline{\gamma }_{RE}}\right) y\right] . \end{aligned}$$

(24)

3 Secrecy performance analysis

In the scenarios where the eavesdropper is passive, the CSI of the eavesdroppers and the intended receiver are not available at the source terminal, hence perfect secrecy is not guaranteed. In this Section, we analyze the PHY secrecy performance of the considered system. Considering the AF relaying system shown in Fig. 1, and using the definition of the capacity of additive white Gaussian noise (AWGN) channels, with SNRs ${\gamma }_\mathrm{_M}$ and ${\gamma }_\mathrm{_W}$, we can express the channel capacity of the main channel $C_M$ and that of the wiretap channel $C_W$ as $C_M=\frac{1}{2}\log _2(1+\gamma _M)$ and $C_W=\frac{1}{2}\log _2(1+\gamma _W)$, respectively. Hence, the instantaneous secrecy capacity can be written as

$$\begin{aligned} C_s={\left\{ \begin{array}{ll} \frac{1}{2} \left[ \log _2(1+\gamma _M)-\log _2(1+\gamma _W)\right] &{} \gamma _M > \gamma _W\\ 0 &{} \gamma _M\le \gamma _W \end{array}\right. } \end{aligned}$$

(25)

where the coefficient of 1/2 is due to the fact that transmission in AF relaying system is done in two time-slots.

3.1 Probability of non-zero secrecy capacity (PNZSC)

According to the definition of the instantaneous secrecy capacity in (25), when $\gamma _M> \gamma _W$, the secrecy capacity is positive and when $\gamma _M\le \gamma _W$, the secrecy capacity is zero. Thus, since $\gamma _M$ and $\gamma _W$ are statistically independent, the probability of non-zero secrecy capacity can be expressed as

$$\begin{aligned} \Pr (C_s>0)&=\Pr (\gamma _M>\gamma _W) \nonumber \\&=\int _{x=0}^{\infty }\int _{y=0}^{x}f_{\gamma _M}(x) f_{\gamma _W}(y)\,\mathrm {d}y\,\mathrm {d}x. \end{aligned}$$

(26)

By inserting (18) and (24) into (26) and solving the integrals, we obtain the following expression

$$\begin{aligned}&\Pr (C_s>0)=\sum _{n=1}^{N}\displaystyle {N\atopwithdelims ()n}\frac{n(-1)^{n-1}}{\overline{\gamma }_C-n\overline{\gamma }_{SD}}\sum _{i=0}^{K} \displaystyle {K\atopwithdelims ()i}\sum _{j=0}^{i}\displaystyle {i\atopwithdelims ()j}\nonumber \\&\quad \times \left( \frac{\overline{\gamma }_{SE}}{\overline{\gamma }_{RE}-\overline{\gamma }_{SE}}\right) ^{i-j} \left( \frac{\overline{\gamma }_{RE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^j (-1)^j \nonumber \\&\quad \times \left[ \left( {\frac{n}{\overline{\gamma }_C} +\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}}\right) ^{-1} -\left( {\frac{1}{\overline{\gamma }_{SD}}+\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}}\right) ^{-1}\right] . \end{aligned}$$

(27)

3.2 Secrecy outage probability (SOP)

An important performance measure for evaluating the PHY secrecy is the secrecy outage probability denoted $P_{out}(R_s)$. The secrecy outage probability is a probability that the secrecy capacity is lower than the threshold of $R_s$, and can be written as [17]:

$$\begin{aligned}P_{out}(R_s)&=\Pr (C_s<R_s) \nonumber \\ &=\Pr (C_s<R_s|\gamma _M>\gamma _W)\Pr (\gamma _M>\gamma _W) \nonumber \\ &\quad+\Pr (C_s<R_s|\gamma _M\le \gamma _W)\Pr (\gamma _M\le \gamma _W). \end{aligned}$$

(28)

According to the expression in (25), for $\gamma _M\le \gamma _W$, $C_s=0$, and since $R_s>0$, we can readily conclude that $\Pr (C_s<R_s|\gamma _M\le \gamma _W)=1$. Also, we can write $\Pr (\gamma _M\le \gamma _W)=1-\Pr (\gamma _M>\gamma _W)$. Therefore, using (25), the secrecy outage probability in (28) can be written as:

$$\begin{aligned} P_{out}(R_s) &=\Pr\left(\log_2\left(\frac{1+\gamma_M}{1+\gamma_W}\right)<R_s|\gamma_M>\gamma_W\right) \\&\times \Pr(\gamma_M>\gamma_W)+\bigg[1-\Pr(\gamma_M>\gamma_W)\bigg] \end{aligned}$$

(29)

where assuming $\mu \triangleq \left[ 2^{2R_s}(1+\gamma _W)-1\right]$, the expression in (29) can be written as

$$\begin{aligned}P_{out}(R_s) &=\Pr (\gamma _M<\mu |\gamma _M>\gamma _W) \Pr (\gamma _M>\gamma _W)\nonumber \\ &\quad+\left[ 1-\Pr (\gamma _M>\gamma _W)\right] \nonumber \\& =1+\Pr (\gamma _W\le \gamma _M\le \mu )-\Pr (\gamma _M\ge \gamma _W)\nonumber \\& =1+\int _{y=0}^{\infty } \int _{x=y}^{\mu }f_{\gamma _M}(x)f_{\gamma _W}(y) \,\mathrm {d}x\,\mathrm {d}y \nonumber \\&\quad -\int _{y=0}^{\infty }\int _{x=y}^{\infty }f_{\gamma _M}(x)f_{\gamma _W}(y)\, \mathrm {d}x\,\mathrm {d}y\nonumber \\& =1-\int _{y=0}^{\infty }\int _{x=\mu }^{\infty }f_{\gamma _M}(x)f_{\gamma _W}(y) \,\mathrm {d}x\,\mathrm {d}y. \end{aligned}$$

(30)

Assuming $\lambda =2^{2R_s}$, we solve the inner integral in (30) as follows:

$$\begin{aligned}&P_{out}(R_s)=1-\int _{y=0}^{\infty } \left[ 1-F_{\gamma _M}(\lambda -1+\lambda y)\right] f_{\gamma _W}(y) \,\mathrm {d}y\nonumber \\&\quad =\int _{y=0}^{\infty }F_{\gamma _M}(\lambda -1+\lambda y)f_{\gamma _W}(y)\mathrm {d}y. \end{aligned}$$

(31)

By inserting (19) and (24) into (31) and solving the integral, we obtain the closed-form expression of the secrecy outage probability as follows

$$\begin{aligned}P_{out}(R_s)&=1-\sum _{n=1}^{N}\displaystyle {N\atopwithdelims ()n}\frac{n(-1)^{n-1}}{\overline{\gamma }_C -n\overline{\gamma }_{SD}}\sum _{i=0}^{K}\displaystyle {K\atopwithdelims ()i}\sum _{j=0}^{i}\displaystyle {i\atopwithdelims ()j}\nonumber \\&\quad \times \left( \frac{\overline{\gamma }_{SE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^{i-j} \left( \frac{\overline{\gamma }_{RE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^j(-1)^{j+1}\left( \frac{i-j}{\overline{\gamma }_{SE}} +\frac{j}{\overline{\gamma }_{RE}}\right) \nonumber \\&\quad \times \left[ \frac{\overline{\gamma }_C}{n}\left( {\frac{n\,2^{2R_s}}{\overline{\gamma }_C} +\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}}\right) ^{-1} \exp \left( -\frac{n\,(2^{2R_s}-1)}{\overline{\gamma }_C}\right) \right. \nonumber \\&\quad \left. -\overline{\gamma }_{SD}\left( {\frac{2^{2R_s}}{\overline{\gamma }_{SD}} +\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}}\right) ^{-1} \exp \left( -\frac{(2^{2R_s}-1)}{\overline{\gamma }_{SD}}\right) \right] . \end{aligned}$$

(32)

3.3 Average secrecy capacity (ASC)

The average secrecy capacity can be obtained by averaging the instantaneous secrecy capacity over the joint PDF of $(\gamma _M, \gamma _W)$, where assuming $\gamma _M$ and $\gamma _W$ are statistically independent, it can be expressed as [18]:

$$\begin{aligned} \overline{C}_s=\int _{0}^{+\infty }\int _{0}^{+\infty }C_s(x,y)\,f_{\gamma _M}(x)f_{\gamma _W}(y) \,\mathrm {d}x\,\mathrm {d}y. \end{aligned}$$

(33)

By inserting (25) in above equation, we obtain

$$\begin{aligned}&\overline{C}_s=\frac{1}{2}\int _{x=0}^{\infty } \int _{y=0}^{x}(\log _2(1+x)-\log _2(1+y)) f_{\gamma _M}(x)f_{\gamma _W}(y)\,\mathrm {d}x\,\mathrm {d}y\nonumber \\&\quad =\frac{1}{2}\left( I_1-I_2\right) \end{aligned}$$

(34)

where

$$\begin{aligned} I_1&=\int _{x=0}^{\infty }\int _{y=0}^{x}\log _2(1+x) f_{\gamma _M}(x)f_{\gamma _W}(y)\,\mathrm {d}x\,\mathrm {d}y\nonumber \\&=\int _{x=0}^{\infty }\log _2(1+x) f_{\gamma _M}(x)F_{\gamma _W}(x)\,\mathrm {d}x. \end{aligned}$$

(35)

By inserting (18) and (23) in above equation, and solving the integral, we get

$$\begin{aligned}I_1&=\sum_{n=1}^{N}\displaystyle{N\choose n}\frac{n(-1)^{n-1}}{\overline{\gamma}_C-n\overline{\gamma}_{SD}} \sum_{i=0}^{K}\displaystyle{K\choose i}\sum_{j=0}^{i}\displaystyle{i\choose j}\\&\times\left(\frac{\overline{\gamma}_{SE}}{\overline{\gamma}_{RE}-\overline{\gamma}_{SE}}\right)^{i-j}\left(\frac{\overline{\gamma}_{RE}}{\overline{\gamma}_{RE}-\overline{\gamma}_{SE}}\right)^j(-1)^j \\ & \times \int_{x=0}^{\infty}\log_2(1+x)\left[\exp\left(-\left(\frac{n}{\overline{\gamma}_C}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right)x\right)\right. \\ &\left.-\exp\left(-\left(\frac{1}{\overline{\gamma}_{SD}}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right)x\right)\right].\end{aligned}$$

(36)

Using $\int _{0}^{\infty }\ln (1+x)\exp (-\mu x)\,\mathrm {d}x=\frac{1}{\mu }\exp (\mu )E_1(\mu )$, we obtain the solution of integral, which yields:

$$\begin{aligned} &I_1=\frac{1}{\ln(2)}\sum_{n=1}^{N}\displaystyle{N\choose n}\frac{n(-1)^{n-1}}{\overline{\gamma}_C-n\overline{\gamma}_{SD}}\sum_{i=0}^{K}\displaystyle{K\choose i}\sum_{j=0}^{i}\displaystyle{i\choose j}\\&\times \left(\frac{\overline{\gamma}_{SE}}{\overline{\gamma}_{RE}-\overline{\gamma}_{SE}}\right)^{i-j}\left(\frac{\overline{\gamma}_{RE}}{\overline{\gamma}_{RE}-\overline{\gamma}_{SE}}\right)^j \\&\times \left[\left({\frac{n}{\overline{\gamma}_C}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}}\right)^{-1}\!\!\exp\left(\frac{n}{\overline{\gamma}_C}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right)\right. \\&\times\left.E_1\left(\frac{n}{\overline{\gamma}_C}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right)-\left({\frac{1}{\overline{\gamma}_{SD}}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}}\right)^{-1}\right. \\ &\left.\times \exp\left(\frac{1}{\overline{\gamma}_{SD}}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right)E_1\left(\frac{1}{\overline{\gamma}_{SD}}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right)\right]. \end{aligned}$$

(37)

Similarly, in (34), we have

$$\begin{aligned} I_2&=\int _{y=0}^{\infty }\int _{x=y}^{\infty } \log _2(1+y)f_{\gamma _M}(x)f_{\gamma _W}(y) \,\mathrm {d}x\,\mathrm {d}y \nonumber \\&=\int _{y=0}^{\infty }\log _2(1+y)f_{\gamma _W}(y) \left[ 1-F_{\gamma _M}(y)\right] \,\mathrm {d}y. \end{aligned}$$

(38)

By inserting (19) and (24) in above equation, and solving the integral, we get

$$\begin{aligned} I_2&=\frac{1}{\ln (2)}\sum _{n=1}^{N}\displaystyle {N\atopwithdelims ()n}\frac{n(-1)^{n-1}}{\overline{\gamma }_C-n\overline{\gamma }_{SD}}\sum _{i=0}^{K}\displaystyle {K\atopwithdelims ()i}\sum _{j=0}^{i}\displaystyle {i\atopwithdelims ()j}\nonumber \\&\quad \times \left( \frac{\overline{\gamma }_{SE}}{\overline{\gamma }_{RE}-\overline{\gamma }_{SE}}\right) ^{i-j} \left( \frac{\overline{\gamma }_{RE}}{\overline{\gamma }_{RE}-\overline{\gamma }_{SE}}\right) ^j(-1)^{j+1} \left( \frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}\right) \nonumber \\&\quad \times \int _{x'=0}^{\infty }\log _2(1+y)\left[ \frac{\overline{\gamma }_C}{n} \exp \left( -\frac{ny}{\overline{\gamma }_C}\right) -\overline{\gamma }_{SD} \exp \left( -\frac{y}{\overline{\gamma }_{SD}}\right) \right] \nonumber \\&\quad \times \exp \left( -\left( \frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}\right) y\right) \,\mathrm {d}y. \end{aligned}$$

(39)

By solving above integral, we obtain:

$$\begin{aligned}I_2&=\frac{1}{\ln(2)}\sum_{n=1}^{N}\displaystyle{N\choose n}\frac{n(-1)^{n-1}}{\overline{\gamma}_C-n\overline{\gamma}_{SD}}\sum_{i=0}^{K}\displaystyle{K\choose i}\sum_{j=0}^{i}\displaystyle{i\choose j} \\ &\times\left(\frac{\overline{\gamma}_{SE}}{\overline{\gamma}_{RE}-\overline{\gamma}_{SE}}\right)^{i-j}\left(\frac{\overline{\gamma}_{RE}}{\overline{\gamma}_{RE}-\overline{\gamma}_{SE}}\right)^j(-1)^{j+1} \\ &\times\left(\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right) \left[\frac{\overline{\gamma}_C}{n}\left({\frac{n}{\overline{\gamma}_C}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}}\right)^{-1}\right. \\ &\left.\times \exp\left(\frac{n}{\overline{\gamma}_C}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right)\right. \\ &\left.\times E_1\left(\frac{n}{\overline{\gamma}_C}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right)\right. \\ &\left.-{\overline{\gamma}_{SD}}\left({\frac{1}{\overline{\gamma}_{SD}}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}}\right)^{-1}\right. \\ &\left.\times\exp\left(\frac{1}{\overline{\gamma}_{SD}}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right)\right. \\ &\left.\times E_1\left(\frac{1}{\overline{\gamma}_{SD}}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right)\right].\end{aligned}$$

(40)

Substituting expressions of $I_1$ given in (37) and $I_2$ given in (40) into (34), we obtain the following closed-form expression for the average secrecy capacity:

$$\begin{aligned} \overline{C}_s&=\frac{0.5}{\ln (2)}\sum _{n=1}^{N}\displaystyle {N\atopwithdelims ()n}\frac{n(-1)^{n-1}}{\overline{\gamma }_C-n\overline{\gamma }_{SD}}\sum _{i=0}^{K}\displaystyle {K\atopwithdelims ()i}\sum _{j=0}^{i}\displaystyle {i\atopwithdelims ()j}\nonumber \\&\quad \times \left( \frac{\overline{\gamma }_{SE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^{i-j}\left( \frac{\overline{\gamma }_{RE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^j(-1)^j\nonumber \\&\quad \times \left\{ \left[ \left( \frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}\right) \frac{\overline{\gamma }_c}{n}+1\right] \left( {\frac{n}{\overline{\gamma }_C} +\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}}\right) ^{-1} \right. \nonumber \\&\quad \times \exp \left( \frac{n}{\overline{\gamma }_C}+\frac{i-j}{\overline{\gamma }_{SE}} +\frac{j}{\overline{\gamma }_{RE}}\right) E_1\left( \frac{n}{\overline{\gamma }_C}+\frac{i-j}{\overline{\gamma }_{SE}} +\frac{j}{\overline{\gamma }_{RE}}\right) \nonumber \\&\quad -\left[ \left( \frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}\right) \overline{\gamma }_{SD}+1\right] \left( {\frac{1}{\overline{\gamma }_{SD}} +\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}}\right) ^{-1} \nonumber \\&\quad \times \left. \exp \left( \frac{1}{\overline{\gamma }_{SD}}+\frac{i-j}{\overline{\gamma }_{SE}} +\frac{j}{\overline{\gamma }_{RE}}\right) E_1\left( \frac{1}{\overline{\gamma }_{SD}} +\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}\right) \right\} . \end{aligned}$$

(41)

4 Secrecy performance of the system under outdated CSI

In practice, in the AF system with relay selection, the CSI of $\mathrm {S} \rightarrow \mathrm {R}_{\mathrm {n}} \rightarrow \mathrm {D}$ link, used for relay selection at the decision time t, may differ from its value at the signal transmission time $t+\tau$. This difference can be due to several factors such as channel variations with time, feedback delay and the channel estimation errors. In other words, the best relay selected according to the outdated CSI at time t may not be the best relay at the time of the data transmission (time $t+\tau$). Therefore, it is of interest to evaluate the effects of outdated CSI on the secrecy performance of the system. In the outdated CSI scenario, in general, we have an estimate of the channel h denoted $\widehat{ h }$, defined by the following model:

$$\begin{aligned} \widehat{h}=\rho \, h + (\sqrt{1-\rho ^2})\epsilon \end{aligned}$$

(42)

where $\widehat{h}$ is the estimate of the channel h, and $\epsilon$ is a complex Gaussian noise $\mathcal {CN}(0, \sigma ^2_h)$. The correlation coefficient $\rho$, $0 \le \rho \le 1$ is a constant value which determines the average quality of the channel estimation. That model is a widely used model in the literature, which models the effects of outdated CSI and imperfect CSI [32].

In this Section, we evaluate and analyze the impacts of outdated CSI on the PHY secrecy of considered AF relaying system. To that end, we obtain closed-form expressions for the probability of non-zero secrecy capacity, the secrecy outage probability, and the average secrecy capacity average of the system under outdated CSI. Then using numerical evaluations, we study and evaluate the impacts of outdated CSI on the secrecy performance of the system. According to [20], for the AF cooperative system with relay selection under outdated CSI, the probability density function and the cumulative distribution function of the main channel’s SNR are given by:

$$\begin{aligned}f_{\widehat{\gamma}_M}(x)&=\sum_{n=1}^{N}\displaystyle{N\choose n}\frac{(-1)^{n-1}}{\overline{\gamma}_c[n(1-\rho)+\rho]/n-\overline{\gamma}_{SD}} \\&\times\left[\exp\left(-\frac{nx}{\overline{\gamma}_c[n(1-\rho)+\rho]}\right)-\exp\left(\frac{-x}{\overline{\gamma}_{SD}}\right)\right]\end{aligned}$$

(43)

and

$$\begin{aligned}&F_{\widehat{\gamma }_M}(x)=1-\sum _{n=1}^{N}\displaystyle {N\atopwithdelims ()n} \frac{(-1)^{n-1}}{\overline{\gamma }_c[n(1-\rho )+\rho ]/n-\overline{\gamma }_{SD}}\nonumber \\&\quad \times \left[ \frac{\overline{\gamma }_c}{n}[n(1-\rho )+\rho ]\right. \exp \left( \frac{-nx}{\overline{\gamma }_c[n(1-\rho )+\rho ]}\right) -\overline{\gamma }_{SD}\left. \exp \left( \frac{-x}{\overline{\gamma }_{SD}}\right) \right] \end{aligned}$$

(44)

where $\rho$ is the correlation coefficient between the SNR of $\mathrm {S}\rightarrow \mathrm {R}_{\mathrm {n}} \rightarrow \mathrm {D}$ link, at time t and the SNR of $\mathrm {S}\rightarrow \mathrm {R}_{\mathrm {n}} \rightarrow \mathrm {D}$ link at time $t+\tau$, where $0\le \rho \le 1$ [20]. In fact, there is two extreme cases, where $\rho =1$ corresponds to a perfect CSI case and $\rho =0$ corresponds to a completely outdated CSI case. It is also worthy to notify that for the wiretap channel’s SNR, the PDF and CDF expressions are the same as those given in expressions (23) and (24).

4.1 Probability of non-zero secrecy capacity under outdated CSI

Similarly to the steps shown in Sect.  3, the expression for the probability of non-zero secrecy capacity under outdated CSI can be obtained from:

$$\begin{aligned} \Pr (C_s>0)&=\int _{x=0}^{+\infty }\int _{y=0}^{x}f_{\widehat{\gamma }_\mathrm{_M}}(x) f_{\gamma _\mathrm{_W}}(y) \,d{y}d{x}\nonumber \\&=\int _{x=0}^{+\infty }f_{\widehat{\gamma }_\mathrm{_M}}(x)F_{\gamma _\mathrm{_W}}(x)\,d{x}. \end{aligned}$$

(45)

By substituting (43) and (23) into (45), we obtain:

$$\begin{aligned} \Pr (C_s>0)&= \int _{x=0}^{+\infty } \left\{ \sum _{n=1}^{N}\displaystyle {N\atopwithdelims ()n}\frac{(-1)^{n-1}}{\overline{\gamma }_c[n(1-\rho )+\rho ]/n-\overline{\gamma }_{SD}} \right. \nonumber \\&\quad \left. \times \left[ \exp \left( -\frac{nx}{\overline{\gamma }_c[n(1-\rho )+\rho ]}\right) -\exp \left( \frac{-x}{\overline{\gamma }_{SD}}\right) \right] \right\} \nonumber \\&\quad \times \left\{ \sum _{i=0}^{K}\displaystyle {K\atopwithdelims ()i}\sum _{j=0}^{i} \displaystyle {i\atopwithdelims ()j} \left( \frac{\overline{\gamma }_{SE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^{i-j} \right. \nonumber \\&\quad \left. \times \left( \frac{\overline{\gamma }_{RE}}{\overline{\gamma }_{RE}-\overline{\gamma }_{SE}}\right) ^j(-1)^j \exp \left[ -\left( \frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}\right) x\right] \right\} \,d{x}. \end{aligned}$$

(46)

We solve the integrals in (46), and we obtain a closed-form expression for probability of non-zero secrecy capacity, as follows:

$$\begin{aligned} &\Pr(C_s>0)=\sum_{n=1}^{N}\displaystyle{N\choose n}\frac{(-1)^{n-1}}{\overline{\gamma}_c[n(1-\rho)+\rho]/n-\overline{\gamma}_{SD}} \\ &\times\sum_{i=0}^{K}\displaystyle{K\choose i}\sum_{j=0}^{i}\displaystyle{i\choose j}\left(\frac{\overline{\gamma}_{SE}}{\overline{\gamma}_{RE}-\overline{\gamma}_{SE}}\right)^{i-j}\left(\frac{-\overline{\gamma}_{RE}}{\overline{\gamma}_{RE}-\overline{\gamma}_{SE}}\right)^j (-1)^{j}\\ &\times \left[\left({\frac{n}{\overline{\gamma}_c[n(1-\rho)+\rho]}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}}\right)^{-1}\right. \\ &\left.-\left({\frac{1}{\overline{\gamma}_{SD}}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}}\right)^{-1}\right]. \end{aligned}$$

(47)

4.2 Secrecy Outage Probability under Outdated CSI

Similarly to the steps followed in Section 3, the expression for the secrecy outage probability of the system under outdated CSI can be obtained from:

$$\begin{aligned} P_{out}(R_s)&=\int _{y=0}^{\infty }F_{\widehat{\gamma }_M}(\lambda -1+\lambda y)f_{\gamma _W}(y)\mathrm {d}y, \end{aligned}$$

(48)

where $\lambda =2^{2R_s}$. Substituting (44) and (24) into (48) yields:

$$\begin{aligned} P_{out}(R_s)&=\int _{y=0}^{\infty } \left\{ 1-\sum _{n=1}^{N}\displaystyle {N\atopwithdelims ()n}\frac{(-1)^{n-1}}{\overline{\gamma }_c[n(1-\rho )+\rho ]/n-\overline{\gamma }_{SD}} \right. \nonumber \\&\quad \left. \times \left[ \frac{\overline{\gamma }_c}{n}[n(1-\rho )+\rho ]\right. \exp \left( \frac{-n(\lambda -1+\lambda y)}{\overline{\gamma }_c[n(1-\rho )+\rho ]}\right) -\overline{\gamma }_{SD}\left. \exp \left( \frac{-(\lambda -1+\lambda y)}{\overline{\gamma }_{SD}}\right) \right] \right\} \nonumber \\&\quad \times \left\{ \sum _{i=0}^{K}\displaystyle {K\atopwithdelims ()i} \sum _{j=0}^{i}\displaystyle {i\atopwithdelims ()j} \left( \frac{\overline{\gamma }_{SE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^{i-j} \left( \frac{\overline{\gamma }_{RE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^j \right. \nonumber \\&\quad \left. \times (-1)^{j+1} \left( \frac{i-j}{\overline{\gamma }_{SE}} +\frac{j}{\overline{\gamma }_{RE}}\right) \exp \left[ -\left( \frac{i-j}{\overline{\gamma }_{SE}} +\frac{j}{\overline{\gamma }_{RE}}\right) y\right] \right\} \mathrm {d}y. \end{aligned}$$

(49)

Solving the integrals in (49), yields the closed-form expression for the secrecy outage probability of the system under outdated CSI, which can be written as

$$\begin{aligned} &P_{out}(R_s)=1-\sum_{n=1}^{N}\displaystyle{N\choose n}\frac{(-1)^{n-1}}{\overline{\gamma}_c[n(1-\rho)+\rho]/n-\overline{\gamma}_{SD}} \\ &\times\sum_{i=0}^{K}\sum_{j=0}^{i}\displaystyle{K\choose i}\displaystyle{i\choose j}\left(\frac{\overline{\gamma}_{SE}}{\overline{\gamma}_{RE}-\overline{\gamma}_{SE}}\right)^{i-j}\left(\frac{\overline{\gamma}_{RE}}{\overline{\gamma}_{RE}-\overline{\gamma}_{SE}}\right)^j \\ &\times(-1)^{j+1}\left(\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}\right) \\ &\times\left[\frac{\overline{\gamma}_c}{n}[n(1-\rho)+\rho]\right.\nonumber \\ &\left.\times\left({\frac{n\,2^{2R_s}}{\overline{\gamma}_c[n(1-\rho)+\rho]}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}}\right)^{-1}\right. \\ &\left.\times \exp\left(\frac{-n\,(2^{2R_s}-1)}{\overline{\gamma}_c[n(1-\rho)+\rho]}\right)\right. \\ &\left.-\overline{\gamma}_{SD}\left({\frac{2^{2R_s}}{\overline{\gamma}_{SD}}+\frac{i-j}{\overline{\gamma}_{SE}}+\frac{j}{\overline{\gamma}_{RE}}}\right)^{-1}\exp\left(-\frac{2^{2R_s}-1}{\overline{\gamma}_{SD}}\right)\right]. \end{aligned}$$

(50)

4.3 Average secrecy capacity under outdated CSI

The expression for the average secrecy of the system under outdated CSI can be obtained following similar steps given in Section 3 (using (34)), which can be written as

$$\begin{aligned} \overline{C}_s&=\frac{1}{2}\left( I_1-I_2\right) \nonumber \\&= \frac{1}{2}\int _{x=0}^{\infty }\log _2(1+x) f_{\widehat{\gamma }_M}(x)F_{\gamma _W}(x)\,\mathrm {d}x \nonumber \\&\quad -\frac{1}{2}\int _{y=0}^{\infty }\log _2(1+y)f_{\gamma _W}(y) \left[ 1-F_{\widehat{\gamma }_M}(y)\right] \,\mathrm {d}y. \end{aligned}$$

(51)

By inserting (43), (44), (23) and (24) into (51) and using $\int _{0}^{\infty }\ln (1+x)\exp (-\mu x)\,\mathrm {d}x=\frac{1}{\mu }\exp (\mu )E_1(\mu )$, we solve the integrals and we obtain the following expression for the average secrecy capacity:

$$\begin{aligned} \overline{C}_s&=\frac{0.5}{\ln (2)}\sum _{n=1}^{N}\displaystyle {N\atopwithdelims ()n}\frac{(-1)^{n-1}}{\overline{\gamma }_c[n(1-\rho )+\rho ]/n-\overline{\gamma }_{SD}} \sum _{i=0}^{K}\displaystyle {K\atopwithdelims ()i}\nonumber \\&\quad \times \sum _{j=0}^{i}\displaystyle {i\atopwithdelims ()j}\left( \frac{\overline{\gamma }_{SE}}{\overline{\gamma }_{RE} -\overline{\gamma }_{SE}}\right) ^{i-j} \left( \frac{\overline{\gamma }_{RE}}{\overline{\gamma }_{RE}-\overline{\gamma }_{SE}}\right) ^j \nonumber \\&\quad \times (-1)^j\left[ \frac{\left( \frac{i-j}{\overline{\gamma }_{SE}} +\frac{j}{\overline{\gamma }_{RE}}\right) \left( \frac{\overline{\gamma }_c[n(1-\rho )+\rho ]}{n}\right) +1}{\frac{n}{\overline{\gamma }_c[n(1-\rho )+\rho ]}+\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}} \right. \nonumber \\&\quad \times \exp \left( \frac{n}{\overline{\gamma }_c[n(1-\rho )+\rho ]} +\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}\right) \nonumber \\&\quad \times E_1\left( \frac{n}{\overline{\gamma }_c[n(1-\rho )+\rho ]} +\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}\right) \nonumber \\&\quad -\left. \frac{\overline{\gamma }_{SD}\left( \frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}\right) +1}{\frac{1}{\overline{\gamma }_{SD}}+\frac{i-j}{\overline{\gamma }_{SE}} +\frac{j}{\overline{\gamma }_{RE}}} \exp \left( \frac{1}{\overline{\gamma }_{SD}}+\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}}\right) \right. \nonumber \\&\quad \times \left. E_1\left( \frac{1}{\overline{\gamma }_{SD}}+\frac{i-j}{\overline{\gamma }_{SE}}+\frac{j}{\overline{\gamma }_{RE}} \right) \right] . \end{aligned}$$

(52)

It is worthy to mention that, considering $\rho =1$ (which corresponds to the perfect CSI), expressions (47), (50) and (52), reduce to the expressions (27), (32) and (41), which were obtained for the perfect CSI case in Sect.  3. In other extreme case, setting $\rho =0$ (which corresponds to the completely outdated CSI), into expressions (47), (50) and (52) yield the corresponding expressions for the PHY secrecy of AF relaying system with one relay in the presence of multiple eavesdroppers. This implies that under completely outdated CSI, relay selection is equivalent to the random relay selection, where no diversity advantage can be achieved from using multiple relays.

5 Simulation and numerical results

In this section, we provide numerical and simulation results for three important PHY secrecy performance metrics for the considered AF relaying system, namely, the probability of non-zero secrecy capacity, the secrecy outage probability and the average secrecy capacity under different parameters. Numerical results are obtained from derived expressions (27), (32), (41), (47), (50) and (52), where to verify the validity of the numerical results and the analysis, we also provide Monte-Carlo simulation results. We considered the path loss for the channel to be $\alpha =0$ in all Figures. We also assumed that the links corresponding to the main channel have the same average SNR values, i.e., $\overline{\gamma }_{SD}=\overline{\gamma }_{SR_n}=\overline{\gamma }_{R_nD}$, for $n=1,2,\cdots ,N$, but the SNRs associated to the eavesdroppers $\overline{\gamma }_{SE}$ and $\overline{\gamma }_{RE}$ may have different SNR values.

The simulation results are obtained as follows: First, using Monte Carlo simulations, we generate several realizations of the random Rayleigh distributed channel coefficients. For the outdated CSI case, we use the formula described in (42), in which we first generate several realizations of the random Rayleigh distributed channel coefficients h, and generate $\epsilon$ that is a complex Gaussian noise $\mathcal {CN}(0, \sigma ^2_h)$, then we obtain outdated channel coefficient $\widehat{h}$. We then, calculate instant SNR values for each time-slot, i.e.. the values for ${\gamma }_{SD}$, ${\gamma }_{SR_n}$, ${\gamma }_{R_nD}$, the SNRs associated to the eavesdroppers ${\gamma }_{SE}$, and ${\gamma }_{RE}$. Then, we obtain the instant SNR values for ${\gamma }_{_M}$, and ${\gamma }_{_W}$ using (15) and (17). Then, using (25), we obtain several instantaneous values for the secrecy capacity $\mathcal {C}_{s}$. Finally, for the given system parameters, defined for each figure, and using the obtained several realizations of the secrecy capacity, the average secrecy capacity (ASC), and the probability of non-zero secrecy capacity (PNZSC), the secrecy outage probability (SOP) are calculated for a total number larger than $10^7$ channel realizations, where $\mathrm{ASC}=\texttt {mean}(C_s)$, ${PNZSC}=\mathrm{Pr}\left( {C}_{s}>0\right)$, and $\mathcal {P}_{out}(R_s)=\mathrm{Pr}\left( {C}_{s}\le R_s\right)$, have been used.

Fig. 2

Probability of non-zero secrecy capacity versus $\overline{\gamma }_{SD}$ with $N=K=5$

Fig. 2 shows the probability of non-zero secrecy capacity versus $\overline{\gamma }_{SD}$, for the system assuming $N=5$ relays and $K=5$ eavesdroppers. We observe that increasing $\overline{\gamma }_{SD}$, yields an increase in the probability non-zero secrecy capacity. Also, we can observe that increasing $\overline{\gamma }_{SE}$ and/or $\overline{\gamma }_{RE}$ cause a decrease in the probability of non-zero secrecy capacity, as expected.

Fig. 3

Secrecy outage probability versus $\overline{\gamma }_{SD}$ with $N=K=5$ and $R_s=0.1$ bits/s/Hz

Fig. 3 shows the secrecy outage probability versus $\overline{\gamma }_{SD}$ for the system with $N=5$ relays and $K=5$ eavesdroppers and $R_s=0.1$ bits/s/Hz. We observe that increasing $\overline{\gamma }_{SD}$, decreases the secrecy outage probability. We also observe that increasing $\overline{\gamma }_{SE}$ and $\overline{\gamma }_{RE}$ increases the secrecy outage probability of the system.

Fig. 4

Secrecy outage probability versus $\overline{\gamma }_{SD}$ with $\overline{\gamma }_{SE}=5$ dB, $\overline{\gamma }_{RE}=10$ dB, $K=5$ and $R_s=0.1$ bits/s/Hz

Fig. 4 shows the secrecy outage probability versus $\overline{\gamma }_{SD}$ with $\overline{\gamma }_{SE}=5$ dB, $\overline{\gamma }_{RE}=10$ dB, $K=5$ eavesdroppers and $R_s=0.1$ bits/s/Hz, for different number of relays N. It can be observed that, increasing the number of available relays, decreases the secrecy outage probability. To show the tightness of the upper bound approximation SNR, the SOP results are obtained for both cases of the upper bound approximate SNR $\gamma _{SR_nD}=\min (\gamma _{SR_n},\gamma _{R_nD})$ and the exact SNR expression $\gamma _{SR_nD}=\frac{\gamma _{SR_n}\gamma _{R_nD}}{1+\gamma _{SR_n}+\gamma _{R_nD}}$, which is obtained via simulations. We observe that the approximate results are tight enough to the exact results, especially at the medium to high SNRs.

Fig. 5

Secrecy outage probability versus $R_s$ with $N=K=5$, $\overline{\gamma }_{SE}=0$ dB and $\overline{\gamma }_{RE}=5$ dB

Fig. 5 shows the secrecy outage probability versus $R_s$ with $N=K=5$, $\overline{\gamma }_{SE}=0$ dB and $\overline{\gamma }_{RE}=5$ dB. We observe that increasing $R_s$, increases the secrecy outage probability. Also we can see that increasing $\overline{\gamma }_{SE}$ and $\overline{\gamma }_{RE}$ increases the secrecy outage probability.

Fig. 6

Secrecy outage probability versus $\overline{\gamma }_{SD}$ with $K=5$, $R_s=0.1$ bits/s/Hz, $\overline{\gamma }_{SE}=0$ dB and $\overline{\gamma }_{RE}=5$ dB

The secrecy outage probability versus $\overline{\gamma }_{SD}$ is shown in Fig. 6, where it is assumed that $K=5$, $R_s=0.1$ bits/s/Hz, $\overline{\gamma }_{SE}=0$ dB and $\overline{\gamma }_{RE}=5$ dB. It can be observed that increasing the number of available relays decreases the secrecy outage probability and therefore, the physical layer security is significantly improved.

Fig. 7

Secrecy outage probability versus the number of relays N with $K=5$, $R_s=0.1$ bits/s/Hz and $\overline{\gamma }_{SD}=20$ dB

The secrecy outage probability versus N and K, are shown in Fig. 7 and Fig. 8, respectively, where $R_s=0.1$ bits/s/Hz and $\overline{\gamma }_{SD}=20$ dB are assumed. We observe that increasing N the number of relays, decreases the secrecy outage probability. It is also observed that the secrecy outage probability increases with the number of eavesdroppers.

Fig. 8

Secrecy outage probability versus the number of eavesdroppers K with $N=5$, $R_s=0.1$ and $\overline{\gamma }_{SD}=20$ dB

Fig. 9

Average secrecy capacity versus $\overline{\gamma }_{SD}$ with $N=K=5$

Fig. 9 and Fig. 10 show the average secrecy capacity. We observe that increasing $\overline{\gamma }_{SD}$ and/or N, increases the average secrecy capacity. Also, it can be observed that increasing $\overline{\gamma }_{SE}$ and $\overline{\gamma }_{RE}$ decreases the average secrecy capacity.

Fig. 10

Average secrecy capacity versus $\overline{\gamma }_{SD}$ with $K=5$, $\overline{\gamma }_{SE}=0$dB and $\overline{\gamma }_{RE}=5$ dB

In Fig. 2 to Fig. 10, the results are obtained assuming that the CSI used for relay selection is perfect. However, in the following, we provide the results of PHY secrecy performance under outdated CSI.

Fig. 11

Probability of non-zero secrecy capacity versus $\overline{\gamma }_{SD}$ for $N=5$ and $K=3$

Fig. 11 shows the probability of non-zero secrecy capacity as a function of $\overline{\gamma }_{SD}$, with $N=5$ relays and $K=3$ eavesdroppers. We observe that increasing $\overline{\gamma }_{SD}$, increases the probability of non-zero secrecy capacity and also increasing $\overline{\gamma }_{SE}$ and $\overline{\gamma }_{RE}$, decreases the probability of non-zero secrecy capacity. Also, we can observe that decreasing $\rho$ which corresponds to the case where CSI becomes more outdated, cause a decrease in the probability of non-zero secrecy capacity.

Fig. 12

Secrecy outage probability versus $\overline{\gamma }_{SD}$ for $N=5$, $K=1$, $\overline{\gamma }_{SE}=0$dB, $\overline{\gamma }_{RE}=5$ and $R_s=0.1$ bits/s/Hz

Fig. 13

Secrecy outage probability versus $\overline{\gamma }_{SD}$ for $N=5$, and $K=3$, $\overline{\gamma }_{SE}=0$dB, $\overline{\gamma }_{RE}=5$, and $R_s=0.1$ bits/s/Hz

Fig. 14

Secrecy outage probability versus $\overline{\gamma }_{SD}$ with $\overline{\gamma }_{SE}=0$ dB, $\overline{\gamma }_{RE}=5$ dB, $N=5$, $K=3$ and $R_s=0.1$ bits/s/Hz

Fig. 12 and Fig. 13 show the secrecy outage probability versus $\overline{\gamma }_{SD}$ for $K=1$ and $K=3$ eavesdroppers, respectively, and $N=5$ relays, $\overline{\gamma }_{SE}=0$ dB, $\overline{\gamma }_{RE}=5$ dB and $R_s=0.1$ bits/s/Hz for different value of $\rho$. Increasing $\overline{\gamma }_{SD}$, decreases the secrecy outage probability and increasing K, increases the secrecy outage probability. Also, it can be observed that increasing $\rho$ decreases the secrecy outage probability. Moreover, it can be seen that for $\rho =0$, the secrecy outage probability is equal to that of the considered AF relay system with one relay, indicating that with $\rho =0$, no diversity advantage can be achieved from relay selection. In the other extreme case, with $\rho =1$ (perfect CSI), the diversity order is equal to $N+1$, as expected. For $0\le \rho <1$ (outdated CSI), the outage probability curves have the same slope at high SNRs, implying that the diversity order in the outdated CSI is equal to 2 that is the diversity order of the AF relaying system with a single relay and $\mathrm {S}\rightarrow \mathrm {D}$ direct channel.

Fig. 15

Secrecy outage probability versus N relays with $\overline{\gamma }_{SD}=\overline{\gamma }_{SR_i}=\overline{\gamma }_{R_iD}=20$dB, $\overline{\gamma }_{SE}=0$dB, $\overline{\gamma }_{RE}=5$ and $R_s=0.1$ bits/s/Hz

In order to show the tightness of the upper bound approximation SNR $\gamma _{SR_nD}\simeq \min (\gamma _{SR_n},\gamma _{R_nD})$ to the exact SNR expression $\gamma _{SR_nD}=\frac{\gamma _{SR_n}\gamma _{R_nD}}{1+\gamma _{SR_n}+\gamma _{R_nD}}$, in Fig. 14, the simulation results for the secrecy outage probability versus $\overline{\gamma }_{SD}$ are given assuming that $\overline{\gamma }_{SE}=5$ dB, $\overline{\gamma }_{RE}=10$ dB, $K=5$ eavesdroppers and $R_s=0.1$ bits/s/Hz, for different values of $\rho$. We can see that the approximate results are tight enough to the exact results, especially at the medium to high SNR values.

Fig. 15 shows the secrecy outage probability versus N with $\overline{\gamma }_{SD}=\overline{\gamma }_{SR_n}=\overline{\gamma }_{R_nD}=20$ dB, $\overline{\gamma }_{SE}=0$ dB, $\overline{\gamma }_{RE}=5$ dB and $R_s=0.1$ bits/s/Hz. It can be seen that increasing K, causes an increase in the secrecy outage probability. Also, we can observe that increasing $\rho$, decreases the secrecy outage probability. However, when $\rho$ decreases to ($\rho =0.5$), the improvement in the secrecy outage probability due to the increasing of N, is small because of poor channel knowledge. Moreover, when $\rho =0$, increasing N, the secrecy outage probability does not increase, since the system behaves similar to the AF relay system with one relay and $\mathrm {S}\rightarrow \mathrm {D}$ direct link.

Fig. 16

Secrecy outage probability versus $\rho$ with $N=5$, $K=3$, $\overline{\gamma }_{SE}=0$dB, $\overline{\gamma }_{RE}=5$dB and $R_s=0.1$ bits/s/Hz

Fig. 16 shows the secrecy outage probability versus $\rho$ with $N=5$, $K=3$, $\overline{\gamma }_{SE}=0$ dB, $\overline{\gamma }_{RE}=5$ dB and $R_s=0.1$ bits/s/Hz. We observe that increasing $\rho$, decreases the secrecy outage probability.

Fig. 17

Average secrecy capacity versus $\overline{\gamma }_{SD}$ with $N=5$, $K=3$, $\overline{\gamma }_{SE}=0$dB and $\overline{\gamma }_{RE}=5$ dB

The average secrecy capacity versus $\overline{\gamma }_{SD}$ is shown Fig. 17 with $N=5$, $K=3$, $\overline{\gamma }_{SE}=0$ dB and $\overline{\gamma }_{RE}=5$dB . We observe that increasing $\overline{\gamma }_{SD}$ and/or $\rho$, increases the average secrecy capacity.

Fig. 18

Average secrecy capacity versus N, with $K=3$, $\overline{\gamma }_{SE}=0$ dB and $\overline{\gamma }_{RE}=5$ dB

Fig. 18 shows the average secrecy capacity versus N with $K=3$, $\overline{\gamma }_{SE}=0$ dB and $\overline{\gamma }_{RE}=5$ dB. We can observe that in the case of completely outdated CSI, $\rho =0$, by increasing N, the average secrecy capacity does not change. This is the extreme case and implies that the relay selection based on the completely outdated CSI does not provide diversity to the system, as explained earlier.

In Fig. 2 to Fig. 18, it can be observed that the obtained numerical results obtained from theoretical mathematical formulas derived in this paper match closely with the simulation results, indicating the validity of the obtained mathematical expressions.

6 Conclusion

In this paper, we have analyzed and evaluated the PHY secrecy performance of an AF relaying system with relay selection under two cases, namely, perfect CSI and outdated CSI cases. We derived closed-form expressions for the probability of non-zero secrecy capacity, the average secrecy capacity and the secrecy outage probability. We provided numerical results to show the significant advantages of relay selection for improving the physical layer security. Moreover, we evaluated the effects of outdated CSI for relay selection on the physical layer security of the AF relaying cooperative communications systems with relay selection. It is observed that when the information used to select the relay is outdated, the PHY secrecy performance can be deteriorated. We also used Monte-Carlo simulation to verify the validity of the obtained mathematical expressions.