1 Introduction

WSN comprises of a network of sensors that are deployed either in static or mobile conditions randomly in a given geographical area to gather, process, and communicate data collected from the environment to a special node considered as the common point of contact referred as a sink [1, 2]. In WSN, sensor nodes re-locate their positions to collect the data about the sudden change occurring in the field. The information gathered by the sensors is communicated periodically or after a sudden change, depending on the nature of particular application. WSN consists of many applications like environmental monitoring, healthcare, medical research, defense and military affairs etc. Sensor nodes are unreliable and consumes more energy [3] but are cheaper and deployed everywhere in the coming future. To meet up with these requirements, the exact locations of unknown target nodes (TNs) must be known. The determination of their exact location in WSN is commonly referred to as the localization problem. There are numerous solutions to assign location to the nodes, it can be done either manually or using GPS. But assigning it manually is a complex and challenging task in WSN. It is also not feasible to use GPS feature in every node because of cost constraints in deploying sensor nodes with this feature [4]. There are various localization techniques available in the literature to detect the exact location of localized nodes. By using anchor nodes (ANs), it is possible to estimate the exact location of the TNs but AN location must be known prior and only few nodes with this feature are deployed in field due to certain cost constraints [5].

The range-based algorithms determine the distance among the sensors based on received signal strength indicator (RSSI), time of arrival (ToA) and angle of arrival (AoA) [6, 7]. Similarly, the algorithms that calculates the hop counts between nodes are classified as Range free techniques. Multidimensional signalling, Distance vector hop, and adhoc positioning system provides the position of various targeted nodes with lesser infrastructure requirements.

In WSN, accurate location estimation is one of the biggest challenges. In static nodes, localization can be achieved precisely but in case of moving nodes this task is quite challenging. In this paper, we deployed a single anchor to locate all unknown TNs and by using the projection of the ANs virtually in six directions using hexagonal projection for targeting the unknown nodes using Adaptive Flower Pollination Algorithm (AFPA). As soon as the TNs drop under the range of AN; the AN itself, and three virtual nodes are selected (as minimum four ANs are required to determine 3D positions). The problem of Line of Sight (LoS) is minimised by deploying AN virtually in other six directions.

The following benefits were offered for localization using the proposed method in this paper:

  • A new technique of projecting VAs employing umbrella projection in the field for determining the exact locations of deployed sensors in 3D environment is proposed using Adaptive FPA Algorithm.

  • By using the concept of VA, the line of sight (LoS) issues is minimized to a greater extent.

  • Flip ambiguity issues in range-based methods are also reduced.

The rest of the paper is organized as follows: Sect. 2 describes the literature review on 3D localization. Section 3, AFPA is presented in detail. In Sect. 4 statistical testing of AFPA with other meta-heuristics is presented. Section 5 deals with concept of deploying a single AN and TNs to locate unknown nodes in the deployed region. Section 6 deals with results and discussions on proposed algorithm. In Sect. 7, conclusion, limitations, and future scope are presented.

2 Literature review

WSN comprises of multiple homogeneous and/or heterogeneous sensor nodes. Each node collects the data, measures it, transmits it to the corresponding node, and forward it to the sink node. By knowing the exact location of the TNs, the data obtained and transmitted is useful and meaningful. The manual incorporation of the location information in every node is very tedious and even impossible in many applications. Generally, localization is applied in two dimensional (2D) planes. But for the localization of sensor nodes in applications like sea, forests, hilly areas and in free space, 3D algorithms are required. Although, determining 3D scenario is more complex than 2D but the algorithms used for 2D needs to be modified and applied for 3D localization with some exceptions.

Bulusu et al. [8] discussed unconstrained open-air environment using different localization algorithms for low-cost devices that does not contains GPS. They proposed an RF-based localization method in that the receiver is located using Centroid method. Graefenstein et al. [9] suggested technique that is energy efficient in which RSSI method is employed to calculate the approximate separation among the target and reference nodes deployed in the field using trilateration approach. Sumathi and Srinivasan [10] have suggested a method that requires a single AN for localizing the unknown nodes using RSSI method. The least square approach for locating the fixed TNs is used in this algorithm. Guo et al. [11] developed a perpendicular intersection (PI) mobile based approach that does not specifically map RSS distances. The measurement of the node position is carried out using the geometric PI relation. Ultra-Wide Band, and ToA technique to compute node location in 3D environment is proposed by Shi et al. [12]. By using this technique, the AN and TN separation is calculated more efficiently. Distance Vector-Hop based approach for locating sensor nodes is introduced by Wang et al. [13]. The main reason behind the failure of this algorithm is complexity and its increased cost. Xu et al. [14] introduced another enhanced 3D localization technique which adopted DV-Distance with quasi-newton optimization method for optimizing the results. By considering localization accuracy and coverage, authors further tested the effectiveness of the proposed algorithm. Li et al. [15] suggested the 3D WSN localization method based on irregular RSSI model in order to calculate the relation among DOIs and the variability in signal transmission range. Ahmad et al. [16] suggested a parametric loop-division algorithm for 3D localization, in which the deployed nodes are located in an area surrounded by a group of ANs. In this method network shrink toward the centre accurately and provides accurate localization results.

In order to get the best approximate locations of TNs various meta-heuristic optimization algorithms are used for 2D and 3D scenarios. A computationally efficient swarm intelligence approach for locating static nodes is suggested by Gopakumar and Jacob [17]. Easier implementation and low memory requirements are the key benefits of this approach. Chuang and Wu [18] use RSS ranging technique for locating sensor nodes efficiently using PSO based approach. This scheme has a higher success rate in terms of localization. Kumar et al. [19] uses H-best PSO and BBO algorithm to predict the optimum position of the randomly deployed TNs. HPSO provides mature and fast convergence, and higher accuracy is achieved using BBO.

Suyatha and Siddappa [20] implemented a hybrid localization optimization technique using differential evolution (DE) and Dynamic Weight PSO to achieve better localization accuracy. Lower localization error, better localization accuracy and improved stability results are achieved using the proposed algorithm. Arora and Singh [21] suggested a BOA optimization algorithm to optimize the location of unknown sensor nodes. The performance of this proposed algorithm, in 2D scenarios is compared and contrasted with PSO and FA. The authors concluded that this approach outperforms in terms of convergence time and location accuracy as compared to other meta heuristics.

Due to the higher accuracy, the range-based methods are commonly used but flip ambiguity is the major drawback of range-based methods. In order to address this important challenge, several researchers proposed different strategies [22,23,24,25]. Various computational intelligence techniques were introduced [26,27,28,29,30,31,32,33] for determining the location of the moving TNs using a single anchor in WSNs. Virtual ANs were deployed at the corners of the sensing field, and this algorithm is divided into two stages. Calculations of distance were performed based on RSSI during the first stage. In the later stage, virtual ANs were assumed to locate unknown TNs with the help of anchor and virtual anchors (VAs). Centroid calculations are obtained in these stages along with optimization algorithms namely PSO, HPSO, BBO, FA, and their results show better convergence time. In this work, authors proposed the concept of single anchor and VAs. Singh and Mittal proposed a hybrid DA-FA [34] approach to locate TNs in 2D environment using single anchor, and six VAs; and their results show less localization error and faster convergence as compared with PSO, HPSO, BBO, FA. Singh and Mittal [35] proposed various NMRA variants and are applied it to 3D localization problem and their results show faster convergence and least localization error in comparison to state-of-the-art algorithms.

3 The proposed adaptive FPA algorithm

Flower Pollination Algorithm (FPA) is inspired from the natural process of pollination occurring in flowering plants [36]. In FPA, each flower stands for a feasible solution and the objective function value is regarded as the fitness value. To mimic the pollination process, two different pollination phases: Global and local pollination phase are used for each flower to mimic the pollination process with a switch probability \({p}_{s}\). The specific process is described as follows.

Global pollination phase: For each individual, a random number rand is generated. If rand < \({p}_{s}\), then global pollination should be carried out. In the global pollination process, each flower updates its position according to the following equation [34]:

$${X}_{i}^{t+1}={X}_{i}^{t}+\upgamma L(\lambda )({X}_{best}^{t}-{X}_{i}^{t})$$
(1)

where \({X}_{i}^{t}\) and \({X}_{i}^{t+1}\) are the old and new positions of ith flower, respectively, \({X}_{best}^{t}\) is the best flower at current iteration t, which has the best fitness value in the whole population, and γ is the scaling factor that controls the step size of global pollination. Parameter L, the L´evy flight, is used as the strength of pollination in the basic FPA, and the step size (λ) obeys the L´evy distribution:

$$L\sim \frac{\lambda \Gamma (\lambda )\mathrm{sin}(\pi \lambda /2)}{\pi } \frac{1}{{s}^{1+\lambda }}, (s\gg {s}_{0}>0)$$
(2)

where Γ(λ) is the gamma function.

Local pollination phase: If rand > \({p}_{s}\), the local pollination process should be carried out. Flower \({X}_{i}^{t}\) obtains its new position \({X}_{i}^{t+1}\) according to the difference between its old position and the position of two neighboring flowers \({X}_{p}^{t}\) and \({X}_{q}^{t}\). This process is considered as local search, and the updating equation [34] is defined as

$${X}_{i}^{t+1}={X}_{i}^{t}+ r({X}_{p}^{t}-{X}_{q}^{t})$$
(3)

where \(r\) is drawn from a uniform distribution [0, 1], and it is considered as a local random walk.

After pollination is completed, the new individuals update their positions by comparing fitness values. If the fitness of \({X}_{i}^{t+1}\) is better than that of \({X}_{i}^{t}\), the new position of ith flower will be replaced by \({X}_{i}^{t+1}\). Otherwise, ith flower remains at \({X}_{i}^{t}\).

FPA has gained attention due to its linear nature and its effectiveness in the recent past and large number of improvements in its basic form as been done since its inception.

The revised improved FPA seeks to achieve enhanced performance by enhancing the basic FPA's exploration and exploitation capabilities. Exploration has been improved by the introduction of the Elite Opposition-Based Learning (EOBL) strategy [37], Global pollination phase has been improved by Cauchy based step size that helps to explore the search space more effectively [38], exploitation has been enhanced by Local Neighborhood Search (LNS) driven by knowledge of the best solution so far found in a small neighborhood of the current solution [39]. A balance between the exploration and exploitation is achieved using the dynamic switch probability \({(p}_{t})\) [40], The catfish-effect mechanism [41] is presented to circumvent premature convergence. The major alterations are discussed as follows:

3.1 Strategy for elite opposition-based learning (EOBL)

In basic FPA, once the algorithm falls to the local optimal, it is difficult to achieve the optimal global solution. So, directing the current solution space approximation to the global optimal solution space is very important. The EOBL approach is adopted to improve the FPA's global search capabilities [39].

We would clarify opposition-based learning (OBL) first, before presenting the EOBL. OBL's main idea is that it produces the current solution's opposition solution, simultaneously compares the current solution and the opposition solution, and selects the stronger one to join the next iteration. We assume that \(x=({x}_{1}, {x}_{2}, {x}_{3},. . . , {x}_{D})\) is a point in the population (\(D\) is the search space dimension; \({x}_{j}\in \left[{a}_{j}, {b}_{j}\right], j=1, 2, . . ., D)\) and its opposition point is defined by \(\stackrel{\sim }{x}=({\stackrel{\sim }{x}}_{1}, {x}_{2}, {\stackrel{\sim }{x}}_{3}, . . . , {\stackrel{\sim }{x}}_{D})\) as follows:

$${\stackrel{\sim }{x}}_{j}={a}_{j}+{b}_{j}-{x}_{j}$$
(4)

Sometimes the created OBL opposition solution may not be promising than the current search space to search for the optimal global solution, we can therefore use EOBL strategy [39] in this paper. EOBL is an intelligence computing technique. In this, suppose the elite (optimal) individual in the current population is \({X}_{e}=({x}_{e,1}, {x}_{e,2}, {x}_{e,3},. . . , {x}_{e,D})\). For the individual\({X}_{i}\), the elite opposition solution \(\tilde{X}_{i}\) is given by

$$ \tilde{x}_{i,j} = \eta *\left( {da_{j} + db_{j} } \right) - x_{e,j} $$
(5)

where i = 1, 2,..., NP, j = 1, 2,..., D, NP is the population size, and η ∈ U(0, 1) is a generalized coefficient, and [\(da_{j} , db_{j}\)] is the dynamic boundary of the jth dimensional search space and is represented by:

$$ da_{j} = \min \left( {x_{i,j} } \right) $$
$$ db_{j} = \max \left( {x_{i,j} } \right) $$
(6)

The dynamic boundary is used instead of fixed boundary in order to preserve the search experience to make the opposite solution situated in the narrowing search space. In addition, if the dynamic boundary operator makes \(\tilde{x}_{i,j}\) jump from [\(da_{j} , db_{j}\)], the following approach is employed to reset \(\tilde{x}_{i,j}\):

$$ \tilde{x}_{i,j} = rand\left( {da_{j} , db_{j} } \right) $$
(7)

In EOBL, opposition population is generated according to the elite individual. It makes full use of the elite individuals characteristics to provide more useful search information which will help to enhance the diversity of the population, and hence the global exploration tendency of FPA.

3.2 Cauchy distribution based global pollination phase

Each flower in the global pollination phase of basic FPA updates its position according to the following equation:

$$ X_{i}^{t + 1} = X_{i}^{t} + {\upgamma }L\left( \lambda \right)\left( {X_{best}^{t} - X_{i}^{t} } \right) $$
(8)

where \(X_{i}^{t}\) and \(X_{i}^{t + 1}\) are the previous and current positions of ith flower, respectively, \(X_{best}^{t}\) is the flower with best fitness at iteration t, and γ is the scaling factor to control the global pollination phase step size. The function of L´evy flight parameter L is to strengthen the pollination in the conventional FPA, and the step size (λ) obeys the L´evy distribution:

$$ L\sim\frac{{\lambda \Gamma \left( \lambda \right){\text{sin}}\left( {\pi \lambda /2} \right)}}{\pi } \frac{1}{{s^{1 + \lambda } }}, (s \gg s_{0} > 0) $$
(9)

where Γ(λ) is the gamma function.

In the proposed AFPA, heavy tailed and highly directed Cauchy based step size is utilized instead of Lèvy flights used in conventional FPA [36]. Due to its heavy tailed distribution, this Cauchy based step size is better at exploring the search space and is given by

$$ dis = \frac{1}{2} + \frac{1}{\pi }{\text{arctan}}\left( {\frac{\delta }{g}} \right) $$
(10)

The Cauchy density function is represented as

$$ f_{{Cauchy\left( {0,g} \right)}} \left( {dis} \right) = \frac{1}{\pi }\frac{g}{{g^{2} + x^{2} }} $$
(11)

where g is a scaling parameter with value equals to 1, \(\delta\) is the Cauchy random operator and dis is a uniform random number. The position updating equation for global pollination phase using Cauchy distribution function is given by:

$$ X_{i}^{t + 1} = X_{i}^{t} + C\left( \delta \right)\left( {X_{best}^{t} - X_{i}^{t} } \right) $$
(12)

3.3 Local Neighborhood Search (LNS)

FPA makes use of the best current solution and random solutions to improve local search in the local pollination phase. The local neighborhood search model (LNS) [41] is introduced to further strengthen the local search functionality of basic FPA.

The main idea is to use the current best solution to change the current solution in a small neighborhood of the current solution. For updating the position of the individual, the knowledge of an individual's neighborhood (i.e. the graph of their interconnections called the neighborhood structure) is utilized.

Suppose the population \(X = \left( {X_{1} , X_{2} , X_{3} ,. . . , X_{NP} } \right), X_{i} \left( {i \in \left[ {1, NP} \right]} \right)\) is a vector in the current population. Here, the indices of each vector are random in order to maintain the diversity of each neighborhood. Next, we can define the radius r neighborhood (r is a nonzero integer and 2r + 1 < NP), for each vector \(X_{i}\), neighborhood of \(X_{i}\) consists of \(X_{i - k} , . . . , X_{i} , . . . , X_{i + k}\). Figure 1 shows the notion of local neighborhood model in that the vectors can be organized into a ring topology according to their indices.

Fig. 1
figure 1

Neighborhood ring topology of radius 2

Full size image

Mathematically, the LNS model is defined as

$$ L_{i} = X_{i} + m*\left( {X_{n\_opt} - X_{i} } \right) + n*\left( {X_{p} - X_{q} } \right) $$
(13)

where \(p\), \(q\) ∈ [i − r, i + r] (p \(\ne\) q \(\ne\) i) and m and n are the scaling factors, where m, n ∈ rand() and \(X_{n\_opt}\) is the best solution in the \(X_{i}\) neighborhood. The enhanced version of FPA updates the best solution according to (13), and the modified solution performs the local pollination step as

$$ X_{i}^{t + 1} = L_{i}^{t} + r*\left( {X_{k}^{t} - X_{m}^{t} } \right) $$
(14)

where \(L_{i}\) is the best solution updated by LNS and \(X_{k}^{t} and X_{m}^{t}\) are the random solutions of kth and mth flower where \(k \ne m\) and \(r\) is a scaling factor, where \(r\) ∈ rand().

3.4 Dynamic switch probability

In adaptive FPA, instead of using a fixed switch, an adaptive switch \((p_{t} )\) has been designed to balance the exploitation and exploration tendency during the search process [42]. The search agents can adapt this strategy to update their next position in accordance with the present fitness value variation, as follows:

$$ X_{i}^{t + 1} = \left\{ {\begin{array}{*{20}l} {X_{i}^{t} + C\left( \delta \right)\left( {X_{best}^{t} - X_{i}^{t} } \right),} \hfill & {rand > p_{t} } \hfill \\ {X_{i}^{t} + m*\left( {X_{n\_opt}^{t} - X_{i}^{t} } \right) + n*\left( {X_{p}^{t} - X_{q}^{t} } \right) + r*\left( {X_{k}^{t} - X_{m}^{t} } \right) ,} \hfill & { rand \le p_{t} } \hfill \\ \end{array} } \right. $$
(15)

here \(p_{t}\) is evaluated in the previous iteration. To accelerate the optimizer convergence, the exploitation must be preferred with a higher probability as compared with the exploration mode. So, the switch \(p_{t + 1}\) is defined in the range [0.5, 1] with the initial switch value as 0.5, the adaptive transition is given as [36],

$$ p_{t + 1} = \left\{ {\begin{array}{*{20}l} {\frac{1}{{1 + {\text{exp}}\left( { - \frac{{f_{t}^{*} }}{{f_{t - 1}^{*} }}} \right)}}, } \hfill & {log_{10} \left| {f_{t}^{*} } \right| \ne log_{10} \left| {f_{t - 1}^{*} } \right|} \hfill \\ {\frac{1}{{1 + {\text{exp}}\left( { - \frac{{f_{t}^{*} - \theta .\frac{{f_{t}^{*} }}{\theta }}}{{f_{t - 1}^{*} - \theta .\frac{{f_{t - 1}^{*} }}{\theta }}}} \right)}},} \hfill & {otherwise} \hfill \\ \end{array} } \right. $$
(16)

In Eq. 16, \(f_{t}^{*}\) is the finest fitness value obtained at the tth iteration,\(.\) is the floor function, \(\theta\) is the threshold value of adaptive scale parameter that helps to auto-recognize the search state and is given by,

$$ \theta = 10^{{log_{10} \left| {f_{t}^{*} - f_{t - 1}^{*} } \right| + 1}} $$
(17)

For the case \(f_{t}^{*} { \ggg }f_{t - 1}^{*}\), there is a large difference in fitness values between two iterations. So, the adaptive switch \(p_{t + 1}\) attains value 1. Therefore, the algorithm switches to the exploitation mode for next iteration. For \(f_{t}^{*} { \lll }f_{t - 1}^{*}\), the adaptive switch \(p_{t + 1}\) will be 0.5 and the exploration mode is selected for next iteration. A local minima has been found for the situation \(log_{10} \left| {f_{t}^{*} } \right| = log_{10} \left| {f_{t - 1}^{*} } \right|\). In order to make this adaptive switch more sensitive, the adaptive switch ratio is modified by the term \(\frac{{f_{t}^{*} - \theta .\frac{{f_{t}^{*} }}{\theta }}}{{f_{t - 1}^{*} - \theta .\frac{{f_{t - 1}^{*} }}{\theta }}}\). This improvement allows the search agents to jump out of potential traps with higher probability [40].

3.5 Catfish effect mechanism

In real life, fishermen always place catfish into a sardine pond to maintain the freshness of sardines. The catfish disturb the sardines' living environment to activate their ability to survive. This phenomenon derives the catfish effect and was successfully incorporated into PSO [43].

This mechanism is employed to avoid premature convergence by forcing the worst individuals to explore new regions and possibly get better candidate solutions. According to this mechanism if in n consecutive iterations the fitness value of the current best solution has not been enhanced, the 10% worst “sardine” individuals \(WX\) will be replaced by new “catfish” individuals \(CX\). The “catfish” individuals are considered as opposition “sardine” individuals, and can be calculated as follows:

$$ CX_{id} = a_{d} + b_{d} - WX_{id} $$
(18)

where i is the “sardine” individuals index and \(WX\) is 10% worst “sardine” individuals.

Main Procedure of the AFPA. The modified approach AFPA is developed by integrating the EOBL technique, Cauchy distribution based Global pollination phase, the LNS model, dynamic switch probability and catfish effect mechanism in the conventional FPA. To demonstrate our proposed algorithm, the detailed pseudocode of the AFPA is shown in Algorithm 1.

figure c

4 Statistical testing of adaptive FPA algorithm

A set of 10 CEC 2019 benchmark functions (see Appendix Table 5) termed as the "100-Digit Challenge" [38] is selected for AFPA evaluation. Out of these 10 benchmarking functions few of them are shifted and rotated (CEC04-CEC-10), whereas CEC (01–03) are taken as it is. These are all scalable test functions. Comparison with FPA [36], GWO [43], SSA [44], CS [45], and SCA [46] is done to check the effectiveness of AFPA. For every algorithm a total of 500 iterations are performed using 30 agents. The parameter settings for abovesaid algorithms are given in Table 1. For all the algorithms under evaluation, the outcomes are described in terms of the worst, best, mean and standard deviation values for 30 independent runs. AFPA achieves better results than competitive algorithms, except in CEC04, CEC06, and CEC9 as shown in Table 2. Figure 2 displays the convergence graph and box plot of various algorithms for the different benchmark functions.

Table 1 Parameter settings
Full size table
Table 2 Results of competitive algorithms for CEC 2019 test suite
Full size table
Fig. 2
figure 2figure 2

Convergence graph and boxplot for CEC 2019 test suite

Full size image

It has been found that AFPA's results for function CEC01 are better in terms of the worst, average, and median values obtained in compassion to other algorithms, but GWO outperforms in terms of the best fitness performance obtained. GWO, SSA, CS and AFPA are able to find optimal solution for function CEC02, but it is found that AFPA is the better for minimum standard deviation achieved. For the CEC03 function, most of the algorithms can achieve almost globally optimal solution; but overall, in terms of minimum standard deviation, AFPA is found to be better.

For function CEC04, GWO outperforms in terms of the best fitness value achieved, but it has been found that AFPA's results are better for the worst, average, and median values attained. AFPA is better than others in the case of CEC05, in terms of all performance metric obtained. SSA's and AFPA’s results are better compared with competitive algorithms for function CEC06 and CEC07 functions respectively. AFPA's results for function CEC08 are better for the worst, average, and median values obtained, however, the results of SSA achieved best fitness function value. AFPA's results are competitive with other algorithms for function CEC09 and CEC10.

Figure 2 displays the box-plots of competitive algorithms for CEC 2019 benchmark functions. The box-plots here are used to measure algorithm efficiency in terms of fitness values. It can be shown that in most cases the proposed AFPA is cost-effective as median of fitness values for AFPA is lower. Therefore, AFPA's overall performance is found to be consistent with other algorithms for optimization.

5 Location determination using single anchor node

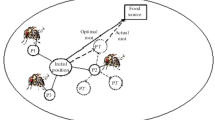
The concept of deploying a single AN in the sensor field is used to locate target nodes. These nodes are deployed into three different layers, anchors are placed at the top, whereas at the bottom and middle layer TNs are deployed randomly. These ANs transmit a beacon signal that helps the TNs to locate themselves. As TNs fall within the range of AN, then by using the beacon signal, TNs obtain the RSSI information of an anchor and then calculating Euclidean distance between AN and TN. After calculating Euclidean distance six VAs are projected at 60 degrees each using umbrella projection concept to locate TNs, as shown in Fig. 3. For locating TNs in 3D scenario, minimum 4 anchors are required (as shown in Fig. 4), one anchor and three VAs are used to obtain the centroid. Then using this centroid information, Adaptive FPA algorithm is applied for optimization.

Fig. 3
figure 3

Umbrella projection for deploying anchor and virtual anchors

Full size image
Fig. 4
figure 4

Anchor and projection of VA in 3D environment

Full size image

By using this concept of VAs, LoS issues are also minimized to a greater extent.

$$ d_{i} = \sqrt {(x_{t} - x)^{2} + (y_{t} - y)^{2} + (z_{t} - z)^{2} } $$
(19)

where \((x_{t}\), \(y_{t} , z_{t} )\) represents the TN position and (\(x\),\( y,z)\) represents current location of the AN.

The centroid position \((x_{c}\), \(y_{c} ,z_{c} )\) is calculated using AN and the respective virtual ANs (\(xv_{1}\),\(yv_{1} ,zv_{1} )\), (\(xv_{2}\),\(yv_{2} , zv_{2} ),and \left( {xv_{3} ,yv_{3} , zv_{3} } \right)\) as shown in Fig. 5.

Fig. 5
figure 5

Calculating centroid in 3D scenario

Full size image

The centroid coordinates are determined as

$$ (x_{c,} y_{c} ,z_{c,} ) = \left( {\frac{{x + xv_{1} + xv_{2} + xv_{3} }}{3}, \frac{{y + yv_{1} + yv_{2} + yv_{3} }}{3}, \frac{{z + zv_{1} + zv_{2} + zv_{3} }}{3}} \right) $$
(20)

After obtaining the centroid, random particles are deployed as shown in Fig. 6. Adaptive FPA is used to locate all the moving TNs and to estimate the coordinates as \(x_{s,} y_{s} ,z_{s,} .\) The fitness function is obtained by calculating mean square error between actual and estimated coordinates distances of actual and estimated nodes as given in (21) is minimized.

$$ f(x_{{s,}} y_{{s,}} z_{{s,}} ) = \frac{1}{M}\sum {\text{ }}\left( {{\text{ }}\sqrt {(x_{e} - x_{i} )^{2} + (y_{e} - y_{i} )^{2} + (z_{e} - z_{i} )^{2} } - d_{i}^{ \wedge } {\text{ }}} \right)^{2} $$
(21)
Fig. 6
figure 6

Adaptive FPA deployed around centroid

Full size image

Here \(x_{i} , y_{i} , z_{i}\) represents the location of placed beacon node and \(x_{e} , y_{e} , z_{e}\) represents the estimated location of TNs (M > 4 to compute 3D location).

Other meta-heuristic algorithms perform in the similar fashion to localize themselves.

Each algorithm obtains the optimum location as shown in Fig. 7, and localization error is calculated as given in (22)

$$ E_{t} = \frac{1}{{N_{L} }}\sum \sqrt {(x_{e} - x_{t} )^{2} + (y_{e} - y_{t} )^{2} + (z_{e} - z_{i} )^{2} } $$
(22)

where \(N_{L}\) represents localized TNs.

Fig. 7
figure 7

Target estimation using adaptive FPA

Full size image

6 Results and discussions

In this research work, a novel approach of using a single anchor with their projection in hexagonal directions to obtain 3D locations of TNs using various meta-heuristic optimization algorithms. Using MATLAB software, various meta-heuristic algorithms are tested for 80 TNs deployed at middle and bottom layer (40 each). The results were performed in WSN field with single AN on the MacBook Air i5 with 4 GB RAM processing. A cubic structure with different properties of TNs and three-layer structure is considered. In this, three-layer arrangement at the top most layer a single AN and at bottom and middle layer 40 TNs are deployed randomly. For obtaining 3D coordinates at least four anchors (one anchor and minimum three VAs) are required. Whenever, the moving TNs fall within the range of AN, the above said scenario is considered. An umbrella projection is formed with the help of anchor and VAs is formed for determining the 3D positions of target nodes.

Various meta heuristic algorithms are applied in this research for obtaining 3D coordinate. Different parameters chosen for meta-heuristic algorithms are as shown in Table 3.

Table 3 Parameter settings
Full size table

In mobility based scenario, various meta-heuristic algorithms are evaluated in the following section. The TNs are deployed initially in a random fashion at bottom and middle layers and at the top most layer is equipped with AN. AN is fixed while mobility is applied for TNs. The fitness function is calculated using the average of localization error. The results of various meta-heuristic algorithms are shown in Figs. 8, 9, 10, 11, 12, 13, 14, 15, 16. From these results, it is clear that the anchor forms umbrella projection pattern with VAs and TN to determine the 3D positions. By using VA concept, the problem of LoS is minimized to greater extent. From these observations it is quite clear that Adaptive FPA outperforms in context of other meta-heuristic optimization algorithms and have faster convergence rate.

Fig. 8
figure 8

Target node movement using BBO

Full size image
Fig. 9
figure 9

Target node movement with HPSO

Full size image
Fig.10
figure 10

Target node movement with FA

Full size image
Fig.11
figure 11

Target node movement with HPSO

Full size image
Fig.12
figure 12

Target node movement with GWO

Full size image
Fig.13
figure 13

Target node movement with FPA

Full size image
Fig.14
figure 14

Target node movement with NMRA

Full size image
Fig.15
figure 15

Target node movement with NMRV 3.0

Full size image
Fig.16
figure 16

Target node movement with adaptive FPA

Full size image

In static scenario, a smaller range and only few anchors are considered. All TNs get localized using this AN and referred as pseudo anchor once it is localized. Then pseudo anchors and initially deployed anchors collectively work together to locate the other unlocated TNs. In static deployment the convergence rate is slow and requires a greater number of rounds to locate all TNs. Whereas in dynamic scenarios, AN with higher range is considered and more number of TNs are located in shorter time.

Initially, anchors and TNs are deployed in similar fashion for all meta-heuristic algorithms. To compare the results in mobility scenario various performance metrics are considered as described in Table 4. The convergence time of Adaptive FPA is quite less as compared to other competitive algorithms tested for the same scenario.

Table 4 Comparison of meta-heuristic algorithms
Full size table

7 Conclusions and future scope

Range based and range free localization techniques are the popular available techniques to locate unknown nodes. In this research, range-based techniques along with various meta-heuristic algorithms are used to obtain 3D coordinates of TNs using single AN concept. Anchor node and the VAs form an umbrella projection for locating all TNs. Whenever the moving targets fall within the scope of AN, three VAs and anchor itself works unitedly to locate the TNs (as minimum 4 nodes are required to obtain 3D positions). In this approach, node is estimated with least localization error along with lesser computational time in Adaptive FPA. The computation time for PSO and HPSO is of the order of one fourth of the second, but for BBO and FA, the convergence rates are higher (close to a second) respectively whereas for Adaptive FPA the convergence time is only 0.1234 s.

The implemented algorithm can be used in a variety of applications, such as animal tracking, logistics, monitoring of coal mine workers and industrial applications. The limitation of this work is that the algorithm is relying only upon a single AN for locating TNs in 3D environment and due to power issues if a single AN gets non-operational, the network gets terminated. So, there is trade-off using the concept of single AN, as only a single AN is required to locate TNs in 3D environment which is cost effective.