1 Introduction

Vehicular ad hoc networks (VANETs) are one of the most interesting commercial applications of ad hoc networks. Vehicular communication is characterized by a dynamic environment but relatively predictable movability. Although vehicular mobility is constrained by road or highway topology and layout, modeling the movability in a VANET is quite involved; the movement of each vehicle is affected by many factors such as highway traffic situation, movements of neighboring vehicles, traffic signs, and driver’s reactions to these factors [1–4]. Vehicles as mobile hosts can communicate with each other directly if and only if their Euclidean distance is not longer than the radio propagation range [5]. Each vehicle in this environment operates not only as a host but also as a router [6]. Utilizing dedicated short-range communications (DSRC) enables a wide variety of driver-assisting applications such as vehicle-to-vehicle (V2V) and vehicle-to-roadside (VRC) messaging of traffic and accident information as well as allowing timely and intelligent communication to improve road safety and traffic stream [7–10].

Vehicles, due to their non-uniform and different types have dissimilar movability patterns and adopt different speeds. This in turn results in variations in the density of a cluster, and the possibility of splitting or merging VANET connectivity [11, 12]. In VANET literature, connectivity and cluster are interchangeable quantities, and are used for defining a sequence of vehicles such that each pair of consecutive vehicles is within radio range of one another. In the rest of this paper we use these expressions similarly. Hereinafter, we study the connectivity related measurements in VANETs by evaluating the probability density function (pdf) of connectivity, cluster size (i.e. defined as the total number of vehicles inside the connectivity) and connectivity distance (i.e. defined as the maximum spatial length of the connected vehicle).

Differences and variation in the speed of vehicles involved in a VANET causes the number of nodes in each cluster to vary dynamically. As a result, the topology of the network changes frequently and nodes come into intermittent contact with vehicles traveling in other lanes in the same or opposite direction. These opportunistic contacts can be utilized to aid message propagation via multihop forwarding using intermediate nodes who overhear the message, regardless of being in a single lane or multiple lanes [13–15]. Networked environments that operate under such intermittent connectivity are also referred to as episodically connected, delay tolerant, or disruption tolerant networks (DTNs) [16–20].

The main contributions of this paper are as follows:

  • Using a time-varying vehicular speed assumption, the mobility model of the head, tail and intermediate vehicles inside connectivity are mathematically presented. According to this, a novel solution for computation of the connectivity distance and also a realistic closed-form equation for pdf of the connectivity are proposed.

  • Joint Poisson vehicular distribution in a multilane highway, expected number of vehicles and tail probability of the expected number of vehicles inside a lane in a multilane highway are modeled.

This paper is organized as follows: in Sect. 2 we summarize the related works and show vehicular connectivity taxonomy and discuss future requirements. Section 3 describes some definitions and presents the network architecture. Our analytical model is given in Sect. 4. We evaluate the proposed model by extensive simulations in Sect. 5. Finally, Sect. 6 concludes this paper.

2 Related work

Connectivity analysis and its related applications, was previously investigated as a classical and attractive problem in wireless communication networks [21–26]. With the introduction of VANETs, and increased possibilities of VANET enabled consumer applications, the topic of connectivity analysis has gained even a higher momentum and attracted higher attention from research communities [11, 12, 27–32].

2.1 A taxonomy of vehicular connectivity

Previous research on the connectivity through intervehicle distances, attempts to disclose the relationship between the connectivity and the distance which is defined as the length of connected path. To reflect the high dynamics of the connectivity due to different mobility patterns, previous work explored the influence of velocity [11, 27, 32], vehicle density [11, 24, 33], radio propagation range [24, 25, 32, 33], node degree [34], connection duration [35] and etc.

2.1.1 Queuing theory technique

In [21], Yousefi et al. provided analytical results on the exponential distribution of intervehicle distance in a 1-D VANET under different constant-speed model and Poisson arrival model. The number of vehicles passing an observation point on the road during any time interval follows a homogeneous Poisson process with intensity of λ. They introduced an equivalent M/D/∞ queuing model that studied the busy period in queuing theory. They further analyzed the connectivity distance and denoted the Laplace transform of the pdf of connectivity distance and tail probability of connection distance. Since their Laplace expression might not explicitly be inverted, they resorted to numerical inverting and did not provide a closed-form formula for the distribution of the cluster length. However, their numerical results showed that increasing the traffic flow and radio propagation range of vehicles correspondingly leads to the increase of the discussed connectivity in terms of platoon size and connection distance. Moreover, in, the authors claim that multiple lanes can be neglected in their model because the difference between the coverage range of the devices and the distance between lanes is negligible. However, some new applications in VANETs may be dependent on multiple lanes.

2.1.2 Constant speed techniques

In [12], Agarwal et al. studied the information propagation speed (IPS) in a 1-D VANET where vehicles are Poisson distributed and move at the same speed but in the opposite directions. Using the alternating periods of disconnection and multihop connectivity, they derived the upper and lower bounds for the IPS, which provided a hint on the impact of vehicle density on the IPS. However, in their model bounds are not tight, and many factors, e.g., speed variation and therefore connectivity variation, were ignored.

In [36], Wu et al. considered a 1-D VANET where vehicles are Poisson distributed and the vehicle speeds are uniformly distributed in a designated range. They provided a numerical method to compute the IPS under two special network models; when the vehicle density is either very low or very high which are obviously oversimplified models [12, 37]. They showed that the message propagation process can be modeled as a renewal reward process in which message propagation cyclically alternates between catch-up and forward processes. Using different constant-speed model of vehicle mobility, they approximated the average connectivity size in forwarding process.

Baccelli et al. in [28] provide a full analysis of the IPS in bidirectional vehicular delay tolerant networks such as roads or highways. They proved that under a certain traffic intensity threshold, on average, information propagates at the vehicle speeds. In while above this threshold, in a situation that, vehicles are connected in an obtained cluster, information propagates much faster. They defined a westbound (respectively, eastbound) cluster as a cluster made exclusively out of westbound (respectively, eastbound) vehicles. A full cluster is made of westbound and eastbound vehicles. They considered a bidirectional vehicular network, such as a highway, where vehicles move in two opposite directions at constant speed v and denoted the Laplace transform of the cluster length.

Chen et al. in [29] defined a metric based on different but constant-speed model, to consider both direct (provides one-hop connections between nodes) and indirect (i.e. multihop forwarding) connectivity. In [34], the distance distribution is expressed by a tuple (h, v, ρ), where h denotes the intervehicle distance, v indicates the velocity, and ρ is the market penetration ratio, respectively. After taking specific propagation model and the radio range into consideration, the connectivity formula was given. The expression was then further extended to the connectivity of a node with degree n.

In [35], the connection duration between two adjacent vehicles was introduced, given their speeds, directions, and the radio ranges. According to the calculated connection period expression, an admission control strategy was proposed to determine whether the next vehicle is allowed to be injected into the current traffic flow without interrupting the ongoing connections. In [22] metrics for evaluating nodal connectivity in VANETs, considering the different nodal mobility patterns, was presented. The connection period distribution was characterized by average duration of the k-hop path existing between any two nodes. They also presented simulation data that suggests multihop paths have much poorer connectivity performance than the single-hop connectivity in VANETs. In [26], the paper demonstrated that, under free flow traffic, the number of connected vehicles increases as either the vehicle density or the number of lanes grows. They found that the intervehicle distances had a major impact on connectivity when it is within 3–4 times larger than the radio range. Beyond this distance, the connectivity declines slowly. In [23], a simple geometrical analysis of the connectivity in vehicular networks under a distance-based radio communication model was proposed. The authors presented the notion of the connectivity robustness based on intervehicle distances, whereby a local computable function could be obtained to provide a sufficient condition for the connectedness of the network.

2.1.3 Time-varying speed techniques

Zhang et al. in [11, 27] provided a closed-form formula for the pdf of the connectivity using a different method inspired by the study on the connectivity of random interval graph [38] and theory of coverage processes [39]. They considered a model in which time is divided into intervals of equal length and each vehicle changes its speed at the beginning of each time slot, independent of its speed in other time slots. In their analysis n vehicles are Poisson distributed in a cluster length of x 0, and vehicles follow a uniform distribution. However they did not precisely determine how the parameter x 0 can be computed.

2.1.4 Motivations

In the context of vehicular networks, many previous connectivity related studies are based on simplistic assumption that vehicle speeds are either equal at all times [12, 28, 34] or different from vehicle to vehicle but constant for a given vehicle at all times [21, 29, 34, 35]. Only a few studies, without clarification of the mechanism of computing the connectivity distance, proposed pdf of the connectivity allowing vehicle speed variation [11, 27].

To the best of our knowledge, none of the prior connectivity related VANET-literature has considered the simultaneous spatial and temporal analysis in such time-varying vehicular speed networks. The focus of this work is to analyze and address the impact of dynamic movement of vehicles on forming instantaneous connectivity. In this work we propose a time dependent analytical model for calculating the pdf of connectivity. This model is derived based on time-varying vehicular mobility model of tail, head and intermediate vehicles in a cluster. Our proposed model is also capable of analyzing connectivity distance that is not solved by the prior literature accurately.

2.2 Future requirements

The broadcast nature of the wireless medium can be advantageous to support multi-path capabilities that information-centric networking (ICN) can enable for transport of information in VANETs [40, 41]. Mobile and wireless communications as well as mobile cloud computing are a profoundly important technology that is rapidly growing and continuously changing human life [42–49]. The taxonomy of cloud-based vehicular networks is addressed from the standpoint of the service relationship between cloud computing and VANETs [10]. It is extremely necessary to efficiently provide comprehensive study for future vehicular networks especially cloud-based VANETs. In this regard, we study the vehicular spatial distribution and mathematically investigate joint Poisson vehicular distribution.

Therefore, we highlight that this paper investigates two distinguished challenges in VANETs (i.e. connectivity related analysis and vehicular related spatial distribution), which provides future vehicular networks with possible solutions and exploits promising directions for future research.

3 System model

In this section, the network architecture is explained. This paper considers a set of legal movement changes, such as changing lanes, slowing down, speeding up, and overtaking, in which vehicles are capable of communication and broadcasting information to the vehicles traveling in the same direction on a multilane highway.

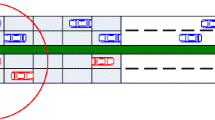
As shown in Fig. 1, following the convention in prior VANTE literature, the highway is annotated as eastbound and westbound. It is assumed that vehicles are able to communicate with each other using fixed radio range, referred to by r. Without loss of generality, in the rest of this paper, we focus on analyzing the V2V communication in single direction of a multilane highway (e.g. eastbound) [12]. However, our model could be applied to scenarios of V2V and VRC on both eastbound and westbound directions as well.

Fig. 1
figure 1

VANET example and connectivity model of vehicles on eastbound direction

Full size image

The arrival and distribution of a vehicle in each lane can be modeled as an independent Poisson process in which vehicles travel in each lane of the highway at different speeds. As illustrated in Fig. 1, tail is defined as the leftmost vehicle inside the cluster in the eastbound direction and head is defined as the foremost vehicle inside that cluster.

While traveling, vehicles may change their speed. In order to provide dynamic movability, a synchronized random walk mobility model is considered. It is considered that time is divided into equal intervals, and which interval duration is referred to by τ, where the ith time slot is \( t \in \left( {\left( {i - 1} \right)\tau , i\tau } \right]. \) The vehicle speed’s may vary at the beginning of each interval, independent of other vehicles [11, 27]. Therefore, at any time interval, the spatial distribution of the vehicles on the road follows a homogeneous Poisson process with intensity \( \rho = \lambda \int_{ - \infty }^{\infty } {\left( {f_{v} \left( v \right)/v} \right)dv} \) in which f v (v) is a zero-mean normal speed distribution and λ is Poisson intensity (veh/s).

We consider a dynamic VANET with a set of n nodes. For clarity, as shown in Fig. 2, we assume that H m denotes the mth vehicle to the left side of the observer H 0 (start point). Let’s define w m to be the Euclidean distance between H m and H 0 at time t 0 = 0 and f wm (w m ) to be the pdf of w m which is given by (11). As illustrated in Fig. 2, there exist N(t 0) = n vehicles at the left side of the observer. During [t 0, t 1] vehicles passing the observer are allowed to change their speed at the beginning of each interval independent of other intervals as well as other vehicles. We consider that at time t 1 = t the total of n vehicles take part to form connectivity at right side of the observer if and only if the conditions given in Sect. 4.1.5 hold. As shown in Fig. 2, at time t the tail is in H tail with minimum distance to the observer (i.e. y tail (t)) and the head is in H head with maximum distance to the observer (i.e. y head (t)). Furthermore, x m (t) − w m is the Euclidean distance between H m and H 0 at time t where x m (t) is the difference between the position of the vehicle H m at time t 0 = 0 and its position at time t. Considering a Poisson process, when N(t) = n the following property holds:

$$ p_{r} (N(t) = n) = \frac{{e^{ - \lambda t} (\lambda t)^{n} }}{n!} $$
(1)
Fig. 2
figure 2

Example of connectivity in VANET. The observer is located in H 0 and there exist N(t 0) = n vehicles in left side of the observer at time t 0 = 0. During [t 0, t 1) all n vehicles pass the H 0, and at time t 1 = t form a connectivity at right side of the observer. The connectivity distance will be determined as y c (t) = y head (t) − y tail (t) in which H tail is considered as location of the tail and H head shows the head location

Full size image

4 Analysis

4.1 Connectivity analysis

In this section we study the connectivity in a VANET in which the vehicular speeds follow a generic pdf f v (v). This section is organized as follows: using time-varying vehicular speed assumption, the mobility model of a single vehicle is described. Next mobility model of the head, tail and intermediate nodes inside a cluster are mathematically formulated. Afterwards, the connectivity distance and pdf of the connectivity is proposed.

4.1.1 Mobility model of a single vehicle based on normal speed distribution

In this subsection, commonly used assumptions and analytical formulations of the connectivity process under the normal speed distributions of VANETs is summarized: For a zero-mean normal speed distribution with standard deviation of σ, the pdf f v (v) of the vehicle speed [11, 21, 27, 37, 50, 51] is defined as

$$ f_{v} (v) = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left( {\frac{{ - v^{2} }}{{2\sigma^{2} }}} \right) $$
(2)

Let’s consider that time is equally divide into i slots of size \( \tau \) such that t = iτ. In addition let’s assume that speed of each vehicle may change at the beginning of each time interval independent of the other intervals. Let p(x, τ) be the probability that displacement of a vehicle at time τ is equal to x. Because the speed does not change during a time slot, p(x, τ) can be easily obtained from f v (v) [11]. At the end of the first time slot, i.e. t = τ, it is straightforward to show that [11]

$$ p(x,\tau ) = \frac{1}{{\sigma \tau \sqrt {2\pi } }}\exp \left( {\frac{{ - x^{2} }}{{2(\sigma \tau )^{2} }}} \right) $$
(3)

Since vehicle speeds are modeled as independent random variables at different time slots, their displacements are also independent random variables. Therefore at time \( t = i\tau \):

$$ p(x,t) = p(x,i\tau ) = \overbrace {(p * p * \cdots * p * p)(x,\tau )}^{i {\text{-}} fold\,convolution} $$
(4)

The calculation of the aforementioned i-fold convolution can be simplified by using the Fourier and inverse Fourier transformations. Note that convolution of i normal functions is a normal function [52],

$$ p(x,i\tau ) = \frac{1}{{\sigma_{i} \sqrt {2\pi } }}\exp \left( {\frac{{ - x^{2} }}{{2\sigma_{i}^{2} }}} \right) $$
(5)

where σ 2 i  = i(στ)2,

Indeed, moment generating function of the sum of independent random variable is equal to the product of individual moment generating functions [52]. Using this property for i zero-mean normal functions of p(x, τ) with standard deviation στ we arrive at the following definition of join moment generating function:

$$ \phi_{i\tau } = (\phi_{\tau } (t))^{i} = \exp \left\{ {\frac{{i(\sigma \tau )^{2} t^{2} }}{2}} \right\} $$
(6)

ϕ iτ (t) is the joint moment generating function of i normal displacements in which σ 2 i  = i(στ)2,

4.1.2 Mobility model of head inside the cluster

Let us first consider the movement of the head in a cluster. As shown in Fig. 2, let’s define y head (t) as the displacement of the vehicle with the maximum position coordinate among those N(t) = n vehicles passing location H 0 at time t. Note that the head may be overtaken by another vehicle during time \( \left[ {0, t} \right) \). Based on this definition:

$$ y_{head} (t) = \hbox{max} (x_{m} (t) - w_{m} ),m = 1,2, \ldots ,N(t) $$
(7)

Since \( x_{1} , x_{2} , \ldots , x_{n} \) and \( w_{1} , w_{2} , \ldots , w_{n} \) are independent identically distributed (i.i.d.) random variables, the cumulative distribution function (cdf) of displacement for the head at time t among N(t) = n connected vehicles is defined as:

$$ F_{{Y_{head} (t)}} (y|N(t) = n) = p_{r} [y_{head} (t) \le y|N(t) = n] $$
(8)
$$ \begin{aligned} & = p_{r} \left( {x_{1} (t) - w_{1} \le y} \right), \ldots ,p_{r} \left( {x_{n} (t) - w_{n} \le y} \right) \\ & = F_{{x_{1} (t) - w_{1} }} (y), \ldots ,F_{{x_{n} (t) - w_{n} }} (y) \\ & = \left( {F_{{x_{m} (t) - w_{m} }} (y)} \right)^{n} \\ \end{aligned} $$
(9)
$$ = \left( {\int\limits_{0}^{\infty } {\int\limits_{ - \infty }^{{y + w_{m} }} {p(x,t)f_{{w_{m} }} (w_{m} )dxdw_{m} } } } \right)^{n} $$
(10)

where p(x, t) is given by (4) and \( f_{{w_{m} }} \left( {w_{m} } \right) \) is the pdf of w m which is shown below. As a consequence of using the Poisson distribution for vehicle arrival [11], the intervehicle distance follows an exponential distribution. Therefore

$$ f_{{w_{m} }} (w_{m} ) = \frac{{\rho e^{{ - \rho w_{m} }} (\rho w_{m} )^{m - 1} }}{(m - 1)!},\quad {\text{for}}\,m \ge 1 $$
(11)

Since \( w_{1} , w_{2} , \ldots , w_{n} \) are (i.i.d.), the cdf of intervehicle distance can be easily obtained by:

$$ F_{W} (l) = 1 - \sum\limits_{k = 0}^{m - 1} {\frac{{e^{ - \rho l} (\rho l)^{k} }}{k!}} = e^{ - \rho l} \sum\limits_{k = m}^{\infty } {\frac{{(\rho l)^{k} }}{k!}} $$
(12)

Therefore, the tail probability of intervehicle distance is:

$$ P(w > l) = 1 - F_{W} (l) = e^{ - \rho l} \sum\limits_{k = 0}^{m - 1} {\frac{{(\rho l)^{k} }}{k!}} $$
(13)

Define \( f_{{Y_{head} \left( t \right)}} (y|N\left( t \right) = n) \) to be the pdf of head displacement among N(t) = n connected vehicles at time t:

$$ \begin{aligned}& f_{{Y_{head} (t)}} (y|N(t) = n) \\& = \frac{\partial }{\partial y}F_{{Y_{{_{head} (t)}} }} (y|N(t) = n)\, \\ & = n \cdot f_{{x_{m} (t) - w_{m} }} (y) \cdot \left( {F_{{x_{m} (t) - w_{m} }} (y)} \right)^{n - 1} \\ \end{aligned} $$
(14)

where,

$$ \begin{aligned} f_{{x_{m} (t) - w_{m} }} (y) & = \frac{\partial }{\partial y}F_{{x_{m} (t) - w_{m} }} (y) \\ & = \frac{\partial }{\partial y}\left( {\int\limits_{0}^{\infty } {\int\limits_{ - \infty }^{{y + w_{m} }} {\frac{1}{{\sigma_{i} \sqrt {2\pi } }}\exp \left( {\frac{{ - x^{2} }}{{2\sigma_{i}^{2} }}} \right)} \cdot \frac{{\rho e^{{ - \rho w_{m} }} (\rho w_{m} )^{m - 1} }}{(m - 1)!}dxdw_{m} } } \right) \\ \end{aligned} $$
(15)

The cdf of the displacement for the head at time t independent of the cluster size is:

$$ \begin{aligned}& F_{{Y_{head} (t)}} (y) \hfill \\& = \sum\limits_{n = 1}^{\infty } {p_{r} [y_{head} (t) \le } y|N(t) = n] \cdot p_{r} [N(t) = n] \hfill \\ \end{aligned} $$
(16)
$$ = \sum\limits_{n = 1}^{\infty } {\left( {\left( {\int\limits_{0}^{\infty } {\int\limits_{ - \infty }^{{y + w_{m} }} {p(x,t)f_{{w_{m} }} (w_{m} )dxdw_{m} } } } \right)^{n} \cdot \frac{{e^{ - \lambda t} (\lambda t)^{n} }}{n!}} \right)} $$
(17)

Define \( f_{{Y_{head} \left( t \right)}} \left( y \right) \) to be the pdf of displacement of head at time t unconditional of vehicle numbers. Then:

$$ f_{{Y_{head} (t)}} (y) = \frac{{\partial F_{{Y_{{_{head} (t)}} }} (y)}}{\partial y} $$
(18)

4.1.3 Mobility model of tail inside the cluster

Following a formulation process similar to that described in Sect. 4.1.2, the distribution of the tail can be obtained. As shown in Fig. 2, y tail (t) is the displacement of the tail from start point at time \( t. \) Cluster tail at time t is the one of the n connected vehicles with the minimum position among all the vehicles passing location H 0. Note that the tail may overtake another vehicle(s) during time \( \left[ {0, t} \right) \). It follows that

$$ y_{tail} (t) = \hbox{min} (x_{m} (t) - w_{m} ),m = 1,2, \ldots ,N(t) $$
(19)

Since x m and \( w_{m} m = 1, 2, \ldots , N\left( t \right) \) are i.i.d., this leads to

$$ p_{r} [y_{tail} (t) > z|N(t) = n] = \left( {\int\limits_{0}^{\infty } {\int\limits_{{z + w_{m} }}^{\infty } {p(x,t).f_{{w_{m} }} (w_{m} )dxdw_{m} } } } \right)^{n} $$
(20)

where p(x, t) can be obtained from (4) and f wm (w m ) is given by (11). Considering cluster size of N(t) = n, the cdf of the tail displacement at time t is

$$ \begin{aligned} &F_{{Y_{tail} (t)}} (z|N(t) = n) \\ & = 1 - p_{r} [y_{tail} (t) > z|N(t) = n] \\ & = 1 - \left( {P_{r} [x_{m} (t) - w_{m} > z]} \right)^{n} \\ & = 1 - \left( {\int\limits_{0}^{\infty } {\int\limits_{{z + w_{m} }}^{\infty } {p(x,t).f_{{w_{m} }} (w_{m} )dxdw_{m} } } } \right)^{n} \\ \end{aligned} $$
(21)

Let \( f_{{y_{tail} \left( t \right)}} (z|N\left( t \right) = n) \) be the pdf of the tail displacement at time t conditioning on cluster size N(t) = n, which is defined as:

$$ \begin{aligned} & f_{{Y_{tail} (t)}} (z|N(t) = n) \\ & = \frac{\partial }{\partial z}F_{{Y_{tail} (t)}} \left( {z|N(t) = n} \right) \\ & = - n\left( {P_{r} [x_{m} (t) - w_{m} > z]} \right)^{n - 1} \frac{\partial }{\partial z}\left( {P_{r} [x_{m} (t) - w_{m} > z]} \right) \\ \end{aligned} $$
(22)

The cdf of the tail displacement at time t independent of the number of connected vehicles is given by

$$ \begin{aligned} F_{{Y_{tail} (t)}} (z) \hfill \\ = 1 - \sum\limits_{n = 0}^{\infty } {p_{r} [y_{tail} (t) > } z|N(t) = n].p_{r} [N(t) = n] \hfill \\ \end{aligned} $$
(23)
$$ = 1 - \sum\limits_{n = 0}^{\infty } {\left( {\left( {p_{r} [x_{m} (t) - w_{m} > z]} \right)^{n} \cdot \frac{{e^{ - \lambda t} (\lambda t)^{n} }}{n!}} \right)} $$
(24)

let’s define \( f_{{y_{tail} \left( t \right)}} \left( z \right) \) to be the unconditional pdf of displacement of the tail at time t. \( f_{{y_{tail} \left( t \right)}} \left( z \right) \) is defined as:

$$ f_{{Y_{tail} (t)}} (z) = \frac{{\partial F_{{Y_{tail} (t)}} (z)}}{\partial z} $$
(25)

4.1.4 Mobility model of intermediate vehicles inside the cluster

Let \( x_{1} \left( t \right) - w_{1} , x_{2} \left( t \right) - w_{2} , \ldots ,x_{n} \left( t \right) - w_{n} \) be i.i.d. continues random variables with probability distribution F and density function \( f_{ = } F^{\prime}, \) where x m (t) − w m denotes the mth smallest vehicles distance to the observer. With this definition, \( x_{1} \left( t \right) - w_{1} , x_{2} \left( t \right) - w_{2} , \ldots ,x_{n} \left( t \right) - w_{n} \) is denoted as order statistics [52]. The distribution of x m (t) − w m , given that size of cluster is N(t) = n, is obtained from (26). Note that x m (t) − w m will be less than or equal to α if and only if at least m of the N(t) = n random variables \( x_{1} \left( t \right) - w_{1} , x_{2} \)(t) − w 2, …, x n (t) − w n are less than or equal to α. Hence,

$$ \Pr (x_{m} (t) - w_{m} \le \alpha |N(t) = n) = \sum\limits_{k = m}^{n} {\left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)} (F(\alpha ))^{k} (1 - F(\alpha ))^{n - k} $$
(26)

Differentiation (26) yields the density function of x m (t) − w m as:

$$ f_{{x_{m} (t) - w_{m} }} (\alpha ) = \frac{n!}{(n - m)!(m - 1)!}f(\alpha )(F(\alpha ))^{m - 1} (1 - F(\alpha ))^{n - m} $$
(27)

Equation (27) is quite intuitive; in order for x m (t) − w m to equal \( \alpha \), m − 1 of the n values \( x_{1} \left( t \right) - w_{1} , x_{2} \left( t \right) - w_{2} , \ldots ,x_{n} \left( t \right) - w_{n} \) must be less than \( \alpha \), n − m of them must be greater than \( \alpha \), and one must be equal to \( \alpha \). The probability density that (I): \( m - 1 \) members of this set satisfy the conditions x m (t) − w m  < α, (II): n − m members of this set to satisfy the condition x m (t) − w m  > α and (III): one member satisfies the x m (t) − w m  = α, is equal to (F(α))m−1(1 − F(α))n−m f(α). Since there are \( n!/\left[ {\left( {m - 1} \right)!\left( {n - m} \right)!} \right] \) different partitions of n random variables in the three specified groups, the Eq. (27) is obtained [52]. Moreover, the distribution of vehicles x m (t) − w m inside the cluster independent of the cluster size can be obtained by

$$ \Pr (x_{m} (t) - w_{m} \le \alpha ) = \sum\limits_{n = 1}^{\infty } {\left[ {\left( {\sum\limits_{k = m}^{n} {\left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)} \left\{ {(F(\alpha ))^{k} (1 - F(\alpha ))^{n - k} } \right\}} \right) \times \Pr (N(t) = n)} \right]} $$
(28)

4.1.5 Probability of connectivity

As explained in Sect. 3 we consider that at time t 1 = t all of n vehicles are at the right side of observer H 0. These vehicles take part in forming the connectivity if certain conditions hold. As illustrated in Fig. 2, at time t the tail is in H tail with minimum distance to the start point and the head is locate at H head with maximum distance to the observer. Therefore the connectivity distance is defined by y c (t) = y head (t) − y tail (t). Vehicles are assumed to be point objects meaning that length of vehicles is ignored when computing the connectivity distance. Hence, N(t) = n vehicles can form connectivity with length of y c (t) = y head (t) − y tail (t) if and only if the following conditions hold:

  • ɛ 1: the tail vehicle locates in H tail

  • ɛ 2: the head vehicle locates in H head

  • ɛ 3: the intervehicle distance between any two adjacent vehicles for those n vehicle in \( \left[ {H_{tail} , H_{head} } \right] \) is smaller than or equal to the radio range r.

  • ɛ 4: there is no vehicle in \( \left( {H_{head} , H_{head} + r} \right] \).

  • ɛ 5: there is no vehicle in \( \left[ {H_{tail} - r, H_{tail} } \right) \).

Denote by Pr(ɛ m ) the probability of event ɛ m in the preceding list. Due to the Poisson distribution of vehicles, it is straightforward to show that

$$ \Pr (\varepsilon_{1} ) = f_{{Y_{tail} (t)}} (z|N(t) = n) $$
(29)
$$ \Pr (\varepsilon_{2} ) = f_{{Y_{head} (t)}} (y|N(t) = n) $$
(30)
$$ \Pr (\varepsilon_{3} ) = \sum\limits_{m = 0}^{{\hbox{min} \left\{ {n - 1,\left\lfloor {y_{c} (t)/r} \right\rfloor } \right\}}} {\left( {\begin{array}{*{20}c} {n - 1} \\ m \\ \end{array} } \right)( - 1)^{m} } (1 - m\frac{r}{{y_{c} (t)}})^{n - 2} $$
(31)
$$ \Pr (\varepsilon_{4} ) = e^{ - \rho r} $$
(32)
$$ \Pr (\varepsilon_{5} ) = e^{ - \rho r} $$
(33)

Equation Pr(ɛ 3) which is given by (31), is completely depicted in [38, Lemma 1], which was used for the connectivity of random interval graph. Moreover, (31) is denoted in [53] as the probability of connectivity for the 1D linear VANET. In this model n vehicles, that are Poisson distributed, form a cluster with length of y c (t). By normalizing the connectivity distance y c (t) to 1 and, consequently, the radio range to r/y c (t), we have (31) from [38] and [53] where m is an integer, and. is the floor function. For the convenience let’s assume \( \left( {\begin{array}{*{20}c} {n - 1} \\ m \\ \end{array} } \right) = 0 \) for m > n − 1 [11]. Thus, the preceding summation is from m = 0 to y c (t)/r.

Events ɛ 1 and ɛ 2 define the minimum and maximum distances to the observer among n vehicles in the cluster. Assuming non-outgoing and nonstop scenarios of vehicle movement for the remaining n − 2 vehicles, and using event ɛ 3, it is guaranteed that all n vehicles are connected. Consequently, the connectivity length is at least y c (t) = y head (t) − y tail (t); because regarding to the events ɛ 4 and ɛ 5 there may exist some other vehicles within the radio range of the tail vehicle or head vehicle. As a result, the cluster length will be larger than the spatial distance between head and tail vehicles. Therefore, events ɛ 4 and ɛ 5 guaranty that connectivity distance is y c (t) = y head (t) − y tail (t) definitely. Let’s define \( f\left( {y_{c} \left( t \right), N\left( t \right) = n} \right) \) to be the probability that the connectivity distance lies in y c (t), and there are n vehicles in this connectivity. It is evident that:

$$ f(y_{c} (t),N(t) = n) = \Pr (\varepsilon_{1} ) \cdot \Pr (\varepsilon_{2} ) \cdot \Pr (\varepsilon_{3} ) \cdot \Pr (\varepsilon_{4} ) \cdot \Pr (\varepsilon_{5} ) $$
(34)
$$ \begin{aligned} &= f_{{Y_{tail} (t)}} (z|N(t) = n) \times f_{{Y_{head} (t)}} (y|N(t) = n) \hfill \\ & \quad \times \sum\limits_{m = 0}^{{\left\lfloor {y_{c} (t)/r} \right\rfloor }} {\left( {\begin{array}{*{20}c} {n - 1} \\ m \\ \end{array} } \right)( - 1)^{m} } (1 - m\frac{r}{{y_{c} (t)}})^{n - 2} \times e^{ - 2\rho r} \hfill \\ \end{aligned} $$
(35)

Equation (35) shows the pdf of connectivity regarding to y c (t) if and only if N(t) = n vehicles participate in forming the connectivity. Without loss of generality \( f\left( {c\left( t \right), N\left( t \right) = n} \right) \) can be defined as the pdf of connectivity for N(t) = n vehicles passing the observer regardless of exact connectivity distance. Since the necessary condition for the validation of this scenario is the occurrence of events \( \varepsilon_{1} ,\varepsilon_{2} ,\varepsilon_{3} \cdot f\left( {c\left( t \right), N\left( t \right) = n} \right) \) could be formulated as:

$$ f(c(t),N(t) = n) = \Pr (\varepsilon_{1} ) \cdot \Pr (\varepsilon_{2} ) \cdot \Pr (\varepsilon_{3} ) $$
(36)
$$ \begin{aligned} = f_{{Y_{tail} (t)}} (z|N(t) = n) \times f_{{Y_{head} (t)}} (y|N(t) = n) \hfill \\ \times \sum\limits_{m = 0}^{{\left\lfloor {y_{c} (t)/r} \right\rfloor }} {\left( {\begin{array}{*{20}c} {n - 1} \\ m \\ \end{array} } \right)( - 1)^{m} } (1 - m\frac{r}{{y_{c} (t)}})^{n - 2} \hfill \\ \end{aligned} $$
(37)

Moreover, f(N(t) = n, y c (t)) can be derived using Bayes’ formula. Equation (38) is the probability that n vehicle that pass an observer are connected at time t, and the connectivity distance is y c (t):

$$ f(N(t) = n,y_{c} (t)) = \frac{{f(y_{c} (t),N(t) = n) \cdot f(N(t) = n)}}{{f_{{y_{c} (t)}} (y_{c} (t))}} $$
(38)

Equation (38) is derived from (1), (35) and (39). If the connectivity consists of just one vehicle (where there are no neighbors in the vehicle’s radio range), the connectivity distance is 0, and the probability of this event is Pr(N(t) = 1) = e −ρr [11]. On the other hand, if the connectivity consists of more than one vehicle [with probability of Pr(N(t) ≥ 2) = 1 − e −ρr], then the pdf of connectivity with length of y c (t), independent of the connectivity size, is:

$$ f_{{y_{c(t)} }} (y_{c} (t)) = \frac{{\sum\limits_{n = 2}^{\infty } {f(y_{c} (t),N(t) = n)} }}{{p_{r} (N(t) \ge 2)}} $$
(39)

Moreover, f(N(t) = n, c(t)) can be derived using Bayes’ formula on (36). Compared with (38), (40) shows the probability that n vehicle that pass the observer will be connected at time t. It is obvious, according to ɛ 4 and ɛ 5 there may exist either some other slow vehicles in same direction that passed the observer during \( \left[ { - t ,0} \right) \), or vehicles in opposite direction and situated on radio propagation range of either tail vehicle (behind it) or head vehicle (in front of it). Hence (40) guaranties that the cluster length will be at least y c (t).

$$ f(N(t) = n,c(t)) = \frac{f(c(t),N(t) = n) \cdot f(N(t) = n)}{{f_{c(t)} (c(t))}} $$
(40)

When connectivity consists of more than one vehicle with probability of (1 − e −ρr), then the pdf of connectivity, independent of the number of vehicles, is:

$$ f_{c(t)} (c(t)) = \frac{{\sum\limits_{n = 2}^{\infty } {f(c(t),N(t) = n)} }}{{p_{r} (N(t) \ge 2)}} $$
(41)

4.2 Joint Poisson distribution

In this section probability of joint Poisson distribution for one direction of a VANET is investigated. For the sake of clarity, we consider a highway model including two lanes in each direction. Although, the proposed model can be easily extended to more lanes. Let’s consider that the spatial distribution of vehicles traveling in both lanes follows a homogeneous Poisson process with intensity ρ (veh/m). Without loss of generality we define ρ i as vehicle density of lane i, in which \( \sum\nolimits_{i = 1}^{2} {\rho_{i} = } \rho \). The probability that a vehicle travels in lane 1 or 2 is P 1 = ρ 1/ρ 1 + ρ 2 or P 2 = 1 − P 1 = ρ 2/ρ 1 + ρ 2 respectively where \( \sum\nolimits_{i = 1}^{2} {P_{i} = 1} \). Moreover, let N 1(t) = n 1 and N 2(t) = n 2 be the number of vehicles travelling in lane 1 and lane 2 at time t respectively. Therefore, the vehicle size is \( N(t) = N_{1} (t) + N_{2} (t). \) Moreover, N 1(t) and N 2(t) are independent Poisson variables with means ρ 1 ζ(t) and ρ 2 ζ(t) respectively. Hence, the joint Poisson distribution that exactly n 1 vehicles from lane 1 and n 2 vehicles from lane 2, at time t travel in a spatial distribution with length of \( \zeta \left( t \right) \) and mean ρζ(t) is:

$$ \begin{aligned}& \Pr \left\{ {N_{1} (t) = n_{1} ,N_{2} (t) = n_{2} } \right\} \\ & = \sum\limits_{m = 0}^{\infty } {\Pr \left\{ {N_{1} (t) = n_{1} ,N_{2} (t) = n_{2} |N(t) = m} \right\}\Pr \left\{ {N(t) = m} \right\}} \\ & = \Pr \left\{ {N_{1} (t) = n_{1} ,N_{2} (t) = n_{2} |N(t) = n_{1} + n_{2} } \right\} \\ & \quad \times e^{ - \rho \zeta (t)} \frac{{\rho \zeta (t)^{{n_{1} + n_{2} }} }}{{\left( {n_{1} + n_{2} } \right)!}} \\ \end{aligned} $$
(42)

Let’s assume that n 1 + n 2 vehicles at time t,  are Poisson distributed in a single direction of a road with intensity of ρ in a spatial distribution with length of ζ(t). Because each of these n 1 + n 2 vehicles independently belongs to lane 1 with probability P 1, the conditional probability that n 1 of vehicles are from lane 1 (and n 2 are from lane 2) is the binomial probability of n 1 successes in n 1 + n 2 trials. Therefore,

$$ \begin{aligned}& \Pr \left\{ {N_{1} (t) = n_{1} ,N_{2} (t) = n_{2} } \right\} \\ & = \left( {\begin{array}{*{20}c} {n_{1} + n_{2} } \\ {n_{1} } \\ \end{array} } \right)p_{1}^{{n_{1} }} p_{2}^{{n_{2} }} e^{ - \rho \zeta (t)} \frac{{\left( {\rho \zeta (t)} \right)^{{n_{1} + n_{2} }} }}{{\left( {n_{1} + n_{2} } \right)!}} \\ & = \frac{{\left( {n_{1} + n_{2} } \right)!}}{{n_{1} !n_{2} !}}p_{1}^{{n_{1} }} p_{2}^{{n_{2} }} e^{{ - \rho (t\zeta )p_{1} }} e^{{ - \rho \zeta (t)(1 - p_{1} )}} \\ & \quad\times \frac{{\left( {\rho \zeta (t)} \right)^{{n_{1} }} \left( {\rho \zeta (t)} \right)^{{n_{2} }} }}{{\left( {n_{1} + n_{2} } \right)!}} \\ & = e^{{ - \rho_{1} \zeta (t)}} \frac{{(\rho_{1} \zeta (t))^{{n_{1} }} }}{{n_{1} !}} \times e^{{ - \rho_{2} \zeta (t)}} \frac{{(\rho_{2} \zeta (t))^{{n_{2} }} }}{{n_{2} !}} \\ \end{aligned} $$
(43)

Equation (43) is factored into two products; one of which depends only on n 1 and other only on n 2. It is now clear that when each of a Poisson number of vehicles is independently classified as either belonging to lane 1 with probability P 1 = ρ 1/ρ 1 + ρ 2 or belonging to lane 2 with probability P 2 = 1 − P 1 = ρ 2/ρ 1 + ρ 2,  the numbers of vehicles from lane 1 and lane 2 are independent Poisson random variables.

The result of (43) could be further generalized to include a highway consisting of k lanes. Inside lane i vehicles are Poisson distributed with number of N i (t), and mean ρ i ζ(t), with the probability \( p_{i} i = 1, \ldots ,k \), \( \sum\nolimits_{i = 1}^{k} {P_{i} = 1} \). If N i (t) is the vehicle size of lane i, then N 1(t), …, N k (t) are independent Poisson random variables with respective means ρ 1 ζ(t),…, ρ k ζ(t). Therefore, the joint probability distribution of \( n = \sum\nolimits_{i = 1}^{k} {n_{i} } \) vehicles in k random lanes, in which Poisson distributed in a Euclidean distance of ζ(t) and mean ρζ(t), is

$$ \begin{aligned} &\Pr \left\{ {N_{1} (t) = n_{1} , \ldots ,N_{k} (t) = n_{k} } \right\} \\ & = \Pr \left\{ {N_{1} (t) = n_{1} , \ldots ,N_{k} (t) = n_{k} |N(t) = n} \right\}\Pr (N(t) = n) \\ & = \frac{n!}{{n_{1} ! \ldots n_{k} !}}p_{1}^{{n_{1} }} \cdots p_{k}^{{n_{k} }} e^{ - \rho \zeta (t)} \frac{{\left( {\rho \zeta (t)} \right)^{n} }}{n!} \\ \end{aligned} $$
(44)
$$ = \prod\limits_{i = 1}^{k} {e^{{ - \rho_{i} \zeta_{(t)} }} \frac{{\left( {\rho_{i} \zeta (t)} \right)^{{n_{i} }} }}{{n_{i} !}}} $$
(45)

4.2.1 Expected number of vehicles inside a lane in a multilane highway

As shown in Fig. 2, and like Sect. 4.2, let us consider a part of a highway with length of ζ(t) in which vehicles traveling in eastbound direction at time t. Conditional expected number of vehicles from lane 1, assuming that the total number of vehicles in this geographic region is \( N_{1} (t) + N_{2} (t) = n \), is given by

$$ E\left\{ {N_{1} (t)|N_{1} (t) + N_{2} (t) = n} \right\} = n\frac{{\rho_{1} }}{{\rho_{1} + \rho_{2} }} $$
(46)

Proof

$$ \begin{aligned} \Pr \left\{ {N_{1} (t) = k|N_{1} (t) + N_{2} (t) = n} \right\} \hfill \\ = \frac{{\Pr \left\{ {N_{1} (t) = k} \right\}\Pr \left\{ {N_{2} (t) = n - k} \right\}}}{{\Pr \left\{ {N_{1} (t) + N_{2} (t) = n} \right\}}} \hfill \\ \end{aligned} $$
(47)

where (47) is the result of assuming N 1(t) and N 2(t) are independent. Recalling that N 1(t) + N 2(t) has a Poisson distribution with mean ρ 1 ζ(t) + ρ 2 ζ(t),  the preceding equation could be expressed as:

$$ \begin{aligned} \Pr \left\{ {N_{1} (t = k|N_{1} (t) + N_{2} (t) = n} \right\} \hfill \\ = \frac{{e^{{ - \rho_{1} \zeta (t)}} \left( {\rho_{1} \zeta \left( t \right)} \right)^{k} }}{k!} \times \frac{{e^{{ - \rho_{2} \zeta (t)}} \left( {\rho_{2} \zeta (t)} \right)^{n - k} }}{(n - k)!} \hfill \\ \times \left[ {\frac{{e^{{ - (\rho_{1} \zeta (t) + \rho_{2} \zeta (t))}} (\rho_{1} \zeta (t) + \rho_{2} \zeta (t))}}{n!}} \right]^{ - 1} \hfill \\ = \frac{n!}{(n - k)!k!}\frac{{\left( {\rho_{1} \zeta (t)} \right)^{k} \left( {\rho_{2} \zeta (t)} \right)^{n - k} }}{{(\rho_{1} \zeta (t) + \rho_{2} \zeta (t))^{n} }} \hfill \\ = \left( {\begin{array}{*{20}l} n \hfill \\ k \hfill \\ \end{array} } \right)\left( {\frac{{\rho_{1} }}{{\rho_{1} + \rho_{2} }}} \right)^{k} \left( {\frac{{\rho_{2} }}{{\rho_{1} + \rho_{2} }}} \right)^{n - k} \hfill \\ \end{aligned} $$
(48)

In other words, the conditional distribution for expected number of vehicles traveling in lane 1, given that the total number of vehicles is \( N_{1} (t) + N_{2} (t) = n \), is a binomial distribution with parameters n and ρ 1/ρ 1 + ρ 2 expressed as:

$$ E\left\{ {N_{1} (t)|N_{1} (t) + N_{2} (t) = n} \right\} = n\frac{{\rho_{1} }}{{\rho_{1} + \rho_{2} }} $$
(49)

Moreover, the tail probability of the expected number of vehicles from lane 1, \( {\text{N}}_{1} (t) \) (i.e., the probability that at least \( {\text{k}} \) vehicles are inside lane 1), assuming that \( {\text{N}}_{1} (t) + {\text{N}}_{2} (t) = {\text{n}} \), is given by:

$$ \begin{aligned} \Pr \left( {N_{1} (t) \ge k|N_{1} (t) + N_{2} (t) = n} \right) \hfill \\ = 1 - \sum\limits_{j = 0}^{k} {\left( {\begin{array}{*{20}c} n \\ j \\ \end{array} } \right)\left( {\frac{{\rho_{1} }}{{\rho_{1} + \rho_{2} }}} \right)^{j} \left( {\frac{{\rho_{2} }}{{\rho_{1} + \rho_{2} }}} \right)^{n - j} } \hfill \\ \end{aligned} $$
(50)

Consider that vehicles traveling in a k lane highway with size of \( N_{1} (t) + \cdots + N_{k} (t) = n \). Using (44) the conditional expected number of vehicles in each lane has a multinomial distribution with parameters (n, p 1, …, p k ). Consequently the conditional expected size of lane 1 in a k lane highway could be expressed as:

$$ \begin{aligned} E\left\{ {N_{1} (t)|N_{1} (t) + \cdots + N_{k} (t) = n} \right\} \hfill \\ = np_{1} = n\frac{{\rho_{1} }}{{\rho_{1} + \cdots + \rho_{k} }} \hfill \\ \end{aligned} $$
(51)

5 Simulation analysis

To check the validity and accuracy of our analytical results, using MATLAB (similar to previous research done in [13, 21]) an interrupted 1-D highway is simulated. The simulation assumes that, at any time slot, the spatial distribution of the vehicles on the road remains a homogeneous Poisson process with intensity ρ veh/m. The simulation closely tracks the unidirectional highway in which n vehicle following Poisson arrival with intensity λ veh/s passing an observer located in H 0. In the rest of this paper, in order to configure the simulations, similar to the related publications, the following assumptions are made: The radio propagation range is r =  250 m [36], the average vehicle speed is E[v] = 25 m/s, the standard deviation σ = 7.5 m/s [11], the time slot τ = 5 s [11] and the simulation time is t = 2000 s up to t = 8000 s. Simulation results depicted in the figures are obtained from averaging across 100 iterations.

It should be noted that vehicular connectivity through the simulation area can be implemented independent of complicated V2V interactions. In such a dynamic network, when the intervehicle distance is not larger than the radio range, V2V communication is provided. In other words, implementing the connectivity through the simulation can be studied based on the vehicular spatial distribution. As a result, we utilize our simulation platform similar to previous research done in [11, 27, 41] and [54–56]. In this paper using MATLAB, regardless of physical and MAC layer complexities, a simple VANET environment is implemented.

Figure 3 captures the analytical and simulation results for the tail probability of intervehicle distances over two choices of traffic flows with the intensity of ρ =  0.015 and 0.020 veh/m. Simulations results, when averaged over 100 simulations, closely follow the predicted behavior of the analytical model. In this figure the average intervehicle distance is 1/ρ (i.e. ≈66, 50 m for two mentioned Poisson intensity, respectively). Note that a large Euclidean intervehicle distance results in a large tail probability of intervehicle distance.

Fig. 3
figure 3

Tail probability of the intervehicle distance

Full size image

Considering a vehicle intensity of λ = 0.3 veh/s, spatial distribution of vehicles follows a homogeneous Poisson process with intensity of \( \rho = \lambda \int_{ - \infty }^{\infty } {\left( {f_{v} \left( v \right)/v} \right)dv = 0.012{\text{ veh}}/{\text{m}}} \) (i.e. a low traffic density). Figure 4 illustrates the pdf of connectivity. This figure compares the prediction of our analytical model to the behavior obtained from the simulations results when r, the radio propagation range, is 250 m. As expected, for a small cluster size, the pdf of connectivity is large. However, when the cluster size increases the pdf of connectivity decreases. In our model, at the beginning of each time interval, the speed of each vehicle can vary. Moreover, this change in the speed is independent of other vehicles as well as other time intervals. In the result of the speed variation, connectivity interruption may occur, resulting in adjacent vehicles losing connection.

Fig. 4
figure 4

Pdf of connectivity

Full size image

Using an invariable traffic flow of ρ = ρ 1 + ρ 2 = 0.06 veh/m, the simulation and analytical results for the tail probability of the expected number of vehicles of lane 1 for a two-lane highway is shown in Fig. 5. For this purpose, vehicle intensity of lane 1 is ρ 1 =  0.004, 0.006 and 0.008 veh/m. It is evident that the tail probability of three mentioned values decreases as the number of vehicles in lane 1 increases. Moreover, for a given vehicle count, increasing the Poisson intensity increases the related tail probability.

Fig. 5
figure 5

Tail probability of the expected number of vehicles in lane 1

Full size image

In practice different lanes of a highway follow a heterogeneous mobility pattern. These differences in vehicular movability is mainly because of the differences in the speeds of vehicles (e.g. cars move fast but trucks and buses move slow) and/or difference in type of vehicles (e.g. bus and truck movements not allowed in lane 1). According to this, we consider a time-varying vehicular speed assumption for single direction of a two-lane highway in which traffic flow of lanes dynamically vary, however the highway’s Poisson intensity remains constant (i.e. ρ = ρ 1 + ρ 2 =  0.03 veh/m). Figure 6 shows the variations of the expected number of vehicles inside lane 1 over three choices of traffic flows with intensity of ρ 1 =  0.006, 0.008 and 0.01 veh/m. When the number of vehicles travelling in the same direction varies from 10 to 100 veh, the expected number of vehicles in both lane 1 and 2 varies accordingly. Because the Poisson intensity of the highway remains constant, if the expected number of vehicles of lane 1 increases, the expected number of vehicles of lane 2 decreases.

Fig. 6
figure 6

Expected connectivity size of lane 1

Full size image

Figure 7 shows expected number of vehicles inside a lane in a VANET based on Poisson intensity variations. In this simulation 200 vehicles travel in a two-lane highway on eastbound direction. The spatial distribution of the vehicles inside lane 1 follows a heterogeneous Poisson process with density ρ 1 = 0.002 veh/m that increases to ρ 1 = 0.06 veh/m. As depicted in Fig. 7, when the traffic flow of lane 1 increases, the expected number of vehicles in lane 1 among N = 200 veh also increases. The analytical and simulation results are shown for two different traffic flows of lane 2 (i.e. ρ 2 =  0.002 and 0.004 veh/m). If the vehicle intensity of lane 2 increases, the expected number of vehicles in lane 1 decreases.

Fig. 7
figure 7

Expected number of vehicles in lane 1 based on Poisson intensity variations

Full size image

To investigate the joint Poisson distribution in a VANET we simulate single direction of a highway in which 100 vehicles following Poisson process travel in two lanes with density of ρ = ρ 1 + ρ 2 =  0.004 veh/m. Figure 8 shows the analytical and simulation results of joint Poisson distribution in a spatial distribution with a length of ζ(t) (i.e. joint Poisson spatial distribution). As mentioned earlier, in our model, time is equally slotted and at the beginning of each time interval speed variation is allowed. As a result, vehicles move faster/slower independent of other vehicles as well as other times. Whenever Poisson intensity of eastbound direction is equal to ρ = ρ 1 + ρ 2 =  0.004 veh/m, the expected intervehicle distance is 1/ρ = 250 m. As depicted in Fig. 8, whenever the number of vehicles is N = 100 veh, simulation and analytical results confirm that the maximum joint Poisson distribution belongs to the spatial distribution with a length of ζ(t) = 25,000 m. The results in Fig. 8 are depicted based on three choices of Poisson intensity for ρ 1 and ρ 2 consisting of (ρ 1, ρ 2) = (0.002, 0.002), (0.001, 0.003) and (0.0005, 0.0035) in which the spatial distribution of the vehicles on the road for these three scenarios is equal and remains a homogeneous Poisson process with density ρ = ρ 1 + ρ 2 =  0.004 veh/m. The minimum probability belongs to the scenario that both lanes have equal Poisson intensities. As the intensity difference of the traffic flows in two lanes increases, the difference in the number of vehicles in two lanes also increases; moreover, the joint Poisson distribution increases accordingly.

Fig. 8
figure 8

Variations of joint Poisson distribution based on three different traffic flows where \( \rho = \rho_{1} + \rho_{2} = 0.004\,{\text{veh}}/{\text{m}} \), the analytical (Ana) and simulation (Sim) results are shown

Full size image

Figure 9 illustrates the variation in spatial distribution, ζ(t) given that N = 200 vehicles following Poisson process travel in two different lanes in an equal direction with Poisson intensity of ρ 1 = ρ 2 = 0.001, 0.0015, and 0.002 veh/m in three different scenarios. As depicted in Fig. 9, if the vehicle intensity (i.e. ρ = ρ 1 + ρ 2) increases, the intervehicle distance and therefore the spatial distribution decreases. Considering the simulation time of t = 8000 s, and time varying vehicular speed assumptions of v min  = 20 m/s and v max  = 30 m/s the analytical results perfectly match the simulation results.

Fig. 9
figure 9

Variations of vehicular spatial distribution based on variations in traffic flow

Full size image

In Fig. 10, in order to investigate the joint Poisson distribution of a single direction of a free-flow highway, it is assumed that 100 vehicles following the Poisson process travel in two different lanes on equal direction with intensity of (ρ 1, ρ 2) = (0.001, 0.002), (0.001, 0.003) and (0.001, 0.004) in three different test scenarios. As depicted in Fig. 10, when the eastbound traffic flow is ρ = ρ 1 + ρ 2 =  0.003 veh/m, the maximum joint Poisson distribution belongs to the spatial distribution with length of ζ(t) = 33,000 m. But whenever the traffic flow increases (e.g. ρ =  0.004 veh/m), the maximum joint Poisson distribution also increases (i.e. belongs to the spatial distribution with length of ζ(t) = 25,000 m). As expected, if the traffic flow increases, the vehicular spatial distribution noticeably decreases. Figure 10 illustrates that the predicted behavior from the analytical model closely tracks the simulation results.

Fig. 10
figure 10

Variations of joint Poisson distribution and spatial distribution based on three choices of ρ 2. Traffic flow in lane 1 is constant (i.e. ρ 1 =  0.001 veh/m) and vehicle size is N = 100 veh

Full size image

We showed that if the traffic flow of at least one lane varies, the joint Poisson distribution also varies. In Fig. 11, we investigate the impact of the number of vehicles on joint Poisson distribution in a highway where N = 200 vehicles following poisson process travel in two different lanes on equal direction with Poisson intensity of (ρ 1, ρ 2) = (0.0025, 0.002), (0.0026, 0.002) and (0.0027, 0.002) in three different simulations. Whenever the vehicle intensity of lane 1 increases, the number of vehicles traveling in this lane among N = 200 veh increases too. However, it is interesting to note that joint Poisson distribution decreases slightly.

Fig. 11
figure 11

Variations of joint Poisson distribution and number of vehicles inside lane 1 based on traffic flow of lane 1

Full size image

In Fig. 12, unlike the assumption made in Fig. 11, the Poisson intensity of lane 1 is constant (i.e. ρ 1 = 0.001 veh/m). In this situation, variations in the probability of joint Poisson distribution and also the number of vehicles in lane 1 are determined based on changes in vehicle intensity of lane 2 (i.e. ρ 2 = 0.00230, 0.00235, and 0.00240 veh/m). This is straightforward to show that by increasing the traffic flow of lane 2 the expected number of vehicles from lane 1 among N = 200 veh, decreases. Moreover, the probability of joint Poisson distribution slightly decreases. This is because the difference between the traffic flow of lane 1 and lane 2 increases.

Fig. 12
figure 12

Variations of joint Poisson distribution and number of vehicles in lane 1 based on traffic flow of lane 2

Full size image

As indicated in Fig. 12, simulation results are in line with the predicted behavior of our analytical model. In this experiment, simulation time is set to t = 2500 s, minimum speed is set to 20 m/s, maximum speed is set to 30 m/s, time is equally slotted and speed variation is allowed at the beginning of each interval.

Figure 13 shows the impact of variation in vehicle size on joint Poisson distribution in three different scenarios corresponding to the choices of N = 200, 210, and 220 veh. Vehicles following the Poisson process travel in two different lanes in an equal direction with equal intensity of ρ 1 = ρ 2 = 0.002 veh/m. It is clear that by increasing the total number of vehicles from N = 200–220 veh, the expected number of vehicles travelling in these two lanes increases uniformly. As shown in Fig. 13, when the vehicle size of lane 1 is N 1 = 100 veh, the maximum joint Poisson distribution is 0.0014, i.e. belongs to scenario that the total number of vehicles is N = 200 veh. In other words, whenever the vehicle intensity in both of lane 1 and 2 remains equal, the joint Poisson distribution confirms that the number of vehicles traveling in these two lanes is similar.

Fig. 13
figure 13

Variations of joint Poisson distribution and number of vehicles inside lane 1 based on total number of vehicles

Full size image

Conditional probability of vehicle size of lane 1 based on two different Poisson intensity (i.e. ρ 1 = 0.001, 0.002 veh/m), is shown in Fig. 14. According to this, N = 100 vehicles following Poisson process travel in two different lanes in an equal direction with Poisson intensity of ρ = ρ 1 + ρ 2 = 0.004 veh/m. If the traffic flow of lane 1 increases, the number of vehicles in this lane among N = 100 vehicles also increases. However, the related conditional probability of the number of vehicles in this lane decreases noticeably. This is acceptable because compared with lane 2, the vehicle intensity of lane 1 is sparse. On the other hand, by increasing the Poisson intensity of lane 1, the related conditional probability of number of vehicles in this lane increases. Using determined Poisson intensity for a 1-D two lane highway through at least 100 simulations and duration time of t = 2000 s, a minimum speed of 20 m/s and a maximum speed of 30 m/s, simulation results confirm the accuracy of the analytical model.

Fig. 14
figure 14

Conditional probability of number of vehicles in lane 1

Full size image

6 Conclusion and future work

In this paper, we proposed an analytical model for measurement of connectivity. In suggested formulations, we considered a single direction of a free-flow highway in which n vehicles were Poisson distributed, and passed an observer with different speeds. The proposed model used a time-varying vehicular speed assumption that allowed vehicles to change their speed independent of the other vehicles as well as the other time intervals. To the best of our knowledge this is the first work that mathematically analyzed the connectivity distance based on the temporal mobility of head, tail and intermediate vehicles inside a cluster over a time-varying vehicular speed environment. According to this we proposed an accurate analytical model for calculating the pdf of connectivity. Then, the joint Poisson distribution of vehicles in a multilane highway, the expected number of vehicles and also the tail probability of the expected number of vehicles inside a lane in a multilane highway were mathematically investigated. We validated the accuracy of the proposed model through extensive simulations.

The model developed in this study can be easily extended to determine the connectivity measurements between vehicles traveling in opposite directions of a free-flow highway. We believe this fundamental work can provide a novel insight for further development of VANETs.

Our future research includes extending the proposed model using other simulation platforms such as NS2/3 and a VANET simulator written in C++ [57]. Furthermore, additional optimizations and further enhancements for connectivity related measurement will be planned, such as taking into account employing metaheuristic algorithms, queuing and game theory, fuzzy logic and other schemes (i.e. utilized in many kind of wireless networks [58–66]).