1 Introduction

Water distribution networks (WDNs) are continuously exposed to numerous factors that affect distribution service sustainability and lead to component deterioration. This deterioration can increase operating and maintenance costs, increase water losses, and reduce service quality. Factors that influence pipe deterioration can be classified into three categories: intrinsic pipe factors (e.g., diameter, material, and age), environmental factors (e.g., weather, soil, and hydrogeological conditions), and operational factors (e.g., pressure and previous failure) (Barton et al. 2019). Most previous studies have focused on the age, pipe materials, and surrounding conditions (type of soil and temperature) as factors contributing to breaks in WDNs (Rezaei et al. 2015).

Leaks and breaks represent the two basic types of pipe deterioration. Leaks are small holes or cracks that allow water to slowly escape from active supply pipes. Liemberger and Wyatt (2018) estimated that the global volume of such “non-revenue” water was 126 billion cubic meters a year. In Montreal, Canada, water losses through the distribution system account for approximately 30% of the water volume produced (Ville de Montreal 2022). This suggests that preventing leaks could help to save large quantities of water, the waste of which is a global concern in the context of climate change, particularly in regions already facing water shortages. Based on the recommendations of the American Water Works Association (AWWA), the actions normally implemented by governments and WDN managers to reduce water loss through leaks and breaks comprise a combination of active leakage control, asset management, rapid high quality repair, and pressure management (AWWA 2016). Breaks are complete pipe failures that result in loss of service. Pipe breaks are often used as indicators of the structural condition of a WDN (Mailhot et al. 2003). In 2023, the pipes with the highest break rates in Canada and the USA were made of cast iron, which had a break rate nearly ten times higher than that of PVC (Barfus 2023).

Among the operating factors affecting the deterioration of water pipes, frequent variations in pressure and overpressure lead to a higher frequency of leaks (Lambert 2001; Savic and Walters 1995), and when combined with other factors (e.g., pipe corrosion, defects in manufacturing, and material), higher pressure increases the probability of breaks in WDN pipes (Barton et al. 2019). Indeed, when a pipe material is degraded owing to corrosion or other factors, the stress imposed by cyclic pressure fluctuations on cracks can cause pipe breaks (Rezaei et al. 2015). Furthermore, previous investigations on the relationship between the operating pressure and pipe break rate have shown that a decrease in pressure reduces the probability of pipe breaks. Konstantinou et al. (2024) applied a random forest model to relate the total number of water pipe breaks to various operational factors; the mean pressure and pressure variation (amplitude and frequency) were found to exhibit the best fit with the observed number of breaks. Akbarkhiav and Imteaz (2021) reported a strong relationship between the pipe break rate and a pressure index integrating the number of service connections in predefined pressure ranges. Martínez-Codina et al. (2015a) used data from four district metered areas (DMAs) in Madrid, Spain, to identify a threshold above which a small increase in the maximum pressure could lead to a significant increase in the probability of pipe breaks. This probabilistic approach, based on Bayes’ theorem, used pipe break data and pressure measurements to estimate the cumulative distribution functions (CDFs) of the maximum pressure values under normal operating conditions and when they coincide with a recorded pipe break. The probability ratio (PR) was subsequently computed as the ratio of the break-conditional CDF to the unconditional CDF of maximum pressure in six equal intervals. The maximum pressure threshold was defined as the first maximum pressure interval in which the conditional probability value exceeded the unconditional probability value. Martínez-Codina et al. (2015a) suggested that the threshold values should be updated according to the age and level of pipe deterioration. Moslehi and Jalili_Ghazizadeh (2020) also applied Bayes’ theorem to two groups of pipes sharing the same material (ductile iron or polyethylene) in a large zone of the WDN of Tehran, Iran. The number of annual recorded pipe breaks and annual maximum pressure corresponding to the maximum hourly average pressure over a specific time window (set to 24 h), were used to develop a break rate function for different pipe materials using the maximum pressure as the independent variable. Similar to the method applied by Martínez-Codina et al. (2015a), Moslehi and Jalili_Ghazizadeh (2020) determined the maximum pressure threshold by comparing the unconditional and break-conditioned CDFs of the maximum pressure range associated with each material; they divided this range into 17 equal intervals and calculated the PR for each. The first maximum pressure interval exceeding PR = 1 was identified as the maximum pressure threshold for that pipe material. The results indicated that the maximum pressure threshold for ductile iron pipes was greater than that for polyethylene pipes. Finally, Jara-Arriagada and Stoianov (2021) developed a model for predicting pipe breaks based on logistic regression using polynomial terms. They estimated the probabilities of breaks according to different pressure variations and subsequently identified the influence of the pressure variation on the probability of pipe break occurrence using a sensitivity analysis combined with machine learning. The results indicated that a decrease of 20 m in the mean pressure led to a reduction of 18% and 30% in the rate of breaks for asbestos cement and cast iron pipes, respectively.

Owing to the scarcity of reported data and the difficulty of collecting pressure measurements, few studies have quantitatively investigated the influence of pressure on pipe breaks using actual pressure data. Instead, the pressure values used in most previous pipe break modeling studies were estimated from hydraulic simulation models based on uncertain parameters, including demand and pipe roughness; therefore, considerable uncertainty is associated with these results (Ghorbanian et al. 2016). Pressure indicators were calculated by Martínez-Codina et al. (2015a, 2015b) and Moslehi and Jalili_Ghazizadeh (2020) by exploiting the water pressure time series recorded at a single point in their respective studied DMAs. For the former, this specific point was the entry point of the DMA; for the latter, it was a point where pressure variations could represent the average of the area under study.

Furthermore, most previous studies have investigated the influence of operating pressure on the occurrence of pipe breaks by first assuming a specific pressure covariate as the most significant indicator. However, Martínez-Codina et al. (2015b) compared the impacts of seven pressure indicators (maximum pressure, minimum pressure, average pressure, pressure range, pressure variability, pressure change, and pressure change rate) calculated for different time windows (between one and five days) on the occurrence of pipe breaks to determine which was the most influential. Their methodology was based on the comparison of a CDF conditioned on pipe breaks with 100 CDFs obtained from random sets for each pressure indicator. The results indicated that the pressure range indicator had the most significant influence on pipe breaks.

The primary objective of this study was to identify the pressure covariates that have a significant impact on pipe breaks. In contrast to previous studies, in which pressure was either measured over a short period that covered only a small portion of historical pipe break records (Konstantinou et al. 2024), simulated with a hydraulic model that did not rely on pressure measurements (Jara-Arriagada and Stoianov 2021), or considered globally for a DMA but not for each pipe (Akbarkhiav and Imteaz 2021; Moslehi and Jalili_Ghazizadeh 2020; Martínez-Codina et al. 2015a, 2015b), the proposed methodology relies on the estimation of pressure covariates for all pipes of a specific water DMA based on pressure and flow rate measurements taken at the supply and outlet junctions of that DMA.

2 Case Studies

Two datasets from two DMAs (designated as Zones A and B for confidentiality reasons) of Quebec City’s WDN were used for the analyses presented in this paper. The first dataset contained a record of pipe breaks recorded from 1987 to 2020 as well as the installation date, length, diameter, and material of all pipes in the DMAs. The second dataset included recorded 15-min measurements of water pressures and flow rates at the inlets and outlets of each DMA from 2015 to 2021. Representations of the two studied DMAs in the EPANET software are presented in Fig. 1 along with the locations of their inlets and outlets. The figure shows that water is supplied by three inlets for Zone A and two inlets for Zone B, and that Zone A has four outlets and Zone B has two outlets. Notably, Zone B contains two multifunctional junctions that behave as inlets or outlets according to the water consumption balance. All input and output junctions are equipped with measurement sensors for flow rate and pressure, except for outlets G and H in Zone B, which only contain flow rate sensors (i.e., no pressure data were recorded at these two outlets).

Fig. 1
figure 1

EPANET models of a) Zone A and b) Zone B

Full size image

The primary characteristics of Zones A and B are listed in Table 1. Zone B is larger than Zone A in terms of the number of pipes and total pipe length. In addition, Zone B is older, with 63% of its pipes over 40 years old, compared to 54% in Zone A.

Table 1 Physical characteristics of the studied DMAs
Full size table

From 2015 to 2020, the average recorded number of annual breaks was 15 and 67 in Zones A and B, respectively, corresponding to 0.3 and 0.4 breaks/year/km, respectively.

3 Methods

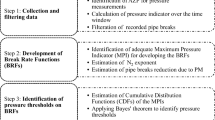
The pressure time series at the inlets and the input and output flow rates measured in the two DMAs every 15 min were used to run successive hydraulic simulations and obtain the pressure in each pipe in 15-min time steps. These calculated pressures were subsequently applied to estimate the pressure indicators for each pipe. Finally, five pipe break models were calibrated with different pressure covariates and the statistical significance of these covariates was assessed using a likelihood ratio test. As shown in Fig. 2, the associated methodology comprises four primary steps.

  1. 1.

    Cleaning and preparing data: First, the outliers in the database of recorded pressures and flow rates were detected and removed or modified.

  2. 2.

    Hydraulic simulations: For each 15-min step, the pressures at water supply junctions, flow rates at water outlet junctions, and water demands were attributed to the corresponding water network elements. A hydraulic simulation was subsequently executed using the EPANET 2.2 software (Rossman et al. 2020) to compute the pressures at all nodes, based on which the pressure indicators were calculated for each pipe in the water network.

  3. 3.

    Calibration of the pipe break model: Based on the pipe break records, two different pipe break models were calibrated by maximizing their likelihood functions. One model had no pressure covariates; the other included a single pressure covariate.

  4. 4.

    Likelihood ratio test: The two pipe break models were compared based on the ratio between their respective maximum likelihood function values.

Fig. 2
figure 2

Flowchart describing the applied pipe break analysis methodology

Full size image

The Python programming language was used to implement all steps of the proposed methodology.

3.1 Data Cleaning

Outliers in the water pressure (P) and water flow rate (Q) time series were identified as values outside the following limits:

$${Ul=Q}_{3}+ 1.5\text{ IQR }; {Ll=Q}_{1}- 1.5 IQR$$

where \(Ul\) denotes the upper limit, \({Q}_{1}\) denotes first quartile value, \({Q}_{3}\) denotes the third quartile value, \(IQR ={Q}_{3}-{Q}_{1},\text{ and }Ll\) denotes the lower limit.

Each identified outlier i was removed or modified according to the following conditions:

  1. 1.

    For an outlier Q[i] (P[i]), if Q[i + 1] (P[i + 1]) or Q[i-1] (P[i-1]) were also defined as outliers, then all measurements for both Q and P in this time step were removed.

  2. 2.

    Otherwise, Q[i] was defined as mean(Q[i + 1], Q[i-1]) and P[i] was defined as mean(P[i + 1], P[i-1]).

3.2 Hydraulic Simulations

The pressure in each pipe in the studied DMAs must be known to compute the pressure covariates of the pipe break model. Because the monitored pressure values are only available at the inlet and outlet junctions of the DMAs, the pressure in each pipe was computed using the EPANET 2.2 software (Rossman et al. 2020) in 15-min time steps. The pressures at the upstream junctions and the inlet and outlet flow rates were used to run these hydraulic simulations, and the monitored pressures at the downstream junctions were compared to the corresponding calculated pressures to validate the model.

The upstream monitored pressure values were included in the EPANET model as fixed-level reservoirs. As there were no flowmeters for consumers in the studied DMAs, the demand at each node was computed based on the initial water demand values in the EPANET model. As the EPANET models provided by the City of Quebec contain the demands at each node for an average day of water consumption, the sum of the water demands at each node e, \({Q}_{e}\), for this average day was used to calculate the demand weighting factor, \({p}_{e}\), for that node. This factor represents the portion of total water consumed, \({Q}_{t}\), at node e in a DMA containing K nodes. The corresponding equations are:

$${Q}_{t}=\sum_{e=1}^{K}{Q}_{e}$$
$${p}_{e}=\frac{{Q}_{e}}{{Q}_{t}}$$

Thus, for each simulation, the demand value assigned to node e at time ts, \({Q}_{e,{t}_{s}}\), was computed from the total measured flow rate of water consumed in the DMA at time ts, \({Q}_{C,{t}_{s}}\), as follows:

$${Q}_{e,{t}_{s}}={p}_{e}{Q}_{C,{t}_{s}}$$

where \({Q}_{C,{t}_{s}}=\sum {Q}_{I,{t}_{s}}-\sum {Q}_{O,{t}_{s}}\), in which \({Q}_{I,{t}_{s}}\) denotes the total input water flow rate for the DMA at time ts and \({Q}_{O,{t}_{s}}\) denotes the total output water flow rate from the DMA at time ts.

Successive EPANET simulations (one in each 15-min time step) were performed using the Python Water Network Tool for Resilience (Klise et al. 2018). The Python script was based on a “for” loop that first assigned the corresponding water demand at each node and water elevation at each reservoir, then ran a hydraulic simulation for that time step and saved the results.

3.3 Hydraulic Model Validation

The hydraulic model was validated by analyzing the relative root mean square deviation (RRMSE) between the observed and simulated pressures at each outlet junction. The RRMSE was calculated for each year z of the recorded period as follows:

$$\%RRMSE = \frac{\sqrt{\frac{{\sum }_{{t}_{s}=1}^{m}{ ({\widehat{P}}_{{t}_{s}}-{P}_{{t}_{s}})}^{2}}{m}}}{\overline{{P }_{{t}_{s}}} } x100$$

where \({\widehat{P}}_{{t}_{s}}\) is the simulated pressure at time ts, \({P}_{{t}_{s}}\) is the measured pressure at time ts, m is the number of simulation time steps, and \(\overline{{P }_{{t}_{s}}}\) is the mean observed pressure.

3.4 Pressure Covariates

For a DMA containing N pipes, the pressure covariates for each pipe j were computed as the mean of the corresponding covariates at the upstream and downstream nodes of that pipe. Because the pipe breaks were recorded in one-year time steps (i.e., only the year of occurrence of the break and its location were known), the pressure covariates listed in Table 2 were also calculated for a one-year time step.

Table 2 Annual and mean pressure covariates for a pipe
Full size table

The stationarity of the annual covariates (Table 2) for the recording period was tested using the Mann–Kendall test; only the pressure covariates that exhibited a non-significant trend in their annual values were retained. Finally, the pressure covariates selected for inclusion in the pipe break model were provided as average annual values over the recording period, as listed in Table 2.

3.5 Pipe Break Model

Barton et al. (2022) provided an exhaustive review of statistical pipe failure models for drinking water networks. They noted that available pipe failure records were typically short, potentially precluding the development of reliable pipe break models. Mailhot et al. (2000) and Pelletier (2000) developed a statistical method to model the evolution of pipe breaks in WDNs by considering breaks that could have occurred before the beginning of the historical pipe break record. Their model was based on two statistical distributions: a Weibull distribution to model the time of appearance of the first break following the installation date of a pipe and an exponential distribution to model the time between subsequent breaks. This model was applied to estimate the evolution of pipe breaks in a WDN and thereby evaluate proposed replacement scenarios (Pelletier et al. 2003). Mailhot et al. (2000) and Pelletier (2000) also proposed other models comprising various combinations of these two distributions, including the Weibull–exponential–exponential (WEE) and Weibull–Weibull–exponential models. However, explanatory variables other than the pipe age were not considered in these models. Toumbou et al. (2014) developed a pipe break model incorporating additional explanatory variables based on the WEE model by Mailhot et al. (2000). This pipe break model, which was applied in the present study, combines a Weibull distribution to model the time elapsed between the pipe installation date and its first break with a first exponential distribution associated with the time between the first and second breaks and a second exponential distribution linked to the time between subsequent breaks. Notably, the WEE model facilitates estimations of the influences of various factors (e.g., pipe diameter, length, and material, pressure, etc.) on the occurrence of breaks.

According to Toumbou et al. (2014), the average number of breaks for a pipe between T and T + DT, \(\mu \left(T,T+DT\right)\), can be computed using the WEE model as follows:

$$\mu \left(T,T+DT\right)=\left(\frac{{k}_{3}}{{k}_{2}}-1\right)\left\{\left[{e}^{-{k}_{2}\left(T+DT\right){e}^{x\beta }}-{e}^{-{k}_{2}T{e}^{x\beta }}\right]Int0+{e}^{-{k}_{2}\left(T+DT\right){e}^{x\beta }}Int1\right\}-{k}_{3}{e}^{x\beta }Int2 +{k}_{3}DT{e}^{x\beta }+\left(\frac{{k}_{3}}{{k}_{2}}-2\right)\left[{F}_{1}\left(T+DT\right)-{F}_{1}\left(T\right)\right]$$

where

$$Int0={\int }_{t{^{\prime}}_{1}=0}^{T}{f}_{1}\left(t{^{\prime}}_{1}\right){e}^{{k}_{2}t{^{\prime}}_{1}{e}^{x\beta }}dt{^{\prime}}_{1};Int1={\int }_{{t}_{1}=0}^{T+DT}{f}_{1}\left({t}_{1}\right){e}^{{k}_{2}{t}_{1}{e}^{x\beta }}d{t}_{1}; Int2={\int }_{{t}_{1}=T}^{T+DT}{F}_{1}\left({t}_{1}\right)d{t}_{1}$$

and x is the covariate vector, β is the covariate coefficient vector, t is the time, ki and pi are scalar parameters of distribution i, and F1 and f1 are the survival and probability density functions of the Weibull distribution, respectively, given by:

$${F}_{1}={e}^{-{\left({k}_{1}t{e}^{x.\beta }\right)}^{{p}_{1}}}$$
$${f}_{1}={p}_{1}{k}_{1}{e}^{x.\beta }{\left({k}_{1}t{e}^{x.\beta }\right)}^{{p}_{1}-1}{e}^{-{\left({k}_{1}t{e}^{x.\beta }\right)}^{{p}_{1}}}$$

The values of parameters k1, p1, k2, and k3 were estimated during the calibration of the WEE model, which was performed by maximizing its likelihood function using the historical record of pipe breaks. The covariates included in vector x were those linked to pressure (\({\overline{P}}_{{j}_{max}}\), \({\overline{P}}_{{j}_{mean}}\), \({\overline{P}}_{{j}_{var}}\), \({\overline{M}}_{j}\), and \({\overline{L}}_{j}\), as defined in Table 2), which were considered successively, whereas the other covariates were linked to pipe physical characteristics (diameter, length, and material).

3.6 Calibration of Pipe Break Model

The WEE model was calibrated by maximizing the natural logarithm of its likelihood function (Pelletier 2000; Mailhot et al. 2000; Toumbou et al. 2014) as follows:

$$\begin{array}{c}\mathit{ln}\left(L\right)=\sum_{i=1;{n}_{i}=0}^{N}\mathit{ln}\left[{P}_{i}\left(0\right)\right]+\sum_{i=1;{n}_{i}=1}^{N}\mathit{ln}\left[{P}_{i}\left(1\right)\right]+\sum_{i=1;{n}_{i}\ge 2}^{N}\mathit{ln}\left[{P}_{i}\left({n}_{i}\right)\right]\\ =\sum_{i=1;{n}_{i}=0}^{N}\mathit{ln}\left\{{e}^{-{\left({k}_{1}{T}_{a}{e}^{x.\beta }\right)}^{{p}_{1}}}+\left[1-{F}_{1}\left({T}_{b}\right)\right]{e}^{-{k}_{3}\left({T}_{a}-{T}_{b}\right){e}^{x.\beta }} +\left[{e}^{-{k}_{2}{T}_{a}{e}^{x.\beta }}-{e}^{-{k}_{2}{T}_{b}{e}^{x.\beta }}{e}^{-{k}_{3}\left({T}_{a}-{T}_{b}\right){e}^{x.\beta }}\right]Int0\right\} \\ +\sum_{i=1;{n}_{i}=1}^{N}\text{ln}\left\{{f}_{1}\left({t}_{1}\right){e}^{{k}_{2}{t}_{1}{e}^{x\beta }}{e}^{-{k}_{2}{T}_{a}{e}^{x\beta }}+{k}_{3}{e}^{x\beta }{e}^{-{k}_{3}\left({T}_{a}-{T}_{b}\right){e}^{x.\beta }}\left[1-{F}_{1}\left({T}_{b}\right)\right]\right.\\ \left.+{e}^{x.\beta }{e}^{-{k}_{3}{T}_{a}{e}^{x.\beta }}\left[{k}_{2}{e}^{\left({k}_{3}-{k}_{2}\right){t}_{1}{e}^{x.\beta }}-{k}_{3}{e}^{\left({k}_{3}-{k}_{2}\right){T}_{b}{e}^{x.\beta }}\right]Int0\right\}\\ +{\sum }_{i=1;{n}_{i}\ge 2}^{N}\text{ln}\left({e}^{-{k}_{3}{T}_{a}{e}^{x\beta }}\{{k}_{2}{f}_{1}\left({t}_{1}\right){e}^{{k}_{2}{t}_{1}{e}^{x\beta }}{e}^{\left({k}_{3}-{k}_{2}\right){t}_{2}{e}^{x\beta }}+{{k}_{3}}^{2}{e}^{x\beta }{e}^{-{k}_{3}{T}_{b}{e}^{x.\beta }}\left[1-{F}_{1}\left({T}_{b}\right)\right]\right)\\ +{k}_{3}{e}^{x.\beta }\left[{k}_{2}{e}^{\left({k}_{3}-{k}_{2}\right){t}_{1}{e}^{x.\beta }}-{k}_{3}{e}^{\left({k}_{3}-{k}_{2}\right){T}_{b}{e}^{x.\beta }}\right]Int0{e}^{x.\beta })\\ +{\sum }_{i=1;{n}_{i}\ge 2}^{N}\left[\left({n}_{i}-2\right)\mathit{ln}\left({k}_{3}{e}^{x.\beta }\right)\right]\end{array}$$

where Pi(n) is the probability of having n breaks in pipe i between T and T + DT regardless of the number of breaks between the time of pipe installation and T, N is the number of pipes in the DMA, ni is the number of breaks between T and T + DT, and Tb and Ta represent the start and end of the data collection period, respectively.

The pipe break models (with and without a pressure covariate) were calibrated for each DMA. Subsequently, a database combining the data from the two DMAs was created to calibrate the pipe break model. This database included the most significant pressure covariate identified based on the individually obtained results for each DMA.

In addition to the most significant pressure covariate, the pipe length, diameter, and material were included in the pipe break model calibration for the combined DMAs. This model was subsequently compared with the pipe break model calibrated using only the physical covariates (pipe diameter, length, and material) for the combined DMAs to verify the impact of the pressure covariate on pipe breaks when combined with physical covariates.

3.7 Likelihood Ratio Test

The likelihood ratio (LR) was used to compare the pipe break model calibrated without a pressure covariate with that calibrated with a pressure covariate. It was computed by

$${\varvec{L}}{\varvec{R}}=-2{\varvec{ln}}\left(\frac{{\varvec{L}}({{\varvec{\theta}}}_{0})}{{\varvec{L}}(\widehat{{\varvec{\theta}}})}\right)=-2\left[{\varvec{l}}\left({{\varvec{\theta}}}_{0}\right)-{\varvec{l}}\left(\widehat{{\varvec{\theta}}}\right)\right]$$

where \(l\left({\theta }_{0}\right)\) and \(l\left(\widehat{\theta }\right)\) are the maxima of the logarithms of the likelihood functions of the models without (\(L\left({\theta }_{0}\right)\)) and with (\(L\left(\widehat{\theta }\right)\)) the pressure covariate, respectively.

The null hypothesis of this test was that the difference between the two models was insignificant and could be neglected. If the null hypothesis was true, LR would follow a chi-squared distribution, \({\rm X}_{k}^{2}\), where k is the degree of freedom (i.e., the difference between the number of covariates of the two tested models). A significance level of α = 5% was considered for this test.

4 Results and Discussion

4.1 Data Cleaning

The analyses were performed using the pressure, flow rate, and break data recorded from 2015 to 2020. During the process of cleaning these data, 11% and 16% of records were removed from Zones A and B, respectively.

4.2 Hydraulic Simulations

The validation results for the hydraulic model are provided in Table 3, which indicates that the average RRMSE for the outlet pressures were 4.8% and 3.5% for Zones A and B, respectively. As these values were less than 5%, the hydraulic model was considered valid for computing the annual pressure covariates for each pipe in the two DMAs.

Table 3 Validation results for the hydraulic model
Full size table

4.3 Pressure Covariates

The results of the Mann–Kendall trend test performed on the annual covariates defined in Table 2 for each pipe in the two DMAs during the 2015–2020 period indicate that there was no temporal trend in any pressure covariate values for any pipes, except 2% of the pipes exhibited a trend in \(L\) for Zone A and 1% of the pipes exhibited a trend in \({P}_{mean}\) for Zone B. For both DMAs, the absence of a significant trend in the annual pressure covariates permitted the calculation of all pressure covariates as mean annual values, as listed in Table 2. Thus, these covariates can be considered to characterize the entire recorded period.

4.4 Likelihood Ratio Test

The WEE model was calibrated using a combination of variables related to time (installation date and break date) and covariates (x) under the constraint \({k}_{1}<{k}_{2}<{k}_{3}\), applied according to the hypothesis that successive breaks occur more frequently (Duchesne et al. 2016).

The results of the LR test are provided in Table 4 for the separately calibrated models for Zones A and B and for the models calibrated by combining the data from both DMAs. These results indicate that the covariates \({\overline{P}}_{max}\), \({\overline{P}}_{mean},\) and \({\overline{P}}_{var}\) had significant impacts on pipe breaks in Zone A and \({\overline{P}}_{max}\) and \({\overline{P}}_{mean}\) had significant impacts on pipe breaks in Zone B. The results also show that \({\overline{P}}_{max}\) had a significant impact on pipe breaks when the pipes of both DMAs were combined.

Table 4 Comparison between pipe break models with and without pressure covariates for Zones A and B (gray cells indicate covariates that had a significant impact on pipe breaks)
Full size table

The results presented in Table 4 for the individual DMAs can be further analyzed using Fig. 3, which shows the distributions of the mean and maximum pressure values and the mean pressure variation for the pipes in Zones A and B.

Fig. 3
figure 3

Distributions of the a) maximum pressure covariate for Zones A and B; b) mean pressure covariate for Zones A and B; and c) mean pressure variation covariate for Zones A and B

Full size image

The \({\overline{P}}_{max}\) and \({\overline{P}}_{mean}\) values were observed to have a significant impact on the occurrence of pipe breaks in both DMAs, although the two zones exhibited differences in terms of pipe age, pipe break rate, and the distributions of \({\overline{P}}_{max}\) and \({\overline{P}}_{mean}\). As previously mentioned, the pipes in Zone B were older than those in Zone A; thus, the pipe break rate was higher in the former. Moreover, Figs. 3a and 3b show that the variations in \({\overline{P}}_{max}\) and \({\overline{P}}_{mean}\) for Zone B were greater than those for Zone A. The impacts of these two covariates on the pipe break rate have been demonstrated in previous studies, which showed that decreasing the maximum pressure (Martínez-Codina et al. 2015a; Moslehi and Jalili_Ghazizadeh 2020) and mean pressure (Jara-Arriagada and Stoianov 2021) led to reduced pipe break rates. However, these studies applied different methods to determine the pressure covariates, either estimating them from the time series of pressures measured at specific points of the DMA assuming that each covariate was representative of all pipes in that DMA (Martínez-Codina et al. 2015a; Moslehi and Jalili_Ghazizadeh 2020), or estimating them for each pipe using a hydraulic model that was not adjusted to represent the actual hydraulic conditions (Jara-Arriagada and Stoianov 2021). In the former case, the covariates were conditioned to the occurrence of breaks; i.e., for each reported break, a pressure covariate was calculated from the pressure time series that preceded the break using a specific window width (generally between one and five days). However, Martínez-Codina et al. (2015b) pointed out that the maximum and mean pressures do not always affect the probability of pipe breaks, such as when the values of \({\overline{P}}_{max}\) and \({\overline{P}}_{mean}\) are low.

In addition, the results in Table 4 show that the p-values from the LR test of \({\overline{P}}_{max}\) and \({\overline{P}}_{mean}\) for Zone B were significantly lower than those for Zone A. This difference can be explained by the relative distributions of the two covariates, which were wider in Zone B (Fig. 3).

The comparison between the WEE models without a pressure covariate and with \({\overline{P}}_{var}\), shown in Table 4, provided contradictory results according to DMA: \({\overline{P}}_{var}\) had a significant impact on pipe breaks in Zone A but not on those in Zone B. The distribution of \({\overline{P}}_{var}\) across the pipes in the two DMAs (Fig. 3c) may explain this difference. The values of \({\overline{P}}_{var}\) were higher and covered a wider range in Zone A (0.300 m to 1.100 m) than in Zone B (0.001 m to 0.250 m). Therefore, the pressure variation in Zone B was insufficient to affect the occurrence of pipe breaks. This can be related to the results reported by Martínez-Codina et al. (2015b), who demonstrated that indicators linked to the variability of pressure, such as the pressure variation rate, pressure variation, and range of pressure, influenced the occurrence of pipe breaks in six considered DMAs.

The results presented at the end of Table 4 strengthen this conclusion regarding the impact of the maximum pressure covariate on pipe breaks. These results indicate that \({\overline{P}}_{max}\) had an even more significant influence on pipe breaks when data from the two DMAs were combined. Finally, the results in Table 4 also show that \({\overline{P}}_{max}\) had a significant impact on pipe breaks, even when the physical covariates were included in the calibration of the WEE model.

5 Conclusion

The impact of pressure on the occurrence of pipe breaks was investigated considering five explanatory water pressure covariates (mean annual maximum pressure, mean pressure, mean pressure variation, mean annual number of times the pressure variation exceeded \({\overline{P} }_{Var}+2\sigma\), and mean annual number of times the pressure variation exceeded \({\overline{P} }_{Var}+3\sigma\)) in pipe break models for two DMAs from the WDN of Quebec, Canada.

First, a hydraulic model was simulated and validated based on the recorded pressure and flow rate time series. This hydraulic model was used to estimate the aforementioned pressure covariates for each pipe in the studied DMAs. The results indicated that the maximum and mean pressure values had significant impacts on the occurrence of pipe breaks in both DMAs when considered separately; this was also verified when the data from the two DMAs were combined. The link between the maximum pressure and pipe break rate was verified by combining the pipe break model using this covariate with that using the physical characteristics (pipe diameter, length, and material) for the two DMAs combined. The results confirmed that pressure management strategies that aim to reduce pressure variations can reduce the occurrence of pipe breaks. Predicting the probability of pipe breaks as a function of pressure-related covariates could help water utilities decide between several intervention scenarios such as implementing pressure management valves or replacing older pipes.

Note that the pressure and flow rate time series employed in this study covered only six years for the two studied DMAs. The use of a longer record period could strengthen the conclusions regarding the significant pressure covariates or help identify other critical covariates. Furthermore, the limits \(Ul\) and \(Ll\) imposed to detect outliers in the time series could be overly restrictive. Indeed, several actual extremely high water consumption rates could have been considered measurement errors when applying the proposed data cleaning method. This could specifically affect the results for the mean pressure variation, which was identified as exerting a significant impact on the deterioration of the WDN pipes in Zone A but not in Zone B. Finally, the pressure covariates were estimated assuming that they represented the entire recording period. The pipe break model is limited to such stationary covariates; however, when the recording period extends, the possibility of detecting a trend in the annual pressure covariates increases. Indeed, trends in pressure covariates can be caused by interventions in WDNs, such as changing the inlet pressure settings. In this case, including a nonstationary pressure covariate in the calibration of the WEE model could affect the validity of the results.

The primary findings of this study confirm the impact of the maximum and mean pressure values on the occurrence of pipe breaks and can help WDN managers develop intervention plans such as implementing pressure reducers with fixed or variable setpoints or developing real-time pressure management strategies.