1 Introduction

Water use is set to increase over the next few decades even in arid or semi-arid areas (Bajany et al. 2021) as a result of population growth and planned increases in irrigation. Under water scarcity conditions groundwater can be seen as an opportunity to access secure water (MacDonald and Calow 2009). Nevertheless, this trend leads to increased stress upon groundwater resources, which are also finite.

In any case, water resources management can be expressed as an optimization problem. Traditionally, the respective objective function represents water or energy consumption, or pollutants’ concentration and needs to be minimized. In certain cases, the extrema of the objective function might be calculated analytically (Harvey et al. 1994; Nagkoulis and Katsifarakis 2020) or numerically (Saez and Harmon 2006; Stratis et al. 2016). Moreover, many optimization techniques have been used, from linear programming to evolutionary techniques, such as Genetic Algorithms (GA), which have been extensively used to solve difficult optimization problems in water resources management (Kontos and Katsifarakis 2017; Moutsopoulos et al. 2017; Nicklow et al. 2010).

The aforementioned traditional approach fails to include social interactions, which might be important (Walker et al. 2015; Nikolic and Simonovic 2015). To take them into account, water resources can be approached as common pool recourses, as the use of the resource by one individual reduces the possibilities for others to consume this good (Héritier 2015), which, in turn, raises moral issues (Hardin 1968; Cox 1985) (e.g. poorer farmers might not be able to carry the cost of pumping from larger depths). In this framework, game theory is increasingly used, in order to consider interests and conflicts of water users, defined as players (Eyni et al. 2021; Parsapour-Moghaddam et al. 2015). Some of the important water resources issues approached using game theory are international rivers’ conflicts (Eleftheriadou and Mylopoulos 2008; Safari et al. 2014; Zeng et al. 2019), shared aquifers (Müller et al. 2017; Penny et al. 2021) and water market’s implications (Galaz 2004). A useful review, covering a period of 70 years, is presented by Dinar and Hogarth (2015), representing game theory’s contribution in water resources aspects and presenting ideas and priorities for future research.

Regarding groundwater resources in particular, literature includes some game-theoretic approaches, in which players take into consideration groundwater extraction externalities to reduce over-exploitation’s drawbacks (Loáiciga 2004; Raquel et al. 2007). Moreover, fuzzy models have been used to incorporate uncertainties in aquifer parameters and in decision maker’s preferences, while analyzing and resolving water conflicts (Alizadeh et al. 2017); they have also performed satisfactorily, combined with GA and Rubinstein Sequential Bargaining Theory, in developing optimal operating policies for conjunctive use of surface and groundwater resources (Kerachian et al. 2010). Recently, Kicsiny and Varga (2019) derived a solution to water allocation problem, taking into consideration aquifer recharge and water consumption. Nevertheless, it cannot be directly used in groundwater resources management, as basic aquifer characteristics, like storativity and transmissivity, are not taken into consideration. Dynamic games have been also applied to groundwater resources (Nazari et al. 2020) to find an equilibrium between local farmers and government. Farmers want to pump large water quantities to maximize their economic profit and government wants low amounts of water to be drained in order to protect the aquifer. Cooperative games have also been applied in order to allocate the benefit between cooperating stakeholders in common aquifers (Sadegh et al. 2010).

In this paper, we deal with groundwater extraction, putting emphasis on pumping schedules. In a previous work (Nagkoulis 2021), it has been shown that alternate pumping schedules can be used to reduce energy consumption and pumping cost of a system of wells. A simplified relationship is proposed to calculate the benefit of alternate pumping. However, if all players choose their favorite pumping schedule, (most probably during the day) the overall financial optimum will not be achieved. To include players’ preferences, we have formulated the problem as an anti-coordination graph coloring game. To solve it, we propose an algorithm that can find the Nash equilibria using the transient hydraulic head level drawdowns, due to pumping. Moreover, we have used GA to find the best Nash equilibrium, since the problem is non-linear and the objective function presents many optima.

Applications of graph and network games to represent social interactions and predict their outcomes are numerous (Bramoullé et al. 2014; Bramoullé and Kranton 2007). Graph Congestion games have been studied because of their importance on resources allocation (Chien and Sinclair 2011; Southwell et al. 2012). In these games, neighbors receive an extra cost when they follow the same strategy. Coordination games are a typical category of graph games (Apt et al. 2017; Cai and Daskalakis 2011). In a coordination game the payoff of a node is defined as the total weight of all edges to neighbors that are in the same coalition. If the weights of the edges are negative, we get an anti-coordination game (Carosi and Monaco 2020). We have modelled our groundwater management problem as such a game, because simultaneous pumping (in particular from neighboring wells) increases overall cost, as explained in Sect. 2.1. Moreover, we have opted to represent pumping schedules using colors. Subsequent optimization is based on the coloring method of Panagopoulou and Spirakis (2008).

In the following sections, firstly the groundwater flow problem is described and then it is modelled as a coloring graph game, explaining why an iterative computation of Nash Equilibrium has been chosen. Finally, examples and applications of the algorithm created are presented.

2 Preliminaries

2.1 Transient Flow Hydraulic Head Level Drawdowns

Suppose that a system of NW wells is used to pump at different flowrates from an infinite confined aquifer. Then, using the Theis formula (Theis 1935) and the superposition principle, the transient hydraulic head level drawdown (from here on mentioned simply as drawdown) at point i and at time t, is given as:

$${s}_{i,t}=\frac{1}{4\pi T}\sum_{j=1}^{j=NW}{Q}_{j} W\left({u}_{i,j,t}\right)$$
(1)

where

$$W\left({u}_{i,j,t}\right)=-{\gamma }_{eul}-\mathrm{ln}\left({u}_{i,j,t}\right)-\sum_{k=1}^{\infty }\frac{{\left(-1\right)}^{k}{\left({ u}_{i,j,t}\right)}^{k}}{k k!}$$
(2)
$${u}_{i,j,t}=\frac{S {r}_{i,j}^{2}}{4 T \Delta t}$$
(3)

In the above formulas, T(m2/s) and S are the aquifer’s transmissivity and storativity, respectively, Qj(m3/s) is the flow rate of well j, γeul is the Euler’s constant,, ri,j(m) is the distance between point i and well j (ri,i is equal to the radius of the well r0) and \(\Delta t\) the time period between the beginning of pumping to and t (\(\Delta t=t-{t}_{0}\)).

For two wells, Nagkoulis (2021) has examined two pumping schedules with two phases each (I and II). In Schedule A the wells are pumped during different phases, while in Schedule B they are pumped simultaneously.

The pumping energy consumption Ki for well i can be calculated using relationship (4):

$${K}_{i}=\gamma {\int }_{0}^{{t}_{final}}{Q}_{i,t} {s}_{i,t} dt$$
(4)

where “γ” is the specific weight of water (γ = 9.81kN/m3), “Qi,t” (m3/s) is the flow rate of well “i” for every moment “t” and “si,t” is the drawdown for every moment t at well “i” (no matter which well causes this drawdown). K is measured in kW∙s, or kWh/3600. Finally, it has been proved that there is an economic benefit Beni for each player i from pumping alternately (schedule A) instead of simultaneously (schedule B). Beni is given as:

$${Ben}_{i}={C}_{1}\left({K}_{i}^{B}-{K}_{i}^{A}\right)$$
(5)

In Eq. (5) C1 is a coefficient transforming watts to monetary units, depending on local energy price (\({C}_{1}\) units: € kW−1 s−1). The results indicate that the profit of each player is maximized by pumping alternately with as many players as possible and that the higher the interference of the wells (which results in larger drawdown), the larger the benefit obtained from alternate pumping. This behavior of a system of wells which is already indicated in literature (Nagkoulis 2021), is because the drawdown function is cumulative. Then, include player’s schedule preferences in our model, we construct a graph coloring game.

3 Game Formulation

Our approach is based on the work of Carosi and Monaco (2020), which offers the theoretical tools to model the graph coloring game. Using similar notations to these authors, we define an undirected simple graph G = (V, E, w), where |V| is the number of nodes, |E|= m is the number of edges, and \(w:E\to {\mathbb{R}}_{\ge 0}\) is the edge-weight function that associates a positive weight to each edge. In our paper each node represents a well and |V|= NW. If a well is affected by another well, then the two wells are connected using an edge. We suppose that pumping from a well affects all of them. Then all wells are connected with each other and the resulting graph is full. The weights of the edges represent how much each player is affected by another player’s choices and depend on wells’ interference.

An instance of the generalized graph k-coloring game is a tuple (G, K, P), supposing that K is a set of available colors and \(P :V x K\to {R}_{\ge 0}\) is a color profit function that defines how much a player likes a color. We use two colors (k = 2) to indicate the two pumping phases (I and II). Supposing that each period is equivalent to 24 h (day and night), players can either pump during phase I (6:00 to 18:00) or during phase II (18:00 to 6:00). We will refer to these choices as D (choosing phase I) and N (choosing phase II). These phases have been chosen as typical. In future research more complicated schedules can be used.

Supposing that these are the available schedules, we can plausibly assume that most players would prefer to pump during the day, if there were not any benefit from alternate pumping. To model this preference, we use function P as follows: if player \(i\) chooses to pump during the day then he/she gains monetary units equivalent to \({P}_{i}\left(D\right)\ge 0\), whereas if he/she chooses to pump during the night then he/she gains \({P}_{i}\left(N\right)=0\). In practice, \({P}_{i}\left(N\right)\le 0\) and \({P}_{i}\left(D\right)\)=0, as players do not want to pump during the night. However, we preferred to reverse the payoffs in order to use positive P values, as the models are equivalent. As \({P}_{i}\left(N\right)\) has been set to 0, we simplify the notation from \({P}_{i}\left(D\right)\) to Pi.

A state of the game \(c=({c}_{1}, \dots , {c}_{n})\) is a coloring, where \({c}_{i}\) is the color chosen by player \(i\). We will call “objective payoff” \({\delta }_{i}(G)\) of a player \(i\) the sum of the weights of the edges \((i,j)\) incident to \(i\), such that the color chosen by \(i\) is different than the one chosen by j. It is given by Eq. (6). This definition results in an anti-coordination game, as players increase their payoffs when they choose different colors. Moreover, we define the “subjective” payoff μc(i) of a player as the respective objective payoff plus the profit due to the use of the chosen color. It is given by Eq. (7). We have chosen to use two payoff functions, although the game is played using the subjective payoffs, because the objective payoffs are useful environmental indicators. This will be made clear in the following sections.

$${\delta }_{i}\left(\mathrm{G}\right)=\sum_{j\in V:{c}_{j}\ne {c}_{i}}\mathrm{w}(\left\{\mathrm{i},\mathrm{j}\right\})$$
(6)
$${\upmu }_{\mathrm{c}}\left(\mathrm{i}\right)={\delta }_{i}\left(\mathrm{G}\right)+{\mathrm{P}}_{\mathrm{i}}\left({\mathrm{c}}_{\mathrm{i}}\right)$$
(7)

Summing the objective payoffs of all players we get the objective utilitarian social welfare (OSW), while summing the subjective payoffs we get the subjective utilitarian social welfare (SSW).

Finally, an improving move of player \(i\) in a coloring profile \(c=\left({c}_{1}, \dots , {c}_{n}\right)\), is a strategy \({c}_{i}^{^{\prime}}\) such that \({\mu }_{({c}_{-i},{c}_{i}^{^{\prime}})}\left(i\right)> {\mu }_{({c}_{-i},{c}_{i})}\left(i\right)\). A state of the game \({c}^{*}=({c}_{1}^{*}, \dots , {c}_{n}^{*})\) is a pure Nash equilibrium if and only if no player can perform an improving move. This means that: \({\mu }_{({c}_{-i}^{*},{c}_{i}^{*})}\left(i\right)\ge {\mu }_{({c}_{-i}^{*},{c}_{i})}\left(i\right)\) \(\forall i\in V\).

4 Methodology

4.1 Pure and Mixed-Strategy Equilibrium

At first, we examine two players’ payoffs (Table 1) in a static game. The players aim at maximizing their subjective payoffs. Each player prefers to pump during the day (D), while at the same time pumping alternately with the other player.

Table 1 Two Players, Static Game
Full size table

Let us examine pure Nash equilibria; if \(\mathrm{min}({\mathrm{P}}_{1}\&{\mathrm{P}}_{2})\ge \mathrm{w}(\left\{\mathrm{1,2}\right\})\) we get (D, D), if \(\mathrm{max}({\mathrm{P}}_{1}\&{\mathrm{P}}_{2})<\mathrm{w}(\left\{\mathrm{1,2}\right\})\) we get two pure Nash equilibria (D, N) and (N, D), if \({\mathrm{P}}_{1}<\mathrm{w}\left(\left\{\mathrm{1,2}\right\}\right)\mathrm{ and} {\mathrm{P}}_{2}>\mathrm{w}(\left\{\mathrm{1,2}\right\})\) we get (N, D) and if \({\mathrm{P}}_{1}>\mathrm{w}\left(\left\{\mathrm{1,2}\right\}\right)\mathrm{and} {\mathrm{P}}_{2}<\mathrm{w}(\left\{\mathrm{1,2}\right\})\) we get (D, N). After these notes one could say that the players will reach a pure Nash equilibrium by just examining the possible moves of the other players. However, we should take into consideration that if \({\mathrm{P}}_{1}\&{\mathrm{P}}_{2}<\mathrm{w}(\left\{\mathrm{1,2}\right\})\) the players do not know if the other player will choose (D) or (N). Therefore, when we examine a population of players, it makes more sense to use mixed strategy profiles instead of stationary, in order to model the actual situation.

Assuming that player 1 chooses (D) with a probability a1 and player 2 chooses (D) with a probability a2 we will find the mixed strategy Nash equilibrium. A mixed strategy Nash equilibrium of a finite strategic game is a mixed strategy profile a* with the property that for every player i, every action in the support of ai* is a best response to ai* (Osborne and Rubinstein 1994). To find the probabilities distribution we need to calculate the expected payoffs of the players: \({\mu }_{1}={a}_{1}{a}_{2}{P}_{1}+{a}_{1} {P}_{1}(1-{a}_{2})+{a}_{1} \mathrm{w}(\left\{\mathrm{1,2}\right\})(1-{a}_{2})+{a}_{2}\mathrm{w}(\left\{\mathrm{1,2}\right\})-{a}_{1}{a}_{2}\mathrm{w}(\left\{\mathrm{1,2}\right\})\) and \({\mu }_{2}={a}_{1}{a}_{2} {P}_{2}+{a}_{2} {P}_{2}(1-{a}_{1})+{a}_{2} \mathrm{w}(\left\{\mathrm{1,2}\right\})(1-{a}_{1})+{a}_{1}\mathrm{w}(\left\{\mathrm{1,2}\right\})-{a}_{1}{a}_{2} \mathrm{w}(\left\{\mathrm{1,2}\right\})\). We will get the distribution a* as follows:

$$\frac{\partial {\mu }_{1}}{\partial {a}_{1}}=\frac{\partial {\mu }_{2}}{\partial {a}_{2}}=0\to {a}_{1}^{*}=\frac{{P}_{1}+\mathrm{w}(\left\{\mathrm{1,2}\right\})}{2\mathrm{w}(\left\{\mathrm{1,2}\right\})}\, and\; {a}_{2}^{*}=\frac{{P}_{2}+\mathrm{w}(\left\{\mathrm{1,2}\right\})}{2\mathrm{w}(\left\{\mathrm{1,2}\right\})}$$
(8)

From relationship (8) for \({P}_{1}\in \left(0,\mathrm{w}\left(\left\{\mathrm{1,2}\right\}\right)\right)\) we get \({a}_{1}^{*}\in \left(0.5, 1\right)\), which means that player 1’s possibility of choosing Day will be higher than 50%. Considering that the same applied for player 2, for \({P}_{2}\in \left(0,\mathrm{w}\left(\left\{\mathrm{1,2}\right\}\right)\right)\), we easily get a mixed strategy equilibrium (D, D). In practice, the outcome (D, D) should be expected in a static game. As each player has only one opportunity to play, it is more beneficial for them to play (D) and hope that the other players will play (N). However, this is not the case when the players have the opportunity to play in turns. In this paper, iterative play is chosen, in order to promote alternate pumping.

5 Improving Moves

In case that players play in turns and each player can see what the others have played, they can change their strategy to maximize their benefit. From Carosi and Monaco (2020) we get that such a sequence of moves in this specific coloring game converges to a Nash equilibrium. The proof is simple and derives from the fact that the game is a potential game (Babichenko and Tamuz 2016). Thus, each improving move increases the value of the potential function. It follows that, after a finite number of improving moves, no player can increase their utility (subjective benefit) anymore, that is, the resulting coloring is Nash stable. The authors also prove that Price of Anarchy (PoA) is equal to 2 and Price of Stability (PoS) is equal to 1.5 for \({P}_{i}>0, \forall i\in V\). It was already known that (PoA) is equal to 2 and PoS is equal to 1 for \({P}_{i}=0, \forall i\in V\). This means that the Nash equilibria, even though they are stable solutions, they do not necessarily maximize the benefit of the system of the players, regardless if the objective or the subjective benefit is examined.

Moreover, we suppose that the players are myopic, namely they make their moves based on the existing condition and they do not take into consideration that the other players might change their strategy during the next rounds. This is done, because it is important to “simulate real conflicts” so that “the applied stability definitions better reflect characteristics of the players” (Madani and Hipel 2011).

As an example, let us suppose that i) P1 = P2 = 0 in Table 1, ii) the initial condition is (D, D) iii) player 1 plays first. We get the following sequence of moves: At first player 1 can choose between (N, D) and (D, D), therefore he/she chooses (N, D). Then player 2 can choose between (N, D) and (N, N) therefore player 2 chooses (N, D). Finally, player 1 can choose between (N, D) and (D, D), therefore he/she chooses again (N, D). The profile c* = (N, D) is a Nash equilibrium, as no player increases their benefit by changing their option anymore. On the other hand, it is important to take into consideration the sequence of the moves of the players. If player 2 played first, the Nash equilibrium would have been c* = (D, N). We believe that this game play fits to the actual players, who might not be aware of the full game theoretical literature or might not have the willingness to take into consideration the actions of the other players. Institutions can promote cooperation, helping to escape the tragedy of the commons’ trap (Madani and Dinar 2012). In this paper we have chosen to use researchers and authorities as externalities that will inform the player about the results of their options, each time they consider pumping during the day or during the night. Their role is to inform the players about their energy consumption for both options.

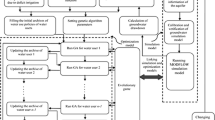
The algorithm used to reach a Nash equilibrium is presented in Fig. 1. In Fig. 1 we can see the iterative game play process. Each player takes the previous moves of the other players as granted and plays the best move according to the existing situation (Fig. 1). The payoffs of the players are calculated from the drawdowns of the pumping wells. When identical \(c={(c}_{1}, \dots , {c}_{n})\) profiles appear for two consecutive rounds, the game stops, because a Nash Equilibrium profile \({c}^{*}=({c}_{1}^{*}, \dots , {c}_{n}^{*})\) has been reached. The players are assumed to be rational, therefore, two consecutive identical profiles indicate that the profiles will not change, regardless of the number of rounds following.

Fig. 1
figure 1

Iterative game play. The red arrows represent the moves played by the players. We can see that player 1 has played (N). Player 2 is the “active” player, which means that they are going to play (D) or (N) based on the previous moves of the other players

Full size image

Improving the payoff of each edge w({i, j}), namely increasing the benefit of the players, is equivalent to reducing the subjective cost of the players. This way: player i chooses to pump during the Day if: \({\mu }_{({c}_{-i},D)}\left(i\right)> {\mu }_{({c}_{-i},N)}\left(i\right)\), which is equivalent to \({K}_{({c}_{-i},D)}\left(i\right)<{K}_{({c}_{-i},N)}\left(i\right)+{\mathrm{P}}_{\mathrm{i}}\). The costs are calculated using Eqs. (1), (2), (3) and (4). In Fig. 1, for example, each player choses the strategy that minimizes their subjective cost.

5.1 Genetic Algorithms and Optimization

Before moving to the results section, it is necessary to mention how the results of this paper can be applied in practice, as excessive assumptions about the players can make game theory seem repulsive to practitioners. Specifically, we need to mention that well users are mostly unaware of the economic benefit that can be obtained through pulsed pumping; therefore, we should take into consideration in our analysis the researcher or the authorities that make the players aware of their potential benefit. Actually, narrowing the gap between research, policy making and end users, is essential to improve water resources management in praxis (Azhoni and Goyal 2018).

This researcher (or authorities) practically acts as an external player aiming at his/her own benefit. In this paper we assume that the external player’s target is to minimize the pumping energy consumption, which is identical to maximizing the objective utilitarian social welfare (OSW). Nevertheless, as the external player cannot force the well users to pump following the schedules that he/she wants, recommendation of a Nash Equilibrium strategy profile is the best choice, because no player will obtain a payoff advantage by switching away from it. To increase the applicability of this research, we assume that it is necessary that the Nash Equilibrium does not need many rounds to be reached, because this will increase the players’ cost. This idea is similar to Rubinstein’s “time is valuable” concept (Rubinstein 1982). In this paper instead of inserting a cost parameter, which is difficult to be defined in our problem, we limit our results to the solutions that require just one round of moves to reach a Nash Equilibrium. Summarizing, the following can be thought to be the targets of the external player:

  1. 1.

    The coloring solution \({c}^{*}=({c}_{1}^{*}, \dots , {c}_{n}^{*})\) is a Nash equilibrium.

  2. 2.

    The Nash equilibrium obtained maximizes the OSW.

  3. 3.

    The Nash equilibrium is obtained from the first round.

The first target is reached using the iterative play introduced in the previous chapter. The other two targets are reached using genetic algorithms (Coley 1999; Holland 1992), which have been widely used in water resources management problems (Ketabchi and Ataie-Ashtiani 2015; Perea et al. 2020). The target is to optimize sequence of the players (meaning who plays first and who is next). Using different players’ sequences, we can get different outcomes, as indicated in the example used in the previous section. Since the number of the wells is NW, the number of combinations, namely of possible sequences is NW!. We use the R package GA (Scrucca 2013), with the following parameter values: population size: 15, generations: 200, mutation probability: 0.45, crossover probability: 0.8. The choice of crossover and mutation probability is based on the results of Kontos and Katsifarakis (2012). Moreover, elitism is included in the selection process. The sequences that result in the highest OSW values survive until the end of the optimization process. In some of the following examples, the solutions that result in a Nash Equilibrium after the first round are removed, in order to find the sequence of the players that reaches the best Nash Equilibrium that can be reached from the first round. This extension could increase the applicability of this research.

It should be mentioned that, in order to run the algorithm the external player (researcher / authority) needs the following data:

  1. 1.

    The aquifer characteristics (T, S) and the locations of the wells, in order to calculate the w(i,j) values.

  2. 2.

    The time schedules preferences of the players, in order to make an estimation for Pi parameter. The simplest way to find that is to ask the players what is the monetary compensation that they would accept, in order to pump during the night.

6 Results – Applications

Example 1:

In this example we use NW = 3 wells–players, in a confined aquifer with T = 10−3m2/s and S = 5*10–7. We suppose that the pumping cost coefficient is A’ = 0.06€/kWh, the duration of the pumping schedule is 5 days, and the pumping flow rate of each well is q = 0.01m3/sec. We use the following values to represent the unwillingness to pump during the night (N) or the willingness to pump during the day (D): P = (0.30, 0.24, 0.14) €/day. The possible sequences of the players are the following 6 (NW!): (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1). In this example we will find the Nash equilibrium of the first sequence.

Each player minimizes their “subjective” cost, which is the cost due to energy consumption plus the unwillingness to pump during the night. This results also in a reduction in the overall “objective” cost, namely the cost of energy consumption by the system of the wells. Table 2 represents the subjective costs matrix for the players for the first round. Each player minimizes their own pumping cost (equivalently maximizes their benefit), choosing between Day and Night each turn.

Table 2 Objective costs matrix (€/Day)
Full size table

This way in the 1st turn of the 1st round, the first player choses to pump during the Night because this offers them lower Subjective cost (1.71€/day for Night, instead of 2.036€/day for Day). The next player (2nd turn, 1st round) chooses to pump during the Day (1.64€/day for Day, instead of 2.04€/day for Night). The last player (3rd turn, 1st round) chooses to pump during the Day (1.64€/day for Day, instead of 1.789€/day for Night).

As no player changes their strategy after the 1st round, the Nash Equilibrium is c* = (N, D, D). The players decide based on their Subjective benefit; however, this results in an Objective benefit as well. Table 2 represents the economic benefit (objective benefit) obtained from the optimization. Initially all players were pumping during the day, however after the Nash Equilibrium is reached, all players have benefited financially.

Summing the objective benefit values, we can get the overall daily economic benefit of the system. The benefit is 1.3€/day, which is equivalent to 21.6kWh/day.

Example 2:

In this example we use 10 wells / players, in a confined aquifer with T = 10−3m2/s and S = 5*10–7. We suppose that the pumping cost coefficient is A’ = 0.06€/kWh, the duration of the pumping schedule is 5 days, and the pumping flow rate of each well is q = 0.01m3/sec. We suppose that P values are the following: P = (0.986, 1.359, 1.716, 2.089, 1.77, 1.70, 0.527, 1.137, 2.611, 2.038). The possible sequences of the players are 10!. All these combinations are expected to end up to Nash Equilibria with iterative moves. However, the payoffs of these equilibria might differ. In this example genetic algorithms will be used to find the sequence of the players that minimizes the overall objective cost (equivalently, the energy consumption).

In Fig. 2 we can see the strategic profiles at the beginning of the 2nd round and at the end of the 2rd round. The active player has to choose the best strategy based on the existing situation. It is clear that the players are trying to pump during a different period from their neighbors, while at the same time avoiding pumping during the night. The sequence of the players is (10, 6, 3, 7, 4, 9, 5, 2, 1, 8) and the Nash Equilibrium profile is (N, D, D, D, N, D, N, D, D, D), reached after 2 rounds. We know that a Nash Equilibrium is reached because no player changed their strategy during the 3rd round. This means that even if 5 rounds were used, the strategic profile would be the same. If there were any willingness from any player to change their move, they would have done it during the 3rd round. Overall, when the algorithm created notices that a strategic profile is identical for two consecutive rounds, the next rounds are cancelled, and the solution is saved. The initial objective costs and the objective costs after a Nash Equilibrium has been reached, are summarized in Table 3. The overall objective economic benefit is 15.569 €/Day which is equivalent to 259.486 kWh/day.

Fig. 2
figure 2

The strategic profiles at the beginning and at the end of the 2nd round

Full size image
Table 3 Objective costs matrix (€/Day)
Full size table

Then we insert a penalty in the objective function of the genetic algorithms, that gives a zero-fitness value to those player sequences that fail to reach a Nash Equilibrium from the first round. We believe that such a penalty increases the applicability of this research, because the players might not have the patience to play a long game, as explained in the methodology section. The new sequence is (5, 7, 3, 1, 9, 4, 6, 10, 2, 8). The Nash Equilibrium profile and the objective costs matrix are identical to those obtained in the previous case, however in this case 1 round is used instead of 2. We can see that, in these examples, inserting a penalty, improves the applicability of the solution, reducing the rounds needed to reach a Nash Equilibrium. Even though in this case the profiles are identical, this should not be generalized. In most cases reducing the available number of rounds will result in Nash Equilibria that will be linked with lower economic benefits.

Finally, we set P value to zero, to find the solution in case that players are indifferent to pumping during the day or during the night. Moreover, we remove the penalty inserted previously. The new sequence is (5,10, 8, 3, 2, 1, 7, 4, 6, 9) and the Nash Equilibrium profile is (D, N, N, D, N, D, D, N, D, N). The overall objective economic benefit is 17.91€/day, which is equivalent to 298,51kWh/day, and the Nash Equilibrium is reached from the first round. Regarding cost reduction, the results are better than those of the previous cases. The players that are indifferent to pumping during the day or during the night have more opportunities to achieve a better solution, as they have a higher willingness to change this behavior in order to minimize their pumping cost. It is interesting to mention that the final players’ pumping schedule profile is very close to a 2-chromatic Nearest Neighbor Graph (Fig. 3), which is promising in terms of future research.

Fig. 3
figure 3

Nash equilibrium profile (red for Day, yellow for Night)

Full size image

7 Conclusion

In this paper we propose an algorithm that can be applied to a system of wells, pumping groundwater from a common aquifer. The researcher – authorities using the algorithm can help the well users to change their pumping schedules, so that they pump alternately, in a way that a Nash equilibrium is reached. When the schedules’ allocation has reached a Nash equilibrium, no player has any benefit from changing their pumping schedule. Genetic Algorithms are used to improve the optimization process by finding the Nash equilibrium that minimizes the overall energy consumption and pumping cost. Finally, to improve applicability, genetic algorithms keep only the solutions that reach a Nash equilibrium from the first round. This way we avoid long games that might make the players tired and lead them to “irrational” behaviors. Finally, one interesting application of this research can be finding the amount of money that should be paid by the authorities, in order to increase the number of players pumping during inconvenient time periods. Overall, the algorithm can be considered as the first approach to model an alternate pumping game, in order to reduce pumping cost and energy consumption.

In terms of future research, it should be mentioned that the algorithm is built in a way that the pumping flow rates of the players do not need to be identical. However, this asset was not used, because it has not been proved yet that the players are still benefiting from alternate pumping in this case. Another parameter that can be inserted in the algorithm is the radius of influence of each well. In this case, the edges of the graph that represent influences that do not exist can be removed, in order to examine how the graph decomposition can affect the player strategies. Reducing the number of edges might lead to approximate simple to use solutions.