1 Introduction

Drought is defined as the abnormally prolonged dry weather condition that results in hydrological imbalance for a particular region. Irrespective of the deficit in the availability of water, it is one of the challenging issues which human society is confronting. The drought monitoring for a particular area can be handled through various indices. Many authors have developed univariate drought indices, viz., Standardized Precipitation Index, SPI (McKee et al. 1993), Standardized Runoff Index, SRI (Shukla and Wood 2008), and Standardized Soil moisture Index, SSI (Hao and AghaKouchak 2013). Various studies have also concentrated on the multivariate drought indices such as the Joint Deficit Index, JDI, (Kao and Govindaraju 2010), Standardized Precipitation Evapotranspiration Index, SPEI, (Vicente-Serrano et al. 2010); Integrated Drought Index, IDI (Shah and Mishra 2020b); Copula-based Joint Drought Index, CJDI (Won et al. 2020) and Reconnaissance Trivariate Drought Index, RTDI (Dixit and Jayakumar 2021a). Indian agronomy and cropping pattern are dependent on the onset and withdrawal of monsoon, distribution of rainfall and water storage capacities. Moreover, drought during the year 2014–15 caused severe inadequacy of water by affecting around 330 million people (Mishra et al. 2016). A study by Poonia et al. (2021a) indicated that drought vulnerability will increase throughout India. Hence, adequate attention must be paid to understand the multi-scalar drought assessment, especially an agrarian country like India.

Stationarity refers to the parameters of the climate that are invariant and free of trends (Wang et al. 2015). Nevertheless, the outcome of environmental changes exhibits non-stationary behaviour in climatic parameters and hence, indicators have been developed for identifying drought status in non-stationary conditions (NSPI, Russo et al. 2013; NRDI, Bazrafshan and Hejabi 2018). The large-scale climate indices (external covariates) based on El Niño Southern Oscillation (ENSO) should not, however, be neglected in the computation of nonstationary indices (Bazrafshan and Hejabi 2018). Some of the studies proved the linkage between the global climate indices and Indian climatic conditions (Tamaddun et al. 2019; Shah and Mishra 2020a; Kumar et al. 2021a, b). It can, hence, be concluded that covariates provide greater insight into the climatic factors which influence the climatic parameters over time in a greater dimension.

Drought characteristics must have a dependence structure and hence a multivariate analysis of drought is widely accepted in hydro-meteorological studies for drought risk assessment. Copula function could preserve the multivariate dependence structure of drought characteristics (Saghafian and Mehdikhani; 2014; Mortuza et al. 2019; Poonia et al. 2021b; Dixit et al. 2021). Nevertheless, the higher dimensional multivariate Student’s t copulas are not effective enough to model the complex dependence structure of extreme event variables (Aas et al. 2009). Due of the limitation of the vine or pair-copulas, an efficient way of copula construction method to model the complex dependence pattern emerged (Aas et al. 2009). Many studies have been conducted in the past to define the vital role of pair copula model in hydrological analysis (Song and Kang 2011; Gräler et al. 2013; Xu et al. 2022). Daneshkhah et al. (2016) developed a multivariate pair copula model using the flood properties in River Beas of the Himalayan region indicating that the Himalayan rivers are highly affected by the monsoon fluctuations and stored snow cover. Therefore, an extensive study based on drought characteristics must be carried out considering the multivariate dependent pattern of the drought variables.

Many studies have been carried out in the past for the non-stationary drought frequency analysis (Wang et al. 2015; Rashid and Beecham 2019) and the non-stationary flood frequency analysis (Villarini et al. 2009; Lopez and Frances 2013; Debele et al. 2017; Chen et al. 2021) using GAMLSS model. To the best of the knowledge, study focused on non-stationary drought analysis for the Godavari River Basin (GRB) have not been carried out in the past. GRB is the second largest river basin in India which spreads from Western Ghats to the Eastern coastal region, having a wide variation in climatic pattern. Most of the areas in the river basin have severe impacts on the economical, agricultural and social factors due to drought events (Dixit and Jayakumar 2021b). Hence, the nonstationary assessment of drought considering large-scale climate indices is an appropriate approach for this basin. The objectives of this study are: (i) use of GAMLSS package in R developed by Rigby and Stasinopoulos (2005) for the non-stationary modelling of SPI and RDI in the Godavari River basin; (ii) construction of dependence among drought characteristics is studied by using the trivariate Student’s t copula and PCC models; and (iii) the return period analysis for a better understanding of the statistical behaviour of drought events. The awareness regarding the extreme events and their response in river basin scale with the changing climate will be useful in planning, managing and combating the impacts on water resources systems.

2 Study Area and Data

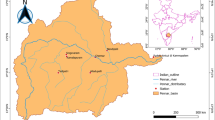
Godavari is the second largest river basin in India and flows through the states of Maharashtra, Telangana, Andhra Pradesh, Odisha, Chhattisgarh and some parts of Karnataka, Madhya Pradesh. The total area of the Godavari basin is approximately 3, 12,810 sq. km., which is about 10% of the total area of the country. The length and width are about 995 km and 585 km respectively. The basin has a tropical climate and as a whole receives on an average 85% of the annual rainfall during the South-west monsoon. The annual precipitation in the river basin varies from 600 to 1200 mm. Most part of the river basin is rain-fed and the distribution of rainfall is highly irregular. The average temperature in the basin varies from 15o C in the winter to 45o C in the peak of summer. High variability in temperature and precipitation in the river basin affects the evapotranspiration and relative humidity of the basin. Therefore, it is essential to estimate the non-stationary drought condition related to precipitation and evapotranspiration variability. In this study, two sub-basins of GRB namely Upper Godavari River Basin (UGRB) and Lower Godavari River Basin (LGRB) are selected for non-stationary assessment of drought. The location map of the study area is given in Fig. 1.

Fig. 1
figure 1

Location map of the study area

Full size image

In the present study, the Indian Meteorology Department (IMD) daily precipitation datasets of resolution 0.25 × 0.25 for the period of 1950 to 2017 are obtained from the IMD website. The Non-stationary Reconnaissance Drought Index (NRDI) requires both precipitation and evapotranspiration data to estimate the meteorological drought. Hence, the monthly 0.5 × 0.5 resolution evapotranspiration data has been downloaded from the Climate Research Unit (CRU) 4.03TS data sites for the same period. Recently, many studies have been conducted considering the CRU 4.03TS dataset (Zarch et al. 2015; Harris et al. 2020). Then the data is extracted and regridded to the IMD grids. There is an effect of large-scale climate indices on a non-stationarity evaluation of drought phenomenon. So, the non-stationary drought indices were computed based on the association with four large-scale climate indices such as Indian Ocean Dipole (IOD), Southern Oscillation Index (SOI), Sea Surface Temperature (SST) and Multivariate ENSO Index (MEI) and are presented in Table 1.

Table 1 Large-scale climate indices and their data site
Full size table

3 Methodology

3.1 Non-stationary Reconnaissance Drought Index (NRDI) and Non-stationary Standardized Precipitation Index (NSPI) Development

The stationary RDI is calculated based on the assumption that the parameters related to initial values \(\left({\delta }_{0}\right)\) are constant with time (Tsakiris et al. 2007). Under non-stationarity condition, some parameters of the distribution function of \({\delta }_{0}\), the initial value, can get changed. \({\delta }_{0}\) is taken as the ratio of precipitation series \(\left({\mathrm{P}}_{\mathrm{j}}\left(t\right)\right)\) to evapotranspiration series \({(\mathrm{PET}}_{\mathrm{j}}\left(\mathrm{t}\right))\) in different time windows (3-, 6- and 12-month), computed using the Eq. (1).

$${\delta }_{0}\left(\mathrm{t}\right)=\frac{\sum_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{P}}_{\mathrm{j}}\left(\mathrm{t}\right)}{\sum_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{PET}}_{\mathrm{j}}\left(\mathrm{t}\right)}$$
(1)

For the computation of NSPI and NRDI, correlation analysis between the precipitation and large-scale climate indices and the computed \(\delta\) 0 values and the large-scale climate indices of different lags (1–12) are performed using Kendall’s method (Kendall 1955) at a significance level of 0.05. The significant covariates from potential large-scale climate indices are evaluated from the best lags based on the minimum p-value. NSPI and NRDI can be developed using the filtered covariates by fitting the GAMLSS model.

3.2 GAMLSS Model Development

In the present study, the random variable \({y}_{i}\) (precipitation series and the initial value series) was assumed to have a parametric cumulative distribution function. The related time varying parameters can be modelled as a function of selected covariates by using the GAMLSS model. The selected covariates based on the Kendall’s \(\tau\) lag correlation method for different time windows of precipitation and the series of initial values \(\left({\delta }_{0}\right)\) were varied linearly with the parameters (\({\upmu }_{\mathrm{t}}\)) is a time varying parameter) of the distribution. The step by step details on the use of GAMLSS analysis is available in Rigby and Stasinopoulos (2005).

In the present work, for computing the NSPI for a particular location, a two parametric Gamma distribution was fitted to the precipitation series with linearly varying location and constant scale parameter considering the explanatory variables given in Eq. (4), using Eqs. (2) and (3).

$${\mathrm{y}}_{\mathrm{t}}\sim \mathrm{Gamma}\left({\upmu }_{\mathrm{t}},\upsigma \right)$$
(2)
$${\upmu }_{\mathrm{t}}={\mathrm{a}}_{\mathrm{o}}+ {\mathrm{a}}_{1}{\mathrm{I}}_{1}\left(\mathrm{t}\right)+ {\mathrm{a}}_{2}{\mathrm{I}}_{2}\left(\mathrm{t}\right)+\dots + {\mathrm{a}}_{\mathrm{n}}{\mathrm{I}}_{\mathrm{n}}\left(\mathrm{t}\right)$$
(3)

where \({\mathrm{a}}_{\mathrm{o}},\dots\ \dots\ ..,{\mathrm{a}}_{\mathrm{n}}\) are estimated mean coefficients for the linear variability for a particular location for fitted Gamma distribution and \({\mathrm{I}}_{1},\ \dots\ \dots ,\ {\mathrm{I}}_{\mathrm{n}}\) represent the explanatory climate variables at time t.

$$\mathrm{f}\left({y}_{t},{\mu }_{t},\sigma \right)= \frac{1}{{\left({\sigma }^{2}{\mu }_{t}\right)}^{{1}/{{\sigma }^{2}}}}\frac{{\mathrm{y}}^{\frac{1}{{\sigma }^{2}}-1}{e}^{{-\mathrm{y}}/ {\left({\sigma }^{2}{\mu }_{t}\right)}}}{\left({1}\!\left/ \!{{\sigma }^{2}}\right.\right)}$$
(4)

The cumulative distribution functions of the aggregated rainfall series were computed by fitting the non-stationary model and transformed into standard normal values using Eq. (5).

$$\mathrm{NSPI}={\upvarphi }^{-1}\left(\mathrm{f}\left({y}_{t},{\upmu }_{t},\upsigma \right)\right)$$
(5)

where \(f\left({y}_{t},{\mu }_{t}, \sigma \right)\) are the CDFs of the aggregated precipitation series, \({y}_{t}\) is the aggregated precipitation at any time t, and \({\varphi }^{-1}\) is the inverse CDF values.

Further, non-stationary Log-normal distribution with linearly varying location parameter (\({\mu }_{t})\) with time considering the respective covariates and with the constant scale parameter (σ), was fitted to the \(\delta\) 0 values as shown in Eqs. (6) and (7).

$${\mathrm{y}}_{\mathrm{t}}\sim \mathrm{LogNormal }\left({\upmu }_{\mathrm{t}},\upsigma \right)$$
(6)
$${\upmu }_{\mathrm{t}}={\mathrm{b}}_{\mathrm{o}}+ {\mathrm{b}}_{1}{\mathrm{I}}_{1}\left(\mathrm{t}\right)+ {\mathrm{b}}_{2}{\mathrm{I}}_{2}\left(\mathrm{t}\right)+\dots + {\mathrm{b}}_{\mathrm{n}}{\mathrm{I}}_{\mathrm{n}}\left(\mathrm{t}\right)$$
(7)

where \({\mathrm{b}}_{\mathrm{o}},\dots ,{\mathrm{b}}_{\mathrm{n}}\) are estimated mean coefficients for the linear variability for a particular location for the fitted non-stationary Log-normal distribution and \({\mathrm{I}}_{1},\dots ,{\mathrm{I}}_{\mathrm{n}}\) are the explanatory climate variables at time t. Then, using the time variant location parameter and the invariant scale parameter, the NRDI is estimated using the Eq. (8).

$$\mathrm{NRDI}\left(\mathrm{t}\right)=\frac{{\mathrm{y}}_{\mathrm{t}}- {\upmu }_{\mathrm{t}}}{\upsigma }$$
(8)

Here, \({y}_{t}=\mathrm{ln}\left({\delta }_{0}\right)\); \({\upmu }_{\mathrm{t}}\) is the time varying arithmetic mean and \(\sigma\) is the standard deviation of the observational variable. The parameters for Log-normal and Gamma distribution are estimated by Rigby and Stasinopoulos (RS) algorithm in the GAMLSS framework. The selection of both the models was evaluated in terms of lowest Akaike information criterion (AIC) values.

The classification of NSPI and NRDI is similar to the standard SPI (Mckee et al. 1993) and RDI (Tsakiris et al. 2007). The drought characteristics can be estimated using the widely accepted method Run theory analysis (Ganguli and Reddy 2012; Dixit et al. 2021). A run is defined as the values below a preferred truncation level by considering the positive and negative run (Yevjevich 1967). In the present study, a value of -0.8 is considered as the threshold value below which all the values are taken to represent drought events. Duration (D), peak (P) and severity (S) are the three drought characteristics considered in the study.

3.3 Multivariate Dependence Modelling Using Copula Constructions

The multivariate drought frequency analysis based on copula theory can be used to overcome the limitations of univariate drought frequency analysis. A trivariate distribution function, fitted to three dependent drought characteristics P, D and S with marginal CDFs \({\mathrm{F}}_{\mathrm{P}}, {\mathrm{F}}_{\mathrm{D}}\ {\mathrm{and\ F}}_{\mathrm{S}}\) can be represented based on copula function that guarantees the existence of a unique function c such that, \(\mathrm{P},\mathrm{ D}\) and \({\mathrm{S}}_{,}\in \mathrm{R}\). The trivariate joint probability distribution resulting in the parameter associated with the specified copula function is presented by Eq. (9).

$$\mathrm{f}\left(\mathrm{P},\mathrm{D},\mathrm{S}\right)={\mathrm{f}}_{\mathrm{P}}\left(\mathrm{P}\right)\times {\mathrm{f}}_{\mathrm{D}}\left(\mathrm{D}\right)\times {\mathrm{f}}_{\mathrm{S}}\left(\mathrm{S}\right)\times \mathrm{c}\left[{\mathrm{F}}_{\mathrm{P}}\left(\mathrm{P}\right),{{\mathrm{F}}_{\mathrm{D}}\left(\mathrm{D}\right),\mathrm{F}}_{\mathrm{S}}\left(\mathrm{S}\right)\right]$$
(9)

Different types of copula families like Frank, Gaussian, Gumbel, Clayton, and Student’s t copula are used in many hydro-meteorological studies. The dependency status between the interrelated drought variables is represented by the respective copula parameter. In this study, the parameters of copula families are estimated using the Maximum Likelihood Estimation (MLE) method based on its fitted marginal distribution. The best fitted copula was estimated based on the Goodness of Fit (GoF) measures such as Kolmogorov–Smirnov test (KS), Cramer-von Misses (CVM), and Chi-square (Chsq) tests (Genest and Favre 2007), AIC criteria and the maximum likelihood function. The copula parameters and their constructions carried out in this study are presented briefly (in Eqs. (10) to (14)). For more details regarding copula, Nelsen (2006) may be referred.

$$\mathrm{Clayton}:{\mathrm{C}}_{\uptheta }\left(\upalpha ,\upbeta \right)={\left({\upalpha }^{-\uptheta }+{\upbeta }^{-\uptheta }-1\right)}^{-\uptheta }\mathrm{for\ all\ \uptheta }\left(0,\infty \right)$$
(10)
$$\mathrm{Frank}:{\mathrm{C}}_{\uptheta }\left(\upalpha ,\upbeta \right)=-\frac{1}{\uptheta }\mathrm{log}\left(1+\frac{\left(\mathrm{exp}\left(-\uptheta \upalpha \right)-1\right)\left(\mathrm{exp}\left(-\uptheta \upbeta \right)-1\right)}{\mathrm{exp}\left(-\uptheta \right)-1}\right)\mathrm{for}\ \theta \in \mathrm{R}\left\{0\right\}$$
(11)
$$\mathrm{Gaussian}:{\mathrm{C}}_{\uptheta }\left(\upalpha ,\upbeta \right)=\underset{-\infty }{\overset{{\upvarphi }^{-1(\upalpha )}}{\int }}{\int }_{-\infty }^{{\upvarphi}^{-1(\upbeta )}}\frac{1}{2\pi \sqrt{1-{\theta }^{2}}}{\mathrm{e}}^{\frac{2\uptheta \mathrm{uv}-{\mathrm{u}}^{2}-{\mathrm{v}}^{2}}{2\left(1-{\uptheta }^{2}\right)}}\mathrm{dudv}$$
(12)
$$\mathrm{Gumbel}:{\mathrm{C}}_{\theta }\left(\alpha ,\beta \right)=\mathrm{exp}\left\{{-[-(-{\mathrm{log}\alpha )}^{\theta }+(-{\mathrm{log}\beta )}^{\theta }]}^{{1}/{\theta}}\right\},\ \mathrm{for\ \theta\ \epsilon }\left[1,\infty \right)$$
(13)
$$\mathrm{Student}\operatorname{-}\mathrm{t}:{\mathrm{C}}_{\uptheta }\left(\upalpha ,\upbeta \right)=\underset{-\infty }{\overset{{{\mathrm{T}}_{\upgamma }}^{-1(\upalpha )}}{\int }}{\int }_{-\infty }^{{{\mathrm{T}}_{\upgamma }}^{-1(\upbeta )}}\frac{\Gamma \left(\frac{\upnu +2}{2}\right)}{\Gamma \left(\frac{\upnu }{2}\right)\mathrm{\upnu \uppi }\sqrt{1-{\uptheta }^{2}}}\left\{1+\frac{{\mathrm{u}}^{2}+{\mathrm{v}}^{2}-2\mathrm{\uptheta uv}}{\upnu \left(1-{\uptheta }^{2}\right)}\right\}\ \mathrm{dudv}$$
(14)

Daneshkhah et al. (2016) and Brechmann and Schepsmeier (2013) showed the complex structure of the dependencies between multivariate data. For example, the parameters of Student’s t copula showed a single degree of freedom which is the driving force for the dependency of all other pair of variables. Because of this limitation, a unique method of copula construction named as vine copula is introduced (Aas et al. 2009). Regular vines are broadly categorised into two subsets i.e. D-vine and Canonical vine (Kurowicka and Cooke 2006). Vine is a flexible graphically represented tree-like structure that computes the pairwise construction of variables that are mutually dependent, known as PCC model.

The D-vine structure that is used to model joint probability related to the drought characteristics \(\mathrm{P},\mathrm{D},\mathrm{and\ S}\) with the given marginal densities \({\mathrm{F}}_{\mathrm{P}},{\mathrm{F}}_{\mathrm{D}},{\mathrm{F}}_{\mathrm{S}}\) respectively. Here D-vine structure is selected for the joint density decomposition as shown in Eq. (15).

$$\begin{array}{l}\mathrm{F}\left(\mathrm{P},\mathrm{D},\mathrm{S}\right)={\mathrm{f}}_{\mathrm{P}}\left(\mathrm{P}\right)\times {\mathrm{f}}_{\mathrm{D}}\left(\mathrm{D}\right)\times {\mathrm{f}}_{\mathrm{S}}\left(\mathrm{S}\right){\mathrm{c}}_{\mathrm{PD}}\left\{{\mathrm{F}}_{\mathrm{P}}\left(\mathrm{P}\right),{\mathrm{F}}_{\mathrm{D}}\left(\mathrm{D}\right)\right\}\\\qquad\qquad\qquad\times {\mathrm{c}}_{\mathrm{DS}}\left\{{\mathrm{F}}_{\mathrm{D}}\left(\mathrm{D}\right),{\mathrm{F}}_{\mathrm{S}}\left(\mathrm{S}\right)\right\}\times {\mathrm{c}}_{\mathrm{PS}|\mathrm{D}}\left\{{\mathrm{F}}_{\mathrm{PD}}\left(\mathrm{P}|\mathrm{D}\right),{\mathrm{F}}_{\mathrm{SD}}\left(\mathrm{S}|\mathrm{D}\right)\right\}\end{array}$$
(15)

\({\mathrm{c}}_{\mathrm{PD}}\left\{{\mathrm{F}}_{\mathrm{P}}\left(\mathrm{P}\right),{\mathrm{F}}_{\mathrm{D}}\left(\mathrm{D}\right)\right\}\) represents the bivariate copula fitted between \({\mathrm{F}}_{\mathrm{P}}\left(\mathrm{P}\right)\) and \({\mathrm{F}}_{\mathrm{D}}\left(\mathrm{D}\right)\). \({\mathrm{c}}_{\mathrm{PS}|\mathrm{D}}\left\{{\mathrm{F}}_{\mathrm{PD}}\left(\mathrm{P}|\mathrm{D}\right),{\mathrm{F}}_{\mathrm{SD}}\left(\mathrm{S}|\mathrm{D}\right)\right\}\) represents the bivariate copula fitted to the second tree variables \({\mathrm{F}}_{\mathrm{PD}}\left(\mathrm{P}|\mathrm{D}\right),{\mathrm{F}}_{\mathrm{SD}}\left(\mathrm{S}|\mathrm{D}\right).\)

3.4 Estimation Methods for Pair-Copula Models

The dependency measurement between drought characteristics like P–D, D – S and S–P are estimated using Kendall’s τ and Spearman’s ρ and presented in supplementary Table S7. Then, an appropriate D-vine model was chosen in terms of the dependency of variables. Graphical tools like Kendall plot (K-plot) and Chi-plots are useful for the optimum choice of bivariate copula models (Genest and Favre 2007). The GoF tests such as Vuong and Clarke tests, were also implemented to find the suitable copula family for this study (Vuong 1989). Commonly used AIC criteria to distinguish between models were also used to find an optimum solution regarding the selection of copula family.

After deciding the pairwise copula models, the parameters were estimated based on the MLE method. For more details regarding the vine copula and process of parameter estimation for the distribution function, Aas et al. (2009) can be referred. Drought frequency analysis was carried out to identify the changes in the return period with respect to the trivariate copula model. The return period can be obtained by selecting the appropriate copula family based on the dependent parameters.

4 Results and Discussions

4.1 Non-stationary SPI and RDI Indices

The basis for this study to incorporate large-scale climate indices was that the global climatology is highly affected by the climatic phenomenon over the Pacific and Indian oceans (Rashid and Beecham 2019). The large-scale climate indices are considered as external covariates for evaluating the NSPI and NRDI. For the LGRB and URGB, the monthly aggregation (3-, 6- and 12- month moving average) of precipitation and evapotranspiration data were prepared. In addition, the moving average of climate indices were obtained and then organised into 13 different lag values from 0 to 12. MLE method is used for the evaluation of parameters of Gamma and Log-normal distributions. Comparison between the stationary and non-stationary models was carried out by estimating the two stationary based indices namely SSPI and SRDI by keeping the parameters invariant with time.

Kendall correlation analysis was carried out at a significance level of 0.05 for the assessment of significant large-scale climate indices based on different lags for different time scales. Table 2 displays the dominant covariates for parameters of fitted distributions. It was observed that the 3-month cumulative precipitation and initial values (\({\updelta }_{0}\)) showed a significant correlation with SOI and IOD for the UGRB and SOI for the LGRB for different lags respectively. Similarly, SOI was identified as the most influential covariate for 6-month aggregated precipitation and \({\delta }_{0}\) series for the UGRB whereas SOI and SST showed a quantitative influence in the LGRB for different lag values. The MEI, SOI and SST are significantly associated with 12-month cumulative precipitation and \({\delta }_{0}\) for both the sub-basins.

Table 2 Significant lag for different large-scale climate oscillations
Full size table

The stationary and non-stationary models are optimised by minimizing the AIC. Table 3 represents the AIC values for non-stationary and stationary models. The AIC values obtained from non-stationary models are consistently lesser than those obtained from the stationary models. Hence, it can be concluded that the non-stationary models achieved better performance than the stationary models.

Table 3 Comparison between stationary and non-stationary models using AIC values
Full size table

4.2 Comparison of Historical Drought Characteristics

The outputs in the form of rationales are the drought indices that are transformed from the cumulative probability of rainfall and initial values (\({\updelta }_{0}\)). There are many differences of signals between the stationary and non-stationary time series, which are due to the inclusion of the external covariates. Large dissimilarities of signals were observed between NSPI and SSPI for 3-, 6- and 12-month aggregation levels for both the sub-basins as seen in Figs. 2 and 3. These dissimilarities are apparent in case of drought characteristics SPI and RDI and are fairly different from the NSPI and NRDI. For comparing stationary and non-stationary models, the box plots for 3-, 6-and 12-month time windows are shown in Figs. 4 and 5 for UGRB and LGRB to identify the variations of the drought characteristics. In these figures, P1, D1 and S1 refer to non-stationary drought characteristics while P2, D2 and S2 refer to stationary characteristics. After comparing 3-month NSPI and SSPI, significant differences are identified in the drought characteristics in the LGRB (Fig. 4b) compared to the UGRB (Fig. 4a). Larger differences were evident in the drought severity and peak between NSPI and SSPI for the LGRB for 3-month time scale. In the case of duration, the UGRB showed significant variations between NSPI and SSPI for 3-month time scale whereas the LGRB showed less variations. Figure 5 shows the comparison between NRDI and SRDI for the spatial and temporal variability of drought characteristics for the 3-month time scale. The estimated severities of SRDI series were lower than the severity from NRDI series in the case of UGRB whereas the estimated peaks of SRDI series were higher than those estimated from the NRDI series (Fig. 5a). In case of 3-month time series, the LGRB, the peak and severity estimated from SRDI were higher than that of the NRDI (Fig. 5b). The comparison between NRDI and SRDI showed some variations in drought duration. From Fig. 4c, it is observed that the UGRB displayed significant changes in peak, duration and severity of the 6-month NSPI and SSPI series. For LGRB, there were significant variations of peak and severity whereas lesser variations of NSPI and SSPI were detected for the drought duration (Fig. 4d). From Fig. 5c and d, no significant variations of the drought characteristics were observed for NRDI and SRDI for both the sub-basins for the 6-month time scale. Comparison of the non-stationary approach and stationary for the 12-month time scale for the drought events in both sub-basins showed significant deviations in drought characteristics (Fig. 5e and f). It can, hence, be concluded that substantial variations of drought characteristics were evident in the case of 12-month time window comparing to 3- and 6-month time window.

Fig. 2
figure 2

NSPI and SSPI drought signals during 1951–2017 for 3-, 6- and 12-month time scales: (a) 3-month time scale for UGRB; (b) 3-month time scale for LGRB; (c) 6-month time scale for UGRB; (d) 6-month time scale for LGRB; (e) 12-month time scale for UGRB; (f) 12-month time scale for LGRB

Full size image
Fig. 3
figure 3

NRDI and SRDI drought signals during 1951–2017 for 3-, 6- and 12-month time scales: (a) 3-month time scale for UGRB; (b) 3-month time scale for LGRB; (c) 6-month time scale for UGRB; (d) 6-month time scale for LGRB; (e) 12-month time scale for UGRB; (f) 12-month time scale for LGRB

Full size image
Fig. 4
figure 4

Comparison by box plots for drought variables peak (P), duration (D) and severity (S) for NSPI and SSPI for different time scales: (a) 3-month time scale for UGRB (b) 3-month time scale for LGRB; (c) 6-month time scale for UGRB (d) 6-month time scale for LGRB; (e) 12-month time scale for UGRB (f) 12-month time scale for LGRB

Full size image
Fig. 5
figure 5

Comparison by box plots for drought variables peak (P), duration (D) and severity (S) for NRDI and SRDI for different time scales (a) 3-month time scale for UGRB (b) 3-month time scale for LGRB; (c) 6-month time scale for UGRB (d) 6-month time scale for LGRB; (e) 12-month time scale for UGRB (f) 12-month time scale for LGRB

Full size image

The differences observed in the drought characteristics between the stationary and non-stationary models have significant role in the implementation of sustainable water resources systems planning and management. In this study, non-stationary models have been considered for further analysis using trivariate and pairwise copula.

4.3 Trivariate Copula Models

The Archimedean copulas (Gumbel, Frank and Clayton) and elliptical copulas (Gaussian and Student’s t) are used in this study to evaluate the dependence structure of drought characteristics. Different types of distributions namely Gumbel, Gamma, Log-normal, Weibull and Exponential distributions were fitted to the drought characteristics. The best fitted distributions for several time scales were obtained based on AIC criteria and the log-likelihood values to find the marginal distributions are provided in Supplementary Tables S1-S6.

The best fitted trivariate copula model among the copulas was decided by analysing the GoF measures–KS, CVM, Chsq considering 2000 sample runs including AIC, log-likelihood values and their estimated parameters are represented in Tables 4 and 5. The results from the tables show that the Student’s t copula performed better rather than the other trivariate copula models. The parameter estimation of trivariate copula analysis was conducted using the MLE method. Higher dimensional Student's t copula is more popular in hydrological studies for modelling of different extreme events (Ganguli and Reddy 2013). The main limitation of modelling of the higher dimensional Student’s t copula is that it has only a single degree of freedom for each pair of parameters (Aas et al. 2009). However, this limitation can be further efficiently modified by the PCC models (Tables 4 and 5).

Table 4 Trivariate copula analysis for non-stationary reconnaissance drought characteristics
Full size table
Table 5 Trivariate copula analysis for non-stationary standardized precipitation drought characteristics
Full size table

4.4 Drought Characteristics Modelling Using Pair-Copula Models

Suitable vine structure between C-vine and D-vine models and the copula families must be selected for the dependent pair variables viz., peak (P)–duration (D), duration (D)–severity (S) and severity (S)–peak (P). The dependency measures between pair variables of drought events are given in Supplementary Table S7. This supporting document explains the stronger dependence between D and S. The next stronger dependency was observed between S and P. It can, hence, be concluded that S must be present between D and P for the D-vine structure. D-vine structure was selected for further analysis since it has more flexibility towards forming the pair copula rather than the C-vine structure because it creates a relationship of variables with a particular root variable that defines the key elements of the structure (Aas et al. 2009). Kendall’s plots and Chi-plots of the pair variables P–D, D–S and S–P are given in the Supplementary Figs. S1-S12 signifying positive dependencies between the pair variables. The dependency measures and the Kendall’s and Chi-plots of the pair variables signifies that D – S showed the strongest dependency than other pairs. The copula families for the pair variables were selected from various copulas based on Clarke and Vuong tests.

In the first phase of parameter estimation method, the sequential parameters were estimated using the MLE method for these pairs of drought variables D/S (\({\uptheta }_{\mathrm{DS}}\)) and S/P (\({\uptheta }_{\mathrm{SP}}\)). Then for the second phase of parameter estimation, the respective h functions (conditional distribution function) were computed between the pair variables D/S and S/P. The parameter, \({\uptheta }_{\mathrm{DP}/\mathrm{S}}\) was then estimated for drought variables (D/S, S/P). The copula families selected for the pair variables and the parameters estimated in the second phase (\({\uptheta }_{\mathrm{DP}/\mathrm{S}}\)) considering the best fitted copula for the LGRB and UGRB for different time scales are given in Table 6.

Table 6 Pairwise Copula Construction (PCC) for NSPI and NRDI drought characteristics
Full size table

In the second phase of parameter estimation, the copula was selected from the first phase of copula families fitted for estimation of the sequential parameter. For example, in the case of the generated drought characteristics from 3- month NRDI, Gaussian copula was selected for estimation of the second phase of the parameter. Finally, the PCC model, accounting for the drought variables was compared with the derived trivariate copula using the AIC criteria. It can be observed from Supplementary Table S8 that the AIC of the trivariate model showed higher AIC value compared to PCC based model. It can, hence, be justified that the PCC model can flexibly model the drought characteristics by transforming the bivariate model to a higher dimensional model.

4.5 Return Period Analysis of Drought Variables

The frequency analysis of droughts can be related to the occurrence of extreme events and their probability distributions. Here, the values of peak (P), duration (D) and severity (S) that exceed their truncation level (\(\mathrm{S}\ge \mathrm{s},\mathrm{D}\ge \mathrm{d},\mathrm{P}\ge \mathrm{p}\)) were considered for analysing the multivariate drought frequency. The joint return period analysis was carried out by using the two probability cases i.e. (i) ‘‘AND” and ‘‘OR” return periods for the drought variable using the approach suggested by Salvadori and Michele (2004). For annual drought analysis, the mathematical expressions for return period considering the ‘‘AND” and ‘‘OR” case are shown in Eqs. (16) and (17).

$$\begin{array}{l}{\mathrm{T}}_{\left(\mathrm{SDP}\right)}^{\mathrm{AND}}=\frac{\varepsilon }{\mathrm{P}\left(\mathrm{S}\ge \mathrm{s},\mathrm{D}\ge \mathrm{d},\mathrm{P}\ge \mathrm{p}\right)}=\frac{\varepsilon }{1-{\mathrm{F}}_{\mathrm{S}}\left(\mathrm{s}\right)-{\mathrm{F}}_{\mathrm{D}}\left(\mathrm{d}\right)-{\mathrm{F}}_{\mathrm{P}}\left(\mathrm{p}\right)+{\mathrm{F}}_{\mathrm{S},\mathrm{D}}\left(\mathrm{s},\mathrm{d}\right)+{\mathrm{F}}_{\mathrm{D},\mathrm{P}}\left(\mathrm{d},\mathrm{p}\right)+{\mathrm{F}}_{\mathrm{P},\mathrm{S}}\left(\mathrm{p},\mathrm{s}\right)-{\mathrm{F}}_{\mathrm{S},\mathrm{D},\mathrm{P}}\left(\mathrm{s},\mathrm{d},\mathrm{p}\right)}\\\qquad\;\;\;=\frac{\varepsilon }{1-{\mathrm{F}}_{\mathrm{S}}\left(\mathrm{s}\right)-{\mathrm{F}}_{\mathrm{D}}\left(\mathrm{d}\right)-{\mathrm{F}}_{\mathrm{P}}\left(\mathrm{p}\right)+\mathrm{C}\left({\mathrm{u}}_{1},{\mathrm{u}}_{2}\right)+\mathrm{C}\left({\mathrm{u}}_{2},{\mathrm{u}}_{3}\right)+\mathrm{C}\left({\mathrm{u}}_{3},{\mathrm{u}}_{1}\right)-\mathrm{C}\left({\mathrm{u}}_{1},{\mathrm{u}}_{2},{\mathrm{u}}_{3}\right)}\end{array}$$
(16)
$$\begin{array}{l}{\mathrm{T}}_{\mathrm{SDP}}^{\mathrm{OR}}=\frac{\varepsilon }{\mathrm{P}(\mathrm{S}\ge \mathrm{s},\mathrm{D}\ge \mathrm{d},\mathrm{P}\ge \mathrm{P})}=\frac{\varepsilon }{1-\mathrm{P}(\mathrm{S}\ge \mathrm{s},\mathrm{D}\ge \mathrm{d},\mathrm{P}\ge \mathrm{P})}\\\qquad\;=\frac{\varepsilon }{1-{\mathrm{F}}_{\mathrm{S},\mathrm{D},\mathrm{P}}\left(\mathrm{s},\mathrm{d},\mathrm{p}\right)}=\frac{\varepsilon }{1-\mathrm{C}({\mathrm{u}}_{1},{\mathrm{u}}_{2},{\mathrm{u}}_{3})}\end{array}$$
(17)

Supplementary Tables S9-S12 show the joint return periods (‘‘AND” and ‘‘OR” cases) obtained from the trivariate copula and PCC models using the drought characteristics for NSPI and NRDI for 3-, 6- and 12- month time scale. Here \({\mathrm{T}}_{\left(\mathrm{SDP}\right)}^{\mathrm{AND}}\mathrm{TC}\) and \({\mathrm{T}}_{\left(\mathrm{SDP}\right)}^{\mathrm{AND}}\mathrm{ PCC}\) represent the joint return periods for trivariate Student’s t copula and PCC model respectively. Similarly, the joint return period of “OR” case can be denoted as \({\mathrm{T}}_{\mathrm{SDP}}^{\mathrm{OR}}\mathrm{TC}\) and \({\mathrm{T}}_{\left(\mathrm{SDP}\right)}^{\mathrm{OR}}\mathrm{PCC}\) for trivariate Student’s t copula and PCC models respectively. The ‘‘OR” joint return periods are less compared to ‘‘AND” return periods in both trivariate Student’s t copula and PCC models. It can, hence, be concluded that the frequency of drought is more in the ''OR” case when compared to the "AND" case.

5 Conclusions

The concept of non-stationarity was employed by aggregating the precipitation and initial value series with the large-scale climate indices with lag time of 0–12 months. It can be concluded that the non-stationary meteorological droughts considering the large-scale climate indices are capable of capturing the drought events in comparison with stationary drought indices. Both precipitation and evapotranspiration based non-stationary drought indices can be applied to identify more complex aspect of drought occurrence. The probabilistic estimation of drought characteristics must be carried out to estimate the recurrence intervals of droughts. The standard multivariate copulas are not flexible enough to model the higher dimensional copula for assessment of extreme events. The drawbacks of multivariate copulas can be removed using D-vine copula models. D-vine PCC model was also used to find the drought return periods. The conclusions derived in the present study are:

  1. 1.

    The non-stationary models performed better compared to the stationary models as the AIC values are lower in case of non-stationary models. UGRB, showed a significant influence at various lags for 3-, 6- and 12- month time scales. SOI, MEI and SST are the most influential large oscillations at different time scales are the most influential covariates.

  2. 2.

    The non-stationary and stationary models showed variations in their time signals. The box plots between drought variables revealed that the drought properties significantly varied under stationary and non-stationary conditions in the both the basins for 12-month time scale.

  3. 3.

    The "AND" and "OR’ joint return periods for PCC models are higher compared to those obtained from the trivariate Student’s t copula model for both the non-stationary models. The drought frequencies for PCC model is higher as compared to the trivariate copula model.

  4. 4.

    After analysing the trivariate and PCC models, the return periods showed variations between “AND” and “OR” return periods for drought indices in different time scales. The variations of return periods between trivariate Student’s t copula and PCC model are significant in case of 12-month time scale for both the non-stationary drought events. To summarize, the ‘AND’ and ‘OR’ return periods predicted by PCC model are more reliable compared to trivariate Student’s t-copula model as PCC model performed better than the trivariate Student’s t copula.