1 Introduction

Floods are among the most devastating natural disasters that cause mortalities and financial losses in the affected areas. They are important not only for their destructive effects at the time of occurrence but also for their post-disaster damaging effects persisting for a long time. Global Assessment Report on Disaster Risk Reduction (UNISDR 2015) indicates that flood mortality rate is increasing in developing countries such as Iran. The flood mortality rate has increased by 11% in the Middle East and North Africa compared to the last century (Ghomian and Yousefian 2017). Over the past few years, floods have been the most serious natural disaster in Iran. The recent flood of March 2019 affected many parts of the country with a loss of 76 people and damages of 476 million US dollars.

Knowledge of flood magnitudes and frequencies is critical for flood preparedness by adopting preventive measures to mitigate their destructive effects. Flood frequency analysis (FFA) is employed for estimating flood magnitudes for given return periods; economically safe designs of hydraulic structures such as dams, culverts, bridge, and spillways and it can be also used to determine flood insurance premiums under potential flood damages.

Single-site FFA is performed by fitting appropriate univariate probability distributions to peak stream flow data (Modarres 2008). In the case of interconnected rivers, where two mainstreams with different drainage areas, land-use/land-cover schemes and consequently different probability distributions join together, FFA can however be challenging, especially when the two mainstreams marge at a dam where the historical streamflow data are usually not available. Fitting univariate probability distributions to the sums of flows may not be appropriate, because different pairs of flood quantiles which have the same probability of occurrence may have different severities of impact. Also, the stochastic nature of interconnected rivers with different drainage areas and hydro-geomorphic characteristics may differ from each other. Thus, the use of bivariate probability distributions will not guarantee reliable flood quantile estimation, as they assume that the flood records of the joining rivers share the same probability distributions. To our best knowledge, little literature provides the solution to the estimation of design flood at the confluence of the interconnected rivers, especially where two rivers merge at a reservoir dam.

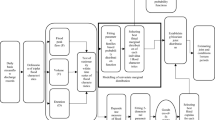
In this study, an innovative application of copula functions (Sklar 1959) for design flood estimation at the confluence of interconnected rivers is presented by mapping from bivariate to univariate peak flow quantile estimation. Copulas have the capability of preserving the dependence structure of random variables having similar or different marginal probability distributions (Zhang and Singh 2019). Copulas have been applied to drought frequency analysis (Shiau and Modarres 2009; Mirakbari et al. 2010, 2012; Janga Reddy and Ganguli 2012; Madadgar and Moradkhani 2012; Lee et al. 2013; Saghafian and Mehdikhani 2014; Dodangeh et al. 2017), rainfall frequency analysis (Kao and Govindaraju 2007, 2008; Zhang and Singh 2007; Zhang et al. 2013), flood frequency analysis (Grimaldi and Serinaldi 2006; Shiau et al. 2006; Zhang and Singh 2006; Fu and Butler 2014), rainfall-runoff frequency analysis (Golian et al. 2012; Dodangeh et al. 2019), water quality analysis and other analyses (Zhang and Singh 2019). The copula model was applied to peak flow magnitudes estimation at the Sefidrud dam (where the Qezel Ozan and Shahrud Rivers merge). Various combinations of copula functions and univariate probability distributions were assessed to select the best combination to fit the joint cumulative distribution functions (CDFs) of annual peak flows of Qezel Ozan River and corresponding flows of Shahrud River. Then, the joint flood quantile and the uncertainty of joint flood quantile was estimated using a non-parametric bootstrapping method. Figure 1 demonstrates the general flowchart of the methodology used.

Fig. 1
figure 1

Flowchart of methodology

Full size image

2 Description of Study Area

The study area is Sefidrud (Manjil) lake dam at the intersection of Qezel Ozan and Shahrud Rivers. The dam is located 75 km south of Rasht and is adjacent to the Manjil city. The main objective of the Sefidrud dam is to regulate inflows into the Sefidrud River to irrigate 189,832 ha of grasslands in Guilan and Foumanat Plain downstream of the dam. There are also secondary objectives, such as flood control, production of hydroelectric power with a nominal capacity of 87.5 MW, drinking water supply and urban industries of Central to and East of Guilan, and meeting the needs of fishery, aquaculture, and animal husbandry (Dodangeh 2010).

The drainage area of the Sefidrud lake is approximately 56,200 km2 and the volume of the lake is 1756–106 m3 which is supplied by two mainstreams, namely Qezel Ozan River in the west and Shahrud River in the east of the dam. The Shahrud River with a length of 180 km originates in the Taleghan, Alamkooh, Takht-e-Solaiman and central Alborz mountain ranges and it is the main river of the Qazvin province. The Qezel Ozan River with a length of 800 km is one of the longest rivers of the country that originates in the Chehel Cheshmeh mountain ranges in Kurdistan and East Azarbaijan province (Dodangeh et al. 2014). In the south of Guilan province, in the waters of Sefidrud dam, it joins the Shahrud River and forms the Sefidrud River.

Sefidrud dam is one of the most sediment-silting dams in the world and more than half of the reservoir capacity is filled with sediment (Kavian et al. 2016). Since the 1980s, Shas operation has been used to overcome siltation. However, considering the overflow discharge of about 5000 m3/s, which was estimated at the time of dam construction, severe floods in Qezel Ozan and Shahrud Rivers may endanger the dam stability and the lives of residents of the areas adjacent to the lake (as illustrated in Fig. 2). Therefore, flood frequency and magnitude estimation are essential for determining the extent of flooding around the lake and for estimating potential damages caused by flooding. For this purpose, historical data for a 49-year period (1963–2011) from the Gilvan (#17–033) (GPF) and Loshan (#17–041) (LCF) gauging stations, located on Qezel Ozan and Shahrud Rivers, respectively, were used.

Fig. 2
figure 2

Location of the study area

Full size image

3 Methods

3.1 Copulas

For bivariate cases, the joint CDF, FX, Y(x, y), of random variables X and Y can be expressed using the copula function as:

$$ {F}_{X,Y}\left(x,y\right)=C\left({F}_X(x),{F}_Y(y)\right) $$
(1)

where C is the copula function, and FX(x) and FY(y) are the marginal cumulative distribution functions (CDFs) of random variable X and Y, estimated using the univariate probability distributions. For the cestimation of univariate CDFs of the X and Y variables, the probability distributions suggested by Rao and Hamed (2002) were used (Table 1). Parameters of the marginal distributions were estimated independently and then the copula parameter was estimated based on the dependence between the marginal variables. Equation 1 can be rewritten in the form:

$$ {F}_{X,Y}\left(x,y,\theta \right)=C\left({F}_X\left(x,{\theta}_x\right),{F}_Y\left(y,{\theta}_y\right),{\theta}_c\right) $$
(2)

where θx and θy are the parameters of the univariate marginal distributions, θ is the parameter of bivariate distribution and θc is the copula parameter (Dung et al. 2015). Of the various copula functions used for multivariate frequency analysis of random variables (Joe 1997; Nelsen 2006; Sungur and Nelson 2006; Zhang and Singh 2019), Archimedean, Gaussian, Student’s t and Plackett copulas were used to model the joint GPF-LCF pairs.

Table 1 Goodness of fit test of univariate probability distributions
Full size table

3.2 Parameter Estimation for Bivariate Distributions

Reliable parameter estimation is required to identify the best fit distributions (de Melo e Silva Accioly and Chiyoshi 2004). Both parametric and nonparametric approaches, such as Kendall’s tau and Maximum likelihood estimation (MLE) method (Genest and Rivest 1993), have been employed. The non-parametric Kendall’s tau estimation method is based on the association between Kendall’s tau and copula parameters (Mirakbari et al. 2010). Kendall’s tau estimation can be used for single-parameter copula families (Zhang and Singh 2006; Mirakbari et al. 2010; Janga Reddy and Ganguli 2012). However, for one- and two- parameter copula families such as Student’s t copula, the maximum likelihood estimation method, which is more appropriate (Joe 1997), was used. For the estimation of copula parameters using the MLE method, the log likelihood (LL) can be expressed as:

$$ L\left(\theta \right)=\sum \limits_{i=1}^n\log \left[{c}_{\theta}\left\{{F}_X\left({x}_i\right),{F}_Y\left({y}_i\right)\right\}\right] $$
(3)

where F denotes the marginal distributions, cθ denotes the copula density function with parameter θ, X and Y denote random variables and xi and yi denote historical observations (Dodangeh et al. 2019). Using the MLE method, the bivariate model parameter (θ) was estimated as the value for which the negative LL function is minimized.

3.3 Copula Model Selection Criteria

For identifying the copula which best fitted the GPF-LCF pairs, various performance measures and goodness-of-fit tests (GOF) were utilized. The Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) are commonly used performance measures (Breymann et al. 2003). The AIC and BIC values were computed as follows:

$$ AIC=2L\left(\theta \right)+2/\left(n\ast k\right) $$
(4)
$$ BIC=2L\left(\theta \right)+\mathit{\ln}(n)/\left(n\ast k\right) $$
(5)

In Eqs. 4 and 5, k denotes to the number of estimated parameters, n is the data length, and L(θ) denotes to the log-likelihood value. For small data samples with n/k < 40, the second order variant of AIC, named AICc, was estimated as (Viglione 2008):

$$ {AIC}_c=2L\left(\theta \right)+2/\left(n\ast k\right)\ast \left(n/\left(n-k-1\right)\right) $$
(6)

These performance measures are however only useful for comparative assessment between the models but are not capable of representing the degree-of-fit of the copula models (Genest and Rivest 1993). For verification of the copula model selection using the AIC, BIC and AICc measures, the White test (White 1982) was employed to test if the copula belonged to the selected copula family.

3.4 Bivariate Quantile Estimation

The joint return period of a GPF-LCF quantile was estimated from the best fit copula with the joint CDFs of the GPF and LCF data:

$$ {T}_{GPF- LCF}=T\left( GP F\ge GP{F}^{\prime }, LPF\ge LC{F}^{\prime}\right)=\frac{E(L)}{1-{F}_{GPF}\left( GP{F}^{\prime}\right)-{F}_{LCF}\left( LC{F}^{\prime}\right)+C\left[{F}_{GPF}\left( GP{F}^{\prime}\right),{F}_{LCF}\left( LC{F}^{\prime}\right)\right]} $$
(7)

Here C is the copula function, TGPF-LCF is the joint return period of GPF ≥ GPF′ and LCF ≥ LCF′. GPF′ and LCF′ are the specified values of the Gilvan peak flows and the corresponding Loshan flows. E(L) denoted the expected inter-arrival time of GPF ≥ GPF′ and LCF ≥ LCF′ events, that is calculated based on the historical data; FGPF(GPF′) and FLCF(LCF′) are CDFs of GPF and LCF.

3.5 Uncertainty Analysis of Bivariate Quantile Estimation

Bivariate quantile estimation has uncertainties associated with parameters of marginal distributions, parameter of copulas, and inappropriate univariate or copula model selection. There is an additional uncertainty for bivariate quantile associated with the quantile selection on the p-level curves. There are indefinite combinations of x and y (PF data points) on a given p-level curve with the same probability of occurrence. However, they have different implications for engineering applications (Salvadori and De Michele 2011). The point with the highest density on the p-level curve is the event with the highest likelihood and is considered as a design event in hydrologic engineering applications. For the estimation of this point a line that best fits the dependence between X and Y variables, is plotted. Intersection of this line with the p-level curve identifies the design event. For this purpose, the Acceptance-Rejection Sampling (ARS) algorithm (Martino and Míguez 2010) was employed to estimate the bivariate design event on the p-level curves. The following steps were followed to estimate the design event based on the ARS algorithm:

  • [1] Set the number of bootstrap samples at a sufficient large number Nb (Nb = 500).

  • [2] Generate Nb bootstrap samples by sampling with replacement from the observed x-y pairs. The size of all Nb bootstrap samples should be identical to the size of the original sample of observed x-y pairs.

  • [3] Fit Nb separate copulas to the generated Nb bootstrap samples.

  • [4] Generate a random integer number in [1, Nb], and select the corresponding copula from the fitted copulas.

  • [5] Simulate a point along the level curve (at a specific p-level, for instance, p = 0.95) of the copula selected in step 4. Such a point is also referred to as the p-th quantile. Points along a level curve are simulated using the acceptance-rejection algorithm.

  • [6] Iterate steps 4 and 5 Ns = 50,000 times.

  • [7] Identify the confidence range around the p-level curves using the Ns points.

4 Results and Discussion

4.1 Homogeneity and Randomness Tests

Randomness and homogeneity of the GPF and LCF data were examined before doing the joint FFA. The run test (Rodrigo et al. 1999) checks the homogeneity of the GPF and LCF data at the 95% confidence level and investigates the variation of data around the median (Modarres 2008). Results showed that both GPF and LCF were homogeneous at 95% confidence level with p > 0.05. Randomness of the GPF and LCF time series is examined with the Autocorrelation and Partial autocorrelation functions (ACF and PACF), i.e., autocorrelation between the unique data points is calculated at various time lags. If the ACF values were near zero, especially at the first lag, then the data set was considered random. The zero and near zero values of PACF at the first lag also indicated the randomness of data sets (see Fig. 3). It shows that the ACF coefficients are close to zero, which indicated that the streamflow data are randomly distributed over time.

Fig. 3
figure 3

ACF and PACF values of the GPF (a) and LCF (b) data series

Full size image

4.2 Univariate GPF and LCF Quantile Estimation

Univariate FFA is performed by fitting the probability distributions to the GPF and LCF data. Fourteen probability distributions, including the normal, 2-parameter log-normal (LN2), Gumbel, Extreme values type II (EV2), Generalized extreme values (GEV), Pearson III (P3), Log-Pearson III (LP3), Weibull, Gamma, Logistic, exponential, 3-parameter Weibull (Weibull3p), generalized Pareto (GPAR), and 3-parameter log-normal (LN3) (Rao and Hamed 2002), are considered. Parameters of these distributions are estimated using the MLE method and their goodness-of-fit was evaluated based on the AIC, AICc, BIC criteria and Kolmogorove-Smirnove (KS) test. Results of the best fit distributions are given in Table 1. The best fit distribution is that with the least AIc, AICc and BIC values. The Weibull and gamma distributions best fitted the GPF (AIC =724, AICc = 725, BIC = 725) and LCF (AIC =544, AICc = 544, BIC = 549) peak flow data. The KS test also supported the selection of the Weibull and gamma distributions to fit the GPF (p value = 0.66) and LCF data (p value = 0.72). Past studies also found the Weibull distribution fitting annual maximum rainfall and river discharge (Aksoy 2000; Burn and Goel 2001; Chandrasekhar 2002; Ghorbani et al. 2010). The gamma distribution has also been used for flood frequency analyses (Haan 1977; Yevjevich and Obeysekera 1984; Singh 1998). Figure 4 illustrates the satisfactory fit of Weibull and gamma distributions to univariate GPF and LCF data.

Table 2 Performance evaluation and goodness of fit test of copula functions
Full size table
Fig. 4
figure 4

Univariate frequency analysis of GPF and LCF using Weibull and Gamma distributions

Full size image

4.3 Joint GPF-LCF Quantile Estimation

For the joint quantile estimation of the GPF-LCF, bivariate distributions based on nine copula functions, as given in Table 2, were built. According to the White test, all of the copulas had an acceptable fit (at 95% significant level) to the joint CDFs of the GPF-LCF data. The Gaussian copula was identified as the best fit copula based on the AIC, AICc and BIC criteria (AIC = −17.84, AICc = −17.83, BIC = −17.80). Visual inspection of the degree of fit of the Gaussian copula was also considered using the Q-Q plot. Figure 5 illustrates the empirical CDFs (Kn(t)) of the GPF-LCF pairs against that obtained by the Gaussian copula (K(t)). Clearly, empirical points fit will with Gaussian copula, which has a symmetric structure without tail dependency. It is selected because of its weaker dependencies of the most peak GPF and LCF events which may be attributed to the different GPF and LCF generation mechanisms.

Fig. 5
figure 5

Q-Q plot of the Gaussian copula

Full size image

For the joint quantile estimation of GPF-LCF using the Gaussian copula, the univariate CDFs derived by Weibull and gamma distributions were used (see the joint probabilities of occurrence and return periods of the GPF-LCF pairs in Figs. 6 and 7). It shows that most of GPF-LCF events (95%) occurs with a return period less than 100 -years, indicating the high risk of concurrent flooding in the Qezel Ozan and Shahrud Rivers. The comparison of the univariate and joint quantile estimates of the GPF and LCF in Figs. 4 and 7 indicates that univariate GPF and LCF quantiles occurred with shorter return periods than joint GPF-LCF quantiles. For example, the GPF quantile equal to 2000 m3/s and LCF quantile equal to 300 m3/s occurred with a 50-yr return period. However, the joint quantile of GPF-LCF equal to 2000–300 m3/s exceeded the 100-yr return period. For clarification, we constructed the conditional probability and return periods of the LCF quantiles given the various quantiles of GPF. Figure 8a, b shows the conditional return period and the probability of occurrence of LCF for different GPF quantiles and it demonstrates that the return period and probability of occurrence of LCF varies with GPF levels. The return period of LCF ≈ 330 m3/s is 50-yr return period for GPF ≥ 313 m3/s, while the return period of the same LCF quantile is 200 years for GPF ≥ 895 m3/s. Because the Sefidroud lake on the Sefidroud River is formed from two rivers, the univariate flood frequency analysis of GPF and LCF is not sufficient for optimal reservoir management and flood risk analysis around the lake. Thus the results of joint GPF-LCF quantile estimates can be helpful.

Fig. 6
figure 6

Joint probability of occurrence of the GPF and LCF data

Full size image
Fig. 7
figure 7

Joint return period (RT) of the GPF and LCF

Full size image
Fig. 8
figure 8

Conditional RT (a) and probability (b) of LCF given GPF

Full size image

4.4 Evaluation of Uncertainty of the Joint GPF-LCF Quantiles Estimates

The joint quantile estimates of GPF-LCF have uncertainties stemming from sample size, and inappropriate univariate and copula model selection and their associated parameter estimations. The non-parametric bootstrapping algorithm proposed in section 3.5 was used to estimate the uncertainties of the joint GPF-LCF quantiles. Figure 9 shows the uncertainty of bivariate GPF-LCF quantiles at various probability levels of p = 0.9 (≈10-yr return period), p = 0.95 (≈ 20-yr return period), p = 0.98 (≈ 50-yr return period) and p = 0.99 (≈ 100-yr return period). The 25–95% confidence regions (CRs) display the uncertainties of GPF-LCF quantile estimates. The parallel extent of CRs with p-level curves indicates the uncertainties caused by inefficient univariate distribution and copula function selection and associated parameter estimations (PU). Besides, the extent of CRs along the bottom left to top right direction demonstrates the sampling uncertainty (SU). The figures show that the dimension of CRs along the bottom left to top right direction increased for larger p-level curves. That implies that the GPF-LCF quantile estimates at larger hazard levels were more sensitive to sample size.

Fig. 9
figure 9

Uncertainty estimation of GPF-LCF quantiles at various probability levels

Full size image

4.5 Mapping from Bivariate to Univariate FFA

Finally, we estimate the peak flows generated at the confluence of two rivers by mapping from the bivariate to univariate FFA. For this purpose, the return period of the sum of the GPF and LCF was derived from the fitted copula. Figure 10 illustrates the return periods of peak flows of Qezel Ozn and Shahrud Rivers against the sum of the two river peak flows. It shows that a significant number of historical peak flows >1000 m3/s at the confluence of two rivers occurs with return periods less than 10 -years. This should be attached great importance from policymakers for flood control around the dam lake. Also, the same quantile of peak flows could occur with different return periods, which is caused by different combinations of GPF-LCF pairs and marginal probabilities. For example, both of 470–200 and 560–111 GPF-LCF events generated approximately the same inflow of 670 m3/s to the Sefidrud reservoir (Fig. 10), however, they lead to different occurrence probabilities of marginal events and affect flood control differently. This finding shows that simply fitting univariate distributions to the annual maxima of the sums of peak flows does not satisfy the requirement of FFA for interconnected rivers. Thus, this study provides a simple guide for statistical properties analysis of interconnected rivers using copulas, which does not seem to have received much attention.

Fig. 10
figure 10

Univariate peak inflow estimation at the Sefidrud dam location

Full size image

The flood dynamics and characteristics might be impacted by anthropogenic climate changes mainly due to increasing greenhouse gas emissions. As governed by the Clausius-Clapeyron relationship, the holding vapor capacity of atmosphere is increasing at rates with about 7% per degree warming, and thus lead to a substantial intensification of extreme precipitations and flooding in most areas of the globe. The change to flood characteristics is of great importance for water resources planning and management (Yin et al. 2018), which is not considered in this study due to lack of space. Future works can be devoted to investigate the bivariate flood quantiles under changing environments. Moreover, our developed methods can also be extended to estimate design floods at the confluence of more than two rivers, in which a trivariate or higher-dimensional copulas can be further employed.

5 Conclusions

Flood frequency analysis considering the confluence of interconnected rivers is of great importance in water resources engineering, but it has not yet been addressed in the literature. In this study we used potential of copulas for peak flow quantile estimation at the confluence of two interconnected rivers through mapping from bivariate to univariate peak flow quantile estimation.

The following conclusions can be drawn from this study:

  1. (1)

    The Gaussian copula with Weibull and gamma margins fits best for the estimation of the joint CDFs of the GPF-LCF data, based on its performance in terms of AIC, AICc, BIC. The efficiency of the copula function was also ascertained by White GOF test.

  2. (2)

    The joint probability distribution of the GPF-LCF pairs was derived for flood frequency analysis at the confluence of two rivers.

  3. (3)

    Bivariate quantile estimation uncertainties increased with increasing probability of hazard levels. The joint GPF-LCF quantiles at higher probability levels lead to higher uncertainties.

  4. (4)

    For FFA at the confluence of the two rivers, mapping from the bivariate to univariate quantile estimation was done by plotting the joint return period of GPF-LCF pairs against their sum. Floods of greater than 1000 m3/s occurred with return periods less than 10 years at the confluence of two rivers.

  5. (5)

    Flood quantiles with the same magnitudes and different impacts occurred with different return periods which cannot be isolated in univariate FFA of summed GPF-LCF pairs. As there is one-one mapping between the probability and quantiles in univariate FFA, the marginal probabilities of GPF and LCF are not taken into account by simply fitting the univariate probability distributions to the summed GPF-LCF pairs. Thus all of the summed GPF-LCF pairs with the same magnitudes are assigned by the same return period which is not the case in practice. By using the copula-based method, we are able to isolate the same magnitudes of peak flows with different impacts at the confluence of the rivers.

The results of this study can be used to determine the extent of flooding with different return periods around the dam lake to prepare dam safety plans and to adopt preventive measures for reducing flood damages especially in the residential areas adjacent to the lake dam. As there is no direct literature addressing FFA for interconnected rivers, this study can be a good reference for future works for appropriate FFA at the confluence of the interconnected rivers.