1 Introduction

The supply of water to end users is energy demanding, due to the requirements of treatments and the need for pumping. Due to these energy demands and processes involved, the greenhouse gas emissions related to water supply are high (McNabola et al. 2014b). As an example, in the UK, water distribution has been estimated to be the fourth most energy intensive sector, with a total amount of 5 million tons of C O 2 per year (Ainger et al. 2009). In the US, the total amount of energy associated with water can be accounted as nearly 4 billion dollars per year (Zilberman et al. 2008). Water supply systems are generally characterized by low efficiency. A large amount of energy used to pump water is lost because most of the water supply and distribution systems are affected by water leakage (Olsson 2012).

Because the maintenance, rehabilitation or replacement of old and damaged pipes are expensive, water leakage is often kept under control by reducing the working pressure of the network through dissipation valves (Karadirek et al. 2012). This is conducted to face the variations in ground elevation and to set optimal pressure values within district metered areas (Alvisi and Franchini 2014). A preliminary study by Cabrera et al. (2010) showed that 40–60% of energy used to distribute water is lost due to leakage and head losses, while 30–60% of energy is effectively used to supply the end users.

Awareness about the scarcity of energy sources and impact of human activities on the environment has been increasing, while the cost of energy has been raising for the last decades. These issues suggest that the optimal management of a water system should be focused on the reduction of both energy consumption and greenhouse gas emissions, in order to increase efficiency and reduce the carbon footprint.

1.1 Energy Recovery in Water Networks

In this context, every effort should be made to reduce both leakage and energy dissipation in water networks, and several authors suggest the replacement of pressure regulating valves with turbines to reduce pressure and also recover energy (Ramos et al. 2010; McNabola et al. 2014a; Gallagher et al. 2015). The use of Pump As Turbines (PATs) has been recently demonstrated to be a viable and economical solution due to the large availability and the lower cost of pumps when compared to classical turbines (Carravetta et al. 2011; Fecarotta et al. 2015). Several works have been presented to show their hydropower potential in water distribution (Ramos et al. 2005; Fontana et al. 2012; McNabola et al. 2014b). Some authors propose different technical solutions for the regulation (Carravetta et al. 2014a; Fontana et al. 2016). Some others investigate the behaviour of PATs (Fecarotta et al. 2016; Carravetta et al. 2014b; Pugliese et al. 2016). Finally, some studies analyze the mutual behaviour of water network and hydropower devices (Arriaga 2010; De Marchis et al. 2016; Fecarotta et al. accepted). However, detailed methodologies on the optimal locations of turbines—and their optimal number—to be placed in a given network, are still lacking.

1.2 Optimal Location of Turbines

Few investigations analyze the problem of the optimal location of a hydropower device within a water network. The complexity of the problem lies in the nature of the network. The placement of a concentrated head loss, i.e. a turbine, along a pipe of a closed loop network affects the distribution of discharge among the branches of the network, as well as the available power. Moreover, the equations that are used to model fluid motion and water losses are non-linear. Furthermore, the location problem is a mixed integer problem, since it involves continuous variables (e.g. discharge, pressure) and integer variables (the presence of the turbine within a branch). Finally, the number of variables can be very large, depending on the size of the network and on the type of the simulation (steady, quasi-steady, transient). Fecarotta et al. (2015) showed a simplified two steps method where first the problem of optimal location of PRVs was solved and then some valves were replaced by PATs, with a good economic viability. Giugni et al. (2014) showed that two different objective functions can be selected with the purpose of optimizing either pressure reduction or power output potential, with consequent differing results. In the latter case, the author introduced a penalty factor within the objective function to avoid low values of service pressure. A genetic algorithm was used to find the optimal location of a fixed number of turbines under steady conditions, while an external solver was used to model the hydraulic behaviour of the network. A second run of the optimization model was used to set the optimal values of head losses within the turbines under daily variable conditions, assuming the location to be known. Corcoran et al. (2015) performed a two steps optimization: in the first step, the optimal location of a fixed number of turbines was found to maximize the power production under steady average conditions then, the turbines were regulated according to the daily demand. A mixed integer non-linear solver was used to find the optimal solution and the hydraulic equations were written as equality constraints of the optimization problem. In both researches, the turbines were simulated as simple head losses, while Samora et al. (2016) used the affinity equations to better simulate the behaviour of real turbines within the network. A simulated annealing technique was performed to assess the best location of a fixed number of turbines, to optimize the energy production within the real water network in Lausanne. The size of the turbine of each branch was assigned while the presence of the turbine was a result of the optimization. The produced power was calculated with reference to the yearly variability of the monthly-averaged daily pattern.

1.3 Aim of the Paper

The novelty of this paper lies in the investigation of an objective function not considered by previous authors, and one which provides a more holistic assessment of the benefits of PATs in water networks. Despite the encouraging results of previous investigations, none of these have considered optimising both the income due to energy production and savings due to reduced water losses. In addition, in all of the previous works, the total number of turbines installed in a network was assigned as a constraint.

A new single objective function, i.e. the net present value (NPV) of the turbine investment, has been proposed here to pursue maximum energy production and minimum water losses. NPV takes into account the incomes due to the energy production and the economic saving due to the reduction of water losses and the outcomes due to the cost of installation of the turbines at the same time. The total number of turbines has not been constrained. It is a result of the new optimization procedure. The complete set of constraints, which comprise both the hydraulic equations to simulate the network behaviour and several operating constraints, have been written and a Mixed Integer Non-Linear Programming (MINLP) algorithm has been applied to solve the problem. The model has been applied to a literature synthetic network (Jowitt and Xu 1990) both considering the average demand and the whole daily pattern. Different scenarios have been investigated to study the variability of the solution with the design parameters. The solutions are compared with previous studies on the same network to show the improvements introduced.

2 Optimization Model

2.1 Variables

Given a network of n nodes and l links, the aim of the optimization model is to determine the best number and location of turbines to reduce the pressure and produce energy. The k th pipe of the network can be equipped or not with a turbine, producing at t time the \({H^{T}_{k}}(t)\) head-loss. Thus, a binary variable that indicates the presence of the turbine, I k should be introduced for each link of the network. The total number of turbines can then be calculated as the sum of I k . The operations of the turbine affect the hydraulic behaviour of the network, thus the discharge Q k (t) flowing through the k th pipe and the head H i (t) at the i th node are variables of the problem as well. If the node is a reservoir, its head is a boundary condition, while the inflow or outflow discharge is unknown. The network can be modeled as a directed graph, so that each link of the network has a direction and the discharge is positive if it has the same direction of the pipe and negative otherwise. The network is modeled in quasi-steady conditions, meaning that the hydraulic transient due to the demand variation are neglected. The demand of each node \({q^{d}_{i}}(t)\) is time dependent and can be calculated as:

$$ {q^{d}_{i}}(t)=c_{d}(t) \cdot \overline{{q^{d}_{i}}} $$
(1)

where \(\overline {{q^{d}_{i}}}\) is the average demand of the i th node and c d (t) is the demand coefficient which depends on time but is independent of the network nodes. If the daily pattern is divided in n t timesteps of Δt i hours, then the number of variables can be accounted as:

$$ \left\{\begin{array}{ll} I_{k} & l \\ {H^{T}_{k}}(t) & l \cdot n_{t} \\ Q_{k}(t) & l \cdot n_{t} \\ H_{i} (t) & n \cdot n_{t} \\ \end{array}\right. $$
(2)

The demand coefficient can assume the same values at two or more different time steps, so that the solution is the same and does not need to be calculated. More efficiently, if the frequency distribution of the demand coefficient is evaluated, the daily pattern can be divided into a small number of n d ranges of the demand coefficient, with an associated duration of Δt d . Thus, if n d < n t , the number of variables can be significantly reduced as follows:

$$ \left\{\begin{array}{ll} I_{k} & l \\ {H^{T}_{k}}(c_{d}) & l \cdot n_{d} \\ Q_{k}(c_{d}) & l \cdot n_{d} \\ H_{i} (c_{d}) & n \cdot n_{d} \\ \end{array}\right. $$
(3)

2.2 Objective Function

The objective function has been chosen as the NPV of the investment:

$$ \text{maximize} \left( NPV = \sum\limits_{y=0}^{Y} \frac{C^{in}_{y}-C^{out}_{y}}{(1+r)^{y}} \right) $$
(4)

where Y is the number of y years, \(C^{in}_{y}\) and \(C^{out}_{y}\) are the cash inflow and outflow, respectively, at the y − t h year and r is the discount rate, set equal to 0.05.

The cash outflow only occurs when y = 0 and is considered as the sum of the turbines cost, c T. It can be calculated as:

$$ c^{T} = c_{P} {P^{T}_{r}} + c_{z} + c_{inst} $$
(5)

where c T is the total cost of the turbine in euros, \({P^{T}_{r}}\) is the rated power of the turbine in kW and c P and c z are coefficient specific to the cost of PATs, predetermined in previous studies, set to 220 € /kW and 450 € respectively (Ramos et al. 2009). Y has been selected as 10 years, so that the maintenance cost of the turbines can be neglected. The sum c i n s t of the piping cost and the grid connection has been assigned as 2500 € (Fecarotta et al. 2015).

The cash inflow is the sum of the incomes due to the produced energy and water savings.

The energy income \({E^{p}_{y}}\) at the y − t h year has been calculated as:

$$ {E^{p}_{y}} = c_{e} \sum\limits_{k=1}^{l}{365 {\int}_{day}{\gamma I_{k} {H^{T}_{k}}(t) Q_{k}(t) \eta^{T} dt}} $$
(6)

where γ is the specific weight of water (9806 N/m 3), \({H^{T}_{k}}\) is the turbined head of the k th pipe, η T is the turbine efficiency and t is the daily time. The turbine efficiency should vary depending on the discharge, according to the efficiency curve of the selected machine. At this stage, in order to simplify the model, a conservative constant value equal to 0.65 has been considered. The energy unit selling price c e has been considered constant and equal to 0.1 € /kWh. Equation 6 can be modified with reference to the discrete distribution of the demand:

$$ {E^{p}_{y}} = c_{e} \sum\limits_{k=1}^{l}{365 \sum\limits_{d=1}^{n_{d}}{\gamma I_{k} {H^{T}_{k}}(c_{d}) Q_{k}(c_{d}) \eta^{T} {\Delta} t_{d}}} $$
(7)

The annual water saving \({W^{s}_{y}}\) is calculated as the difference between the leaked water volume without the pressure control \({V_{l}^{0}}\) and the volume leaked by the network with turbines \({V_{l}^{T}}\). A water unit cost c w of 0.3 € /kWh has been considered (Fecarotta et al. 2015). Thus,

$$ {W^{s}_{y}} = c_{w} \left( {V_{l}^{0}}-{V_{l}^{T}} \right)=c_{w} \left( {\int}_{day}{{Q_{l}^{0}}dt}-{\int}_{day}{{Q_{l}^{T}}dt} \right) $$
(8)

where Q l is the total leakage through the all pipes of the network. Equation 8 can be modified as follows:

$$ {W^{s}_{y}} =c_{w} \left( \sum\limits_{d=1}^{n_{d}}{{Q_{l}^{0}}(c_{d}) {\Delta} t_{d}} - \sum\limits_{d=1}^{n_{d}}{{Q_{l}^{T}}(c_{d}) {\Delta} t_{d}} \right) $$
(9)

As suggested by Araujo et al. (2006), the leakage can be allocated in the nodes of the network as a pressure-driven demand, so that:

$$ Q_{l} = \sum\limits_{i=1}^{n}{{q^{l}_{i}}} $$
(10)

where n is the number of nodes and \({q^{l}_{i}}\) is the leaked discharge through the i th node, that can be assessed as:

$$ {q^{l}_{i}} = f_{i} \cdot p_{i}^{\beta} $$
(11)

where p i is the pressure head (in meters) of the i th node, β an exponent depending on the material of the pipe and on the shape of the orifice (Greyvenstein and van Zyl 2007). For the sake of simplicity and in order to compare this study to some literature results, such exponent is kept constant and equal to 1.18 (Araujo et al. 2006). The leakage coefficient, f i , is constant for each node and is estimated as:

$$ f_{i} = c \sum\limits_{j=1}^{K_{i}}{0.5L_{i,j}} $$
(12)

where c is a coefficient equal to 0.00001 l/(s ⋅ m 1 + β) (Araujo 2005) and K i is the number of pipes approaching the i th node and connecting the nodes i and j, whose lengths are L i,j .

2.3 Constraints

The optimization problem is subject to a certain number of linear and non-linear constraints, representing the physical modelling of the hydraulic network and the technical or practical limit of the variables related to the behaviour of the network.

2.3.1 Hydraulic Constraints

There are two kinds of hydraulic constraint: the mass continuity equations within the nodes and the momentum balance along the pipes. The continuity equation can be written as:

$$ \sum\limits_{k \in K_{i}}{Q_{k}^{in}} - \sum\limits_{k \in K_{i}}{Q_{k}^{out}} - f_{i}p_{i}^{\beta} = {q^{d}_{i}} $$
(13)

where Q k is the discharge flowing through the k th link contained in the set K i of links connected to the i th node and the superscript in and out indicate either the discharge is flowing into or out of the node. A continuity equation can be written for each node and each Δt d , so that they are n ⋅ n d . The momentum balance equation can be written as:

$$ H_{i} - H_{j} - r_{k}L_{k} - I_{k} \cdot {H_{k}^{T}} \cdot sign(Q_{k}) = 0 $$
(14)

where k is the pipe that connects the i th and j th nodes and r k are the unit head loss along the pipe. \({H_{k}^{T}}\) is always positive and is multiplied by the sign of Q k to ensure that the head loss produced by the turbine has the same direction as the flow. The unit head loss has been calculated by the Hazen-Wlliams formula:

$$ r_{k} = \frac{10.67}{{C_{k}}^{1.852}} \frac{\left|Q_{k}\right|^{1.852}}{{D_{k}}^{4.8704}}\cdot sign(Q_{k}) $$
(15)

where C k and D k are the roughness coefficient and the diameter of the k th pipe. There is a momentum balance equation for each pipe and for each demand interval, so that l ⋅ n d equations can be written.

2.3.2 Linear Constraints

The linear constraints can be further divided in boundary constraints and proper linear constraints. The boundary constraints are used to force the pressure head at the nodes within an allowable range. These two boundaries, p m i n and p m a x have been set to 25 m and 100 m respectively. Such boundary constraint can be written as:

$$ p_{min} \leq H_{i} - z_{i} \leq p_{max} $$
(16)

where z i is the elevation of the i th node. Such constraints can be written for each node, excluding the reservoirs, where the head is constant. For each demand interval, so that 2 ⋅ (n − s) inequalities can be written, with a total number of 2 ⋅ (n − s) ⋅ n d . The head loss within the turbines should be always positive, according to Eq. 14, thus:

$$ {H_{k}^{T}} \geq 0 $$
(17)

This inequality ensures that the head loss has always the same direction as the discharge. This means that, if the discharge reverses due to the demand change, the head loss reverses too, but this is generally not admissible for a turbine unless it is placed in a complex hydraulic circuit. Thus, the consistency of the solution of the optimization problem should be further analysed with reference to such a limitation of the model (i.e. the flow cannot reverse through a PAT and still produce energy).

Finally, two linear constraints have been introduced, as follows:

$$\begin{array}{@{}rcl@{}} \overline{{H_{k}^{T}}} & \geq& \overline{{H_{k}^{T}}}_{min} \cdot I_{k} \end{array} $$
(18)
$$\begin{array}{@{}rcl@{}} {H_{k}^{T}}(c_{d}) & \leq& {{H_{k}^{T}}}_{max} \cdot I_{k} \end{array} $$
(19)

where \(\overline {{H_{k}^{T}}}\) is the time average head loss of the k th turbine and \({{H_{k}^{t}}}_{min}\) is a fixed value fixed to 0.5 m. The first inequality forbids the algorithm to select turbines with an average head loss smaller than \(\overline {{H_{k}^{t}}}_{min}\) and can be written for each node of the network (l inequalities). The second inequality forces the value of \({H_{k}^{T}}\) to be zero if I k is zero and to be less than \({{H_{k}^{T}}}_{max}\) if I k is one. \({{H_{k}^{T}}}_{max}\) has been calculated as the difference between the maximum and the minimum allowable head within the network. Figure 1 shows the feasible region on the plane \(({H_{k}^{T}}(c_{d}),I_{k})\) for the continuous relaxed problem and the allowable values of \({H_{k}^{T}}(c_{d})\) in the mixed integer problem.

Fig. 1
figure 1

Graphical description of the feasible region of (H k T(c d ),I k )

Full size image

2.3.3 Tolerances

Most of the equations that are used to create the mathematical model are strongly non-linear, so that the resolution of the optimization can be very difficult and time demanding. In order to simplify the problem the two Eqs. 13 and 14 have been substituted with the two following inequalities, where small tolerances (t o l Q and t o l H ) are admitted:

$$\begin{array}{@{}rcl@{}} \left|\sum\limits_{k \in K_{i}} Q_{k}^{in} - \sum\limits_{k \in K_{i}} Q_{k}^{out} - f_{i}p_{i}^{\beta} - {q^{d}_{i}} \right| & \leq& to{l_{i}^{Q}} \end{array} $$
(20)
$$\begin{array}{@{}rcl@{}} \left|H_{i} - H_{j} - r_{k}L_{k} - I_{k} \cdot {H_{k}^{T}} \cdot sign(Q_{k}) \right| & \leq& to{l_{k}^{H}} \end{array} $$
(21)

Such modification increases the dimension of the feasible region and help the algorithm to find the optimal solution in a reasonable time. The value of \(to{l_{i}^{Q}}\) has been calculated for each node and for each demand as follows:

$$ to{l_{i}^{Q}} = \varepsilon_{Q} \left( {q^{d}_{i}} + \sum\limits_{j \in J_{i}} {q^{d}_{j}} \right) $$
(22)

where J i is the set of the j nodes connected to the i th node by a single pipe, while \(to{l_{i}^{H}}\) has been calculated as follows:

$$ to{l_{k}^{H}} = \varepsilon_{H} {{H_{k}^{T}}}_{max} $$
(23)

ε Q and ε H have constant values equal to 0.01. The two tolerances introduce errors in the evaluation of the best solution and in the hydraulic modelling of the network. The introduction of such errors, which are small due to the small values of ε Q and ε H , can be acceptable if the uncertainties in the determination of the demand and in the results of the application of the Hazen-Williams equation (15), are taken into account.

2.4 Optimization Algorithm

The optimization model, as described above, can be written as follows:

$$ \left\{\begin{array}{ll} \underset{I_{k}, {H_{k}^{T}}}{\operatorname{maximize}} & \displaystyle\qquad NPV = \sum\limits_{k=1}^{l}{ - {c^{T}_{k}} \cdot I_{k} + \sum\limits_{y=1}^{Y}{\frac{{E^{p}_{y}}+{W^{s}_{y}}}{(1+r)^{y}}}} \\ \\ & \qquad\displaystyle\left|\sum\limits_{k \in K_{i}} Q_{k}^{in} - \sum\limits_{k \in K_{i}} Q_{k}^{out} - f_{i}p_{i}^{\beta} - {q^{d}_{i}} \right| \leq to{l_{i}^{Q}} \\ & \qquad\left|H_{i} - H_{j} - r_{k}L_{k} - I_{k} \cdot {H_{k}^{T}} \cdot sign(Q_{k}) \right| \leq to{l_{k}^{H}} \\ &\qquad p_{min} \leq \left( H_{i} - z_{i} \right) \leq p_{max} \\ &\qquad {H_{k}^{T}} \geq 0 \\ \text{subject to} & \qquad\overline{{H_{k}^{T}}} \geq \overline{{H_{k}^{T}}}_{min} \cdot I_{k} \\ &\qquad {H_{k}^{T}}(c_{d}) \leq {{H_{k}^{T}}}_{max} \cdot I_{k} \\ &\qquad 0 \leq I_{k} \leq 1 \\ & \\ & \qquad I_{k} \in \mathbb{Z}, \quad H_{k} \in \mathbb{R}, \quad Q_{k} \in \mathbb{R}, \quad H_{i} \in \mathbb{R} \\ &\qquad \forall i,j = 1 {\ldots} n, \quad \forall k = 1 {\ldots} n_{l}, \quad \forall d = 1 {\ldots} n_{d} \end{array}\right. $$
(24)

In the second constraint, as well as in the objective function (for the calculation of E p, as expressed by Eqs. 6 and 7), the product between \({H^{T}_{k}}\) and I k increase the non-linearity of the model and is apparently redundant, since the fourth and the fifth constraints force \({H^{T}_{k}}\) to be 0 if I k is zero. Nevertheless, several simulations that have been carried out showed that such configuration of the model gives the best results in terms of both optimal solution and computational time.

The Basic Open-source Nonlinear Mixed INteger programming (BONMIN) (Belotti et al. 2013) code has been chosen to solve the optimization. A branch-and-bound based algorithm has been selected (Bonami et al. 2008) to investigate all the different solution. The code used the Interior Point OPTimizer (IPOPT) (Wächter and Biegler 2006) to solve the continuous relaxed problem and the Coin-or branch and cut (Cbc) algorithm (Schoenemann 2010) to solve the mixed integer problem. Even if the algorithm is designed for convex problems, it can retrieve heuristic solutions in case of non-convex problems and several options allow improvement in the quality of the solutions (Bonami and Lee 2009). Due to the complexity of the problem described by Eq. 24, the convexity has not been proven and all the options for the resolution of non-convex problems have been selected.

For the resolution of the network without turbines, the MATLAB FMINCON optimization algorithm (Byrd et al. 2000) for continuous problems has been used. The mathematical model of the network without turbines can be obtained from Eq. 24 by setting I k and \({H_{k}^{T}}\) to zero. Due to the simplification of the problem, even \(to{l_{i}^{Q}}\) and \(to{l_{k}^{H}}\) can be set to zero. The resulting optimizing function is null as well, so that the algorithm searches for the solutions which satisfies the constraints.

3 Case Study: a Synthetic Network

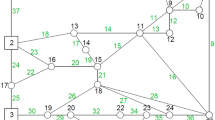
The optimization procedure has been applied to the literature synthetic ‘anytown’ network first proposed by Sterling and Bargiela (1984) and detailed in Figure ORF1 (Online Resource) and table ORT1 (Online Resource). The network had 25 nodes and 37 pipes. This means that there are more than 137.4 billion combinations of turbines within the network. The network is fed by gravity by three water reservoirs whose level was kept constant for the sake of simplicity. The same network was used in many studies about optimal valve location (Jowitt and Xu 1990) and was also used by Corcoran et al. (2015) and Giugni et al. (2014) in their research about the optimal location of turbines. The users’ demand is concentrated in the nodes of the network and the daily variability is modeled by introducing the demand coefficient c d , as expressed by Eq. 1. The variability of c d during the day is shown in Figure ORF2 (Online Resource) Leakage are concentrated in the nodes of the network as well, according to Eq. 11. Two kinds of simulations have been carried out, investigating only the average flow conditions as well as the whole daily pattern. For each of the two conditions, three scenarios have been considered: in the first one, the network was simulated in the theoretical situation of zero leakage, while in the second and in the third scenarios the leakage are taken into account. The economic value of water is taken into account only in the third scenario. Table 1 illustrates the difference among the scenarios.

Table 1 Summary of the different conditions and scenarios
Full size table

3.1 Average Conditions

The optimization procedure was first tested with the average demand (see Online Resource ORF2). In this case, the problem is smaller because n d = 1 and thus the number of variables significantly decreases. The results for the three scenarios, in terms of installation pipes, produced power and node pressure are shown in Fig. 2. In the first scenario, the model set the optimal location of four turbines at links 1, 5, 8 and 11 with a produced power of 1.47, 1.91, 0.58, and 8.85 kW respectively (total = 12.81 kW). The pressure plot shows that the gain in terms of pressure reduction is relevant, if the node pressure is compared with the no-dissipation condition (in white). Both the power plot and the pressure plot also show the solution proposed by Corcoran et al. (2015). The new optimization ensures better results in terms of both power production and pressure reduction. The NPV has been calculated both for the new model and for the solution proposed by Corcoran et al. (2015), and resulted as 72′051 and 64′915 € respectively, with a benefit increase of 11%.

Fig. 2
figure 2

Results of the optimization model for scenario 1 (a, b, c), scenario 2 (d, e, f) and scenario 3 (g, h, i) in average conditions: turbines locations, turbines power and nodes pressure

Full size image

For the second scenario, the model proposed the same location of turbines with an increase in the energy production, accounted as 1.65, 2.00, 0.59 and 9.17 kW for pipes 1, 5, 8 and 11 respectively, (total = 13.4 kW). The total amount of saved water has been accounted as 275′870 m 3 per year while the NPV resulted as 75′936 €.

The results of the third scenario are quite different, because, in this case, the economic value of lost water is taken into account. The high income due to the water saving pushes the algorithm to select more dissipation points because the increase in NPV due to water saving is higher than the decrease due to the installation of a new turbine. The pressure plot shows that the pressure is slightly different from its minimum value in the whole network and the water saving can be accounted as 339′240 m 3 per year. The calculated NPV was 833′740 €. The power plot shows that the produced power of some of the 16 proposed turbines is very low and for them the installation is probably not realistic. The total produced power is 14.53 kW. The introduction of a minimum allowable power constraint could avoid the selection of low power turbines but, due to its non-linear nature it is not suitable for this algorithm. All the attempts that have been made in this direction resulted in failures. Regardless, the selection of the turbine can be based on technical and practical considerations, such as the real installation costs, the location of the pipe, the ease of grid connection. In this study, a minimum power constraint is set a-posteriori, with a minimum value of 0.5 kW per turbine, and only 6 turbines have been selected among the solution, with a total power of 14.06 kW. For all the other dissipation points, pressure reducing valves can be placed, in order to pursue the same benefit in pressure reduction and water saving.

All the results are summarized in Table 2.

Table 2 Summary of the results for the different scenarios for the average condition
Full size table

3.2 Daily Pattern

The optimization model (24) has been designed to deal with the daily pattern of user demand. Thus, a simulation has been run with the pattern shown in the Figure ORF2 (Online Resource). The main results, obtained for the proposed scenarios, are reported in Table 3, where the results obtained by Giugni et al. (2014) are also shown for comparison. Note that, Giugni et al. (2014), in their work, proposed six different solutions, with two different objective functions (O F 1 and O F 2 respectively) and one, two or three installed turbines (a, b and c respectively). Figure 3 shows the daily pattern of the turbine characteristics for the three scenarios, in terms of turbined head, turbined discharge and produced power, while Fig. 4 shows the optimal location of turbines for scenario 1, 2 and 3 respectively.

Table 3 Summary of the results for the different scenarios for the daily variable demand, and comparison with Giugni et al. (2014)
Full size table
Fig. 3
figure 3

Results of the optimization model for scenario 1 (a, b, c), scenario 2 (d, e, f) and scenario 3 (g, h, i) in daily variable conditions: turbined head, turbined discharge and turbines power during the day

Full size image
Fig. 4
figure 4

Optimal location of turbines and node pressure values for the daily pattern simulation for scenario 1 (a), 2 (b) and 3 (c) respectively

Full size image

Again, in scenario 3, the number of installed turbines is quite high, due to the nature of the optimization function. If only the devices with an average power greater than 0.5 kW are selected (where all the others can be replaced with PRVs), then the total power reduces to 10.87 kW, while the total number of installed turbines reduces to 6.

4 Discussion

The results obtained by the application of the new algorithm are quite promising. Comparing the results obtained by Corcoran et al. (2015) with the results of the first scenario for average conditions, an increase in the produced energy and in the resulting NPV is observed. The new algorithm obtains very good results even if the leakage is taken into account, and Table 2 shows that the produced energy further increases when the water losses are modeled and the water cost is considered in the evaluation of the objective function. Therefore, even though Corcoran et al. (2015) set an objective function to maximize power production for average conditions, using the NPV objective function proposed here resulted in 11% higher power production.

The comparison between the results of the daily pattern simulations and the results obtained by Giugni et al. (2014) shows that a single objective function, which contains both the energy selling price and the economic saving due to leakage reduction, allows an optimal solution to both reduce leakage and produce power: Table 3 shows that the energy production obtained by the simulations of scenario 2 and 3 is close to the energy production obtained by Giugni et al. (2014) in O F 2, and is much larger than the value obtained for O F 1. Furthermore, the values of the water saving obtained with the new algorithm, both for scenario 2 and 3, are larger than the values obtained by Giugni et al. (2014), even if O F 1 was specifically designed to reduce the pressure within the network.

Although it contains promising results, the new model presents some weakness. First of all, the PATs are not simulated as real machines, but only as head losses along the pipes, and a conservative value of 0.65 has been chosen as average turbine efficiency in the calculation of the produced power. After the algorithm has selected the best PATs locations and operations, a machine should be selected and installed, for example by the application of the Variable Operating Strategy (Carravetta et al. 2014a), in order to maximize the energy production.

In the second instance, when the cost of water is taken into account in the objective function, the high economic saving due to the reduction of leakage pushes the algorithm to select a high number of PATs. The comparison of the results of scenario 2 and 3 shows that the installation of more PATs in scenario 3 reduces the pressure at the nodes, and the income produced by saving water is larger than the outcome due to the installation of more PATs. Furthermore, the additional PATs of scenario 3 present very little power and the installation of such low power devices is probably not viable. A minimum power constraint would avoid this problem but it is not suitable due to its non-linearity. Thus, in this paper, an empirical approach is proposed: after the algorithm identifies the optimal location, only the PATs that exceed a certain power are chosen for the installation, while the low power PATs are replaced by valves, in order to achieve the same results in terms of water saving and reduce the installation costs.

Finally, with reference to Fig. 3g, h and i, for certain PATs, during the day, the flow reverses. This is a limitation of the model, since no constraints have been introduced to avoid this kind of result and this is physically not acceptable because, unless the PAT is inserted in a very complex hydraulic circuit, the flow cannot reverse through a PAT and still produce power. Fortunately, in the analyzed case study, this situations happens only for the low power turbines, that are likely to be replaced by valves. In future studies, further constraints can be introduced in order to reduce the solution space only to those pipes where the flow does not reverse. Unfortunately, the list of not-suitable pipes cannot be set a-priori, since the installation of a turbine modifies the behaviour of the network. Thus, the new constraints would be non-linear.

5 Conclusions

Reduction of both leakage and energy dissipation is crucial in order to increase the efficiency and reduce the energy impact of water networks. Many studies are focused on the replacement of existing valves with turbines, analyzing the issues related to the installation, regulation, operation and efficiency. Few studies are related to the optimal location of turbines within a water network and this paper is proposing a new model aimed at the maximization of both energy production and water saving.

The calculated NPV of the three scenarios for the average discharge have been resulted as 72 051, 75 936 and 833 740 €, the third one being much larger due to the large income due to the water saving. When the whole daily pattern is considered, the NPV values reduce by 7.5%, 4.8% and 5,2%. The results have been compared with the results obtained by Corcoran et al. (2015) and by Giugni et al. (2014) who proposed two different optimization model to locate hydropower devices within the network. The proposed model showed 11.0% increase of NPV and 13.6% increase of energy production with reference to the results presented by Corcoran et al. (2015), whose model did not take into account the water leakage. When compared with the results obtained by Giugni et al. (2014), the proposed model showed higher or comparable values of energy production and higher values of water saving.

Despite the promising results of the model, it present some weakness, such as i) the complete behaviour of PATs is not modelled, ii) there is no constraint related to the minimum power of the installed turbine and iii) the flow through the turbine can reverse due to the change of the demand during the day. Such problems should be investigated by future research.

6 List of symbols

β

Exponent in the relation between leaking discharge and pressure

γ

Specific weight of water

Δt d

Sum of timesteps with the same the demand coefficient

Δt i

Timestep

𝜖 H

Coefficient in the evaluation of t o l H

𝜖 Q

Coefficient in the evaluation of t o l i Q

η T

Efficiency of the turbine

c

Coefficient in the evaluation of f i

c T

Total turbine cost

c d

Demand coefficient

c i n s t

Installation cost of the turbine (piping and grid connection)

c P , c z

Coefficients for the evaluation of the turbine total cost

c w

Cost of water

C k

Roughness coefficient of the k − t h pipe of the Hazen-Williams formula

C y i n

Cash inflow at the y − t h year

C y o u t

Cash outflow at the y − t h year

D k

Diameter of the k-th pipe

E y p

Energy production during the y − t h year

f i

Coefficient in the evaluation of leakage through the i th node

H i

Head at the i th node

H k T

Head loss within the turbine installed along the k th pipe

\(\overline {{H_{k}^{T}}}\)

Average head loss within the turbine

H k T m a x

Maximum head loss within the turbine

\(\overline {{H_{k}^{T}}}_{min}\)

Minimum average head loss within the turbine

i, j

Indexes for nodes

I k

Binary variable representing the presence of a turbine along the k th pipe

k

Index for pipes

K i

Number of pipes approaching the i th node

l

Number of pipes of the network

L i, j

Length of the pipe connecting nodes i and j

L k

Length of the k th pipe

n

Number of nodes of the network

n d

Number of ranges in the frequency distribution of the demand coefficient

n t

Number of timesteps

NPV

Net present value

p m a x

Maximum allowable pressure

p m i n

Minimum allowable pressure

p i

Pressure of the i th node

P r T

Rated power of the turbine

q i d

Instantaneous i th node demand

\(\overline {{q_{i}^{d}}}\)

Average i th node demand

q i l

Leaking discharge through the i th node

Q k

Discharge through the k th pipe

Q k i n

Discharge flowing through k th pipe into the i th node

Q k o u t

Discharge flowing through k th pipe out of the i th node

Q l0

Leaking discharge without turbines

Q l T

Leaking discharge with turbines

r

Discount rate

r k

Resistance coefficient of the k th pipe calculated by Hazen-Williams formula

s

Number of reservoirs

t

Time

t o l i H

Allowable tolerance in the momentum equation

t o l i Q

Allowable tolerance in the continuity equation

V l0

Leaked volume of water without turbines

V l T

Leaked volume of water with turbines

W y s

Water saving at the y − t h year

Y

Number of years considered for the NPV calculation

y

Year

z i

Elevation of the ith node