1 Introduction

The estimation of extreme events is a crucial problem in hydrology specially when dealing with rainfall or flood, due to the impact that these events can have on society and economy (e.g. Shabri et al. 2011). A good solution for many hydrologic engineering problems is based on the proper knowledge of extreme rainfall. For a certain place, rainfall intensity and its duration affect the maximum discharge that can be expected. Thus, information on the magnitude and frequencies of extreme rainfall is essential. Intensity-duration-frequency (IDF) relationships allow to compute the design storm which is the expected rainfall value for a given duration and a given occurrence probability (Di Baldassarre et al. 2006). When extreme rainfall data series for different durations are available, there are many IDF models that can be fitted to the rainfall quantiles. If the series are long enough, local frequency analysis techniques can be applied to obtain the quantiles. Since reliable estimations require very long station records that are not usually available, the regional frequency analysis appear as an alternative technique to provide a framework for hazard characterization of the extreme events (Norbiato et al. 2007).The RFA increases the data at the site of interest considering data from other places that share the same probability distribution functions. The RFA leads to more accurate quantile estimations than those from local frequency analysis (Lettenmaier and Potter 1985; Wallis and Wood 1985; Hosking and Wallis 1997) when working with rain (Hosking and Wallis 1997). The improvement of the RFA over the local one depends on the regional homogeneity, always considering that in cases of extreme regional heterogeneity, local estimations could be better than those based on RFA (Lettenmaier and Potter 1985).

The regional frequency analysis method introduced by Hosking and Wallis (1993, 1997) is widely used in rainfall studies over different climatic areas (Lee and Maeng 2005; Fowler and Kilsby 2003; Di Baldassarre et al. 2006; Norbiato et al. 2007; Wallis et al. 2007; Castellarin et al. 2009; Ngongondo et al. 2011; García-Marín et al. 2011, 2015a, b; Satyanarayana and Srinivas 2011; Malekinezhad and Zare-Garizi 2014; Liu et al. 2015).This method is based on lineal moments estimations (Hosking 1990, 1992) of the data series analyzed, and their values are used in all its steps (Hosking and Wallis 1993; Hosking and Wallis 1995; Hosking and Wallis 1997; Rao and Hamed 2000). Within all the steps on RFA the determination of homogeneous regions is the most difficult task and it conditions the final results.

Two important aspects have to be considered in order to finally obtain homogeneous regions: the grouping methodology used and the at-site characteristics to be considered in the joining process. Different methodologies have been applied in rainfall regionalization including spatial correlation analysis (Gadgil et al. 1993), principal component analysis (García-Marín et al. 2011), cluster analysis (Easterling 1989; Bonell and Sumner 1992; Venkatesh and Jose 2007), combination of principal component analysis and cluster analysis (e.g. Dinpashoh et al. 2004), and clustering combined with artificial neuronal networks (Jingyi and Hall 2004; Srinivas et al. 2008; Satyanarayana and Srinivas 2011), among others.

The more common characteristics that have been used in rainfall regionalization include climatological and geographical information, statistical values and location attributes (García-Marín et al. 2011) or even atmospheric variables (e.g. Satyanarayana and Srinivas 2011). Some multifractal parameters of rainfall data series have been recently used with this aim with very good results (García-Marín et al. 2015a; b). The multifractal character of rainfall has been widely studied from a descriptive use (e.g. de Lima and Grasman 1999) to any application in engineering models (García-Marín et al. 2013). Several methodologies exist to analyze the multifractal behavior of rainfall. All of them have in common that the multifractal paremeters are independent of the available data for the different scales, and that no probability distribution function has to be assumed for the data set. The multifractal analysis based on the strange attractor formalism (e.g. Hentschel and Procaccia 1983; Grassberger 1983; Halsey et al. 1986) deals with the fractal dimensions of a data set.

Thus, the objective of this work is to compound homogeneous regions of extreme annual daily rainfall by using the fractal dimensions of the daily rainfall data sets available in the Maule Region of Chile.

2 Materials and Methods

2.1 Rainfall Data

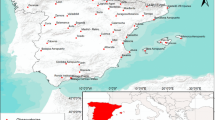
Daily precipitation data from 53 stations located in the Maule Region of Chile and supplied by the “Dirección General de Aguas”,DGA, were used to carry out this work. The geographical distribution of the stations throughout the Region ofMaule is shown in Fig. 1. Site elevations range from 10to 1058 m abovemeansealevel, longitude, from 70° 48′ 43”to72° 25′ 17″ W and latitude, from34° 54′ 41″ to36° 21′ 29″S (Table 1).

Fig. 1
figure 1

Study Area: The Maule Region, Chile

Full size image
Table 1 ID of the location, name, data time-period analysed, and coordinates of the weather stations used in this study (Maule Region, Chile)
Full size table

Maule Region is located in the semiarid region of Chile (from 34°41′ to 36°33′ S latitude), withannualaveragerainfallrangingbetween 600 and 2.300 mm. As central Chile, its physiography is characterized by the Andes mountains at the Eastside (withaltitudesbordering the 4.000 m.a.s.l.), followed by a central valleyof 40 km width, the Coast mountains (withheightsof 300 and 1000 m), and the coastalplain, whichreaches a widthof 5 km and is interrupted by the riversthatflowinto the Pacific Ocean. The Maule region is located in a transition area of Chile, from the semi-arid zone and the wetzone, showing a north-south gradient in annualrainfall. Besides, the orography lets an increase of precipitation from the coastto the Andes Mountains.

Validation procedures are part of the quality control systems and their purpose is to identify erroneous data from meteorological sensor measurements in order to make optimal use of them (Estévez et al. 2011a). In the validation process, data of a doubtful quality must be detected and appropriately flagged. Many methods exist to validate meteorological data (Feng et al. 2004; Zahumensky 2004; Kunkel et al. 2005; Estévez et al. 2011b).The available data for Maule Region were previously validated (García-Marín et al. 2015a). For this validation, Range (Estévez et al. 2011b) and Persistence (e.g. Hubbard et al. 2005) tests were applied.

2.2 Multifractal Analysis Based on the Strange Attractor Formalism

Multifractal formalisms find their origin in the theory of measures. Multifractal measures are related to the study of the distribution of a quantity over a geometric support (De Bartolo et al. 2000). The strange attractor (Hentschel and Procaccia 1983; Grassberger 1983; Halsey et al. 1986) formalism is used here to perform the multifractal analysis on daily rainfall data sets with the aim of obtaining homogeneous regions. This formalism deals with the fractal dimensions of the geometric sets associated with singularities of the measure.

The fractal dimension of a set is defined as the scaling exponent D 0

$$ N(r)=\frac{A}{r^{d_0}}\kern1em \left( r\to \infty \right) $$
(1)

Where N(r) is the number of boxes of length or size r, that are necessary to cover the set, and A is a constant (Mandelbrot 1982; Feder 1988). Suppose the set is represented by a large number of points. If these points are uniformly distributed across the set, then the fractal dimension completely characterizes the dimension of the set. If the points are not distributed uniformly it is possible that the mass distribution of the points varies. Then, at a given box length r, it is possible to identify regions of the same masses μ (Feeny 2000). The mass can be estimated within a box of size r asμ i  = n i /n, where n i is the number of points in the box, and n the total number of points. Then a measure can be constructed as follows,

$$ {M}_d\left( q, r\right)=\sum_{i=1}^N{\mu}_i^q{r}^d $$
(2)

Where N is the number of boxes that cover the set; d = τ q is called the mass exponent. Defining \( Z\left( q, r\right)=\sum_{i=1}^N{\mu}_i^q \) as the partition function (i.e. Feder 1988), then \( Z\left( q, r\right)\sim {r}^{-{\tau}_q} \)and thus,

$$ {\tau}_q=\underset{r\to 0}{ \lim}\frac{ \log Z\left( q, r\right)}{ \log r} $$
(3)

τ q can be obtained as the slope of the linear segment of a log-log plot of Z(q, r) versus r. For q> > 1, the value of Z(q, r) is mainly determined by the high data values, while the influence of the loB55w data values contributes most to the partition function for q < < −1 (Kravchenko et al. 1999).

The generalized fractal dimension, D q , of moment order q is defined as,

$$ {D}_q=\underset{r\to 0}{ \lim}\frac{ \log Z\left( q, r\right)}{\left( q-1\right) \log r} $$
(4)

In the limit as q → 1Eq. 4 reduces to

$$ {D}_1=\underset{r\to 0}{ \lim}\frac{\sum_{i=1}^N{\mu}_i \log {\mu}_i}{ \log r} $$
(5)

Among the generalized fractal dimensions, D 0, D 1 and D 2 are frquently used to describe the measure. Thus, D 0 is the fractal dimension of the set over which the measure is carried out.D 1 is the information dimension that describes the degree of heterogeneity in the distribution of the measure. In addition, according to Davis et al. (1994), D 1 characterizes the distribution and intensity of singularities with respect to the mean. If D 1 becomes smaller, the distribution of the singularities will be sparse. On the contrary, if D 1 increases, the singularities will have lower values that exhibit a more uniform distribution.D 2 is the correlation fractal dimension, which is associated with the correlation function, and it determines the average distribution of the measure (Grassberger 1983; Grassberger and Procaccia 1983). D q is a decreasing function with respect to q for a multifractally distributed measure (e.g., Saa et al. 2007) where D 0 > D 1 > D 2.

The relation between the spectrum of generalised fractal dimensions (Rényi spectrum), D q , and multifractal spectrum, f(α), with α being the Lipschitz–Hölder exponent (that quantifies the strength of the measured singularities), is given through the sequence of mass exponents τ q (Hentschel and Procaccia 1983) according to the expression:

$$ {\tau}_q=\left( q-1\right){D}_q $$
(6)

The multifractal or singularity spectrum f(α) can be obtained through (4) by means of the Legendre transform (Halsey et al. 1986) (Eq. 7). The spectrum is an inverted parabola for measures multifractally distributed. For monofractal measures, α value is identical for all the regions of the same size and f(α) consists of a single point (Kravchenko et al. 1999). Multifractal spectrum highest value,f(α 0), corresponds to the fractal dimension D 0 of the support of the measure.

$$ \begin{array}{l}{\alpha}_q=-\frac{d{\tau}_q}{ d q}\\ {} f\left({\alpha}_q\right)= q{\alpha}_q+{\tau}_q\end{array} $$
(7)

2.3 The Homogeneous Regions in Regional Frequency Analysis

The delimitation of homogeneous regions is usually the most difficult and important stage of the RFA (e.g Greis and Wood 1981; Hosking et al. 1985a, Lettenmaier and Potter 1985). If the available data cannot be joined into one homogeneous region or more, the RFA cannot be carried out. Several methodologies exist to group stations into potential homogeneous regions (e.g. Bonell and Sumner 1992; García-Marín et al. 2011; Jingyi and Hall 2004; Srinivas et al. 2008; Satyanarayana and Srinivas 2011; Yürekli and Modarres 2007) being cluster analysis of site characteristics the most practical one (Hosking and Wallis 1997). This technique has been widely used in hydrology (e.g. Burn 1989; Hall and Minns 1999; Lecce 2000; Jingyi and Hall 2004; Kyselý et al. 2007; Srinivas et al. 2008; Meshgi and Khalili 2009; Satyanarayana and Srinivas 2011; García-Marín et al. 2015a; b).

Once the potential regions have been determined, the quality of the following steps of RFA is conditioned by the degree of homogeneity found for the regions. In this work, the RFA proposed by Hosking and Wallis (1997) is followed. This methodology is based on L-Moments which are linear functions of the probability weighted moments (Greenwood et al. 1979) and were introduced by Hosking (1990, 1992). The L-Moments methodology includes from the probability distribution function characterization to the fitting of these functions to the data. For any distribution, the first four L-moments (λ 1 , λ 2, λ 3, λ 4) and their ratios have to be obtained (Hosking 1990),

$$ \tau =\frac{\lambda_2}{\lambda_1}\uptau =\frac{\uplambda_2}{\uplambda_1};{\tau}_3=\frac{\lambda_3}{\lambda_2}{\uptau}_3=\frac{\uplambda_3}{\uplambda_2};\kern0.5em \mathrm{and}\kern0.5em {\uptau}_4=\frac{\uplambda_4}{\uplambda_2}{\tau}_4=\frac{\lambda_4}{\lambda_2} $$
(8)

Where τ, τ 3 and τ 4are the L-coefficient of variation (L-C v ), L-coefficient of skewness (L-C s ) and L-coefficient of kurtosis (L-C k ), respectively. The first L-moment λ 1 is equal to the mean, hence it is a measure of location, and, τ, τ 3 and τ 4are measures of a distribution’s scale, skewness and kurtosis, respectively, which is analogous to the ordinary moments σ, γandκ, respectively (Hosking 1990).

For any step in RFA, L-Moments and their corresponding L-Moments ratios (L-CV, L-C s and L-C k ) have to be previously obtained for all the data series used in the analysis. Each data series will be considered as a site or station that could be potentially joined with other stations into a homogeneous region. The sample L-Moments ratios of a certain site is firstly considered as a point in a three-dimensional space. A group of sites will then yield a cloud of such points. Any point that is far from de centre of the cloud is considered as discordant. Mathematically, the discordance can be measured with the statistic Di (Hosking and Wallis 1993, 1997),

$$ {D}_i=\frac{1}{3} N{\left({u}_i-\overline{u}\right)}^T{A}^{-1}\left({u}_i-\overline{u}\right) $$
(9)

being, \( A=\sum_{i=1}^N\left({u}_i-\overline{u}\right)\left({u}_i-\overline{u}\right),\overline{u}={N}^{-1}\sum_{i=1}^N{u}_i,{u}_i=\left[{LC}_v^i,{LC}_s^i,{LC}_k^i\right] \) and N = the number of stations. Hosking and Wallis (1997) suggested some critical values for the discordancy test which are dependent on the number of sites in the study region. D i is used to identify unusual sites in a potential region. If any discordant site is identified, it has to be removed from the region.

In order to asses if a proposed region is homogeneous, the heterogeneity measure H-statistic can be used. It is used to compare the between-site variation in sample L-moments for a group of sites with what would be expected for a homogeneous region (Hosking and Wallis 1997).There are three measures of the H-statistic, H 1 , H 2 , H 3 , defined as

$$ {H}_i=\frac{\left({V}_{obs_i}-{\mu}_{v_i}\right)}{\sigma_{v_i}}\kern2.75em i=1,2,3 $$
(10)

Where μ v and σ v are the mean and standard deviation of the simulated values of V while V obs is calculated from the regional data and is based on a corresponding V-statistic, defined as (Hosking and Wallis 1997)

$$ \left.\begin{array}{c}{V}_1={\left[\sum_{i=1}^N{n}_i{\left({t}^{(i)}-{t}^R\right)}^2/\sum_{i=1}^N{n}_i\right]}^{1/2}\\ {}{V}_2=\sum_{i=1}^N{n}_i{\left[{\left({t}^{(i)}-{t}^R\right)}^2+\left({t}_3^{(i)}-{t}_3^R\right)\right]}^{1/2}/\sum_{i=1}^N{n}_i\\ {}{V}_3=\sum_{i=1}^N{n}_i{\left[{\left({t}_3^{(i)}-{t}_3^R\right)}^2+{\left({t}_4^{(i)}-{t}_4^R\right)}^2\right]}^{1/2}/\sum_{i=1}^N{n}_i\end{array}\right\} $$
(11)

where V 1 is the standard deviation, weighted according to records length, of the at-site L-CVs. V 2 and V3 are the average distances from the site coordinates to the regional averages on a plot of L-CV versus L-skewness and a plot of L-skewness versus L-kurtosis, respectively; \( {t}^{(i)},{t}_3^{(i)} \)and \( {t}_4^{(i)} \) are the sample L-moment ratios at site i; t R, \( {t}_3^R \) and \( {t}_4^R \) are the regional averages of the L-moment ratios; n i is the record length at site i; and N is the number of sites in the region.The realization of at least 500 simulations let to obtain the mean and standard deviation values \( {\mu}_{v_i} \) and \( {\sigma}_{v_i} \).

The H-statistics (Eq. 10) indicate that the region under consideration is acceptably homogeneous when H < 1; possibly heterogeneous when 1 < H < 2 and definitely heterogeneous when H > 2. The statistic H 1, based on V 1 measurements, is the most decisive when discriminating between homogeneous or heterogeneous regions (Hosking and Wallis 1993; Castellarin et al. 2001), whereas H 2 has no power as a heterogeneity measurement (Viglione et al. 2007).

For any region that can be catalogued as homogeneous, the following steps of RFA can be successfully performed.

3 Results and Discussion

3.1 Aplication of Strange Attractor Formalism for Multifractal Analysis of Rainfall Data

No data from the stations were flagged by range test and very few with the persistence one (García-Marín et al. 2015a). After de validation proccess of the 53 available daily rainfall data series in the Maule region, the fractal behaviour was studied through their fractal dimensions. The strange attractor formalism was applied and the Rényi dimensions (Eqs. 4 and 5) obtained at each site. Figure 2 shows the generalized fractal dimensions Dq for q values from −10 to 10 for a selection of 4 sites: Agua Fría, Bullileo, Liguay and San Rafael. The expected decreasing behaviour of Dq function can be observed for all the stations with a strong dependence of Dq on the values of q, confirming the multifractal nature of the series analysed. The values of D 0 are 1 for all the sites which shows a full fill in the entire 1D domain. For lower and higher q values, different values of D q are obtained, with D 0  > D 1  > D 2 . For q values lower than 0 the highest D q values are obtained for Agua Fria station, followed by San Rafael and Liguay, being the lowest values those from Bullileo Station. An opposite behaviour is found for q values higher than 0, being Bullileos’ D q values the highest ones, followed by Liguay and San Rafael, being Agua Fria’s the lowest D q . Table 2 shows the values of D 1 and D 2 for all the data series analysed. The information dimension D 1 provides a measure of the degree of heterogeneity (Davis et al. 1994) and characterize the distribution and intensity of singularities with respect to the mean (Ariza-Villaverde et al. 2013).The lowest value of D 1 is the one obtained for Rio Maule Salto (0.877382) showing a more sparse distribution of singularities than in the rest data series, for which greater D 1 values were obtained (Table 2) and a more homogeneous distribution of singularities can be expected. The highest D 1 value is the one of La Sexta station (0.984788). Correlation dimension values (D 2 ) are also shown in Table 2 with the lowest and highest values obtained for the same stations as D 1 , being 0.793721 and 0.969889 for Rio Maule Salto and La Sexta, respectively. The correlation dimension describes the probability of finding data belonging to the set within a given distance when starting on a data belonging to the set (Ariza-Villaverde et al. 2013).

Fig. 2
figure 2

The generalized fractal dimension function D q for the stations Agua Fria, Bullileo, Liguay and San Rafael

Full size image
Table 2 Values of fractal dimensions D1 and D2, and the multifractal degree (MD) for the available sites (ID) in the Maule Region
Full size table

Once the multiscaling of the rainfall data series were detected and analysed from the D q function, the multifractal spectrums f(α) (Eq. 7) were obtained for all of them. For the same stations of Fig. 2, the multifractal spectrums are shown in Fig. 3. For all of them, the spectrum show as an inverted parabola. The singularity spectrum quantifies in details the long- range correlation properties of a series. It gives information about the relative importance of various fractal exponents present in the series. It is a measure of how wide the range of fractal exponents found in the signal is and, thus, it measures the multifractality degree (MD) of the series (Telesca and Lovallo 2011). Greater the value of the width, greater will be the multifractality of the spectrum. For a monofractal set, the width will be zero (Maity et al. 2015). According to Telesca et al. (2004) the width of the spectrum can be obtained from the D q function, being the difference between D-5 and D5 values. The higher the MD value the larger the heterogeneity. For all the stations, Table 2 shows the values of the MD for all the stations, with the minimum and maximum values of 0.137865 for La Sexta station and 1.481674 for Rio Ancoa station, respectively. If we focus on the sites shown in Fig. 2, the highest multifractal degree is found for Agua Fria (0.920359), followed by San Rafael (0.822637) and Liguay (0.632138). The lowest multifractal degree corresponds to Bullileo (0.468812).Some information can also be obtained from the shape of the multifractal spectra (Fig. 3) (Serrano et al. 2013). Rounder and wider spectra correspond to higher variability in the distribution of the values. Agua Fria and Bullileo stations’ spectra are different in shape, being Agua Fria’s rounder and wider than Bullileo’s. The different behaviour between rainfall data series for both stations were previously detected by García-Marín et al. (2015a) being related to the percentage of no-rain days and with the presence of rare and extreme events in the time series.

Fig. 3
figure 3

The multifractal spectrum f(α) for the stations Agua Fria, Bullileo, Liguay and San Rafael

Full size image

3.2 RFA: Looking for Homogeneous Regions

As the objective is to test if the available stations in the Maule region can be grouped into regions according to the extreme annual daily rainfall, 53 extreme daily annual rainfall data series were obtained from the validated daily rainfall data series. Each site was characterized by its L-moments values and ratios (L-C v , L-C s and L-C k ) (Table 3). With all the L-moments data from Table 3 a region called Maule was firstly tested and a RFA of extreme annual daily rainfall was performed. Considering Hosking and Wallis’ (1997) criteria for regions with more than 15 sites, all the stations showing D i values (Eq. 9) higher than 3.00 had to be removed from the region. Thus, five stations showed discordance and were eliminated: Agua Fria (D i  = 3.35), Quella (D i  = 3.01), Río Ancoa (D i  = 3.96), Río Loncomilla (D i  = 5.04) and San Rafael (D i  = 4.66). The values of the H-statistic (Eq. 10) for the region (now composed by 48 sites) were 2.35, 1.17 and 1.38, for H 1 , H 2 and H 3 , respectively (Table 4). H 1 , the most restrictive heterogeneity measurement, shows the heterogeneity of the Maule Region and new groups of stations (Sub-regions) had to be composed.

Table 3 L-Moment Ratios for the 53 stations
Full size table
Table 4 Results of the homogeneity tests for the regions formed by using cluster analysis
Full size table

Since different values of the Rénji spectrum were obtained at each site, these differences were used as the basis of the joining criteria. Thus, with the D 1 and D 2 values as the at-site vector characterization (Table 2) a cluster analysis was performed and two sub regions were obtained, composed by 19 and 34 sites, respectively. For the first sub regions, only one station showed as discordant and was removed (San Rafael station, D i  = 3.45). The H-statistic values for the group were 0.33, −0.34, and 0.44, for H 1 , H 2 and H 3 , respectively (Table 4). The group with 34 sites showed as possibly heterogeneous, with a final value of H 1 of 1.89 after removing the discordant stations (Liguay, Los Queñes, Quella and Talca) from the analysis.

A new cluster analysis was then performed with all the stations that were not included in the first homogeneous region (Region 1 in Table 4). Two groups were obtained, with 20 stations and 15 stations respectively. The stations Liguay (D i  = 3.23), San Rafael (D i  = 3.55) and Talca (D i  = 3.03), showed as discordant in the first new group. The rest of stations (17) behaved as a homogeneous region, with H-statistic values of 0.76, −0.33, and 0.60, for H 1 , H 2 and H 3 , respectively (Region 2 in Table 4).The sub-region with the 15 stations had no discordant sites and the value of H 1 was 1.00. This last value is the lowest value to classify a region as a possibly heterogeneous. Since some spare stations were available (those removed from Region 2 for being discordant), a new group or region was formed by adding them to the sub-region with the 15 stations. Thus, an 18-site region was available and its homogeneity was tested. Only one station was discordant (San Rafael station, D i  = 3.18), but the 17 stations left, behaved as an homogeneous region (Region 3 in Table 4) with H-statistic values of 0.80, 0.46, and 1.17, for H 1 , H 2 and H 3 , respectively.

Figure 4 shows the three homogeneous regions obtained by colouring each station with the reference colour of the region: red for Region 1, blue for Region 2, and green for Region 3. Only one station (San Rafael) stays in black in Fig. 4 because it was not possible to include it in any of the three homogeneous regions detected (Table 4). For this station, only the local frequency analysis of extreme annual daily rainfall is then possible. Moreover, if the results that the authors present in this work are compared to those in García-Marín et al. (2015a), the latter let five spare sites that could not be included into any homogeneous region. This fact shows a clear improvement in the process of forming homogeneous regions. Thus the methodology presented in this work is the easiest and most direct when looking for homogeneous regions.

Fig. 4
figure 4

The final regions obtained (red, blue and green sites) and the sparse station (black)

Full size image

4 Summary and Conclusions

This paper presents a new methodology for grouping stations into regions when performing a RFA of extreme daily annual rainfall data. According to the results, grouping daily rainfall data series into homogeneous regions using the generalized fractal dimensions (also known as Rénji spectrum) of daily rainfall data is a useful method. The novelty of this work is that only with two fractal dimensions, D 1 and D 2 , from the Rénji spectrum, homogeneous regions in RFA are easily obtained.

The Regional Frequency Analysis methodology used in this work was the one proposed by Hosking and Wallis (1997). This method is widely used in hydrology and is based on the L-moments of the data series analysed. Thus, the main L-moments and L-moments ratios of extreme annual daily rainfall data series from 53 sites in the Maule region (Chile) were obtained. Considering each station characterized by it L-moments, a first RFA was made considering a region composed by the whole sites. This region showed heterogeneous and had to be divided into new sub-regions potentially homogeneous.

Cluster analysis was performed in order to divide the whole region into new sub-regions. For this purpose, each station was characterized by two fractal dimensions from the Rénji Spectrum. The spectrum was obtained by applying the box counting method to each daily rainfall data (previously validated). The differences between the Rénji spectrums indicated that some of their fractal dimensions could be used as site characteristics in the cluster analysis. Two representative dimensions in fractal analysis, D 1 and D 2 , were then used. D 1 characterizes the distribution of the rainfall data series and D 2 is related to the correlation function.

The fractal dimension-based cluster analysis led to form three fully homogeneous regions of 17, 18 and 17 stations respectively. Only one site stayed out of these homogeneous regions being the local frequency analysis the only option when dealing with its extreme annual daily rainfall data.