1 Introduction

Due to increasing water demands and global warming, water shortages are occurring more frequently. Expanding human populations and economic development have increased the water demand (Chang et al. 2009; Braga et al. 1985; Rosegrant and Cai 2002; Jenkins et al. 2004; Pulido-Velazquez et al. 2006). Global warming also causes extreme climate conditions, such as droughts and floods, which are occurring more often than in previous decades (Tung et al. 2006). These extreme climate conditions greatly influence water resource stability. The two conditions mentioned above increase the shortage risk of water supply in general. Because of the high interaction between climate conditions and surface water resources, groundwater is more stable than surface water. Thus, the highly efficient conjunctive use of surface and subsurface water is a good way to reduce the water shortage risk with minimal environmental impact for an area with plentiful groundwater aquifer (Mishra and Desai 2006). Therefore, developing a conjunctive use management model (CUMM) to manage the surface and subsurface water efficiently and simultaneously has become an important issue (Vedula et al. 2005; Pulido-Velazquez et al. 2006).

Traditionally, the simulation-optimization method is one of the most widely used approaches for water resource management planning (Yeh 1985; Dhar and Datta 2008). The simulation-optimization method simulates the water resource using a numerical simulation model. This simulation model is then embedded in an optimization algorithm to determine the optimal operation policy of water supply. However, this simulation-optimization method for developing a CUMM requires the construction of numerical simulation models for both a multi-reservoir system and a groundwater system. Because the behaviors of reservoirs are linear, the implementation of the simulation model for the multi-reservoir system can be formed as a set of linear equations.

Although the model implementation for the multi-reservoir system is simple, the implementation for the groundwater system especially for unconfined aquifer is more complicated. Gorelick (1983) determined that the groundwater simulation approaches used in groundwater management models can be classified as embedded or response matrix methods, depending on how the management model performs groundwater modeling. The embedded method uses a full function numerical model for groundwater simulation to represent the relationship between the pumping rates and groundwater head. Wang and Zheng (1998) embedded MODFLOW, one of the most commonly used models for groundwater flow simulation, in an optimal groundwater management model. Chang et al. (1992, 2009) and Hsiao and Chang (2002) also embedded ISOQUAD, a finite element model for groundwater simulation proposed by Pinder and Frind (1972), in their optimal management model. This embedded method describes the groundwater system with less simplification than the response matrix method, and can be directly applied to confined or unconfined aquifers. The embedded method computes the state variables, hydraulic heads, for all numerical grids and provides detail description of the groundwater system. However, it also requires a large amount of computational resources. A management model generally requires only the information at the monitoring locations, and not all the numerical grids. From the management model perspective, the embedded method uses a great amount of computational resources to compute information that are not required. Therefore, the embedded method is not a computationally efficient approach for conjunctive use management problems.

The response matrix method simplifies the groundwater simulation as a linear matrix equation and computes only the information required for a management model. Psilovikos (2006) used the response matrix method to simulate the groundwater system for a confined aquifer. The advantage of the response matrix method is its high computational efficiency compared to the embedded method. However, due to its linear assumption, the response matrix method is not directly applicable to nonlinear systems, such as unconfined aquifers. However, unconfined aquifers are normally the top layers of groundwater system and provide much more water resources than confined aquifers.

Based on the discussion above, the embedded method and response matrix approach both have their limitations for conjunctive use management problems with unconfined aquifers. An Artificial Neural Network (ANN) is a computationally efficient alternative for addressing the problem. Rogers and Dowla (1994) integrated ANN and the Nonlinear Programming (NLP) into a groundwater remediation model. They used an ANN model to represent the groundwater system behaviors, including groundwater flow and pollutant transport. Based on previous research, Rogers et al. (1995) applied a combination of an ANN with the Genetic Algorithm (GA). The GA avoids the convergence problem of NLP induced by initial solutions. Coppola et al. (2003) proposed an ANN model for field groundwater simulation. Chang et al. (2005) applied an ANN model in a real-time reservoir operation. Chu and Chang (2009) combined the recursive ANN with Constrained Differential Dynamic Programming (CDDP) for a groundwater resource planning problem. They used the ANN model in the planning model instead of using ISOQUAD, effectively reducing the computational time by up to 94.5 %.

For the optimization algorithm of solving surface water allocation problems, LP is the most popular choice because of the linearity of reservoir systems (Labadie 2004; Wei and Hsu 2008). In the optimization of groundwater management or conjunctive use problems, because of the nonlinearity of groundwater systems, algorithms which have ability to deal with the nonlinearity such as NLP are required (Rogers and Dowla 1994). Without the derivation of optimization formulation, GA also becomes an attractive alternative (Rogers et al. 1995; Wang et al. 2011).

The behaviors of multi-reservoir system and groundwater system in the CUMM are linear and nonlinear, respectively. Therefore, the CUMM optimization algorithm used must deal with mixed linear and nonlinear problems. These problems are complicated and difficult to solve using single algorithms. Thus, this study proposes a decomposition method to decompose the problem into several sub-problems based on problem characteristics such as integer, linear, nonlinear or time-variant characteristics. A hybrid architecture of optimal algorithms can then solve the set of sub-problems and each algorithm for solving different sub-problems can be chosen based on the characteristics of sub-problem itself. For example, LP is usually the best choice for linear sub-problems because of its high searching efficiency and low computational burden. Watkins and McKinney (1998) applied two decomposition methods, generalized Benders decomposition (GBD) and outer approximation (OA), to a mixed-integer nonlinear programming (MINLP) problem. They decomposed the MINLP problem into a mixed-integer linear programming (MILP) sub-problem and a nonlinear programming (NLP) sub-problem. Hsiao and Chang (2002) and Chang et al. (2009) also used decomposition methods in their groundwater management models. They proposed optimal groundwater management models to minimize the total costs, including fixed costs for well network design and operational costs for groundwater pumping. The models in both studies simultaneously determined the optimal design of well networks and the associated time-variant pumping quantities. Because the determination of a network design contains integer characteristics and the determination of pumping quantities contains time-variant characteristics, the entire problem becomes a mixed integer and time-variant problem. They decomposed the entire problem into an integer sub-problem, which is a network design problem, and another time-variant sub-problem, which is a pumping quantity determination problem. Based on the sub-problem characteristics, the algorithms for both sub-problems respectively are GA, a good choice for integer programming problems, and CDDP (Chang et al. 1992), which a dynamic programming-based algorithm and also the most powerful algorithm for time-variant problems. These studies show that the decomposition method can successfully decompose the complicated water resource management problem into several sub-problems. The proposed hybrid architecture, unlike a purebred architecture, can combine the advantages of multiple algorithms for solving these sub-problems.

This study proposes a stepwise optimization CUMM for unconfined aquifer. The proposed model uses the decomposition method to decompose the entire optimization problem into a linear sub-problem (a surface water system), and another nonlinear sub-problem (an unconfined aquifer system). The proposed model uses LP and GA to solve these two sub-problems. This study uses a recursive ANN model to simulate the behavior of unconfined aquifer.

2 Methodology

This section describes the methodology of developing the proposed CUMM. Section 2.1. demonstrate the model architecture of CUMM. Section 2.2. uses the recursive ANN model to simulate the behavior of an unconfined aquifer. Section 2.3. further describes some basic operating concepts, including the rule curve operating method, the index value theory, the index balance method (IBM), and the mathematical formulation for CUMM. Section 2.4. presents a hybrid architecture including ANN, LP, and GA, which is then used to determine the supply strategies for CUMM.

2.1 Model Architecture

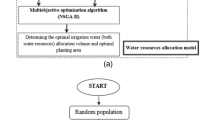
Figure 1 shows the model architecture of the proposed CUMM. In Fig. 1, the model architecture contains three elements, include GA, LP and ANN. The ANN instead of numerical modeling for unconfined aquifers is trained to simulate an unconfined groundwater system (Eq. 12) and the construction of ANN is further described in Section 2.2. The combination of GA and LP is the optimization solver of CUMM which determine the optimal pumping rates for well networks and release quantities for reservoirs. Because the behavior of reservoir system and the behavior of unconfined aquifers respectively are linear and nonlinear, a decomposition method is applied to decompose the CUMM into two sub-problems, linear and nonlinear parts. GA and LP are respectively used to solve the different parts. The combination of two algorithms can remain the high computational efficiency of LP for the linear part and the robust, flexibility and nonlinear ability of GA for the nonlinear part.

Fig. 1
figure 1

The model architecture for CUMM

Full size image

2.2 Groundwater ANN Model Development

The governing equation for unconfined aquifer is a nonlinear equation which describes the temporal and spatial variations of groundwater levels. In traditional groundwater numerical simulation, only the groundwater levels of the first time step are directly assigned as the initial condition. The groundwater levels of later time steps are recursively calculated based on the previous time step. This subsection proposes a recursive ANN model to replace the usage of traditional numerical models. Due to the recursive procedure of the time variation problem mentioned above, the recursive ANN model also simulates as the recursive procedure mentioned above.

Figure 2 shows a structural diagram of the recursive ANN model. The structure can be divided into two stages: a training stage (Fig. 2a), and a prediction stage (Fig. 2b). The training stage has a structure similar to other ANN models. The input nodes of the structure contain state variables and decision variables of the t-th time step. The output nodes only contain state variables of the next time step. In CUMM, the state variables mean the groundwater levels for each observation well, \(\vec{h}\left(t\right)\) and \(\vec{h}\left(t+1\right)\), and the decision variables mean the pumping rates for each pumping well, \(\vec{P}\left(t\right)\). The training stage normally collects data pairs between input nodes and output nodes from field data observations or numerical model generation. The prediction stage modifies the structure of the recursive ANN model (Fig. 2b). Similar to the recursive procedure mentioned above, the results calculated from output nodes are recursively assigned to the input nodes for the next step simulation, except for the first time step.

Fig. 2
figure 2

Recursive ANN structure diagram a Training stage; b Prediction stage

Full size image

Figure 3 illustrates the creation procedure of the recursive ANN model. This procedure can be divided into two parts: data creation for ANN model training and verification and ANN model training and verification. The first part contains two steps: data creation by groundwater numerical model and data preprocessing for ANN. The first step uses the numerical groundwater model, MODFLOW 96, to generate data for ANN training and verification. Figure 4 depicts the groundwater system structure. Five pumping wells, well #A to #E, and five observation wells, wells #1 to #5, and five observation wells, wells #1 to #5, were installed on a homogeneous and isotropic unconfined aquifer whose area is 17×17 (km2) (shown as Table 1). The aquifer thickness was 110 (m). The aquifer was divided into 170×170 cells whose area was 100×100 m2 each. The left side and right side of the aquifer were assigned as the Dirichlet boundary conditions, which were respectively assigned as 100 and 80 (m). The other two sides were assigned as no flow boundary condition (Fig. 4). The length of simulation time step was 10 (days) and the entire simulation period was 365 time steps (10 years total). Table 1 shows the hydrogeological and other simulation parameters.

Fig. 3
figure 3

Flowchart of training and verification of groundwater ANN simulation model

Full size image
Fig. 4
figure 4

Map of groundwater system

Full size image
Table 1 Table of aquifer properties and simulation parameters
Full size table

The training data set was generated by repeating MODFLOW simulations with different pumping rates. A random number generator was used to create ten series of time varying pumping rates with 365 time steps for the five pumping wells, and ten matrixes labeled as P 365×5 were created to store the pumping rates. After repeating MODFLOW simulations, the groundwater levels, including the initial time step and other 365 time steps observed from the five observation wells, were stored in another ten matrixes labeled as h 366×5.

The data preprocessing step can be divided into two sub-steps, including data collection and data normalization (Fig. 3). The data collection sub-step collects training data and verification data from the matrixes, P 365×5 and h 366×5. In the data normalization sub-step, a linear transformation transfers the variable values varied between 1 to -1 is applied. Both the aquifer thickness (110 m) and maximum pumping rate (0.5 cms) are used to normalize h 366×5 and P 365×5, as Eq. 1 shows.

$$ \begin{cases} P^{i}_{N, 365\times 5}=\dfrac{P_{365 \times 5}^{i} \times 2}{0.5\; (\rm cms)} - 1\\[6pt] h^{i}_{N, 366\times 5}=\dfrac{h_{366 \times 5}^{i} \times 2}{110\; (\rm m)} - 1 \end{cases}\qquad,\; {\rm for}\; i=1,...,10\\ \label{eq:normalization} $$
(1)

The ANN groundwater simulation model training and verification stage uses the MATLAB Neural Network toolbox to construct the proposed ANN model. Table 2 lists the ANN parameters used in this study. The proposed model uses a three-layer backward propagation network (BPN), including an input layer, a hidden layer, and an output layer. The number of nodes in the hidden layer is 20 and the transfer function of hidden layer and output layer are respectively tan-sigmoid transfer function (Eq. 2), and linear transfer function (Eq. 3). The assignment for the number of output layer is based on the size of the observation wells. To avoid the affect of over fitting, a try-and-error approach is used to determine the proper number of hidden nodes. The number of hidden nodes increases gradually when the ability of the ANN model with fewer hidden nodes can not deal with the complexity and nonlinearity of data. Until the model errors for both the training set and the validation set can satisfy the model criteria, the current number of hidden nodes is the proper number. The BFGS method, a qusai-Newton method, is the training algorithm. The ANN convergence criterion is that the root mean-square error (RMSE) must be smaller than 10 − 7.

$$ f\left(x\right)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \label{eq:ann1} $$
(2)
$$ f\left(x\right)=x \label{eq:ann2} $$
(3)
Table 2 Table of ANN parameters
Full size table

After finishing the training stage, model verification involving another set of data pairs is necessary to verify model reliability. The ANN model structure after the training stage becomes the prediction stage (Fig. 2b). Therefore, by applying the initial groundwater levels and other sets of pumping rates, the RMSE between the simulated levels and the observation levels is an index of model reliability.

Two types of time series for pumping created by an uniform random number, type A, and a step function, type B, are used to train and verify the robustness and ability. The type A was generated by the uniform random number generator which varied from 0 to 0.5 (cms). The type B was generated by the step function generator which pumps 0.3 (cms) for 18 continuous time steps and stops for the next 18 time steps. Each verification cases simulate 3,650 time steps (100 years). The verification results in Table 3 indicate that the relative root-mean-square error (relative RMSE) of a 100-year simulation is less than 3.0 %. These result confirm the reliability of the proposed ANN model and indicate that the ANN groundwater simulation model is well trained.

Table 3 ANN model verification error
Full size table

On a computer with Intel(R) Xeon(R) CPU E5620 @2.40GHz, the computational burden of the groundwater simulation with 25,000 time steps for the MODFLOW model with 170×170 grids consumes about 131 seconds. However, the computational burden of the simulation with the same time steps for the groundwater ANN model just requires two seconds. The ANN model is about 65 times faster than the MODFLOW model. The high computational efficiency of the ANN model make the proposed conjunctive-use model attractive in a operation with large number of time steps.

2.3 Formulation of Conjunctive-Use Management Model (CUMM)

This section describes three operational concepts: Rule Curve Operating Method (Section 2.3.1), Index Value Theory (Section 2.3.2) and Index Balancing Method (Section 2.3.3). The Rule Curve Operating Method is traditionally used to determine the total supply quantity based on current reservoir storage. The Index Value Theory linearly demonstrates the status of reservoir storage. The Index Balancing Method is used to allocate the supply quantities between different reservoirs in a multi-reservoir system. Because this study develops a CUMM, it applies the Rule Curve Operating Method and Index Value Theory to groundwater systems and extends the Index Balancing Method to allocate the supply quantities between surface water system and groundwater system. Section 2.3.4 describes the formulation of the proposed CUMM.

2.3.1 Rule Curve Operating Method

The rule curve operating method is one of the most widely used approaches in practice because engineers can easily operate the reservoirs basing on the predefined rule curves. These rule curves vertically divide the entire reservoir volume into several layers. Each layer associates a discounting ratio, which varies from 0 to 1, and the ratio for upper layer is normally larger than the ratio for lower layer. The ratio is calculated based on the sum of reservoir storage and inflow quantity (Eq. 4).

$$ D^{t}=\begin{cases} \gamma^{1}D^{\star t} & if\; \nu^{2}>V^{t}+IF^{t}\geq \nu^{1}\\ \gamma^{2}D^{\star t} & if\; \nu^{3}>V^{t}+IF^{t}\geq \nu^{2}\\ & \vdots\\ \gamma^{N_{r}}D^{\star t} & if\; \nu^{N_{r}+1}>V^{t}+IF^{t}\geq \nu^{N_{r}} \end{cases} \label{eq:discounting_single} $$
(4)

In Eq. 4, V t is the reservoir storage at the t-th time step, IF t is the reservoir inflow quantity at the same time step, ν i is the volume of the reservoir storage below the bottom of the i-th layer, γ i is the discounting ratio associated with the i-th layer, N r is the number of the rule curves, D  ⋆ t is the original water demand, and D t is the discounted water demand and also is the supply quantity for the current time step. The discounting ratios for upper layers are normally equal to 1.0 and those for lower layers are less than 1.0. The reason for the discounting ratio assignment is that the reservoir can fully satisfy the water demand when the reservoir storage is plentiful. Otherwise, the reservoir should save water to go through the entire draught period. The upper layers and the lower layers can respectively be called the full supply layer (FSL) and partial supply layer (PSL).

The rule curve operating method also can be applied to a multi-reservoir system. The equation of discounting ratio determining should be modified as Eq. 5. The storage quantities, inflow quantities, and reservoir volumes of each reservoir are summed to form the equivalent reservoir values for the entire system.

$$ D^{t}=\begin{cases} \gamma^{1}D^{\star t} & if\; \sum_{j=1}^{N_{s}}\nu_{j}^{2}>\sum_{j=1}^{N_{s}}\left(V_{j}^{t}+IF_{j}^{t}\right)\geq \sum_{j=1}^{N_{s}}\nu_{j}^{1}\\ \gamma^{2}D^{\star t} & if\; \sum_{j=1}^{N_{s}}\nu_{j}^{3}>\sum_{j=1}^{N_{s}}\left(V_{j}^{t}+IF_{j}^{t}\right)\geq \sum_{j=1}^{N_{s}}\nu_{j}^{2}\\ & \vdots\\ \gamma^{N_{r}}D^{\star t} & if\; \sum_{j=1}^{N_{s}}\nu_{j}^{N_{r}+1}>\sum_{j=1}^{N_{s}}\left(V_{j}^{t}+IF_{j}^{t}\right)\geq \sum_{j=1}^{N_{s}}\nu_{j}^{N_{r}} \label{eq:discounting_multi} \end{cases} $$
(5)

2.3.2 Index Value Theory

The index value for a reservoir is linearly normalized by the volume of the reservoir storage and its associating rule curves (Eq. 6). In Eq. 6, \(I_{SW,j}^{t}\) means the index value at the t-th time step for the j-th reservoir, \(V_{j}^{t}\) means the volume of the water storage at the same time step, \(\nu_{j}^{i}\) means the reservoir storage at the bottom of the i-th layer and \(\nu_{j}^{i+1}\) means the reservoir storage at the bottom of the i + 1-th layer (i.e., the top of the i-th layer). Therefore, an index value between i and i + 1 means that the water level occupies the i-th layer.

$$ I_{SW,j}^{t}=i+{\left(V_{j}^{t}-\nu_{j}^{i}\right)}/{\left(\nu_{j}^{i+1}-\nu_{j}^{i}\right)},\; i=1, ... ,N_{r} \label{eq04} $$
(6)
$$ I_{GW}^{t}=i+{\left(\widetilde{h}^{t}-\widetilde{\mu}^{i}\right)}/{\left(\widetilde{\mu}^{i+1}-\widetilde{\mu}^{i}\right)},\; i=1,...,N_{r} \label{eq:indexGW} $$
(7)

The concept of the Index Value Theory can be further applied in a conjunctive use system. The definition of the index value of a groundwater system can be also written as Eq. 7. In Eq. 7, \(I_{GW}^{t}\) means the index value of groundwater system at the t-th time step, \(\widetilde{h}^{t}\) means the average groundwater level at the same time step, \(\widetilde{\mu}^{i}\) means the average groundwater level at the bottom of the i-th layer and \(\widetilde{\mu}^{i+1}\) means the average level at the top of the same layer. Therefore, an index value between i and i + 1 means that the average level occupies the i-th layer.

2.3.3 Index Balancing Method

Equations 4 and 5 calculate the discounted water demand. In a multi-reservoir system, the supply quantities for each reservoir and the pumping quantities for groundwater aquifers must be further allocated. This study uses the index balance method (IBM) to allocate the supply quantities in a multi-reservoir system or a conjunctive use system.

The IBM is an operating policy in which the index values of each reservoir should equal to the values of other reservoirs during operation. The goal of the IBM is to avoid overuse of single reservoir in contrast to the entire water resource system, and to guarantee that the storage of each reservoir has similar status. The IBM of a conjunctive use system is similar to that of a multi-reservoir system. The index value of a surface water system and the value of a groundwater system should be the same or nearly equal.

2.3.4 CUMM Formulation

The operation of the proposed CUMM is based on the predefined operation rule curve. The discounted ratio and discounted water demand for each time step is calculated directly using the rule curve. Although the discounted demand at each time step can be calculated, the supply quantities for each reservoir and the pumping quantities for groundwater system must obey the IBM and the pre-calculated discounted demand (Eqs. 4 and 5). The determination of supply quantities and pumping quantities can be formed as a stepwise optimization problem. Equation 8 through 20 show this formulation.

$$ \big[\rm Problem~~\#1~~(Original~~problem~~for~~CUMM)\big] $$

Objective function:

$$ Z_{CUMM}^{t}=\min\limits_{\vec{X}^{t}, \vec{P}^{t}} \sum\limits_{i=1}^{N_{d}}\omega_{SH,i}SHR_{i}^{t}+\omega_{GAP}\sum\limits_{m=1}^{N_{s}}\sum\limits_{n=1}^{N_{s}}GAP_{SW,mn}^{t}+ \label{eq:problem1_object} $$
(8)
$$\omega_{GAP}GAP_{SYS}^{t}+\omega_{SL}\left(\sum\limits_{j=1}^{N_{s}}SL_{SW,j}^{t}+SL_{GW}^{t}\right) ,\qquad \omega_{SH,i}>\omega_{GAP}>\omega_{SL}$$

s.t.

$$ SHR_{i}^{t}=SH{}_{i}^{t}/\left(\sum\limits_{k=1}^{N_{d}}D_{k}^{t}\right),\quad\forall i\in N_{d} \label{eq:problem1_shortage} $$
(9)
$$ D_{i}^{t}=\sum\limits_{j=1}^{\forall j\in N_{s}}\lambda_{ij}X_{j}^{t}+\sum\limits_{k=1}^{\forall k\in N_{p}}\lambda_{ik}P_{k}^{t}+SH_{i}^{t},\quad\forall i\in N_{d},\quad X_{j}^{t}\in\vec{X}^{t},\quad P_{k}^{t}\in\vec{P}^{t} \label{eq:problem1_shortage_continuity} $$
(10)
$$ V_{j}^{t+1}=V_{j}^{t}+\sum\limits_{m=1}^{\forall m \in N_{IF}}\lambda_{jm}IF_{m}^{t}-\sum\limits_{i=1}^{\forall i \in N_{d}}\lambda_{ij}X_{j}^{t}-OF_{j}^{t},\quad\forall j\in N_{s} \label{eq:problem1_swcontinuity} $$
(11)
$$ \vec{h}^{t+1}=f_{ANN}\left(\vec{h}^{t},\vec{P}^{t}\right) \label{eq:problem1_gwcontinuity} $$
(12)
$$ GAP_{SW,mn}^{t}=|I_{sw,m}^{t}-I_{sw,n}^{t}|,\quad\forall m,n\in N_{s} \label{eq:problem1_indexgap1} $$
(13)
$$ GAP_{SYS}^{t}=|\widetilde{I}_{SW}^{t}-I_{GW}^{t}| \label{eq:problem1_indexgap2} $$
(14)
$$ I_{SW,j}^{t}=\begin{cases} 1+\frac{V_{j}^{t}-\nu_{j}^{1}}{\nu_{j}^{2}-\nu_{j}^{1}} & if\: \nu_{j}^{2}> V_{j}^{t} \geq \nu_{j}^{1}\\ 2+\frac{V_{j}^{t}-\nu_{j}^{2}}{\nu_{j}^{3}-\nu_{j}^{2}} & if\: \nu_{j}^{3}> V_{j}^{t} \geq \nu_{j}^{2}\\ & \vdots\\ N_{r}-1+\frac{V_{j}^{t}-\nu_{j}^{N_{r}}}{\nu_{j}^{N_{r}+1}-\nu_{j}^{N_{r}}} & if\: \nu_{j}^{N_{r}+1}> V_{j}^{t} \geq \nu_{j}^{N_{r}}\\ \end{cases},\quad \forall j\in N_{s} \label{eq:problem1_swindex} $$
(15)
$$ I_{GW}^{t}=\begin{cases} 1+{\left(\widetilde{h}^{t}-\widetilde{\mu}^{1}\right)}/{\left(\widetilde{\mu}^{2}-\widetilde{\mu}^{1}\right)} & if\: \widetilde{\mu}^{2}> \widetilde{h}^{t} \geq \widetilde{\mu}^{1}\\ 2+{\left(\widetilde{h}^{t}-\widetilde{\mu}^{2}\right)}/{\left(\widetilde{\mu}^{3}-\widetilde{\mu}^{2}\right)} & if\: \widetilde{\mu}^{3}> \widetilde{h}^{t} \geq \widetilde{\mu}^{2}\\ & \vdots\\ N_{r}+{\left(\widetilde{h}^{t}-\widetilde{\mu}^{N_{r}}\right)}/{\left(\widetilde{\mu}^{N_{r}+1}-\widetilde{\mu}^{N_{r}}\right)} & if\: \widetilde{\mu}^{N_{r}+1}> \widetilde{h}^{t} \geq \widetilde{\mu}^{N_{r}}\\ \end{cases} \label{eq:problem1_gwindex} $$
(16)
$$ SL_{SW,j}^{t}=\frac{V_{j,{\rm max}}-V_{j}^{t}}{V_{j,{\rm max}}-V_{j,{\rm min}}},\quad\forall j\in N_{s} \label{eq:problem1_swsparevolume} $$
(17)
$$ SL_{GW}^{t}=\frac{\widetilde{h}_{\rm max}-\widetilde{h}^{t}}{\widetilde{h}_{\rm max}-\widetilde{h}_{\rm min}} \label{eq:problem1_gwsparevolume} $$
(18)
$$ V_{j,{\rm min}}\leq V_{j}^{t}\leq V_{j,{\rm max}},\quad\forall j\in N_{s} \label{eq:problem1_noneq_constrain_sw} $$
(19)
$$ \widetilde{h}_{\rm min}\leq\widetilde{h}^{t}\leq\widetilde{h}_{\rm max} \label{eq:problem1_noneq_constrain_gw} $$
(20)

where \(\vec{X}^{t}\) and \(\vec{P}^{t}\) respectively represent the water supply quantities and groundwater pumping quantities at the t-th time step and also are the decision variables for [Problem #1]. The terms N d , N s , N p , N IF , and N r are the number of water demands, reservoirs, pumping wells, inflow nodes and rule curve levels, respectively. The lengths of \(\vec{X}^{t}\) and \(\vec{P}^{t}\) are N s and N p , respectively. \(SHR_{i}^{t}\) is the ratio of the water shortage to water demand for the i-th demand node (Eq. 9). \(GAP_{SW,mn}^{t}\) means the index value discrepancy between the m-th and the n-th reservoirs (Eq. 13). \(GAP_{SYS}^{t}\) means index value discrepancy between the surface water system and the groundwater system (Eq. 14). \(SL_{SW,j}^{t}\) means the ratio of spare volume to system capacity for the j-th reservoir (Eq. 17). \(SL_{GW}^{t}\) means ratio of spare volume to system capacity for groundwater system (Eq. 18). \(D_{i}^{t}\) means the discounted water demand for the i-th demand node and is already pre-determined based on Eq. 4 or 5. \(SH_{i}^{t}\) means water shortage for the i-th demand, while \(V_{j}^{t}\) means water storage of the j-th reservoir. The terms \(\vec{h}^{t}\) and \(\widetilde{h}^{t}\) respectively means the groundwater levels of different observation points and the average groundwater level, while \(IF_{m}^{t}\) and \(OF_{j}^{t}\) respectively mean the inflow quantity for the m-th inflow node and the overflow quantity for the j-th reservoir. \(I_{SW,j}^{t}\) and \(\widetilde{I}_{SW}^{t}\) respectively mean the index value of the j-th reservoir and the average index value for entire surface water system. \(I_{GW}^{t}\) means the index value for groundwater water system. \(\nu_{j}^{m}\) and \(\widetilde{\mu}^{m}\) respectively mean the volume of the m-th level of rule curve for the j-th reservoir and that for groundwater system. V j, min and V j, max are the minimum and maximum volumes of the j-th reservoir, respectively, while \(\widetilde{h}_{\rm min}\) and \(\widetilde{h}_{\rm max}\) are the minimum and maximum average groundwater levels. The term λ ij means the active index between the i-th node and the j-th node. If the i-th node and the j-th node are connected, the value of λ ij is 1; otherwise, the value is 0.

Equation 8 is an objective function that sums shortage rates for each demand (\(SHR_{j}^{t}\)), the summation of discrepancy of index value (\(GAP_{SW,mn}^{t}\) and \(GAP_{SYS}^{t}\)) and the summation of the ratio of spare volume to system capacity (\(SL_{SW,j}^{t}\) and \(SL_{GW}^{t}\)). Three weight values, ω SH, j , ω GAP and ω SL , represent the priority between different sub-objectives. The shortage rate of each demand is further defined by Eq. 9 in which the water shortage, \(SH_{j}^{t}\), is defined through Eq. 10, a mass balance equation for each demand. In this study, the priority of the summation of shortage rates is higher than the other two sub-objectives. The second sub-objective, which minimizes the summation of discrepancy of index value, tries to balance the index value among reservoirs or different systems. \(GAP_{SW,mn}^{t}\) and \(GAP_{SYS}^{t}\), respectively are defined in Eqs. 13 and 14, are the discrepancy of index value between different reservoirs or different systems. The third term of objective function, minimizing the summation of the ratio of spare volume to system capacity, tries to keep more water resource in the supply system and also be further formed as Eqs. 17 and 18.

Equations 11 and 12, which are the continuity equations of reservoirs and groundwater system, present the behavior of reservoirs and groundwater system. The implementation of Eq. 12 repuires a recursive ANN model instead of a traditional numerical model or a response matrix, as introduced in Section 2.2. Equations 19 and 20 respectively are constraint functions for reservoirs and the groundwater system. These constraint functions require that the reservoir levels or groundwater levels must vary in predefined ranges.

Since the unconfined groundwater transfer function, Eq. 12, is a nonlinear constraint, the optimal problem, [Problem #1], becomes a complicated nonlinear optimization problem. However, this problem can be reformulated as a linear sub-problem and another nonlinear sub-problem by exploring the problem structure. The original problem is denoted as [Problem #1], and the decomposed problem is denoted as [Problem #2].

$$ \big[\rm Problem~~\#2~~(Decomposed~~problem~~for~~CUMM)\big] $$

Objective function of primary sub-problem

$$ Z_{CUMM}^{t}=\min_{\vec{P}^{t}}\left[J^{\star}\left(\vec{P}^{t}\right)+\omega_{GAP}GAP_{SYS}^{t}+\omega_{SL}SL_{GW}^{t}\right] \label{eq:problem3_object} $$
(21)

s.t.

                           Equations 12, 14, 16, 18 and 20

Objective function of secondary sub-problem

$$ J^{\star}\left(\vec{P}^{t}\right)=\min\limits_{\vec{X}^{t}}\sum\limits_{i=1}^{N_{d}}\omega_{SH,i}SHR_{i}^{t}+\omega_{GAP}\sum\limits_{m=1}^{N_{s}}\sum\limits_{n=1}^{N_{s}}GAP_{SW,mn}^{t}+\omega_{SL}\sum\limits_{j=1}^{N_{s}}SL_{SW,j}^{t} \label{eq:problem4_object} $$
(22)

s.t.

                           Equations 9, 10, 11, 13, 15, 17 and 19

[Problem #2] contains a primary sub-problem and a secondary sub-problem. The primary sub-problem, which determines the pumping quantities (\(\vec{P}^{t}\)) on an unconfined aquifer system, is still a nonlinear problem. However, the secondary sub-problem, which just deals with the surface water system under the pre-determined pumping quantities (\(\vec{P}^{t}\)), is a linear problem.

2.4 Hybrid Architecture for Solving CUMM

As described previously, this study uses a hybrid architecture to solve [Problem #2]. Figure 1 shows the model architecture of the proposed CUMM. In Fig. 1, GA and LP are respectively used to solve the primary sub-problem and the secondary sub-problem. The ANN described in Section 1 is also adapted to simulate the unconfined groundwater system (Eq. 12). Figure 5 shows the computation steps of the hybrid architecture, as illustrated in detail below.

  1. 1.

    The initial population in GA is generated for the solution of the primary sub-problem. Each chromosome is encoded as a binary string.

  2. 2.

    Decoding each binary string, chromosome, into a set of decimal value, a set of pumping rates (\(\vec{P}^{t}\)).

  3. 3.

    The groundwater ANN model (Eq. 12) computes the average groundwater level (\(\widetilde{h}^{t+1}\)) for the next time step reacted by assigning the set of pumping rates decoded from each chromosome. If the average level is not satisfied the groundwater level constrain (Eq. 20), a penalty function will be added; otherwise, LP further solves the secondary sub-problem to obtain the objective value, \(J^{\star}\left(\vec{P}^{t}\right)\), which is also the first term of Eq. 21. Because the second and the third term of Eq. 21 are functions of the average groundwater level, the objective function value of secondary sub-problem for each chromosome can be determined based on the Eqs. 12, 14, 16 and 18.

  4. 4.

    After calculating the fitness (the value of objective function in primary sub-problem), examining the convergence criteria. If it is not convergent, apply selection, crossover, and mutation operators to generate a new population of chromosomes and return to Step 2; otherwise, stop entire process.

Fig. 5
figure 5

The model flowchart for the hybrid architecture (CUMM)

Full size image

Using the proposed hybrid architecture has several benefits. First, solving surface water allocation problem (the secondary sub-problem) is computationally more efficient using LP than other algorithms, such as GA. Second, because the value of \(J^{\star}(\vec{P}^{t})\) in the objective function of the primary sub-problem is the optimal value of the secondary sub-problem, the gradient of \(J^{\star}(\vec{P}^{t})\) is difficult to be derived. Therefore, GA is a better choice than traditional gradient-based optimal algorithms such as NLP. Therefore, the GA-LP hybrid architecture for the entire problem, the primary and the secondary sub-problems, not only achieves higher computational performance for the linear part, but also has ability to deal with the nonlinear part.

3 Results and Discussion

This section introduces the study cases and their associated setting in Section 3.1. Section 3.3 then describes the operation results of the cases and compares different cases to show the advantages of the proposed CUMM.

3.1 Cases Introduction

The length of operation time step is ten days, same as the length of simulation time step used in the recursive ANN model. Table 4 compares four numerical cases with the same water requirement, 15 ×106 (\(\rm m^{3}/{ten\: days}\)). Case #1 only uses surface water resources to satisfy the water requirement, and thus a pure surface water operation case (refers to SW case). The formulation of supply strategy determination for the SW case is determined using only the secondary sub-problem in Problem #2. Because the objective function of the secondary sub-problem is conditioned with the predefined pumping quantities, \(\vec{P}^{t}\), the value of \(\vec{P}^{t}\) is directly assigned as zero in Case #1, a SW case.

Table 4 Numerical case list table
Full size table

Cases #2, #3 and #4 are conjunctive use cases. Case #2 uses both surface water and groundwater resources in a prearranged supply priority called surface water supply first (SWSF) policy. This case is also called a decoupling conjunctive use (refers to DCU) case. The groundwater system supplies only during the water demand cannot be satisfied by only using the surface water system. The determination of the supply strategy for the surface water system in this case is equal to that in Case #1. After determining the supply quantities of the surface water system, the pumping quantities can be assigned as either the gap between the surface water supply quantities and the water demand or the maximum pumping productivity constraint. The DCU model has been widely applied in Taiwan because of its ease of implementation.

Cases #3 and #4 use both surface water and groundwater resources with the proposed CUMM. Contrast to the Case #2, the supply priority which is not predefined before model operating is determined by the CUMM. Different operation rule curves of the groundwater resource which define the priority of resource usage are applied in Cases #3 and #4. Both of them are coupled conjunctive use (refers to CCU) cases.

  • Case #1:

The surface water system contains two reservoirs, reservoir A and reservoir B, with maximum storages of 70×106 and 50×106 (m3), respectively. These two reservoirs supply water a water demand node with a parallel connection. Figure 6 is a system diagram. The Fig. 7 shows the variations of inflow quantities for two reservoirs. The average inflow quantities for the two reservoirs are 8.4×106 and 4.95×106 (\(\rm m^{3}/{ten\: days}\)), respectively. The average inflow quantity of entire surface system, 13.35×106 (\(\rm m^{3}/{ten\: days}\)) is a little smaller than the water requirement quantity, 15×106 (\(\rm m^{3}/{ten\: days}\)). Figures 8 and 9 show the operation rule curve diagrams of reservoirs A and B, respectively. In this case, the discounting ratios for each layers are assigned as 1.0 and each layers are FSLs.

Fig. 6
figure 6

System diagram of surface water system (SW case)

Full size image
Fig. 7
figure 7

The inflow quantity diagram for both reservoir A and B

Full size image
Fig. 8
figure 8

The diagram of operation rule curve for reservoir A

Full size image
Fig. 9
figure 9

The diagram of operation rule curve for reservoir B

Full size image

  • Case #2, #3, #4:

The other three cases are all conjunctive use operation cases. The two-reservoir surface water system mentioned above and an additional five-well groundwater system construct the entire supply system (Fig. 10). This study uses a recursive ANN model as the simulation model for the five-well groundwater system, as described in Section 2.2. The reservoir assignment of the surface water system, including maximum capacities, inflow quantities, and operation rule curves, is the same in all four cases, from Cases #1 to #4. In the groundwater system, the maximum pumping rate of each well is 0.26×106 (\(\rm m^{3}/{ten\: days}\)). Therefore, the maximum supply productivity of the entire groundwater system is 1.30×106 (\(\rm m^{3}/{ten\: days}\)).

Fig. 10
figure 10

System diagram of conjunctive use system(CU system)

Full size image

Because Cases #3 and #4 are both CCU cases, their supply priorities are determined by comparing the gap of SI between surface and groundwater system, which is related to the assigned operation rule curves for both systems. Groundwater operation rule curves #1 and #2 (Figs. 11 and 12, respectively) are applied to Cases #3 and #4. The third layer, whose index value varies from 3.0 to 4.0, in Fig. 11 is thinner than the layer in Fig. 12. On the contrary, the first layer, whose index value varies from 1.0 to 2.0, in Fig. 11 is thicker than the layer in Fig. 12. Figure 13 plots the relationship between the average groundwater level and the groundwater index value for both rule curves #1 and #2. For example, if the groundwater level is 85 (m), the index values based on different rule curves are 2.0 and 3.67, and if the groundwater level is 75 (m), the index values are 1.33 and 3. Therefore, the index value based on the rule curve #1 is always smaller than the value based on the rule curve #2 for the same groundwater level. The lower index values mean the lower priority of groundwater usage in rule curve #1.

Fig. 11
figure 11

Operation rule cuve #1 of groundwater system

Full size image
Fig. 12
figure 12

Operation rule cuve #2 of groundwater system

Full size image
Fig. 13
figure 13

The relationship diagram between groundwater level and index value for rule curve #1 and #2

Full size image

3.2 Model Parameters for Genetic Algorithm

Table 5 lists the model parameters for GA. The GA population contains 50 chromosomes. The mutation rate and crossover rate respectively are 0.01 and 0.8. The proposed model based on two stopping criteria. The first one is the model will be stopped while the model generations is exceeded the maximum generation. The second one is the model will be stopped while the optimal fitness of each generation is continuously fixed without improvement in a specific length of generations. The maximum generation of the proposed model is 200 and the number of non-improved generation is 20.

Table 5 Table of GA parameters
Full size table

3.3 Case Results

Table 6 lists the simulation results of four cases.

  • Case #1:

In Case #1 (SW), because the average supply amount of surface water system, 13.55×106 (\(\rm m^{3}/{ten\: days}\)), is 90.33 % of the water requirement quantity, 15×106 (\(\rm m^{3}/{ten\: days}\)), the average supply amount is almost equal to the average inflow quantity mentioned above. The shortage index (SI) of Case #1 is 2.93 and the number of supply shortage time steps (labels as SSTSN) is 135.

  • Case #2:

In Case #2 (DCU), the average supply amount of surface water system is also 13.55×106 (\(\rm m^{3}/{ten\: days}\)) and the operation behavior is the same as that of Case #1. The groundwater system is worked within the water demand cannot be satisfied by using only the surface water system. The average supply amount of groundwater system is 0.48×106 (\(\rm m^{3}/{ten\: days}\)), which is just 3.20 % of the entire requirement. Because of the additional groundwater resource, the SI of Case #2 decreases from 2.93 to 1.54 and the SSTSN decreases from 135 to 125. Although the supply ratio of groundwater system is just 3.20 %, the additional groundwater resource still can significantly decrease the SI in a DCU case.

A comparison between Cases #1 and #2 indicates that a small but stable water resource also can significantly relax the deficit status of water supply shortage. Comparing the average pumping quantity, 0.48×106 (\(\rm m^{3}/{ten\: days}\)), and the maximum productivity constrain, 1.30×106 (\(\rm m^{3}/{ten\: days}\)), the production efficiency of the groundwater system in Case #2 is just 36.87 %. Because the production efficiency caused by the SWSF policy is still low, the production efficiency of this groundwater system remains great potential to improve with various conjunctive use policies.

  • Case #3 and #4:

In Cases #3 and #4, both CCU cases, the operation priority between two systems is determined by the assignment of rule curves for surface water system and groundwater system. In both cases, the average supply amounts of surface water respectively are 13.48×106 (\(\rm m^{3}/{ten\: days}\)), which is 89.87 % of the entire water requirement, and 13.53×106 (\(\rm m^{3}/{ten\: days}\)), 90.20 %. The amounts of groundwater respectively are 0.68×106 \((\rm m^{3}/{ten\: days})\), 4.53 %, and 0.89×106 \(\rm (m^{3}/{ten\: days})\), 5.93 %. The SI values respectively are 1.13 and 0.79, while the SSTSNs are 111 and 89.

Table 6 Table of simulation results
Full size table

A comparison of the DCU case, Case #2A comparison of the DCU case, Cases #3 and #4, shows that the average supply ratios of groundwater system increase from 3.20 % to 4.53 % and to 5.93 %. The production efficiencies also increase from 36.87 % to 52.31 % and to 68.46 %. The SIs further decrease from 1.54 to 1.13 and to 0.79. These results indicate that the proposed conjunctive use policy can increase the production efficiency of the groundwater system and also decrease the system SI to relax the shortage status of water supply.

The improvement of productivity efficiency for the groundwater systems between Cases #2 and Case #4 is more significant than that between Case #2 and Case #3. The reason of the difference on improvement is that the different height of operation rule curves of groundwater system (Figs. 11 and 12). Figure 14 compares SW and GW index values for the operation results of Case #3 and #4, while Fig. 15 shows the associated groundwater level. Because of the effect of the operation rule curves (Fig. 13), the slope of GW level and index value for rule curve #1 is steeper than the slope for rule curve #2 when the index values vary from 3.0 to 4.0 (the third layer of the rule curve). Besides, because the IBM is the supply principle to allocate quantities between groundwater system and surface water system, the groundwater usage in Case #3 has lower priority and shorter pumping period than in Case #4. Counting the number of time steps whose GW index value is higher than the associated SW index value from Fig. 14, the number of Case #3, which is 187 within 365 time steps, is less than that of Case #4, which is 247.

Fig. 14
figure 14

The variation diagram of SW and GW index value for Case #3 and #4

Full size image
Fig. 15
figure 15

The variation diagram of groundwater level for Case #3 and #4

Full size image

Figure 16 demonstrates the convergency of GA of Case #3 for the 15-th time step. In the figure, the red line demonstrates the variation of the optimal fitnesses in each generations and the blue points demonstrates the fitness values for each chromosomes. The model converges at the 59-th generation while the optimal fitnesses remain 1.1228 from the 40-th to the 59-th generation. For the convergency of GA, the optimal fitness is stable indicate that the proposed model has had high possibility to find the optimal solution.

Fig. 16
figure 16

The diagram of GA convergency (for the 15-th time step)

Full size image

4 Conclusion

The CUMM, the proposed stepwise optimal model for conjunctive use management, has been developed in this study and a hybrid architecture, the combination of LP, GA and a recursive ANN, is also proposed in CUMM. In the hybrid architecture, LP is applied to determine the optimal amounts of supply quantities for each reservoir, GA is applied to connect a surface water system and a groundwater system and is also used to determine the optimal amounts of pumping quantities for each wells, and the recursive ANN is trained to represent the behaviors of an unconfined aquifer. The hybrid architecture used in the CUMM has several advantages. First, for groundwater simulation, the usage of the recursive ANN can remain both the high computational efficiency of the response matrix method and the nonlinear simulation ability of the embedded method for unconfined aquifers. In simulations of unconfined aquifers with large number of time steps, the recurse ANN is 65 times faster than the MODFLOW model and, besides, the error of the ANN related to the MODFLOW model remains small. Therefore, the high computational efficiency and the nonlinear simulation ability make the proposed model have the potential to apply on a real case planning for unconfined aquifer. Second, for supply policy determination, the optimal algorithm combination in the hybrid architecture, LP and GA, can remain the high computational efficiency of LP for solving the linear sub-problem and the robust, flexibility and nonlinear ability of GA for solving the nonlinear sub-problem. Based on not only the high computational efficiency of the recursive ANN groundwater simulation but also the advantages of the hybrid optimal algorithms, the proposed hybrid architecture can be further extending to a field case.

The usage of the operation rule curves for multi-reservoir systems is the most widely-used approach to determine the priority between different reservoirs and allocate reservoir supply quantities. In this study, the operation rule curves were further applied to determine the priority between multi-reservoir and groundwater systems. Compared with the DCU case, the proposed CCU model, CUMM, could improve the SI from 1.54 to 1.13 or 0.79. The different improvement efficiencies depend on the definition of the groundwater operation rule curves. The thicker the upper layer of groundwater system, the lower the SI for the CCU model. The comparison of different rule curves shows that the different thickness of the upper layer defined by rule curves significantly affected water usage priority between reservoir system and groundwater system. Comparing Case #3 and #4 shows that the average production efficiency for groundwater system significantly increased from 52.31 % to 68.46 %.

The operation rule curves for traditional reservoir operation typically vary with seasons. Because water resources are more plentiful during flood seasons, the heights of the operation rule curves are lower, increasing the usage priority of reservoir storage. Because the heights of the operation rule curves for groundwater system remain static over seasons, the variation of the groundwater rule curves allows the CUMM to further improve the system SI in future study.

Finally, this study uses the operation rule curve theory as a new type of framework for conjunctive use management. Because the operation rule curve theory is widely used for practical reservoir management, the framework is easy to understand for not only academic researchers, but also engineers, who are responsible for practical water management.