A Riemannian Bayesian Framework for Estimating Diffusion Tensor Images

Abstract

Diffusion tensor magnetic resonance imaging (DT-MRI) is a non-invasive imaging technique allowing to estimate the molecular self-diffusion tensors of water within surrounding tissue. Due to the low signal-to-noise ratio of magnetic resonance images, reconstructed tensor images usually require some sort of regularization in a post-processing step. Previous approaches are either suboptimal with respect to the reconstruction or regularization step. This paper presents a Bayesian approach for simultaneous reconstruction and regularization of DT-MR images that allows to resolve the disadvantages of previous approaches. To this end, estimation theoretical concepts are generalized to tensor valued images that are considered as Riemannian manifolds. Doing so allows us to derive a maximum a posteriori estimator of the tensor image that considers both the statistical characteristics of the Rician noise occurring in MR images as well as the nonlinear structure of tensor valued images. Experiments on synthetic data as well as real DT-MRI data validate the advantage of considering both statistical as well as geometrical characteristics of DT-MRI.

1 Introduction

Diffusion tensor magnetic resonance imaging (DT-MRI) allows estimating diffusion tensor images.¹ Each voxel contains a second order tensor represented by a $3 \times 3$ symmetric positive definite matrix. Basis of this technique builds a physical model of water self-diffusion, here the Stejskal–Tanner equation (Stejskal and Tanner 1965), which relates the observed DT-MRI data with the diffusion tensor image. In this paper we generalize estimation theoretical concepts from Euclidean space to non-Euclidean spaces, i.e. the Riemannian manifold of diffusion tensor images. This allows us to estimate diffusion tensor images from DT-MRI data in a way respecting the specific geometry of diffusion tensor images as well as considering the statistical properties of DT-MRI data.

To this end, a likelihood function based on the statistical properties of the DT-MRI data and the Stejskal–Tanner equation is derived. We examine prior distributions and relate them to their deterministic counterparts. In particular, we generalize the concept of anisotropic diffusion filtering from gray-scale images to diffusion tensor images within the Riemannian framework. This paper closes with experimental evaluations of our framework.

1.1 Related Work

Our approach combines reconstruction with regularization of diffusion tensor images. Consequently, it is related to both techniques that have been proposed in this field since the seminal work of Bihan et al. (1986, 2001).

The maybe most common way to reconstruct diffusion tensors is based on a linearized version of the Stejskal–Tanner equation (1) combined with a least squares estimator (cf. Bihan et al. 2001). In order to obtain a consistent and effective estimator from a least squares approach requires the image noise to be identical independent Gaussian distributed. For high signal-to-noise ratios the underlying Gaussian assumption on the image noise has been shown to be satisfied (Gudbjartsson and Patz 1995). However, the independent assumption does not hold for the linearized Stejskal–Tanner equation. Moreover, the linear estimator of Bihan et al. (2001) does not account for the nonlinear structure of the space of diffusion tensors and therefore may lead to physical meaningless non-positive definite diffusion tensors.

There are reconstruction methods considering Rician noise and/or positive definiteness. Andersson (2008) proposed a Bayesian estimator for diffusion tensor images including a Rician noise model. Landman et al. (2007a) proposed a maximum likelihood estimator based on the Rician noise model. A robust variant, considering observations beyond the Rician noise model, has been proposed in Landman et al. (2007b). Cox and Glen (2006) force positive definiteness, but did not consider Rician noise. All methods (Cox and Glen 2006; Landman et al. 2007a; Andersson 2008) do not account for the nonlinear structure of diffusion tensor images. A Riemannian approach respecting the nonlinear structure has been proposed in Lenglet et al. (2006). Unfortunately, no Rician noise has been considered. Both approaches, Landman et al. (2007a) and Lenglet et al. (2006) did not incorporate any denoising or regularization strategies.

Besides the reconstruction of diffusion tensor images from DTI-MRI data, numerous methods for denoising and regularization of diffusion tensor images have been proposed. These methods can be classified into ones based on the Euclidean metric (Tschumperlé and Deriche 2001; Martin-Fernandez et al. 2003; Weickert and Brox 2002; Coulon et al. 2001; Feddern et al. 2006; Burgeth et al. 2007, 2009) and others based on the Riemannian metric (Gur and Sochen 2005; Moakher 2005; Fletcher and Joshi 2004, 2007; Lenglet et al. 2005, 2006; Batchelor et al. 2005; Fillard et al. 2005; Pennec et al. 2006; Castano-Moraga et al. 2007; Zéraï and Moakher 2007a; Gur et al. 2007, 2009, 2012). Methods using the Euclidean metric consider the diffusion tensor image to be embedded in the space of symmetric matrix-valued images which constitutes a vector space. Distances between tensors are computed with respect to the Euclidian metric of the space of symmetric matrices. To keep tensors positive definite, they are projected back onto the manifold of positive definite tensors (Tschumperlé and Deriche 2001), only positive definite tensors are accepted within stochastic sampling steps (Martin-Fernandez et al. 2003), additional constraints are incorporated (Tschumperlé and Deriche 2002) or image processing is restricted to operations assuring positive definiteness, e.g. convex filters (Weickert and Brox 2002; Westin and Knutsson 2003; Krajsek and Mester 2006; Burgeth et al. 2007). Although tensors are forced to be positive definite within such approaches, the Euclidean metric turns out to be less appropriate for regularizing diffusion tensor images as tensors become deformed. This is known as eigenvalue swelling effect and can be circumvented by using the Riemannian metric (Chefd’hotel et al. 2004; Pennec et al. 2006; Castano-Moraga et al. 2007).

Riemannian approaches consider diffusion tensor images as a Riemannian manifold² equipped with a metric on the tangent bundle which is invariant under affine transformations. For instance, Fillard et al. (2005) and Pennec et al. (2006) proposed a ‘Riemannian framework for tensor computing’ which generalizes several well established image processing techniques, originally developed for gray-scale images, to diffusion tensor images, including interpolation, restoration and nonlinear isotropic diffusion filtering. The framework is based on the matrix representation of diffusion tensors and heavily uses computational costly matrix operations like the exponential and the logarithmic map. A computational more efficient approach than the Riemannian framework of Pennec et al. (2006) is based on the so called log-Euclidean metric (Arsigny et al. 2005, 2006; Fillard et al. 2007). The log-Euclidean metric is not invariant under affine coordinate transformations and consequently it depends on the position of the origin of the coordinate system. Zéraï and Moakher (2007a), Gur et al. (2007, 2009, 2012) propose Riemannian regularization approaches which are based on local coordinates and therefore less computationally demanding as the matrix representation of Fillard et al. (2005), Pennec et al. (2006).

In principle, Euclidean denoising and regularization approaches are compatible with the reconstruction approach of Landman et al. (2007a), i.e. they can be combined with the Rician noise model to obtain a simultaneous reconstruction and denoising method but in general suffer from the eigenvalue swelling effect. On the other hand, Riemannian denoising and regularization approaches do not show the eigenvalue swelling effect and are compatible with the Riemannian reconstruction approach proposed by Lenglet et al. (2006). However, such a reconstruction scheme leads to a bias towards smaller diffusion tensors as it does not consider the Rician distributed noise in the DT-MRI data as we will show in this paper.

In summary, we observe that in the literature on diffusion tensor image reconstruction several approaches have been proposed either considering the Rician noise in DT-MRI data or considering the Riemannian geometry of the diffusion tensor images. However no method has been published so far, that simultaneously

• (a) assures positive definiteness,

• (b) considers the Riemannian geometry of diffusion tensor images,

• (c) considers Rician noise, and

• (d) provides a Bayesian estimator with error bounds.

All previous papers fail in providing at least two of the points (a)–(d). For instance, the method proposed in Andersson (2008) covers (a) and (c) but does not include (b) and (d). The approach proposed in Lenglet et al. (2006) does not provide (c) leading to biased estimates and does not cover (d).

1.2 Own Contribution

We present a Riemannian approach to Bayesian estimation of diffusion tensor images from DT-MRI data covering (a) to (d). To this end, we derive a Bayesian estimation framework for diffusion tensor images from DT-MRI data considering both the statistical characteristics of the measured DT-MRI data as well as the specific Riemannian geometry of diffusion tensor images. To the best of our knowledge, only classical statistical (frequentistic) methods or deterministic regularization approaches have been generalized to diffusion tensor images within the Riemannian framework. Thus this Bayesian framework is new.

In a first step, we reformulate estimation theoretical concepts, e.g. the Bayesian risk, from Euclidean spaces to the Riemannian space of diffusion tensor images in Sect. 5. In Sect. 6 we derive a likelihood model for diffusion tensor images that accounts for the Rice distribution. In Sect. 7.2 we generalize the regularization taxonomy for gray-scale images to diffusion tensor images needed for the covariance estimator in Sect. 9. To this end, we relate already known regularization schemes to their MRF counterparts but also derive new ones that have not been considered in the literature so far. The latter are linear and nonlinear anisotropic regularization schemes. In Sect. 7.1.1 we derive mixed second order derivatives needed for anisotropic regularization. In Sect. 7.1.3 we derive discrete approximations for the continuous regularization schemes and demonstrate their stability in numerical experiments in Sect. 10.1.1. Our approach is based on the matrix representation introduced by Fletcher and Joshi (2004, 2007), Fillard et al. (2005), Pennec et al. (2006). A major drawback of the matrix representation is its large computational costs due to the heavy use of matrix operations. In Sect. 7.1.4 we introduce an analytical computation of these matrix functions leading to a considerable speedup compared to commonly used numerical computations. In Sect. 7.1.2 we relate the matrix representation of the diffusion tensor used here to the local coordinate representation used in e.g. Zéraï and Moakher (2007a), Gur et al. (2007) and show that numerical cumbersome Christoffel symbols can be avoided within our approach. In addition to the maximum a posteriori (MAP) estimator, we derive in Sect. 9 an estimator for the covariance matrix of the posterior probability distribution.

Parts of this paper have already been presented at two conferences Krajsek et al. (2008) as well as Krajsek et al. (2009). In addition to the work in Krajsek et al. (2008, 2009) the current paper introduces (1) the speedup of the matrix operations via analytic matrix operations, (2) new stable discretization schemes compared to less stable ones presented in Krajsek et al. (2008), (3) a robust likelihood function in order to cope with noise statistics beyond the Rice distribution, (4) a regularization taxonomy generalizing Euclidean approaches to Riemannian ones, as well as (5) new experiments evaluating the new framework in detail.

In addition to the above mentioned contributions, Sects. 2–4 introduce diffusion tensor imaging, Riemannian manifolds, and treatment of diffusion tensors as Riemannian manifolds, in order to introduce notations and make the paper more self-contained.

2 Diffusion Tensor Imaging

In this section we give a brief overview on the physical diffusion process of water molecules within biological tissues and how it can be measured by means of an NMR scanner. It is beyond the scope of this contribution to give a detailed introduction in diffusion tensor imaging (DTI). We refer the interested reader to the review paper (Bihan et al. 2001).

DTI is a variant of magnetic resonance imaging (MRI) that allows measuring the tensor of water self-diffusion. The basic characteristics of diffusion tensors like their trace or fractional anisotropy (FA) have been shown to be valuable indicators in medical diagnostic/therapy (Müller et al. 2007; Alexander et al. 2007), e.g. being used in medical imaging to delineate infarcted tissue from healthy brain (Edlow et al. 2016). Therefore a precise estimate of the diffusion tensors is a crucial step, helping to provide reliable diagnostics in these cases. However, the clinical application of our method goes far beyond the scope of this paper.

Self diffusion of water origins from thermally induced Brownian motion and takes place irrespective from the concentration gradient of the water molecules. The diffusion can be described by means of the diffusion tensor, i.e. a symmetric positive definite $3 \times 3$ matrix. The eigenvalues of the diffusion tensor encode the amount of diffusion along the principal directions given by the corresponding eigenvectors. The most common model for estimating the diffusion tensor $\varSigma _k$ at spatial position $x_k$ is given by the Stejskal–Tanner equation (Stejskal and Tanner 1965)

$$\begin{aligned} A_{j k}\!=\!A_{0 k} \exp \big (- b_j g_j^T \varSigma _k g_j \big ), \quad j\!=\!1,\ldots ,L , \; k=1,\ldots ,N, \end{aligned}$$

(1)

where N denotes the number of pixels. It relates the diffusion tensor $\varSigma _k$ with the diffusion weighted (DW) image values $A_{j k}$, the reference signal $A_{0 k}$, and the so called ‘b-value’ $b_j$, a scalar value containing a few material constants and experimental parameters, as well as the L unit vectors $g_j \in {\mathbb {R}}^3, \Vert g_j\Vert =1$ indicating the direction of the diffusion encoding. The ‘b-values’ as well as the diffusion encoding directions $g_j$ are usually determined by the experimental design. Thus, by measuring the DW image values for different ‘b-values’ and different diffusion encoding directions allows to estimate the diffusion tensor components by means of the Stejskal–Tanner equation (1). Six or more signals per image pixel measured with non-collinear $g_j$ vectors can be used to estimate the diffusion tensor by minimizing a cost functional of the residua of the corresponding Stejskal–Tanner equations.

3 Riemannian Manifolds

This section gives a short introduction into Riemannian manifolds (cf. Helgason 1978). A manifold ${\mathcal {M}}$ is an abstract mathematical space that locally looks like the Euclidean space. A typical example of a 2D manifold is the sphere ${\mathcal {S}}^2$ embedded in the 3D Euclidean space. In general, an n-dimensional manifold can at least be embedded into a 2n dimensional Euclidean space according to Whitney’s embedding theorem (Whitney 1944; Cohen 1985). Thus, each manifold can be represented by a surface in a higher dimensional Euclidean space which is denoted as the extrinsic view. Except from the extrinsic view, we can describe an n-dimensional manifold locally by the n-dimensional real space ${\mathbb {R}}^n$ which is denoted as the intrinsic view. A local chart $(\vartheta ,U)$ is an open subset of the manifold $U \subseteq {\mathcal {M}}$ together with a one to one map $\vartheta :U\rightarrow {\mathbb {R}}^n$ from this open subset to an open set of the Euclidean space. The image $\vartheta (p) \in {\mathbb {R}}^n$ of a point of the manifold $p \in {\mathcal {M}}$ is denoted as local coordinates. The piecewise one to one mapping to the Euclidean space allows the generalization of concepts developed for the Euclidean space onto manifolds. For instance, a function $f: {\mathcal {M}}\rightarrow {\mathbb {R}}$ defined on the manifold is denoted as differentiable at point $p\in {\mathcal {M}}$ if the function $f_{\vartheta }:=f \circ \vartheta ^{-1}$ is differentiable under the chart at point $\vartheta (p)$. At each point on the manifold $p \in {\mathcal {M}}$ we can attach a tangent space $T_p{\mathcal {M}}$ that contains all directions one can pass through p. More precisely, let $\gamma (t): {\mathbb {R}}\rightarrow {\mathcal {M}}$ denote a continuously differentiable curve in the manifold going through $\gamma (0)=p \in {\mathcal {M}}$ and $\gamma _\vartheta (t)=\vartheta \circ \gamma (t)$ its representation in a local chart $(\vartheta ,U)$. A representation of a tangent vector $\overrightarrow{p v}_\vartheta$ is then given by the instantaneous speed $\overrightarrow{pv}_\vartheta :=\left. \partial _{t}\gamma _\vartheta (t)\right| _{t=0}$ of the curve and the speed vectors of all possible curves constitute the tangent space at p. The definition of the tangent vector is independent of the chosen local chart and is denoted as $\overrightarrow{p v} \in T_p{\mathcal {M}}$. The set of all tangent spaces of the manifold is denoted as the tangent bundle. A Riemannian manifold owns additional structure that allows to define distances between different points on the manifold. Each tangent space is equipped with an inner product

$$\begin{aligned} \langle \overrightarrow{px} |\overrightarrow{py} \rangle _{p}=\overrightarrow{px}_\vartheta ^{T} G_{p}^\vartheta \overrightarrow{py}_\vartheta \end{aligned}$$

(2)

defined by the Riemannian metric $G_p: T_p{\mathcal {M}}\times T_p{\mathcal {M}} \rightarrow {\mathbb {R}}$ (with its matrix representation $G_p^\vartheta$ in the local chart) that smoothly varies from point to point on the manifold. The inner product induces the norm $||\overrightarrow{px}||_p=\sqrt{\langle \overrightarrow{px}, \overrightarrow{px} \rangle _p }$ on the manifold. The curve length $\mathcal {L}_{q_1}^{q_2}(\gamma )$ of the curve $\gamma (t)$ between two points $q_1$ and $q_2$ with $q_1=\gamma (a)$, $q_2=\gamma (b)$ is then given in a natural way by integrating the norm of the instantaneous speed $\dot{\gamma _\vartheta }(t):=\partial _t \gamma _\vartheta (t)$ along the curve³

$$\begin{aligned} {\mathcal {L}}_{q_1}^{q_2}(\gamma )=\int _{a}^{b} \sqrt{\langle \dot{\gamma _\vartheta }(t),\dot{\gamma _\vartheta }(t) \rangle _{\gamma _{\vartheta }(t)}} dt. \end{aligned}$$

(3)

The distance $\text{ dist }(q_1,q_2)$ between two points $q_1,q_2 \in {\mathcal {M}}$ is defined by the infimum of the set of curve lengths of all possible curves between them. The locally shortest path between two points is denoted as a geodesic $\gamma ^g$. The Riemannian metric is intrinsic as it does not make use of any space in which the manifold might be embedded and allows the computation of distances on the manifold without using the extrinsic view. Important tools for working on manifolds are the Riemannian logarithmic and exponential map. The exponential map $\exp _p: T_p{\mathcal {M}} \rightarrow {\mathcal {M}}$ is a mapping between the tangent space $T_p{\mathcal {M}}$ and the corresponding manifold ${\mathcal {M}}$. It maps the tangent vector $\overrightarrow{px}$ to the element of the manifold $\exp _p(\overrightarrow{px})=x$ that is reached by the geodesic at time step one, i.e. $x=\gamma ^g(1)$ with $p=\gamma ^g(0)$. The manifold of positive definite tensors considered in this paper is equipped with additional structure, namely, it is a so called homogenous space with non-negative curvature from which follows that the exponential map is one to one (Helgason 1978). In particular there exists an inverse, the logarithmic map $\log _p(x)=\overrightarrow{px}$.

Minimizing a function f defined on the manifold might require the computation of its gradient $\nabla f$. Let us denote with $\gamma (t)$ a curve in ${\mathcal {M}}$ passing through p at time $t=0$ with its corresponding tangent vector $\overrightarrow{px}$. Furthermore, let us assume that the directional derivative

$$\begin{aligned} X_{\overrightarrow{px}}(f):=\left. \frac{d f(\gamma (t))}{d t} \right| _{t=0} \end{aligned}$$

(4)

exists for all possible tangent vectors $\overrightarrow{px} \in T_p{\mathcal {M}}$. The gradient $\nabla f$ at point p and its representation $\nabla f_{\vartheta }$ in the chart $(\vartheta ,U)$ is then uniquely defined by the relation

$$\begin{aligned} X_{\overrightarrow{px}}(f)= & {} \big \langle \nabla f, \overrightarrow{px} \big \rangle _{p} = \nabla f_{\vartheta }^{T} G_p^{\vartheta }\overrightarrow{px}_{\vartheta }. \end{aligned}$$

(5)

Applying the chain rule, we can rewrite the directional derivative

$$\begin{aligned} X_{\overrightarrow{px}}(f)= & {} \sum _{j=1}^n \left. \partial _j f_{\vartheta } \partial _{t} \gamma _{\vartheta _{j}}(t) \right| _{t=0} = \nabla \!_{\perp }f_{\vartheta }^{T} \overrightarrow{px}_{\vartheta }, \end{aligned}$$

(6)

where $\gamma _{\vartheta _j}(t)=\vartheta _j \circ \gamma (t)$ denotes the j coordinate in the chart $\vartheta$ and we introduce the abbreviation $\nabla \!_{\perp }f_{\vartheta }:=(\partial _1 f_{\vartheta } ,\ldots ,\partial _n f_{\vartheta })^T$. Comparing (5) with (6) allows us to express the gradient in a local chart by means of the partial derivatives and the inverse metric tensor

$$\begin{aligned} \nabla f_{\vartheta } = \big (G_{p}^{\vartheta }\big )^{-1} \nabla \!_{\perp }f_{\vartheta }. \end{aligned}$$

(7)

As the gradient points in the direction of largest ascent of the function value, the gradient can be used for designing a gradient descent scheme which will be discussed in Sect. 4.3.

4 Diffusion Tensor Riemannian Manifolds

A diffusion tensor image contains at each pixel (or voxel in case of a three dimensional image domain) position x a symmetric positive definite $n \times n$ matrix (also denoted as a tensor in the following). Mathematically, such an image can be described by a tensor valued function $f: \Omega \rightarrow {\mathcal {P}}(n)$ from the image domain $\Omega \subset {\mathbb {R}}^m$, (usually $m=2$ or $m=3$) into the space of $n \times n$ positive definite tensors ${\mathcal {P}}(n):=Sym^{+}(n,{\mathbb {R}})=\{A \in {\mathbb {R}}^{n \times n}|A^T=A, A \succ 0 \}$ where the symbol $\succ$ denotes the positive definiteness. In case of a discrete image domain we consider one tensor at each spatial position. Such an image can be described by a point in the N-times Cartesian product ${\mathcal {P}}^N(n):={\mathcal {P}}_1(n) \times {\mathcal {P}}_2(n)\times \cdots \times {\mathcal {P}}_N(n)$ of the individual tensor manifolds at each of the N grid points. Independent from a continuous or discrete modeling, image processing techniques, e.g. denoising or interpolation, need some mechanism to compare image values at different spatial positions which can be done by a metric on the space of tensors.

4.1 The Euclidean Metric of ${\mathcal {P}}(n)$

The space of positive definite tensors can be considered as a manifold embedded into the vector space of symmetric matrices $Sym(n,{\mathbb {R}})=\{A \in {\mathbb {R}}^{n \times n}|A^T=A \}$. The space $Sym(n,{\mathbb {R}})$ together with the Frobenius norm $||A||_F=\sqrt{\text{ trace }\left( A^T A \right) }$ (Golub and Loan 1996) is isometric to the $n^2$-dimensional Euclidean space with the usual Euclidean metric ($L_2$ norm), i.e. there exists a distance preserving isomorphism $\text{ Vec }: {\mathcal {P}}(n)\rightarrow {\mathbb {R}}^{n^2}$ that is commonly denoted as vectorization by stacking the columns (or alternatively the rows) of a matrix $A \in Sym(n,{\mathbb {R}})$ on top of one another yielding the $n^2$-dimensional column vector $\text{ Vec }(A)=(A_{11},\ldots ,A_{n 1},A_{12},\ldots ,A_{n n})^T$ where $A_{i j}$ denote elements of A. Due to the redundancy of symmetric tensors, ${\mathcal {P}}(n)$ is even isometric to the $\frac{n(n+1)}{2}$ dimensional Euclidean space which can be obtained by a projection $v:{\mathbb {R}}^{n^2}\rightarrow {\mathbb {R}}^{\frac{n(n+1)}{2}}$ with a $\frac{n(n+1)}{2} \times n^2$ projection matrix P

$$\begin{aligned} v(A)= & {} P\text{ Vec }(A) \end{aligned}$$

(8)

$$\begin{aligned}= & {} \Big (A_{11},\ldots ,A_{n n},\sqrt{2}A_{12},\ldots ,\sqrt{2}A_{1 n}\Big )^T. \end{aligned}$$

(9)

The factor $\sqrt{2}$ takes the redundance of the off-diagonal elements into account such that the Frobenius norm in the matrix notation corresponds to the canonical inner product within the vector representation, i.e. $||A||_{F}^2=(P \text{ Vec }(A))^T P \text{ Vec }(A)$.

The inverse mapping $v^{-1}:{\mathbb {R}}^{\frac{n(n+1)}{2}}~\rightarrow ~{\mathbb {R}}^{n^2}$ from the reduced Euclidean representation v(A) to the vectorized matrix representation is given by the pseudo inverse $P^{\dagger }$ of the projection matrix.

The space of positive definite tensors ${\mathcal {P}}(n)$ lies within the vector space of symmetric tensors, i.e. $Sym^{+}(n,{\mathbb {R}}) \subset Sym(n,{\mathbb {R}})$. However, $Sym^{+}(n,{\mathbb {R}})$ does not form a vector space but a curved sub-manifold of ${\mathbb {R}}^{\frac{n(n+1)}{2}}$ which will be denoted with ${\mathcal {D}}$. Using the Euclidean metric within ${\mathcal {P}}(n)$ restricted on ${\mathcal {D}}$ corresponds to an exterior view, i.e. distances are measured in the Euclidean space $Sym(n,{\mathbb {R}})$ in which the manifold is embedded.

Fig. 1

Illustration of ${\mathcal {P}}(2)$ embedded in the 3D Euclidean space. We neglect the factor $\sqrt{2}$ of the off-diagonal term for visualization purpose. The space ${\mathcal {P}}(2)$ is the interior of a cone. The plot shows surfaces in ${\mathcal {P}}(2)$ for which tensors have the same determinant. The solid line shows the distance between two points on ${\mathcal {P}}(2)$ with respect to the flat Euclidean metric. The dotted curve illustrates the corresponding geodesic with respect to the affine invariant metric

An argument against applying the exterior view in the context of diffusion tensors is illustrated in Fig. 1 showing the space ${\mathcal {P}}(2)$ being isomorphic to the interior of a cone embedded in the 3D Euclidian space. The factor $\sqrt{2}$ of the off-diagonal term has neglected for visualization purpose, i.e. each axis shows the value of the corresponding matrix entry. The iso-surfaces of different colors depict surfaces of constant values of the tensor determinant. The determinant is directly related to the size of the tensor as it is given by the product of its eigenvalues and each eigenvalue determines the length of the corresponding principal axis. In case of DTI, diffusion tensors encode the average thermal induced Brownian motion of water molecules within some local area. It is evident that the encoded average amount of motion should not be changed by image processing operations applied to the diffusion tensor image. However, the Euclidean metric does not fulfill this requirement. The straight line indicates the distance between two tensors having the same determinant. As the average of two points in a metric space lies on the geodesic between them (Helgason 1978), the average of both tensors lies somewhere on the straight line above the isosurface of both original tensors. Consequently, the corresponding determinant increases through the average process. This phenomenon is known as the eigenvalue swelling effect (Tschumperlé and Deriche 2001; Chefd’hotel et al. 2004; Pennec et al. 2006; Castano-Moraga et al. 2007).

4.2 The Affine Invariant Metric of ${\mathcal {P}}(n)$

Alternative to the extrinsic view, we can consider the space of positive definite tensors ${\mathcal {P}}(n)$ as a Riemannian manifold where distances are defined by its interior metric.⁴ At each position $\varSigma \in {\mathcal {P}}(n)$ a tangent space $T_{\varSigma }{\mathcal {P}}(n)$ is attached equipped with an inner product

$$\begin{aligned} \langle \cdot , \cdot \rangle _{\varSigma }: T_{\varSigma }{\mathcal {P}}(n)\times T_{\varSigma }{\mathcal {P}}(n) \rightarrow {\mathbb {R}} \end{aligned}$$

(10)

that smoothly varies from point to point inducing a metric on ${\mathcal {P}}(n)$. A preferred property of a metric is affine invariance. On ${\mathcal {P}}(n)$ such metric has been shown to be induced by the inner product

$$\begin{aligned} \langle \varLambda _1,\varLambda _2 \rangle _{\varSigma }= & {} \text{ trace }\left( \varSigma ^{-\frac{1}{2}}\varLambda _1^T\varSigma ^{-1}\varLambda _2\varSigma ^{-\frac{1}{2}} \right) . \end{aligned}$$

(11)

where the matrix square-root of a symmetric matrix is defined by the square root of its eigenvalues. This affine invariant inner product and the corresponding metric have been motivated from information geometric arguments (Rao 1945) by considering the space of probability distributions as Riemannian manifolds with the Fisher information matrix as an appropriate metric. In case of multivariate normal distributions with fixed mean the Fisher information matrix boils down to the affine invariant metric (Atkinson and Mitchell 1981; Skovgaard 1981; Lenglet et al. 2006). The metric properties of (11) have been examined in Förstner and Moonen (1999). Originally developed as a distance measure between fixed mean normal distributions, the affine invariant metric has been extensively used in conjunction with tensor valued data (Fletcher and Joshi 2004; Lenglet et al. 2005, 2006; Fillard et al. 2005; Pennec et al. 2006; Zéraï and Moakher 2007a).

4.3 The Geodesic Marching Scheme

As our diffusion tensor image reconstruction approach is formulated as an energy minimization problem some optimization method is required. The geodesic marching scheme (GMS) (Pennec 1999, 2006) is a generalization of the classical gradient descent approach to Riemannian manifolds. The main components of the GMS are the exponential and logarithmic map. Besides its theoretical justifications, e.g. independence of the chosen coordinate system, the affine invariant metric allows to derive analytical expressions of the Riemannian exponential map

$$\begin{aligned} \exp _{\varSigma }\left( \varLambda \right) =\varSigma ^{\frac{1}{2}}\exp \Big ( \varSigma ^{-\frac{1}{2}} \varLambda \varSigma ^{-\frac{1}{2}}\Big ) \varSigma ^{\frac{1}{2}} \end{aligned}$$

(12)

with $\varLambda \in T_{\varSigma }{\mathcal {P}}(n)$ and logarithmic map

$$\begin{aligned} \log _{\varSigma }\left( \Xi \right) =\varSigma ^{\frac{1}{2}} \log \left( \varSigma ^{-\frac{1}{2}}\Xi \varSigma ^{-\frac{1}{2}}\right) \varSigma ^{\frac{1}{2}} \end{aligned}$$

(13)

for any $\Xi \in {\mathcal {P}}(n)$ (Fletcher and Joshi 2004) and the matrix exponential and matrix logarithm are defined by the exponentials of their eigenvalues. According to Eq. (7), the gradient of a function $f: {\mathcal {P}}(n)\rightarrow {\mathbb {R}}$ is the product of the inverse metric tensor times the partial derivatives, i.e. $\nabla f = G^{-1} \nabla _{\perp }f$. Before we describe the GMS, we derive a general expression of the gradient in the matrix notation needed for diffusion tensor images.

By means of the definition of the inner product (2) and the vectorization map (8), the inner product can be expressed as a matrix vector product

$$\begin{aligned} \langle \varLambda _1,\varLambda _2 \rangle _{\varSigma }=v\left( \varLambda _1\right) ^T G v\left( \varLambda _2\right) , \end{aligned}$$

(14)

where G denotes the matrix representation of the affine invariant metric. On the other hand, we can transform the affine invariant metric (11) using the (cyclic) permutation invariance property of the trace, i.e. $\text{ trace }\left( \varSigma \varLambda \right) =\text{ trace }\left( \varLambda \varSigma \right)$, as

$$\begin{aligned} \langle \varLambda _1,\varLambda _2 \rangle _{\varSigma }= & {} \text{ trace }\left( \varSigma ^{-\frac{1}{2}}\varLambda _{1}^{T}\varSigma ^{-1}\varLambda _{2}\varSigma ^{-\frac{1}{2}} \right) \end{aligned}$$

(15)

$$\begin{aligned}= & {} \text{ trace }\left( \varLambda _{1}^{T}\varSigma ^{-1}\varLambda _{2}\varSigma ^{-1} \right) \end{aligned}$$

(16)

$$\begin{aligned}= & {} \langle \varLambda _1, \varSigma ^{-1} \varLambda _{2} \varSigma ^{-1} \rangle _{I}\end{aligned}$$

(17)

$$\begin{aligned}= & {} v\left( \varLambda _1\right) ^T v\left( \varSigma ^{-1} \varLambda _2 \varSigma ^{-1}\right) . \end{aligned}$$

(18)

Comparing $v\left( \varLambda _1\right) ^T v\left( \varSigma ^{-1} \varLambda _2 \varSigma ^{-1}\right)$ with $v\left( \varLambda _1\right) ^T G v\left( \varLambda _2\right)$ reveals that the left multiplication of a vectorized tangent vector at $\varSigma$ with the matrix form of the metric tensor G equals the vectorized tangent vector translated by $\varSigma ^{-1}$, i.e. $G v\left( \varLambda _2\right) =v\left( \varSigma ^{-1} \varLambda _2 \varSigma ^{-1}\right)$. Thus, the left multiplication of the inverse metric tensor $G^{-1} v\left( \varLambda _2\right)$ equals the vector version of vector translated by $\varSigma$, i.e. $G^{-1} v\left( \varLambda _2\right) =v\left( \varSigma \varLambda _2 \varSigma \right)$. Finally, the matrix valued gradient $\nabla f$ at $\varSigma$

$$\begin{aligned} \nabla f = \varSigma \left( \nabla _{\perp } f \right) \varSigma =: \varSigma *\nabla _{\perp } f \end{aligned}$$

(19)

can be computed conveniently by means of the partial derivative $(\nabla _{\perp } f)_{i j}=\partial _{\varSigma _{i j}}f$ with respect to the i, j-th matrix element followed by a transformation with $\varSigma$.

So far we considered only a single tensor manifold ${\mathcal {P}}(n)$. In case of a tensor valued image we are confronted with a tensor at each position in the image domain. As we minimize only functions on a discrete image domain we restrict our discussion to this case. Such a tensor valued image is described by the N-tuple $\varSigma =(\varSigma _1,\varSigma _2,\ldots ,\varSigma _N)^T$ with the corresponding tangent vector $\varLambda =(\varLambda _1,\varLambda _2,\ldots ,\varLambda _N)^T \in T_{\varSigma }{\mathcal {M}}$. Affine transformations of tensors of such a tensor valued image are explained by an n-tuple of invertible matrices $W=(W_1,W_2,\ldots ,W_N)^T$ where the transformation is applied element wise, i.e. $W *\varSigma =(W_1 *\varSigma _1,W_2 *\varSigma _2,\ldots ,W_N *\varSigma _N)^T$ and $W *\varLambda =(W_1 *\varLambda _1,W_2 *\varLambda _2,\ldots ,W_N *\varLambda _N)^T$ with $W_i *\varSigma _i:=W_i \varSigma _i W_{i}^{T}$ and $W_i *\varLambda _i:=W_i \varLambda _i W_{i}^{T}$. The affine invariant inner product generalized to

$$\begin{aligned} \langle \varLambda _1,\varLambda _2 \rangle _{\varSigma }= \sum _{j=1}^N \text{ trace }\left( \varSigma _{j}^{-\frac{1}{2}}\varLambda _{1 j}^{T}\varSigma _{j}^{-1}\varLambda _{2 j}\varSigma _{j}^{-\frac{1}{2}} \right) \end{aligned}$$

(20)

and the gradient of a function $f:{\mathcal {P}}^N(n) \rightarrow {\mathbb {R}}$ generalizes to

$$\begin{aligned} \nabla f= & {} \left( \varSigma _1 *\nabla _{\perp }^1 f,\varSigma _2 *\nabla _{\perp }^2 f,\ldots , \varSigma _N *\nabla _{\perp }^N f \right) \end{aligned}$$

(21)

with components

$$\begin{aligned} \big (\nabla _{\perp }^{k} f\big )_{i j}= & {} \partial _{\left( \varSigma _k\right) _{i j}}f. \end{aligned}$$

(22)

The geodesic marching scheme is based on the fact that the gradient $\nabla f$ is an element of the tangent space, $\nabla f \in T{\mathcal {P}}^N(n)$, and indicates the direction of steepest ascent. Thus we can find an argument with a lower value of f by going a sufficiently small step in the negative direction of the gradient $\varLambda =- dt \nabla f$ and mapping this point back on the manifold using the exponential map (12). This procedure is then iterated until convergence (cf. with Sect. 8).

5 Bayesian Estimation

5.1 Probabilities on Tensor Fields

Based on (Pennec 2006) we introduce basic concepts of probability theory on manifolds and extend them with respect to Bayesian interpretation of probability and estimation theory.

Let $\left( \varTheta ,{\mathcal {F}},P \right)$ denote the probability space consisting of the sample space $\varTheta$, the $\sigma$-algebra ${\mathcal {F}}$ of events and a probability measure P and let ${\mathcal {M}}$ denote the state space with corresponding $\sigma$-algebra ${\mathcal {E}}$. A ${\mathcal {M}}$-valued random variable $\varSigma :\varTheta \rightarrow {\mathcal {M}}$ is a function from the sample space $\varTheta$ to the state space ${\mathcal {M}}$ which is $({\mathcal {F}},{\mathcal {E}})$ measurable. The state space ${\mathcal {M}}$ consists of the Cartesian product ${\mathcal {M}}={\mathcal {P}}^N(n)$ of the space of tensors.

To each subset ${\mathcal {A}}\in {\mathcal {E}}$ a probability $P(\varSigma \in {\mathcal {A}}):=P(\left\{ \omega \in {\mathcal {F}}: \varSigma (\omega ) \in {\mathcal {A}}\right\} )$ can then be assigned describing the chance to find a realization of the random variable $\varSigma$ within ${\mathcal {A}}$. Generalizing the concept of probability density functions to Riemannian manifolds requires a measure which is induced in a natural way by the volume form $d{\mathcal {M}}$ on ${\mathcal {M}}$. In a local coordinate system $z=(v(\varSigma _1);v(\varSigma _2);\ldots ;v(\varSigma _N)) \in {\mathcal {D}} \subset {\mathbb {R}}^{\frac{nN(n +1)}{2}}$ the volume form reads

$$\begin{aligned} d{\mathcal {M}}(z)=\sqrt{|G|}d z. \end{aligned}$$

(23)

The metric tensor G can be inferred from the definition of the affine invariant inner product (20) and the isometry (8) between the space of $n \times n$ symmetric tensors and the $\frac{n(n +1)}{2}$ Euclidean space (cf. Zéraï and Moakher 2007b)

$$\begin{aligned} G^{-1}(\varSigma _j)=(P^{\dagger })^T \text{ Vec }\left( \varSigma _j\otimes \varSigma _j \right) P^{\dagger }, \end{aligned}$$

(24)

where $\otimes$ denotes the tensor product and $P^{\dagger }$ denotes the pseudo inverse of P. The determinant of the metric tensor at position $\varSigma _j$ can then be calculated from (24) and using the relation $\det {\left( G^{-1}\right) }=\left( \det {G}\right) ^{-1}$.

A function $p:{\mathcal {M}}\rightarrow {\mathbb {R}}^{+}_0$ is then denoted as probability density function (pdf) with respect to the volume form $d{\mathcal {M}}$ if the probability of any event ${\mathcal {A}} \in {\mathcal {E}}$ can be expressed in the form

$$\begin{aligned} P(z \in {\mathcal {A}}) = \int _{{\mathcal {A}}} p \, d {\mathcal {M}}. \end{aligned}$$

(25)

In order to stress the special choice of the reference measure $d{\mathcal {M}}$, the pdf is also denoted as a volumetric probability in the literature (Tarantola and Valette 1982; Tarantola 2005).

The expectation value ${\mathbb {E}}_{\varSigma }\left[ \cdot \right]$ of a function $f:{\mathcal {M}}~\rightarrow ~{\mathbb {R}}$ with respect to the pdf $p(\varSigma )$ is defined by

$$\begin{aligned} {\mathbb {E}}_{\varSigma }\left[ f \right]= & {} \int _{{\mathcal {M}}}f(\varSigma ) p(\varSigma ) \, d {\mathcal {M}}\end{aligned}$$

(26)

$$\begin{aligned}= & {} \int _{{\mathcal {D}}}f(z) p(z) \, \sqrt{|G(z)|}d z. \end{aligned}$$

(27)

Important expectation values are the moments of a distribution, in particular the mean and the variance. The variance can be defined as the expectation value of the squared distance $\sigma ^2_{\bar{z}}\left( z \right) ={\mathbb {E}}_{z}\left[ \text{ dist }(z,\bar{z})^2 \right]$ from the mean value $\bar{z}$. However, on manifolds the mean is not necessarily unique. Furthermore, a mean value $\bar{z}$ cannot be defined by an integral or sum over a random variable as the concept of addition and integration is not defined for elements of a manifold. The Frechét mean is defined by the set (if it exists) minimizing the variance (Pennec 2006)

$$\begin{aligned} \bar{z}:=\arg \min _{y} {\mathbb {E}}_{z}\left[ \text{ dist }(z,y)^2 \right] \end{aligned}$$

(28)

Alternatively to the Frechét mean, Karcher means (Karcher 1977) are defined by all local minima in (28). The covariance matrix (Pennec 2006) is defined by the expectation value of the outer product of tangent vectors $u \in T_{\bar{z}}{\mathcal {D}}$ attached at a mean value

$$\begin{aligned} {{\varvec{C}}}=\int _{T_{\bar{z}}{\mathcal {D}}} u u^T p_{\bar{z}}(u)\sqrt{|G_{\bar{z}}(u)|}d u \end{aligned}$$

(29)

with $p_{\bar{z}}(u):=p(\exp _{\bar{z}}(u))$.

5.2 Estimation Theory

Bayesian decision theory in Euclidean space ${\mathbb {R}}^n$ (cmp. with Kay 1993) defines a Bayesian estimator of a random vector $z \in {\mathbb {R}}^n$ given some observation $g \in {\mathbb {R}}^m$ by the minimum of a Bayesian risk $\mathcal {R}(\varepsilon )={\mathbb {E}}_{z|g}[L(\varepsilon )]$. The Bayesian risk depends on a loss function $L(\varepsilon )$ weighting the error $\varepsilon =z-{\hat{z}}$ between the estimate ${\hat{z}} \in {\mathbb {R}}^n$ and the current realization z. Commonly used loss functions are the quadratic loss function $L_2(\varepsilon )=||\varepsilon ||^2$ penalizing the squared norm of the error leading to the minimum mean squared error (MMSE) estimator ${\hat{z}}={\mathbb {E}}_{z|g}[z]$. The hit and miss loss function penalizes all errors equal whose norm is above a small threshold $\rho$ and zero otherwise and leads to the maximum a posteriori (MAP) estimator ${\hat{z}}=\arg \max _{z}\{p(z|g)\}$.

When we generalize the concept of Bayesian decision theory to the manifold of diffusion tensors⁵ we have to assure the estimators to be invariant with respect to the chosen chart (Jermyn 2005). We denote with $g \in {\mathcal {X}}$ an observation which is an entity of the observation manifold ${\mathcal {X}}$ and with $z \in {\mathcal {D}}$ the entity which we like to estimate based on the posterior pdf p(z|g). We define the quadratic loss function as $L_2(z,{\hat{z}})= \text{ dist }(z,{\hat{z}})^2$. The condition of the minimum of the corresponding Bayesian risk is obtained by setting its gradient with respect to the estimate ${\hat{z}}$ equal zero

$$\begin{aligned} \nabla _{{\hat{z}}}{\mathcal {R}}= & {} \nabla _{{\hat{z}}} \int _{{\mathcal {D}}} \text{ dist }(z,{\hat{z}})^2 p(z|g) \, \sqrt{|G(z)|}d z \end{aligned}$$

(30)

$$\begin{aligned}= & {} \int _{{\mathcal {D}}} \nabla _{{\hat{z}}} \text{ dist }(z,{\hat{z}})^2 p(z|g) \, \sqrt{|G(z)|}d z \end{aligned}$$

(31)

$$\begin{aligned}= & {} \int _{T_{{\hat{z}}}{\mathcal {D}}} \nabla _{{\hat{z}}} \Vert u \Vert _{{\hat{z}}}^2 \, p_{{\hat{z}}}( u|g) \, \sqrt{|G_{{\hat{z}}}(u)|}d u \end{aligned}$$

(32)

$$\begin{aligned}= & {} -2 \int _{T_{{\hat{z}}}{\mathcal {D}}} u p_{{\hat{z}}}(u|g) \, \sqrt{|G_{{\hat{z}}}(u)|}d u \end{aligned}$$

(33)

$$\begin{aligned}&\overset{!}{=}&0 \end{aligned}$$

(34)

where we denote with $u:=\overrightarrow{{}{\hat{z}} z}$ the element of the tangent space attached at ${\hat{z}}$ that is mapped to z by the exponential map. From (30) to (31) we exchange differentiation and integration and from (31) to (32) we apply a coordinate transformation by means of the logarithmic map $\log _{{\hat{z}}}$ where $G_{{\hat{z}}}(u)$ denotes the metric tensor in the transformed coordinate system. From (32) to (33) we use $\nabla _{{\hat{z}}} \Vert u \Vert _{{\hat{z}}}^2 = -2 u$ which directly follows from Theorem 2 in Pennec (2006). The Riemannian MMSE estimator is invariant with respect to the chosen coordinate system as it is fully defined by the integral equation (33,34).

A loss function sharing the same idea as the hit and miss loss function, i.e. giving the same weight to all errors, is given by the negative delta distribution $L_{\delta }(z,{{\hat{z}}}):=-\delta _{{\hat{z}}}(z)$. It gives no weight to all points $z\ne {\hat{z}}$ and a negative ‘infinitive’ weight to $z = {{\hat{z}}}$. The corresponding Bayesian risk yields

$$\begin{aligned} \mathcal {R}({{\hat{z}}})= & {} \int _{{\mathcal {M}}} L_{\delta }(z,{{\hat{z}}}) p(z|g) d{\mathcal {M}}(z) = -p({{\hat{z}}}|g), \end{aligned}$$

(35)

which is obviously minimized by the value ${\hat{z}}$ maximizing the volumetric probability function p(z|g).

Thus, we can take over the concepts of Euclidean estimation theory by considering volumetric probability functions, i.e. pdfs defined with respect to the volume form. In particular, the Bayesian rule holds for volumetric probability functions such that we can derive the posterior pdf by means of a corresponding likelihood function and prior distribution as in case of the Euclidean space (Jermyn 2005; Tarantola 2005).

6 Likelihood Models

6.1 Noise in NMR Images

Examinations on NMR noise characteristics can be traced back to Hoult and Richards (1976), Libove and Singer (1980), Edelstein et al. (1983, 1984), Ortendahl et al. (1983, 1984), Henkelman (1986). The Rician distribution, also denoted as Rice distribution (Rice 1944), has first been examined by Bernstein et al. (1989) as a theoretical model for the noise in the NMR signal. Since then, a large number of different analyzing and denoising methods based on the Rician noise model have been proposed, e.g. McGibney and Smith (1993), Gudbjartsson and Patz (1995), Macovski (1996), Andersen (1996), Sijbers et al. (1998, 2007), Nowak (1999), Wood and Johnson (1999), Sijbers and Dekker (2004), Koay and Basser (2006). NMR imaging systems provide at each spatial position $x_k$ and direction $g_j$ a quadrature pair $I_{j k}, R_{j k}$ of signal values that can be interpreted as a complex image value $R_{j k}+ j I_{j k}$. The magnitude image $S_{j k}:=S_j(x_k)$ is related with the complex NMR image via

$$\begin{aligned} S_{j k}=\sqrt{I_{j k}^2+R_{j k}^2}. \end{aligned}$$

(36)

The noise in the real part $R_{j k}$ as well as in the imaginary part $I_{j k}$ are well described by additive Gaussian noise components with same standard deviation $\sigma$ for both channels (Wang and Lei 1994). Furthermore, the noise at different spatial positions $x_k$ as well as in different channels can be assumed to be statistically independent (Wang and Lei 1994). Due to the nonlinear relation (36) between the complex valued NMR signal and real valued magnitude signal the latter is not Gaussian distributed any more, but follows a Rician distribution (Rice 1944)

$$\begin{aligned} p(S_{j k}|A_{j k},\sigma )=\frac{S_{j k}}{\sigma ^2} \exp \!\left( -\frac{S_{j k}^2\!+\!A_{j k}^2}{2 \sigma ^2}\right) \!I_0\!\left( \frac{S_{j k} A_{j k}}{\sigma ^2} \right) , \end{aligned}$$

(37)

where $A_{0 k}$ denotes the noise free reference image, $A_{j k}$, $j>0$ the noise free DW images at position $x_k$ and $I_0$ the zero order modified Bessel function of first kind⁶In accordance with the literature on DTI reconstruction, e.g. (Chen and Hsu 2005), we define the signal-to-noise ratio (SNR) as the quotient $\text{ SNR }=\mu /\sigma _{b}$ of the mean $\mu$ of the image magnitude in the region of interest divided by the background standard deviation. The background standard deviation can be estimated from regions containing no tissue. For high signal-to-noise ratios (i.e. approx. $\text{ SNR }\ge 3$) the Rician distribution is quite well approximated by a Gaussian distribution (cf. Fig. 2, lower right) with standard deviation $\sigma$ and mean $\sqrt{\mu ^2+\sigma ^2}$ (Gudbjartsson and Patz 1995). But due to the nonlinear relationship between the signal and noise, the observed signal $S_{i k}$ is not related by an additive noise term with the true underlying noise free signal $\mu$, i.e. the mean of the Gaussian approximation does not correspond with the true underlying signal value $\mu$.

Fig. 2

Upper left Rician probability density function $p(x|\mu ,\sigma )$ with $\mu =1$ and different standard deviations: red curve $\sigma =0.3$, $\text{ SNR } \approx 5.1$, green curve $\sigma =0.9$, $\text{ SNR } \approx 1.7$, blue curve $\sigma =1.4$, $\text{ SNR } \approx 1.1$; Upper right image and lower row The Rician pdfs and corresponding Gaussian approximations (dotted curves) with same standard deviation as the Rician pdfs. In case of high SNR (lower right image) also a Gaussian distribution (dotted dashed curve) of the additive Gaussian noise model with mean $\mu =1$ and standard deviation $\sigma =0.3$ is shown (Color figure online)

For low SNR (Fig. 2, upper right) and medium SNT (Fig. 2, lower left) SNR the distribution is skewed with a longer right tail distinguished clearly from the corresponding Gaussian approximation with standard deviation $\sigma$ and mean $\sqrt{\mu ^2+\sigma ^2}$. In particular, for all SNRs, the observed DW image is not related to true underlying noise free signal $\mu$ by an additive noise term. Our real data set (cmp. with Sect. 10.2.2) has a SNR of 5.2. We conclude that an additive Gaussian model for NMR signal is not always a good idea even in the case of high signal-to-noise ratios.

6.2 The Likelihood Model

Although the Rician noise model has been applied for restoration MMR magnitude images for a long time (McGibney and Smith 1993; Gudbjartsson and Patz 1995; Macovski 1996; Andersen 1996; Sijbers et al. 1998, 2007; Nowak 1999; Wood and Johnson 1999; Sijbers and Dekker 2004; Koay and Basser 2006), as a noise model for the likelihood function of diffusion tensors images it has been proposed quite recently (Landman et al. 2007a; Andersson 2008; Jeong and Anderson 2008). In contrast to (Landman et al. 2007a; Andersson 2008; Jeong and Anderson 2008) where the likelihood function has been formulated within an Euclidean setting, we formulate the likelihood function within the Riemannian framework. In order to relate the observations $S_{j k}$ with the diffusion tensor image $\varSigma _k:=\varSigma (x_k)$ we insert the Stejskal–Tanner equation (1) of the jth measurement into the Rician noise model (37)

$$\begin{aligned} p\!\left( S_{j k}|A_{0 k},\varSigma _k,\sigma \right) :=p\!\left( S_{j k}|A_{0 k} \exp \!\left( -b_j g_j^T\!\varSigma _k g_j \right) ,\sigma \right) \end{aligned}$$

(38)

where $A_{0 k}$ denotes the noise free reference signal at position $x_k$. The noise in each DW signal $S_{j k}$ for j different ‘b-values’ is mutually independent as DW images are acquired in independent measurements steps.

As we can assume statistical independence (Gudbjartsson and Patz 1995) of signal magnitudes at different spatial positions $x_k$ we can express the overall sampling distribution by the product of sampling distributions at different spatial positions and different ‘b-values’

$$\begin{aligned} p(\underline{S}|\underline{A}_0,\underline{\varSigma },\sigma )=\prod _{k=1}^N \prod _{j=1}^L p\left( S_{j k}|A_{0 k},\varSigma _k,\sigma \right) , \end{aligned}$$

(39)

where we introduced the abbreviations $\underline{S}=\{S_{j k}\}$, $\underline{A}_0=\{A_{0 k}\}$ and $\underline{\varSigma }=\{\varSigma _k\}$. After inserting the measurements $\underline{S}$, the sampling distribution (39) serves as the likelihood function of the tensor image $\varSigma$, the noise free reference image $\underline{A}_0$ and the noise levels $\sigma$. In a next step, we decouple the estimation of nuisance parameters $(\underline{A}_0,\sigma )$ from the estimation of the tensor valued image $\varSigma$. We first estimate the noise level directly from water-free regions in NMR data volume such that all signal values above zero are due to noise. Using a non-informative prior for the noise variance, i.e. $p(\sigma )\propto 1/\sigma$, and the Rician pdf $p(S_{j k}|0,\sigma )$ for mean value⁷ equal 0 we estimate noise variance by the MAP estimator

$$\begin{aligned} {{\hat{\sigma }}}= & {} \arg \max _{\sigma } p(\sigma |\underline{S})\end{aligned}$$

(40)

$$\begin{aligned}= & {} \arg \max _{\sigma }\prod _{jk} p(S_{j k}|0,\sigma )/\sigma \end{aligned}$$

(41)

The estimate $\hat{\underline{A}}_0$ of the noise-free reference image $\underline{A}_0$ can be estimated from the observed reference image $\underline{S}_{0}$ using one the denoising approaches for Rician distributed data proposed by Sijbers et al. (1998).

6.2.1 Maximum Likelihood

Applying the geodesic marching scheme to the posterior pdf

$$\begin{aligned} p\Big (\underline{\varSigma }|\underline{S},{\hat{\underline{A}}}_0,{\hat{\sigma }}\Big ) \propto p\Big (\underline{S}|\hat{\underline{A}}_0,\underline{\varSigma },{\hat{\sigma }}\Big ) p(\underline{\varSigma }) \end{aligned}$$

(42)

requires the calculation of the gradient of the likelihood function or its negative logarithm. According to (19) the gradient of the negative log likelihood, $E_L:=-\log (p_L)$, with $p_L$ given by (38) with respect to the tensor at spatial position m yields

$$\begin{aligned} \nabla _{\!\varSigma _m}\!E_L = \sum _{j=1}^L \chi _{j m} b_j \hat{A}_{0 m}e^{- b_j g_{j}^{T} \varSigma _m g_j} \varSigma _m g_j g_{j}^{T} \varSigma _m, \end{aligned}$$

(43)

with

$$\begin{aligned} \chi _{j m} = \left( \frac{I_1}{I_0}\frac{ S_{j m} }{\sigma ^2} - \frac{{\hat{A}}_{0 m}e^{-b_jg_{j}^{T} \varSigma _m g_j}}{\sigma ^2}\right) . \end{aligned}$$

(44)

We left out the arguments of the modified Bessel functions of zero order $I_0(x)$ and first order $I_1(x)$ in favor of an uncluttered notation. Let us compare this gradient with the gradient of the log likelihood model we would obtain for an additive Gaussian noise model, i.e. $S_{i k} =A_{i k}+\varepsilon _{j k}$ with $\varepsilon _{i k}\sim \mathcal {N}(0,\sigma )$ and $p(S_{i k}|A_{i k})= \mathcal {N}(A_{i k},\sigma )$ proposed by Lenglet et al. (2006). The likelihood function for the tensor image is then obtained by inserting the Stejskal–Tanner equation in the noise model

$$\begin{aligned} p\!\left( S_{j k}|{\hat{A}}_{0 k},\varSigma _m,\sigma \right) = {\mathcal {N}} \left( {\hat{A}}_{0 k}\exp \left( -b_j g_{j}^{T} \varSigma _m g_j \right) ,\sigma \right) . \end{aligned}$$

(45)

The gradient of the negative log likelihood of (45) equals the gradient of the Rician noise model (43) except for the correction term $\frac{I_1(x)}{I_0(x)}$ which equals one for the additive Gaussian noise model. The correction term $S_j\mapsto S_j \frac{I_1}{I_0}$ accounts for the skewed Rician probability density function with heavy right tail. For the Rician noise model, the correction term becomes nearly one for large arguments, e.g. $\frac{I_1(x)}{I_0(x)}>0.99$ for $x=\frac{\hat{A}_{0 k} S_{j k}}{\sigma ^2}>51$. However, one should be careful in applying the Gaussian approximation as the DW magnitude depends on the diffusion process. Even a high SNR in the reference image $A_{0 m}$ might correspond with low SNRs in the DW images (cf. Eq. (1)) making the correction term indispensable. In order to better understand the influence of the correction term on the estimated diffusion tensor image we examine the maximum of the likelihood function (39). For the moment being we neglect the influence of the prior distribution which occurs for instance in case of flat priors or in case of a sufficient large amount of observations. At the maximum of the likelihood function the term (44) needs to be zero⁸ for each observation j and each spatial position m, i.e.

$$\begin{aligned} {\hat{A}}_{0 m} e^{-b_{j}g_{j}^{T} \varSigma _m g_j}=\frac{I_1}{I_0} S_{j m} \end{aligned}$$

(46)

The term $g_{j}^{T} \varSigma _m g_j$ describes the diffusion component in direction $g_j$. As $\frac{I_1(x)}{I_0(x)}<1$ for finite arguments x the right hand side of (46) is smaller compared to the additive Gaussian noise model. In return, the term on the left hand side must also be smaller at the likelihood maximum which can be accomplished by a larger diffusion component $g_{j}^{T} \varSigma _m g_j$. Consequently, the correction term leads to estimates ${\hat{\varSigma }}_m$ encoding larger diffusion as for the additive Gaussian noise model or reversely, the Gaussian noise model leads to a bias towards too small diffusion.

6.2.2 Robust Likelihood Functions

So far, we assumed the MRI images, i.e. the imaginary and real part, to be corrupted by additive Gaussian noise. However, outliers that do not follow the assumed statistical model might lead to serious estimation errors. If the statistical distribution of other error sources are available, the estimators can be made robust by modifying the potential function of the error model as illustrated with the following example.

Example

Figure 3 (left) shows a Gaussian distribution (red curve) with mean $\mu =1$ and standard deviation $\sigma =1$ and Fig. 3 (right) the corresponding Rician distribution $p(x|\mu ,\sigma )$ (red curve). If we model outliers by Gaussian distributions with larger standard deviation ($\sigma =4$) we end up with a mixture of Gaussian distributions [(Fig. 3 (left, blue bar plot)] with larger tails than the single Gaussian distribution. These tails in the Gaussian mixture distribution lead to a larger tail on the right side of the distribution of the signal magnitude $S=\sqrt{x^2+y^2}$ where x, y follow the Gaussian mixture distribution [(cf. Fig. 3 (right, blue bar plot)].

The modified distribution explains both types of random variables such that outliers with respect to the Rician noise model become part of the new probability model. However, such outlier model might not be available in closed form.

Fig. 3

Left The normal distribution (red curve) with mean $\mu =1$ and standard deviation $\sigma =1$ as well as the (normalized) histogram of $10^6$ samples of a Gaussian mixture model, i.e. $p_m(x)=0.7 \, {\mathcal {N}}(1,1)+ 0.3 \, {\mathcal {N}}(1,4)$. Right The Rician distribution (red curve) and the (normalized) histogram (blue bars) of the magnitude distribution $S=\sqrt{x^2+y^2}$ where x, y follow the Gaussian mixture distribution shown on the left side (Color figure online)

Instead of explicitly modeling outlier distributions we use the idea of robust statistics: outliers are detected and excluded (or at least their influence is reduced) from the estimation process without modeling them explicitly (Huber 1981; Hampel et al. 1986). Additive Gaussian noise models can be made robust against outliers by introducing potential functions depending on the residua of the constraint equations. These potential functions have a lower slope than the quadratic potential function of the Gaussian noise model for residua which are unlikely to occur. As a consequence the influence function, as the derivative of the potential function, reduces the influence of the corresponding terms in the gradient or constraint equation. A corresponding modification of Rician noise model is not that obvious as the residua of the constraint equation cannot be isolated from the true signal due to the nonlinear relation between magnitude image and noise. Thus, instead of modifying the likelihood function, we change the negative log likelihood gradient by introducing the influence functions $\psi (\zeta _{j m})$ depending on the likelihood function

$$\begin{aligned} \zeta _{j m}=p\left( S_{j m}|\hat{A}_{0 m} \exp \left( -b_j g_{j}^{T} \varSigma _m g_j \right) ,{\hat{\sigma }} \right) \end{aligned}$$

(47)

Multiplying each summand in (43) by the influence function

$$\begin{aligned} \nabla _{\!\varSigma _m}\!E_L = \sum _{j=1}^L \zeta _{j m} b_j {\hat{A}}_{0 m}e^{- b_j g_{j}^{T} \varSigma _m g_j} \varSigma _m g_j g_{j}^{T} \varSigma _m \psi (\zeta _{j m}),\nonumber \\ \end{aligned}$$

(48)

allows outliers to be suppressed or reduced by choosing a low value $\psi (\zeta _{j m})$ for unlikely arguments.

7 Prior Models

7.1 Mathematical Issues

In this subsections several mathematical concepts are discussed that will be useful for the subsequent analysis.

7.1.1 Energy Functionals

An intrinsic linear isotropic regularization scheme for tensor valued images has been derived in Pennec et al. (2006) and has been used to define nonlinear anisotropic regularization schemes by giving different weights to different directions of the linear regularizer. In Fillard et al. (2005) an intrinsic nonlinear isotropic regularization has been derived from a corresponding energy functional. A semi-intrinsic nonlinear isotropic diffusion scheme has been derived in Gur et al. (2007, 2009), i.e. the data term has been handled extrinsic whereas the regularization term has intrinsically been handled. In this section we extend the intrinsic approach of Pennec et al. (2006) to the linear anisotropic case which serves as a basis for a further generalization to nonlinear isotropic and nonlinear anisotropic regularization/diffusion schemes. Let us denote with $\partial _i\varSigma (x)$ the partial derivatives of the diffusion tensor images in the direction $i=1,\ldots ,n$ and with $d^{i j}$ the components of the diffusion tensor⁹ which locally controls the amount and direction of the regularization and does not depend on the tensor valued image $\varSigma$. We define the energy functional for linear anisotropic regularization by

$$\begin{aligned} E(\varSigma )= & {} \frac{1}{2}\int \sum _{i,j} d^{i j} \langle \partial _i \varSigma , \partial _j \varSigma \rangle _{\varSigma } \, d x \\\nonumber \text{ with }&\langle \partial _i \varSigma , \partial _j \varSigma \rangle _{{\small \varSigma }}=\text{ trace }\left( (\partial _i \varSigma )\varSigma ^{-1} (\partial _j \varSigma ) \varSigma ^{-1}\right) . \end{aligned}$$

(49)

A stationary image $\varSigma$ is an image for which the energy attains a (local) extremum. A variation of the image is parameterized with the test vector field $W:\Omega \rightarrow T{\mathcal {P}}(n)$ and defined by $\varSigma _{\varepsilon }=\exp _{\varSigma }(\varepsilon W)$. According to the fundamental lemma of calculus of variations (Courant and Hilbert 1953), the functional derivative $\delta E$ can then be deduced by the relation

$$\begin{aligned} \left. \frac{\partial E(\varSigma _{\varepsilon })}{\partial \varepsilon }\right| _{\varepsilon =0}= & {} \int \langle \delta E , W \rangle _{\varSigma } dx, \end{aligned}$$

(50)

leading to

$$\begin{aligned} \delta E= & {} - \sum _{i,j}\left( \partial _j \left( d^{i j} \partial _i \varSigma \right) - d^{i j} (\partial _i \varSigma )\varSigma ^{-1} (\partial _j \varSigma )\right) . \end{aligned}$$

(51)

For $i=j$ and $d^{i j}=1$ (51) reduces to the operator $\Delta =\sum _i \Delta _{i i}$ derived in Pennec et al. (2006) with the components

$$\begin{aligned} \Delta _{i i}\varSigma := \partial _i \partial _i \varSigma - (\partial _i \varSigma )\varSigma ^{-1} (\partial _i \varSigma ), \end{aligned}$$

(52)

In addition to Pennec et al. (2006), we also derive the mixed components

$$\begin{aligned} \Delta _{i j}\varSigma = \partial _i \partial _j \varSigma - (\partial _i \varSigma )\varSigma ^{-1} (\partial _j \varSigma ), \quad i \ne j \end{aligned}$$

(53)

needed for anisotropic regularization. The nonlinear anisotropic regularizer can then be deduced from (51) by making the diffusion tensor $d^{i j}$ dependent on the tensor field $\varSigma$.

7.1.2 Local Coordinate Representation

In this section, we discuss the relation of our energy formulation (49) to the energy formulation proposed by Gur et al. (2007, 2009). Firstly, the energies in both approaches are different. The authors in Gur et al. (2007, 2009) motivate their energy from a differential geometric point of view, i.e. they consider the tensor valued image as a section in the fibre bundle of the trivial product space of image—and tensor domain and derive their energy from high energy physics (Polyakov action). We motivate our energy functional from a generalization of the linear anisotropic diffusion scheme for gray-scale images. Explaining the whole idea of Gur et al. (2007, 2009) goes beyond the scope of this paper and we have to refer the interested reader to the original work. The point we would like to make here concerns the different representations of both approaches. In our energy formulation we use the metric in the form (11). We call this the matrix representation in the following. The approach of Gur et al. uses a matrix form of the metric with vectorized tangent vectors which will be denoted as local coordinate representation in the following.

These are two equivalent ways for writing down the same mathematical entity. But the matrix representation leads to considerable practical simplifications of the variational problem: We write our energy functional in the local coordinate representation with Einstein summation convention¹⁰

$$\begin{aligned} E(\varSigma )= & {} \frac{1}{2}\int \left( d^{i j} g_{\alpha \beta } \partial _i \varSigma ^\alpha \partial _j \varSigma ^\beta \, \right) d x. \end{aligned}$$

(54)

where $g_{\alpha \beta }$ denote the $\alpha , \beta$th component of the metric tensor. The variation yields

$$\begin{aligned} \left. \frac{\partial E(\varSigma _{\varepsilon })}{\partial \varepsilon }\right| _{\varepsilon =0}= & {} -\int \left( \partial _j\left( d^{i j} \partial _i\varSigma ^\alpha \right) \right. \nonumber \\&+ \left. d^{i j} \Gamma ^{\alpha }_{\eta \gamma } \partial _i\varSigma ^\eta \partial _j\varSigma ^\gamma \right) g_{\alpha \beta }W^{\beta } dx \end{aligned}$$

(55)

with the Christoffel symbols $\Gamma ^{\eta }_{\alpha \beta }$ defined by

$$\begin{aligned} g_{\eta \gamma } \Gamma ^{\eta }_{\alpha \beta }= & {} \frac{1}{2}\left( \partial _{\varSigma ^\beta }g_{\alpha \gamma } +\partial _{\varSigma ^\alpha }g_{\beta \gamma }- \partial _{\varSigma ^\gamma }g_{\alpha \beta }\right) \end{aligned}$$

(56)

From (55) we can infer the $\alpha$th component of the functional derivative as

$$\begin{aligned} \delta E^{\alpha }= & {} - \partial _j\left( d^{i j} \partial _{i}\varSigma ^\alpha \right) - d^{i j} \Gamma ^{\alpha }_{\eta \gamma } \partial _{i}\varSigma ^{\eta } \partial _{j}\varSigma ^\gamma \end{aligned}$$

(57)

Although of outstanding importance in theory, Christoffel symbols become a nuisance if they have to be computed explicitly. In the case of DTI (Gur et al. 2007, 2009) have been faced with 78 nontrivial Christoffel symbols when using the standard matrix chart¹¹ resulting in numerical difficulties when computing the functional derivative. As a solution, they proposed a particular chart, given by the so called Iwasawa decomposition of the tensors, which allows them to reduce the number of nonzero Christoffel symbols to 26. If we compare (57) with the $\alpha$th component of the functional derivative in matrix form in (51) we see that the term containing the Christoffel symbols is given implicitly in the matrix representation

$$\begin{aligned} \left( (\partial _i \varSigma )\varSigma ^{-1} (\partial _j \varSigma )\right) ^\alpha = - \Gamma ^{\alpha }_{\eta \gamma } \partial _{i}\varSigma ^{\eta } \partial _{j}\varSigma ^{\gamma }. \end{aligned}$$

(58)

Consequently, the matrix representation allows to compute the functional derivative without the need for explicitly computing any Christoffel symbols at all.

7.1.3 Discretization of Differential Operators

So far we assumed the tensor valued image $\varSigma (x)$ to be defined on a continuous image domain $\Omega$. In an experiential setting we are confronted with diffusion tensor images defined on a discrete grid $\mathcal {G}_h$ where h denotes the width between the nodes of the regular grid. Consequently, we require discrete approximations of $\partial _i \varSigma$ and $\Delta _{i j} \varSigma$. In principle, we could apply finite difference approximations as proposed in Moakher (2005), Gur et al. (2007, 2009), Zéraï and Moakher (2007a) but such a treatment might lead to unstable regularization schemes (cmp. with Sect. 10.1.1).

Alternatively, we can rely on intrinsic approximation schemes that make use of the tangent space in order to approximate partial derivatives. In the following we denote with $T\varSigma _x^{\pm e_j}:=\overrightarrow{\varSigma (x)\varSigma (x \pm h e_j)}$ the tangent vector defined by the logarithmic map (13)

$$\begin{aligned} T\varSigma _{x}^{\pm e_{j}} =\varSigma ^{\frac{1}{2}} \log \left( \varSigma ^{-\frac{1}{2}}\varSigma (x \pm h e_{j}) \varSigma ^{-\frac{1}{2}}\right) \varSigma ^{\frac{1}{2}}, \end{aligned}$$

(59)

and we denote with $e_j$ the unit vector pointing in jth direction.

Proposition 1

The second order discrete approximation of the partial derivative in direction j reads

$$\begin{aligned} \partial _j \varSigma =\frac{1}{2 h} \left( T\varSigma _x^{+ e_j}- T\varSigma _x^{-e_j}\right) +O(h^2). \end{aligned}$$

(60)

Proposition 2

The second order discrete approximation of $\Delta _{i i} \varSigma$ reads

$$\begin{aligned} \Delta _{i i} \varSigma =\frac{1}{h^2} \left( T\varSigma _x^{e_{i}}+ T\varSigma _x^{-e_{i}} \right) +O(h^2). \end{aligned}$$

(61)

where $e_i$ denotes a unit vector in direction i.

The proofs of Proposition I and II can be found in (Fillard et al. 2005; Pennec et al. 2006). For the anisotropic regularization schemes, we also need the mixed derivative operator $\Delta _{i j} \varSigma$ provided by Proposition III

Proposition 3

The second order discrete approximation of the mixed derivative operator $\Delta ^{[i j]}:=\Delta _{i j} \varSigma + \Delta _{j i} \varSigma$ in direction $e_i$ and $e_j$ is given by

$$\begin{aligned} \Delta ^{[i j]}= & {} \frac{T\!\varSigma _x^{x_{n}}+ T\!\varSigma _x^{-x_{n}}-T\!\varSigma _x^{x_{p}}-T\!\varSigma _x^{-x_{p}}}{2 h^2} +O(h^2) \end{aligned}$$

(62)

with the unit vectors $e_n=\frac{e_i+e_j}{\sqrt{2}}$ and $e_p=\frac{e_i-e_j}{\sqrt{2}}$ pointing towards the diagonal adjacent grid points $x_n:=\sqrt{2}e_n$ and $x_p:=\sqrt{2}e_p$.

Proof

We start with expanding the tangent vector in a Taylor series

$$\begin{aligned} T\varSigma _x^{x_{n}} = \sqrt{2} h \partial _{n} \varSigma + h^2 \partial _{n}^2 \varSigma - h^2 (\partial _{n} \varSigma ) \varSigma ^{-1} (\partial _{n} \varSigma ) + O(h^3). \end{aligned}$$

(63)

In a second step we express the derivative in direction n by derivatives along the coordinate axes in i and j direction , $\partial _{n}=\frac{1}{\sqrt{2}}\partial _i+\frac{1}{\sqrt{2}}\partial _j$, yielding

$$\begin{aligned} T\varSigma _x^{x_{n}}= & {} h(\partial _i \varSigma \!+\!\partial _j \varSigma )\!+\!\frac{h^2}{2}\left( \left( \partial _i^2 \varSigma \!+\!\partial _j^2 \varSigma \!+\!2 \partial _i \partial _j \varSigma \right) \right. \nonumber \\&-\,(\partial _i \varSigma ) \varSigma ^{-1} (\partial _i \varSigma )-(\partial _j \varSigma ) \varSigma ^{-1} (\partial _j \varSigma ) \nonumber \\&-\, \left. (\partial _i \varSigma ) \varSigma ^{-1} (\partial _j \varSigma )- (\partial _j \varSigma ) \varSigma ^{-1} (\partial _i \varSigma )\right) \!+\!O(h^3).\nonumber \\ \end{aligned}$$

(64)

Computing the sum $T\varSigma _x^{\Delta x_{n}}:=T\varSigma _x^{x_{n}}+T\varSigma _x^{-x_{n}}$ becomes a fourth order approximation as all uneven terms with respect to h cancel out

$$\begin{aligned} T\varSigma _x^{\Delta x_{n}}= & {} h^2\left( \!\left( \partial _i^2 \varSigma \!+\!\partial _j^2 \varSigma \!+\!2 \partial _i \partial _j \varSigma \right) \!-\!(\partial _i \varSigma ) \varSigma ^{-1} (\partial _i \varSigma ) \right. \nonumber \\&-\left. (\partial _j \varSigma ) \varSigma ^{-1} (\partial _j \varSigma ) -(\partial _i \varSigma ) \varSigma ^{-1} (\partial _j \varSigma ) \right. \nonumber \\&-\left. (\partial _j \varSigma ) \varSigma ^{-1} (\partial _i \varSigma ) \right) +O(h^4). \end{aligned}$$

(65)

Expanding $T\varSigma _x^{\Delta x_p}:=T\varSigma _{x}^{x_p}+T\varSigma _{x}^{-x_p}$ in the same way yields

$$\begin{aligned} T\varSigma _x^{\Delta x_p}= & {} h^2\left( \!\left( \partial _i^2 \varSigma + \partial _j^2 \varSigma \!-2 \partial _i \partial _j \varSigma \right) \!-\!(\partial _i \varSigma ) \varSigma ^{-1} (\partial _i \varSigma ) \right. \nonumber \\&-\left. ( \partial _j \varSigma ) \varSigma ^{-1} (\partial _j \varSigma ) +(\partial _i \varSigma ) \varSigma ^{-1} (\partial _j \varSigma ) \right. \nonumber \\&+ \left. (\partial _j \varSigma ) \varSigma ^{-1} (\partial _i \varSigma )\right) +O(h^4) . \end{aligned}$$

(66)

By subtracting Eqs. (66) from (65) and dividing by $2 h^2$ we obtain the second order approximation for the mixed derivative $\Delta _{i j}\varSigma +\Delta _{j i} \varSigma$ which concludes the proof. $\square$

7.1.4 Analytic Matrix Functions

In addition to its theoretical justification, the affine invariant metric has outperformed the flat Euclidean metric in numerous applications (Gur and Sochen 2005; Moakher 2005; Fletcher and Joshi 2004; Lenglet et al. 2005, 2006; Fillard et al. 2005; Pennec et al. 2006; Zéraï and Moakher 2007a). In order to become an established method in DTI image processing, the involved matrix functions need to be computed in an effective way. In this section we present an analytical method for matrix functions $f:{\mathcal {P}}(3)\rightarrow {\mathcal {P}}(3)$ which allows us to evaluate them much faster than their numerical counterparts. This analytical scheme has been extensively examined in the context of finite element computation (Morman 1986; Hartmann 2003) but has not been applied in the context of DTI estimation so far. In fact, an analytical scheme for eigenvector and eigenvalue computation has been proposed in Hasan et al. (2001). However, this scheme can only deal with pairwise different eigenvalues not being guarantied in DTI. For instance, at convergence of the geodesic marching scheme, the energy gradient converges to the zero matrix such that we also need to handle the case of three identical eigenvalues, i.e. zero eigenvalues in this case.

In the following we discuss the direct analytical computation of matrix functions by means of eigendyades (Morman 1986). The starting points are the three principle matrix invariants

$$\begin{aligned} {\mathcal {I}}_1=\text{ tr }\left( {\varSigma } \right) ,\, {\mathcal {I}}_2= \frac{1}{2}\left( \left( \text{ tr }\varSigma \right) ^2\!-\!\text{ tr }\varSigma ^2\right) , \, {\mathcal {I}}_3=\det {A} , \end{aligned}$$

(67)

from which eigenvalues $\lambda _k$, $k=1,2,3$ can then analytically be computed using Cardano’s formula (Dunham 1990)

$$\begin{aligned} \lambda _k= & {} \frac{1}{3} \left( {\mathcal {I}}_1 + 2 \sqrt{ {\mathcal {I}}_1^2-3 {\mathcal {I}}_2} \cos \frac{\beta +(k-1)2\pi }{3} \right) \end{aligned}$$

(68)

$$\begin{aligned} \beta= & {} \text{ arcos }\frac{2 {\mathcal {I}}_1^3-9 {\mathcal {I}}_1{\mathcal {I}}_2 +27 {\mathcal {I}}_3}{2 \sqrt{\left( {\mathcal {I}}_1^2-3 {\mathcal {I}}_2 \right) ^3}} \,\text{ for } \, {\mathcal {I}}_1^2>3 {\mathcal {I}}_2. \end{aligned}$$

(69)

In case of ${\mathcal {I}}_1^2=3 {\mathcal {I}}_2$ all three eigenvalues are identical equal $\lambda _k = {\mathcal {I}}_1/3$. The case ${\mathcal {I}}_1^2<3 {\mathcal {I}}_2$ does not occur which can be simply proven by inserting $\text{ tr }\left( \varSigma \right) =\sum _k \lambda _k$ in the matrix invariants ${\mathcal {I}}_1$ and ${\mathcal {I}}_2$. For computing the matrix functions f(A) we have to distinguish the cases of (a) three pairwise different eigenvalues, (b) exact two identical eigenvalues and (c) three identical eigenvalues. In the first case (a) the matrix function in analytical form is given by Morman (1986)

$$\begin{aligned} f(A)=\sum _{i=1}^3 f(\lambda _i)\mathbf {n}_{i}\otimes \mathbf {n}_{i} \end{aligned}$$

(70)

where the eigendyades read

$$\begin{aligned} \mathbf {n}_{i}\otimes \mathbf {n}_{i}=\left( {\mathcal {I}}_3 \lambda _{i}^{-1} I+(\lambda _{i}-{\mathcal {I}}_1)A + A^2 \right) D_{i}^{-1} \end{aligned}$$

(71)

with

$$\begin{aligned} D_{i}=2\lambda _{i}^2-\lambda _{i} {\mathcal {I}}_1+{\mathcal {I}}_3 \lambda _i^{-1}. \end{aligned}$$

(72)

The analytical matrix function requires besides the matrix invariants, only the computation of the squared matrix $A^2$ and basic algebraic operations. In the second case (b), i.e. $\lambda _i=\lambda _{j}\ne \lambda _k$, the analytical tensor function reads

$$\begin{aligned} f(A)=f(\lambda _i)I +(f(\lambda _k)-f(\lambda _i))\mathbf {n}_k\otimes \mathbf {n}_k. \end{aligned}$$

(73)

Finally, for three identical eigenvalues (c), i.e. $\lambda =\lambda _i$, $i=1,2,3$ the analytical matrix function is given by

$$\begin{aligned} f(A)=f(\lambda ) I. \end{aligned}$$

(74)

We evaluate the run-time of our analytical Matlab implementation both on the CPU as well as on the GPU. As a reference method we implemented a matrix function in C based on the Lapack library.¹² Table 1 shows the run-times (averaged over $\varepsilon$) for different numbers of matrices and confirms a significant speedup of the analytical approach by a factor 2.8–7.2

It is a well known fact that the analytical computation of eigenvalues are sensitive to numerical inaccuracies,¹³ especially in the case of similar eigenvalues $\lambda _i\simeq \lambda _j$ (Hartmann 2003) when the nominator in (69) tends to become nearly zero. We examine these numerical inaccuracies by computing the matrix logarithm subsequently followed by the matrix exponential function of the matrices

$$\begin{aligned} A_{\varepsilon }=\begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} 1+\frac{\varepsilon }{4} &{} \frac{\sqrt{3}\varepsilon }{4} \\ 0 &{} \frac{\sqrt{3}\varepsilon }{4}&{} 1+\frac{\sqrt{3}\varepsilon }{4} \end{pmatrix}, \quad \varepsilon =10^{-4},\ldots ,10^{-10}, \end{aligned}$$

(75)

using the build-in Matlab functions expm and logm as well using our own analytical implementation. As an error measure we compute the Frobenius norm of the difference original matrix and the transformed one i.e. error$=\Vert A_{\varepsilon }-\exp \left( \log \left( A_{\varepsilon }\right) \right) \Vert _{F}$.

Table 2 shows the numerical error for the function $\exp \left( \log (A_{\varepsilon })\right)$. As expected, we observe a significant smaller error for the numerical approach. The error of the analytical implementation depends on the transformed matrices and its largest value is in the range of $10^{-14}$.

Table 1 Run-time (in seconds) for the matrix exponential function implemented with the proposed analytical schemes in Matlab executed on the CPU and the GPU compared to our numerical implementation based on the Lapack library

Table 2 Numerical errors of the matrix function $\exp \left( \log (A_{\varepsilon })\right)$ implemented with the proposed analytical scheme and with the build-in Matlab functions expm and logm

One has to keep this differences in mind and examine if the precision of the analytical schemes is sufficient for the problem at hand. For our purpose, i.e. reconstruction and diffusion/regularization of tensor valued images, we observed no increase of the estimation error when applying the analytical matrix valued functions. In order to prevent the nominator in (69) to become zero we add or subtract a small $\varepsilon =10^{-10}$ to one eigenvalue if two of them are closer than $10^{-10}$.

7.2 Regularization Taxonomy

In this section we present the regularization taxonomy for tensor valued images. We discuss the energy functionals and derive the functional derivatives as well as their discrete approximation. If possible, we derive for each energy functional the corresponding MRF energy function which is later needed for estimating the posterior covariance (cmp. with Sect. 9).

7.2.1 Isotropic Regularization

In order to define an edge-preserving regularizer, we need a proper definition of edges within tensor valued images. In case of gray-scale images, region boundaries have been characterized by significant changes in the intensity indicated by a sufficiently large local change in the gradient norm $|\nabla f(x)|$ (e.g. Canny 1986). In analogy to gray-scale images, we characterize region boundaries of tensor valued images by means of the norm of the spatial gradient $||\nabla \varSigma (x)||_{\varSigma (x)}=\sqrt{\sum _{j=1}^m \left\langle \partial _j \varSigma (x), \partial _j \varSigma (x) \right\rangle _{\varSigma (x)}}$ of the image manifold. Here, the feature space ${\mathcal {P}}(n)$ consists of a multidimensional manifold such that region boundaries might origin from changes in different degrees of freedom of the image features. However, changes in each particular degree of freedom in ${\mathcal {P}}(n)$ yield a change in the gradient magnitude.

Example

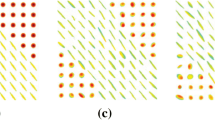
Different types of image boundaries occurring in tensor valued images are illustrated with a synthetically generated tensor valued image $\varSigma (x): {\mathbb {R}}^2\rightarrow {\mathcal {P}}(2)$ defined on a 2D image domain (see Fig. 4). The feature space, i.e. the domain of the diffusion tensor images, has three degrees of freedom as a symmetric $2 \times 2$ matrix is uniquely determined by its two eigenvalues $\lambda _j$ and the orientation $\alpha$ of eigenvectors. Figure 4 illustrates some possible boundaries due to changes of either one of the eigenvalues or the eigenvector orientation. General boundaries have their origin in a combination of changes in all degrees of freedom.

Fig. 4

Illustration of different kind of image boundaries in $\varSigma (x): {\mathbb {R}}^2 \rightarrow {\mathcal {P}}(2)$. The left and the middle image show a change in eigenvalues in the upper triangle and the right image shows a change of the eigenvector directions in the corresponding area

Variational formulation In Fillard et al. (2005) an energy functional for nonlinear isotropic regularization has been defined by

$$\begin{aligned} E_p(\varSigma )= & {} \frac{1}{2} \int \phi \left( ||\nabla \varSigma (x)||_{\varSigma (x)} ^2 \right) dx, \end{aligned}$$

(76)

with the corresponding functional derivative

$$\begin{aligned} \delta E = - \sum _{i j} \varSigma \partial _i\big ( \phi ' \varSigma ^{-1}\!(\partial _j \varSigma ) \varSigma ^{-1}\!\big ) \varSigma + \phi '(\partial _i \varSigma ) \varSigma ^{-1}\!(\partial _j \varSigma ) \end{aligned}$$

(77)

They discretize (77) approximating $\Delta _{i i}\varSigma$ and $\partial _i \varSigma$ using Proposition I (60) and II (61), respectively. Partial derivatives $\partial _i \phi '$ have been approximated by standard finite difference technique. As we will show in Sect. 10.1.1, such a scheme leads to an unstable diffusion process. Furthermore it is, according to Pennec et al. (2006), considered as ineffective.

We do not have a stability proof for numerical regularization schemes for diffusion tensor images. However, we require that a numerical scheme is consistent with a stable scheme in a special Riemannian space, the flat Euclidean space, i.e. it converges to the Euclidean counterpart in the Euclidean limit.

Such a numerical scheme can be derived from (77) via basic algebraic manipulations and approximating $\delta E_p(x_s)=\nabla \!_{\varSigma _{s}}\!E_p(x_s) + O(h)$ with

$$\begin{aligned} \nabla \!_{\varSigma _{s}}\!E_p(x_s)= & {} \!-\sum _{i=1}^m \frac{\phi '(x_s)\!+ \!\phi '(x_{s}\!+\!he_i)}{2 h^2} T\varSigma _{s}^{e_{i}}\nonumber \\&-\sum _{i=1}^m \frac{\phi '(x_s)\!+\!\phi '(x_{s}\!-\!he_i)}{2 h^2} T\varSigma _{s}^{- e_{i}}. \end{aligned}$$

(78)

This scheme converges to the vector version of a well known scheme in the Euclidean limit (cf. with Weickert (1999b), pp. 436) which can be proven easily by setting $T\varSigma _{s}^{\pm e_{i}}\approx \pm \left( \varSigma _{x_s \pm h e_i} \mp \varSigma _{s} \right)$.

MRF formulation The gradient of the MRF energy

$$\begin{aligned} E_p(\underline{\varSigma })= \frac{1}{4 h^2}\sum _{k=1}^N\sum _{j=1}^m \phi \left( \sum _j ||T\varSigma _{x_i}^{e_{j}}||^2_{\varSigma _i}+ ||T\varSigma _{x_i}^{-e_{j}}||^2_{\varSigma _i} \right) , \end{aligned}$$

(79)

with respect to the tensor at position $x_s$ leads directly to (78).

7.2.2 Anisotropic Regularization

Variational formulation In a similar way as in case of gray-scale images (cf. Weickert 1996), we design the diffusion tensor $d^{i j}$ at position x by analyzing the structure of the image $\varSigma$ in a local neighborhood V around x. Let us denote with $\nabla _{\perp } \varSigma (x)=(\partial _1 \varSigma (x), \ldots ,\partial _m \varSigma (x))^T$ the vector containing the partial derivatives along all m spatial coordinate directions and let a denote a unit vector in ${\mathbb {R}}^m$ such that directional derivatives in direction a can be written as $\partial _{a}\varSigma (x) =a^{T} \nabla _{\perp } \varSigma (x)$. The direction $a_{\min }$ of least variation of the image value around position $x_m$ can then be inferred by minimizing the local energy, i.e. $a_{\min }= \arg \min _{a} E(a)$ with

$$\begin{aligned} E(a)= & {} \int _{V} w_m(x) \langle \partial _{a} \varSigma (x), \partial _{a} \varSigma (x) \rangle _{\varSigma (x)} dx \end{aligned}$$

(80)

$$\begin{aligned}= & {} a^T J a. \end{aligned}$$

(81)

where $w_m(x)$ denotes a weighting mask around the position $x_m$. In the last term (81) we defined the structure tensor J by its components

$$\begin{aligned} J_{i j}=\int _{V}w_m(x) \langle \partial _{i} \varSigma (x), \partial _{j} \varSigma (x) \rangle _{\varSigma (x)} dx. \end{aligned}$$

(82)

The direction of least/largest variation is characterized by a minimum/maximum of the energy E(a) and can be deduced by a spectral decomposition of the structure tensor. The diffusion tensor $D=\underline{\psi }(J)$ is finally obtained by applying a (matrix valued) influence function $\underline{\psi }$ to the structure tensor J, i.e. a scalar valued influence function $\psi$ is applied to the eigenvalues of J.

As for the gray-scale counterpart (Weickert 1996), nonlinear anisotropic diffusion filtering schemes with a diffusion tensor D defined above cannot be derived from a corresponding energy formulation (cf. Scharr et al. 2003). However, we can define such a nonlinear diffusion scheme as a generalization of the corresponding linear scheme by making the components of the diffusion tensor $d^{i j}$ depended on the evolving diffusion tensor image.

Table 3 Diffusion filtering based on the geodesic marching scheme

In order to approximate (51) on a discrete grid we split the functional derivative $\delta E_{p}(x)=\delta E^1_{p}(x)+\delta E^2_{p}(x)$ in a part $\delta E^1_{p}(x):=\delta E_{p;i=j}(x)$ containing the diagonal terms of the diffusion tensor and a part $\delta E^2_{p}(x):=\delta E_{p;i j \in \chi }(x)$ with $\chi :=\{i,j: i \ne j \text{ and } \, i,j \in \{1,\ldots ,m\} \}$, containing the off-diagonal terms of the diffusion tensor. We observe that terms with $i=j$ can directly be deduced from the corresponding derivation of the isotropic regularizer [(cf. Eq. (78)] by exchanging $\phi '$ with $d^{i i}$. In addition, we have to approximate the mixed derivative terms

$$\begin{aligned} \delta E_{p}^2(x)= - \sum _{ij \in \chi } d^{i j}(x) \Delta _{i j}\varSigma (x) - \sum _{ij \in \chi } \partial _i d^{i j}(x) \partial _j \varSigma (x) \end{aligned}$$

(83)

An approximation scheme¹⁴ being consistent with its Euclidean limit is given by $\delta E^2_{p}(x_s)=\nabla \!_{\varSigma _{s}}\!E_{p}^2(x_s) + O(h)$ with

$$\begin{aligned} \nabla \!_{\varSigma _{s}}\!E_{p}^2(x_s)\!= & {} -\!\sum _{ij \in \chi } \frac{ d^{i j}(x_s)\!+\!d^{i j}\Big (x_s+\sqrt{2}he_{n}\Big )}{4 h^2}T\!\varSigma _{x_s}^{x_{n}}\nonumber \\&-\!\sum _{ij \in \chi } \frac{ d^{i j}(x_s)\!+\!d^{i j}\Big (x_s-\sqrt{2}he_{n}\Big )}{4 h^2} T\!\varSigma _{x_s}^{-x_{n}}\nonumber \\&+\!\sum _{ij \in \chi } \frac{ d^{i j}(x_s)\!+\!d^{i j}\Big (x_s+\sqrt{2}he_{p}\Big )}{ 4 h^2} T\!\varSigma _{x_s}^{x_{p}}\nonumber \\&+\!\sum _{ij \in \chi } \frac{ d^{i j}(x_s)\!+\!d^{i j}\Big (x_s-\sqrt{2}he_{p}\Big )}{4 h^2} T\!\varSigma _{x_s}^{-x_{p}}.\nonumber \\ \end{aligned}$$

(84)

MRF formulation In order to find the MRF energy whose gradient leads to the discrete approximated linear¹⁵ anisotropic diffusion scheme, we first make use of the fact that the condition equation is the sum of terms involving second derivatives, i.e. $i=j$ and terms involving mixed derivatives, i.e. $i \ne j$. Due to the linearity property of the gradient, we can model energies for each of these terms separately denoted as $E_{iso}$ for terms with $i=j$ and $E_{an}$ for terms with $i \ne j$ with $E( \underline{\varSigma }) = E_{iso}( \underline{\varSigma })+E_{an}( \underline{\varSigma })$. The energy $E_{iso}( \underline{\varSigma })$ is obtained from the MRF energy of the linear isotropic regularizer

$$\begin{aligned} E_{iso}( \underline{\varSigma })= \frac{1}{4 h^2}\!\sum _{k i}\!d^{i i}(x_k)\left( ||T\varSigma _{x_k}^{e_{i}}||^2_{\varSigma _k}\!+\!||T\varSigma _{x_k}^{-e_{i}}||^2_{\varSigma _k} \right) , \end{aligned}$$

(85)

by exchanging $\phi '(x_k)$ with $d^{i i}(x_k)$. For the anisotropic part it is not difficult to see that the gradient of the energy

$$\begin{aligned} E_{an}( \underline{\varSigma })= & {} \frac{1}{8 h^2}\sum _{k,ij \in \chi } d^{i j}(x_k)\left( ||T\varSigma _{x_{k}}^{x_{n}}||^{2}_{\varSigma _k} \right. \nonumber \\&+\left. ||T\varSigma _{x_k}^{-x_{n}}||^{2}_{\varSigma _k} -||T\varSigma _{x_k}^{x_{p}}||^2_{\varSigma _k}-||T\varSigma _{x_k}^{-x_{p}}||^2_{\varSigma _k} \right) .\nonumber \\ \end{aligned}$$

(86)

leads to (84).

Table 4 Diffusion tensor image reconstruction based on the geodesic marching scheme with a isotropic prior

8 Point Estimation

We consider two point estimates: diffusion filtering on given diffusion tensor images and reconstruction of a diffusion tensor images from MRI data.

8.1 Diffusion Filtering

Diffusion filtering can be applied for denoising or interpolating observed diffusion tensor images. To this end, the observed image $\underline{\varSigma }^0$ is evolved by means of the geodesic marching scheme (cf. Table 3): In a first step, the gradient

$$\begin{aligned} \left. \nabla \!_{\underline{\varSigma }}\!E_{p}\right| _{\underline{\varSigma }=\underline{\varSigma }^{\tau =0}} := \left( \begin{array}{c} \left. \nabla \!_{\varSigma _{1}}\!E_{p}(x_1)\right| _{\varSigma _1=\varSigma _1^{\tau =0}} \\ \left. \nabla \!_{\varSigma _{2}}\!E_{p}(x_2)\right| _{\varSigma _2=\varSigma _2^{\tau =0}}\\ \ldots \\ \left. \nabla \!_{\varSigma _{N}}\!E_{p}(x_N) \right| _{\varSigma _N=\varSigma _N^{\tau =0}} \end{array} \right) ^T \end{aligned}$$

(87)

is computed by one of the discrete schemes presented in Sect. 7.2. In a second step, we map the negative gradient (scaled by some time step dt) onto the manifold by means of the exponential map. This process is repeated until the maximum number of iteration steps have been accomplished. Table 3 summarizes the diffusion filtering algorithm in pseudo-code.

8.2 Image Reconstruction

In addition to isotropic and anisotropic diffusion filtering, we consider the MAP estimation of diffusion tensor images from MRI data, i.e. by minimizing the posterior energy

$$\begin{aligned} E(\underline{\varSigma })= & {} -\log \Big (p\Big (\underline{\varSigma }|\underline{S},{\hat{\underline{A}}}_0,{\hat{\sigma }}\Big )\Big )\end{aligned}$$

(88)

$$\begin{aligned}\propto & {} E_L(\underline{\varSigma })+\lambda E_p(\underline{\varSigma }) \end{aligned}$$

(89)

Due to page number limitations we restrict the MAP estimate to isotropic regularization terms. The posterior energy $E(\underline{\varSigma })$ is proportional to the linear-combination of likelihood $E_L(\underline{\varSigma })$ and prior energy $E_p(\underline{\varSigma })$ where the regularization parameter $\lambda$ balances both terms. In a first step, diffusion tensor image $\underline{\varSigma }^{\tau =0}$ is initialized, e.g. by isotropic diffusion tensors. In a next step, the energy gradient $\left. \nabla \!_{\underline{\varSigma }}\!E \right| _{\underline{\varSigma }=\underline{\varSigma }^{\tau =0}}$ is evaluated at the initial diffusion tensor image $\underline{\varSigma }^{\tau =0}$. The posterior energy gradient consists of the sum of likelihood (sampling) energy gradient $\nabla \!_{\underline{\varSigma }}\!E_L$ which is either based on the Gaussian noise model (45) or the Rician noise model (43), as well as the prior energy gradient $\nabla \!_{\underline{\varSigma }}\!E_p$ (87). As the energy gradient points in the direction of the largest ascent, we can minimize the energy by going in the opposite direction. To this end, we map the negative gradient, scaled by some small ‘time’ step dt, back on the manifold by means of the exponential map. This process is repeated until convergence, i.e. the change in the evolved diffusion tensor image falls below some threshold. Table 4 summarizes the geodesic marching based MAP estimator in pseudo-code.

9 Covariance Estimation

In case of image reconstruction (cf. Sect. 8.2) we can make use not only of the maximum of the posterior pdf but also use its width as a reliability measure of the point estimate. We apply the Laplace approximation to the posterior pdf to approximate the posterior covariance. To this end, we expand the negative log posterior pdf $E(\underline{\varSigma })=-\log (p(\underline{\varSigma }|\underline{S},\hat{\underline{A}}_0,{\hat{\sigma }}))$ in a second order Taylor series around its minimum $\underline{\varSigma }_{\min }$

$$\begin{aligned} E(a)\approx & {} E(0)+\frac{1}{2}a^{T}Ha . \end{aligned}$$

(90)

which requires the computation of the Hessian. On general manifolds, the computation of the Hessian H in local coordinates of a function $f:{\mathcal {M}}\rightarrow {\mathbb {R}}$ reads (cf. Pennec 2006)

$$\begin{aligned} H_{i j}(f)=\partial _{i}\partial _{j}f-\Gamma _{i j}^{k}\partial _{k} f \end{aligned}$$

(91)

requiring the cumbersome evaluation of the Christoffel symbols $\Gamma _{i j}^k$. For our Riemannian manifold ${\mathcal {P}}^{N}\!(n)$, the exponential/logarithmic map allows us to define an exponential chart $\varphi := v \circ \log _{\underline{\varSigma }_a}\!\left( \underline{\varSigma } \right)$ mapping each point $\underline{\varSigma }$ of the manifold first to the tangent space attached at $\underline{\varSigma }_a$ and subsequently mapped on an element of the Euclidean space ${\mathbb {R}}^{\frac{n(n+1)}{2}}$ by means of the projection map $v: Sym(n,{\mathbb {R}}) \rightarrow {\mathbb {R}}^{\frac{n(n+1)}{2}}$ , $A \mapsto a$, defined in Sect. 4.1.

In the exponential chart $\varphi$ all Christoffel symbols become zero, i.e. $\Gamma _{i j}^k=0$. In order to see this, let us remind (cf. Sect. 3) that geodesics $\gamma (t)$ between $\underline{\varSigma }_a$ and $\underline{\varSigma }_b$ are mapped on straight lines by the exponential chart, i.e. $v \circ \varphi \circ \gamma (t)=a t$ with $a := v \circ \overrightarrow{\underline{\varSigma }_a\!\underline{\varSigma }_b} \in {\mathbb {R}}^{\frac{n(n+1)}{2}}$. Each geodesic is represented as a curve $\underline{\gamma }(t):=v \circ \varphi \circ \gamma (t)=a t$ in the Euclidean space ${\mathbb {R}}^{\frac{n(n+1)}{2}}$. On the other hand, a geodesic in local coordinates needs to fulfill the geodesic equations (Helgason 1978)

$$\begin{aligned} \frac{d^2 (\underline{\gamma }(t))^k}{d t^2}+\Gamma _{i j}^k\frac{d (\underline{\gamma }(t))^i}{d t}\frac{d (\underline{\gamma }(t))^j}{d t}=0, \end{aligned}$$

(92)

which reduces to $\Gamma _{i j}^k a_i a_j =0$ in our exponential chart. In general, this geodesic equation can only be fulfilled for zero Christoffel symbols leading to the Hessian components $H_{i j}(f)=\partial _i \partial _j f$ evaluated in the exponential chart. In favor of an uncluttered notation we define $P_j:=\varSigma _{\min }(x_j)$, $A_j:= \overrightarrow{P_j \varSigma (x_j)}$, $A_{s p q}:=(A_s)_{p q}$, $J^{p q}_s:=\frac{\partial A_s}{\partial A_{s p q}}$. A rather length but straightforward computation of the second derivative of the energy of the isotropic regularization energy reads

$$\begin{aligned}&\left. \frac{\partial ^2 E_L(A)}{\partial A_{s p q}\partial A_{\ell m n}} \right| _{A=0}\nonumber \\&\quad =\frac{b_i^2}{\sigma ^2}\sum _{i=1}^L\left( \frac{I_1}{I_0} S_{i s} S_{0 s} \right. +\left( \frac{(I_0+I_2)}{2 I_0}-\frac{I_1^2}{I_0^2}\right) \frac{S_{i s}^2 S_{0 s}^2}{\sigma ^2 }\nonumber \\&\qquad -\left. 2 S_{0 s}^2 \right) g_{i}^{T} P_{s} J_{s}^{p q} P_{s} g_{i} g_i^{T} P_\ell J_\ell ^{m n} P_\ell g_i \delta _{s \ell }\nonumber \\&\qquad +\frac{b_i}{\sigma ^2}\sum _{i=1}^{L}\left( \frac{I_1}{I_0}S_{i m} S_{0 m} - S_{0 m}^2 \right) \nonumber \\&\qquad \times \frac{g_{i}^{T} P_s^{\frac{3}{2}} \left( J_{s}^{p q} J_{s}^{m n}+ J_{s}^{m n} J_{s}^{p q} \right) P_{s}^{\frac{3}{2}}g_i}{2} \delta _{s \ell } \end{aligned}$$

(93)

The Hessian of the nonlinear isotropic energy can directly be deduced from (78) as

$$\begin{aligned} \left. \frac{\partial ^2 E_{iso}(a)}{\partial a_{s t} \partial a_{\ell w}} \right| _{a=0}= \sum _{j=1}^m \frac{2 \phi '(x_s) +\phi '(x_{s}^{+j})+\phi '(x_{s}^{-j}) }{2 h^2}\delta _{s \ell } \end{aligned}$$

(94)

where we introduce the abbreviation $a_{s t}:= a_t(x_s)$ as well as $x_{s}^{+j}:=x_{s}+he_j$ and $x_{s}^{-j}:=x_{s}-he_j$. Finally, we estimate the covariance matrix by means of a Gauss Markov random sampling algorithm. To this end, we consider (29) as the expectation

$$\begin{aligned} C={\mathbb {E}}\Big [a a^T\sqrt{|G_{x}(a)|}\Big ] \end{aligned}$$

(95)

of the outer product of the tangent vectors times the Jacobian factor $\sqrt{|G_x(a)|}$ with respect to the pdf in the tangent space at x. The inverse of H is estimated via Gauss Markov Monte Carlo sampling. To this end let $p_k \sim \mathcal {N}(0,I)$, $k\in {1,\ldots ,K}$ be K samples from the zero mean Gaussian distribution with identity covariance matrix I. Further let $H=LL^T$ be the Cholesky decomposition of H. The solutions $q_k$ of the linear equation systems $L^{T} q_k=p_k$ have then the desired covariance matrix $C(q)=C(L^{-T} p)=\left( L L^T \right) ^{-1}=H^{-1}$, and thus $C \approx \sum _k \sqrt{|G_x(a_k)|} q_k q_{k}^{T}/K$. In contrast to the case of gray-scale images, here the empirical mean has to be weighted by the Jacobian factor $\sqrt{|G_x(a_k)|}$.

10 Experiments

In this section, we experimentally examine our diffusion image estimation framework. The following experiments have been carried out: (a) a quantitative and qualitative evaluation of our Riemannian diffusion filtering approaches (b) a qualitative demonstration of the edge enhancing property of our anisotropic diffusion filter scheme on a real data set, (c) qualitative as well as quantitative comparison of our DTI reconstruction approach to reference methods on synthetic data, (d) qualitative demonstrations of the covariance estimates (e) the runtime performance of the DTI reconstruction approach as well as a (f) qualitative comparison on real NMR data.

10.1 Diffusion Filtering

In this experiment we examine the image reconstruction properties of our Riemannian isotropic and anisotropic diffusion scheme, i.e. we apply the corresponding regularization terms without data term to a given tensor valued image.

10.1.1 Synthetic Data

First, we examine diffusion filtering schemes on synthetic tensor valued images. In order to generate noisy diffusion tensor images we add symmetric matrices $W \in Sym(n,{\mathbb {R}})$ with zero mean i.i.d Gaussian random variables with standard deviation $\sigma$ at each entry to the tangent vectors of the noise free diffusion tensor image. In a first step, each tensor of the noise free diffusion tensor image $\varSigma _0$ is mapped to its tangent space at the identity matrix by the standard matrix logarithm, $\varLambda _0=\log _{I}\!\left( \varSigma _0 \right)$. In a second step, all elements of the tangent vectors are corrupted by additive Gaussian noise, i.e. symmetric matrices W containing random variables as matrix elements are added to each tangent vector $\varLambda =\varLambda _0+W$. In a third step, all tangent vectors are mapped back to the manifold by means of the standard matrix exponential to obtain the noisy image $\varSigma =\exp _{I}\!\left( \varLambda \right)$. Figure 5 shows the noise free and noisy diffusion tensor images with five different noise scales ($\sigma =0.1,0.2,0.3,0.4,0.5$).

In a first experiment we evaluated the denoising potential of our Riemannian isotropic diffusion (RID) and Riemannian anisotropic diffusion (RAD) compared to its Euclidean counterparts, i.e. Euclidean nonlinear isotropic (EID) and Euclidean anisotropic diffusion (EAD) proposed by Weickert and Brox (2002). We applied the influence function $\psi (x^2)=1/(1+\kappa x^2)$ with varying contrast parameter in the range $\kappa \in \{ 10^{-2},10^{-1},\ldots ,10^{3} \}$.

Fig. 5

Synthetic diffusion tensor images. Upper row from left to right: noise free image, noisy images with noise variance $\sigma =0.1,0.2$, respectively. Lower row from left to right: noisy images with noise variance $\sigma =0.3,0.4,0.5$

We applied the diffusion schemes to the noisy images (Fig. 5) with a constant time step of $dt=0.1$ for all schemes except for the Euclidean anisotropic scheme which has been evolved with $dt=0.01$ as it otherwise leads to non-positive diffusion tensors.

For each diffusion filtering scheme at each noise level we choose the contrast parameter and stopping time with the lowest error measure under consideration. This means that we look at the potential of the four schemes to denoise images. On real noisy images we cannot compute this distance and thus cannot choose the best suitable contrast parameter for each individual image. Nonetheless we can observe the maximal possible image reconstruction quality of the different schemes.

In order to measure the performance of the four different diffusion schemes we estimate the mean and its standard deviation of the Riemannian as well as the Euclidean distance distribution over the image. As the Euclidean anisotropic scheme might lead to non-positive definite diffusion tensor images and the Riemannian distance is not defined for non-positive tensors, we project such tensors to the space of positive definite tensors ${\mathcal {P}}(n)$ by replacing negative eigenvalues by a small constant, i.e. 10e$-$9 in our case.

Furthermore, we consider the absolute difference between the noise free and the denoised image for the following different tensor entities: the determinant of each diffusion tensor as well as the fractional anisotropy (FA) (Basser and Pierpaoli 1996). The determinant of the diffusion tensor is directly related to the strength of the physical diffusion process: the larger the determinant the larger the physical diffusion process. The fractional anisotropy (FA) is computed from the eigenvalues $(\lambda _1,\lambda _2,\lambda _3)$ of the tensor and their mean $\bar{\lambda }=\frac{1}{3}(\lambda _1+\lambda _2+\lambda _3)$ via

$$\begin{aligned} \text{ FA }=\sqrt{\frac{1}{2}}\sqrt{\frac{\big (\lambda _1-\bar{\lambda }\big )^2+\big (\lambda _2-\bar{\lambda }\big )^2+ \big (\lambda _3-\bar{\lambda }\big )^2}{\lambda _{1}^2+\lambda _{2}^2+\lambda _{3}^2}}. \end{aligned}$$

(96)

FA is a scalar measure characterizing the degree of anisotropy of the diffusion process. It is zero for isotropic diffusion tensors and one for maximal anisotropic diffusion tensors. Figure 6 shows the mean and its standard deviation for all four error measures.

Fig. 6

Estimated mean and its standard deviation of the error measure distribution over the image versus the noise level for different diffusion filtering methods: Euclidean isotropic (EID), Euclidean anisotropic (EAD), Riemannian isotropic (RID), Riemannian anisotropic (RAD)

Fig. 7

Denoising results. The contrast parameter $\kappa$ has been chosen such that the Riemannian error is minimized for each filtering scheme and each noise level. From left to right noise levels $\sigma =0.1,0.2,0.3,0.4,0.5$. From upper row to lower row EID, EAD, RID, RAD

Fig. 8

Upper row: discretization RID diffusion scheme proposed in Fillard et al. (2005) for $\sigma =0.1$, $dt=0.1$, and for different diffusion times (from left to right) $t=10,20,30,40$. Lower row our discretization scheme (78) for the same parametrization as above

Our RID scheme shows the best denoising properties with respect to all considered error measures for all noise levels. Our RAD scheme performs twice as good with respect to all considered error measures for higher noise levels and performs less accurate as the Euclidean isotropic scheme for lower noise levels ($\sigma =0.1,0.2$) with respect to the Euclidean distance, the Determinant and FA error measure. We also observe an artefact at the border of the line (cmp. Fig. 7, lower row), especially for higher noise levels: the diffusion tensors become more isotropic and point in different directions. This artefact persists also for different influence functions and also for alternative diffusion schemes. In particular, we applied the influence functions $\psi (x^2)=\sqrt{10^{-4}/(10^{-4}+x^2)}$ and $\psi (x^2)=\exp {\left( -\kappa x^2\right) }$.

Visual inspection of the denoised images (Fig. 7) of the Euclidean schemes confirms the eigenvalue swelling effect reported in Pennec et al. (2006), i.e. the volume of the tensors in the line structure increases due to the iterative local averaging with respect to the Euclidean metric.

Furthermore, the anisotropic Euclidean diffusion scheme can lead to non-positive definite tensors (Fig. 7, upper right: shown by the corresponding non-closed second order surface) in accordance with our considerations in Sect. 4. In order to obtain a stable anisotropic diffusion scheme (cmp. with Weickert 1996; Scharr 2000) strict conditions on the eccentricity of the diffusion tensor steering the filtering process has to be imposed, i.e. the ratio between smallest and largest eigenvalues is not allowed to fall below a certain value. We conclude that anisotropic diffusion filtering steered by general diffusion tensors, i.e. applying an influence function to the eigenvalues of the structure tensor without bounding the eccentricity of the resulting diffusion tensor, does not provide a reliable denoising method for tensor valued images.

In a second experiment we compared the performance of our discretization scheme (78) with the scheme proposed in Fillard et al. (2005) in which the terms in (77) have been directly discretizised. Figure 8 shows the temporal evolution of both schemes for $t=10,20,30,40$. While our approach shows the desired denoising property the approximation scheme of Fillard et al. (2005) reveals numerical instabilities, i.e. the tensors at the border of the line structure as well as the tensors of the line structures increase their anisotropy for increasing diffusion time. We observe this behavior also for varying time steps as well as for different influence functions. Our scheme reduces to a stable scheme for gray scale images when we replace tangent vectors on the manifold by tangent vectors in the Euclidean space, i.e. $T_{x}^{e_i}\varSigma \simeq \varSigma (x+h e_i)- \varSigma (x)$, whereas the approximation scheme of (Fillard et al. 2005) reduces to a non-stable scheme (cf. Weickert 1999b, pp. 423). A sound theoretical proof of stability for general diffusion images, i.e. ${\mathcal {P}}(n)$, $n>1$, is still an open issue and will be postponed to future research.

In a third experiment, we examine the diffusion schemes to close gaps in line structures of tensor valued images. This is the most prominent property of the anisotropic diffusion concept in case of gray-scale images and has successfully been applied to enhance fingerprint images (Weickert 1996). In diffusion tensor images such line structures occur in nerve fiber bundles of the human brain as well as in transport systems in biological tissues. Due to errors in the imaging process such gaps also occur in line structures within diffusion images. We applied the RAD scheme to the tensor valued image (Fig. 9, left) where several tensors in the line structure have been replaced by tensors of the surrounding. For the RAD scheme we modify the diffusion tensor in that we only apply the influence function to the largest eigenvalue of the structure tensor and set the smallest eigenvalue equal one. This scheme is known as edge-enhancing diffusion in the scalar valued case (Weickert 1999a) and has been generalized to matrix valued data in an Euclidean setting (Burgeth et al. 2009). In each step of the geodesic marching scheme only tensors in this gap are allowed to change. As starting points for the diffusion process we choose unit tensors, i.e. tensors with eigenvalues $(\lambda _1=\lambda _2=\lambda _3=1)$.

The RAD filtered image after $10^3$ iteration of the geodesic marching scheme is shown in Fig. 9, right. Due to the local orientation encoded by the structure tensor (cmp. with Sect. 7.2.2), the anisotropic scheme (RAD) is steered by the average direction in the local region. Thus, the diffusion process in the gab is steered by the local line structure allowing to fill the gab with tensors pointing in the direction of the line structure. We conclude that we generalized the coherence-enhancing diffusion concept to tensor valued images within the Riemannian framework.

Fig. 9

From left to right: original synthetic image, RID scheme ($t=100,dt=0.1$), RAD scheme ($t=100,dt=0.1$)

10.1.2 Real Data

In order to illustrate the application of our Riemannian diffusion schemes on real data we consider the post-processing of a diffusion tensor image of a plant, i.e. a fresh rhubarb (Fig. 10, upper left). Plants build sophisticated architectures to transport water and nutrients. While plant anatomy can be assessed invasively, dynamics and pathways of long distance transport need to be investigated non-invasively. To this end, water mobility has to be measured using a non-invasive technique, e.g. DT-MRI (Scheenen et al. 2007). The diffusion tensor image (Fig. 10, the main diffusion direction has been color-coded) of a fresh rhubarb (Rheum rhabarbarum) has been reconstructed in conjunction with a Ph.D.-thesis (Menzel 2002) by means of a least squares estimate¹⁶ using the Stejskal–Tanner Equation (1). The reconstructed tensor image is noisy and it is difficult to identify the plant transport systems from the surrounding tissue.

We applied the Riemannian nonlinear isotropic (RID, Fig. 10 lower left) and Riemannian anisotropic diffusion (RAD, Fig. 10 lower right) to the noise tensor valued image (Fig. 10, upper right) with a time step $dt=0.1$. We stopped the diffusion process according to subjective criteria from observing the evolving image.

The Riemannian anisotropic diffusion process enhances the pathways of the plant (the dark blue spots) much better than the Riemannian isotropic diffusion. However, evaluating the use-fullness of this methods in the context of restoring biological based diffusion tensor images requires further examinations involving expertise from the biological science.

Fig. 10

Upper left cross section of two rhubarbs; upper right Least squares estimated diffusion image; Lower right: RID diffusion filtered image; lower right: RAD diffusion filtered image; The color code is red, green, blue indicating the three spatial dimensions (Color figure online)

10.2 DTI Reconstruction

This section provides an experimental evaluation of our diffusion tensor image reconstruction MAP and covariance estimator from synthetic and real NMR data.

10.2.1 Synthetic Data

In this experiment we reconstruct several diffusion tensor images from synthetic generated DW and reference images corrupted by Rician distributed noise. We start with a set of synthetic diffusion tensor images. Based on the Stejskal–Tanner equation (1) we generate the corresponding noise free magnitude DW images $A_{i k}(x)$, where we set the reference signal equal to one, i.e. $A_{0 k}=1$. The ‘b-values’ are set to the same values as in our experiment on real data described in Sect. 10.2.2. The DW images $A_{i k}(x)$ are the norm of the complex valued NMR images. As we know the noise free magnitude DW images, we can define the imaginary $\mathfrak {I}(A_{R j}(x))=S_j(x) \sin (\eta )$ and real $\mathfrak {R}(A_{R j}(x))=S_j(x) \cos (\eta )$ part of the NMR magnitude image values (DW and reference image) where $\eta$ can be chosen to an arbitrary value within $[0,2 \pi ]$. Noisy DW images are then generated by choosing $\eta$ from a uniform distribution in the interval $[0,2 \pi ]$ and additive noise components for the imaginary as well as real NMR signal that both follow a zero mean Gaussian distribution with standard deviation $\sigma$. We corrupt the ground truth NMR signals with five different noise levels ($\sigma =0.04,0.08,0.12,0.16,0.2$), compute the corresponding DW signals $S_j$ as well as the reference image $S_0(x)$ for each spatial position ${{\varvec{x}}}$. The five chosen noise levels correspond to average SNRs of (7.5:1,4.5:1,3.5:1,3.0:1,2.7:1). Based on the noisy images, we reconstruct the tensor field using the reference methods as well as our method.

The least squares estimator on the linearized Stejskal–Tanner equation (1) leads to some non-positive definite tensors for all considered noise levels. Consequently, this method does not lead to physical meaningful reconstruction results and will not be considered in the following analysis.

As reference methods we consider the method of Lenglet et al. (2006) which uses a Gaussian noise model within the Riemannian framework as well as the method of Landman et al. (2007a) which uses a Rician noise model in the Euclidean geometry. Both approaches do not apply spatial regularization. Additional to the original reference methods we adapt them by applying a nonlinear isotropic spatial regularization term. Our approach is denoted as Rician–Riemannian¹⁷ using the same non-linear spatial regularization term. As influence function we choose $\psi (x)=10^{-3} /\sqrt{10^{-3}+x^2}$ and optimize the regularization parameter $\lambda$ for each noise level on the image shown in Fig. 12. For subsequent experiments we fix these ‘learned’, optimal regularization parameters. We initialize the geodesic marching scheme with identity matrices I. The geodesic marching scheme is considered to be in convergence when the diffusion tensor components change less $10^{-5}$ on average.

Figure 11 shows the different error measures versus the five noise levels for the different reconstruction methods.

Fig. 11

Estimated mean and its standard deviation of the error measures (Euclidean error, Riemanian error, FA error, determinant error) versus the noise level ($\sigma =0.04,0.08,0.12,0.16,0.2$) for the different reconstruction methods: Gaussian–Euclidean, Gaussian–Riemannian, Rician–Euclidean, Rician–Riemannian

Our Rician–Riemannian approach performs best on all noise levels and with respect to all error measures. The Gaussian–Riemannian approach, i.e. the approach of (Lenglet et al. 2006) combined with our Riemannian regularization scheme, yields similar results as our Rician–Riemannian approach for small noise levels, but its performance breaks down for medium and larger noise levels.

Visual inspection of the reconstructed diffusion tensor images (Figs. 12 and 13) supports the quantitative results: For the smallest noise level all approaches show similar reconstruction results. Methods without regularization become very noisy for larger noise levels in the NMR images. For methods utilizing the Gaussian likelihood model we observe, in accordance with our theoretical considerations in Sect. 6.2.1, a bias towards smaller diffusion tensors whereas the Rician noise model leads to reconstruction results much closer to ground truth. For medium ($\sigma =0.08$) and larger noise scales our Rician–Riemannian approach visually outperforms all reference methods, i.e. it keeps closest to the ground truth.

In a second experiment we examine our covariance estimator described in Sect. 9. To this end, we compute the posterior covariance matrices for our approach for the NMR image data also used for the results shown in Fig. 12. The bottom row in Fig. 12 shows the trace of the estimated covariance for each spatial position encoded in a gray scale image. As expected the covariance increases at the edges within the image. This is due to the reduced influence of the prior term in the vicinity of edges indicated by a larger image gradient.

Fig. 12

Reconstructed diffusion tensor images for different noise levels (from left to right; $\sigma =0.04,0.08,0.12,0.16,0.2$), for the different reconstruction methods (from upper to lower row): Gaussian without regularization, Rician without regularization, Gaussian–Euclidean, Gaussian–Riemannian, Rician–Euclidean, Rician–Riemannian. The last row shows the trace of the estimated covariance at each pixel position for the Rician–Riemannian method

Fig. 13

Reconstructed diffusion tensor images from four different synthetic DTI data corrupted with Rician noise ($\sigma =0.16$) and different reconstruction methods (from left to right): Gaussian–Euclidean, Gaussian–Riemannian, Rician–Euclidean, Rician–Riemannian. The underlying noise free images are composed from the same two tensor types (green and magenta ellipsoids) as the line image in Fig. 5 (Color figure online)

Fig. 14

Reconstruction of a synthetic DTI from DW images corrupted by outliers: Upper row: Rician noise model with nonlinear isotropic regularization (left), Robust noise model with nonlinear isotropic regularization (middle), DW image corrupted by non Gaussian noise at one spatial position; lower row covariance estimation (trace of the covariance matrix) of the Rician noise model with nonlinear isotropic (left), covariance estimation of the robust noise model with nonlinear isotropic (middle), covariance estimation (trace of the covariance matrix) of the Rician noise model with nonlinear isotropic reconstructed from DW image without outliers (right)

In the next experiment we examine the influence of outliers in DW and reference images on reconstructed diffusion tensor images. To this end, we corrupted the components of the complex MRI images $\mathfrak {R}(A_{R j}(x))$ and $\mathfrak {I}({A_{R j}(x)})$ used in the previous experiment (cf. Fig. 12) with noise following a Gaussian mixture distribution $p_{\varepsilon }(x)=0.7 \mathcal {N}(1,0.01) + 0.3 \mathcal {N}(0,1)$ at one spatial position $x_s$. MRI images at other positions were corrupted with Gaussian noise $\mathcal {N}(0,0.01)$. Figure 14 (upper right) shows a DW image as a gray-scale image with an outlier at lower right. We reconstructed the diffusion tensor image using our Rician–Riemannian approach with the same parametrization described in the previous section. The outlier at position $x_s$ in the DW image leads to a significant error in the estimated diffusion tensor at the corresponding position as shown in Fig. 14 (upper left). The influence function of the regularizer reduces the regularization such that the error in the DW image and reference images proceed to the estimated diffusion tensor. As the regularization is only reduced and not completely suppressed also neighbor tensor values are affected by the non-Rician noise distribution in the DW and reference images at position $x_s$.

Next, we applied our robust likelihood function (cmp. with Sect. 6.2.2 ). As influence function we chose a constant function with value one for arguments equal or larger than 0.01 and with a value of zero for arguments smaller than 0.01. Applying the robust likelihood term allows to reconstruct a diffusion tensor image that visually does not differ from the image reconstructed without any outliers [(cf. Fig. 14 (upper middle)]. The usefulness of the covariance estimator becomes obvious in this experiment. In case of the Rician noise model, the covariance estimator indicates a reduction of the reliability of the estimator due to the reduced prior distribution (Fig. 14 (lower left)). In case of the robust likelihood term, the covariance estimator also indicates slightly less reliability (Fig. 14 (lower middle)) compared to the outlier free image (Fig. 14 (lower right)).

In a last experiment we examine the runtime of the four approaches: Gaussian–Euclidean, Gaussian–Riemannian, Rician–Euclidean and Rician–Riemannian. To this end we reconstructed images with a line like structure with noise level $\sigma =0.12$ for different image sizes and measured the time until convergence of the corresponding method. Figure 15 shows the measured run-time of the four methods versus the size of the reconstructed image indicated by the square root of the number of pixels. As expected the Euclidean approaches are faster than the Riemannian approaches. However, due to the analytical computation of the required matrix functions (cf. Sect. 7.1.4), the Riemannian approaches are only about a factor of two slower than the Euclidean ones. Runtime of an approach using numerical matrix function computation is about a factor of four slower than its Euclidean counterpart (data not shown).

Fig. 15

Runtime versus square root of number of pixels for the four reconstruction methods (Gaussian–Euclidean, Gaussian–Riemannian, Rician–Euclidean, Rician–Riemannian) for a line-like structure (cmp. Fig. 12) with noise level $\sigma =0.12$ (Color figure online)

10.2.2 Real Data

In this experiment, we apply the different reconstruction methods: Gaussian, Rician, Gaussian–Euclidean, Gaussian–Riemannian, Rician–Euclidean, Rician–Riemannian, to 3D MRI images measured from a human brain in-vivo. A single-shot diffusion-weighted twice-refocused spin-echo echo planar imaging sequence was used with the following measurement parameters: TR = 6925 ms, TE = 104 ms, 192 matrix with 6/8 phase partial Fourier, 23 cm field of view, and 36 2.4-mm-thick contiguous axial slices. The in-plane resolution was 1.2 mm/pixel. For each of the 36 slices, diffusion weighted images were acquired involving diffusion gradients with eight different b values (250, 500, 750, 1000, 1250, 1500, 1750, 2000 s/mm$^2$), each being applied along six non-collinear directions [ (x, y, z) gradient directions were (1, 0, 1), ($-$1, 0, 1), (0, 1, 1), (0, 1, $-$1), (1, 1, 0), ($-$1, 1, 0)], and an individual set of reference images without diffusion weighting (b = 0 s/mm$^2$).

We estimated a SNR of 5.2 by estimating the background standard deviation $\sigma _b$ from regions of MRI images containing no brain tissue and by estimating the mean from the region of interest. All parameters of the algorithms, e.g. regularization parameters, are set to interpolated values of the optimized values obtained in the synthetic experiment.

Figure 16 shows the tensor characteristics for the reconstructions without regularization, namely the method proposed in Lenglet et al. (2006) as well as the method proposed in Landman et al. (2007a). Figure 17 shows the tensor characteristics for the regularized reconstruction methods. We observe that the images from the non-regularized methods are quite noisy, especially the FA images, whereas all regularized methods appear significant less noisy, as expected. We additionally observe that the four regularized methods lead to significant different tensor characteristics. The evaluation of the medical use of these results goes beyond the scope of this paper and requires corresponding expertise.

Fig. 16

The matrix properties: Fractional anisotropy (left column), determinant (middle column) and the trace (right column) of the reconstructed diffusion tensor images for the Rician (upper row) and the Gaussian (lower row) noise model without any regularization (Color figure online)

Fig. 17

The matrix properties: fractional anisotropy (upper row), determinant (middle row) and trace (lower row) of the reconstructed diffusion tensor images with regularization for (from left to right): the Rician–Riemannian, the Rician–Euclidean, the Gaussian–Riemannian and the Gaussian–Euclidean reconstruction method (Color figure online)

Table 5 Tensor characteristics for the synthetic (synth.) and real MRI data

As no ground truth is available we cannot make any quantitative comparisons between the methods by means of a Riemannian or Euclidean error measure.

What we can do here, though, is the comparison of the tensor characteristics with results obtained from synthetic MRI images. To this end we compute the mean of the tensor characteristics, i.e. fractional anisotropy (FA), determinant, and trace, for synthetic and real (Table 5) NMR signals.

For the FA we could not observe any correspondences between real and synthetic data which is reasonable as the FA should not show any distinct bias for the different methods, i.e. the FA is sometimes too large and sometimes too small. Evidently, the sign of the FA error depends on the considered data and we cannot expect it to be comparable for synthetic and real data sets.

For the determinant and the trace, on the other hand, all reconstruction methods show the same qualitative behavior on both MRI data sets which is again reasonable as these values show a clear bias according to our theoretical considerations and already validated by experiments on synthetic data. The determinant and trace are lower for the Gaussian noise model in accordance with our theoretical consideration in Sect. 6: The Gaussian noise model leads to a bias towards smaller diffusion tensors and hence to smaller traces and determinants. The eigenvalue swelling effect of the Euclidean regularization approaches leads to the opposite effect, an increase of determinant and trace which explains the larger values for Gaussian–Euclidean approach compared to the Gaussian–Riemannian approach.

We observe that the tensor characteristics of real data is well in accordance with our findings on synthetic data and theoretical considerations.

11 Summary and Outlook

In this paper we formulated a Bayesian estimation framework for tensor valued images. We formulated a likelihood function for diffusion tensor images based on the Rician noise model. We provide a regularization taxonomy for tensor valued images within the matrix representation. In particular, we derived anisotropic diffusion equations within this representation. We introduced discrete approximations for the regularization schemes and experimentally validated their stability. Last but not least we formulate an estimator for the covariance matrix as a confidence measure for the point estimate. In order to speed up the estimator we introduced analytical matrix functions which have not been used in the context of DTI so far. Experiments on synthetic data demonstrate that our fully intrinsic one-step reconstruction approach yields more accurate and reliable results than competing algorithms. Overall we conclude that the consequent usage of the intrinsic view for model derivation in conjunction with suitable Bayesian estimation schemes yields the most accurate and reliable approach to DTI reconstruction from DW images presented so far.

It is evident that we cannot cover all aspects of Bayesian estimation theory which have been investigated for Euclidean spaces so far such that there is plenty of room for future research. For instance, learning and estimation techniques for model parameters have not been tackled at all. However, supervised learning requires suitable training data which is not available, yet. A further research topic is a sound theoretical stability analysis of the geodesic marching scheme including an analysis of different approximation schemes of the continuously formulated diffusion equation.

DTI has its limitations where the model assumption, i.e. the Stejskal–Tanner equation, is violated, e.g. at crossing fiber structures in the brain tissue. In such cases models allowing multiple orientations like orientation distribution functions based on high angular resolution diffusion imaging can extend the approach presented here, cmp. e.g. (Krajsek and Scharr 2012). Adapting our approach to the more general framework of Finsler geometry (Melonakos et al. 2007; Florack and Fuster 2014) might be another interesting future research direction.