1 Introduction

In this paper, we consider images captured under unknown distant point source illumination and satisfying the Lambertian model, i.e., where surface brightness looks the same from any viewing direction. We show that locations of maximal diffuse brightness in the captured images carry very useful geometrical information about shape (in the form of a unit normal field) and light. We demonstrate their potential in the case of uncalibrated photometric stereo, where no prior knowledge about the illumination, geometry, and reflectance albedo is available. In the most general formulation of this problem, the normal field of the object can be obtained from the Lambertian reflectance model only up to a nine-parameter linear ambiguity (Hayakawa 1994). This ambiguity can be further reduced to three parameters, the so-called generalized bas-relief ambiguity (GBR) (Belhumeur et al. 1999), via the integrability constraint, which enforces that a valid surface can be reconstructed from the estimated normal field.

Finding a way to fix the GBR parameters with assumptions as realistic as possible is still an open research problem. We make the assumption that one can detectFootnote 1 and exploit maxima of the Lambertian diffuse reflectance (LDR) component (as opposed to the specular reflectance component (Drbohlav and Chantler 2005; Drbohlav and Sara 2002; Lagger and Fua 2008; Oren and Nayar 1997) or the temporal maxima (Koppal and Narasimhan 2006)). We show that each of these maxima restricts the space of GBR ambiguities to a semi-circle in 3-D space, and that as few as two maxima from differently illuminated images yield a unique solution for the GBR parameters (see Fig. 2). Moreover, the semi-circles can be efficiently computed in closed-form (see Sect. 6.1).

Fig. 1
figure 1

Some Lambertian diffuse reflectance (LDR) maxima on the surface of a face in one input image. The lighting direction is shown at the very top with gray arrows. For illustration purposes, we look only at a 1D profile (blue solid line) of the 3D surface. Along this profile we show some of the normals to the surface as blue arrows. Those normals that are parallel to the illumination direction are shown as red arrows and their corresponding point (shown in red) on the surface is an LDR maximum (Color figure online)

Full size image
Fig. 2
figure 2

GBR ambiguity solved via LDR constraints. The integrability constraint alone allows the GBR parameters \((\mu ,\nu ,\lambda )\) to take any value in the 3D space. A single LDR maximum constrains the GBR parameters to a semi-circle (which can be written in closed-form). Two different LDR maxima are sufficient to generate a unique solution. Indeed, two maxima correspond to two semi-circles, and these intersect at one point (whose calculation is very efficient). All LDR maxima define other semi-circles all intersecting at the true GBR parameters (which shows the consistency of this constraint)

Full size image

The most fundamental challenge that we address in this paper is the consistency of the assumptions, i.e., when the assumptions uniquely identify the same solution. We show that there is a limited choice of constraints that satisfy the consistency property. As we argue in the next sections, our proposed solution is one such choice. Consistency is not only needed to guarantee that the solution is reliable, but also to make the algorithm fast. Indeed, current inconsistent state-of-the-art methods obtain a stable estimate by running their algorithms several times with different initial conditions and by averaging all the estimates, a process that may take several minutes and yield a solution with low confidence. In contrast, our algorithm needs to be run only once and yields a reliable estimate in about \(14\) s with non optimized code, as we show in Sect. 6.

2 Prior Work and Contributions

Photometric stereo (Woodham 1980) is a method for estimating shape and reflectance of an object, using three (Woodham 1980) or more (Wu and Tang 2005) images of a static object taken from a fixed viewpoint and under different lighting conditions. When the illumination directions and intensities are known, the problem can be solved via a linear system.Footnote 2

When no prior knowledge about the illumination, geometry, and reflectance is available, the problem is called uncalibrated photometric stereo (UPS). UPS has been addressed with a variety of techniques that make explicit or implicit use of the GBR ambiguity (Belhumeur et al. 1999):

2.1 Explicit GBR Disambiguation Methods

In (Alldrin et al. 2007), the GBR ambiguity is solved by minimizing the entropy of the albedo distribution following the argument that incorrect GBR parameters result in spreading albedo values. This approach relies on the assumption that albedos are based on a few intensity values. A similar philosophy is to group the normal-albedo distribution based on intensity-color appearance (Shi et al. 2010). The use of color, when available, allows albedo clustering based on the chromaticity. Another example is to introduce additional constraints to determine the GBR ambiguity by exploiting specularities of glossy surfaces (Drbohlav and Chantler 2005; Drbohlav and Sara 2002; Tan et al. 2007). These methods rely on the ability to correctly detect specularities and on the assumption that objects in the scene have a non-negligible specular component. In other investigations, the GBR ambiguity has been eliminated by exploiting inter-reflections (Chandraker et al. 2005) or by considering the Torrance and Sparrow reflectance model (Georghiades 2003). Lagger and Fua (2008) notice that both specular and diffuse maxima provide useful information about the illumination direction. However, they discard diffuse maxima and focus only on specular ones.

2.2 Implicit GBR Disambiguation Methods

Other approaches instead exploit shadows (Okabe et al. 2009; Sunkavalli and Zickler 2010), dimensionality reduction (Sato et al. 2007), the bilateral symmetry of isotropic bidirectional reflectance distribution function (BRDF) (Alldrin and Kriegman 2007) or consider changing the viewpoint and exploit the Helmoltz reciprocity principle (Zickler et al. 2002). Hertzmann and Seitz (2005) use a reference object in the scene to generate intensity-normal look-up tables, and can handle fairly general reflectance functions (more precisely, all materials of a single object must be a linear combination of a given basis of materials). A recent work of Chandraker et al. (2011) exploits a particular image acquisition setup and spatial and temporal image derivatives to obtain an uncalibrated photometric invariant that can deal with a general isotropic BRDF. Other methods generalize the lighting environment and implicitly extend the Lambertian model so that different normals see a different portion of the illumination hemisphere (Basri and Jacobs 2001).

2.3 Contributions

We introduce LDR maxima (Favaro and Papadhimitri 2012) to solve the GBR ambiguity in UPS explicitly. Our main contributions are:

  • A closed-form solution given an LDR maximum;

  • A robust estimator to find the GBR parameters that tolerates up to 80 % incorrect LDR maxima;

  • A proof that the solution is GBR-consistent.

Finally, we experimentally demonstrate that our method handles a wide range of real-world scenes (with varying albedo distribution), is the most computationally efficient UPS algorithm, and achieves state-of-the-art results.

3 Photometric Stereo

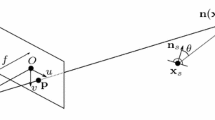
Photometric stereo is the task of recovering the surface of an object with normal field \(\mathbf {n}\), given \(K\) input images taken from a fixed viewpoint, and illuminated by known distant point light sources with direction \(\mathbf {l}\). We denote the unit-normal to the surface at the pixel index \(p\) with \(\mathbf {n}_{p}\in S^{2}\) for \(p=1,\ldots ,P\), where \(P\) is the total number of pixels in an image. Similarly, we denote with \(\mathbf {l}_{k}\in S^{2}\) the unit-normal corresponding to the \(k\)-th illumination direction. Now, let us call \(\mathbf {L}_{k}=e_{k}\mathbf {l}_k\) the light vector, where \(e_{k}\) denotes the light intensity. Also, let \(\mathbf {N}_{p}=\rho _{p}\mathbf {n}_p\) represent the generic normal vector and \(\rho _{p}\) be the albedo coefficient (i.e., the intensity of the surface texture). Then, the intensity measured at a pixel index \(p\) with illumination \(k\) for the Lambertian case (and under the assumption of a linear response of the camera and orthographic projection) is:

$$\begin{aligned} I_{p,k}= \rho _{p}\langle \mathbf {n}_p,\mathbf {l}_k\rangle e_{k} = \mathbf {N}_{p}^\top \mathbf {L}_{k} \end{aligned}$$
(1)

where \(\langle \cdot ,\cdot \rangle \) denotes inner product and \((\cdot )^\top \) the transpose of a vector (or of a matrix). By sorting the pixels in lexicographical order we can rearrange all the generic normal vectors in a matrix \(\mathbf {N} = [\mathbf {N}_{1}~\ldots ~\mathbf {N}_{P}]\in \mathbb {R}^{3\times P}\), which we call normal matrix; similarly we can rearrange the light vectors into a matrix \(\mathbf {L} = [\mathbf {L}_{1}~\ldots ~\mathbf {L}_{K}]\in \mathbb {R}^{3\times K}\), which we call light matrix. Then, we can write Eq. (1) in the following compact matrix form

$$\begin{aligned} \mathbf I =\mathbf N ^\top \mathbf L \end{aligned}$$
(2)

where \(\{\mathbf {I}\}_{p,k} = I_{p,k}\).If light directions and intensities are given, solving photometric stereo is equivalent to solving the linear system (2) in the unknown normal matrix \(\mathbf {N}\). Finally, extracting the albedo \(\rho _{p}\) from the generic normal vectors \(\mathbf {N}_{p}\) can be done via \(\rho _{p} = \Vert \mathbf {N}_{p}\Vert _{2}\), where \(\Vert \cdot \Vert _{2}\) denotes the \(\ell _2\) norm.

4 Uncalibrated Photometric Stereo

If the light matrix is unknown, \(\mathbf {N}\) and \(\mathbf {L}\) can be obtained up to a linear ambiguity \(\mathbf {G}\in GL(3)\) (Hayakawa 1994), where:

$$\begin{aligned} \mathbf {I}=\mathbf {N}^\top \overbrace{\mathbf {G}^{-1}\mathbf {G}}^{identity}\mathbf {L}. \end{aligned}$$
(3)

It can be shown (Belhumeur et al. 1999) that if we impose the integrability constraint, then the ambiguities take the form

$$\begin{aligned} \mathbf {G}= \left[ \begin{array}{lll} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ \mu &{} \nu &{} \lambda \end{array} \right] \end{aligned}$$
(4)

where the three parameters \(\lambda \ne 0\), \(\mu ,\nu \in \mathbb {R}\) represent the group of GBR transformations. In this formulation it is apparent that solving UPS amounts to fixing these three parameters. For simplicity, we also fix the sign of \(\lambda \) to be positive. Define \(\hat{\mathbf {N}} \doteq \mathbf {G}^{-\top } \mathbf {N}\), the pseudo-normals, and \(\hat{\mathbf {L}} \doteq \mathbf {G} \mathbf {L}\), the pseudo-lights. An initial pair \((\hat{\mathbf {N}},\hat{\mathbf {L}})\) can be computed with the algorithm of Yuille and Snow (1997). Our task is to find \(\hat{\lambda }\), \(\hat{\mu }\), and \(\hat{\nu }\) such that \(\hat{\mathbf {G}}^\top \hat{\mathbf {N}} = \mathbf {N}\) and \(\hat{\mathbf {G}}^{-1} \hat{\mathbf {L}} = \mathbf {L}\) where

$$\begin{aligned} \hat{\mathbf {G}}^\top = \left[ \begin{array}{lll} 1 &{} 0 &{} \hat{\mu }\\ 0 &{} 1 &{} \hat{\nu }\\ 0 &{} 0 &{} \hat{\lambda }\end{array} \right]&\quad {\text{ and }} \quad \hat{\mathbf {G}}^{-1}= \left[ \!\!\!\begin{array}{lll} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ -\frac{\hat{\mu }}{\hat{\lambda }} &{} -\frac{\hat{\nu }}{\hat{\lambda }} &{} \frac{1}{\hat{\lambda }} \end{array} \right] . \end{aligned}$$
(5)

5 Reconstruction Consistency

As mentioned in the introduction and in the discussion on prior work, the main unsolved challenge in uncalibrated photometric stereo is that most proposed solutions do not yield a unique estimate for the normal matrix. In this section we define this issue more formally and show how it can be addressed.

Given the pseudo-normals \(\hat{\mathbf {N}}\) and a GBR solution \(\hat{\mu }\), \(\hat{\nu }\) and \(\hat{\lambda }\), the reconstructed normal matrix \(\tilde{\mathbf {N}}\) can be written as follows

$$\begin{aligned}&\tilde{\mathbf {N}} = \hat{\mathbf {G}}^\top \mathbf {G}^{-\top } \mathbf {N} = \left[ \begin{array}{rrr} 1 &{} 0 &{} \hat{\mu }\\ 0 &{} 1 &{} \hat{\nu }\\ 0 &{} 0 &{} \hat{\lambda }\end{array} \right] \left[ \!\!\!\begin{array}{llr} 1 &{} 0 &{} -\frac{\mu }{\lambda } \\ 0 &{} 1 &{} -\frac{\nu }{\lambda } \\ 0 &{} 0 &{} \frac{1}{\lambda } \end{array} \right] \qquad \quad \quad \quad \nonumber \\&\mathbf {N} = \left[ \!\!\!\begin{array}{lll} 1 &{} 0 &{} \frac{\hat{\mu }-\mu }{\lambda } \\ 0 &{} 1 &{} \frac{\hat{\nu }-\nu }{\lambda } \\ 0 &{} 0 &{} \frac{\hat{\lambda }}{\lambda } \end{array} \right] \mathbf {N}.\qquad \quad \quad \quad \end{aligned}$$
(6)

When the estimated GBR parameters match the true ones, the vector \([\frac{\hat{\mu }-\mu }{\lambda }~\frac{\hat{\nu }-\nu }{\lambda }~\frac{\hat{\lambda }}{\lambda }]^\top \) is equal to \([0~0~1]^\top \) and \(\tilde{\mathbf {N}} = \mathbf {N}\). In general, however, we might have some error in our estimate of the parameters. Let us define such error as

$$\begin{aligned} \eta = \begin{bmatrix}\frac{\hat{\mu }-\mu }{\lambda }\\ \frac{\hat{\nu }-\nu }{\lambda }\\ \frac{\hat{\lambda }}{\lambda }\end{bmatrix} - \begin{bmatrix} 0\\0\\1 \end{bmatrix} = \frac{1}{\lambda }\begin{bmatrix}\hat{\mu }-\mu \\ \hat{\nu }-\nu \\ \hat{\lambda }-\lambda \end{bmatrix}. \end{aligned}$$
(7)

Current algorithms return an error vector \(\mathbf {\eta }\) that depends on the true GBR parameters \(\mu ,\,\nu \), and \(\lambda \). Hence, for any pseudo-normal \(\hat{\mathbf {N}}\) one obtains a different \(\tilde{\mathbf {N}}\) estimate. This is a highly undesirable behavior of a UPS algorithm, and to obtain a stable result, the current strategy is to average several estimates obtained with different pseudo-normals. The implicit assumption is that the error \(\mathbf {\eta }\) is zero-mean. Current published results on real data (Alldrin et al. 2007; Shi et al. 2010), however, show relatively large average angular errors, which indicate that these assumptions are unfounded.

We therefore argue that one should only introduce constraints that result in estimates that do not change with the GBR parameters. We formalize this in the next definition.

Definition 1

Given a pseudo-normals and pseudo-lights pair \((\hat{\mathbf {N}},\hat{\mathbf {L}})\), we define a constraint on \(\hat{\mu },\,\hat{\nu }\) and \(\hat{\lambda }\), to be GBR-consistent when the error \(\mathbf {\eta }\) is independent of the true parameters \(\mu ,\,\nu \), and \(\lambda \).

The next question is then: Given the pseudo-normals and the pseudo-lights, what type of GBR-consistent constraints in the estimated GBR parameters can one devise? In general, an algorithm will introduce \(M\) constraints that can be written as

$$\begin{aligned} f_j(\hat{\mu },\hat{\nu },\hat{\lambda },\hat{\mathbf {N}},\hat{\mathbf {L}}) = 0 \quad \quad \forall j=1,\ldots ,M. \end{aligned}$$
(8)

We can then see how the constraints depend on the true GBR parameters by explicitly writing the pseudo-normals at a pixel \(p\) and the pseudo-lights in the \(k\)-th image as

$$\begin{aligned} \begin{array}{ll} \begin{bmatrix} \hat{n}_{1,p}\\ \hat{n}_{2,p}\\ \hat{n}_{3,p} \end{bmatrix} =&{} \begin{bmatrix} n_{1,p}-\frac{\mu }{\lambda }n_{3,p}\\ n_{2,p}-\frac{\nu }{\lambda }n_{3,p} \\ \frac{n_{3,p}}{\lambda } \end{bmatrix}\\ \\ \begin{bmatrix} \hat{l}_{1,k}\\ \hat{l}_{2,k}\\ \hat{l}_{3,k} \end{bmatrix} =&{} \begin{bmatrix} l_{1,k}\\ l_{2,k}\\ \mu l_{1,k} +\nu l_{2,k} +\lambda l_{3,k} \end{bmatrix}. \end{array} \end{aligned}$$
(9)

Then, according to the GBR-consistency definition, it must be possible to write the constraints such that the estimates \(\hat{\mu }\), \(\hat{\nu }\), and \(\hat{\lambda }\) are in the form

$$\begin{aligned} \hat{\mu }&= \mu + \lambda \eta _1\end{aligned}$$
(10)
$$\begin{aligned} \hat{\nu }&= \nu + \lambda \eta _2\end{aligned}$$
(11)
$$\begin{aligned} \hat{\lambda }&= \lambda (1+\eta _3) \end{aligned}$$
(12)

where \(\mathbf {\eta } = [\eta _1~\eta _2~\eta _3]^\top \) and \(\nabla _{\mu ,\nu ,\lambda }\mathbf {\eta }=\mathbf {0}\) (i.e., the error is independent of the true GBR parameters). Therefore, we can conclude that the constraints will be GBR-consistent if there exists an \(\mathbf {\eta }\) such that for any \(\mu ,\nu \), and \(\lambda \), and \(\forall j=1,\ldots ,M\)

$$\begin{aligned} f_j\Bigg (&\mu + \lambda \eta _1,\nu + \lambda \eta _2,\lambda (1+\eta _3),\nonumber \\&\left\{ n_{1,p}-\frac{\mu }{\lambda }n_{3,p}, n_{2,p}-\frac{\nu }{\lambda }n_{3,p}, \frac{n_{3,p}}{\lambda }\right\} _{p=1,\ldots ,P},\\&\left\{ l_{1,k}, l_{2,k}, \mu l_{1,k} +\nu l_{2,k} +\lambda l_{3,k}\right\} _{k=1,\ldots ,K}\Bigg ) = 0.\nonumber \end{aligned}$$
(13)

We will show in the next sections that the constraints based on LDR maxima are indeed GBR-consistent. However, as an illustration of the analysis presented so far, let us introduce a simple example of a GBR-consistent constraint. Suppose that a novel algorithm for UPS can reliably detect a pixel \(p\) where the true normal is \([0~0~-1]^\top \). Then, one could devise the constraint

$$\begin{aligned} f(\hat{\mu },\hat{\nu },\hat{\lambda },\hat{\mathbf {N}},\hat{\mathbf {L}}) = \frac{\hat{\mu }}{\hat{\lambda }}-\hat{n}_{1,p} = 0 \end{aligned}$$
(14)

i.e., that \(\hat{\mu }\) and \(\hat{\lambda }\) are linearly related through \(\hat{n}_{1,p}\). By substituting the expression of \(\hat{\mu }\) and \(\hat{\lambda }\) and \(\hat{n}_{1,p}\) above, one obtains

$$\begin{aligned} \frac{\mu }{\lambda (1+\eta _3)}+ \frac{\eta _1}{1+\eta _3}-n_{1,p} + \frac{\mu }{\lambda }n_{3,p} = 0 \end{aligned}$$
(15)

which is verified for any \(\lambda \) and \(\mu \) with error \(\eta _1 = -n_{1,p}/n_{3,p}\) and \(\eta _3 = -1-1/n_{3,p}\). Finally, notice that the estimators would achieve \(\mathbf {\eta } = \mathbf {0}\) because \(\mathbf {n}_{p}=[0~0~-1]^\top \). Of course, this example is not sufficient to uniquely determine all the GBR parameters and also it is not clear how one can detect such pixels directly from images. Indeed, this shows how the design of an algorithm that is feasible, robust, and satisfying the GBR-consistency, is challenging.

6 Lambertian Diffuse Reflectance Maxima

We assume that the scene contains curved objects such that there exists a nonempty set \({\fancyscript{S}}_{k}\) of spatial maxima (where “spatial” refers to the image domain) of the inner product \(\langle \mathbf {n}_{p},\mathbf {l}_{k}\rangle \), for a given \(k\)-th illumination. Geometrically, we assume that there exist points in the scene where both principal curvatures are positive. We call such points Lambertian diffuse reflectance maxima. Notice that we have a maximum only when \(\mathbf {n}_{p}\) and \(\mathbf {l}_{k}\) point in the same direction. Since both vectors are unit-normal, they must also coincide.

In the next sections we introduce the LDR maxima constraints. We first impose them by looking for the maximum of the inner product between normals and lights (see Sect. 6.1). Then, we show that this formulation fully represents all the constraints by carrying out analysis imposing that at LDR maxima normals and lights must be parallel (see Sect. 6.2). Our proof is based on the fact that both approaches yield the same set of solutions (i.e., semi-circles), albeit through different calculations.

6.1 A Closed-Form Solution

For each \(k\), an LDR maximum at \(p\in {\fancyscript{S}}_{k}\) constrains the GBR ambiguity to the following set

$$\begin{aligned} (\tilde{\mu },\tilde{\nu },\tilde{\lambda }) \in \arg \max _{\hat{\mu },\hat{\nu },\hat{\lambda }} \left\langle \frac{\hat{\mathbf {G}}^\top \hat{\mathbf {N}}_{p}}{\Vert \hat{\mathbf {G}}^\top \hat{\mathbf {N}}_{p}\Vert }, \frac{\hat{\mathbf {G}}^{-1} \hat{\mathbf {L}}_{k}}{\Vert \hat{\mathbf {G}}^{-1} \hat{\mathbf {L}}_{k}\Vert } \right\rangle . \end{aligned}$$
(16)

Notice the use of the symbol \(\in \), as the solution of the above maximization problem is not unique given a single LDR maximum. The entire set of solutions can be fully characterized in closed-form. First, by using \(I_{p,k} = \langle \hat{\mathbf {G}}^\top \hat{\mathbf {N}}_{p}, \hat{\mathbf {G}}^{-1} \hat{\mathbf {L}}_{k}\rangle \), let us rewrite the above problem as

$$\begin{aligned} (\tilde{\mu },\tilde{\nu },\tilde{\lambda }) \in \arg \min _{\hat{\mu },\hat{\nu },\hat{\lambda }} \Vert \hat{\mathbf {G}}^\top \hat{\mathbf {N}}_{p}\Vert \Vert \hat{\mathbf {G}}^{-1} \hat{\mathbf {L}}_{k}\Vert . \end{aligned}$$
(17)

Next, we are ready to state the main result in this manuscript:

Theorem 1

The set of minima

$$\begin{aligned} (\mu ,\nu ,\lambda ) \in \arg \min _{\hat{\mu },\hat{\nu },\hat{\lambda }} \Vert \hat{\mathbf {G}}^\top \hat{\mathbf {N}}_{p}\Vert \Vert \hat{\mathbf {G}}^{-1} \hat{\mathbf {L}}_{k}\Vert ,\quad \forall p\in {\fancyscript{S}}_{k} \end{aligned}$$
(18)

lies on a segment between the 2-D points \([\mu _{0}~\nu _{0}]^\top \) and \([\mu _{1}~\nu _{1}]^\top \), where

$$\begin{aligned} \begin{array}{llr} \mu _{0} &{}=\mu _{1}+ \frac{\hat{l}_{1,k}}{\sqrt{\hat{l}_{1,k}^{2}+\hat{l}_{2,k}^{2}}} \theta &{}\quad \quad \quad \quad \quad \mu _{1} = -\frac{\hat{n}_{1,p}}{\hat{n}_{3,p}}\\ \nu _{0} &{}= \nu _{1}+ \frac{\hat{l}_{2,k}}{\sqrt{\hat{l}_{1,k}^{2}+\hat{l}_{2,k}^{2}}} \theta &{} \quad \quad \quad \quad \quad \nu _{1} = -\frac{\hat{n}_{2,p}}{\hat{n}_{3,p}}\\ \theta &{}= \frac{\hat{\mathbf {N}}_{p}^\top \hat{\mathbf {L}}_{k}}{\hat{n}_{3,p}\sqrt{\hat{l}_{1,k}^{2}+\hat{l}_{2,k}^{2}}}&{} \end{array} \end{aligned}$$
(19)

and we defined \(\hat{\mathbf {L}}_{k} = [\hat{l}_{1,k}~\hat{l}_{2,k}~\hat{l}_{3,k}]^\top \) and \(\hat{\mathbf {N}}_{p}=[\hat{n}_{1,p}~\hat{n}_{2,p}~\hat{n}_{3,p}]^\top \). Given a 2-D point \([\hat{\mu }~\hat{\nu }]^\top = [\mu _{0}~\nu _{0}]^\top +(1-\alpha )([\mu _{1}~\nu _{1}]^\top -[\mu _{0}~\nu _{0}]^\top )\) onto the segment, where \(\alpha \in [0,1]\), the third GBR parameter is uniquely determined via

$$\begin{aligned} \textstyle \hat{\lambda }= \sqrt{\alpha (1-\alpha )}|\theta | \end{aligned}$$
(20)

and the trajectory of the 3-D point \([\hat{\mu }~\hat{\nu }~\hat{\lambda }]^\top \) in the parameter \(\alpha \in [0,1]\) forms a semi-circle of diameter \(|\theta |\).

Proof

See Appendix. \(\square \)

The next result tells us how many LDR maxima we need to solve the GBR ambiguity.

Lemma 1

If two Lambertian diffuse reflectance maxima correspond to two different pseudo-normals \(\hat{n}_{p_a}\) and \(\hat{n}_{p_b}\) with

$$\begin{aligned} \frac{\hat{n}_{1,p_{a}}}{\hat{n}_{2,p_{a}}}\ne \frac{\hat{n}_{1,p_{b}}}{\hat{n}_{2,p_{b}}}. \end{aligned}$$
(21)

then there exists a unique solution in the GBR parameters.

Proof

See Appendix. \(\square \)

To illustrate the results, we show in Figs. 2 and 3 how LDR maxima constrain the GBR parameters segments in the \((\mu ,\nu )\) plane and to semi-circles in the \((\mu ,\nu ,\lambda )\) space. All segments or semi-circles intersect at the same point, which corresponds to the correct solution.

Fig. 3
figure 3

GBR ambiguity solved via LDR constraints. Each segment is the set of solutions in the parameters \(\tilde{\mu }\) and \(\tilde{\nu }\) for one LDR maximum. Segments must intersect at the correct GBR solution

Full size image

Next, we prove a remarkable property of LDR maxima: The GBR parameters obtained from the LDR maxima are GBR consistent. In practice, this means that our method yields the same solution every time it is run, unlike competing methods (see Sect. 7).

Proposition 1

The constraints on the GBR parameters introduced by an LDR maximum are GBR-consistent.

Proof

See Appendix. \(\square \)

6.2 Using Pseudo-Normals as Pseudo-Lights

In the previous section, given an LDR we have defined a single equation based on the inner product between a normal vector and a light. However, from the definition of LDR one can derive up to \(3\) equations in \(4\) unknowns. The question is then of whether LDRs carry any extra constraint in the GBR solution beyond what has been already presented in Theorem 1. As we will find out, the answer is negative: All the constraints of an LDR point are fully captured in Theorem 1.

Suppose that the set \({\fancyscript{S}}_{k}\) is given and that one is also given \(\hat{\mathbf {N}} = \mathbf {G}^{-T} \mathbf {N}\), the pseudo-normals, and \(\hat{\mathbf {L}} = \mathbf {G} \mathbf {L}\), the pseudo-lights. We now impose that the LDR constraint corresponds to having \(\mathbf {N}_{p}\) parallel to \(\mathbf {L}_{k}\) when \(p\in {\fancyscript{S}}_{k}\):

$$\begin{aligned} \frac{\hat{\mathbf {G}}^\top \hat{\mathbf {N}}_{p}}{\Vert \hat{\mathbf {G}}^\top \hat{\mathbf {N}}_{p}\Vert }= \frac{\hat{\mathbf {G}}^{-1} \hat{\mathbf {L}}_{k}}{\Vert \hat{\mathbf {G}}^{-1} \hat{\mathbf {L}}_{k}\Vert }. \end{aligned}$$
(22)

We can write the above equation as

$$\begin{aligned} c_{p,k}\hat{\mathbf {L}}_k =\hat{\mathbf {G}}\hat{\mathbf {G}}^\top \hat{\mathbf {N}}_{p} \end{aligned}$$
(23)

where \(c_{p,k} =\frac{\Vert \hat{\mathbf {G}}^\top \hat{\mathbf {N}}_{p}\Vert }{\Vert \hat{\mathbf {G}}^{-1} \hat{\mathbf {L}_{k}}\Vert }\). Notice that although the scalar \(c_{p,k}\) depends on the GBR parameters, it also depends on the (unknown) albedo and (unknown) light intensity. Therefore, it can be considered as a free variable. Then, we can finally solve these equations in the \(4\) unknowns \(\hat{\mu },\,\hat{\nu },\,\hat{\lambda }\), and \(c_{p,k}\).

One can verify that these equations are satisfied by the solution in Theorem 1 for any \(\alpha \in [0,1]\) with

$$\begin{aligned} c_{p,k} = \alpha \frac{\theta n_3}{\sqrt{\hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}}}. \end{aligned}$$
(24)

Hence, Eq. (22) does not provide any additional constraints to the solution in Theorem 1.

6.3 Existence of LDR Maxima

One may wonder whether LDR maxima are commonly found in images. Indeed, surfaces that do not generate LDR maxima do exist. These are surfaces whose normals are never parallel to any light direction; for example, this can easily occur with slopes or cylinders. In these cases it is not possible to detect LDR maxima reliably. Similarly, more general surfaces can also have no LDR maxima. However, in practice this is rarely a problem for general surfaces of interest with a sufficiently uniform sampling of illumination directions. Indeed, we experimentally find an average of \(251\) LDR maxima per dataset, among those used in Sect. 7. These statistics are very favorable as only \(2\) LDR maxima are sufficient to solve UPS.

6.4 Detection and Localization of LDR Maxima

In this section we describe a procedure to detect LDR maxima. The main idea is that we can do so by detecting local intensity maxima. In general, however, intensity maxima do not correspond to LDR maxima. In fact, detection of the maxima of \(I_{p,k}\) requires

$$\begin{aligned} \nabla I_{p,k} = \nabla \rho _{p}\mathbf {N}_{p}^\top \mathbf {l}_{k} e_{k} +\rho _{p}\nabla \mathbf {N}_{p}^\top \mathbf {l}_{k} e_{k}=0, \end{aligned}$$
(25)

while the LDR maxima are determined by

$$\begin{aligned} \nabla \mathbf {N}_{p}^\top \mathbf {l}_{k} =0. \end{aligned}$$
(26)

Thus, even small variations of the albedo could result in a displacement of the detected maximum. However, we show that an LDR maximum can be found within a small disc around the detected intensity maximum, whose radius \(\Delta \) depends on the albedo gradient magnitude and the curvature of the surface.

We approximate the surface of the object around an intensity maximum with a hemisphere. Let

$$\begin{aligned} \mathbf {P} \doteq [p_{1}~p_{2}~\sqrt{R^{2}-p_{1}^{2}-p_{2}^{2}}]^\top \in \mathbb {R}^{3}, \end{aligned}$$
(27)

with \(p_{1}^{2}+p_{2}^{2} \le R^{2}\), be a point on the hemisphere with radius \(R\in \mathbb {R}_{+}\). If a pixel index \(p\) corresponds to the pixel coordinates \([p_{1}~p_{2}]^\top \), then the normals to this surface region can be directly defined as \(\mathbf {N}_{p} = \mathbf {P}/\Vert \mathbf {P}\Vert \). Notice that in this case the correct LDR maximum lies at the pixel coordinates \(R[l_{1,k}~l_{2,k}]^\top \). If \([p_{1}~p_{2}]^\top \) denotes the detected intensity maximum, we are interested in finding an estimate of the disc radius \(\Delta \) via the distance

$$\begin{aligned} \Delta = \left\| R\begin{bmatrix} l_{1,k}\\ l_{2,k} \end{bmatrix} - \begin{bmatrix} p_{1}\\ p_{2} \end{bmatrix} \right\| . \end{aligned}$$
(28)

Suppose that the surface is Lambertian and we capture an image with illumination direction \(\mathbf {l}_{k}\), where \(l_{3,k}>0\), then the measured intensity is \(I_{p,k} = \rho _{p}\left\langle \mathbf {P}/\Vert \mathbf {P}\Vert ,\mathbf {l}_{k}\right\rangle e_{k}.\) Detection of the maxima of \(I_{p,k}\) requires

$$\begin{aligned} \nabla I_{p,k} = \nabla \rho _{p}\frac{\mathbf {P}^\top \mathbf {l}_{k}}{\Vert \mathbf {P}\Vert } e_{k} +\rho _{p}\frac{\nabla \mathbf {P}^\top }{\Vert \mathbf {P}\Vert }\left( \mathbf {I_{d}} - \frac{\mathbf {P}\mathbf {P}^\top }{\Vert \mathbf {P}\Vert }\right) \mathbf {l}_{k} e_{k}=0 \end{aligned}$$
(29)

where \(\mathbf {I_{d}}\) denotes the identity matrix. Notice that since

$$\begin{aligned} \nabla \mathbf {P}^\top = \begin{bmatrix} 1&0&-\frac{p_{1}}{\sqrt{R^{2}-p_{1}^{2}-p_{2}^{2}}}\\ 0&1&-\frac{p_{2}}{\sqrt{R^{2}-p_{1}^{2}-p_{2}^{2}}} \end{bmatrix} \end{aligned}$$
(30)

we have \(\nabla \mathbf {P}^\top \mathbf {P} = \mathbf {0}\), which, combined with Eq. (25), yields the constraint

$$\begin{aligned} \nabla \rho _{p}\mathbf {P}^\top \mathbf {l}_{k} +\rho _{p}\nabla \mathbf {P}^\top \mathbf {l}_{k}=0. \end{aligned}$$
(31)

Assume that the ratio between the albedo gradient and the albedo magnitude is bound by a constant \(B>0\), i.e., \(\left\| \frac{\nabla \rho _{p}}{\rho _{p}}\right\| \le B\). Then, we can write

$$\begin{aligned} \left\| \nabla \mathbf {P}^\top \mathbf {l}_{k}\right\| =\left\| \frac{\nabla \rho _{p}}{\rho _{p}}\mathbf {P}^\top \mathbf {l}_{k}\right\| \le \left\| R\frac{\nabla \rho _{p}}{\rho _{p}}\right\| \le B R, \end{aligned}$$
(32)

where we used the identity \(\Vert \mathbf {P}\Vert =R\). Finally, we obtain

$$\begin{aligned} \left\| \begin{bmatrix} l_{1,k}\\ l_{2,k} \end{bmatrix} - \begin{bmatrix} p_{1}\\ p_{2} \end{bmatrix} \frac{l_{3,k}}{\sqrt{R^{2}-p_{1}^{2}-p_{2}^{2}}}\right\| \le B R. \end{aligned}$$
(33)

For a reliable detection and localization we consider LDR maxima that are not too far off the detected maxima. This means that locally, we can approximate \(\mathbf {P}\) with the hemisphere tangent plane at \(R\mathbf {L}_{k}\). This means that

$$\begin{aligned} \sqrt{R^{2}-p_{1}^{2}-p_{2}^{2}}\simeq R l_{3,k} \end{aligned}$$
(34)

and we obtain

$$\begin{aligned} \Delta = \left\| R\begin{bmatrix} l_{1,k}\\ l_{2,k} \end{bmatrix} - \begin{bmatrix} p_{1}\\ p_{2} \end{bmatrix} \right\| \le B R^{2}. \end{aligned}$$
(35)

Therefore, the correct localization of LDR maxima will be a tradeoff between the curvature of the local surface and the albedo gradient: Surfaces with high curvature can tolerate high albedo gradients and, vice versa, surfaces with small curvature can tolerate little albedo variation. We experimentally find that \(\Delta = 1\) is a good tradeoff.

As done in Lagger and Fua (2008), we improve the selection of LDR maxima by discarding maxima that appear at the same spatial location under different illuminations (two are sufficient to decide) as they are most likely generated by the albedo texture. Third, we discard maxima with low pixel intensities, e.g., maxima from the \(k\)-th input image with intensity less than \((\max _{p}{I_{p,k}}-\min _{p}{I_{p,k}})/2\). We experimentally found that such maxima tend to be less reliable than those with high intensity.

6.5 Dealing with Outliers

In practice, the sets \(\{{\fancyscript{S}}_{k}\}_{k=1,\ldots ,K}\) contain many outliers. We take outliers into account by using a robust estimation procedure.

To simplify the notation, let us define \(\mathbf {y} \doteq [\mu ~\nu ~\lambda ]^\top \), the vector of GBR parameters. Let \(S\) be the sum of the cardinalities of the sets \(\{{\fancyscript{S}}_{k}\}_{k=1,\ldots ,K}\). Also, let \(\{\mathbf {y}_{i}\}_{i=1,\ldots ,S(S-1)/2}\) be the set of all the intersections between any two semi-circles defined by two detected maxima lying in one of the sets \(\{{\fancyscript{S}}_{k}\}_{k=1,\ldots ,K}\). We consider the intersections \(\{\mathbf {y}_{i}\}_{i=1,\ldots ,S(S-1)/2}\) as samples of a random variable \(\mathbf {Y}\) defining the GBR parameters. We can obtain an approximation to the distribution \(\mathbf {f}_{\mathbf {Y}}\) of the random variable \(\mathbf {Y}\) via the empirical distribution

$$\begin{aligned} \mathbf {f}_{\mathbf {Y}}(\mathbf {y}) \simeq \frac{2}{S(S-1)}\sum _{i=1}^{\frac{S(S-1)}{2}} \delta \left( \mathbf {y}-\mathbf {y}_{i} \right) . \end{aligned}$$
(36)

Then, the GBR parameters can be chosen as the median \(\bar{\mathbf {y}}\) of the empirical distribution, i.e.,

$$\begin{aligned} (\tilde{\mu },\tilde{\nu },\tilde{\lambda }) \equiv \bar{\mathbf {y}} = \arg \min _{\hat{\mathbf {y}}} \mathbf {E}_{\mathbf {f}_{\mathbf {Y}}}\left[ \left| \hat{\mathbf {y}}- \mathbf {y}\right| \right] \end{aligned}$$
(37)

where \(\mathbf {E}_{\mathbf {f}_{\mathbf {Y}}}\) denotes the expectation with respect to the distribution \(\mathbf {f}_{\mathbf {Y}}\). This formalization makes it possible to further improve this outlier rejection method by using other approximations for \(\mathbf {f}_{\mathbf {Y}}\) (for example, with a Kernel density estimator).

Remark 1

As we have seen in the previous section, the localization of an LDR maximum via a local brightness maximum is affected by the albedo of the surface. However, as long as the albedo introduces a small random error, the likelihood of distinguishing the correct LDRs via the median is high. That is because with high likelihood only the correct detected LDR maxima will agree on the same correct GBR solution. It is however possible to find albedos that introduce a non-random error leading to agreement on an incorrect GBR solution. Fortunately, although these cases are possible, they are extremely rare: Such albedos must be a function of the normal components so as to consistently introduce the same error at corresponding normals. One artificial example of such albedos can be built by taking the ratio between two images captured under different illumination (see right image in Fig. 4). In this case the albedo becomes the inverse of a linear combination of the normals. Let us briefly analyze the ratio of two images \(k\) and \(i\). The detection of LDR maxima on these “image ratios” relies on the brightness maxima, which can be found at pixels \(p\) where

Fig. 4
figure 4

Detected image brightness maxima are shown as green dots. The image regions where the normals are almost parallel to the light direction are shown in red. We show the detection of LDR maxima in the original image (left) and in the ratio image (right). Notice that as the albedo is no longer independent of the normal map, the ratio may cause the LDR maxima to vote with strong consensus for one or many incorrect GBR solutions. In this illustration the detected LDR maxima in the ratio image (right) are quite far from the correct ones (Color figure online)

Full size image
$$\begin{aligned} \nabla \left( \frac{I_{p,k}}{I_{p,i}}\right) =\nabla \left( \frac{\mathbf {N}_{p}^\top \mathbf {l}_{k} e_{k}}{\mathbf {N}_{p}^\top \mathbf {l}_{i} e_{i}}\right) =0 \Rightarrow \frac{\nabla \mathbf {N}_{p}^\top \mathbf {l}_{k}}{\mathbf {N}_{p}^\top \mathbf {l}_{k}}=\frac{\nabla \mathbf {N}_{p}^\top \mathbf {l}_{i}}{\mathbf {N}_{p}^\top \mathbf {l}_{i}}. \end{aligned}$$
(38)

Notice that LDR maxima would instead require \(\nabla \mathbf {N}_{p}^\top \mathbf {l}_{k}=0\), but the above equation may instead impose that \(\nabla \mathbf {N}_{p}^\top \mathbf {l}_{k}\ne 0\) as LDR maxima are typically not shared across different input images.

6.6 Robustness

Because the proposed algorithm can compute the GBR parameters very efficiently, we can evaluate how well it can tolerate several levels of outliers and errors in the detected LDR maxima. We show that the algorithm can tolerate very high levels of outliers, while it is more sensitive to persistent misalignments between normals and lights. We synthetically generate a set of \(K=12\) light directions. Then, we generate \(P=500\) maxima by matching each normal to one of the light directions. With reference to Fig. 5, to simulate outliers in the detected LDR maxima, we corrupt outliers ratio normals every \(100\) normals. To simulate errors in the detected LDR maxima, we add to all the normals uniform noise in the range uniform noise ratio \(\times [-0.1~+~0.1]\) (notice that the normals have magnitude equal to \(1\)). Uniform noise corresponds to persistent misalignment. The performance is computed as the relative error \(\epsilon = \frac{\Vert \mathbf {y}-\bar{\mathbf {y}}\Vert _{2}}{\Vert \mathbf {y}\Vert _{2}}\), where \(\mathbf {y}\) is the correct vector of GBR parameters and \(\bar{\mathbf {y}}\) the estimated one. In Fig. 5 we show the results for several outlier and noise ratios. To ease visualization we smooth the error map and then quantize it. The outlier ratio is shown in the abscissa and ranges from \(0\,\%\) (left) to \(100\,\%\) (right). Similarly, the uniform noise ratio is shown in the ordinate axis and ranges from \(0\,\%\) (bottom) to \(100\,\%\) (top). Notice that the darkest region (bottom-left) denotes no more than \(0.3\,\%\) relative error and it allows up to \(75\,\%\) outliers even when the remaining \(25\,\%\) of the maxima have around \(10\,\%\) uniform additive noise.

Fig. 5
figure 5

Color coding of the estimation error against outliers and noise ratios. Error levels are shown with solid green lines and the corresponding values are indicated in the cyan box (Color figure online)

Full size image

7 Experiments

To validate our method we use nine real object datasets: Redfish and Octopus of 5 images each (courtesy of Neil AlldrinFootnote 3); Cat, Buddha, Owl, Horse and Rock of 12 images each (courtesy of Dan Goldman and Steven SeitzFootnote 4); Puppet of 15 images taken in our lab with a Canon 5D Mark II; Face of 64 images (Yale Face Database (Georghiades et al. 2001)). All the experiments were run with Matlab on a Mac (2.66 GHz CPU, Intel Core Duo) platform.

7.1 Image Acquisition of the Puppet

To take the photos of the Puppet, we used a Canon 5D Mark II camera and a \(30\)-watt incandescent light source attached on a tripod. We placed the light source in \(15\) different positions (far enough from the object in order to satisfy the distant point light source assumption) and took three photos for each position. The three photos were then averaged to reduce noise. Ambient image subtraction was also performed. Because the light source has constant intensity, we scaled each image with a random scalar between 0.5 and 1.5 (this was done for the face dataset as well). An object mask was also created by simple thresholding.

7.2 Image Pre-processing

Equation (2) dictates that the intensity matrix \(\mathbf {I}\) should have rank \(3\). Because real world data are affected by noise, shadows, specularities and other non/Lambertian effects, the rank will be different, typically bigger, than \(3\). Hence, we perform a pre-processing step based on a recent convex optimization approach (Lin et al. 2009; Wu et al. 2011) that recovers the low-rank intensity matrix without having any information about what entries are corrupted:

$$\begin{aligned} \min _{\mathbf {A},\mathbf {E}} ||\mathbf {A}||_{*} + \gamma ||\mathbf {E}||_{1} \quad s.t \quad \mathbf {I}=\mathbf {A}+\mathbf {E} \end{aligned}$$
(39)

where \(\mathbf {A}\) is the noise-free low-rank data and \(\mathbf {E}\) is a sparse matrix with the outliers. \(||\cdot ||_{*}\) and \(|| \cdot ||_{1}\) denote the nuclear and \(L^{1}\) norm respectively. \(\gamma >0\) is a weighting parameter that defines the amount of outliers in the data. This parameter depends on the input images and, as suggested in Wright et al. (2009), we fix it to \(\gamma =\frac{\kappa }{\sqrt{P}}\) where \(\kappa \) is a constant and \(P\) is the total number of pixels of a single input image. We fixed \(\kappa =1.7\) for all datasets having at least \(12\) images and \(\kappa =3\) for the others. Figure 6 shows how the pre-processing algorithm removes shadows and specularities in the case of the Face dataset.

Fig. 6
figure 6

Removal of non Lambertian effects. On the left we show one of the input images. In the middle image we show the detected non Lambertian components (shadows and specularities) via the low-rank matrix recovery pre-processing step. Finally, on the right image we show the low-rank and noise-free data used in our algorithm

Full size image

7.3 Implementation Details

We impose the integrability constraint as described in Yuille and Snow (1997) and the surface pseudo-normals \(\hat{\mathbf {N}}\) and pseudo-lights \(\hat{\mathbf {L}}\) are obtained up to the GBR ambiguity. The initial group of all the LDR maxima is detected by using the built-in Matlab function “imregionalmax” after applying a small Gaussian smoothing to all the input images. This function gives as output a set of single pixels for each image corresponding to the intensity local maxima. As described in Sect. 6.4 we select as local maxima all pixels in a disc neighborhood of radius \(1\) pixel. Then, we discard all local maxima that appear (at least twice) at the same spatial location for different illumination conditions and those that have low intensity values.

7.4 Results

Because no ground truth data is available for these datasets, we consider as ground truth for the normal maps the ones obtained from the calibrated photometric stereo method. We compare our experimental results with the state-of-the-art in uncalibrated photometric stereo (Shi et al. 2010; Alldrin et al. 2007). For the accuracy evaluation we consider the mean angular error of the estimated normals with respect to the calibrated case. In Table 1 we show the performance comparison of all methods in the case of datasets with \(12\) input images (top) and in the case of datasets with \(5\) and \(15\) input images (bottom). Notice that \(\sigma < 10^{-12}\) in all the reconstructions via LDR maxima as predicted by our analysis (see Proposition 1). Since our method provides a GBR-consistent solution, we always get the same estimate no matter what pseudo-normals and pseudo-lights we start from. This is a major advantage over prior work.

Table 1 Performance comparison with the entropy minimization (EM) method (Alldrin et al. 2007) and the self calibrating photometric stereo (SCPS) method (Shi et al. 2010)
Full size table

Figure 7 shows the comparison of the obtained normal and depth maps for the methods (Shi et al. 2010; Alldrin et al. 2007) in the case of the Buddha dataset. The depth map is obtained by integrating the normal map with a Poisson solver (Agrawal and Raskar 2006). Figure 8 shows all the depth maps obtained by our method across all the datasets (bottom row) and the depth maps obtained from the calibrated photometric stereo method (middle row).

Fig. 7
figure 7

Comparison of reconstructed normal and depth maps. From left to right, each column corresponds to the first (x axis), second (y axis), and third (z axis) components of the normal map n and the depth map, respectively. We show the results obtained from the calibrated photometric stereo method (top row), the results obtained from our method (second row), the results obtained from the entropy minimization method (third row) and the results obtained from the SCPS method (bottom row)

Full size image
Fig. 8
figure 8

Reconstructed depth maps. One of the input images (top row). Graylevel-coded depth map reconstructed with calibrated photometric stereo (middle row). Graylevel-coded depth map obtained with our method (bottom row)

Full size image

All datasets yield visually reasonable surface reconstructions. However, in the Owl dataset one might notice an artifact (a spike) of the reconstructed surface on the left eye. This artifact is caused by specular highlights (probably because the eye is made of glass) that were not removed by the preprocessing step. Notice that this artifact is present also in the calibrated reconstruction. One possible explanation for the failure of the preprocessing algorithm (Lin et al. 2009; Wu et al. 2011) is that the outliers in this case have very low intensities that can be confused with small Gaussian noise. In Fig. 9 we show an enlargement of that region in one of the input images. To demonstrate that outliers are the cause of the artifact, we mask out these pixels (by using some simple thresholding) before reconstructing the surface. In Fig. 9 one can also see the comparison of the surface reconstruction around the eye with and without outliers. The reconstruction without outliers is much smoother and looks qualitatively correct.

Fig. 9
figure 9

On the top we show one of the input images of the Owl dataset. In red we show the selected patch. In the second row—left image we show the selected patch where some outliers are visible inside the pupil. In the second row—right image we show the reconstructed depth map without outlier rejection. Notice that the outliers cause sharp discontinuities in the depth map. In the bottom—left image we show the detected specular highlights (simple thresholding based on the standard deviation across different illumination settings). Finally in the bottom—right image we show the reconstructed depth map after rejection of the detected specular highlights. Notice that, unlike in the previous case, the recovered depth map does not have sharp discontinuities (Color figure online)

Full size image

Finally, the average time Footnote 5 to run our method, implemented in non/optimized Matlab code, on all the datasets is 13.5 s (we also include the preprocessing step). Notice that the average time for Alldrin et al. (2007) is 62 s, while for Shi et al. (2010) is 10 min. Moreover, since our standard deviation is zero, we only need to run the algorithm once, while the other methods need to be run several times. To appreciate the fine details of the reconstructed surfaces, in Fig. 10 we show two views of the surfaces obtained for all datasets. The first and the third columns are the results obtained with photometric stereo. The other two columns are obtained with our method. We also tested our method on face reconstruction by using data from Yale’s face database and the reconstructed depth map and surfaces are shown in Fig. 11.

Fig. 10
figure 10

Surface reconstructions. Rendered surfaces obtained with the calibrated photometric stereo method (first and third column). Rendered surfaces obtained with our method (second and fourth column)

Full size image
Fig. 11
figure 11

Results on Yale’s Face database. One of the input images (left). Reconstructed depth map (second from the left). Two views of the reconstructed surface (third and fourth from the left)

Full size image

7.5 Discussion

In the second row (from the bottom) of each table in Table 1, we also show the performance when the LDR maxima are guaranteed to be true LDR maxima (as they are selected from the ground truth normal map—obtained with calibrated photometric stereo). The performance based on the ground truth shows that the algorithm would not achieve \(0\) error even if the detected maxima were correct. As the theory is exact, this limitation can only be due to non Lambertian components still present in the model. Indeed, the pre-processing step (Lin et al. 2009; Wu et al. 2011) may not fully remove specularities and shadows as already observed in the case of the Owl dataset. Finally, in the last row we show the mean angular errors without the pre-processing step. Although we still achieve lower error rates compared to prior methods on many datasets, the reconstruction accuracy degrades. This is true especially for datasets (e.g., Horse) where there is a non-negligible specular component.

7.6 Limitations and Future Work

Our method is entirely based on the diffuse component of the images. Even though the detection of maxima is very robust, their estimation degrades in the presence of shadows, noise, interreflections and specularities. We found the latter ones particularly important. Thus, a possible suggestion of future work is to find a way to detect/model specularities and use them (at the moment we just discard them) together with the LDR maxima to better disambiguate the uncalibrated photometric stereo problem.

8 Conclusion

In this paper we presented a simple and fast method for solving the generalized bas relief (GBR) ambiguity of the uncalibrated photometric stereo problem. Our method makes no stringent assumptions about the distribution of lights, only that they are sufficiently different, and can handle a wide variety of albedos and surfaces. We introduce a novel Lambertian constraint for the distribution of lights and normals, which can be computed in closed-form. We use this new constraint to design a very robust algorithm that achieves the best results to date and provides the same estimate regardless of the GBR ambiguity. Key to our approach is a reliable detection of Lambertian diffuse reflectance maxima in the input images and a robust formulation of the GBR estimation process.

9 Appendix

In this section we provide the detailed proofs for the LDR solutions, how a unique solution can be identified given \(2\) LDR maxima, and that these solutions satisfy the GBR consistency property. First, we need to introduce a simple technique to obtain analytical solutions in a minimization problem.

Lemma 2

Let \(\phi \) be a function of two variables and \(\phi _{\xi _1}\) be its derivative with respect to the first argument \(\xi _1\). Then, if \(\phi _{\xi _1}(\xi _1,\xi _2) = 0\) if and only if \(\xi _1=f(\xi _2)\) for any \(\xi _2\), the following two minimization problems yield the same extrema

$$\begin{aligned} (P_1)\quad \min _{\xi _1,\xi _2}&\phi (\xi _1,\xi _2) \\ (P_2)\quad \min _{\xi _2}&\phi (f(\xi _2),\xi _2)\quad \text{ with }\quad \xi _1 = f(\xi _2).\nonumber \end{aligned}$$
(40)

Proof

Problem \(P_1\) gives the following conditions on the gradients of \(\phi \):

$$\begin{aligned} \phi _{\xi _1}(\xi _1,\xi _2) = 0\quad \quad \phi _{\xi _2} (\xi _1,\xi _2)= 0 \end{aligned}$$
(41)

since \(\phi _{\xi _1} (\xi _1,\xi _2)= 0\) implies that \(\xi _1 = f(\xi _2)\), we must have

$$\begin{aligned} \phi _{\xi _1}(f(\xi _2),\xi _2) = 0\quad \quad \phi _{\xi _2}(f(\xi _2),\xi _2)&= 0 \end{aligned}$$
(42)

Problem \(P_2\) gives the following condition on the gradients of \(\phi \):

$$\begin{aligned} \phi _{\xi _1}(f(\xi _2),\xi _2)\times f_{\xi _2}(\xi _2)+\phi _{\xi _2}(f(\xi _2),\xi _2) = 0. \end{aligned}$$
(43)

Since \(\phi _{\xi _1}(f(\xi _2),\xi _2) = 0\) by definition of \(f\), the first term in the above equation disappears and we have exactly the same set of equations as problem \(P_1\). Notice that the same result can be easily extended to more than \(2\) variables. \(\square \)

We intend to use the above lemma in the Theorem 1 to derive an analytic solution.

Proof of Theorem 1 Firstly, rather than minimizing Eq. (17) we can equivalently minimize the cost function

$$\begin{aligned} \textstyle \min _{\hat{\mu },\hat{\nu },\hat{\lambda }} \Vert \hat{\mathbf {G}}^\top \hat{\mathbf {N}}_{p}\Vert ^{2} \Vert \hat{\mathbf {G}}^{-1} \hat{\mathbf {L}}_{k}\Vert ^{2},\quad \forall p\in {\fancyscript{S}}_{k}. \end{aligned}$$
(44)

Now, recall that

$$\begin{aligned} \hat{\mathbf {G}}^\top = \left[ \begin{array}{lll} 1 &{} 0 &{} \hat{\mu }\\ 0 &{} 1 &{} \hat{\nu }\\ 0 &{} 0 &{} \hat{\lambda }\end{array} \right]&\quad \text{ and }&\hat{\mathbf {G}}^{-1}= \left[ \begin{array}{lll} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ -\frac{\hat{\mu }}{\hat{\lambda }} &{} -\frac{\hat{\nu }}{\hat{\lambda }} &{} \frac{1}{\hat{\lambda }} \end{array} \right] ; \end{aligned}$$
(45)

then, \(\forall p\in {\fancyscript{S}}_{k}\) the cost function can be explicitly written as

$$\begin{aligned} \min _{\hat{\mu },\hat{\nu },\hat{\lambda }}&\displaystyle \frac{1}{\hat{\lambda }^{2}}\left( (\hat{n}_{1,p}+\hat{\mu }\hat{n}_{3,p})^{2}+(\hat{n}_{2,p}+\hat{\nu }\hat{n}_{3,p})^{2}+\hat{\lambda }^{2} \hat{n}_{3,p}^{2}\right) \nonumber \\&\times \left( \hat{\lambda }^{2}\left( \hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}\right) + \left( -\hat{\mu }\hat{l}_{1,k}-\hat{\nu }\hat{l}_{2,k}+\hat{l}_{3,k}\right) ^{2}\right) . \end{aligned}$$
(46)

Notice that the cost is a convex function in the parameter \(\hat{\lambda }\in (0,\infty )\). Consider the case \(\hat{l}_{1,k}^{2}+\hat{l}_{2,k}^{2}=0\), then, the minimization problem has infinite solutions with \(\hat{\lambda }= \infty \) and any \(\hat{\mu },\hat{\nu }\in \mathbb {R}\). This is a degenerate case not only for the LDR constraint theory, but also for photometric stereo in general. Notice that the first two components of the normalized pseudo-lights always coincide with the first two components of the true lights. Then, in this case, the true light direction can be immediately obtained from the pseudo-light. Notice that with this type of illumination the normals can never be retrieved from the Lambertian model. Now, suppose that \(\hat{l}_{1,k}^{2}+\hat{l}_{2,k}^{2}\ne 0\) and the values of \(\hat{\mu }\) and \(\hat{\nu }\) are given; then, a necessary condition for a minimum is that the first order derivative of the cost with respect to \(\hat{\lambda }\) is zero,

$$\begin{aligned} \textstyle \hat{n}_{3,p}^{2}\hat{\lambda }^{4}\left( \hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}\right) =&\left( (\hat{n}_{1,p}{+}\hat{\mu }\hat{n}_{3,p})^{2}+(\hat{n}_{2,p}{+}\hat{\nu }\hat{n}_{3,p})^{2}\right) \nonumber \\&\times \left( -\hat{\mu }\hat{l}_{1,k}-\hat{\nu }\hat{l}_{2,k}+\hat{l}_{3,k}\right) ^{2} \end{aligned}$$
(47)

which immediately yields the unique solution (in \((0,\infty )\))

$$\begin{aligned} \textstyle \hat{\lambda }=\root 4 \of {\frac{\Big [(\hat{n}_{1,p}+\hat{\mu }\hat{n}_{3,p})^{2}+\left( \hat{n}_{2,p}+\hat{\nu }\hat{n}_{3,p}\right) ^{2}\Big ] \left( -\hat{\mu }\hat{l}_{1,k}-\hat{\nu }\hat{l}_{2,k}+\hat{l}_{3,k}\right) ^{2}}{\hat{n}_{3,p}^{2}\left( \hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}\right) }}. \end{aligned}$$
(48)

Now, let us use Lemma 2, substitute the above solution in the cost (46) and solve the minimization in the two remaining unknowns \(\hat{\mu }\) and \(\hat{\nu }\); one obtains the equivalent problem

$$\begin{aligned} \arg \min _{\hat{\mu },\hat{\nu }}&\textstyle \sqrt{\hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}}\sqrt{(\hat{n}_{1,p}+\hat{\mu }\hat{n}_{3,p})^{2}+(\hat{n}_{2,p}+\hat{\nu }\hat{n}_{3,p})^{2}}\nonumber \\&\textstyle +|\hat{n}_{3,p}| \left| -\hat{\mu }\hat{l}_{1,k}-\hat{\nu }\hat{l}_{2,k}+\hat{l}_{3,k}\right| \end{aligned}$$
(49)

which is a convex function in both \(\hat{\mu }\) and \(\hat{\nu }\) (as each energy term is convex in the unknowns). Let us assume that \(\hat{\mu },\hat{\nu }\) are such that \(-\hat{\mu }\hat{l}_{1,k}-\hat{\nu }\hat{l}_{2,k}+\hat{l}_{3,k}\ne 0\). Then, we can compute the first order derivatives of the cost in Eq. (49) in both \(\hat{\mu }\) and \(\hat{\nu }\); by equating them to zero we obtain

$$\begin{aligned} \textstyle \hat{\nu }= \frac{\hat{l}_{2,k}}{\hat{l}_{1,k}\hat{n}_{3,p}}\left( \hat{n}_{1,p}+\hat{n}_{3,p}\hat{\mu }\right) -\frac{\hat{n}_{2,p}}{\hat{n}_{3,p}}. \end{aligned}$$
(50)

Now suppose that \(\hat{\mu },\hat{\nu }\) are such that \(-\hat{\mu }\hat{l}_{1,k}-\hat{\nu }\hat{l}_{2,k}+\hat{l}_{3,k}=0\); then, we have

$$\begin{aligned} \textstyle \hat{\nu }= \frac{\hat{l}_{3,k}-\hat{\mu }\hat{l}_{1,k}}{\hat{l}_{2,k}}. \end{aligned}$$
(51)

To find the minimum we plug both solutions in the cost and look for \(\hat{\mu }\) yielding the smallest value among the two cases. In the first case, we can simplify the minimization to

$$\begin{aligned} \min _{\hat{\mu }} \textstyle \frac{\hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}}{|\hat{l}_{1,k}|}\left[ \left| \hat{n}_{1,p}+\hat{\mu }\hat{n}_{3,p}\right| +\left| \hat{n}_{1,p}+\hat{\mu }\hat{n}_{3,p} - \frac{\hat{l}_{1,k} \hat{\mathbf {N}}_{p}^\top \hat{\mathbf {L}}_{k}}{\hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}}\right| \right] \end{aligned}$$
(52)

and, in the second case, we have

$$\begin{aligned}&\min _{\hat{\mu }}\textstyle \sqrt{\hat{l}_{1,k}^{2}+\hat{l}_{2,k}^{2}}\nonumber \\&\quad \times \sqrt{(\hat{n}_{1,p}+\hat{\mu }\hat{n}_{3,p})^{2}+\left( \hat{n}_{2,p}+ \frac{\hat{l}_{3,k}-\hat{\mu }\hat{l}_{1,k}}{\hat{l}_{2,k}} \hat{n}_{3,p}\right) ^{2}}\nonumber \\ \end{aligned}$$
(53)

In the first case, the solutions in \(\hat{\mu }\) are readily obtained as \(\hat{\mu }\in [\min (\hat{\mu }_{0},\hat{\mu }_{1}),\max (\hat{\mu }_{0},\hat{\mu }_{1})]\) where

$$\begin{aligned} \hat{\mu }_{1} =\textstyle -\frac{\hat{n}_{1,p}}{\hat{n}_{3,p}}\quad \quad \hat{\mu }_{0} =\textstyle \frac{\hat{l}_{1,k} \hat{l}_{2,k}\hat{n}_{2,p} - \hat{l}_{2,k}^{2}\hat{n}_{1,p}+\hat{l}_{3,k}\hat{l}_{1,k}\hat{n}_{3,p}}{\hat{n}_{3,p} \left( \hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}\right) }. \end{aligned}$$
(54)

The gradient of the second cost gives

$$\begin{aligned} \textstyle \hat{\mu }_{*} = \frac{-\hat{l}_{2,k}^{2}\hat{n}_{1,p}+\hat{l}_{1,k}\hat{l}_{2,k}\hat{n}_{2,p}+\hat{l}_{1,k}\hat{l}_{3,k}\hat{n}_{3,p}}{\hat{n}_{3,p}\left( \hat{l}_{1,k}^{2}+\hat{l}_{2,k}^{2}\right) } \end{aligned}$$
(55)

which is identical to \(\hat{\mu }_{0}\). Hence, we only need to substitute \(\hat{\mu }_{0}\) in both costs. A few calculations show that the value of both Eqs. (52) and (53) is \(|\hat{\mathbf {N}}_{p}^\top \hat{\mathbf {L}}_{k}|\) and, therefore, the solutions are \(\hat{\mu }\in [\min (\hat{\mu }_{0},\hat{\mu }_{1}),\max (\hat{\mu }_{0},\hat{\mu }_{1})]\). Now, given all the solutions in \(\hat{\mu }\) we can substitute in the previous expressions and obtain an explicit solution for \(\hat{\nu }\) and for \(\hat{\lambda }\). By using the relationship in Eq. (50), we have \(\hat{\nu }\in [\min (\hat{\nu }_{0},\hat{\nu }_{1}),\max (\hat{\nu }_{0},\hat{\nu }_{1})]\) where

$$\begin{aligned} \hat{\nu }_{1} =\textstyle -\frac{\hat{n}_{2,p}}{\hat{n}_{3,p}}\quad \quad \hat{\nu }_{0} =\textstyle \frac{\hat{l}_{1,k} \hat{l}_{2,k}\hat{n}_{1,p} - \hat{l}_{1,k}^{2}\hat{n}_{2,p}+\hat{l}_{2,k}\hat{l}_{3,k}\hat{n}_{3,p}}{\hat{n}_{3,p} \left( \hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}\right) }. \end{aligned}$$
(56)

Notice also that given \(\theta = \frac{\hat{\mathbf {N}}_{p}^\top \hat{\mathbf {L}}_{k}}{\hat{n}_{3,p}\sqrt{\hat{l}_{1,k}^{2}+\hat{l}_{2,k}^{2}}}\), the following identities hold

$$\begin{aligned} \textstyle \hat{\mu }_{0} = \hat{\mu }_{1}+\frac{\hat{l}_{1,k} \theta }{\sqrt{\hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}}}\quad \quad \quad \hat{\nu }_{0} = \hat{\nu }_{1}+\frac{\hat{l}_{2,k} \theta }{\sqrt{\hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}}}. \end{aligned}$$
(57)

Equation (20) can be readily obtained by direct substitution of the point \([\hat{\mu }~\hat{\nu }]^\top = [\mu _{0}~\nu _{0}]^\top +(1-\alpha )([\mu _{1}~\nu _{1}]^\top -[\mu _{0}~\nu _{0}]^\top )\) in Eq. (48). Finally, we show that the solution in \(\alpha \) is a semi-circle by computing its center and diameter. Firstly, define \((\bar{\mu }, \bar{\nu }, 0)\) as the center of the circle. By using Eq. (57), we obtain

$$\begin{aligned} \bar{\mu }\textstyle = \hat{\mu }_{1}+\frac{\hat{l}_{1,k} \theta }{2\sqrt{\hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}}}\quad \quad \quad \bar{\nu }\textstyle = \hat{\nu }_{1}+\frac{\hat{l}_{2,k} \theta }{2\sqrt{\hat{l}_{1,k}^{2}+ \hat{l}_{2,k}^{2}}} \end{aligned}$$
(58)

and

$$\begin{aligned} (\hat{\mu }-\bar{\mu })^{2}&\textstyle =\left( \alpha -\frac{1}{2}\right) ^{2}\frac{\hat{l}_{1,k}^{2}\theta ^2}{\hat{l}_{1,k}^{2}+\hat{l}_{2,k}^{2}}\nonumber \\ (\hat{\nu }-\bar{\nu })^{2}&\textstyle =\left( \alpha -\frac{1}{2}\right) ^{2}\frac{\hat{l}_{2,k}^{2}\theta ^2}{\hat{l}_{1,k}^{2}+\hat{l}_{2,k}^{2}}\nonumber \\ \hat{\lambda }^{2}&\textstyle =\alpha \left( 1-\alpha \right) \theta ^2. \end{aligned}$$
(59)

By summing the above equations and by taking the square root, one can immediately draw the conclusion that the diameter is the constant \(\theta \).

Proof of Lemma 1 If two Lambertian diffuse reflectance maxima correspond to two different pseudo-normals \(\hat{n}_{p_a}\) and \(\hat{n}_{p_b}\) with

$$\begin{aligned} \frac{\hat{n}_{1,p_{a}}}{\hat{n}_{2,p_{a}}}\ne \frac{\hat{n}_{1,p_{b}}}{\hat{n}_{2,p_{b}}}. \end{aligned}$$
(60)

then there is a unique solution in the GBR parameters.

Proof

Suppose that two LDR maxima with pixel indices \(p_{a}\) and \(p_{b}\), obtained with illumination \(k_{a}\) and \(k_{b}\) respectively, correspond to two pseudo-normals with different directions; then, by using the LDR maxima constraint, the pseudo-normals will have the same direction as the pseudo-light directions, and therefore the corresponding pseudo-lights will be different and satisfy an inequality corresponding to the one above. Now, to find the explicit intersection between the two segments identified by these two LDR maxima, we need to solve

$$\begin{aligned}&\textstyle \begin{bmatrix} \mu _{1,a}\\ \nu _{1,a} \end{bmatrix} +\alpha \left( \begin{bmatrix} \mu _{0,a}\\ \nu _{0,a} \end{bmatrix} -\begin{bmatrix} \mu _{1,a}\\ \nu _{1,a} \end{bmatrix}\right) \nonumber \\ \textstyle&\quad \quad \quad \quad =\begin{bmatrix} \mu _{1,b}\\ \nu _{1,b} \end{bmatrix} +\beta \left( \begin{bmatrix} \mu _{0,b}\\ \nu _{0,b} \end{bmatrix} -\begin{bmatrix} \mu _{1,b}\\ \nu _{1,b} \end{bmatrix} \right) \end{aligned}$$
(61)

in the unknown \(\alpha \) and \(\beta \). Let us define

$$\begin{aligned} \textstyle \theta _{a} \doteq \frac{\hat{\mathbf {N}}_{p_{a}}^\top \hat{\mathbf {L}}_{k_{a}}}{\hat{n}_{3,p_{a}}^{2}(\hat{l}_{1,k_{a}}^{2}+\hat{l}_{2,k_{a}}^{2})}\quad \quad \theta _{b} \doteq \frac{\hat{\mathbf {N}}_{p_{b}}^\top \hat{\mathbf {L}}_{k_{b}}}{\hat{n}_{3,p_{b}}^{2}(\hat{l}_{1,k_{b}}^{2}+\hat{l}_{2,k_{b}}^{2})}. \end{aligned}$$
(62)

Then, the intersection can be computed by solving the following linear system

$$\begin{aligned} \textstyle \begin{bmatrix} \hat{l}_{1,k_{a}}\theta _{a}&-\hat{l}_{1,k_{b}}\theta _{b}\\ \hat{l}_{2,k_{a}}\theta _{a}&-\hat{l}_{2,k_{b}}\theta _{b} \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} = \begin{bmatrix} \mu _{1,b}-\mu _{1,a}\\ \nu _{1,b}-\nu _{1,a} \end{bmatrix}. \end{aligned}$$
(63)

To have a unique solution the determinant of the \(2\times 2\) matrix on the left hand side must be nonzero. Hence, we find

$$\begin{aligned} -\hat{l}_{1,k_{a}}\hat{l}_{2,k_{b}}\theta _{a}\theta _{b}+\hat{l}_{1,k_{b}}\hat{l}_{2,k_{a}}\theta _{a}\theta _{b}\ne 0 \end{aligned}$$
(64)

which can be simplified as

$$\begin{aligned} \frac{\hat{l}_{1,k_{a}}}{\hat{l}_{2,k_{a}}}\ne \frac{\hat{l}_{1,k_{b}}}{\hat{l}_{2,k_{b}}}. \end{aligned}$$
(65)

The latter constraint is satisfied due to the inequality on the pseudo-normals in the assumptions. \(\square \)

Proof of Proposition 1 The transformation \(\hat{\mathbf {G}}^\top \mathbf {G}^{-\top }\), where \(\mu \), \(\nu \), and \(\lambda \) have been estimated via the LDR constraints is GBR-consistent.

Proof

When we estimate the unit normals from the pseudo-normals we compute

$$\begin{aligned} \tilde{\mathbf {N}} = \hat{\mathbf {G}}^\top \hat{\mathbf {N}}/\Vert \hat{\mathbf {G}}^\top \hat{\mathbf {N}}\Vert = \hat{\mathbf {G}}^\top \mathbf {G}^{-\top }\mathbf {N}/\Vert \hat{\mathbf {G}}^\top \mathbf {G}^{-\top }\mathbf {N}\Vert . \end{aligned}$$
(66)

Hence, if \(\hat{\mathbf {G}}^\top \mathbf {G}^{-\top }\) is GBR consistent, then the recovered normals \(\tilde{\mathbf {N}}\) do not depend on the GBR parameters. By computing \(\hat{\mathbf {G}}^\top \mathbf {G}^{-\top }\) we obtain

$$\begin{aligned} \hat{\mathbf {G}}^\top \mathbf {G}^{-\top }= \left[ \begin{array}{lll} 1 &{} 0 &{} \frac{\hat{\mu }-\mu }{\lambda } \\ 0 &{} 1 &{} \frac{\hat{\nu }-\nu }{\lambda } \\ 0 &{} 0 &{} \frac{\hat{\lambda }}{\lambda } \end{array} \right] . \end{aligned}$$
(67)

Thus, we need to show that \(\frac{\hat{\mu }-\mu }{\lambda }\), \(\frac{\hat{\nu }-\nu }{\lambda }\) and \(\frac{\hat{\lambda }}{\lambda }\) do not depend on the GBR parameters \(\mu \), \(\nu \), and \(\lambda \), when \(\hat{\mu }\), \(\hat{\nu }\), and \(\hat{\lambda }\) are computed from the LDR constraints. By direct substitution and by using \(\hat{\mathbf {L}} = \mathbf {G}\mathbf {L}\) and \(\hat{\mathbf {N}} = \mathbf {G}^{-1}\mathbf {N}\) we obtain the following equalities, which depend only on the data and \(\alpha \),

$$\begin{aligned} \textstyle \eta _1&= \frac{\hat{\mu }-\mu }{\lambda } =\textstyle \alpha \frac{l_{1,k}I_{p,k}}{n_{3,p}\left( l_{1,k}^{2}+ l_{2,k}^{2}\right) }-\frac{n_{1,p}}{n_{3,p}}\end{aligned}$$
(68)
$$\begin{aligned} \textstyle \eta _2&=\frac{\hat{\nu }-\nu }{\lambda } \textstyle = \alpha \frac{l_{2,k}I_{p,k}}{n_{3,p}\left( l_{1,k}^{2}+ l_{2,k}^{2}\right) }-\frac{n_{2,p}}{n_{3,p}}\end{aligned}$$
(69)
$$\begin{aligned} \textstyle \eta _3&=\frac{\hat{\lambda }}{\lambda } \textstyle = \sqrt{\alpha (1-\alpha )}\frac{I_{p,k}}{|n_{3,p}|\left( l_{1,k}^{2}+l_{2,k}^{2}\right) } \end{aligned}$$
(70)

To conclude the proof we need to show that \(\alpha \) does not depend on the GBR parameters. To this purpose, consider the intersection between the segments generated by two LDR maxima as in Eq. (61). Then, by direct substitution we obtain

$$\begin{aligned}&\textstyle \begin{bmatrix} -\frac{n_{1,p_{a}}\lambda }{n_{3,p_{a}}}+\mu \\ -\frac{n_{2,p_{a}}\lambda }{n_{3,p_{a}}}+\nu \end{bmatrix} +\alpha \frac{\lambda I_{p_{a},k_{a}}}{|n_{3,p_{a}}|\left( l_{1,k_{a}}^{2}+l_{2,k_{a}}^{2}\right) } \begin{bmatrix} l_{1,k_{a}}\\ l_{2,k_{a}} \end{bmatrix}\nonumber \\&\quad = \begin{bmatrix} -\frac{n_{1,p_{b}}\lambda }{n_{3,p_{b}}}+\mu \\ -\frac{n_{2,p_{b}}\lambda }{n_{3,p_{b}}}+\nu \end{bmatrix} +\beta \frac{\lambda I_{p_{b},k_{b}}}{|n_{3,p_{b}}|\left( l_{1,k_{b}}^{2}+l_{2,k_{b}}^{2}\right) } \begin{bmatrix} l_{1,k_{b}}\\ l_{2,k_{b}} \end{bmatrix}\nonumber \\ \end{aligned}$$
(71)

this is equivalent to

$$\begin{aligned}&\textstyle \begin{bmatrix} -\frac{n_{1,p_{a}}}{n_{3,p_{a}}}\\ -\frac{n_{2,p_{a}}}{n_{3,p_{a}}} \end{bmatrix} +\alpha \frac{I_{p_{a},k_{a}}}{|n_{3,p_{a}}|\left( l_{1,k_{a}}^{2}+l_{2,k_{a}}^{2}\right) } \begin{bmatrix} l_{1,k_{a}}\\ l_{2,k_{a}} \end{bmatrix}\nonumber \\&\quad \quad = \begin{bmatrix} -\frac{n_{1,p_{b}}}{n_{3,p_{b}}}\\ -\frac{n_{2,p_{b}}}{n_{3,p_{b}}} \end{bmatrix} +\beta \frac{I_{p_{b},k_{b}}}{|n_{3,p_{b}}|\left( l_{1,k_{b}}^{2}+l_{2,k_{b}}^{2}\right) } \begin{bmatrix} l_{1,k_{b}}\\ l_{2,k_{b}} \end{bmatrix} \end{aligned}$$
(72)

which is independent of the GBR parameters. Therefore, \(\alpha \) and \(\beta \) are also independent of the GBR parameters. \(\square \)