The global asymptotical stability of pseudorabies model with age-structure

Abstract

In this paper, the dynamics of an infectious disease is studied by considering age-structured models; a stage structure and an age-structured epidemic model. The respective basic reproduction numbers for the proposed models are calculated, and the local analyses of the equilibria of the models are investigated by using the method of linearization. The global dynamics of the two models are analyzed by using the wave lemma and the Lyapunov function theory. This study establishes a solid theoretical framework and a rigorous mathematical formulation for the prevention and control of pseudorabies.

Introduction

When a pathogenic microbial agent (such as bacteria, fungi, virus etc.) is present in a body, it causes a clinically obvious sickness known as an infectious disease [1]. There has always been a threat to human health from infectious diseases. In the past, emergence and re-emergence of infectious diseases have caused devastating human disasters [2,3,4,5,6]. Since then, epidemiologists and other related health officials have achieved better results in the possible prevention and elimination of infectious diseases by studying its dynamics and introducing a number of pharmaceutical and non-pharmaceutical measures. However, the complete elimination of infectious diseases needs a lot of human efforts and is very costly. Further, such diseases can be controlled by employing variety of experiments, and humanly, research experiments on infectious diseases are unethical and sometime impossible [7]. Therefore, theoretical analysis and simulation are the best way to find out the root causes of the disease, to summarize the associated epidemic characteristics and to predict the future behaviors of the disease [7].

Pseudorabies (PR) is a severe infectious disease caused by pseudorabies virus (PRV) and the virus affects a wide range of domestic and wild animals like pigs, dogs, sheep, and cats. The main symptoms include fever, itching, lethargy, ataxia, and encephalomyelitis [8]. PRV belongs to the herpesviridae family, and the disease was first discovered in the United Statesin 1813. Aujeszky, a Hungarian scientist, recognized it as a novel and distinct disease in 1902 [8]. In 1910, Schniedh offer confirmed it as a virus [9]. Pigs are the main reservoirs and a place of detoxification of the PRV. Pigs infected with a small amount of virus under natural conditions will show no symptoms but could have recessive infection [9]. Once the swine is infected with PRV, it is generally difficult to completely remove the virus from the body. The infected body will continue to retain the virus throughout the incubation period [10], where it can be easily activated by certain environmental stimuli and may cause the disease once again.

Among other known infections in pigs, PR infection is one of the most severe and highly contagious diseases [11]. In general, there is a close relationship between the symptoms and the age of the infected pigs. Further, the infection is asymptomatic in pigs having age more than two months. Piglets have the most obvious symptoms after the disease, which include the rise in temperature, dyskinesia, tremor, diarrhea, etc., and the disease course is short and the mortality is very high [12]. After PRV infection, adult pigs will only suffer from mild diarrhea, temperature rise or slight dyspnea, etc. Sows may experience infertility and decreased appetite in severe cases, as well as temporary blindness [13]. Infected pigs and mice are important sources of PR infection, especially asymptomatic infected pigs, which play the key role in the preservation and transmission of the virus [14]. At present, there are no specific available drugs to treat the disease, and hence one can rely only on the control measures such as weeding out sick pigs, timely isolation of the infected animals, vaccine prevention, and distillation of pigs. In the recent years, PR has been continuously breaking out and popular in pig farms in many countries around the globe [15], which caused a great economic loss to our pig industry.

In order to decrease the spread of pseudorabies in the community, similar to other medical researchers, mathematicians playing their own role by developing and analyzing the models that describe the dynamics of the underlying disease. Due to the complexity of the disease, very little research work related the modeling and control of PRV is available in the literature. This paper mainly focuses on the interior and the exterior spread of pseudorabies within the animals by using the tools of mathematical modeling. By considering the features and characteristics of pseudo rabies infection in pigs and its spreading mechanism, the corresponding stage-structured model for the disease will be formulated using the techniques of differential equations. The models will be analyzed from the dynamic perspectives, and initially, the models will be investigated for possible steady states. The local analysis of the equilibria of the stage-structured model is investigated by using the linearization method. The global stabilities of the disease-free and endemic equilibria of the model are proved with the help of Lyapunov functional theory. We utilized the techniques of partial differential equations and formulated an age-structured model reflecting the effect of age in the dynamics of pseudorabies. Again, the model was checked for the existence of infection-free and endemic steady states. The steady states of the model were investigated from the dynamical aspects. The qualitative analysis of the study provides novel and accurate theoretical results for the prevention and control of pseudorabies disease. Theoretical analysis of the results indicates that clinical symptoms in particular age groups of pigs can be reduced by immunization. The study further suggests that the disease could be effectively controlled with routine vaccination, and hence, all pig farms in China should be vaccinated with a modified live virus. The study is considered to be of sufficient novelty both from methodology and results point of view as the proposed research assumes the effect of age in the modeling. Due to the theoretical and practical importance of the study, the authors expect that this work will open new doors of research in the modeling and control of the pseudorabies disease.

A class of pseudorabies models with stage structure

A significant cause of swine infectious illnesses and a large source of financial losses in the swine business is the pseudorabies virus. The fundamental epidemic models categorize people according to their infection status (susceptible, infected, recovered, immune, etc.), and they calculate the dynamics of the epidemic based on the rates at which people switch between various infection states. A population unit may vary in terms of their age, maturity, size, and reproductive status from another population unit. Stage-structured epidemic models provide a way to study interactions between epidemic and demographic process. Further, such models classify population units according to their infectious and demographic status.

In this section, we will establish a pseudorabies model with stage structure according to different infectious and demographic characteristics of adult and young pigs, the effect of the disease on the two pigs with different age segments, the development law, and the transmission mechanism.

Establishment of model

Here, the pig population is divided into five compartments: susceptible piglet group, infected piglet group, susceptible adult piglet group, infected adult piglet group, and the latent pig group, whose sizes (at any time $t$) are, respectively, denoted by $S_{1} (t)$, $I_{1} (t)$, $I_{2} (t)$ and $L(t)$. Let us assume that the pigs give birth at a constant rate $b$, $\beta_{1}$ and $\beta_{2}$ are, respectively, the rates at which susceptible piglets and susceptible adult piglets moving to the compartments of infected piglet and infected adult piglet. The terms $d_{1}$ and $d_{2},$ respectively, denote the natural death rates of pig and adult pig populations. The notion $\rho$ is the progression rate of piglets into the adult pig’s population. The piglet dies due to the disease at a constant rate $\alpha$ $\gamma$ is the constant rate at which infected adult swine move to the latent compartment and finally, the term $\eta$ stands for the rate at which the exposed adult swine rejoin the infected compartment after completing their latent period.

The proposed model is based on the following assumptions:

(1) We did not consider the mobility of the herd, and it is assumed that all the newborn piglets are the susceptible pigs;

(2) It is assumed that only infected adult pigs are contagious, that is, the disease spread only when the susceptible pigs interact with infected adult pigs.

(3) It is assumed that adult pigs cannot recover from the disease rather they enters into the incubation period and after completing the latent period, the adult pigs rejoin the infected compartment at a constant rate $\eta$.

Based on the above-mentioned assumptions, the following model is formulated which governs the dynamics of pseudorabies:

$$ \left\{ \begin{array}{ll} \frac{{{\text{d}}S_{1} }}{{\text{d}}t} = b - \beta_{1} S_{1} I_{2} - (d_{1} + \rho )S_{1} , \hfill \\ \frac{{{\text{d}}I_{1} }}{{\text{d}}t} = \beta_{1} S_{1} I_{2} - (d_{1} + \alpha + \rho )I_{1} , \hfill \\ \frac{{{\text{d}}S_{2} }}{{\text{d}}t} = \rho (S_{1} + I_{1} ) - \beta_{2} S_{2} I_{2} - d_{2} S_{2} , \hfill \\ \frac{{{\text{d}}I_{2} }}{{\text{d}}t} = \beta_{2} S_{2} I_{2} - (d_{2} + \gamma )I_{2} + \eta L, \hfill \\ \frac{{\text{d}}L}{{{\text{d}}t}} = \gamma I_{2} - (\eta + d_{2} )L. \hfill \\ \end{array} \right. $$

(2.1)

Let $N_{1} (t),N_{2} (t)$ denote the total number of piglets and adult pigs, respectively, that is,$N_{1} = S_{1} + I_{1} ,$$N_{2} = S_{2} + I_{2} + L,$ and hence model (2.1) will take the form:

$$ \left\{ \begin{gathered} \frac{{{\text{d}}N_{1} (t)}}{{\text{d}}t} = b - (d_{1} + \rho )N_{1} (t) - \alpha I_{1} (t), \hfill \\ \frac{{{\text{d}}N_{2} (t)}}{{\text{d}}t} = \rho N_{1} (t) - d_{2} N_{2} (t). \hfill \\ \end{gathered} \right. $$

It is easy to prove that the forward invariant set of model (2.1) is given by

$$ \Omega = \left\{ {\left. {(S_{1} ,I_{1} ,S_{2} ,I_{2} ,L) \in R_{ + }^{5} } \right|0 < S_{1} + I_{1} \le \frac{b}{{d_{1} + \rho }},0 < S_{2} + I_{2} + L \le \frac{\rho b}{{d_{2} (d_{1} + \rho )}}} \right\}. $$

The right hand sides of model (2.1) were set equal to zero, and the disease-free equilibrium point was obtained

$$ E^{0} (S_{1}^{0} ,I_{1}^{0} ,S_{2}^{0} ,I_{2}^{0} ,L^{0} ) = \left( {\frac{b}{{d_{1} + \rho }},0,\frac{\rho b}{{d_{2} (d_{1} + \rho )}},0,0} \right). $$

According to the third part of literature [16], the basic reproduction number for model (2.1) is calculated as

$$ \Re_{0} = \frac{{\beta_{2} S_{2}^{0} (d_{2} + \eta )}}{{(d_{2} + \gamma )(d_{2} + \eta ) - \eta \gamma }} = \frac{{\beta_{2} S_{2}^{0} (d_{2} + \eta )}}{{d_{2} (d_{2} + \eta + \gamma )}}. $$

Local and global asymptotic stabilities of the disease-free equilibrium point

Theorem 2.2.1

When $\Re_{0} < 1$, the disease-free equilibrium point $E^{0}$ is locally asymptotically stable.

Prove By linearizing model (2.1) at the disease-free equilibrium $E^{0} (S_{1}^{0} ,I_{1}^{0} ,S_{2}^{0} ,I_{2}^{0} ,L^{0} )$, we have the following characteristic equation

$$ (\lambda + d_{2} )(\lambda + d_{1} + \rho )(\lambda + d_{1} + \alpha + \rho )(\lambda^{2} + A\lambda + B) = 0. $$

(2.2)

Three roots of Eq. (2.2) are given by

$${\lambda }_{1}=-{d}_{2}, {\lambda }_{2}=-\left({d}_{1}+\rho \right), {\lambda }_{2}=-\left({d}_{1}+\alpha +\rho \right).$$

The remaining two roots of Eq. (2.2) can be determined from the following quadratic equation

$${\lambda }^{2}+A\lambda +B=0,$$

(2.2a)

where

$$ A = d_{2} + \eta + d_{2} + \gamma - \beta_{2} S_{2}^{0} , $$

$$ B = d_{2} (d_{2} + \eta + \gamma ) - (d_{2} + \eta )\beta_{2} S_{2}^{0} = d_{2} (d_{2} + \eta + \gamma )(1 - \Re_{0} ). $$

Clearly for $\Re_{0} < 1$, we have

$$ \beta_{2} S_{2}^{0} < \frac{{(d_{2} + \gamma )(d_{2} + \eta ) - \eta \gamma }}{{d_{2} + \eta }} < d_{2} + \gamma . $$

Thus, the condition ${R}_{0}<1$ guarantees that both $A > d_{2} + \gamma - \beta_{2} S_{2}^{0} > 0,$ and $B>0$. By using the Descartes rule of signs, Eq. (2.2a) has no positive real solution and there exist two negative real roots of Eq. (2.2a) or complex with negative real parts. Therefore, all roots of the characteristic Eq. (2.2) are negative real or complex with negative real parts, so the disease-free equilibrium point $E^{0}$ is locally asymptotically stable.

Mathematically, Theorem 2.2.1 indicates that if the initial conditions are sufficiently close to the disease-free equilibrium point, the respective solution curves will approach the disease-free fixed point. However, if one chose initial conditions far away from ${E}^{0}$, it is not necessary that the solution curves will approach to the equilibrium point in the long run. Biologically, the statement of the theorem suggests that if the size of the population of the initially infected piglets and adults pigs is close to zero and further, if one infected pig/piglet infect less than one pig during their course of infection, the disease will tend to eliminate from the population. However, if one infected pig produces more than one infected pigs, the disease will tend to persist in the pig’s community. Moreover, if the population of the initially infected pigs are not close to zero, then Theorem 2.2.1 does not guarantee that the elimination of the disease.

In the following theorem, we will prove that for $\Re_{0} < 1$, the disease-free equilibrium $E^{0}$ is globally asymptotically stable.

Theorem 2.2.2

The disease-free equilibrium point $E^{0}$ is globally asymptotically stable for ${R}_{0}<1$ and unstable otherwise.

Proof

In order to prove the global stability of the disease-free equilibrium, we will consider the following Lyapunov function.^[26]

$$ V = \left( {d_{2} + \eta } \right)I_{2} + \eta L. $$

The derivative of $V$ with respect to $t$ while considering equations in system (2.1), we have

$$ \begin{aligned} V^{\prime} = & \left( {d_{2} + \eta } \right)\left[ {\beta_{2} S_{2} - \left( {d_{2} + \gamma } \right)} \right]I_{2} + \eta \gamma I_{2} , \\ = & \left[ {\left( {d_{2} + \eta } \right)(\beta_{2} S_{2} - d_{2} - \gamma ) + \eta \gamma } \right]I_{2} , \\ \le & \left[ {\left( {d_{2} + \eta } \right)(\beta_{2} S_{2}^{0} - d_{2} - \gamma ) + \eta \gamma } \right]I_{2} \le 0, \\ \end{aligned} $$

for${R}_{0}<1$. Let $\Gamma = \left\{ {\left( {S_{1} ,I_{1} ,S_{2} ,I_{2} ,L} \right) \in \Omega \left| {V^{\prime}(t) = 0} \right.} \right\} = \left\{ {I_{2} { = 0}} \right\},$ be obtained from model (2.1), and the maximum invariant set of $\Gamma$ is $\left\{ {E^{0} } \right\}$.Thus, according to the LaSalle invariant principle [18], the disease-free equilibrium $E^{0}$ is globally asymptotically stable for ${R}_{0}<1$ and unstable otherwise.

Physically, the global stability of the disease-free equilibrium implies that irrespective of the initial condition of the infected population, the disease will tend to dies out of the pig population if one infected pig infects less than one susceptible pig/piglets.

Existence of the unique positive equilibrium point

In majority of the cases, we are not only interested in the elimination of the diseases rather we are looking for the conditions under which the disease may persist in the community. To find the unique positive endemic equilibrium point $E^{ * } (S_{1}^{ * } ,I_{1}^{ * } ,S_{2}^{ * } ,I_{2}^{ * } ,L^{ * } )$ of model (2.1), again we will set the expressions at the right of each equation in model equal to zero. By solving the resultant simultaneous system of algebraic equations, we have

$$ S_{1}^{ * } = \frac{{b - (d_{1} + \alpha + \rho )I_{1}^{ * } }}{{d_{1} + \rho }},\;S_{{2}}^{ * } = \frac{{(d_{{2}} + \gamma )(d_{{2}} + \eta ) - \eta \gamma }}{{\beta_{2} (d_{{2}} + \eta )}}, $$

$$ I_{{2}}^{ * } = \frac{{(d_{1} + \alpha + \rho )I_{1}^{ * } }}{{\beta_{1} S_{1}^{ * } }},\;L^{ * } = \frac{\gamma }{{d_{{2}} + \eta }}I_{2}^{ * } . $$

The value of ${I}_{1}^{*}$ can be obtained from the following equation

$$ f(I_{1}^{ * } ) = \frac{{(d_{{2}} + \gamma )(d_{{2}} + \eta ) - \eta \gamma }}{{\beta_{2} (d_{{2}} + \eta )}}\left( {d_{{2}} + \frac{{\beta_{2} (d_{1} + \rho )(d_{1} + \alpha + \rho )I_{1}^{ * } }}{{\beta_{1} b - \beta_{1} I_{1}^{ * } (d_{1} + \alpha + \rho )}}} \right) + \frac{{(\alpha I_{1}^{ * } - b)\rho }}{{d_{1} + \rho }} = 0. $$

Since $f^{\prime}(I_{1}^{ * } ) = \frac{{(d_{{2}} + \gamma )(d_{{2}} + \eta ) - \eta \gamma }}{{d_{{2}} + \eta }} \cdot \frac{{b(d_{1} + \rho )(d_{1} + \alpha + \rho )}}{{\beta_{1} \left[ {b - (d_{1} + \alpha + \rho )I_{1}^{ * } } \right]^{2} }} + \frac{\alpha \rho }{{d_{1} + \rho }} > 0,$ which implies that $f$ is monotonically increasing. Further, ${S}_{1}^{*}>0$ if and only if $I_{1}^{ * } < \frac{b}{{d_{1} + \alpha + \rho }},$. However, $I_{1}^{ * } \to \frac{b}{{d_{1} + \alpha + \rho }}$, implies that $f(I_{1}^{ * } ) \to + \infty$. Moreover, $f({0}) = \frac{{\rho b(1 - \Re_{0} )}}{{(d_{1} + \rho )\Re_{0} }},$ and $f\left(0\right)\ge 0$ only if $\Re_{0} \le 1$. This implies that for${R}_{0}<1$, equation $f(I_{1}^{ * } ) = 0$ has no positive root in the interval $\left( {{0},\frac{b}{{d_{1} + \alpha + \rho }}} \right)$, that is, model (2.1) has only the disease-free equilibrium point $E^{0}$ when${R}_{0}<1$. However for $\Re_{0} > 1$, $f({0}) < {0}$, and hence $f(I_{1}^{ * } ) = 0$ has a unique positive solution on interval $\left( {{0},\frac{b}{{d_{1} + \alpha + \rho }}} \right)$, that is, model (2.1) has a unique positive equilibrium point $E^{ * }$ besides disease-free equilibrium point $E^{0}$. Based on the above discussion, we can state the following theorem.

Theorem 2.3.1

If ${R}_{0}>1$, then there exists a unique positive endemic equilibrium ${E}^{*}$ of model (2.1) given by

$$ S_{1}^{ * } = \frac{{b - (d_{1} + \alpha + \rho )I_{1}^{ * } }}{{d_{1} + \rho }},\;S_{{2}}^{ * } = \frac{{(d_{{2}} + \gamma )(d_{{2}} + \eta ) - \eta \gamma }}{{\beta_{2} (d_{{2}} + \eta )}}, $$

$$ I_{{2}}^{ * } = \frac{{(d_{1} + \alpha + \rho )I_{1}^{ * } }}{{\beta_{1} S_{1}^{ * } }},\;L^{ * } = \frac{\gamma }{{d_{{2}} + \eta }}I_{2}^{ * } . $$

where ${I}_{1}^{*}$ is the positive root of the following equation $f(I_{1}^{ * } ) = \frac{{(d_{{2}} + \gamma )(d_{{2}} + \eta ) - \eta \gamma }}{{\beta_{2} (d_{{2}} + \eta )}}(d_{{2}} + \frac{{\beta_{2} (d_{1} + \rho )(d_{1} + \alpha + \rho )I_{1}^{ * } }}{{\beta_{1} b - \beta_{1} I_{1}^{ * } (d_{1} + \alpha + \rho )}}) + \frac{{(\alpha I_{1}^{ * } - b)\rho }}{{d_{1} + \rho }} = 0.$

Local and global asymptotic stability analysis of the endemic equilibrium

If we assume $\alpha = 0$, then it is easy to show that for $t \to \infty$, we have.

$N_{1} (t) \to \frac{b}{{d_{1} + \rho }},\;N_{2} (t) \to \frac{b\rho }{{d_{2} (d_{1} + \rho )}},$ and thus the limit equation of model (2.1) will take the form

$$ \left\{ \begin{gathered} \frac{{{\text{d}}I_{1} }}{{\text{d}}t} = \frac{{\beta_{1} b}}{{d_{1} + \rho }}I_{2} - \beta_{1} I_{1} I_{2} - (d_{1} + \rho )I_{1} , \hfill \\ \frac{{{\text{d}}I_{2} }}{{\text{d}}t} = \frac{{\beta_{2} b\rho }}{{d_{2} (d_{1} + \rho )}}I_{2} - \beta_{2} I_{2}^{2} - \beta_{2} I_{2} L - (d_{2} + \gamma )I_{2} + \eta L, \hfill \\ \frac{{\text{d}}L}{{{\text{d}}t}} = \gamma I_{2} - (d_{2} + \eta )L. \hfill \\ \end{gathered} \right. $$

(2.3)

Here again, if we let $\Re_{0} > 1$, then model (2.3) has a unique positive endemic equilibrium point $\hat{E}^{ * } (I_{1}^{ * } ,I_{2}^{ * } ,L^{ * } )$.

Theorem 2.4.1

If $\alpha = 0$ and $\Re_{0} > 1$, then the unique positive equilibrium point $E^{ * }$ of model (2.1) is locally asymptotically stable.

Proof

By linearizing model (2.1) around the endemic equilibrium $E^{ * } (S_{1}^{ * } ,I_{1}^{ * } ,S_{2}^{ * } ,I_{2}^{ * } ,L^{ * } )$, the following characteristic equation can be easily obtained.

$$ \left| {\begin{array}{*{20}c} {\lambda + \beta_{1} I_{2}^{ * } + d_{1} + \rho } & 0 & 0 & {\beta_{1} S_{1}^{ * } } & 0 \\ { - \beta_{1} I_{2}^{ * } } & {\lambda + d_{1} + \rho } & 0 & { - \beta_{1} S_{1}^{ * } } & 0 \\ { - \rho } & { - \rho } & {\lambda + d_{2} + \beta_{2} I_{2}^{ * } } & {\beta_{2} S_{2}^{ * } } & 0 \\ 0 & 0 & { - \beta_{2} I_{2}^{ * } } & {\lambda - \beta_{2} S_{2}^{ * } + d_{2} + \gamma } & { - \eta } \\ 0 & 0 & 0 & { - \lambda } & {\lambda + d_{2} + \eta } \\ \end{array} } \right|{ = 0,} $$

that is

$$ (\lambda + \beta_{1} I_{2}^{ * } + d_{1} + \rho )(\lambda + d_{1} + \rho )(\lambda^{3} + C_{1} \lambda^{2} + C_{2} \lambda + C_{3} ) = 0, $$

(2.4)

The two roots of Eq. (2.4) can be easily calculated and one can notice that both the roots ${\lambda }_{1}=-({\beta }_{1}{I}_{2}^{*}+{d}_{1}+\rho )$ and ${\lambda }_{2}=-({d}_{1}+\rho )$ are negative only if ${R}_{0}>1$. The other three roots of Eq. (2.4) can be calculated from the following equation

$${\lambda }^{3}+{C}_{1}{\lambda }^{2}+{C}_{2}\lambda +{C}_{3}=0,$$

(2.4a)

where

$$ \begin{gathered} C_{1} { = 2}d_{2} + \beta_{2} I_{2}^{ * } + \eta + \frac{\eta \gamma }{{d_{2} + \eta }} > 0, \hfill \\ C_{2} { = (}d_{2} + \beta_{2} I_{2}^{ * } )(d_{2} + \eta + \frac{\eta \gamma }{{d_{2} + \eta }}) + \beta_{2}^{2} S_{2}^{ * } I_{2}^{ * } > 0, \hfill \\ C_{3} { = }\beta_{2}^{2} S_{2}^{ * } I_{2}^{ * } (d_{2} + \eta ) > 0. \hfill \\ \end{gathered} $$

This means, all of the coefficients of Eq. (2.4a) are positive and further

$$ \begin{aligned} C_{1} C_{2} - C_{3} { = } & {(}d_{2} + \beta_{2} I_{2}^{ * } )^{2} \left( {d_{2} + \eta + \frac{\eta \gamma }{{d_{2} + \eta }}} \right)^{2} + \beta_{2} S_{2}^{ * } \beta_{2} I_{2}^{ * } \left( {d_{2} + \beta_{2} I_{2}^{ * } + d_{2} + \eta + \frac{\eta \gamma }{{d_{2} + \eta }}} \right) \\ & - \beta_{2} S_{2}^{ * } \beta_{2} I_{2}^{ * } (d_{2} + \eta ) \\ { = } & {(}d_{2} + \beta_{2} I_{2}^{ * } )^{2} \left( {d_{2} + \eta + \frac{\eta \gamma }{{d_{2} + \eta }}} \right)^{2} + \beta_{2} S_{2}^{ * } \beta_{2} I_{2}^{ * } \left( {d_{2} + \beta_{2} I_{2}^{ * } + \frac{\eta \gamma }{{d_{2} + \eta }}} \right) > 0. \\ \end{aligned} $$

Thus, at $\alpha = 0$, the application of Routh–Hurwitz criterion [19]to Eq. (2.4a) ensures that all the roots of characteristic Eqs. (2.4) are negative or complex with negative real parts, so the unique positive equilibrium point $E^{ * }$ is locally asymptotically stable.

Biologically Theorem 2.4.1 argued that if we have very small size of the infected pigs and one infectious pig infecting more than one susceptible pigs/piglets, then the Pseudorabies disease will tend to persist in the pigs community.

Theorem 2.4.1

If $\alpha = 0$ and $\Re_{0} > 1$, then the unique endemic equilibrium $E^{ * }$ of model (2.1) is globally asymptotically stable in$\Omega$.

Proof

To prove the global stability of the endemic equilibrium, we will consider the following Lyapunov function.

$$ G = \gamma I_{2}^{ * } G_{1} + \eta L^{ * } G_{2} + G_{3} , $$

where the functions ${G}_{i}$’s for $i=\mathrm{1,2},3,$ are given by

$$ G_{1} = I_{2} - I_{2}^{ * } - I_{2}^{ * } \ln \frac{{I_{2} }}{{I_{2}^{ * } }},G_{2} = L - L^{ * } - L^{ * } \ln \frac{L}{{L^{ * } }},G_{3} = \frac{{\beta_{2} }}{2}I_{2}^{ * } (L - L^{ * } )^{2} . $$

The derivatives of the function G_i's with respect to $t$ along model (2.3) are of the form.

$$ \begin{aligned} G_{1}^{\prime } = & \left( {1 - \frac{{I_{2}^{ * } }}{{I_{2} }}} \right)I_{2}^{\prime } = \left( {1 - \frac{{I_{2}^{ * } }}{{I_{2} }}} \right)\left[ {\beta_{2} I_{2} (S_{2}^{0} - I_{2} - L) + \eta L - (d_{2} + \gamma )I_{2} } \right], \\ = & \left( {1 - \frac{{I_{2}^{ * } }}{{I_{2} }}} \right)\left[ {\beta_{2} I_{2} (I_{2}^{ * } + L^{ * } - I_{2} - L) - \frac{{I_{2} }}{{I_{2}^{ * } }}\eta L^{ * } + \eta L} \right] \\ = & - \beta_{2} (I_{2} - I_{2}^{ * } )^{2} + \beta_{2} (I_{2} - I_{2}^{ * } )(L^{ * } - L) + \eta L^{ * } \left( {\frac{L}{{L^{ * } }} - \frac{{I_{2} }}{{I_{2}^{ * } }} - \frac{{LI_{2}^{ * } }}{{L^{ * } I_{2} }} + 1} \right); \\ \end{aligned} $$

$$ \begin{aligned} G_{{2}}^{\prime } = & \left( {1 - \frac{{L^{ * } }}{L}} \right)L^{\prime } = \left( {1 - \frac{{L^{ * } }}{L}} \right)\left[ {\gamma I_{2} - (\eta + d_{2} )L} \right] \\ = & \left( {1 - \frac{{L^{ * } }}{L}} \right)\left[ {\gamma I_{2} - \frac{{\gamma I_{2}^{ * } }}{{L^{ * } }}L} \right] = \gamma I_{2}^{ * } \left( {\frac{{I_{2} }}{{I_{2}^{ * } }} - \frac{L}{{L^{ * } }} - \frac{{L^{ * } I_{2} }}{{LI_{2}^{ * } }} + 1} \right); \\ \end{aligned} $$

$$ \begin{aligned} G_{{3}}^{\prime } = & \beta_{2} I_{2}^{ * } (L - L^{ * } )L^{\prime} = \beta_{2} I_{2}^{ * } (L - L^{ * } )\left[ {\gamma I_{2} - (\eta + d_{2} )L + (\eta + d_{2} )L^{ * } - \gamma I_{2}^{ * } } \right] \\ = & \beta_{2} I_{2}^{ * } (L - L^{ * } )\left[ {\gamma (I_{2} - I_{2}^{ * } ) - (d_{2} + \eta )(L - L^{ * } )} \right] \\ = & - \beta_{2} I_{2}^{ * } (d_{2} + \eta )(L - L^{ * } )^{2} + \beta_{2} I_{2}^{ * } \gamma (L - L^{ * } )(I_{2} - I_{2}^{ * } ). \\ \end{aligned} $$

Therefore,

$$ \begin{aligned} G^{\prime} = & \gamma I_{2}^{ * } G_{1}^{\prime } + \eta L^{ * } G_{2}^{\prime } + G_{3}^{\prime } \\ = & - \beta_{2} I_{2}^{ * } \gamma (I_{2} - I_{2}^{ * } )^{2} - \beta_{2} I_{2}^{ * } (d_{2} + \eta )(L - L^{ * } )^{2} + \eta \gamma I_{2}^{ * } L^{ * } \left( {2 - \frac{{L^{ * } I_{2} }}{{LI_{2}^{ * } }} - \frac{{LI_{2}^{ * } }}{{L^{ * } I_{2} }}} \right) \le 0. \\ \end{aligned} $$

Let $E = \left\{ {\left( {S_{1} ,I_{1} ,S_{2} ,I_{2} ,L} \right) \in \Omega \left| {G^{\prime}(t) = 0} \right.} \right\} = \left\{ {I_{2} = I_{2}^{ * } ,L = L^{ * } } \right\}$ be obtained from model (2.1), and the maximum invariant set of $E$ is $\left\{ {E^{ * } } \right\}$. According to LaSalle invariant set principle, for $\alpha = 0$ and $\Re_{0} > 1$, the unique positive equilibrium point $E^{ * }$ is globally asymptotically stable.

A pseudorabies model with age structure in the infected class

The infectious disease modeled structured via ordinary differential equations has been widely and deeply studied from the last century by numerous researchers. However, different age groups or populations have different infection degrees to a certain infectious disease, and therefore, it is necessary and practical to consider infectious disease models with age structure in the infectious compartment.

Age-structured models are a special case of the stage-structured models. This means, stage-structured epidemic models include age-classified and stage-classified models.

Formulation of the model

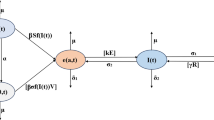
In this part of the paper, for model formulation, the pig population is divided into susceptible pigs, infected pigs, and latent pigs. Let $S(t)$ and $L(t)$ represent the total number of susceptible pigs and latent pigs at any time $t$ and $i(t,a)$ represents the density function of the infected pigs at time $t$ having the age of infectivity$a$. Thus $I(a) = \int_{0}^{\infty } {i(t,a)da}$ represents the total number of infected pigs at time $t$. Let $\Lambda$ be the birth rate of pigs, $d$ is the natural mortality rate of the pigs,$m$ is the killing rate of the pigs, and thus $mX(.)$ will denote the total population of pig being killed at any time$t$,$\eta$ is the reoccurrence rate of adult pigs in the latent period,$a$ is the age of infection. Further, the coefficient of infection rate and the transformation coefficient of the adult pigs from the infectious period to the latent period are related to the age of infection, which are denoted by $\beta (a)$ and $\gamma (a),$ respectively.

Next, we shall assume that the new infections from the susceptible and latent pigs will come to the infected compartment. The rate $\beta$ at which the disease is transferred to susceptible from the infectious now depends on $a$, that is $\beta =\beta \left(a\right)$. Thus, the inflow into the infected compartment is given by

$$S\left(t\right){\int }_{0}^{\infty }\beta \left(a\right)i\left(t,a\right)da+\eta L\left(t\right).$$

This inflow into the infected compartment will be entered via boundary condition.

Based on the above-mentioned assumptions, the following model is established

$$\left\{\begin{array}{l}\frac{dS(t)}{{\text{d}}t}=\lambda -{\int }_{0}^{\infty } \beta \left(a\right)S\left(t\right)i\left(t,a\right)da-\left(m+d\right)S\left(t\right),\\ \frac{\partial i(t,a)}{\partial t}+\frac{\partial i(t,a)}{\partial a}=-\left(\gamma \left(a\right)+m+d\right)i\left(t,a\right),\\ \frac{dL(t)}{{\text{d}}t}={\int }_{0}^{\infty } \gamma \left(a\right)i\left(t,a\right)da-\left(m+d+\eta \right)L\left(t\right),\end{array}\right.$$

(3.1)

with the boundary conditions

$$i\left(t,0\right)={\int }_{0}^{\infty } \beta \left(a\right)S\left(t\right)i\left(t,a\right)da+\eta L\left(t\right),$$

for $t\ge 0$ and the initial conditions

$$S\left(0\right)={S}_{0}, i\left(0,a\right)={i}_{0}\left(a\right), L\left(0\right)={L}_{0},$$

for $a\ge 0$. The parameters $\beta (a)$ and $\gamma (a)$ are from the space ${L}_{+}^{1}$ where $L_{ + }^{1}$ is the set of integrable functions from $(0,\infty )$ to $R_{ + } = \left[ {0, + \infty } \right)$. If we set $N(t) = \left\| {S(t),i(t, \cdot ),L(t)} \right\|$, we get $\frac{{{\text{d}}N(t)}}{{{\text{d}}t}} \le \Lambda - (d + m)N(t).$

For computational convenience, let us define the following function and parameters

$$ \pi (a) = e^{{ - \int_{0}^{a} {(d + m + \gamma (s)){\text{d}}s} }} ,\;K = \int_{0}^{\infty } {\beta (a)\pi (a){\text{d}}} a,\;P = \int_{0}^{\infty } {\gamma (a)\pi (a){\text{d}}} a. $$

Further, we will define the basic reproduction number as

$$ \Re_{0} = \frac{\Lambda K}{{d + m}} + \frac{\eta P}{{d + m + \eta }}. $$

Existence of an equilibrium point of the age-structured model

If $E = \left( {\overline{S},\overline{i},\overline{L}} \right)$ is the equilibrium point of (3.1), then such equilibrium point will satisfy the following system of equations

$$ \left\{ \begin{gathered} 0 = \Lambda - \overline{S}\int_{0}^{\infty } {\beta (a)\overline{i}(a)} da - (d + m)\overline{S}, \hfill \\ \frac{{d\overline{i}(a)}}{{\text{d}}t} = - (d + m + \gamma (a))\overline{i}(a), \hfill \\ \overline{i}(0) = \overline{S}\int_{0}^{\infty } {\beta (a)\overline{i}(a)} da + \eta \overline{L}, \hfill \\ 0 = \int_{0}^{\infty } {\gamma (a)\overline{i}(a)} da - (d + m + \eta )\overline{L}. \hfill \\ \end{gathered} \right. $$

(3.2)

The second equation of system (3.2) is linear and separable, and a solution of this equation is given by

$$ \overline{i}(a) = \overline{i}(0)\pi (a). $$

By substituting this expression in the fourth equation of system (3.2), and we get $\overline{L} = \frac{P}{d + m + \eta }\overline{i}(0)$. Similarly, from the first and third equation of system (3.2), one can obtain

$$ \overline{S} = \frac{{\Lambda - \left( {1 - \frac{\eta P}{{d + m + \eta }}} \right)\overline{i}(0)}}{d + m}. $$

From the third equation of system (3.2), one can notice that $\overline{i}(0)$ is the root of the equation $g(x) = 0$, where

$$g(x) = \frac{{\Lambda - \left( {1 - \frac{\eta P}{{d + m + \eta }}} \right)x}}{d + m}\int_{0}^{\infty } {\beta (a)\pi (a)xda} + \left( {\frac{\eta P}{{d + m + \eta }} - 1} \right)x$$

(3.3)

Obviously $g(0) = 0$. Further, the function $g(x)$ is a concave function as $g(\frac{\Lambda }{{1 - \frac{\eta P}{{d + m + \eta }}}}) = - \Lambda < 0$ and $g^{\prime}(0) = \Re_{0} - 1$. So, for $\Re_{0} \le 1$, we have $g^{\prime}(x) < 0$ and as a result, model (3.1) has only the disease-free equilibrium point ${E}_{0}=(\frac{\lambda }{d+m},\mathrm{0,0})$ of one is However, for $\Re_{0} > 1$,$g^{\prime}(x) > 0$, and hence $g(x)$ has a unique zero point, then model (3.1) in addition to a disease-free equilibrium point $E_{0}$, there is also a positive equilibrium point $E^{ * }$. The following conclusions can be drawn about the steady states of model (3.1):

Theorem 3.2.1

For model (3.1), we have the following results about the existence of the steady states:

• (i) When $\Re_{0} \le 1,$ then model (3.1) has a disease-free equilibrium point $E_{0} = \left( {\frac{\Lambda }{d + m},0,0} \right).$

• (ii) If $\Re_{0} > 1,$ then model (3.1) has the disease-free steady state $E_{0}$ and the positive equilibrium point $E^{ * } = (S^{ * } ,i^{ * } ,L^{ * } )$ where$S^{ * } = \frac{{\Lambda - (1 - \frac{\eta P}{{d + m + \eta }})i^{ * } (0)}}{d + m}$, $i^{ * } (a) = i^{ * } (0)\pi (a)$, $L^{ * } = \frac{P}{d + m + \eta }i^{ * } (0)$, and $i^{ * } (0)$ is the root of function (3.3).

Local stability of equilibrium point

To study the local stability of model (3.1), we need to linearize the model at $\overline{E} = \left( {\overline{S},\overline{i},\overline{L}} \right)$, and the linearized system is as follows

$$ \left\{ \begin{gathered} \frac{{{\text{d}}S(t)}}{{{\text{d}}t}} = - (d + m + \int_{0}^{\infty } {\beta (a)\overline{i}(a)} {\text{d}}a)S(t) - \overline{S}\int_{0}^{\infty } {\beta (a)i(t,a)} {\text{d}}a, \hfill \\ \frac{\partial i(t,a)}{{\partial t}} + \frac{\partial i(t,a)}{{\partial a}} = - (d + m + \gamma (a))i(t,a), \hfill \\ i(t,0) = S(t)\int_{0}^{\infty } {\beta (a)\overline{i}(a)} da + \overline{S}\int_{0}^{\infty } {\beta (a)i(a)} da + \eta L(t), \hfill \\ \frac{{{\text{d}}L(t)}}{{{\text{d}}t}} = \int_{0}^{\infty } {\gamma (a)i(t,a)} {\text{d}}a - (d + m + \eta )L(t). \hfill \\ \end{gathered} \right. $$

(3.4)

The linear system (3.4) has the exponential solution of the form $S(t) = x_{0} e^{\lambda t}$,$i(t,a) = y_{0} e^{\lambda t}$ and $L(t) = z_{0} e^{\lambda t}$. By substituting these solutions in the linearized system (3.4),we have the following characteristic equation.

$$\left| {\begin{array}{*{20}c} {\lambda + d + m + \int_{0}^{\infty } {\beta (a)\overline{i}(a)} {\text{d}}a} & {\overline{S}\int_{0}^{\infty } {\beta (a)\pi (a)e^{ - \lambda a} } {\text{d}}a} & 0 \\ { - \int_{0}^{\infty } {\beta (a)\overline{i}(a)} {\text{d}}a} & {\lambda - \overline{S}\int_{0}^{\infty } {\beta (a)\pi (a)e^{ - \lambda a} } {\text{d}}a} & { - \eta } \\ 0 & { - \hat{P}(\lambda )} & {\lambda + d + m + \eta } \\ \end{array} } \right| = 0,$$

(3.5)

where $\hat{P}(\lambda )\mathop = \limits^{\Delta } \int_{0}^{\infty } {\gamma (a)\pi (a)e^{ - \lambda a} } da$ is the Laplace transform of $\gamma \pi$.

Theorem 3.3.1

• (i) If $\Re_{0} \le 1$, then the disease-free equilibrium $E_{0} = \left( {\frac{\Lambda }{d + m},0,0} \right)$ of model (3.1) is locally asymptotically stable, and unstable otherwise.

• (ii) If $\Re_{0} > 1$, then the positive endemic equilibrium $E^{ * } = (S^{ * } ,i^{ * } ,L^{ * } )$ of model (3.1) is locally asymptotically stable.

Proof:

(i) The characteristic Eq. (3.5) at the disease-free equilibrium point $E_{0}$ is given by

$$(\lambda + d + m)C(\lambda ) = 0,$$

(3.6)

where $C(\lambda ) = (1 - \frac{\Lambda }{d + m}\hat{K}(\lambda ))(\lambda + d + m + \eta ) - \eta \hat{P}(\lambda )$, and $\hat{K}(\lambda )\mathop = \limits^{\Delta } \int_{0}^{\infty } {\beta (a)\pi (a)e^{ - \lambda a} } da$ is the Laplace transform of $\beta \pi$. Obviously, $d + m$ is a root of (3.6), and the other roots are actually the roots of the equation $C(\lambda ) = 0$.

Assume that $\Re_{0} > 1$, then $C(0) = (1 - \Re_{0} )(d + m + \eta )$, and $\mathop {\lim }\limits_{\lambda \to \infty } C(\lambda ) = \infty$. Hence, by mean value theorem, the equation $C(\lambda ) = 0$ has a positive root. Consequently, for $\Re_{0} > 1$, the disease-free equilibrium point $E_{0}$ is unstable.

On the other hand, if $\Re_{0} < 1$, let us assume that the equation $C(\lambda ) = 0$ has a solution with nonnegative real part, then there must exist some $\lambda_{0} \in C$ with ${\text{Re}} (\lambda_{0} ) > 0$ such that $C(\lambda_{0} ) = 0$. Consequently,

$$ \left| {1 - \frac{\Lambda }{d + m}\hat{K}(\lambda_{0} )} \right| = \left| {\frac{{\eta \hat{P}(\lambda_{0} )}}{{\lambda_{0} + d + m + \eta }}} \right|. $$

Further, we assumed that $\Re_{0} < 1$ and ${\text{Re}} (\lambda_{0} ) > 0$, thus

$$ \left| {1 - \frac{\Lambda }{d + m}\hat{K}(\lambda_{0} )} \right| \ge \left| {1 - \left| {\frac{\Lambda }{d + m}\hat{K}(\lambda_{0} )} \right|} \right| \ge 1 - \frac{\Lambda K}{{d + m}} = 1 - \Re_{0} + \frac{\eta P}{{d + m + \eta }}, $$

$$ \left| {\frac{{\eta \hat{P}(\lambda_{0} )}}{{\lambda_{0} + d + m + \eta }}} \right| \le \frac{\eta P}{{d + m + \eta }}. $$

In summary, we have $\Re_{0} \ge 1$, which contradicts the assumption of $\Re_{0} < 1$. Hence, we concluded that for $\Re_{0} \le 1$, the disease-free equilibrium $E_{0}$ is locally asymptotically stable.

(ii) The characteristic Eq. (3.5) at the positive endemic equilibrium point $E^{ * }$ will take the form

$$ \begin{aligned} & (\lambda + d + m)(\lambda + d + m + \eta )S^{ * } \int_{0}^{\infty } {\beta (a)\pi (a)e^{ - \lambda a} } {\text{d}}a + \eta \hat{P}(\lambda )(\lambda + d + m + \int_{0}^{\infty } {\beta (a)i^{ * } (a)} {\text{d}}a) \\ & \quad = (\lambda + d + m + \int_{0}^{\infty } {\beta (a)i^{ * } (a)} {\text{d}}a)(\lambda + d + m + \eta ). \\ \end{aligned} $$

(3.7)

Let us assume that Eq. (3.7) has a solution with positive real parts. Thus, for a solution ${\lambda }_{0}$ of Eq. (3.7), we have ${\text{Re}} (\lambda_{0} ) \ge 0$, and by putting this solution in Eq. (3.7), we have

$$ \begin{aligned} i^{ * } (0) = & \frac{{(\lambda_{0} + d + m)S^{ * } \int_{0}^{\infty } {\beta (a)i^{ * } (0)\pi (a)e^{{ - \lambda_{0} a}} } {\text{d}}a}}{{\lambda_{0} + d + m + \int_{0}^{\infty } {\beta (a)i^{ * } (a)} {\text{d}}a}} + \frac{{\eta \hat{P}(\lambda_{0} )i^{ * } (0)}}{{\lambda_{0} + d + m + \eta }}, \\ \le & \frac{{S^{ * } \int_{0}^{\infty } {\beta (a)i^{ * } (a)} {\text{d}}a}}{{1 + \frac{{\int_{0}^{\infty } {\beta (a)i^{ * } (a)} {\text{d}}a}}{{\lambda_{0} + d + m}}}} + \frac{{\eta Pi^{ * } (0)}}{d + m + \eta } \\ < & S^{ * } \int_{0}^{\infty } {\beta (a)i^{ * } (a)} {\text{d}}a + \frac{{\eta Pi^{ * } (0)}}{d + m + \eta } \\ = i^{ * } (0), \\ \end{aligned} $$

This is a clear contradiction; hence our hypothesis is wrong and the original proposition holds. That is, if $\Re_{0} > 1$, then the positive equilibrium point $E^{ * }$ is of the proposed model is locally asymptotically stable.

Physically, this theorem reflects that a solution that start close to the disease-free fixed point will approach to ${E}^{0}$ whenever ${R}_{0}<1$ and contrary, for ${R}_{0}>1$, a solution closer to ${E}^{*}$ will approach to the endemic equilibrium in the long run.

Global stability analysis of the equilibria of model (3.1)

For convenience, let us define the following function

$$ B(t) = i(t,0) = S(t)\int_{0}^{\infty } {\beta (a)i(t,a)} {\text{d}}a + \eta L(t). $$

If we integrate the second equation of model (3.1) along the characteristic line $t = a$, we get the following piece-wise defined solution

$$ i(t,a) = \left\{ {\begin{array}{*{20}c} {B(t - a)\pi (a),t \ge a,} \\ {i_{0} (a - t)\frac{\pi (a)}{{\pi (a - t)}},t \le a.} \\ \end{array} } \right. $$

(3.8)

For any bounded function $f$ defined on $\left[ {0,\infty } \right)$, we shall denote $f^{\infty } = \mathop {\lim }\limits_{t \to \infty } \sup f(t)$, and $f_{\infty } = \mathop {\lim }\limits_{t \to \infty } \inf f(t)$.

Theorem 3.4.1

If $\Re_{0} < 1$, then the disease-free equilibrium $E_{0}$ of model (3.1) is globally asymptotically stable.

Proof

First of all, we need to prove $B^{\infty } = L^{\infty } = 0$, which means that $\mathop {\lim }\limits_{t \to \infty } B(t) = \mathop {\lim }\limits_{t \to \infty } L(t) = 0$.

According to the wave lemma [20], there exists a sequence $\left\{ {t_{n} } \right\}$ such that $t_{n} \to \infty$,$L(t_{n} ) \to L^{\infty }$ and when $n \to \infty$,$\frac{{dL(t_{n} )}}{{\text{d}}t} \to 0$. From the relation (3.1), we can obtain

$$ \begin{aligned} \frac{{{\text{d}}L(t_{n} )}}{{{\text{d}}t}} = & \int_{0}^{{t_{n} }} {\gamma (a)} B(t_{n} - a)\pi (a){\text{d}}a + \int_{{t_{n} }}^{\infty } {\gamma (a)i_{0} (a - t_{n} )\frac{\pi (a)}{{\pi (a - t_{n} )}}} {\text{d}}a - (d + m + \eta )L(t_{n} ) \\ \le & \int_{0}^{{t_{n} }} {\gamma (a)} B(t_{n} - a)\pi (a){\text{d}}a + e^{{ - (d + m)t_{n} }} \left\| \gamma \right\|_{\infty } \cdot \left\| {i_{0} } \right\|_{1} - (d + m + \eta )L(t_{n} ) \\ \end{aligned} $$

Let $n \to \infty$, and by applying the wave lemma, we get

$$ 0 \le B^{\infty } \gamma - (d + m + \eta )L^{\infty } \Rightarrow L^{\infty } \le \frac{{B^{\infty } \gamma }}{d + m + \eta }. $$

Since

$$ \begin{aligned} B(t) \le & \frac{\Lambda }{d + m}\int_{0}^{\infty } {\beta (a)i} (t - a){\text{d}}a + \eta L(t_{n} ), \\ = & \frac{\Lambda }{d + m}\left( {\int_{0}^{t} {\beta (a)} B(t - a)\pi (a){\text{d}}a + \int_{t}^{\infty } {\beta (a)i_{0} (a - t)\frac{\pi (a)}{{\pi (a - t)}}} {\text{d}}a} \right) + \eta L(t) \\ = & \frac{\Lambda }{d + m}\left( {\int_{0}^{t} {\beta (a)} B(t - a)\pi (a){\text{d}}a + \int_{t}^{\infty } {\beta (a + t)i_{0} (a - t)\frac{\pi (a + t)}{{\pi (a)}}} {\text{d}}a} \right) + \eta L(t) \\ \le & \frac{\Lambda }{d + m}\left( {\int_{0}^{t} {\beta (a)} B(t - a)\pi (a){\text{d}}a + e^{ - (d + m)t} \left\| B \right\|_{\infty } \cdot \left\| {i_{0} } \right\|_{1} } \right) + \eta L(t) \\ \end{aligned} $$

Letting $t \to \infty$, and then by using the wave lemma, we have

$$ B^{\infty } \le \frac{\Lambda }{d + m}B^{\infty } + \eta L^{\infty } \le \Re_{0} B^{\infty } . $$

Since $\Re_{0} < 1$, therefore, we must accept that $B^{\infty } = 0$, and due to $B^{\infty } = 0$, we have $L^{\infty } = 0$.

By the wave lemma, there exists a sequence $\left\{ {s_{n} } \right\}$,such that $s_{n} \to \infty$,$S(s_{n} ) \to S_{{^{\infty } }}$ and then $n \to \infty$,$\frac{{dS(s_{n} )}}{{\text{d}}t} \to 0$. Based on these results, we have the following assertion

$$ \begin{aligned} \frac{{{\text{d}}S(s_{n} )}}{{{\text{d}}t}} = & \Lambda - S(s_{n} )\int_{0}^{\infty } {\beta (a)} i(s_{n} ,a){\text{d}}a - (d + m)S(s_{n} ) \\ \ge & \Lambda - B(s_{n} ) - (d + m)S(s_{n} ) \\ \end{aligned} $$

because of $\mathop {\lim }\limits_{t \to \infty } B(t) = 0$, we get $S_{\infty } \ge \frac{\Lambda }{d + m}$. Also, we have $S^{{_{\infty } }} \le \frac{\Lambda }{d + m}$, then by letting $n \to \infty$, we reach to the conclusion $\mathop {\lim }\limits_{t \to \infty } S(t) = \frac{\Lambda }{d + m}$.

Thus $\mathop {\lim }\limits_{t \to \infty } (S(t),i(t, \cdot ),L(t)) = E_{0}$, that is, if $\Re_{0} < 1$, then disease-free equilibrium $E_{0}$ is globally asymptotically stable.

In the above, by using the wave lemma, we proved that the disease-free steady state is globally asymptotically stable when $\Re_{0} < 1$. In Appendix A, we also proved the global stability of the disease-free equilibrium by using the Lyapunov stability theorem while imposing an additional condition on the model.

The global stability of the endemic equilibrium is presented in the following theorem.

Theorem 3.4.2

If $\Re_{0} > 1$, then the endemic equilibrium $E^{ * }$ of model (3.1) is globally asymptotically stable.

Proof

To prove the result, let us consider a function $\phi :\left( {0,\infty } \right) \to R$ defined by $\phi \left( x \right) = x - 1 - \ln x$ and $x \in \left( {0,\infty } \right)$.

Further, we set $\varphi (a) = \int_{a}^{\infty } {\left( {\beta (s)i^{ * } (s) + \frac{\eta \gamma (s)}{{(d + m + \eta )S^{ * } }}i^{ * } (s)} \right)} {\text{d}}s$, whose derivative with respect to $a$ is given by

$\frac{{{\text{d}}\varphi (a)}}{{{\text{d}}a}} = - \left[ {\beta (a)i^{ * } (a) + \frac{\eta \gamma (a)}{{(d + m + \eta )S^{ * } }}i^{ * } (a)} \right]$ _.

Define

$$ V(t) = V_{S} (t) + V_{i} (t) + \frac{{\eta L^{ * } }}{{(d + m + \eta )S^{ * } }}V_{L} (t), $$

where $V_{S} (t){ = }\phi (\frac{S(t)}{{S^{ * } }})$,$V_{L} (t){ = }\phi (\frac{L(t)}{{L^{ * } }})$,$V_{i} (t){ = }\int_{0}^{\infty } {\varphi (a)} \phi (\frac{i(t,a)}{{i^{ * } (a)}}){\text{d}}a$. This shows that $V$ is bounded on $x(t)$. The derivative of ${V}_{s}$ with respect to $t$ is given by

$\begin{aligned} \frac{{{\text{d}}V_{S} (t)}}{{{\text{d}}t}} = & \left( {1 - \frac{{S^{ * } }}{S(t)}} \right)\frac{1}{{S^{ * } }}\left[ {\Lambda - (d + m)S(t) - S(t)\int_{0}^{\infty } {\beta (a)i(t,a)} {\text{d}}a} \right] \\ = & \left( {1 - \frac{{S^{ * } }}{S(t)}} \right)\frac{1}{{S^{ * } }}\left[ {(d + m)(S^{ * } - S(t)) + S^{ * } \int_{0}^{\infty } {\beta (a)i^{ * } (a)} {\text{d}}a - S(t)\int_{0}^{\infty } {\beta (a)i(t,a)} {\text{d}}a} \right], \\ = & - (d + m)\left( {\frac{{S^{ * } }}{S(t)} + \frac{S(t)}{{S^{ * } }} - 2} \right) + \int_{0}^{\infty } {\beta (a)i^{ * } (a)} {\text{d}}a\left[ {1 - \frac{S(t)i(t,a)}{{S^{ * } i^{ * } (a)}} - \frac{{S^{ * } }}{S(t)} + \frac{i(t,a)}{{i^{ * } (a)}}} \right]{\text{d}}a. \\ \end{aligned}$ _,

By using the relation $d + m + \eta = \frac{{\int_{0}^{\infty } {\gamma (a)i^{ * } (a){\text{d}}a} }}{{L^{ * } }}$, we have

$\begin{aligned} \frac{{{\text{d}}V_{L} (t)}}{{{\text{d}}t}} = & \frac{1}{{L^{ * } }}\left( {1 - \frac{{L^{ * } }}{L(t)}} \right)\left[ {\int_{0}^{\infty } {\gamma (a)i(t,a){\text{d}}a - (d + m + \eta )L(t)} } \right], \\ = & \frac{1}{{L^{ * } }}\left( {1 - \frac{{L^{ * } }}{L(t)}} \right)\left[ {\int_{0}^{\infty } {\gamma (a)i(t,a){\text{d}}a - \frac{{\int_{0}^{\infty } {\gamma (a)i^{ * } (a){\text{d}}a} }}{{L^{ * } }}L(t)} } \right] \\ = & \frac{1}{{L^{ * } }}\int_{0}^{\infty } {\gamma (a)i^{ * } (a)\left( {\frac{i(t,a)}{{i^{ * } (a)}} - \frac{L(t)}{{L^{ * } }} - \frac{{L^{ * } i(t,a)}}{{L(t)i^{ * } (a)}} + 1} \right){\text{d}}a} \\ \end{aligned}$ _,

Next, for $t\in R$ and$a\in {R}^{+}$, we have $\frac{i(t,a)}{{i^{ * } (a)}}{ = }\frac{B(t - a)}{{i^{ * } (0)}}$, and as a result

$\frac{{{\text{d}}V_{i} (t)}}{{{\text{d}}t}} = \int_{0}^{\infty } {\varphi (a)\frac{\partial }{\partial t}\phi \left( {\frac{B(t - a)}{{i^{ * } (0)}}} \right){\text{d}}a}$ _,

Since $\varphi (0) = \int_{0}^{\infty } {\left[ {\beta (a)i^{ * } (a) + \frac{\eta \gamma (a)}{{(d + m + \eta )S^{ * } }}i^{ * } (a)} \right]{\text{d}}a}$, thus

$$ \frac{{{\text{d}}V_{i} (t)}}{{{\text{d}}t}} = \int_{0}^{\infty } {\left[ {\beta (a)i^{ * } (a) + \frac{\eta \gamma (a)}{{(d + m + \eta )S^{ * } }}i^{ * } (a)} \right]\left[ {\phi \left( {\frac{i(t,0)}{{i^{ * } (0)}}} \right) - \phi \left( {\frac{i(t,a)}{{i^{ * } (a)}}} \right)} \right]{\text{d}}a} . $$

Accordingly,

$$ \begin{aligned} \frac{{\text{d}}V(t)}{{{\text{d}}t}} = & \frac{{{\text{d}}V_{S} (t)}}{{\text{d}}t} + \frac{{{\text{d}}V_{i} (t)}}{{\text{d}}t} + \frac{{\eta L^{ * } }}{{(d + m + \eta )S^{ * } }}\frac{{{\text{d}}V_{L} (t)}}{{\text{d}}t} \\ = & - (d + m)\left( {\frac{{S^{ * } }}{S(t)} + \frac{S(t)}{{S^{ * } }} - 2} \right) \\ & + \int_{0}^{\infty } {\beta (a)i^{ * } (a)} \left[ {\phi \left( {\frac{i(t,0)}{{i^{ * } (0)}}} \right) - \phi \left( {\frac{i(t,a)}{{i^{ * } (a)}}} \right) + 1 - \frac{{S^{ * } }}{S(t)} + \frac{i(t,a)}{{i^{ * } (a)}} - \frac{S(t)i(t,a)}{{S^{ * } i^{ * } (a)}}} \right]{\text{d}}a \\ & + \frac{\eta }{{(d + m + \eta )S^{ * } }}\int_{0}^{\infty } {\gamma (a)i^{ * } (a)} \\ & \cdot \left[ {\phi \left( {\frac{i(t,0)}{{i^{ * } (0)}}} \right) - \phi \left( {\frac{i(t,a)}{{i^{ * } (a)}}} \right) + \frac{i(t,a)}{{i^{ * } (a)}} - \frac{{L^{ * } i^{ * } (a)}}{L(t)i(t,a)} + 1 - \frac{L(t)}{{L^{ * } }}} \right]{\text{d}}a \\ = & - (d + m)\left( {\frac{{S^{ * } }}{S(t)} + \frac{S(t)}{{S^{ * } }} - 2} \right) \\ & - \int_{0}^{\infty } {\beta (a)i^{ * } (a)} \left[ {\phi \left( {\frac{{S^{ * } }}{S(t)}} \right) + \phi \left( {\frac{{S(t)i(t,a)i^{ * } (0)}}{{S^{ * } i^{ * } (a)i(t,0)}}} \right)} \right]{\text{d}}a \\ & - \frac{\eta }{{(d + m + \eta )S^{ * } }}\int_{0}^{\infty } {\gamma (a)i^{ * } (a)} \left[ {\phi \left( {\frac{{L(t)i^{ * } (0)}}{{L^{ * } i(t,0)}}} \right) + \phi \left( {\frac{{L^{ * } i^{ * } (a)}}{L(t)i(t,a)}} \right)} \right]{\text{d}}a \\ \le & 0 \\ \end{aligned} $$

Let $E = \left\{ {(S,i,L) \in \Omega \left| {G^{\prime}(t) = 0} \right.} \right\} = \left\{ {S = S^{ * } ,L = L^{ * } } \right\}$ be obtained from model (3.1), and the maximum invariant set of $E$ is $\left\{ {E^{ * } } \right\}$. According to LaSalle invariant set principle, when $\Re_{0} > 1$, the endemic equilibrium $E^{ * }$ of model (3.1) is globally asymptotically stable.

Conclusion

In this paper, we established stage and age-structured pseudorabies models describing the dynamics of the infection in different pig populations. The models are investigated for the existence of possible steady states, and stability of each equilibrium point of the model is analyzed and discussed. The traditional linearization method was used for carrying out the results on the local analysis of the steady states. In the sequel, we employed the well-known Routh–Hurwitz criterion. We developed suitable Lyapunov functions for proving the global stability of some equilibria where others were studied with the help of wave lemma. The findings of the study indicate that one must bring the value of ${R}_{0}$ less than one for eradicating the disease out of the pig populations. Further, the study is considered to be much beneficial for researchers dealing with age-structured models particularly and it provides a platform that how one can apply the tools to study age and stage-structured models.

Appendix 1

From model (3.1), for the sake of simplicity, we make some substitutions. For $a\ge 0$, we denote

$$\epsilon \left(a\right)=\gamma \left(a\right)+m+d,$$

and the notions $\pi \left(a\right), K$ and $P$ in term of $\epsilon \left(a\right)$ are reproduced as

$$\pi (a)={e}^{-{\int }_{0}^{a} \epsilon (s)ds},K={\int }_{0}^{\infty } \beta (a){e}^{-{\int }_{0}^{a} \epsilon (s)ds}da,P={\int }_{0}^{\infty } \gamma (a){e}^{-{\int }_{0}^{a} \epsilon (s)ds}da.$$

(3.9)

Clearly, $\pi (0)=1$ and $0\le \pi (a)\le {e}^{-\left({\gamma }_{0}+m+d\right)}\le 1$. The derivative of $\pi (a)$ is

$$\frac{d\pi (a)}{da}=-\pi \left(a\right)\epsilon \left(a\right).$$

The proposed model exhibits a disease-free steady state, i.e., ${E}^{0}=\left({S}^{0},\mathrm{0,0}\right)$, where

$${S}^{0}=\frac{\Lambda }{m+d}.$$

(3.10)

The basic reproduction number ${\mathfrak{R}}_{0}$ in terms of (A1) and (A2) can be expressed alternatively as

$${\mathfrak{R}}_{0}={S}^{0}K+\frac{\eta P}{m+d+\eta }.$$

Next, we will consider an important Volterra-type function

$$G\left(x\right)=x-1-\mathrm{ln}x, x>0.$$

Obviously, $G(x)\ge 0$ for $x>0$ and $G(x)$ has a global minimum at $x=1$ and $G(1)=0$.

Theorem A1

If ${\mathfrak{R}}_{0}<1$, the DFE is globally asymptotically stable.

Proof

First, we define a positive function as

$${K}^{0}(a)={\int }_{a}^{\infty } {S}^{0}\beta (v){e}^{-{\int }_{a}^{v} \epsilon (\tau )d\tau }d\nu .$$

Note that ${K}^{0}(a)>0$ for $a\ge 0$ and ${K}^{0}(0)={S}^{0}K$. Furthermore, the derivative of ${K}^{0}(a)$ is

$$\frac{d{K}^{0}(a)}{da}={K}^{0}\left(a\right)\epsilon \left(a\right)-{S}^{0}\beta \left(a\right).$$

(3.11)

Now, we set the Lyapunov functional as follows

$$V\left(t\right)={V}_{1}\left(t\right)+{V}_{2}\left(t\right),$$

(3.12)

where

$${V}_{1}\left(t\right)={S}^{0}G\left(\frac{S\left(t\right)}{{S}^{0}}\right), {V}_{2}(t)={\int }_{0}^{\infty } {K}^{0}(a)i(t,a)da.$$

Note that $\Lambda =(m+d){S}^{0}$, calculating the time derivative of ${V}_{1}(t)$ along solution of system (3.1), we obtain

$$\begin{array}{cc}\frac{d{V}_{1}(t)}{{\text{d}}t}& ={S}^{0}\left(1-\frac{{S}^{0}}{S(t)}\right)\frac{1}{{S}^{0}}\left(\lambda -(m+d)S(t)-{\int }_{0}^{\infty } \beta (a)S(t)i(t,a)da\right)\\ & =\left(m+d\right){S}^{0}\left(2-\frac{{S}^{0}}{S\left(t\right)}-\frac{S\left(t\right)}{{S}^{0}}\right)-{\int }_{0}^{\infty } \beta \left(a\right)S\left(t\right)i\left(t,a\right)da+{\int }_{0}^{\infty } \beta \left(a\right){S}^{0}i\left(t,a\right)da.\end{array}$$

(3.13)

Using $(A3)$, we obtain

$$\begin{array}{cc}\frac{d{V}_{2}(t)}{{\text{d}}t}& ={\int }_{0}^{\infty } {K}^{0}(a)\frac{\partial }{\partial t}i(t,a)da\\ & ={\int }_{0}^{\infty } {K}^{0}(a)\left[-\frac{\partial }{\partial a}i(t,a)da-\epsilon (a)i(t,a)\right]da\\ & =-{\int }_{0}^{\infty } {K}^{0}(a)\frac{\partial }{\partial a}i(t,a)da-{\int }_{0}^{\infty } {K}^{0}(a)\epsilon (a)i(t,a)da\\ & =-{\left.{K}^{0}(a)i(t,a)\right|}_{a=0}^{a=\infty }+{\int }_{0}^{\infty } i(t,a)\frac{d}{da}{K}^{0}(a)da-{\int }_{0}^{\infty } {K}^{0}(a)\epsilon (a)i(t,a)da\\ & ={K}^{0}(0)i(t,0)+{\int }_{0}^{\infty } i(t,a)\left({K}^{0}(a)\epsilon (a)-\beta (a){S}^{0}\right)da-{\int }_{0}^{\infty } {K}^{0}(a)\epsilon (a)i(t,a)da\\ & ={K}^{0}\left(0\right)i\left(t,0\right)-{\int }_{0}^{\infty } \beta \left(a\right){S}^{0}i\left(t,a\right)da.\end{array}$$

(3.14)

Let us assume that $\eta =0$ and we will consider the derivative of equation $(A4)$ and then we put $(A5)$ and $(A6)$. Further, keeping in view ${K}^{0}(0)={S}^{0}K$ and $i(t,0)={\int }_{0}^{\infty } \beta (a)S(t)i(t,a)da$ under the assumption of $\eta =0$, we have

$$\begin{array}{cc}\frac{{\text{d}}V(t)}{{\text{d}}t}& =\left(m+d\right){S}^{0}\left(2-\frac{{S}^{0}}{S\left(t\right)}-\frac{S\left(t\right)}{{S}^{0}}\right)-{\int }_{0}^{\infty } \beta \left(a\right)S\left(t\right)i\left(t,a\right)da+{K}^{0}\left(0\right)i\left(t,0\right),\\ & =\left(m+d\right){S}^{0}\left(2-\frac{{S}^{0}}{S\left(t\right)}-\frac{S\left(t\right)}{{S}^{0}}\right)+\left({S}^{0}K-1\right){\int }_{0}^{\infty } \beta \left(a\right)S\left(t\right)i\left(t,a\right)da,\\ & \le \left(m+d\right){S}^{0}\left(2-\frac{{S}^{0}}{S\left(t\right)}-\frac{S\left(t\right)}{{S}^{0}}\right)+\left({\mathfrak{R}}_{0}-1\right){\int }_{0}^{\infty } \beta \left(a\right)S\left(t\right)i\left(t,a\right)da.\end{array}$$

Therefore, ${\mathfrak{R}}_{0}<1$ ensures that ${\text{d}}V(t)/dt\le 0$ holds true. Furthermore, the strict equality holds only if $S(t)={S}^{0}$. Thus, by the Lyapunov–LaSalle invariance principle, the DFE is globally asymptotically stable when ${\mathfrak{R}}_{0}<1$. This finishes the proof.