Optimal Textures for Increasing the Load Support in a Thrust Bearing Pad Geometry

Abstract

We present the calculation results of optimal texture geometries which maximize the supported load for a three-dimensional thrust bearing pad. By making use of the recently developed mean field theory of texture hydrodynamics, we develop an efficient multigrid optimization procedure based on the sequential genetic and conjugate gradient optimization. We show that our model allows to determine optimal solutions based on a two-scale hierarchy of structures, and the existence of particularly effective optimal geometries is presented and discussed.

1 Introduction

The interaction between solids, of interest for the tribological problem, usually occurs in a range of length scales from the macroscopic representative size of the contact (e.g., an Hertzian length, or a bearing nominal contact length for conforming contacts) to the atomic level. In between, it includes the length scales corresponding to the hierarchy of defects (structural, materials inhomogeneity, etc.) commonly available at the interface. By simply restricting our attention to the classical mechanical aspect of a contact, we note that even when those defects are not initially covering the surface, their mesoscale is created as a consequence of wear (in this case permanently) or, in wearless processes as lubricated contacts, simply as a consequence of the gap formation. The reason why this happens in the contact of real solids is that the physics occurring at the mesoscale is needed to bridge the gap between the atomic (where, e.g., friction originates) and the macroscale (where friction is experienced and the motion is imposed). This aspect, in its different outcomes, has been increasingly featured in the wide tribological research of the recent years [1, 2].

Among others, a relatively recent research field involves wet sliding interfaces whose superficial properties are created according to an ordered (periodic) scheme of added defects. In the most common case, those defects are simple microstructural modifications as holes or grooves, e.g., produced with the so-called laser surface texturing (LST) [3, 4]. They are created with the purpose of manipulating the macroscopic friction and load support characteristics of a generic contact pair. However, we have recently theoretically shown that tailored contact characteristics can be gained not only with the physical (i.e., structural) surface texturing, but also with the chemical modification of surfaces (i.e., by adding a slippage texture) [5, 6]. In particular, we made use of a mean field theory of texture hydrodynamics (BTH [5]) for the description of the average flow dynamics induced by the texture. The BTH is based on the homogenization of the Reynolds flow (i.e., the lubrication approximation) within the Bruggeman effective medium (BEM) approach. The theory allows to determine the average flow dynamics at the contact interface in terms of flow and shear stress tensorial factors, which can be analytically calculated as a function of the texture lattice characteristics (e.g., the area density, lattice constants), as well as of the hole depth, shape, etc. The theory can also take into account local slip lengths at the sub-texture scale, as well as a viscosity texturing. In a recent paper, the theory has been intensively tested in comparison with ad hoc numerical calculations [7] as well as with the results of independent investigations [5–7], demonstrating its real suitability to accurately model the texture hydrodynamics problem.

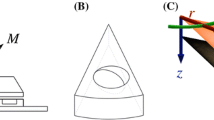
In this paper, we make a step forward in the comprehension of the latter problem and, in particular, we focus on the macroscopic contact conditions given by a single thrust bearing pad (of finite size) in the parallel sliding configuration, see Fig. 1 for the schema. We will make use of the BTH theory, coupled with an ad hoc resolution strategy, to investigate the optimal texture characteristics which maximize the supported load. Different in-plane micro-geometries (e.g., circular or striped) as well as combinations of structural and slippery texturing will be used, for the first time, in a stepped and comprehensive discussion on the optimal surface modifications allowing to maximize the load. The paper is outlined as follows. In Sect. 2, for completeness, we briefly summarize the BTH theory [5], with particular emphasis on the case of circular defects arranged in a squared lattice (Sect. 2.1) and on the striped defects (Sect. 2.2). Then, the BTH is applied to the case of textures constituted by circular or striped defects, both when the micro-defect is structural (Sects. 3.2–3.4), slippery (Sect. 3.5), and structural/slippery (Sec. 3.6). A brief description of the numerical approach is given in the “Appendix”.

Fig. 1

A generic conformal contact (e.g., a thrust bearing pad, as in the schema) subjected to a partial surface texturing. The texture is characterized by an ordered and locally homogeneous lattice of small-scale defects, which in the most general case can be structural defects (e.g., holes, pillars, grooves, ridges, etc.), slippery defects (e.g., elliptic slippage areas, slippage strips, etc.), or even micro-domains where the fluid viscosity is modified with respect to a nominal value. Combinations of the previous mechanisms, e.g., slippery holes, can be modeled as well

2 Summary of the BTH Theory

Here, we summarize the BEM-averaged ([8–10]) texture hydrodynamics theory [5]. We consider the case of a generic-textured surface in relative steady sliding on a smooth mating substrate, see e.g., the schematic of Fig. 3, in the hydrodynamic regime. The lubrication is assumed to occur under isothermal and cavitation-free conditions (however, as recently shown [6], local states of micro-cavitation occurring in a reduced fraction of the contact domain are expected to only marginally affect the model results). In the lubrication approximation, the local (texture scale) hydrodynamics occurring in the representative elementary volume (REV) of interface can be homogenized with the BEM approach, resulting in the effective lubrication equation given by:

$$\nabla \cdot \left[-\varvec{\Uplambda}\left({\bf x}\right) \nabla p\left({\bf x}\right) +\varvec{\Upgamma} \left({\bf x}\right) U_{{\rm m}}\right] =0,$$

(1)

where $p\left({\bf x}\right)$ is the (locally averaged) fluid pressure, U _m the mean surface velocity, $\varvec{\Uplambda}\left({\bf x}\right)$ is the effective hydraulic conductivity tensor and $\varvec{\Upgamma} \left({\bf x}\right)$ is the effective shear flow conductivity tensor, which are functions of the texture characteristics. In particular, $\varvec{\Uplambda}$ and $\varvec{\Upgamma}$ are determined from the tensorial relations [5]:

$$\left\langle {\hbox{d}} \varvec{\Uplambda} \left({\bf I}+{\bf E}_{0}{\hbox{d}} \varvec{\Uplambda}\right) ^{-1}\right\rangle =0$$

(2)

$$\left\langle {\hbox{d}}\varvec{\Uplambda} \left({\bf I}+{\bf E}_{0}{\hbox{d}} \varvec{\Uplambda}\right)^{-1}{\hbox{d}}\varvec{\Uplambda}^{-1}{\hbox{d}} \varvec{\Upgamma}\right\rangle =0,$$

(3)

where the notation $\left\langle \phi \right\rangle$ corresponds to $\left\langle \phi\right\rangle =\sum_{i}c_{i}\phi_{i}$, and where c _i is the texture area density of the generic ith component ϕ _i . Moreover, ${\hbox{d}}\varvec{\Uplambda}= \varvec{\Uplambda}_{i} - \varvec{\Uplambda}$ and ${\hbox{d}}\varvec{\Upgamma}= \varvec{\Upgamma}_{i}-\varvec{\Upgamma}$, where $\varvec{\Uplambda}_{i}$ and $\varvec{\Upgamma}_{i}$ are the hydraulic and shear flow conductivity tensors of the generic ith component, respectively. In this work, we make use of a two-component system, i.e., a texture made of the base material (component of subscript-hf) and the hosted defect (component of subscript-h, circular or striped and characterized by a structural and/or slippage property, see Fig. 2).

Fig. 2

Schema of a two-components system with highlighting of the lattice cell. One component is the circular (or striped, shown elliptical in the figure) defect, whereas the other is the untextured base material

Fig. 3

A surface-textured solid (block) in contact with a rigid solid (substrate) with the untextured surface. The substrate moves with the velocity v ₀, while the block is stationary. The schematic is not equally scaled along horizontal and vertical directions

For the defect, the conductivities are constant and isotropic, resulting into $\varvec{\Uplambda}_{{\rm h}}={\bf I} \alpha_{{\rm h}}h_{{\rm h}}^{3}/ \left(12\eta\right)$ and $\varvec{\Upgamma}_{{\rm h}}={\bf I}\beta_{{\rm h}} h_{{\rm h}}$, where η is the lubricant viscosity, h _h the defect height, I the identity matrix, l _h is the local Navier slip length, and:

$$\begin{aligned} \alpha_{{\rm h}}&= 1+{3}\frac{{l}_{{\rm h}}/h_{{\rm h}}}{1+l_{{\rm h}}/h_{{\rm h}}}\\ \beta_{{\rm h}}&=1+\frac{{l}_{{\rm h}}/h_{{\rm h}}}{1+l_{{\rm h}}/h_{{\rm h}}}. \end{aligned}$$

Similar relations hold for the hosting medium (the base material), where the subscript -h has to be substituted with -hf. Moreover, the tensorial factor E ₀ has to be calculated for each component [5], being a function of (1) the inclusion shape and orientation, and of (2) the same effective hydraulic conductivity tensor $\varvec{\Uplambda}$. Finally, the effective shear stress acting on the unstructured surface reads [5]:

$$\begin{aligned} \left\langle \varvec{\tau}\right\rangle =& \left\langle \frac{\eta/\eta_{0}}{h+l}\right\rangle \eta_{0}{\bf v}_{0}\\ &+\frac{{\bf v}_{0}}{4}\left\langle h \left[1+\frac{l}{h+l}\right] \left[{\bf I}-\left({\bf I}+{\bf E}_{0}d \varvec{\Uplambda} \right)^{-1}\right] d\varvec{\Uplambda}^{-1}d \varvec{\Upgamma}\right\rangle\\ &+\frac{1}{2}\left\langle h\left(1+\frac{l}{h+l}\right) \left({\mathbf{I}}+ {\mathbf{E}}_{0}d\varvec{\Uplambda} \right)^{-1}\right\rangle \nabla p, \end{aligned}$$

(4)

where η ₀ is a reference fluid viscosity (e.g., the low-pressure low-shear viscosity value), and where v ₀ = 2U_m is the velocity of the lower moving untextured surface, see Fig. 3.

2.1 The Flow and Shear Stress Factors for Circular Inclusions in Isotropic Medium

We consider the case of circular defects embedded in an isotropic base conductivity tensor, as it occurs in the case of square grid lattice. In such a case, for both components, we have the following:

$${\bf E}_{0}=\frac{1}{2\lambda}{\bf I},$$

(5)

where λ is the effective hydraulic conductivity of our resulting isotropic interface. By defining the texture area density as $p_{{\rm h}}=\pi d^{2}/\left(4l^{2}\right)$, where l is the lattice constant and d the defect diameter, from Eqs. (2) and (5), we get the following:

$$\left\langle \frac{\lambda -\lambda_{i}}{\lambda +\lambda_{i}}\right\rangle =0.$$

(6)

Since for the defect $\lambda_{i}=\lambda_{{\rm h}}=\alpha_{{\rm h}} h_{{\rm h}}^{3}/ \left(12\eta\right)$ and for the hosting substrate $\lambda_{i}=\lambda_{{\rm hf}}=\alpha_{{\rm f}}h_{{\rm f}}^{3}/\left(12\eta\right)$, and by considering a reference hydraulic conductivity $\lambda_{{\rm s}}=h_{{\rm f}}^{3}/\left(12\eta\right)$, by manipulating Eq. (6), we get the following:

$$\begin{aligned} \tilde{\lambda}=&\lambda/\lambda_{{\rm s}}=\left(2p_{{\rm h}}-1\right) \frac{\tilde{\lambda}_{{\rm h}}-\alpha_{{\rm f}}}{2}\\ &+\frac{1}{2}\sqrt{\left(1-2p_{{\rm h}}\right)^{2} \left(\tilde{\lambda}_{{\rm h}}-\alpha_{{\rm f}}\right)^{2} +4\alpha_{{\rm f}}\tilde{\lambda}_{{\rm h}}}, \end{aligned}$$

(7)

where $\tilde{\lambda}_{{\rm h}}=\lambda_{{\rm h}}/\lambda_{{\rm s}}=\alpha_{{\rm h}}h_{{\rm h}}^{3}/h_{{\rm f}}^{3}$ in the case of constant fluid viscosity. Moreover, from Eq. (3), the effective Couette conductivity γ can be determined as follows:

$$\left\langle \frac{\gamma_{i}-\gamma}{\lambda_{i}+\lambda}\right\rangle =0,$$

(8)

where for the defects γ _i  = γ _h = β _h h _h and for the hosting substrate γ _i  = γ _hf = β _f h _f. Considering a reference conductivity γ _s = h _f, by manipulating Eq. (8), we get the following:

$$\tilde{\gamma}=\gamma/\gamma_{{\rm s}}=\frac{\tilde{\gamma}_{{\rm h}} p_{{\rm h}}\left(\alpha_{{\rm f}}+\tilde{\lambda}\right) +\beta_{{\rm f}}\left(1-p_{{\rm h}}\right) \left(\tilde{\lambda}_{{\rm h}}+\tilde{\lambda}\right)}{p_{{\rm h}}\left(\alpha_{{\rm f}}+\tilde{\lambda}\right) +\left(1-p_{{\rm h}}\right) \left(\tilde{\lambda}_{{\rm h}}+\tilde{\lambda}\right)},$$

(9)

where $\tilde{\gamma}_{{\rm h}}=\gamma_{{\rm h}}/\gamma_{{\rm s}}=\beta_{{\rm h}}h_{{\rm h}}/h_{{\rm f}}$. The effective Reynolds Eq. (1) simplifies then into

$$\nabla \cdot \left[\tilde{\lambda}\frac{h_{{\rm f}}^{3}}{12\eta} \nabla p \right] =\nabla \cdot \left[\tilde{\gamma}h_{{\rm f}}{\mathbf{U}}_{{\rm m}}\right],$$

(10)

where it is clear that $\tilde{\lambda}$ and $\tilde{\gamma}$ corresponds to the pressure and shear flow factors for circular inclusions, respectively (and isotropic lattice).

Finally, the BEM-averaged shear stress acting on the untextured surface, see Fig. 3, reads

$$\left\langle\varvec{\tau}\right\rangle=\phi_{\mathrm{fs}} \eta_{0}\frac{{\bf v}_{0}}{h_{{\rm f}}}+\phi_{{\rm fp}} \frac{1}{2}h_{{\rm f}}\nabla p,$$

(11)

where $\mathbf{v}_{0}$ is the sliding velocity of the lower moving untextured surface, and where the pressure ϕ _fp and sliding ϕ _fs shear stress factors, at constant viscosity, are given by:

$$\begin{aligned} \phi_{{\rm fp}}&=2\tilde{\lambda}\left\langle\frac{\tilde{\gamma}_{i}} {\tilde{\lambda}+\tilde{\lambda}_{i}}\right\rangle\\ \phi_{{\rm fs}}&=\left\langle \left(2-\beta_{i}\right)\beta_{i} \tilde{\gamma}_{i}^{-1}+3\tilde{\gamma}_{i}\frac{\tilde{\gamma}_{i} -\tilde{\gamma}}{\tilde{\lambda}_{i}+\tilde{\lambda}}\right\rangle.\\ \end{aligned}$$

Note in the calculation of the shear stress factors that no new variables are introduced more then a combination of the previously calculated flow factors.

It is always useful to compare the BTH predictions with those available in the literature. In particular, in Fig. 4, we compare the results of Eq. (10) (solid red curves), in terms of nominal film thickness as a function of the applied normal load, with the numerical (solid black curves) and experimental (dashed curves) results reported in Ref. [11] for the case of partially textured thrust bearings. For the contact details, the reader is remanded to the same Ref. [11]. Observe that our predictions are in excellent agreement with those of the independent investigation [11]. The same agreement is confirmed in the comparison of Fig. 5, where we show, for a partially textured thrust bearing, the nominal film thickness (top) and the friction torque (bottom) as a function of the angular speed, as determined from the BTH (red dots), and from the numerical and experimental results of independent investigations [12].

Fig. 4

Nominal film thickness as a function of the applied normal load (solid red curves) compared with the numerical (solid black curves) and experimental (dashed curves) results reported in Ref. [11]. For the case of partially textured thrust bearings (Color figure online)

Fig. 5

Nominal film thickness (top) and friction torque (bottom) as a function of the angular speed. BTH predictions (red dots) are compared with both numerical and experimental results from independent investigations [12]. For a partially textured thrust bearing (Color figure online)

2.2 The Flow and Shear Stress Factors for Striped Inclusions

We consider now the case of striped defects, with major direction aligned along an angle ϕ = π/2 with the reference (transversal texture). In such a case, we have for both components E _0xx = λ ⁻¹₁ , E _0yy = E _0xy = 0 [5], where λ ₁ and λ ₂ are the effective hydraulic conductivities along the x ₁- and x ₂-axis, respectively (note: The effective hydraulic conductivity tensor is principally valued in the adopted reference). Moreover, from Eq. (2), we have the following:

$$\begin{aligned} \left\langle\frac{\lambda_{i}-\lambda_{1}}{\lambda_{i}} \right\rangle & =0\\ \left\langle \lambda_{i}-\lambda_{2}\right\rangle &=0, \end{aligned}$$

and after some algebra we get the following:

$$\frac{1}{\tilde{\lambda}_{1}}=\frac{1-p_{{\rm h}}}{\alpha_{{\rm f}}}+ \frac{p_{{\rm h}}}{\tilde{\lambda}_{{\rm h}}}$$

(12)

$$\tilde{\lambda}_{2}=p_{{\rm h}}\tilde{\lambda}_{{\rm h}}+\left(1 -p_{{\rm h}}\right) \alpha_{{\rm f}},$$

(13)

where as before $\tilde{\lambda}_{1}= \lambda_{1}/\lambda_{{\rm s}}$ and $\tilde{\lambda}_{2}=\lambda_{2}/\lambda_{{\rm s}}$. From Eq. (2), the principal shear flow factors can also be determined:

$$\begin{aligned} \left\langle \frac{\gamma_{i}-\gamma_{1}}{\lambda_{i}}\right\rangle &=0\\ \left\langle \gamma_{i}-\gamma_{2}\right\rangle & =0,\\ \end{aligned}$$

where γ ₁ and γ ₂ are, respectively, the effective shear flow conductivities along the x ₁- and x ₂-axis. After some algebra,

$$\tilde{\gamma}_{1}=\tilde{\lambda}_{1}\left[p_{{\rm h}}{\frac{\tilde{\gamma}_{{\rm h}}}{\tilde{\lambda}_{{\rm h}}}}+ \left(1-p_{{\rm h}}\right)\frac{\beta_{{\rm f}}}{\alpha_{{\rm f}}}\right]$$

and

$$\tilde{\gamma}_{2}=p_{{\rm h}}\tilde{\gamma}_{{\rm h}}+ \left(1-p_{{\rm h}}\right) \beta_{{\rm f}},$$

where $\tilde{\gamma}_{1}=\gamma_{1}/\gamma_{{\rm s}}$ and $\tilde{\gamma}_{2}=\gamma_{2}/\gamma_{{\rm s}}$. Finally, the BEM homogenized shear stress acting on the lower moving untextured surface (sliding at the velocity $\mathbf{v}_{0}$) reads

$$\varvec{\tau}={\tilde{\varvec{\Upphi}}}_{{\rm fs}}\eta \frac{{\mathbf{v}}_{0}}{h_{{\rm f}}}+\frac{h_{{\rm f}}}{2} {\tilde{\varvec{\Upphi}}}_{{\rm fp}}\nabla p,$$

where we have the pressure gradient correction tensor ${\tilde{\varvec{\Upphi}}}_{{\rm fp}}:$

$${\tilde{\varvec{\Upphi}}}_{{\rm fp}}={\tilde{\varvec{\Upgamma}}},$$

where ${\tilde{\varvec{\Upgamma}}}$ has been shown before (i.e., $\tilde{\Upgamma}_{11}=\tilde{\gamma}_{1}$ and $\tilde{\Upgamma}_{22}=\tilde{\gamma}_{2}$). The sliding correction tensor ${\tilde{\varvec{\Upphi}}}_{{\rm fs}}:$

$$\begin{aligned} {\tilde{\varvec{\Upphi}}}_{{\rm fs}}&=\left(p_{\mathrm{h}} \frac{\left(2-\beta_{{\rm h}}\right)\beta_{{\rm h}}}{\tilde{\gamma}_{{\rm h}}} +\left(1-p_{{\rm h}}\right) \left(2-\beta_{{\rm f}}\right)\right) {\mathbf{I}}\\ &\quad+3\left(p_{{\rm h}}\frac{\tilde{\gamma}_{{\rm h}}}{\tilde{\lambda}_{{\rm h}}} \left[\begin{array}{ll} \tilde{\gamma}_{{\rm h}}-\tilde{\gamma}_{1} & 0 \\ 0 & 0 \end{array}\right] +\left(1-p_{{\rm h}}\right) \frac{\beta_{{\rm f}}}{\alpha_{{\rm f}}} \left[\begin{array}{ll} \beta_{\mathrm{f}}-\tilde{\gamma}_{1} & 0 \\ 0 & 0 \end{array}\right]\right).\\ \end{aligned}$$

The reader is kindly remanded to Ref. [7] for an extensive discussion on the BTH for striped inclusions. It is also implicitly understood that in case of striped texture unaligned to form a transversal texture, the effective conductivity tensors as well as the frictional tensors have to be rotationally transformed.

3 Application to Plain Bearings: Optimal Texture to Maximize the Load

In this section, we characterize the problem of texture optimization targeted to maximize the load support in thrust (plain-) bearing geometries. Observe, however, that the mean field theory as well as the developed numerical scheme (see the “Appendix”) is not restricted in their use to the thrust bearing geometry, i.e., the model requires only cosmetic modifications when applied to other macro-contact geometries. We assume a steady sliding contact occurring under the iso-viscous rigid lubrication regime and isothermal conditions. Moreover, we focus on the single pad geometry, as shown in the schematic of Fig. 6. The mean field lubrication is described by Eq. (1), whereas the flow and shear stress tensors, which locally depend on the applied texture, are reported in Sects. 2.1 and 2.2.

Fig. 6

Schematic of the single pad geometry

In Table 1, we summarize the texture schemes adopted in the calculations. For the reasons we show in the following, the circular shape will be used only for the microstructural texturing, whereas the striped geometry, respectively, with (optim. dir.) and without (fixed dir.) the optimization of the strip direction, will be used for both microstructural, micro-slippery, and combined structural/slippery texturing.

Table 1 Texture schemes adopted in the calculations

As previously described, the slippage has been characterized by a Navier’s slip length l. In this work, l = 0 in the case of no-slip, whereas l is set to $\infty$ in the case where a slippage texture is adopted. In reality, of course, the slip length will have a finite value, but this is unimportant for the present discussion.

The numerical procedure, reported in the “Appendix”, is here briefly summarized. Eq. (1) is solved (with Cauchy’s boundary conditions), and the texture (in terms of effective conductivities) is optimized at different degrees of mesh refinement; in particular, at the coarsest level, the texture is optimized recurring to a genetic algorithm (GA), which allows to avoid local maximums to be selected. At successive finer meshes, the texture is refined recurring to a conjugate gradient (CG) optimization. The final texture result is a map describing the (locally averaged) structural, slippery, and in-plane shape properties (e.g., the direction of the strip) to be realized on the pad. In the following, however, we first calculate (optimized) Akers’ pad geometries to be used as reference for the successive optimal texture calculations.

3.1 Optimized Untextured Plain Bearings: The Akers’ Geometry for Different Pad Aspect Ratios

In this section, we determine the optimal pad geometry which maximizes the load in the case where a structural modification, obtained with an uniform material remotion, is applied on the pad. The pad geometry is expected, therefore, to resemble the classical Akers’ construction [13]. Since (in this case) no texture is used, the flow factor tensors in Eq. (1) are simply identity matrices, resulting in the well-known Reynolds equation. The latter is made dimensionless in the in-plane lengths with B (half of the pad width, see Fig. 6), in the vertical lengths with h _f (the nominal separation), and in the pressures with $p^{\ast}=12\eta BU_{{\rm m}}/h_{{\rm f}}^{2}$, resulting in

$$\frac{\partial}{\partial x_{1}}\left( h^{3}\frac{\partial p}{\partial x_{1}} \right) +\frac{\partial}{\partial x_{2}} \left(h^{3}\frac{\partial p}{\partial x_{2}}\right) =\frac{\partial h}{\partial x_{1}}.$$

For each value of the bearing aspect ratio $L/\left(2B\right)$ it is then possible to determine the distribution of material remotion which maximizes the supported load N. As a reference, we have used the load supported by the optimal Akers’ geometry for the square-sized bearing pad N _A [13]:

$$N_{{\rm A}}=0.124\eta v_{0}\left(2B\right)^{3}h_{0}^{-2},$$

where 2B is the side length. Due to the simplicity of the problem, the adopted optimizer at all grid scales has been chosen to be the CG.

In Fig. 7, we thus show the normalized load factor $W_{{\bf e}}=\left[N/L\right]/\left[N_{{\rm A}}/\left(2B\right)\right]$ as a function of the pad aspect ratio $L/\left(2B\right)$, as obtained with the found optimal pad geometrical configuration. N/L as well as $N_{{\rm A}}/\left(2B\right)$ are proportional to the average pressure value at the interface and, therefore, represent the effective load generation capability to be used in comparison between different pad aspect ratios. Note that for 2B/L = 1, W _e = 1. For increasing aspect ratios, the support capability increases up to the 30 % with respect to the square (Akers’) geometry which, therefore, is not the optimal solution for the pad. However, a further increase in the aspect ratio, after a certain plateau, drastically reduces the optimal load.

Fig. 7

Normalized load factor $W_{e}=\left[N/L\right]/ \left[N_{{\rm A}}/\left(2B\right)\right]$ as a function of the pad aspect ratio $L/\left(2B\right)$, as obtained with the calculated optimal pad geometrical configuration. The inserted numbers indicate the optimal solutions shown in Fig. 8a–f

The optimal geometries, corresponding to the inserted numbers of Fig. 7, are shown, respectively, from Fig. 8a–f. First, observe that the geometry reported in Fig. 8a shows a load support equal to N _A, despite the numerically optimized and the Akers’ geometry (see Ref. [13]) do not exactly match. Indeed, our solution does not present a stepped variation of the gap (as for the Akers’ pad), and this suggests that the lubrication problem is not particularly affected by the exact solution close to the borders of the middle-scale structures created inside the domain. Note also that the maximum gap in the worked areas (red dots in the figures) increases by increasing the aspect ratio, reaching the value of h _h/h _f = 3.3 in correspondence of the highest load optimal geometry (given by 2B/L≈2/5). By further increasing the aspect ratio, Fig. 7 shows a plateau in the optimal load. The reason why this occurs can be easily understood by observing Fig. 8e and f. Indeed, by increasing the aspect ratio, the optimal solution is constructed by naturally replicating the optimal geometry of Fig. 8d along the sliding direction, in order to minimize the side leakages. This, however, is not as efficient as it could be imagined, since the optimized geometry placed at the pad outlet (see Fig. 8e) already receives only a fraction of the inlet flow, due to the side leakage occurring in the front gap. However, while for 2 consecutive gaps, this combination still produces normal load (the plateau in Fig. 7), for increasing aspect ratios, the lubrication occurs clearly starved in the average.

Fig. 8

Optimal geometries corresponding to the inserted numbers of Fig. 7. Red dots indicate the positions of largest gap depth (Color figure online)

The pressure field corresponding to the optimal geometry (2B/L ≈ 2/5) is shown in Fig. 9. As it might be expected, the latter geometry makes an efficient use of its nominal area, since the fluid pressure raises in almost the entire pad domain.

Fig. 9

Pressure field corresponding to the optimal geometry (2B/L≈ 2/5) of Fig. 8d. Top values of dimensionless pressure are of order 0.15

3.2 Optimization with Circular Structural Texturing

In this section, the circular defect is investigated in terms of structural texturing. The free variable (to be optimized along the contact domain) is the hole ratio h _h/h _f. The texture area density p _h, instead, is kept to a constant value.

In Fig. 10a, we show the normalized load factor W _e as a function of the pad aspect ratio $L/\left(2B\right)$, obtained with the found optimal pad geometrical configurations for p _h = 0.3 and 0.5. As discussed in a recent work [7], adopting a structural micro-texturing in substitution of a Rayleigh (in two-dimensions) or an Akers’ (in three-dimensions) geometry is not an efficient solution, and this is exactly confirmed in Fig. 10a where the curves lay quite beyond the N _A value. The fluid pressure field corresponding to the optimal geometry at p _h = 0.3 is shown in Fig. 10b. Note that the pressure rise involves only part of the pad domain, resulting in a maximum fluid pressure of order 0.02, about one tenth of the Akers’ optimal pressure.

Fig. 10

Optimization of micro-structuring with circular shape (e.g., micro-holes with square lattice)

The optimal geometries for p _h = 0.5 are shown in Fig. 11a–d. Observe that the textured area generally resembles the Akers’ geometry, both in the worked domain shape and in the values of maximum hole depth. However, the produced normal load is remarkably much lower, and it scales, approximately, with the texture area density p _h. We conclude, for this macro-geometry, that a structural texturing with circular defects does not produce any convenient load support with respect to the adoption of classical optimal geometries.

Fig. 11

Optimal micro-hole textures, for p _h  = 0.5. Red dots indicate the positions of the microstructures with largest depth (Color figure online)

3.3 Optimization with Micro-Grooves in the Longitudinal and Transversal Configuration: The Role of Fluid Redirection

In this section, we will maximize the load recurring to a structural striped texture, i.e., to micro-grooves. While circular defects, arranged in an isotropic lattice, provide isotropic conductivities (with no other exploitable property), striped superficial defects are well known [5–7] to provide anisotropic average flow conductivities, which might be used to practically obtain the so-called flow redirection and retainment widely discussed in the recent literature [6]. Indeed, it has been demonstrated [6] that an effective way to increase load support in bearings, coupled with a decrease in friction, is to improve the entrainment flow as well as to retain it under the sliding interface by minimizing the side leakage. Recent experimental findings show, instead, the opposite, i.e., the grooved geometry is counter-beneficial in terms of friction reduction [4]. The contradiction is, however, only apparent since the reported friction measurements were performed on conformal contacts characterized by a total structural texturing of the surface. Indeed, in the case of total texturing, the load support is basically generated by the collective cavitation of most of the textured area, which generates a strongly reduced bearing pressure with respect to a partial texturing of the surface (see e.g., Ref. [14]). The latter, due to the absence of film rupture (and reformation), allows for the entire bearing area to continuously contribute to the pressure rise at the interface, resulting in the best option for optimizing (if allowed) contact geometries.

In order to shed light on the role of fluid redirection and retainment, we solve the optimization problem with the grooved micro-geometry arranged in the transversal (groove direction perpendicular to the sliding direction) and longitudinal configuration. The free variable is the hole ratio h _h/h _f, whereas the texture area density p _h is kept to a constant value. In Figs. 12a and 13a, we show, respectively for the longitudinal and transversal configuration, the normalized load factor W _e as a function of the pad aspect ratio $L/\left(2B\right)$, obtained with the calculated optimal pad geometrical configurations for p _h = 0.3 and 0.5. The resulting fluid pressure fields are shown, respectively, in Figs. 12b and 13b. It is interesting to observe that despite the texture micro-geometries differ only in their orientation, the resulting effect in terms of optimal bearing load is remarkably different. In particular, the largest optimal support by the transverse texture is less than one-third of the longitudinal texture value. Moreover, the pressure fields of Figs. 12b and 13b show that the transversal texture provides a maximum pressure even less than the one for the circular structural texturing (compare with Fig. 10b). The reason of such huge difference is due to the different amount of side leakage for the two groove directions. Indeed, the transverse configuration provides larger flow conductivities in the direction of the side leakage, facilitating the flow escape and, because of the anisotropic property of the flow factor tensors, reducing the amount of inlet flow. This is confirmed in Fig. 14, where we show the optimal geometries for p _h = 0.3 (the transverse configuration) corresponding to the inserted numbers of Fig. 13a. Note that the maximum groove ratio h _h/h _f ≈ 1.6 for the all pad aspect ratios, confirming that, due to the strong anisotropy of the interface, even if increasing the groove depth would improve the inlet flow, the same increase would determine a build up of a larger side flow, with a consequent negative effect on the average bearing pressure. Therefore, the transverse micro-geometry is simply not effective for the purpose of increasing the supported load.

Fig. 12

Optimizations for a grooved micro-geometry in the longitudinal configuration

Fig. 13

Optimizations for a grooved micro-geometry in the transversal configuration

Fig. 14

Optimal geometries for p _h  = 0.3, in the transverse configuration, corresponding to the inserted numbers of Fig. 13a. Red dots indicate the positions of the microstructures with largest depth (Color figure online)

The inverse occurs for the longitudinal configuration, see Fig. 15. Note that the optimal solutions are characterized by two (obviously-) symmetric suction heads placed at the inlet, indicated by the highest groove ratio (red dots) in Fig. 15. The reason why those macrostructures are generated by the optimization algorithm is related to the improvement of the inlet flow. As also discussed in Refs. [2, 6, 7, 15], the locally averaged surface properties of any generic wet contact, as well as their coupled (long-ranged) interaction required by the fluid mass conservation constraint, cause the macroscopic (i.e., collective) property of the same contact, such as the supported load. Therefore, not only local (texture-scaled) properties have to be optimized, but also their mutual interaction occurring at the length scales in between the micro- and the macro-size of the contact. In order to maximize the entrainment flow, the topography at the inlet is microstructured to make use at best of the entire inlet side as an effective entrainment side. Indeed, despite of the favorable local anisotropic behavior of the texture, the direction of the average pressure gradient at the inlet side borders would produce a certain component of flow in the lateral direction, resulting in the immediate leakage of the entrainment flow. This effect is remarkably reduced by including (at the inlet borders) suction fingers, which allow for the flow to be redirected, at a scale larger than the scale of the grooves, in the internal portion of the domain, as clearly visible in Fig. 15. Anyway, as expected by the previous argumentations, the load support is lower than the one provided by the Akers’ solution.

Fig. 15

Optimal geometries for p _h  = 0.3, in the longitudinal configuration, corresponding to the inserted numbers of Fig. 12a. Red dots indicate the positions of the microstructures with largest depth (Color figure online)

3.4 Optimization of Micro-Grooves with Nonuniform Direction: Fluid Redirection and Restraint Occurring in the Micro-Herringbone Geometry

In this section, we relax the micro-grooves direction, which becomes now a free variable in the optimization process. We decide to perform two investigations; in particular, we optimize by excluding from the optimization the lateral borders (namely, without side-border optimization), and by including those (namely, with side-border optimization), in order to have a better understanding of the flow redirection and restraint in the optimized configurations. The results, in term of optimal geometries for p _h = 0.5 and 2B/L = 1, are shown in Fig. 16a, c, respectively, for the without and with optimization. In the latter figures, the red strips show the local angular alignment of the grooves (in the scaling of the ghaphs), whereas the red circles indicate, hereinafter, that no striped defect is locally present (please consider that the number of strips indicated in the figures has only a qualitative purpose, i.e., they do not represent in any way the lattice and dimensions of the defects, nor they have been somehow scaled. The red strips have been drawn only to show the local directions of the defects, as well as the areas wherein the defects have to be realized). Therefore, in this section, the red circles simply correspond to the untextured areas. Observe in Fig. 16a that suction fingers have been created to increase the inlet flow, as well as the micro-grooves have been aligned in such a way to hinder the side flow and redirect the same toward the inner part of the domain. This determines a large amount of fluid particles sheared at the contact interface and, consequently, an increase in the bearing pressure. When lateral borders are included in the optimization, the resulting optimal geometry is shown in Fig. 16c. Observe in the latter case that the suction fingers are placed at the inlet corners and, moreover, they are coupled with micro-herringbone geometry on the inlet part of the lateral sides. Interestingly, optimal micro-grooved geometries use a certain (inlet) portion of the lateral side to best harvest flow from the environment. Moreover, expulsion fingers are created on the outlet corners of the pad; this allows, in the average, to increase the length of the fluid particle trajectory and, therefore, to obtain a prolonged shearing action on the same fluid particles. Therefore, the flow is only partially exiting from the middle part of the rear side (i.e., moving along the shorter distance), since it is also forced to be routed and sheared through the rear fingers.

Fig. 16

Optimization of the grooved micro-geometry for p _h  = 0.5 and 2B/L = 1. The red circles in a, c indicate the untextured areas (Color figure online)

The neat effect of the micro-groove optimization is shown in Fig. 17 in terms of normalized load factor W _e as a function of the pad aspect ratio $L/\left(2B\right)$, for p _h = 0.3 and 0.5. Observe that the combination of suction fingers, rear fingers, and micro-herringbone geometry allows for an important load support increase only over large values of $L/\left(2B\right)$, as expected due to the increase in the length of the particle routing under the contact. However, accordingly to the previous argumentations, and apart from the optimal solutions at large values of $L/\left(2B\right)$ (which, anyway, do not represent practicable configurations), the Akers’ geometry determine the optimal loads.

Fig. 17

Normalized load factor W _e as a function of the pad aspect ratio $L/\left(2B\right)$, for p _h = 0.3 and 0.5

3.5 Optimization with a Slippery Striped Texture

In the previous sections, we have discussed about the main mechanisms, obtained by the combined genetic/conjugate gradient optimization of microstructural texturing, which mutually contribute to maximize the load support in a generic wet sliding contact. For the case of (plain) thrust bearings, in particular, we have stated that optimized micro-structures do not provide a load support capability larger than the classical Akers’ like geometry would provide. However, surface texturing should not be limited to the micro-structuring; indeed, here, we make use of a different boundary condition describing the defect and, in particular, we focus on a texture made of slippery micro-strips. In such a case, the local micro-strip direction, the slip length l _h describing the defect (slippery strip), and the slip l _hf of the remaining domain (slippery substrate) are the three free scalar fields to be searched for the optimal load support. Since the defect is only slippery, we set h _h/h _f = 1. Note that we have optimized, in alternative to the (unbounded) slip length, its rephrased parameter given by β _h (and β _hf for the substrate) as free variable, which strictly monotonically varies with the slip length and, more important, has bounded values between 1 and 2.

In Fig. 18a, we show the optimal geometry at p _h = 0.5 for $L/\left(2B\right) =1$, whereas the corresponding fluid pressure field is shown in Fig. 18b. Observe that the inlet side of the contact is predicted to be fully slippery, i.e., the applied slippage has no preferential direction. Moreover, the full slippery domain resembles, as expected, the Akers’ shape. Note that, for p _h = 0.5, there is no difference between the slippery strip and slippery substrate texturing; however, when optimizing with different texture area densities, the optimal load curve as a function of the pad aspect ratio is reported in Fig. 19 for p _h = 0.3, 0.5, 0.7, 0.9. Interestingly, the all curves superpose till large values of pad aspect ratios, since the full slippery inlet area solution is common to all cases.

Fig. 18

Optimization with a slippage texture at p _h  = 0.5 for $L/\left(2B\right) =1$. Optimal geometry and corresponding fluid pressure field (Color figure online)

Fig. 19

Optimal load curves as a function of the pad aspect ratio, for the slippery texture. For p _h  = 0.3, 0.5, 0.7, 0.9

Moreover, despite the predicted loads are larger than the Akers’ values of corresponding pad aspect ratios (for relatively small ratios), the maximum load for the slippery surface is not too far from the maximum load obtainable from the Akers’ geometry. This is expected since the Navier’s slippage condition is equivalent to a no-slip condition applied under the surface, i.e., it is formally geometrically equivalent to an Akers’ geometry; therefore, the maximum supported load cannot sensibly differ from the Akers’ one.

3.6 Super-Bearings: Optimization with a Combined Structural/Slippery Striped Texture

In the previous sections, we have shown the role of the grooved micro-geometry and slippery strip, as well as of other larger-scale structures such as suction and expulsion fingers, and micro-herringbones, as mechanisms to increase the load support capability by optimizing the flow redirection and restraint occurring in the contact zone. However, as expected at least for the structural case, none of the geometries obtained from the separate microstructural and micro-slippery surface optimization has showed a neatly improved load support with respect to the Akers’ solution. However, we know, from recent investigations, that the combined structural/slippery texture can remarkably enhance the load support in the case of one-dimensional wedge bearings [6]. Here, we make use of the GA-CG optimization in order to determine whether a mixed texture can provide a greatly improved load as in the 1D case (where the restraint is effectively given by the one-dimensionality of the contact itself). In such a case, the local micro-strip direction, the slip length l _h and the depth h _h/h _f describing the defect (slippery strip), and the slip l _hf of the remaining domain (slippery substrate) are the four scalar fields to be searched for the optimal load support. In Fig. 20a–d, we show the distribution of micro-slippage on the contact domain for the optimal geometries at, respectively, $L/\left(2B\right) =1, 2$ and 4, with a texture area density p _h = 0.5. The distribution of structural micro-grooves, completing the description of the previous optimal geometries, is shown in Fig. 21a–d, where we also report, with blue contour lines, the areas identifying the different slippery boundary domains.

Observe that the optimal geometries show, interestingly, a common rule: Whether slippage is locally included, then also the micro-groove has to be realized on the surface. The opposite, instead, does not hold (see white domains in Fig. 20a–d where red strips are indicated). As a general conclusion, the optimal geometry is characterized by a lattice of grooves, with a certain local angular misalignment with respect to the sliding direction, whose distribution in the contact domain depends on the pad aspect ratio, and where only part of such a distribution domain is subjected to an additional slippage texturing. As a second common feature, we observe that the local angular alignment of the striped defect perfectly accomplishes the middle-scale geometry (e.g., the both slippery or slippery strip domains), see Fig. 20d. This suggests that not only the local slippage improves the local, groove-induced fluid dynamics (targeted to the maximum load support), but also the middle-scale slippage structures are functional to the middle-scale flow dynamics induced by the grooves. This two-scale hierarchy of structures (the micro-scale defects and the middle-scale domains), characterizing the optimal geometries, is interestingly very similar to the few-scales hierarchical solutions optimized by Nature, e.g., as in the case of the Gecko foot (setae and spatulae), the Lotus leave (cuticle and wax crystals), shark skin (dermal denticles and grooves), etc. We stress therefore that our mean field theory, when solved in conjunction with the GA-CG optimization procedure, allows (as shown here for the first time) to calculate bio-mimicking pad geometries, a result which would not be probably possible with a full-scale optimization of the contact.

Fig. 20

Distribution of micro-slippage on the contact domain for the optimal geometries at, respectively, $L/\left(2B\right) =1$, 2 and 4, with a texture area density p _h  = 0.5 (Color figure online)

In Fig. 20a–d, the shape of the domains characterized by the slippery grooves (which basically coincides with the slippery strip domain) is strongly varying depending on the pad aspect ratio. In particular, it increases in its relative extension, coupled with the shrinking of the inlet both slippery domain, when increasing the pad aspect ratio. For the case at $L/\left(2B\right) =4$, the slippery strip domain occurs on the larger part of the contact domain, determining a large extension of the micro-herringbone geometry, whereas the both slippery area is shaped as a funnel to increase the flow restrain under the contact. Moreover, we find very interesting to note that such middle-scaled slippage structures are shaped very closely to the middle-scale structures describing the micro-grooves of almost constant depth, see Fig. 21a–d. Due to the underlying smart aspect of such bio-mimicking geometries, we may expect a great improvement of the load support with respect to the Akers’ solution. This is already clear by observing in Fig. 22 the fluid pressure field, as obtained for the optimal previous configurations, where maximum values are (for the all aspect ratios) larger that the values characterizing the Akers’s optimal geometry.

Fig. 21

Distribution of structural micro-grooves, completing the description of the optimal geometries whose slippage is described in Fig. 20. We also report, with blue contour lines, the areas identifying the different slippery boundary domains shown in Fig. 20a–d (Color figure online)

Fig. 22

Fluid pressure fields as obtained from the optimal configurations shown in Figs. 20 and 21

Finally, in Fig. 23, we report the dimensionless load support as a function of the pad aspect ratio (red curves), in comparison with the predictions for the Akers’ geometry (gray curve) and of the optimal slippery micro-strip texture (black curves, see Sect. 3.5). Note that even for small values of texture area density p _h, the supported load is larger that the Akers’ results for all aspect ratios. In the case of p _h = 0.9, the maximum load is about 70 % larger than for the Akers’ square pad for $L/\left(2B\right) =2$ and 4, so that a super-bearing configuration will occur in between those values. Observe also that the supported load almost increases by increasing the texture area density, suggesting that the middle-scaled structures have a large weight than the local striped defect in contributing to the load support for the plain bearing geometry.

Fig. 23

Dimensionless load support as a function of the pad aspect ratio (red curves), in comparison with the predictions for the Akers’ geometry (gray curve) and for the optimal slippery micro-strip textures (black curves, see Sect. 3.5) (Color figure online)

4 Conclusions

We have discussed on the optimal texture distribution which maximize the supported load for a three-dimensional thrust bearing pad in the parallel configuration. We have used the recently developed mean field theory of texture hydrodynamics (BTH) which allows to accurately calculate the average interface flow dynamics within the lubrication approximation and to easily model circular or elliptical or striped micro-geometries characterized by structural and/or slippery properties. By adopting a multigrid optimization procedure based on the genetic and conjugate gradient optimization, our model has found optimal solutions based on a two-scale hierarchy of structures, bio-mimicking well-known Nature optimized surfaces. The existence of particularly effective optimal geometries (we call super-bearings) has also been presented and discussed. With this work, we demonstrate the ability of an optimized surface texture to remarkably affect the macroscopic properties of a generic sliding contact, confirming the validity of the BTH model as an effective tool for the accurate and low computing cost prediction of texture hydrodynamics.

Appendix: Details on the Numerical Model

Equation (1) has been made dimensionless in the in-plane lengths with B (half of the pad width, see Fig. 6), in the vertical lengths with h _f (the nominal separation) and in the pressures with $p^{\ast}=12\eta BU_{{\rm m}}/h_{{\rm f}}^{2}$, resulting in:

$$\nabla\cdot\left[ -{\tilde{\mathbf{\Lambda}}}\nabla p+{\tilde{\mathbf{\Gamma}}\mathbf{e}}_{1}\right] =0,$$

(14)

to be solved with Cauchy boundary conditions (zero relative pressure at the borders). Equation (14) has been discretized with the control volume approach, leading to the following:

$$\begin{aligned} 0=&\Updelta_{{\rm y}}\left[\lambda_{{\rm xx}}p_{,{\rm x}} +\lambda_{{\rm xy}}p_{,{\rm y}}-\gamma_{{\rm xx}}\right]_{i+1/2}\\ &-\Updelta_{{\rm y}}\left[\lambda_{{\rm xx}}p_{,{\rm x}}+\lambda_{{\rm xy}} p_{,{\rm y}}-\gamma_{{\rm xx}}\right]_{i-1/2}\\ &+\Updelta_{{\rm x}}\left[\lambda_{{\rm yx}}p_{,{\rm x}}+\lambda_{{\rm yy}}p_{,{\rm y}}-\gamma_{{\rm yx}}\right]_{j+1/2}\\ &-\Updelta_{{\rm x}}\left[\lambda_{{\rm yx}}p_{,{\rm x}}+\lambda_{{\rm yy}}p_{,{\rm y}}-\gamma_{{\rm yx}}\right]_{j-1/2}, \end{aligned}$$

(15)

where forward (cross) derivatives have been adopted [e.g., $\left(p_{,{\rm y}}\right)_{i+1/2}\approx\frac{1}{2\Updelta_{{\rm y}}}\left(p_{i,j+1}-p_{i,j}+p_{i+1,j+1}-p_{i+1,j}\right)$] to stabilize the scheme. The set of linear equations represented by Eq. (15) is solved by a simple Jacobi inversion. Simulations have been run on a coarsest grid with n ¹_x  = n ¹_y  = 10 points (first level mesh), with five k-levels of mesh refinement, characterized by the rule $n_{{\rm x}\left({\rm y}\right)}^{k+1}=2n_{{\rm x}\left({\rm y}\right)}^{k}.$

The optimization procedure is drawn in Fig. 24. At the coarsest level, the optimal solution is searched with a Genetic Algorithm (GA), which allows to avoid being trapped in local maxima. On the finer meshes, the optimum search is performed with the conjugate gradient (CG) method, which allows to refine the solution at each length scale. A typical texture optimization output is shown in Fig. 25, where we present the optimal slippage areas for the structural/slippery texture (see Sect. 3.6), and for $L/\left(2B\right) =4$ and p _h = 0.9.

Fig. 24

Optimization procedure. Schematic

Fig. 25

Typical texture optimization output in term of optimal slippage areas for the structural/slippery texture (see Sect. 3.6), and for $L/\left(2B\right) =4$ and p _h  = 0.9