1 Introduction

Porous medium is defined as materiel volume consisting of solid matrix with an interconnected void. The main property of porous medium is characterised by its porosity which is the ratio of void space to total volume of the medium and permeability, i.e. the flow conductivity in porous medium. One of the earliest study of fluid flow in porous media is based on Darcy’s law (Muskat 1937). Brinkman (1947) described extension of Darcy law by using the boundary condition. He found a relation between permeability and particle size density. Brinkman (1949) extended his work in dense porous medium. Whitaker (1986) gave a detailed description about theoretical derivation of Darcy law. He analysed the stokes problem by volume averaging method through rigid porous medium and obtained expression for momentum equation and mass conservation equation analytically in the form of volume averaging velocity and pressure. The flow of non-Newtonian fluid in porous media is also very interesting phenomenon for researchers in these days. Odeh and Yang (1979) discussed power law fluid in porous media and obtained a closed form solution for steady and unsteady flow. Mckinley et al. (1966) also described the aspect of non-Newtonian flow through porous media.

There are various application based on the theory of non-Newtonian flow in biological fluid flow system . The most important fluid of our body is blood, which is very complex in nature. Blood exhibits both nature, Newtonian when it flow under high shear stress(flow in large artery) non-Newtonian when it flow under low shear stress (flow in micro vessels). Sochi (2010) reviewed the various aspects of non-Newtonian flow in porous media. He described the time-dependent and time-independent model of non-Newtonian flow with methods like bundle’s of beds, numerical. The water and other nutrients are carried by blood through microvessels and these nutrients absorbed by permeable vessels wall surrounding by tissues. The study of Pries et al. (1996) gives the overall description of blood flow in microvessels as porous medium. Khaled and Vafai (2003) gave thoroughly reviewed discussion on various aspect of heat and mass transfer in biological tissue by using Darcy and Brinkman models. This study also described briefly the bioconvection, bioheat models and energy transport by different models.

Blood vessels in human circulatory system exhibit the best example of porous media in biological system. Tang and Fung (1975) gave the idea of fluid flow through permeable wall using Darcy flow system which is covered by porous media in pulmonary circulatory system of micro-blood vessels alveoli of human lungs. He found that larger value of permeability gave the larger amount of fluid exchange between channel and porous layer. Goharzadeh et al. (2006) experimentally investigated the existence of thin transition Brinkman layer between fluid porous interface. This study shows the effect of transition Brinkman layer on velocity profile. They found that the velocity decreases continuously downward from fluid in porous layer. In a problem of two fluid layer porous medium, (Nield 1983) discussed the boundary effect for Rayleigh–Darcy convection and found a relation between Brinkman equation and Beavers Joseph boundary condition. Hill and Straughan (2008) and Straughan (2008) have done remarkable work in this field by considering the three layer model of porous media flow in a channel. They considered Newtonian flow overlying thin transition Brinkman layer covered by Darcy layer. They discussed the stability of flow numerically for the depth of Brinkman layer corresponding to fluid layer and found the significant effect of it on the velocity profile, viscosity ratio and porosity etc. A non-Newtonian flow surrounded by Newtonian fluid covered by cylindrical porous layer has been discussed by Sacheti et al. (2008). A numerical simulation of coupled fluid flow system of Newtonian fluid with Brinkman and Darcy porous medium has been discussed by Ehrhardt (2010).

A lot of work has been done in modelling of blood flow in various type of diseased blood vessels. Shukla et al. (1980) have proposed a work on blood flow in small radius artery with mild stenosis by assuming two-layered model of blood flow. The study explained the effect of peripheral layer viscosity on flow rate and velocity. Shivakumar et al. (1986) have modelled the arterial blood flow bounded by varying gap of porous layer. Chakravarty and Datta (1992) discussed the pulsatile flow of blood in constricted artery by assuming the arterial wall as porous and elastic. They configured the wall in Darcy layer (tunica media) filled with Newtonian fluid. They considered blood as viscoelastic in nature which coupled with Newtonian fluid and found the effect of permeability on wall shear stress, velocity and flow rate for different shape and size of constriction. Cardiovascular study says that the blood flow in small radius blood vessels, i.e. under low shear stress behaves like non-Newtonian fluid and hold satisfactorily the Casson model. Srivastava and Saxena (1994) have discussed the blood flow in two-layered model as non-Newtonian Casson model in core region and Newtonian in peripheral region with mild stenosis. Dash and Mehta (1996) studied the non-Newtonian blood flow as Casson fluid in homogeneous porous medium. In this work, they discussed the effect of constant permeability and variable permeability on velocity and flow rate. Haldar and Anderson (1996) have proposed their work for two-layered model of blood flow through stenosed artery. It was found that the yield stress which is an extra stress in Casson fluid made an affect on the flow in terms of velocity, flow rate in homogeneous porous medium and permeability also (Dash et al. 1997). Ponalagusamy (2007) studied the effect of shape of stenosis and slip velocity in two-layered model of arterial blood flow with mild stenosis. Sankar (2009) and Sankar and Lee (2010) have discussed the problem of two-layered Casson fluid model of blood flow in small catheterised artery and artery with mild stenosis. Misra et al. (2011) discussed a mathematical model of double stenotic porous artery under externally applying magnetic field. The study revealed that the pressure gradient increases with rise in hematocrit. Ponalagusamy and Selvi (2011) proposed a theoretical study on two-layered Casson model of blood flow through stenotic artery with axially variable slip velocity on wall. Mehmood et al. (2012) applied the Numerical method of MAC and SOR for multi-irregular porous stenotic artery. Boodoo et al. (2013) developed a theoretical study of two fluid model for porous artery considering micro-polar fluid in core region as non-Newtonian and plasma in peripheral region as Newtonian. The wall of the artery is classified as porous medium consisting a thin transition Brinkman layer followed by a Darcy region. They concluded that the rise in hydraulic resistivity gives slower velocity in both region.

In the present study, we made an effort to develop an analytical solution for porous stenotic artery. We considered the two fluid model approach of blood flow consisting a red blood cell layer in core region as Casson fluid and Cell free layer of plasma fluid in peripheral region as Newtonian. The blood vessels were taken as constricted porous media. The inner layer (tunica intima) consists of a thin transition Brinkman Layer followed by Darcy layer of soft tissue with tissue fluid (tunica media). An analytical expression is obtained for core and peripheral velocity, volume flow rate and wall shear stress. The effect of permeability, yield stress, constriction shape parameter and plasma layer thickness on velocity, wall shear stress and volume flow rate is discussed graphically by using some previous numerical and experimental findings.

2 Mathematical Formulation

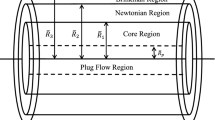
Let us consider the flow of blood through the constricted artery which is modelled as circular cylindrical tube. The wall of the tube assumed as two-layer porous region. The outer layer is modelled as Darcy layer, and the inner layer is modelled as Brinkman layer. The blood flow through the artery is assumed as two-layer model. In peripheral region, it is Newtonian in the form of plasma and in core region it is the suspension of cells (RBC, WBC etc.) in the form of non-Newtonian Casson fluid. The porous region filled with the Newtonian fluid. Let (r, \(\theta \), z) be the cylindrical polar coordinate system in which z axis taken along the axis of constricted segment under the study while r, \(\theta \) are taken as the radial and circumferential region. The geometry (Fig. 1) (Ponalagusamy 2007) of the constricted region is given as:

$$\begin{aligned} R(z)={\left\{ \begin{array}{ll} R_0\left[ 1-a_1\lbrace l_0^{n-1}(z-d)-(z-d)^{n-1}\rbrace \right] &{}\quad d\le z \le d+l_0 \\ 1 &{}\quad \text { other wise} \end{array} \right. } \end{aligned}$$
(1)
Fig. 1
figure 1

Geometry of the porous constricted region

Full size image

where \(a_1 = \frac{\delta _m}{R_0l_0^n}\left[ \frac{n^{n/(n-1)}}{n-1} \right] \) and \(n(\ge 2)\) is a parameter which determines the shape of the constricted region, \(R_0\) is the radius of the normal artery, \(l_0\) is the length of the constricted area, d is the position of the constriction, and L is the length of the artery. Here \(\delta _m\) is the maximum depth of the constricted area appears at \(\displaystyle { z=d+\frac{l_0}{n^{1/(n-1)}}}\) such that ratio of the depth of the constricted area to the radius of the normal artery is much less than unity. We consider \(R_1\), \(R_2\), \(R_3\) and \(R_4\) as the radius of the artery in constricted region for Newtonian, non-Newtonian, Brinkman and Darcy region, respectively. Let us assume that the flow is steady axisymmetric, incompressible, fully developed, laminar, in z direction such that the radial component of velocity is negligibly small in case of low Reynolds number flow. The axial velocity in core, peripheral, Brinkman and Darcy region are taken as \(v_1\), \(v_2\), \(v_3\) and \(v_4\), respectively. Let \(p_1\), \(p_2\), \(p_3\) and \(p_4\) be pressure in the above four region. We assume that the thickness of the transition Brinkman layer is \(h_1\) and Darcy layer is \(h_2\) such that \(h_1 = \frac{h_2}{9}\) (Straughan 2008).

The governing equations for the above-modelled problem will be:

For Non-Newtonian region, i.e. \(0\le \bar{R(z)}\le \bar{R_1(z)}\)

$$\begin{aligned}&\displaystyle \frac{\partial \bar{v_1}}{\partial \bar{z}} = 0 \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle \frac{\partial \bar{p_1}}{\partial \bar{r}} = 0\end{aligned}$$
(3)
$$\begin{aligned}&\displaystyle -\frac{\partial \bar{p}}{\partial \bar{z}} + \frac{1}{\bar{r}} \frac{\partial (\bar{r} \bar{\tau })}{\partial \bar{r}} = 0 \end{aligned}$$
(4)

where the constitutive equation for non-Newtonian Casson fluid is given as:

$$\begin{aligned} \sqrt{\bar{\tau }}&= \sqrt{\bar{\tau _y}} + \sqrt{\bar{\mu _1}\frac{\partial \bar{v_1}}{\partial \bar{r}}} \qquad if \, \bar{\tau }\ge \bar{\tau _y}\nonumber \\&\qquad \frac{\partial \bar{v_1}}{\partial \bar{r}} = 0 \qquad \qquad if \, \bar{\tau }\le \bar{\tau _y} \end{aligned}$$
(5)

For Newtonian region, i.e. \(\bar{R_1(z)} \le \bar{R(z)}\le \bar{R_2(z)}\)

$$\begin{aligned}&\displaystyle \frac{\partial \bar{p_2}}{\partial \bar{r}}=0 \end{aligned}$$
(6)
$$\begin{aligned}&\displaystyle -\frac{\partial \bar{p_2}}{\partial \bar{z}} + \frac{\bar{\mu _2}}{\bar{r}} \frac{\partial }{\partial \bar{r}}\left( \bar{r}\frac{\partial \bar{v_2}}{\partial \bar{r}}\right) = 0 \end{aligned}$$
(7)

For Brinkman region, i.e. \(\bar{R_2(z)} \le \bar{R(z)}\le \bar{R_3(z)}\)

$$\begin{aligned}&\displaystyle \frac{\partial \bar{p_3}}{\partial \bar{r}} = 0 \end{aligned}$$
(8)
$$\begin{aligned}&\displaystyle -\frac{\partial \bar{p_3}}{\partial \bar{z}} + \frac{\bar{\mu }_{eff}}{\bar{r}} \frac{\partial }{\partial \bar{r}}\left( \bar{r}\frac{\partial \bar{v_3}}{\partial \bar{r}}\right) - \frac{\bar{\mu _2}}{\bar{k}} \bar{v_3} = 0 \end{aligned}$$
(9)

where \(\bar{\mu }_{eff}\) is the effective viscosity of Brinkman layer and \(\bar{k}\) is the permeability constant.

For Darcy region, i.e. \(\bar{R_3(z)} \le \bar{R(z)}\le \bar{R_4(z)}\)

$$\begin{aligned}&\displaystyle \frac{\partial \bar{p_4}}{\partial \bar{r}} = 0 \end{aligned}$$
(10)
$$\begin{aligned}&\displaystyle -\frac{\partial \bar{p_4}}{\partial \bar{z}} - \frac{\bar{\mu _2}}{\bar{k}} \bar{v_4} = 0 \end{aligned}$$
(11)

The governing equation for each region can be converted in to non-dimensional form by using the following non-dimensional variable:

$$\begin{aligned} \frac{\bar{r}}{R_0} =\,&r,~ \frac{\bar{R_i}}{R_0} = R_i,~ \frac{\bar{R}}{R_0}=R,~ \frac{\bar{v_i}}{U_0}= v_i,~ \frac{\bar{z}}{R_0}= z, ~ \frac{\bar{p_i}\bar{R_0}}{U_0\bar{\mu _2}}= p_i,~ {\lambda _1} = \frac{\bar{\mu _1}}{\bar{\mu _2}},\nonumber \\&{\lambda _2} = \frac{\bar{\mu _e}}{\bar{\mu _2}},~ \theta = \frac{\bar{\tau _y}R_0}{\mu _2 U_0}, \tau = \frac{\bar{\tau }R_0}{\bar{\mu _2} U_0}, ~ k = \frac{\bar{k}}{R_0^2} \end{aligned}$$
(12)

using above non-dimensional variable, the governing equation in non-dimensional form will become as:

For non-Newtonian region

$$\begin{aligned}&\displaystyle \frac{\partial p_1}{\partial r}=0 \end{aligned}$$
(13)
$$\begin{aligned}&\displaystyle -\frac{\partial p_1}{\partial z} + \frac{1}{r} \frac{\partial (r \tau )}{\partial r} = 0 \end{aligned}$$
(14)

where the constitutive equation for non-Newtonian Casson fluid is given as:

$$\begin{aligned} \sqrt{\tau } =&\sqrt{\theta } + \sqrt{\lambda _1 \frac{\partial v_1}{\partial r}} \qquad if \,\tau \ge \tau _y \nonumber \\&\qquad \frac{\partial v_1}{\partial r} = 0 \qquad \quad if \tau \le \tau _y \end{aligned}$$
(15)

For Newtonian region

$$\begin{aligned}&\displaystyle \frac{\partial p_2}{\partial r}=0 \end{aligned}$$
(16)
$$\begin{aligned}&\displaystyle -\frac{\partial p_2}{\partial z} + \frac{1}{r} \frac{\partial }{\partial r}\left( r \frac{\partial v_2}{\partial r}\right) = 0 \end{aligned}$$
(17)

For Brinkman region

$$\begin{aligned}&\displaystyle \frac{\partial p_3}{\partial r} = 0 \end{aligned}$$
(18)
$$\begin{aligned}&\displaystyle -\frac{\partial p_3}{\partial z} + \frac{\lambda _2}{r} \frac{\partial }{\partial r}\left( r\frac{\partial v_3}{\partial r}\right) - \frac{1}{k} v_3 = 0 \end{aligned}$$
(19)

For Darcy region

$$\begin{aligned}&\displaystyle \frac{\partial p_4}{\partial r} = 0 \end{aligned}$$
(20)
$$\begin{aligned}&\displaystyle -\frac{\partial p_4}{\partial z} - \frac{1}{k} v_4 = 0 \end{aligned}$$
(21)

where \(\lambda _2\) is the non-dimensional effective viscosity and k is the non-dimensional permeability.

3 Solution of the Problem

Let us consider the pressure gradient in all four region be constant, i.e. \(\frac{\partial p_1}{\partial z}=\frac{\partial p_2}{\partial z}=\frac{\partial p_3}{\partial z}= \frac{\partial p_4}{\partial z}=P\).

Therefore from Eq. (14)

$$\begin{aligned} \tau = \frac{rP}{2} + \frac{C_1}{r} \end{aligned}$$
(22)

where \(C_1\) is arbitrary constant which can be obtained by using the condition that \(\tau \) is finite at \(r = 0\) and it will become zero. Thus,

$$\begin{aligned} \tau = \frac{rP}{2} \end{aligned}$$
(23)

now using value of \(\tau \) from Eq. (23) in (15), we get:

$$\begin{aligned} v_1 = \frac{1}{\lambda _1}\left[ \frac{rP}{4} + \theta r - \frac{\sqrt{8 \theta P}}{3} r^{3/2}+ C_2\right] \end{aligned}$$
(24)

Similarly, we can obtain the velocity in peripheral, Brinkman, and Darcy region, respectively, which are:

$$\begin{aligned} v_2&= \frac{r^2P}{4} + C_3 \ln r + C_4 \end{aligned}$$
(25)
$$\begin{aligned} v_3&= C_5 I_0(\gamma r) + C_6 K_0(\gamma r) - Pk \end{aligned}$$
(26)

and from Eq. (21), we have:

$$\begin{aligned} v_4 = - Pk \end{aligned}$$
(27)

where, \(\frac{1}{\lambda _1 k} = \gamma ^2\); \(I_0\) and \(K_0\) are the modified Bessel functions and \(C_2\), \(C_3\), \(C_4\), \(C_5\) and \(C_6\) are arbitrary constant which can be obtained with the help suitable boundary conditions

The suitable boundary conditions which are physically realistic and mathematically consistent are as follows:

  1. 1.

    The stress is finite on the axis \(r=0\), i.e

    $$\begin{aligned} \tau \ \ \text{ is } \text{ finite } \text{ at } \ \ r = 0 \end{aligned}$$
    (28)
  2. 2.

    Continuity of velocity at Newtonian and non-Newtonian interfaces, i.e.

    $$\begin{aligned} v_1 = v_2 \ \ \text {at} \ \ r = R_1 \end{aligned}$$
    (29)
  3. 3.

    Continuity of shear stresses at Newtonian and non-Newtonian interfaces, i.e.

    $$\begin{aligned} \dfrac{\mathrm{d}v_2}{\mathrm{d}r} = \left( \sqrt{\theta } - \sqrt{\lambda _1 \dfrac{\mathrm{d}v_1}{\mathrm{d}r}} \right) ^2 \ \ \text {at} \ \ r = R_1 \end{aligned}$$
    (30)
  4. 4.

    Continuity of velocity across the Newtonian and Brinkman interface, i.e.

    $$\begin{aligned} v_3 = v_4 \ \ \text {at} \ \ r = R_2 \end{aligned}$$
    (31)
  5. 5.

    The stress jump condition of tangential stress at Newtonian and Brinkman interface (Ochoa-Tapia and Whitakeri 1995), i.e.

    $$\begin{aligned} \frac{1}{\phi } \dfrac{\mathrm{d}v_3}{\mathrm{d}r} - \dfrac{\mathrm{d}v_2}{\mathrm{d}r} = \frac{\beta }{\sqrt{k}}v_3 \ \ \text {at} \ \ r = R_2 \ \ \end{aligned}$$
    (32)

    where, \(\phi \) is the porosity and \(\beta \) is stress jump parameter

  6. 6.

    The Beavers and Joseph boundary (Beavers and Joseph 1967) condition at Brinkman and Darcy interface, i.e.

    $$\begin{aligned} \dfrac{\mathrm{d}v_3}{\mathrm{d}r} = \frac{\alpha }{\sqrt{k}} ( v_3 - v_4) \ \ \text {at} \ \ r = R_3 \end{aligned}$$
    (33)

    where \(\alpha \) is Darcy slip parameter.

    Using value of \(v_1\), \(v_2\), \(v_3\) and \(v_4\) in the boundary condition (27)–(33), we have

    $$\begin{aligned}&\frac{PR_1^2(1-\lambda _1)}{4\lambda _1} + \frac{\theta R_1}{\lambda _1} +\frac{\sqrt{8\theta P}R_1^{3/2}}{3\lambda _1} + C_2 - C_3 \ln R_1 - C_4 = 0 \end{aligned}$$
    (34)
    $$\begin{aligned}&R_1^2 P + 2C_3 - 2R_1\left[ \sqrt{\theta } - \sqrt{\mu _1 \left( \frac{R_1P}{2}+ \theta - \sqrt{2R_1P\theta } \right) } \right] ^2 = 0 \end{aligned}$$
    (35)
    $$\begin{aligned}&R_2^2 + 4C_3 \ln R + 4C_2 - C_5 I_0(\gamma R_2) - C_6 K_0(\gamma R_2) + PD = 0 \end{aligned}$$
    (36)
    $$\begin{aligned}&\gamma C_5 I_1(\gamma R_3) + \gamma C_6 K_1(\gamma R_3) - C_3\left( \frac{\phi }{R_3} - \frac{ \ln R_3 \phi \beta }{\sqrt{D}}\right) - C_4\left( \frac{\phi \beta }{\sqrt{D}} \right) \nonumber \\&\qquad - \left( \frac{\phi R_3P}{2} + \frac{R_3^2 P \phi \beta }{4\sqrt{D}} \right) = 0 \end{aligned}$$
    (37)
    $$\begin{aligned}&C_5 \left( \gamma I_1(\gamma R_3) - \frac{\alpha }{\sqrt{D}} I_0(\gamma R_3)\right) + C_6 \left( \gamma K_1(\gamma R_3) - \frac{\alpha }{\sqrt{D}} K_0(\Gamma R_3) \right) = 0 \end{aligned}$$
    (38)

    By solving the above system of Eqs. (34)–(38) and by using the Mathematica-10.3 software, we get the values of arbitrary constants \(C_2\), \(C_3\), \(C_4\), \(C_5\) and \(C_6\), and hence velocity in core, peripheral, Brinkman and Darcy region is given in Appendix-A.

4 Results and Discussion

The purpose of this study is to understand the theory of blood flow in porous constricted blood vessels. Here we are interested to see the effect of permeability k, yield stress \(\theta \), plasma layer thickness h, constriction shape parameter n on core and peripheral region velocity, volume flow rate and wall shear stress. the value of flow rate and wall shear stress is given in next section.

4.1 Volume Flow Rate

The total volume flow rate in non-dimensional form is defined as:

$$\begin{aligned} Q= Q_1+Q_2+Q_3+Q_4 \end{aligned}$$
(39)

where \(Q_1\), \(Q_2\), \(Q_3\) and \(Q_4\) are the volume flow rate in non-dimensional form of the regions I, II, III, and IV, respectively.

The volume flow rate for region-I will be evaluated as:

$$\begin{aligned} Q_1= 2\pi \int _0^{R_1} v_1~r \mathrm{d}r \end{aligned}$$
(40)

Substituting the value of \(v_1\) from Eq. (24) in the above equation and integrating with respect to r, we get:

$$\begin{aligned} Q_1= \frac{1}{2} C_2 R_1^2+\frac{-\frac{1}{21} R_1^{7/2} \left( 4 \sqrt{2 \theta P}\right) +\frac{P R_1^4}{16}+\frac{\theta R_1^3}{3}}{\lambda _1} \end{aligned}$$
(41)

Similarly, we can obtain the expression for \(Q_2\), \(Q_3\) and \(Q_4\) for other three regions as:

$$\begin{aligned} Q_2&= C_4 \left( \frac{R_2^2}{2}-\frac{R_1^2}{2}\right) +C_3 \left( -\left( \frac{R_2^2}{4}-\frac{R_1^2}{4}\right) -\frac{1}{2} R_1^2 \log \left( R_1\right) +\frac{1}{2} R_2^2 \log \left( R_2\right) \right) \nonumber \\&\quad +\frac{1}{16} P \left( R_2^2-R_1^2\right) \end{aligned}$$
(42)
$$\begin{aligned} Q_3&= \gamma C_5 \left( R_3 I_1\left( \gamma R_3\right) -R_2 I_1\left( \gamma R_2\right) \right) +\gamma C_6 \left( R_2 K_1\left( \gamma R_2\right) -R_3 K_1\left( \gamma R_3\right) \right) \nonumber \\&\quad -k P \left( \frac{R_3^2}{2}-\frac{R_2^2}{2}\right) \end{aligned}$$
(43)
$$\begin{aligned} Q_4&= \frac{1}{2} \left( R_4^2-R_3^2\right) (k P) \end{aligned}$$
(44)

Therefore, the total volume flow rate will become:

$$\begin{aligned} Q&= \frac{1}{336 \lambda _1} \bigg [21 \lambda _1 (-16 \gamma C_5 \left( R_2 I_1\left( \gamma R_2\right) -R_3 I_1\left( \gamma R_3\right) \right) \nonumber \\&\quad +16 \gamma C_6 \left( R_2 K_1\left( \gamma R_2\right) -R_3 K_1\left( \gamma R_3\right) \right) \nonumber \\&\quad -4 C_3 R_2^2+8 C_4 R_2^2+8 C_3 R_2^2 \log \left( R_2\right) +8 k P R_2^2-16 k P R_3^2+8 k P R_4^2+P R_2^2) \nonumber \\&\quad -21 \lambda _1 R_1^2 \left( C_3 \left( 8 \log \left( R_1\right) -4\right) -8 C_2+8 C_4+P\right) \nonumber \\&\quad -64 \sqrt{2} R_1^{7/2} \sqrt{\theta P}+21 P R_1^4+112 \theta R_1^3 \bigg ] \end{aligned}$$
(45)

4.2 Wall Shear Stress

The wall shear stress on wall may be obtained in non-dimensional form as:

$$\begin{aligned} \tau _w =-\left[ \dfrac{\mathrm{d}v_2}{\mathrm{d}r}\vert _{r= R_2}+\dfrac{\mathrm{d}v_3}{\mathrm{d}r}\vert _{r= R_3}+\dfrac{\mathrm{d}v_4}{\mathrm{d}r}\vert _{r= R_4} \right] \end{aligned}$$
(46)

substituting the value of \(v_2\), \(v_3\) and \(v_4\) from Appendix-A in Eq. (46), we have:

$$\begin{aligned} \tau _w =&P (R_2(\left( \gamma \sqrt{k} K_1\left( \gamma R_3\right) +\alpha K_0\left( \gamma R_3\right) \right) \left( -\left( \beta \phi I_0\left( \gamma R_2\right) -\gamma \sqrt{k} I_1\left( \gamma R_2\right) \right) \right) +\alpha I_0\left( \gamma R_3\right) \nonumber \\&\left( \gamma \sqrt{k} \left( \phi K_1\left( \gamma R_3\right) +K_1\left( \gamma R_2\right) \right) +\beta \phi K_0\left( \gamma R_2\right) \right) + \gamma \left( -\sqrt{k}\right) I_1\left( \gamma R_3\right) (\gamma \sqrt{k} K_1\left( \gamma R_2\right) \nonumber \\&-\alpha \phi K_0\left( \gamma R_3\right) +\beta \phi K_0\left( \gamma R_2\right) ))-2 \alpha \beta \gamma k \phi \left( I_1\left( \gamma R_3\right) K_0\left( \gamma R_3\right) +I_0\left( \gamma R_3\right) K_1\left( \gamma R_3\right) \right) ) \end{aligned}$$
(47)

To see the influence of k, \(\theta \), h, n on the velocity, volume flow rate, and wall shear stress, we assumed \(\alpha =0.1\), \(\beta =0.1\), \(\phi =0.5\), from Straughan (2008) throughout the analysis. The thickness of the Newtonian fluid Plasma layer h is assumed between 0.015 and 0.05 (Sankar and Lee 2010), and the thickness of the Newtonian fluid layer not in the porous medium is assumed as \(25\%\) of the entire plasma layer.

Fig. 2
figure 2

Velocity variation in core region. a Variation of \(v_1\) outside the constriction region with k for \(\theta =0.1\), \(n=2\), \(h=0.05\), \(z=6\), b Variation of \(v_1\) inside the constriction region with k for \(\theta =0.1\), \(n=2\), \(h=0.05\), \(z=15\), c Variation of \(v_1\) with \(\theta \) for \(k=5\), \(n=2\), \(h=0.05\), \(z=15\)

Full size image

In Figs. 2a–c, the effect of permeability on core region velocity \(v_1\) inside and outside the constricted region has been discussed. In Figs. 2a, b the both region velocity increases with the decrease in permeability parameter k, but the change in radial direction is very small. The visible effect of yield stress on core velocity can be observed in Fig. 2c. The higher value of yield stress gave lower value of velocity \(v_1\) but it increases in radial direction up to Newtonian plasma layer. Figure 3 exhibits the effect of permeability parameter k and degree of shape parameter n on peripheral region velocity \(v_2\) in constricted and non-constricted region. From Fig. 3a, b, it is observed that the velocity decreases with increase in permeability parameter k. It is also noticed that the velocity increases with increase in shape parameter n (Fig. 3c).

Fig. 3
figure 3

Velocity variation in plasma layer region. a Variation of \(v_2\) outside the constriction region with k for \(\theta =0.1\), \(n=2\), \(h=0.05\), \(z=6\), b Variation of \(v_2\) inside the constriction region with k for \(\theta =0.1\), \(n=2\), \(h=0.05\), \(z=15\), c Variation of \(v_2\) with shape parameter n for \(k=5\), \(h=0.05\), \(\theta =0.1\), \(z=15\)

Full size image

Figures 4, 5 and 6 illustrate the effect of permeability k, plasma layer thickness h and degree of constriction n on volume flow rate. During the analysis, it is found that the volume flow rate decreases with the increase in permeability k in constriction region Fig. 4. From this figure, it is also observed that the volume flow rate decreases along the axial direction with increase in constriction region and attains minimum value at the peak of the constriction and after that it increases (Fig. 4). It shows that permeability has remarkable effect on the flow rate in the diseased blood vessels. The variation in volume flow rate with plasma layer thickness h is almost similar in nature to the variation in volume flow rate with k Fig. 5. So the small thickness of plasma layer gives better flow rate. Figure 6 shows the effect of shape parameter n on volume flow rate. At \(n=2\), we obtained the symmetric profile of flow rate, but for \(n=3, 5, 7\) we get the asymmetric profile. The peaks are formed at the maximum arterial constriction but shifted along the axial direction. This explains that the narrower the artery, the maximum the flow rate.

The effect of permeability on wall shear stress is presented in Fig. 7. We concluded that wall shear stress increases with the increase in permeability parameter k. From this figure, we also noticed that the wall shear stress increases or decreases according to increase or decrease in cross-sectional area in the constricted arterial segment. But in case of the Plasma layer thickness, the wall shear stress decreases with the increase in plasma layer thickness (Fig 8). The influence of shape of the constriction region on the wall shear stress is shown in Fig. 9. From this figure, we observed that the wall shear stress profile is symmetric in axial direction when \(n=2\). It increases with the decrease in the cross-sectional area of constricted blood vessel and decreases with the increase in cross-sectional area. For the other value of \(n=3, 5, 7\), we get the asymmetric wall shear stress profile along the axial distance. The peaks are shifted slightly for the maximum value of constriction parameter towards the axial distance. This means that the shape of constriction has a remarkable reflection on the wall shear stress.

Fig. 4
figure 4

Variation of Q with permeability k for \(\theta =0.1\), \(n=2\), \(h=0.05\), \(z=6\ \text {to}\ 24\)

Full size image
Fig. 5
figure 5

Variation of Q with plasma layer thickness h for \(\theta =0.1\), \(n=2\), \(k=5\), \(z=6\ \text {to}\ 24\)

Full size image
Fig. 6
figure 6

Variation of Q with shape parameter n for \(\theta =0.1\), \(k=5\), \(h=0.05\), \(z=6\ \text {to}\ 24\)

Full size image
Fig. 7
figure 7

Variation of wall shear stress with permeability k for \(\theta =0.1\), \(n=2\), \(h=0.05\), \(z=4.5\ \text {to}\ 28\)

Full size image
Fig. 8
figure 8

Variation of wall shear stress plasma layer thickness h for \(\theta =0.1\), \(n=2\), \(k=5\), \(z=4.5\ \text {to}\ 28\)

Full size image
Fig. 9
figure 9

Variation of wall shear stress with shape parameter n for \(\theta =0.1\), \(k=5\), \(h=0.05\), \(z=4.5\ \text {to}\ 28\)

Full size image

5 Conclusion

The discussion on blood flow through porous constricted blood vessels is very important from the pathological point of view. In this present analysis, we made an effort to discussed the flow characteristics of Casson fluid model of blood flow through porous constricted blood vessels. The Brinkman and Darcy model is used to analyse the property of porous wall. The main objective of this study is to find out the effect of permeability and plasma layer thickness on various flow quantity. From the above study, the following points are concluded:

  • The permeability makes direct impact on flow velocity in core and peripheral region both. Velocity decreases with the large value of permeability.

  • The core region velocity decreases with the increasing value of yield stress.

  • The volume flow rate decreases with increase in permeability and increases with decrease in plasma layer thickness. It has a symmetric profile for the shape parameter \(n=2\) and asymmetric profile for other value.

  • The wall shear stress decreases with the increase in permeability and plasma layer thickness in the constriction region.

  • Wall shear stress has a symmetric profile for constriction parameter \(n=2\) and for other value of n it has asymmetric profile.