1 Introduction

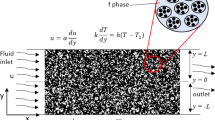
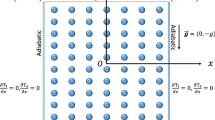
Since the experiments of Chen et al. (2000), a new kind of porous medium called bidisperse porous medium (BDPM) has attracted many heat and fluid flow researchers because of its industrial applications including porous wicks (i.e., used as evaporators in the heat pipes), coal stockpiles, porous absorbent, and geothermal energy extraction, to name a few. A BDPM as defined by Chen et al. (2000) is composed of clusters of large particles that are agglomerations of small particles (see Fig. 1). In other words, as can be seen in Fig. 1a, b, a BDPM can be considered as a Mono-Disperse Porous Medium (MDPM) in which each solid block is replaced by a micro-porous medium. Thus, it can be said, a BDPM consists of an array of micro-porous media (i.e., p-phase) and macro-pores (i.e., f-phase) between the micro-porous media.

Fig. 1
figure 1

Schematic of the studied geometries and corresponding boundary conditions, a detached BDPM, b attached BDPM

Full size image

Nield and Kuznetsov (2005), in a pioneer work, theoretically modeled the heat transfer and fluid flow in BDPM. Invoking the local thermal equilibrium assumption within the micro-porous media, those authors presented a volume-averaged two-velocity two-temperature model with capability of simulating the steady-state fluid flow and heat transfer in BDPM. The presented model was used by many researchers to study different forced convection problems in saturated BDPM (Narasimhan and Reddy 2011a; Narasimhan et al. 2012; Nield and Kuznetsov 2004, 2006a, 2011). Many researchers also used the two-velocity two-temperature model to simulate different natural convection problems in BDPM (Narasimhan and Reddy 2011b; Nield and Kuznetsov 2006b, 2008; Rees et al. 2008; Revnic et al. 2009).

Despite the popularity of the presented model by Nield and Kuznetsov (2005), it includes two unknown parameters namely, the interfacial momentum and heat transfer coefficients and the assumption of the local thermal equilibrium within the micro-porous media is invoked as well. To date, there is an extremely small amount of information in the literature on the value of the mentioned parameters related to the flow and heat transfer in BDPM (Hooman et al. 2015). Therefore, using the two-velocity two-temperature model of Nield and Kuznetsov (2005) depends on the availability of such information. As such, pore scale simulations are needed to fill this gap by providing such information on the interfacial momentum and heat transfer parameters in addition to validating the volume-averaged results and justifying the assumptions invoked by the two-velocity two-temperature model.

To best of the authors’ knowledge, work of Narasimhan and Reddy (2010) is the only effort in which the semi-pore scale simulation of natural convection in an enclosure filled with a BDPM was numerically studied. In their work, by using the finite volume method, fluid flow and heat transfer in the macro-pores was numerically simulated at the pore scale however, in the micro-porous media, in expense of losing some details of the fluid flow and heat transfer, the volume-averaged formulation was used with considering the local thermal equilibrium assumption. Following the researches in the literature that tried pore scale simulation of the natural convection in a MDPM (Braga and de Lemos 2005; Merrikh and Lage 2005; Merrikh et al. 2005; Merrikh and Mohamad 2000, 2001), Narasimhan and Reddy (2010) considered the BDPM to be detached from the enclosure walls which only covered a part of practical applications of the BDPM and did not include applications such as porous wick evaporators (Chen et al. 2000; Wang and Catton 2001).

In view of the above, in this work, natural convection problem in a differentially heated enclosure filled with a BDPM is simulated at the pore scale within both the micro-porous and macro-pores structures. As mentioned before, there are some applications in which the BDPM is attached to walls of the enclosure thus, for the first time, a BDPM attached to the enclosure walls is considered in the present study in addition to the detached one. To see details of fluid flow and heat transfer within a BDPM, effects of pertinent geometrical and thermo-physical parameters on streamlines and isotherms as well as hot wall average Nusselt number in both attached and detached BDPM are investigated. The pore scale results then, for the first time, is used for thoroughly examining the validity of the assumption of the local thermal equilibrium within the micro-porous media of a BDPM which is invoked by the two-velocity two-temperature model. To do so, in the present work, thermal lattice Boltzmann method is employed due to its great ability in pore scale simulation of the fluid flow and conjugate heat transfer in complex geometries (Chen and Doolen 1998; He et al. 1998; Imani et al. 2013) such as the BDPM considered in this study.

2 Mathematical Formulation

In this study, two configurations of the BDPM, namely detached and attached geometries in an enclosure of side H, are considered as shown in Fig. 1a, b, respectively. As seen from Fig. 1a, b, the enclosure is heated and cooled from the sides with assuming the prescribed constant temperatures of \(T_{h}\) and \(T_{c}\) (\(T_{h}>T_{c}\)) applied on the left and right walls, respectively. The bottom and top walls of the enclosure are insulated. This temperature difference between the left and right walls of the enclosure, in presence of the gravitational field, induces a natural convection flow within the enclosure. It is assumed that the flow is steady state, two-dimensional, and remains in the laminar regime. Moreover, the effect of radiation is neglected, the Boussinesq approximation is invoked for modeling the buoyancy term, and all the thermo-physical properties of both solid and fluid constituents are assumed constant. With considering these assumptions, dimensionless form of the continuity, momentum, and energy conservation equations for the fluid and solid constituents are shown here as Eqs. (1)–(4), respectively (Bejan 2004; House et al. 1990; Merrikh and Lage 2005; Merrikh and Mohamad 2001). It should be stated that the dimensional form of the conservation equations also can be found in (Bejan 2004; House et al. 1990; Merrikh et al. 2005; Merrikh and Mohamad 2001) and are not repeated here for sake of the brevity.

$$\begin{aligned} \nabla \cdot \mathbf{V}^{{*}}= & {} 0 \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial \mathbf{V}^{{*}}}{\partial t^{{*}}}+(\mathbf{V}^{{*}}\cdot \nabla )\mathbf{V}^{{*}}= & {} -\nabla p^{{*}}+\Pr \nabla ^{2}{} \mathbf{V}^{{*}}+Ra\,\Pr {\theta }_{\mathrm{f}}{} \mathbf{j} \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial {\theta }_{\mathrm{f}}}{\partial t^{{*}}}+\mathbf{V}^{{*}}\cdot \nabla {\theta }_{\mathrm{f}}= & {} \nabla ^{2}{\theta }_{\mathrm{f}} \end{aligned}$$
(3)
$$\begin{aligned} \left( {\frac{\sigma }{{\lambda }}}\right) \frac{\partial {\theta }_{\mathrm{s}}}{\partial t^{{*}}}= & {} \nabla ^{2}{\theta }_{\mathrm{s}} \end{aligned}$$
(4)

where the dimensionless parameters and groups introduced to derive Eqs. (1)–(4) are taken as follows:

$$\begin{aligned} \left( x^{{*}},y^{{*}}\right)= & {} \frac{(x,y)}{H}, \quad \mathbf{V}^{{*}}=\frac{(u,v)H}{\alpha _{\mathrm{f}}},\quad \theta =\frac{T-T_c}{T_h -T_c}, \quad t^{{*}}=\frac{\alpha _\mathrm{f} t}{H^{2}}, \quad p^{*}=\frac{pH^{2}}{\rho _{\mathrm{f}}\alpha _{\mathrm{f}}^{2}}, \quad \Pr =\frac{\nu _{\mathrm{f}}}{\alpha _{\mathrm{f}}},\nonumber \\ Ra= & {} \frac{g\beta (T_h -T_c)H^{3}}{\alpha _\mathrm{f} v_\mathrm{f}}, \quad \sigma =\frac{(\rho c_p)_\mathrm{s}}{(\rho c_p)_\mathrm{f}}, \quad \lambda =\frac{k_\mathrm{s}}{k_\mathrm{f}} \end{aligned}$$
(5)

where \(\mathbf{V}=(u,v)\) is the velocity vector with u and v being the velocity components in x and y directions, respectively, p is the fluid pressure, \(\mu \) is the fluid dynamic viscosity, \(T_\mathrm{f}\) and \(T_{\mathrm{s}}\) are the fluid and solid temperatures, respectively, \(k_\mathrm{f}\) and \(k_{\mathrm{s}}\) are the fluid and solid thermal conductivities, respectively, \(\beta \) is the isobaric thermal expansion coefficient, and g is the magnitude of the gravitational acceleration. The dimensionless form of the hydrodynamic and thermal boundary conditions applied on the enclosure walls is represented in the following form:

$$\begin{aligned} {\theta }= & {} 1, \quad u^{{*}}=v^{{*}}=0, \quad \hbox {at } x^{{*}}=0 \end{aligned}$$
(6a)
$$\begin{aligned} {\theta }= & {} 0, \quad u^{{*}}=v^{{*}}=0, \quad \hbox {at } x^{{*}}=1 \end{aligned}$$
(6b)
$$\begin{aligned} \frac{\partial {\theta }}{\partial y^{{*}}}= & {} 0, \quad u^{{*}}=v^{{*}}=0, \quad \hbox {at } y^{{*}}=0 \end{aligned}$$
(6c)
$$\begin{aligned} \frac{\partial {\theta }}{\partial y^{{*}}}= & {} 0, \quad u^{{*}}=v^{{*}}=0, \quad \hbox {at } y^{{*}}=1 \end{aligned}$$
(6d)

the conjugate heat transfer conditions (i.e., the compatibility conditions) and the no-slip condition at the solid–fluid interfaces are given as follows:

$$\begin{aligned} \frac{\partial {\theta }_\mathrm{f} }{\partial \mathbf{n}}=\lambda \frac{\partial {\theta }_\mathrm{s}}{\partial \mathbf{n}}, \quad {\theta }_\mathrm{f} ={\theta }_{\mathrm{s}},\quad u^{{*}}=v^{{*}}=0 \end{aligned}$$
(6e)

where \(\mathbf{n}\) is the unit vector along the direction normal to the solid–fluid interfaces.

As one can realize from Eqs. (1)–(6), effect of different parameters on the problem considered in this study is reduced to four dimensionless group and parameters namely, the Rayleigh number Ra, the Prandtl number \(\Pr \), solid–fluid thermal conductivity ratio \({\lambda }\), and solid–fluid volumetric heat capacity ratio \({\sigma }\). Although the macroscopic governing Eqs. (1)–(6) are presented in their unsteady forms, the steady-state simulation is considered in the present investigation.

Furthermore, natural convection heat transfer is significantly influenced by geometrical characteristics of the BDPM (i.e., including the micro-porous media and the macro-pores). The most relevant geometrical parameters are taken as the micro-porous porosity \({\varepsilon }_{\mathrm{mic}}\), macro-pores volume fraction \({\varphi }_{\mathrm{mac}}\), number of blocks in each micro-porous medium \(N_{\mathrm{mic}}^2 \), and number of blocks in the macro-pores \(N_{\mathrm{mac}}^2\). The micro-porous porosity \({\varepsilon }_{\mathrm{mic}}\) is defined as volume of the micro-pores in each micro-porous medium divided by the total volume of the micro-porous medium. The macro-pores volume fraction \({\varphi }_{\mathrm{mac}}\) is defined as the volume of macro-pores divided by the total volume of the BDPM. It should be emphasized that volume of the micro-pores in the micro-porous media is not taken into account in definition of the macro-pores volume fraction. That is why it is referred to as the volume fraction not the porosity. To construct the full geometry of a BDPM, certain parameters are considered to be known priorly, including the macro-pores volume fraction \({\varphi }_{\mathrm{mac}}\), number of blocks in macro-pores \(N_{\mathrm{mac}}^2 \), micro-porous porosity \({\varepsilon }_{\mathrm{mic}}\), and number of blocks in each micro-porous medium \(N_{\mathrm{mic}}^{2}\). With knowing the value of the macro-pores volume fraction and number of blocks in the macro-pores, dimensionless size of the blocks in the macro-pores \(D^{{*}}=D/H\) can be calculated from Eq. (7).

$$\begin{aligned} D^{{*}}=\sqrt{{\left( 1-{\varphi }_{\mathrm{mac}}\right) }/{N_{\mathrm{mac}}^{2}}} \end{aligned}$$
(7)

once \(D^{{*}}\) is determined, the dimensionless clearance between the detached BDPM and the enclosure walls \(\delta ^{{*}}=\delta /H\) and dimensionless size of the micro-porous blocks \(d^{{*}}=d/H\), respectively, is determined from Eqs. (8) and (9).

$$\begin{aligned} \delta ^{{*}}= & {} {\left[ 1-\left( \sqrt{N_{\mathrm{mac}}^2}\right) D^{{*}}\right] }\bigg /{2\sqrt{N_{\mathrm{mac}}^2}} \end{aligned}$$
(8)
$$\begin{aligned} d^{{*}}= & {} \sqrt{{\left( 1-\varphi _{\mathrm{mac}}\right) \left( 1-{\varepsilon }_{\mathrm{mic}}\right) }/{\left( N_{\mathrm{mac}}^2 N_{\mathrm{mic}}^{2}\right) }} \end{aligned}$$
(9)

It should be noted that for the attached geometry (see Fig. 1b) \({\delta }^{{*}}=0\).

3 Lattice Boltzmann method

In the present study, a three-population (i.e., density, fluid internal energy, and solid internal energy distribution functions) thermal lattice Boltzmann model of Peng et al. (2003) is employed. In this method, the velocity and temperature field are solved via evolution of the density and internal energy distribution functions which is numerically applied through two main steps namely, streaming and collision.

3.1 Lattice Boltzmann Equation for the Velocity Field

The hydrodynamic of the problem is simulated by the evolution of the density distribution function including the discrete body force effect proposed by Guo et al. (2002) as follows:

$$\begin{aligned} f_{i}\left( {\mathbf{r}+\mathbf{e}_{i}\delta t,t+\delta t}\right) -f_i \left( \mathbf{r},t\right) =-\frac{1}{\tau _v}\left[ f_i\left( {\mathbf{r},t} \right) -f_i ^{\mathrm{eq}}\left( \mathbf{r},t\right) \right] +\delta tF_i \end{aligned}$$
(10)

where \(\mathbf{e}_i\) is the discrete velocity along direction i, \(f_{i} (\mathbf{r},t)\) is the density distribution function along direction i at position \(\mathbf{r}\) and time \(t, \delta t\) is time step, \(\tau _{v}\) is dimensionless hydrodynamic relaxation time, \(f_{i}^{\mathrm{eq}}\) and \(F_{i}\) are, respectively, the equilibrium distribution function and discrete body force, which for a \(D_2 Q_9\) lattice are calculated from Eqs. (11) and (12), respectively.

$$\begin{aligned} f_i^{\mathrm{eq}}= & {} {\omega }_{i}{\rho }\left[ 1+\frac{\mathbf{e}_{i}\cdot \mathbf{V}}{c_{\mathrm{s}} ^{2}}+\frac{\mathbf{VV}:\mathbf{e}_i \mathbf{e}_i -c_\mathrm{s} ^{2}{} \mathbf{I}}{2c_{\mathrm{s}}^{4}}\right] \end{aligned}$$
(11)
$$\begin{aligned} F_{i}= & {} {\omega }_{i}{\rho }\left( 1-\frac{1}{2\tau _{v}}\right) \left[ {\frac{\mathbf{e}_{i}\cdot \mathbf{F}}{c_\mathrm{s}^{2}}+\frac{\mathbf{VF}:\mathbf{e}_{i} \mathbf{e}_i}{c_\mathrm{s}^{4}}-\frac{\mathbf{V}\cdot \mathbf{F}}{c_\mathrm{s}^{2}}}\right] \end{aligned}$$
(12)

where \(c_{\mathrm{s}}\) is the lattice sound speed related to the lattice velocity c as \(c_\mathrm{s} =c/{\sqrt{3}}\), the lattice velocity c is equal to \({\delta x}/{\delta t}\), and \(\mathbf{F}=\rho \mathbf{g}\beta (T_f -T_c)\) is the buoyancy force term derived using the Boussinesq approximation. For the \(D_2 Q_9 \) lattice arrangement, the discrete velocity \(\mathbf{e}_i\) and the weight factor \(w_i\) in each direction i are given by Eqs. (13) and (14), respectively.

$$\begin{aligned} \mathbf{e}_{i}= & {} \left\{ {\begin{array}{lll} (0,0)\quad i=0 &{}&{}\\ \left( \cos \theta _{i},\sin \theta _{i}\right) c ;&{}\quad \theta _{i}=(i-1)\pi /2 &{} \quad i=1,2,3,4\\ \sqrt{2}\left( {\cos \theta _i ,\sin \theta _i} \right) c ;&{}\quad \theta _{i} =(i-5)\pi /2+\pi /4 &{} \quad i=5,6,7,8 \\ \end{array}}\right. \end{aligned}$$
(13)
$$\begin{aligned} \omega _{i}= & {} \left\{ {\begin{array}{ll} 4/9&{}\quad i=0 \\ 1/9 &{}\quad i=1,2,3,4 \\ 1/36&{}\quad i=5,6,7,8 \\ \end{array}}\right. \end{aligned}$$
(14)

3.2 Lattice Boltzmann Equation for the Temperature Field

The temperature field is modeled using the evolution equation for the internal energy distribution function proposed by Peng et al. (2003) as follows:

$$\begin{aligned} g_{i}\left( \mathbf{r}+\mathbf{e}_i \delta t,t+\delta t\right) -g_{i} \left( \mathbf{r},t\right) =-\frac{1}{\tau _g}\left[ g_i\left( {\mathbf{r},t} \right) -g_{i}^{\mathrm{eq}}\left( {\mathbf{r},t}\right) \right] \end{aligned}$$
(15)

where \(\tau _{g}\) is fluid dimensionless energy relaxation time, \(g_{i} (\mathbf{r},t)\) is internal energy distribution function along direction i at position \(\mathbf{r}\) and time t, and \(g_i^{\mathrm{eq}}\) is internal energy equilibrium distribution function which for a \(D_{2} Q_{9}\) lattice is given by Peng et al. (2003) as follows:

$$\begin{aligned} g_i ^{\mathrm{eq}}=\left\{ {\begin{array}{ll} {-1}/2 \omega _i \rho _f \varepsilon _f \frac{\mathbf{V}\cdot \mathbf{V}}{c_\mathrm{s} ^{2}}&{}\quad i=0 \\ \omega _i \rho _{f} \varepsilon _{f} \left( {\frac{3}{2}+\frac{\mathbf{e}_i \cdot \mathbf{V}}{c_\mathrm{s} ^{2}}+\frac{\left( {\mathbf{e}_i \cdot \mathbf{V}} \right) ^{2}}{2c_\mathrm{s} ^{4}}-\frac{\mathbf{V}\cdot \mathbf{V}}{2c_\mathrm{s} ^{2}}} \right) &{}\quad i=1,2,3,4 \\ \omega _i \rho _{f} \varepsilon _{f} \left( {3+2\frac{\mathbf{e}_i \cdot \mathbf{V}}{c_\mathrm{s} ^{2}}+\frac{\left( \mathbf{e}_i \cdot \mathbf{V}\right) ^{2}}{2c_\mathrm{s} ^{4}}-\frac{\mathbf{V}\cdot \mathbf{V}}{2c_{\mathrm{s}}^{2}}}\right) &{}\quad i=5,6,7,8 \\ \end{array}}\right. \end{aligned}$$
(16)

where \(\mathbf{V}\) is the macroscopic fluid velocity vector and \(\varepsilon \) is the internal energy that for a two dimension can be calculated from \(\varepsilon =RT\) with R being the gas constant.

It should be noted that for the solid phase a separate internal energy distribution function \(g_{\mathrm{si}}\) is used with an evolution equation similar to that of fluid [see Eq. (15)], as the following form:

$$\begin{aligned} g_{\mathrm{si}}\left( {\mathbf{r}+\mathbf{e}_i \delta t,t+\delta t} \right) -g_{\mathrm{si}} (\mathbf{r},t)=-\frac{1}{\tau _{\mathrm{gs}}}\left[ g_{\mathrm{si}} (\mathbf{r},t)-g_{\mathrm{si}} ^{\mathrm{eq}}(\mathbf{r},t)\right] \end{aligned}$$
(17)

where \(\tau _{\mathrm{gs}}\) is solid dimensionless energy relaxation time and \(g_{\mathrm{si}}^{\mathrm{eq}}\) is solid internal energy equilibrium distribution function that can be calculated similar to that of the fluid by setting \(\mathbf{V}=\mathbf{0}\) in Eq. (16) to obtain Eq. (18).

$$\begin{aligned} g_{\mathrm{si}}^{\mathrm{eq}}=\left\{ {\begin{array}{ll} 0 &{}\quad i=0 \\ \frac{3}{2}\omega _{i}\rho _{s}\varepsilon _{s} &{}\quad i=1,2,3,4 \\ 3 \omega _{i}\rho _{s}\varepsilon _{s} &{}\quad i=5,6,7,8 \\ \end{array}} \right. \end{aligned}$$
(18)

Noteworthy is the fact that the macroscopic Eqs. (1)–(6) essentially are recovered from a Chapmann–Enskog expansion applied on the mesoscopic evolution Eqs. (10), (15), and (17) in an incompressible limit (Guo et al. 2002; Peng et al. 2003; He et al. 1998; Mohamad 2011). That is to say, in this paper, instead of solving the nonlinear Eqs. (1)–(6) equivalently, the simple evolution Eqs. (10), (15), and (17) are solved in two main steps namely, streaming and collision. To ensure that the mesoscopic evolution Eqs. (10), (15), and (17) simulate the same problem as described by the macroscopic Eqs. (1)–(6), care should be taken that the dimensionless groups and numbers introduced by Eq. (5) should be identical in two of the frameworks (i.e., Navier–Stokes and lattice Boltzmann).

After evolving on discrete lattices, the macroscopic density, velocity, temperature, local heat flux, and the hydrodynamic and energy dimensionless relaxation times can be calculated from density and energy distribution functions using the following relations, respectively, (Guo et al. 2002; He et al. 1998; Peng et al. 2003).

$$\begin{aligned} \rho= & {} \sum _{i=0}^{8}{f_i}, \quad \mathbf{V}=\sum _{i=0}^{8}{{f_i\mathbf{e}_i}/{\rho _f} +{\delta t}/{\left( 2\rho _{\mathrm{f}}\right) }} \mathbf{F}, \quad \rho \varepsilon =\sum _{i=0}^{8} {g_i}, \mathbf{q}=(\rho c_p)\frac{\tau _{g}-0.5}{\tau _g}\sum _{i=0}^8{g_i}{} \mathbf{e}_i, \nonumber \\ \tau _{v}= & {} 3\nu \frac{\delta t}{\delta x^{2}}+0.5,\quad \tau _g =1.5\alpha _\mathrm{f}\frac{\delta t}{\delta x^{2}}+0.5,\quad \tau _{gs} =1.5\alpha _\mathrm{s}\frac{\delta t}{\delta x^{2}}+0.5 \end{aligned}$$
(19)

where \(\alpha _\mathrm{f}\) and \(\alpha _\mathrm{s}\) are the fluid and solid thermal diffusivities, respectively.

3.3 Boundary Conditions

The macroscopic boundary conditions described by Eqs. (6a)–(6d) are translated to the lattice Boltzmann framework (i.e., mesoscopic level) to calculate and update the unknown density and internal energy populations coming from the outside of each of the fluid and solid media after the streaming step. As such, the method presented by Zou and He (1997) is used to apply the no-slip boundary conditions on the enclosure walls and solid–fluid interfaces. The method proposed by D’Orazio and Succi (2003) based on the idea of the counter-slip internal energy is employed to model the thermal boundary conditions including the two isothermal boundary conditions (as shown in Fig. 1) and two adiabatic conditions (top and bottom walls) as depicted in Fig. 1. At solid–fluid interfaces, the method presented by Meng et al. (2008) is used to model the conjugate heat transfer. It was shown that the presented method by Meng et al. (2008) precisely guaranteed the continuity of the temperature and normal heat flux at solid–fluid interfaces (Imani et al. 2012a, b).

4 Numerical Simulation and Code Validation

The thermal lattice Boltzmann method presented by Peng et al. (2003) is used to solve the natural convection problem in an differentially heated enclosure filled with a BDPM.

4.1 Grid Independence

Four different grids of \(300\times 300, 350\times 350, 400\times 400\), and \(450\times 450\) are considered here to simulate the natural convection problem in a differentially heated enclosure contained a conducting BDPM. The most critical case considered in the present study is selected corresponding to \(Ra=10^{7}, \lambda =100\), and \(N_{\mathrm{mic}}^{2} =81\). It is observed that the result of the average Nusselt number calculated at the hot wall of the enclosure for \(400\times 400\) and \(450\times 450\) grids is within less than only one percent. Therefore, the \(400\times 400\) grid is chosen for all reported results.

4.2 Code Validation

To make sure the developed FORTRAN code works properly, the problem of natural convection flow in a differentially heated enclosure contained a uniform distribution of conducting square solid blocks is considered. For this test case, the related parameters such as the Rayleigh number, solid–fluid thermal conductivity ratio, and Prandtl number are, respectively, chosen as \(Ra= 10^{6}, \lambda =1, 10\), and 100, and \(\Pr =1\), similar to that of Merrikh and Lage (2005). As can be seen in Table 1, the results of the average Nusselt number at the hot wall of the enclosure are in excellent agreement with the work of Merrikh et al. (2005). Further validations of the employed lattice Boltzmann conjugate heat transfer method are available in our previous papers (Imani et al. 2012a, b, 2013) so, we are sure that the prepared code works properly and the presented results are accurate.

Table 1 Hot wall average Nusselt number comparison for an enclosure contained a uniform distribution of conducting solid blocks for \(\Pr =1\)
Full size table

5 Results and Discussion

In the present paper, pore scale numerical simulation of the natural convection flow in a differentially heated enclosure filled with a conducting BDPM with two configurations namely, the detached geometry (Fig. 1a) and the attached geometry (Fig. 1b) is carried out using the thermal lattice Boltzmann method. As stated before, pertinent parameters effect the steady-state heat transfer and fluid flow in the problem under consideration are taken as the Rayleigh number Ra, Prandtl number \(\Pr \), solid–fluid thermal conductivity ratio \(\lambda \), micro-porous porosity \(\varepsilon _{\mathrm{mic}}\), macro-pores volume fraction \(\varphi _{\mathrm{mac}}\), number of blocks in each micro-porous medium \(N_{\mathrm{mic}}^2\), and number of blocks in the macro-pores \(N_{\mathrm{mac}}^2\). The Prandtl number is taken as 1 throughout this study. A complete list of the other parameters considered in this study is given in Table 2.

Table 2 List of parameters considered in this study
Full size table

To examine the effect of presence of the BDPM on natural convection heat transfer in the enclosure, average Nusselt number at the hot wall of the enclosure is defined as follows:

$$\begin{aligned} \overline{{Nu}}=-\int _{0}^1{\left( {{\partial \theta _f}/{\partial x^{{*}}}}\right) }\hbox {d}y^{{*}} \end{aligned}$$
(20)

since for the attached geometry (see Fig. 1b), heat can be transferred from the hot wall to the fluid through both the micro-porous media and the macro-pores, two separate average Nusselt numbers at the hot wall of the enclosure corresponding to the micro-porous media and the macro-pores are, respectively, defined as \(\overline{{Nu}}_{\mathrm{mic}}\) and \(\overline{{Nu}}_{\mathrm{mac}} \) that can be calculated as follows:

$$\begin{aligned} \overline{{Nu}}_{\mathrm{mic,mac}}=-\int \nolimits _{0}^{l_{\mathrm{mic,mac}}^{*}}{\left( { {\partial \theta _{\mathrm{f}}}/{\partial \mathbf{n}^{{*}}}}\right) } dl_{\mathrm{mic,mac}}^{*} \end{aligned}$$
(21)

where \(\mathbf{n}^{{*}}=\mathbf{n}/H\) is dimensionless unit vector normal to the heat transfer surface, \(l_{\mathrm{mic}}^{*}={l_{\mathrm{mic}}}/H\) and \(l_{\mathrm{mac}}^{*}=l_{\mathrm{mac}}/H\) are, respectively, total dimensionless length over which heat is transferred from wall to the micro-porous media and macro-pores.

To assess the validity of the local thermal equilibrium condition in the micro-porous media to be used in available volume-averaged models, percentage of the local thermal non-equilibrium (%LTNE) for each micro-porous medium is defined as Eq. (22).

$$\begin{aligned} \%\hbox {LTNE}=\left| {\langle \theta _{\mathrm{s}}\rangle ^{\mathrm{s}}-\langle \theta _{\mathrm{f}} \rangle ^{\mathrm{f}}}\right| \times 100 \end{aligned}$$
(22)

where \(\langle \theta _{\mathrm{s}}\rangle ^{\mathrm{s}}\) and \(\langle \theta _{\mathrm{f}}\rangle ^{\mathrm{f}}\) are, respectively, solid and fluid intrinsic volume-averaged dimensionless temperatures calculated using the pore scale solid and fluid temperature distributions available from Nield and Bejan (2013).

$$\begin{aligned} \langle \theta _{\mathrm{s,f}}\rangle ^{\mathrm{s,f}}=1/{V_{\mathrm{s,f}}}\int \limits _{V_{\mathrm{s,f}}} {\theta _{\mathrm{s,f}} \hbox {d}V_{\mathrm{s,f}}} \end{aligned}$$
(23)

where \(V_{\mathrm{s,f}}\) is the solid or fluid volumes in the representative elementary volume chosen to calculate \(\langle \theta _{\mathrm{s}}\rangle ^{\mathrm{s}}\) and \(\langle \theta _{\mathrm{f}}\rangle ^{\mathrm{f}}\) in each micro-porous medium.

In view of the above-mentioned, results of interest are streamlines and isotherms in the enclosure filled with a BDPM, average Nusselt number at the hot wall of the enclosure, and the percentage of the local thermal non-equilibrium (%LTNE) in the micro-porous media. These results are presented in two main subsections regarding to the two geometries of the BDPM in the enclosure (see Fig. 1a, b) considered in the present research.

5.1 The Detached BDPM

In this section, effect of pertinent geometrical (\(N_{\mathrm{mac}}^{2}, N_{\mathrm{mic}}^{2}, \varepsilon _{\mathrm{mic}}\), and \(\varphi _{\mathrm{mac}}\)), thermo-physical \((\lambda )\), and flow parameters (Ra) on pore scale streamlines, isotherms, and hot wall average Nusselt number [see Eq. (20)] in an enclosure filled with a detached BDPM (Fig. 1a) is presented as follows.

5.1.1 Pore Scale Streamlines and Isotherms Within a Detached BDPM

In this work, effect of all geometrical, thermo-physical, and flow parameters on streamlines and isotherms is investigated. However, to save some space, only effect of micro-porous porosity on streamlines and isotherms is presented here. In Fig. 2a–c, streamlines and corresponding isotherms in a detached BDPM with \(\varphi _{\mathrm{mac}}=0.64\), \(N_{\mathrm{mac}}^2 =16\), \(N_{\mathrm{mic}}^2 =16\), and \(Ra=10^{6}\) are shown, respectively, for \(\varepsilon _{\mathrm{mic}} =0.50\), \(\varepsilon _{\mathrm{mic}} =0.64\), and \(\varepsilon _{\mathrm{mic}} =0.85\). As seen in Fig. 2a–c, with increasing the micro-porous porosity, the flow is intensified in the BDPM because of the higher permeability to the flow achieved by the higher micro-porous porosity. One can observe from Fig. 2a that, for lower micro-porous porosity \(\varepsilon _{\mathrm{mic}} =0.50\), almost all of the flow is channeling through the macro-pores. This is why isotherms are quite wavy especially near the hot and cold walls. In the other hand, when the micro-porous porosity is increased to the higher values \(\varepsilon _{\mathrm{mic}} =0.85\) (Fig. 2c), as it is obviously seen from the streamlines in Fig. 2c, the flow is enhanced in the micro-porous media as well and the isotherms no longer show the waviness behavior near the hot and cold walls.

Fig. 2
figure 2

Streamlines (left) and isotherms (right) for a detached BDPM with \(Ra=10^{6}, \varphi _{\mathrm{mac}} =0.64\), and \(\lambda =1\), a \(\varepsilon _{\mathrm{mic}} =0.5\), b \(\varepsilon _{\mathrm{mic}} =0.64\), c \(\varepsilon _{\mathrm{mic}} =0.85\)

Full size image

5.1.2 Effect of Pertinent Geometrical Parameters on Hot Wall Average Nusselt Number

In Figs. 3, 4, and 5, respectively, effect of micro-porous porosity and macro-pores volume fraction, number of blocks in the micro-porous medium, and number of blocks in the macro-pores on the hot wall average Nusselt number are shown. As seen in Fig. 3, effect of increasing both micro-porous porosity and macro-pores volume fraction is to enhance the hot wall average Nusselt number. However, it can be seen that changing the macro-pore volume fraction has much more effect on the hot wall average Nusselt number than what the micro-porous porosity does. The same result also can be pointed out from Figs. 4 and 5 where, respectively, effects of number of blocks in the micro-porous medium and macro-pores are investigated on the hot wall average Nusselt number. As can be seen from Figs. 4 and 5, sensitivity of the hot wall average Nusselt number to change in the number of blocks in the macro-pores is more significant compared to that of the micro-porous medium. As another result from Fig. 4, it is seen that beyond \(N_{\mathrm{mic}}^2 =16\) the hot wall average Nusselt number is not affected by the number of blocks in the micro-porous medium.

Fig. 3
figure 3

Effect of micro-porous porosity and macro-pores volume fraction on the average Nusselt number at the hot wall of the enclosure for \(N_{\mathrm{mac}}^{2} =16, N_{\mathrm{mic}}^{2}=16, \lambda =1\), and \(Ra=10^{6}\)

Full size image
Fig. 4
figure 4

Effect of variation of \(N_{\mathrm{mac}}^{2}\) on hot wall average Nusselt number for a detached BDPM with \(Ra=10^{6}, \varepsilon _{\mathrm{mic}}=0.64\), and \(\varphi _{\mathrm{mac}}=0.64\) for different values of \(N_{\mathrm{mic}}^{2}\)

Full size image
Fig. 5
figure 5

Effect of variation of \(N_{\mathrm{mic}}^{2}\) on hot wall average Nusselt number for a detached BDPM with \(Ra=10^{6}\), \(\varepsilon _{\mathrm{mic}}=0.64\), and \(\varphi _{\mathrm{mac}} =0.64\) for different values of \(N_{\mathrm{mac}}^{2}\)

Full size image

To more elaborate on the above-mentioned results, it should be said that a BDPM is a two-scaled porous medium within which fluid flows based on a competing effects between the permeability of the micro-porous medium and macro-pores. By using Eqs. (7) and (9) for calculating the block sizes, respectively, in the macro-pores and micro-porous medium, together with the Carman–Kozeny equation for the permeability of a packed bed available from Nield and Bejan (2013), one can derive a simple analytical relation as Eq. (24) that describes conditions under which the permeability of the micro-porous medium is equal to that of the macro-pores.

$$\begin{aligned} {\varepsilon _{\mathrm{mic}}^3}/{\left[ {\left( 1-\varepsilon _{\mathrm{mic}}\right) N_{\mathrm{mic}}^2}\right] }= {\varphi _{\mathrm{mac}}^3}/{\left( {1-\varphi _{\mathrm{mac}}}\right) }^{2} \end{aligned}$$
(24)

As a first point from Eq. (24), one can realize that the number of blocks in the macro-pores \(N_{\mathrm{mac}}^{2}\) does not affect conditions under which the permeability of the two scales are comparable. As another result, it is seen from Eq. (24) that for the same micro-porous porosity and macro-pores volume fraction, permeability of the micro-porous medium is always lower than that of the macro-pores. According to Eq. (24), the only way that the permeability of the micro-porous medium can exceed that of the macro-pores is for the higher values of the micro-porous porosity together with the lower values of the macro-pores volume fraction and number of blocks in the micro-porous medium. Keeping in mind this analysis, one can take another look at Figs. 3, 4 and 5 to justify that the hot wall average Nusselt number is affected by the micro-porous porosity only for the higher micro-porous porosities together with the lower macro-pores volume fraction and number of blocks in the micro-porous medium.

5.1.3 Effect of the Rayleigh Number and Solid–Fluid Thermal Conductivity Ratio

Effect of variation of the solid–fluid thermal conductivity ratio on the hot wall average Nusselt number for a detached BDPM is presented in Table 3 for different Rayleigh numbers. It is understood from Table 3 that effect of increasing \(\lambda \) on the hot wall average Nusselt number is not in the same direction for different ranges of the Rayleigh number. That is, for lower Rayleigh numbers, this effect is to increase the average Nusselt number, whereas for the higher Rayleigh numbers, it is to slightly decrease the hot wall average Nusselt number. This is because the smaller Rayleigh numbers provide thicker wall thermal boundary layers, which, in turn, helps to thermally activate the conducting blocks adjacent to the hot wall, thereby enhancing the heat transfer. This result is in a good agreement with those considered the pore scale natural convection problem in a differentially heated enclosure filled with a detached MDPM (Merrikh and Lage 2005; Merrikh et al. 2005; Merrikh and Mohamad 2001).

Table 3 Effect of the solid–fluid thermal conductivity ratio and Rayleigh number on the hot wall average Nusselt number for \(N_{\mathrm{mac}}^{2}=16, N_{\mathrm{mic}}^2, \varepsilon _{\mathrm{mic}} =0.64\), and \(\varphi _{\mathrm{mac}}=0.64\)
Full size table

5.1.4 Comparison of the Results of the Detached BDPM with Available Results

The pore scale results presented in this study for the detached BDPM geometry (see Fig. 1a) are compared with those of Narasimhan and Reddy (2010). Those authors, considered the BDPM as homogeneous porous blocks uniformly distributed in an enclosure with considering the volume-averaged model with assumption of the local thermal equilibrium within the micro-porous medium. As can be seen from Fig. 6, the hot wall average Nusselt number of the present study and those obtainable from the correlation given by Narasimhan and Reddy (2010) is plotted versus the modified Rayleigh number \(Ra_\phi Da_E\), as defined by Narasimhan and Reddy (2010). It is observed from Fig. 6 that the results of the present study underpredict the results of Narasimhan and Reddy (2010) with maximum discrepancy of 18 %. It should be noted that this discrepancy between the results of the present study and that of Narasimhan and Reddy (2010) can be attributed to the volume-averaged simulation used by those authors in the micro-porous medium which eliminates some details of the fluid flow and heat transfer in the BDPM compared to the pore scale simulation of the present study.

Fig. 6
figure 6

Comparison of the hot wall average Nusselt number of a detached BDPM calculated for the presented pore scale results with the results of Narasimhan and Reddy (2010)

Full size image

5.2 The Attached BDPM

Pore scale results of streamlines, isotherms and hot wall average Nusselt numbers in an enclosure filled with an attached BDPM (Fig. 1b) is presented as follows. In this section, \(N_{\mathrm{mac}}^2 =16\) and \(N_{\mathrm{mic}}^2 =16\) is considered for the BDPM for all presented results.

5.2.1 Pore Scale Results of Fluid Flow and Heat Transfer Within an Attached BDPM

Figures 7 and 8 show streamlines and corresponding isotherms, respectively, for different values of macro-pores volume fraction and micro-porous porosity. As seen in Figs. 7 and 8, both macro-pores volume fraction and micro-porous porosities effect details of streamlines and isotherms within the BDPM. This change in details of the streamlines and isotherms may be attributed to the change in the fluid flow and heat transfer preferences because of a competing effect between the permeabilities of the macro-pores and micro-porous media as well as change in the thermo-physical properties.

Fig. 7
figure 7

Streamlines and isotherms in an enclosure filled with an attached BDPM for \(Ra=10^{7}\) with \(\varphi _{\mathrm{mac}}=0.64, N_{\mathrm{mac}}^2 =16, N_{\mathrm{mic}}^2 =16\), and \(\lambda =1\). a \(\varepsilon _{\mathrm{mic}} =0.50\), b \(\varepsilon _{\mathrm{mic}} =0.64\), c \(\varepsilon _{\mathrm{mic}} =0.85\)

Full size image
Fig. 8
figure 8

Streamlines and isotherms in an enclosure filled with an attached BDPM for \(Ra=10^{7}\) with \(\varepsilon _{\mathrm{mic}} =0.64, N_{\mathrm{mac}}^2 =16, N_{\mathrm{mic}}^2 =16\), and \(\lambda =1\), a \(\varphi _{\mathrm{mac}} =0.50\), b \(\varphi _{\mathrm{mac}} =0.64\), c \(\varphi _{\mathrm{mac}} =0.85\)

Full size image

Figures 9 and 10 are plotted to show effects of the micro-porous porosity on the pore scale vertical velocity and dimensionless temperature distribution along the x direction at \(y^{*}=0.42\), respectively, for \(\lambda =1\) and \(\lambda =100\). As seen in Figs. 9 and 10, effect of increasing the micro-porous porosity is to increase the vertical velocity within the micro-porous medium for both solid–fluid thermal conductivity ratios. It is interesting to look at Figs. 9 and 10 to see with increasing the solid–fluid thermal conductivity ratio, the flow is enhanced in the micro-porous medium for a given micro-porous porosity. From Figs. 9 and 10, one also can observe that with increasing the micro-porous porosity, the temperature gradient within the micro-porous medium is increased.

Fig. 9
figure 9

Pore scale a vertical velocity and b dimensionless temperature distribution along the x direction at \(y^{*}=0.42\) for \(\lambda =1\) and \(Ra=10^{7}\) for different micro-porous porosities

Full size image
Fig. 10
figure 10

Pore scale a vertical velocity and b dimensionless temperature distribution along the x direction at \(y^{*}=0.42\) for \(\lambda =100\) and \(Ra=10^{7}\) for different micro-porous porosities

Full size image

5.2.2 Effect of Changing the Macro-pores Volume Fraction and Micro-porous Porosity

The above-mentioned results can be better understood by looking at Fig. 11, where \(\overline{{Nu}}_{\mathrm{mac}}\) and \(\overline{{Nu}}_{\mathrm{mic}}\) are plotted versus the macro-pores volume fraction \(\varphi _{\mathrm{mac}}\), for two solid–fluid thermal conductivity ratios \(\lambda =1\) and \(\lambda =100\). As seen in Fig. 11, with increasing \(\varphi _{\mathrm{mac}}\), the macro-pores hot wall average Nusselt number is significantly increased, whereas for the micro-porous media the value of the average Nusselt number at the hot wall is decreased for both \(\lambda =1\) and \(\lambda =100\). As an interesting result, one can observe from Fig. 11 that for a small value of the macro-pores volume fraction \(\varphi _{\mathrm{mac}} =0.50\), the average Nusselt number of the micro-porous media exceeds that of the macro-pores.

Figure 11 also presents the effect of solid–fluid thermal conductivity ratio \(\lambda \) on macro-pores and micro-porous hot wall average Nusselt numbers \(\overline{{Nu}}_{\mathrm{mac}}\) and \(\overline{{Nu}}_{\mathrm{mic}}\). As can be seen from Fig. 11, effect of increasing \(\lambda \) is to increase the micro-porous average Nusselt number \(\overline{{Nu}}_{\mathrm{mic}}\) and decrease the macro-pores average Nusselt number \(\overline{{Nu}}_{\mathrm{mac}}\). It should be noted that, as seen in Figs. 9 and 10, with increasing \(\lambda \) resistance to heat flow from the micro-porous media attached to the wall decreases and more heat flows through this structure thereby reducing the average Nusselt number of the macro-pores.

Fig. 11
figure 11

Effect of variation of the macro-pores volume fraction on the micro-porous and macro-pores hot wall average Nusselt numbers for different solid–fluid thermal conductivity ratios with \(\varepsilon _{\mathrm{mic}} =0.64\) and \(Ra=10^{7}\)

Full size image
Fig. 12
figure 12

Effect of variation of the micro-porous porosity on micro-porous and macro-pores average Nusselt numbers at the hot wall of the enclosure for different Rayleigh numbers

Full size image

As another interesting result, it is seen that effect of solid–fluid thermal conductivity ratio on micro-porous and macro-pores average Nusselt numbers decreases as macro-pores volume fraction increases. A physical explanation for this result is that, as macro-pores volume fraction increases, the intensity of flow in macro-pores adjacent to the wall significantly enhances, which, in turn, drastically decreases contribution of the micro-porous in overall heat transfer from the wall so that the effect of changing \(\lambda \) on the average Nusselt number diminishes within the micro-porous media.

Table 4 Effect of pertinent parameters on maximum percentage of local thermal non-equilibrium \(\max \)(%LTNE) calculated in the micro-porous media for the attached BDPM geometry (see Fig. 1b)
Full size table

Figure 12 is plotted to show the effect of variation of the micro-porous porosity on micro-porous and macro-pores average Nusselt numbers at the hot wall of the enclosure, for two Rayleigh numbers (\(Ra=10^{6}\) and \(Ra=10^{7}\)). As demonstrated by Fig. 12, effect of increasing the micro-porous porosity is to increase both micro-porous and macro-pores average Nusselt numbers for two of the Rayleigh numbers. This is an interesting result because with increasing the micro-porous porosity while keeping other parameters unchanged, it is expected that fluid would choose the micro-porous media over the macro-pores to flow and as a result the micro-porous hot wall average Nusselt number would increase, whereas the macro-pores hot wall average Nusselt number would decrease. But what really happens can be better understood by taking another look at Fig. 8 to see with increasing the micro-porous porosity the fluid flow is intensified in both micro-porous media and macro-pores so that convection heat transfer from the hot wall to both media is enhanced. This is because there are two ways for fluid to flow in the macro-pores: one is to go through the micro-porous media and the other is to go around it. As such, when micro-porous porosity increases, fluid chooses to go through the micro-porous media as well to flow in the macro-pores, that is why \(\overline{{Nu}}_{\mathrm{mac}}\) is increased as well as \(\overline{{Nu}}_{\mathrm{mic}}\). It should be noted that, according to Fig. 11, this is not the case when the macro-pores volume fraction is changed where increasing the macro-pores volume fraction results in increasing \(\overline{{Nu}}_{\mathrm{mac}}\) and decreasing \(\overline{{Nu}}_{\mathrm{mic}}\).

5.2.3 Assessing the Validity of the Local Thermal Equilibrium in the Micro-porous Media

As stated before, in this paper, the pore scale results of the solid and fluid temperature distributions are used to assess the availability of the local thermal equilibrium assumption within the micro-porous media of a BDPM invoked by Nield and Kuznetsov (2005) in their volume-averaged two-velocity two-temperature model and by Narasimhan and Reddy (2010) in their simulation. As such, the percentage of the local thermal non-equilibrium %LTNE, as previously defined by Eqs. (22) and (23), is computed in the attached BDPM for each micro-porous medium (i.e., number of the micro-porous medium in a BDPM is \(N_{{\mathrm{mac}}}^2 )\). Then, the maximum value of the %LTNE denoted as \(\max \)(%LTNE) is presented in Table 4 for all of the considered parameters. Departure from the local thermal equilibrium is confirmed when the criterion \(\max (\%\hbox {LTNE})\ge 5\) is observed in the BDPM (Khashan et al. 2005). As seen in Table 4, the local thermal equilibrium condition is violated for the higher values of the Rayleigh number, micro-porous porosity, solid–fluid thermal conductivity ratio, and the lower values of the macro-pores volume fraction. The maximum departure from the local thermal equilibrium, for the range of parameters considered in this study, is occurred for \(Ra=10^{7}, \varepsilon _{\mathrm{mic}} =0.85\), and \(\lambda =100\). In case of the detached BDPM (see Fig. 1a), for the all ranges of the parameters considered in this study, the thermal equilibrium condition is well justified so that the results of percentage of the local thermal non-equilibrium %LTNE in this case are not presented for sake of the brevity.

6 Conclusion

In the present study, pore scale numerical simulation of the natural convection in a differentially heated enclosure occupied by a conducting bidisperse porous medium (BDPM) is investigated using the thermal lattice Boltzmann method. Based on the different applications, two configurations for the BDPM in the enclosure are considered namely, detached and attached geometries. Effect of pertinent parameters on the streamlines, isotherms, and hot wall average Nusselt number are investigated. The pore scale results of the present study are used to compute the maximum percentage of the local thermal non-equilibrium for two of the bidisperse porous medium configurations. The maximum percentage of the local thermal non-equilibrium then is used to assess the validity of the local thermal equilibrium condition in the micro-porous media invoked by the available volume-averaged two-temperature two-velocity model. The main conclusions of the present study are as follows:

for the detached geometry:

  • The local thermal equilibrium condition within the micro-porous media is justified for all ranges of all parameters considered in this study.

  • Effect of solid–fluid thermal conductivity ratio on the hot wall average Nusselt number is important for lower Rayleigh numbers.

  • Effect of micro-porous geometrical parameters on the hot wall average Nusselt number is only considerable under the conditions that permeability of the micro-porous medium is comparable to that of the macro-pores.

for the attached geometry:

  • It is shown that departure from the local thermal equilibrium condition within the micro-porous media is observed for the higher values of the Rayleigh number, micro-porous porosity, solid–fluid thermal conductivity ratio, and the lower values of the macro-pores volume fraction.

  • Effect of increasing the solid–fluid thermal conductivity ratio is to decrease and increase, respectively, the macro-pores and micro-porous media hot wall average Nusselt numbers.

  • Compared to the detached BDPM, effect of micro-porous geometrical and thermo-physical parameters on the heat transfer characteristics is more important for an attached BDPM.

  • Effect of the micro-porous porosity is to increase both micro-porous and macro-pores hot wall average Nusselt numbers, whereas increasing the macro-pores volume fraction results in, respectively, increasing and decreasing the hot wall average Nusselt number of the macro-pores and micro-porous media.