Pricing algorithms in oligopoly with decreasing returns

Abstract

Pricing algorithms are computerized procedures a seller may use to adapt instantaneously its price to market conditions, including to prices quoted by its rivals. These algorithms are related to the extensive use of web-collectors which contribute in many industries to identifying the best price. In such settings, price competition operates between algorithms, no longer between executives of brick and mortar companies. In this context, the question is to know how implicit forms of collusion may arise between the sellers. This paper is aimed at discussing this conceptual issue in a price-setting homogeneous product oligopoly with decreasing returns to scale where algorithms implement matching policies. Using fixed point argument, we find a family of equilibrium prices encompassing Cournot and Pareto efficient solutions, if matching is allowed upward and downward. Dynamical stability is studied in the linear demand constant return case. When matching operates only for price undercutting, this family is extended up to a bottom value of the market price, close to the Walrasian price. Pricing algorithms may solve the Bertrand–Edgeworth paradox.

1 Introduction

In the digital economy, consumers are better informed on products and prices. Shopping can be done everywhere on smartphones. Information transparency and consumer reactivity stimulate fair competition. But on the supply side, Big Data, search engines, social networks and tutti quanti offer tremendous opportunities to erect monopoly rents and accumulate subnormal profits. Firms are, by nature, better organized than the consumers to exploit or process overwhelming flows of data. The dubious effect on welfare deeply questions competition policies in the digital economy.

In the line of a growing literature on algorithmic pricing (e.g. Brown & MacKay, 2021; for a survey, see Calvano et al., 2019), the book by Ezrachi & Stucke, (2016) exemplifies the role of algorithms in sustaining specific forms of tacit collusion through supra-competitive prices. Pricing algorithms are computerized procedures that a seller may use to adapt instantaneously its price to market conditions, particularly to prices quoted by its rivals. Ezrachi and Stucke identify three collusion scenarios according to the level of AI involved in the pricing bots that operate as substitute for human day-to-day decision-making. This tends to dampen the manager’s antitrust liability since no intent of explicit collusion is involved. Under the third scenario, called “tacit collusion on steroids”, each firm unilaterally adopts its pricing algorithm, which sets its own price. Pricing algorithms act as predictable agents and continually monitor and adjust to each other’s prices and market data.

This scenario is motivated, in the real world, by the Martha’s Vineyard case (White V. R.M. Packer Co., Inc, 2011)¹ (see the recension by The Economist, 2017). Martha’s Vineyard is an island off the coast of Massachusetts, which is deemed to be a nice place for vacationers. Only 9 gas stations operate on the island. Each station prominently posts its prices so that all the consumers are perfectly informed; furthermore, any seller can instantaneously match any deviation of the rivals. The demand from the residents is highly inelastic because alternative sources of gasoline are located on the mainland. The residents constitute a captive segment of the market. In addition, entry of new gasoline sellers is restricted by specific rules and procedures. As a result, gas prices on the island exceed prices on the mainland by an average of 56 cents per gallon. Some residents filed a complaint for collusion among the stations’ owners. The plaintiffs’ antitrust claims failed. The trial and appellate court found no evidence of explicit collusion. The gasoline market in Martha’s Vineyard is oligopolistic and the price fixing mechanism at work is the pure result of a rational, unilateral decision by each competitor, the court said.

1.1 Facts and trends in the digital economy

In the last decades, pricing algorithms have been increasingly used in the digital economy, from services to online retailing. For example:

Since the 2000s, search aggregators such as Kayac, Expedia and Orbitz operate as pricing support tools for airline companies; these aggregators run as pricing algorithms since they mechanically make adjustments to the best offer. In 2001, the four major US airlines decided to team up and create Orbitz which went public in 2003. This has awakened the scrutiny of regulatory authorities (Akca & Rao, 2020): on a similar basis to the Martha’s vineyard case, the Department of Justice ruled in 2003 that Orbitz was not a cartel and that there was no evidence of price fixing² although this have led to increases in markups in the airline industry.

Brown and MacKay (2021) present an empirical analysis of hourly prices of allergy drugs delivered by five online retailers in the United States, in a period of one and a half years. The pricing strategies of these retailers are governed by algorithms which operate in real time. These authors show how the prices of the drugs were consequently boosted in that period.

Third-party software developers of pricing algorithms are now spreading on the net. ChannelAdvisor boasts its software as “constantly monitoring top competitors online.” Repricer.com claims to ”react to changes your competitors make in 90 seconds.” Intelligence Node gives the retailers the opportunity to “have eyes on competitor movements at all times and...automatically update their prices.” Many other software solutions can be found online and advertised as ”dynamic pricing”.

Thus, in various oligopoly situations, prices are likely to be supra-competitive when pricing algorithms are used; explicit collusion is not necessarily involved, as ruled by the antitrust authorities in recent years³. In Martha’s Vineyard case, the court of Appeals based its decision on the analysis of downward (undercutting prices) and upward price-matching policies (raising prices): if one station drops its price to attract more business, the others can quickly drop their prices in response. Conversely, a station acting as a price “leader” risks little by raising its price; if the competitors do not follow the increase, the leader can quickly drop its price again to match his rivals.

This argumentation holds more significantly again in the digital economy, with some specificities:

• (i) Digital economy lacks from insularity; demand in most markets is elastic. Downward matching policy leads to a cut of the market price, which attracts new consumers. Upward matching policy leads to an increase which repels current consumers. The equilibrium price level strongly depends on these marginal consumers.

• (ii) Following a leading firm which raises its price never constitutes a rational and unilateral decision. In classic industries, the “do nothing” option remains the best one any seller can choose in response to rivals’ raising prices. Online driving forces fueled by price web aggregators are more oriented towards price wars than price escalations. It remains, however, that the digital economy opens avenues for pricing algorithms computerizing upward matching policies, especially if these algorithms are opaque to antitrust enforcers.

• (iii) Diseconomies of scale play a key role in some sectors of the digital economy (e.g. in travel industry with online booking) and may interact with the matching policies. As we know from the oligopoly literature, the cost structure of the firms strongly matters. According to the well-known Bertrand–Edgeworth paradox (cf. Tirole, 1988, p. 214), when the firms face strictly decreasing returns to scale, there is no deterministic oligopoly equilibrium⁴; the perfect competitive price is not a pure strategy price equilibrium as the rivals do not want to attract any consumer flying from a price raising firm. This phenomenon may limit the effectiveness of upward matching policies to sustain supra-competitive prices.

In this paper, we want to investigate the theoretical foundations of these issues. Our objective is to analyze the equilibrium conditions when pricing algorithms operate in an oligopoly with decreasing returns. We will prove that the use of algorithms leads to a multiplicity of equilibria with supra-competitive prices.

1.2 Background

The literature on price-matching policies mainly deals with analyzing the price-matching guarantee, namely the commitment made by the seller to sell its product at the lowest price on the market upon proof. Price-matching guarantee is considered an anti-competitive practice as it actually dampens the impact of price undercutting. Salop (1986) shows that the market price ranges from the monopolistic to the Bertrand price when the firms have options to price-match. Monopolistic price may emerge as the dominant strategy (Doyle, 1988). Batsaikhanz and Tumennasan (2018) study the effects of price-matching in a setting in which each firm selects both its price and output simultaneously. They show that the availability of a price-matching option leads to the Cournot outcome (see also Tumennasan, 2013). These contributions consider price-matching guarantees designed to match any vector of prices listed by the rivals (and eventually outputs) in the industry. In a game theoretic setting, this defines specific pricing strategies and equilibrium conditions.

In this literature, the price-matching guarantee is only available to the consumers who are ready to buy the product before the price rebate. Pricing algorithms under consideration in this paper make the rebate to apply to all the potential consumers. This affects the equilibrium conditions especially in the decreasing returns to scale context in which the analysis is made.

1.3 Overview of the results

This paper considers a price setting oligopoly model with decreasing returns to scale (cf. Thépot, 1995 for a Bertrand competition analysis). We formalize the pricing algorithm competition in a static homogeneous product oligopoly as follows: we start from any current state of the oligopoly defined by (i) the clearing market price; (ii) the outputs of the firms. It is an equilibrium if no firm is better off when moving its price (downward and eventually upward) when the rivals systematically use algorithms to match this move. Equilibrium conditions result from a fixed point reasoning similar to that used in general equilibrium theory.

The equilibrium price and outputs depend on the firms’ customers response to market price variation. The original feature of this paper is to distinguish upward and downward matching. Two cases are considered.

• (i) The case where bidirectional matching (upward and downward) is implemented by the algorithms; we get a family of equilibria; these equilibria define a set of oligopoly outcomes including Cournot and Pareto efficient solutions. Dynamical stability in the linear demand constant return case is studied. In the line of the work by Theocharis (1960), we prove that Pareto-efficient equilibria are dynamically stable.

• (ii) The monodirectional matching case where only downward matching is allowed. The family of equilibria extends to a set of prices lower than Cournot but higher than a bottom value (which dominates the competitive price). This bottom price depends on the cost structure of the firms. It is the socially best price achievable through pricing algorithms. It deserves consideration from the antitrust authorities as it deals with a substantial welfare improvement with respect to alternative solutions (Cournot, among others). The existence of pure equilibria in a context of decreasing returns to scale is worth noting: pricing algorithms may solve the Bertrand–Edgeworth paradox; accordingly, they contribute to the market stability.

The remaining of the paper is divided into three parts: the statement of the model is presented in Sect. 2. Sections 3 and 4 are, respectively, devoted to the bidirectional and the monodirectional matching cases; equilibrium analysis are developed and analytical results are illustrated in the linear-quadratic case. Comments are given in Sect. 5.

2 The model

Let us consider an oligopoly with n firms. Each firm produces and sells the same good with a decreasing returns technology. Let $C_{i}(.)$ be the continuously twice differentiable cost function of firm i with $C_{i}(0)=0,$ $C_{i}^{\prime }>0$ and $C_{i}^{\prime \prime }\ge 0.\$The demand D for the good is a function of the market price p with a finite continuous derivative $D^{\prime }(p)<0$ over all the domain where it is positive and such that $\lim _{p\rightarrow {\bar{p}}}D(p)=0,$ for some ${\bar{p}}\in (0,+\infty ].$ Let $q_{i}\ge 0$ the output of firm $i.\$Let us denote $q=(q_{i})_{i=1,\ldots ,n}$ the vector of quantities. Let $\Pi _{i}(p,q_{i})=pq_{i}-C_{i}(q_{i})$ be the profit of firm i.

2.1 Relevant oligopoly states

Let us introduce the firm i’s supply function $s_{i}(p)=C_{i}^{\prime -1}(p)$ if $p\ge C_{i}^{\prime }(0),0$ if not,  which defines the maximum quantity firm i is willing to produce at any given price p (referred to as profitable capacity in Benassy (1989)). Output $q_{i}\ge 0$ is said to be profitable if

$$\begin{aligned} q_{i}\le s_{i}(p), \end{aligned}$$

(1)

or equivalently,

$$\begin{aligned} p\ge C_{i}^{\prime }(q_{i}). \end{aligned}$$

(2)

Definition 1

A feasible oligopoly state is an $n+1$ tuple vector $\left( p,q\right) ,$ such that

• 1. the supply=demand condition $D(p)=\sum \nolimits _{i=1}^{n}q_{i}$ holds.

• 2. The quantities produced by all the firms are nonnegative and profitable, $0\le q_{i}\le s_{i}(p),i=1,\ldots ,n.$

Let ${\mathcal {E}}$ be the set of the feasible oligopoly states. It is a subset of an n-dimensional variety of $\mathfrak {R}^{n+1}.$ Standard feasible oligopoly states are usually considered in economics and defined as follows:

• The competitive (Walrasian) solution $\left( p^{w},q^{w}\right) ,$with $p^{w}=C_{i}^{\prime }(q_{i}^{w}),$ $i=1,\ldots ,n,$ which is not a pure strategy equilibrium when the firms face strictly decreasing returns, according to the Bertrand–Edgeworth paradox.

• The Cournot equilibrium $\left( p^{c},q^{c}\right) ,$ with $q_{i}^{c}+(p^{c}-C_{i}^{\prime }(q_{i}^{c}))D^{\prime }(p^{c})=0,$ $i=1,\ldots ,n.$

• The Pareto efficient oligopoly states $\left( p^{e},q^{e}\right)$ maximizing a positive linear combination of the profits, namely solving the program:

  $$\begin{aligned} \left\{ \begin{array}{l} \max _{p,q_{i}}\sum \limits _{i=1}^{n}\alpha _{i}(pq_{i}-C_{i}(q_{i})) \\ \sum \limits _{i=1}^{n}q_{i}=D(p), \end{array} \right. \end{aligned}$$

  for any coefficients $\alpha _{i}\ge 0,$ $i=1,\ldots ,n.$

Using Lagrangian methods, first-order conditions yield the relations:

$$\begin{aligned} \frac{\alpha _{i}q_{i}}{\sum \nolimits _{j=1}^{n}\alpha _{j}q_{j}}=-\frac{q_{i}}{ (p-C_{i}^{\prime }(q_{i}))D^{\prime }(p)},i=1,\ldots ,n. \end{aligned}$$

(3)

The sum of these relations leads to eliminating the $\alpha _{i}^{\prime }s:$

$$\begin{aligned} 1+\sum \limits _{i=1}^{n}\frac{q_{i}}{(p-C_{i}^{\prime }(q_{i}))D^{\prime }(p)} =0, \end{aligned}$$

(4)

which defines the the Pareto-frontier ${\varvec{F}}\mathcal {\subset \mathfrak {R}} ^{n}$ of the oligopoly (with $\sum \nolimits _{i=1}^{n}q_{i}=D(p)$). Among the efficient states, the collusive solution $\left( p^{m},q^{m}\right)$ is obtained for $\alpha _{i}=1,i=1,\ldots ,n$: conditions (3) thus become $(p^{m}-C_{i}^{\prime }(q_{i}^{m}))=-D(p^{m})/D^{\prime }(p^{m}),$ $i=1,\ldots n,$ which are the standard formulas based on Lerner indices for monopolistic firms.

Then, under the assumptions made, ${\mathcal {E}}$ is not empty. In this paper, we adopt a more restrictive point of view than general equilibrium formulations: we focus here on combinations of prices and quantities where the market is cleared through a single market price. This is consistent with the digital economy functioning where arbitrage opportunities are instantaneously eliminated so that the market price is posted online. Our aim is merely to identify feasible oligopoly states that are robust to unilateral price deviations in the market cleared context.

2.2 Algorithm pricing with homogenous product

At any given feasible oligopoly state, the competitors are assumed to base their pricing policies on algorithms. These algorithms are given and identical for all the firms in the industry, they operate in a very simple way in accordance with the absence of product differentiation. Algorithm pricing is not subject to strategic choice. The firms are price makers in the sense that any of them may unilaterally post a price that differs from the market price prevailing at this particular state. This new post is instantaneously revealed to the rivals and to the consumers (through web collectors, for instance); it mechanically triggers the immediate matching of the rivals to this price value. As a result, a new oligopoly state is found through the adjustment of the quantities. We assume that one firm at most may deviate at any time t.

As explained in the introduction, the pricing algorithm used by all the firm combines two mechanisms: (i) the downward matching in case of price cutting; (ii) the upward matching in case of price boosting. Then equilibrium conditions depend on whether the competitors activate the upward matching mechanism or not.

Let us consider a feasible oligopoly state $\left( p^{0},q^{0}\right) ,$ with $q_{i}^{0}\ge 0$ as a reference point. Let us analyze how stable this oligopoly state is in response to an unilateral price change—up or down—of some firm i when the algorithms make the rivals $k\ne$ i committed to apply both the downward and upward matching policies.

When firm i intends to deviate by charging a price $p_{i}\ne$ $p^{0}$, the rivals are instantaneously informed of this move; the pricing algorithm of firm k is designed to detecting this unilateral price move from rival i and matching this move. Formally this defines a price mapping $\pi _{k}^{i}:\mathfrak {R}^{2+}\rightarrow \mathfrak {R}^{+},$ that computes the new price $p_{k}=\pi _{k}^{i}(p^{0},p_{i})$ charged by firm k, as a response to the unilateral move of firm i.

In the homogenous product case, the price mapping is given by

• $\pi _{k}^{i}(p^{0},p_{i})=p_{i},$ for $k\ne i=1,\ldots ,n,$ in the bidirectional matching case,

• $\pi _{k}^{i}(p^{0},p_{i})=\left\{ \begin{array}{l} p_{i} \mathrm{if} p_{i}\le p^{0}, \\ p^{0} \mathrm{if} p_{i}>p^{0}, \end{array} \right.$ in the monodirectional case.

We assume here that all the firms use the same algorithm, so that $\pi _{k}^{i}(.)=\pi ^{i}(.),$ and that only one firm can move its price at date.

3 The bidirectional matching case

In the bidirectional matching case, the price variation induces a total demand variation $\Delta D=D(\pi ^{i}(p^{0},p_{i}))-D(p^{0})=D(p_{i})-D(p^{0}),$ which represents the gain or loss of consumers according to whether $p_{i}$ is lower or higher than the current price $p^{0}.$ For $n\ge 2,$ firm i guesses this demand variation is shared with the rivals according to a weighted distribution $\left( \gamma _{ik}\right) ,i,k=1,\ldots ,n$. , with $\sum _{k}\gamma _{ik}=1$ and $\gamma _{ik}\ge 0.\$Parameter $\gamma _{ik}$ measures the part of the demand variation borne by the firm k as it is guessed by firm i when price $p_{i}$ deviates from $p^{0}$: it represents a gain of consumers if the market price is lowered, a loss if it is raised. Specifically, firm $i^{\prime }s$ conjectured own output after deviation (with $\gamma _{ii}$ denoted $\gamma _{i}$ for simplicity):

$$\begin{aligned} {\tilde{q}}_{i}=q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0})) \end{aligned}$$

(5)

provided that condition (2) is satisfied at ${\tilde{q}}_{i}$.

The output delivered by rival k is ${\tilde{\xi }}_{ik}=\left[ q_{ki}^{0}+\gamma _{ik}(D(p_{i})-D(p^{0}))\right] ,$ so that $\sum _{k}\tilde{ \xi }_{ik}+{\tilde{q}}_{i}=D(p_{i})$ and the supply=demand condition is still satisfied at the adjusted state. There is no reason to postulate that $\gamma _{ik}=\gamma _{kk}$ since both values are conjectures made by different actors in different contexts (when firm k acts as the initiator of the price move or just as a follower). This does not actually matter here: in quest of equilibrium, the deviating firm does not care about the $\gamma _{ik}$ of the rivals ($k\ne i=1,\ldots n)$.

This formulation means that any move in the market price does not provoke a whole redistribution of all the customers among the sellers. In an online environment, the adjustment takes place instantaneously and triggers marginal changes around the current output levels. The price/quantities adjustments result from the behavior of marginal consumers.

In the following, parameter $\gamma _{i}$ will be termed the marginal consumer responsiveness to firm i (hereafter MCR). It measures the conjectured share of the market demand change that would affect its clientele when it triggers a market price move. The interpretation of MCR will be discussed below.

The profit of the deviating firm i is

$$\begin{aligned} \Pi _{i}(p_{i},p^{0},q_{i}^{0})=p_{i}(q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))-C_{i}(q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0})). \end{aligned}$$

(6)

For $n=1,$ we necessarily have $\gamma =1.$

3.1 Equilibrium conditions

Let us introduce the equilibrium concept associated with the matching policies.

Definition 2

Let $\gamma =(\gamma _{i})_{i=1,\ldots ,n}$ be a vector of MCR. A $\gamma$-equilibrium is an oligopoly state $(p^{*}(\gamma ),q^{*}(\gamma )),$ such that no unilateral price deviation maintaining a positive level of output is beneficial, namely

$$\begin{aligned} \Pi _{i}(p^{*},p^{*},q_{i}^{*})\ge \Pi _{i}(p_{i},p^{*},q_{i}^{*}),\ \forall \ p_{i}\text { st. }q_{i}^{*}+\gamma _{i}(D(p_{i})-D(p^{*}))\ge 0,\text {for }i=1,\ldots n. \end{aligned}$$

(7)

Let us characterize the set of $\gamma$-equilibrium when some firms may remain inactive in the market. For this purpose, we assume that the firms are ranked by increasing order of initial marginal costs:

$$\begin{aligned} C_{1}^{\prime }(0)\le C_{2}^{\prime }(0)\cdots \le C_{n}^{\prime }(0), \end{aligned}$$

(8)

so that the firms are ranked by decreasing order of efficiency. By convention, we introduce a fictitious $n+1$th firm with $C_{n+1}^{\prime }(0)=+\infty ,$ that stays ever out of the market.

Theorem 3

For $r=1,\ldots ,n,$ let $\left\{ p^{r},q^{r}\right\} \in \mathfrak {R}^{+}\times \mathfrak {R}^{n}$ be the $r+1$ tuple solution of:

$$\begin{aligned} q_{i}+\gamma _{i}D^{\prime }(p)\left[ p-C_{i}^{\prime }(q_{i})\right] & = 0,i=1,\ldots ,r, \end{aligned}$$

(9)

$$\begin{aligned} \sum \limits _{i=1}^{r}q_{i} & = D(p). \end{aligned}$$

(10)

Let $r^{*}=\max \left\{ r\text { st. }q_{i}^{r}\ge 0,i=1,\ldots ,r \right\}$. The $\gamma$-equilibrium $(p^{*}(\gamma ),q^{*}(\gamma ))$ is unique and defined by

$$\begin{aligned} \left\{ \begin{array}{l} q_{i}^{*}(\gamma )=q_{i}^{r^{*}}\ge 0, \mathrm{for}\; i=1,\ldots ,r^{*}. \\ q_{i}^{*}(\gamma )=0, \mathrm{for}\; i=r^{*}+1,\ldots ,n. \\ p^{*}(\gamma )=p^{r*}\in \left[ C_{r^{*}}^{\prime }(0),C_{r^{*}+1}^{\prime }(0)\right] . \end{array} \right. \end{aligned}$$

As a result, the $\gamma$-equilibrium quantities are profitable.

Proof

See Appendix 1. $\square$

Hence, the family of $\gamma$-equilibria is parametrized by the $(\gamma _{i}),$with $0\le \gamma _{i}\ \le 1.\$Vector $\gamma =\left( \gamma _{i}\right) _{i=1,\ldots ,n}$ encompasses the behavior of the consumers facing a move of the market price, as this behavior is perceived by the firm initiating the move. The concept of $\gamma$-equilibrium covers standard equilibrium solutions: when $\gamma _{i}\rightarrow \infty ,$ the $\gamma$-equilibrium tends to the Walrasian equilibrium, although values of $\gamma _{i}\ge 1$ are economically irrelevant in our context.

Let us characterize now the standard oligopoly states introduced above.

Proposition 4

Any $\gamma$-equilibrium with $q^{*}(\gamma )>0$ and $\sum \limits _{i=1}^{n}\gamma _{i}=1$ is Pareto-efficient.

Proof

Relations (9), with $r^{*}=n,$ imply $\gamma _{i}=-\frac{q_{i}}{ (p-C_{i}^{\prime }(q_{i}))D^{\prime }(p)}$ so that relation (4) is satisfied. Hence, $q^{*}(\gamma )\in {\varvec{F}}.$ $\square$

Efficient outcomes particularly prevail when the pricing algorithms operate while preserving the market shares of all the competitors, namely for $\gamma _{i}=q_{i}^{0}/\sum \nolimits _{i=1}^{n}q_{i}^{0}$. The collusive solution is a particular efficient $\gamma$-equilibrium with $\gamma _{i}=\gamma _{i}^{m}=$ $q_{i}^{m}/\sum \nolimits _{i=1}^{n}q_{i}^{m}.$ Note that in this case the conjectures concerning the parameters $\gamma _{ik}$ are consistent, for any Pareto-efficient $\gamma$-equilibrium since $\gamma _{ik}$ can be taken equal to $\gamma _{k}.\forall i,k.\$In other words, any individual price deviation generates a distribution of the variation of demand which does not depend on the initiator of the deviation.

Many other combinations for $\gamma \in$ $\left[ 0,1\right] ^{n}$ are allowed since the consumers can differently appreciate the intentions of the deviating firms. Experimental economics investigations may be useful to evaluate the MCR in real life situations

Proposition 5

For $\gamma _{i}=1$ $,i=1,\ldots ,n,$ the $\gamma$-equilibrium duplicates the Cournot equilibrium.

Proof

immediate. $\square$

Cournot equilibrium outcomes prevail when any deviating firm bears the whole demand variation. The consumers recognize the prominent role played by the deviating firm: it gains or looses all the consumers who are the more sensitive to a price cut or boost even though the rivals instantaneously match the price move. This is close to the genuine formulation made by Cournot himself:

In 1838, Cournot introduced the quantity-setting equilibrium which carries his name. The reasoning he used is implicitly based on price matching policies so that the Cournot quantity-setting equilibrium can be interpreted in a price-setting context as a $\gamma$-equilibrium for $\gamma _{i}=1,\forall i$. In the duopoly case, Cournot formulates this as follows: “Firm 1 can have no direct influence on the determination of $q_{2}$ : all that he can do, when $q_{2}$ has been determined by firm 2, is to choose for $q_{1}$ the value which is best for him. This he will be able to accomplish by properly adjusting his price, except as firm 2, who, seeing himself forced to accept this price and this value of $q_{1}$, may adopt a new value for $q_{2}$ more favorable to his interests than the preceding one” (Cournot, 1838, p. 80, rewritten here with the standard terminology).

Cournot characterizes here the best response function $q_{1}(q_{2}),$ as it will be called later. For this purpose, he considers that choosing $q_{1}$ does not affect $q_{2}$ while assuming that the market is cleared. These conditions are met (i) “by properly adjusting his price” (ii) by knowing that the opponent is “forced to accept this price”. This is exactly the price matching mechanism we introduce in this paper.

3.2 Interpretation and evaluation of the MCR $\gamma _{i}^{\prime }s$

The assumptions on matching prices and demand change sharing rule are together reminiscent of conjectural variations which are extensively considered in the literature on quantity-setting competition (see Perry, 1986, among many others). In our price-setting world, the algorithms are incarnations of conjectural variations that map any price move into rivals’ reaction. It is then not surprising to get a wide range of equilibrium prices.

In our model, the rivals’ reactions are written in the code of the algorithms; they are not subjective expectations. Beside this operational feature, the novelty of our approach lies in the interpretation of the MCR parameters that generate the solution set. These parameters characterize the expected behavior of a fringe of consumers—those switching between buying and not buying when the market price moves. Assessing the values of $\gamma _{i}$ amounts firm i to make the following reasoning in petto : “If I lower the price by $\delta$ € and if all my rivals match this move, what proportion of new consumers may I attract ? The more I guess, rightly or wrongly, some consumers will recognize (and award) me as the first mover, the closer of 1 is my $\gamma _{i}$”. Of course, this guess is related to the visibility of the firm on the market and its reputation/positioning as a hard discounter for instance. MCR may also adjust in time through learning processes incorporating historical data in more sophisticated algorithms. But what is going on the supply-side among the rivals does not really matter.

3.2.1 MCR and visibility

Let us consider a market of N one-unit consumers. The consumers are classified in terms of reservation prices. There are M different reservation prices $v_{s},$ranked in decreasing order, i.e. $v_{s}>v_{s+1},$ for $s=1,\ldots ,M.$ Consumer $\left( s,k\right)$ is the kth consumer with reservation price $v_{s},$ for $k=1,\ldots ,N$. with $\sum _{s=1}^{M}N_{s}=N.$ Let $A_{s}=\left\{ (s,k),k=1,.;,N_{s}\right\}$ the class of the consumers with reservation price $v_{s}.$ The current state of the oligopoly is defined by the market price $p^{0}$ equal to some $v_{s^{0}},$ so that the current industry output is $q^{0}=\sum _{s=1}^{s^{0}}N_{s}$ since the consumers with reservation price higher than $v_{s^{0}}$ buy the product. This output is shared among the oligopolists. If firm i plans to lower its price down to $v_{s^{0}+u},$ with $u\ge 1,$ it expects an immediate matching from his rivals and a potential gain in output $\gamma _{i}(\sum _{s=s^{0}}^{s^{0}+u}N_{s}).$

It is convenient to consider that each firm has specific connections on the web with the consumers through social networks, smartphones app, etc. which contribute to the visibility of each firm. Let $\xi _{i}\in \left[ 0,1\right]$ the visibility rate of firm i,  namely the proportion of consumers in the whole market that are connected to firm $i.\$Assuming that $\xi _{i}$ is independent of the reservation prices, $\xi _{i}(\sum _{s=s^{0}}^{s^{0}+u}N_{s})$ is the number of new buyers that can recognize firm i as the instigator of the drop in market price. It is then reasonable to estimate the MCR $\gamma _{i}$ as a fraction of the visibility rate $\xi _{i}$. In the model, $\gamma _{i}$ is assumed to be independent of u.

3.2.2 MCR and elasticity

Let us consider a small price decrease dp triggered by firm i. Relation (5) becomes $\mathrm{d}q_{i}=\gamma _{i}\mathrm{d}D,$ namely $\frac{\mathrm{d}q_{i}}{\mathrm{d}p}=\gamma _{i}D^{\prime }.$ Multiplying both sides by p/D yields the relations:

$$\begin{aligned} s_{i}\varepsilon _{i}=\gamma _{i}\varepsilon , i=1,\ldots ,n, \end{aligned}$$

(11)

where $\varepsilon _{i}=\dfrac{p\mathrm{d}q_{i}}{q_{i}\mathrm{d}p}$ stands for the individual elasticity of firm $i ,$ $\varepsilon =\dfrac{p\mathrm{d}q}{q\mathrm{d}p}$ for the market elasticity and $s_{i}=q_{i}/D$ denotes the market share of firm i. Relation (11) captures the key argument of the model: each firm makes a guess on its own elasticity on the basis on the market elasticity, the market share and the MCR. The equilibrium prevails when these guesses make no unilateral move beneficial to any firm. When the equilibrium is Pareto efficient, summing relations (11) yields:

$$\begin{aligned} \sum _{i=1}^{n}s_{i}\varepsilon _{i}=\varepsilon , \end{aligned}$$

so that the weighted sum of the individual elasticities equal the market elasticity. This relation could be used in empirical studies to build a test to detect collusive practices.

3.2.3 MCR and competitive toughness

Demand-side interpretation of MCR connects with supply-side considerations. d’Aspremont and Dos Santos Ferreira (2009) introduce a parameter $\theta _{i}\in \left[ 0,1\right]$ to measure the competitive toughness displayed by firm i in the industry, namely the capacity of firm i to bite the rivals’ clientele. A wide range class of equilibrium solutions are characterized according to the value of these parameters (Cournot equilibrium, for $\theta _{i}=0$ and Walrasian equilibrium for $\theta _{i}=1,i=1,\ldots ,n$, as polar cases). Confronting their Eq. (12) p. 68 with Eq. (9) indicates that the competitive toughness parameter $\theta _{i}$ is positively related to $\gamma _{i}$ through the relation $\gamma _{i}=1/(1-\theta _{i})$. When index $\theta _{i}$ is extended to take negative values, so that $\gamma _{i}\in \left[ 0,1\right] ,$ it can be interpreted as the “competitive kindness” of firm i measuring its capacity to spare or accommodate the rivals’ clientele. Accordingly, MCR can be viewed as extending the competitive toughness index to generate oligopoly solutions including efficient outcomes and collusion.

3.3 No limit pricing

Theorem (3) yields a characterization of entry strategies. Equilibrium conditions state that price $p^{r^{*}}$ belongs to interval $\left[ C_{r^{*}}^{\prime }(0),C_{r^{*}+1}^{\prime }(0)\right] .$ Assume that inactive firm $r^{*}+1$ drops its initial marginal cost up to ${\tilde{C}}_{r^{*}+1}^{\prime }(0)$ $\in \left[ C_{r^{*}}^{\prime }(0),p^{r^{*}}\right] .$ The prospect of entering sounds profitable since the new initial marginal cost is lower than the current market price, although the entrant is less efficient than the incumbents in terms marginal cost. Theorem (3) implies that price $p^{r^{*}}$ is no longer the post-entry equilibrium price, which is now $p^{r^{*}+1},$ with ${\tilde{C}}_{r^{*}+1}^{\prime }(0)\le p^{r^{*}+1}.$ Hence, equilibrium conditions never hold with the incumbent firms charging exactly $p^{*}= {\tilde{C}}_{r^{*}+1}^{\prime }(0)$ so as to prevent the entry of firm $r^{*}+1.\$At this particular price $p^{*}={\tilde{C}}_{r^{*}+1}^{\prime }(0),$ any incumbent firm would be better off by increasing its price up to $p^{r^{*}+1},$ knowing that the rivals imitate her according to the algorithmic pricing rule. Entry strategy reduces to a simple rule: compare the current market price and the initial marginal cost. Note that the MCR to the entrant does not matter.

3.4 The linear quadratic symmetric case

Let us consider the case where the firms are identical, with a linear market demand $D(p)=1-p$ and a quadratic cost function $C_{i}(q_{i})=cq_{i}+uq_{i}^{2},$ with $c\ge 0,u\ge 0$ and $c\le 1.$ We assume that $\gamma _{i}=\gamma \in \left[ 0,1\right] ,$ $i=1,\ldots ,n.$ Equation (9) become $q_{i}-\gamma (1-nq_{i}-(c+2uq_{i}))=0.$ Hence, the following values of price and quantities:

$$\begin{aligned} p^{*}(\gamma ) & = \frac{\left( 2u\gamma +cn\gamma +1\right) }{n\gamma +2u\gamma +1}, \end{aligned}$$

(12)

$$\begin{aligned} q_{i}^{*}(\gamma ) & = \frac{\gamma \left( 1-c\right) }{\gamma \left( n+2u\right) +1}. \end{aligned}$$

(13)

The profit of any firm is $\Pi _{i}=\gamma \left( u\gamma +1\right) \frac{ \left( 1-c\right) ^{2}}{\left( n\gamma +2u\gamma +1\right) ^{2}}.$ The social welfare is $W=\frac{1}{2}n\gamma \frac{\left( 1-c\right) ^{2}\left( n\gamma +2u\gamma +2\right) }{\left( n\gamma +2u\gamma +1\right) ^{2}}.$ Clearly the equilibrium price (as well as the profit) is a decreasing function of the responsiveness. Among all the feasible $\gamma$-equilibria, Cournot equilibrium corresponds to the greatest social welfare value.

3.5 Dynamical stability in the linear demand/constant returns case

The dynamical stability of the Cournot solution has been analyzed from the seminal work by Theocharis (1960). In the linear demand and constant return case, this author proves that Cournot oligopoly solution is dynamically unstable when the number of firms exceeds 3. Canovas et al. (2008) reconsider the problem when positivity conditions on quantities and profits are introduced; under similar linearity assumptions, they establish that the oligopoly dynamics goes to a monopoly, a duopoly or else to an endless oscillation. These results questions the Cournot-type solutions which do not necessarily ensure the external stability of the industry. This is more crucial as to our $\gamma$-equilibrium concept which derives from a real adjustment process generated by algorithms.

Pricing algorithms are implemented through a dynamical process defined as follows. At time $t\ge 0,$ the oligopoly state is determined by market price p(t) and quantities $q_{i}(t)>0,$with $D(p(t))= \sum _{i=1}^{n}q_{i}(t).$ Each firm computes the best price $p_{i}(t+1)$ it wishes to post at time $t+1$ when the matching mechanism of the algorithms operates. With constant marginal costs, the best price $p_{i}(t+1)$ is given by the first order condition (cf. relations (29) of Appendix 1):

$$\begin{aligned} (q_{i}(t)+\gamma _{i}(D(p_{i}(t+1))-D(p(t)))+\gamma _{i}D^{\prime }(p_{i}(t+1))\left[ p_{i}(t+1)-c_{i})\right] . \end{aligned}$$

In the linear demand case, this provides the value of the best price $p_{i}(t+1)=\frac{1}{2\gamma _{i}}\left( q_{i}(t)+c_{i}\gamma _{i}+\gamma _{i}p(t)\right) )$ as function of the oligopoly state at time t,  which determines in turn the quantity $q_{i}(t+1)=q_{i}(t)+\gamma _{i}(p(t)-p_{i}(t+1)).$

At any time t,  all the algorithms simultaneously compute such best price expectations.⁵ The process generating all the quantities together is then governed by the linear dynamics:

$$\begin{aligned} q_{i}(t+1) & = \frac{1-\gamma _{i}}{2}q_{i}(t)-\frac{\gamma _{i}}{2} \sum _{j\ne i}q_{j}(t)+\gamma _{i}\frac{(1-c_{i})}{2}, \\ q_{i}(0) & = q_{i}^{0},i=1,\ldots ,n. \end{aligned}$$

The Jacobian J of the dynamical system is

$$\begin{aligned} J=\left[ \begin{array}{cccc} \frac{1-\gamma _{1}}{2} &{} \frac{-\gamma _{1}}{2} &{} . &{} \frac{-\gamma _{1}}{2} \\ . &{} . &{} . &{} . \\ \frac{-\gamma _{i}}{2} &{} \frac{1-\gamma _{i}}{2} &{} . &{} \frac{-\gamma _{i}}{2} \\ . &{} . &{} . &{} . \\ \frac{-\gamma _{n}}{2} &{} \frac{-\gamma _{n}}{2} &{} . &{} \frac{1-\gamma _{n}}{2} \end{array} \right] . \end{aligned}$$

There are $n-1$ eigenvalues $\lambda _{j}=1/2,$ $j=1,\ldots ,n-1$ and one last $\lambda _{n}=-\frac{\left( \sum _{i=1}^{n}\gamma _{i}\right) -1}{2}.$ Following standard techniques in dynamical systems, the equilibrium is stable when the eigenvalues are less than unity in absolute value. Accordingly the equilibrium is stable for $\left( \sum _{i=1}^{n}\gamma _{i}\right) <3;$ for a great number of firms, the equilibrium may be stable only if the $\gamma _{i}^{\prime }s$ are small. With $\gamma _{i}=1,$ namely in the Cournot case, this is the result of Theocharis (1960) (cf. also Canovas et al., 2008).

Proposition 6

In the linear demand and constant return case, any Pareto-efficient $\gamma$-equilibrium is dynamically stable.

Proof

By Corollary (4), efficiency holds with $\sum _{i=1}^{n}\gamma _{i}=1$ and $\lambda _{n}=0.$ $\square$

Oligopoly with collusive firms may be viable when pricing algorithms operate in the industry. Although this result is probably strongly dependent on the linearity assumptions, it questions the conventional view about collusion which is strategically unstable in game-theoretical approaches of oligopoly. In our pricing algorithm context, the firms merely adapt to the main actor in the industry which is the group of marginal consumers: Pareto efficiency and stability prevail, for instance, when the marginal consumers behave in a conservative way, by preserving the current market shares in response to any market price shift.

3.6 Extension to other matching mechanisms

Pricing algorithms considered here operate as an intermediary aimed at building a market price from unilateral price deviations of any competitor, with the nice property that this is made instantaneously. The algorithms used in retailing (Brown & MacKay, 2021) update the prices with a frequency that differs from one firm to another, so that the algorithms operate in a sluggish way with some memory of the past prices. A way to cope with this issue is to distinguish the market price p and the prices $\psi _{i}$ posted by the firms. In any feasible oligopoly state, the posted prices are assumed to coincide with the market price, $\psi _{i}=p,i=1,\ldots ,n.\$Starting from a feasible state $\left( p^{0},q^{0}\right)$, if firm i posts a different price $\psi _{i}\ne p^{0},$ the pricing algorithms generates a new market price ${\hat{p}}(\psi _{i},p^{0})$ which differs from $\psi _{i}$ according to the time lag and inertia of reaction of the system. Function ${\hat{p}}(.,.)$ is assumed to be well behaved, with $\frac{\partial {\hat{p}}(\psi _{i},p)}{\psi _{i}}>0,\frac{ \partial {\hat{p}}(\psi _{i},p)}{p}\ge 0$ and ${\hat{p}}(p,p)=p,\forall p.$ For instance ${\hat{p}}(s_{i},p^{0})=(\psi _{i}+(n-1)p^{0})/n,$ when the new market price is equal to the average posted price. Function ${\hat{p}}$ is a particular case of the pricing schemes introduced by d’Aspremont et al. (1991) in a general oligopoly setting where the market price is built from signals emitted by the firms. Here the posted prices play the role of signals and pricing scheme ${\hat{p}}$ merely applies for unilateral deviations around current oligopoly states. The profit of the deviating firm i becomes

$$\begin{aligned} \Pi _{i}(\psi _{i},p^{0},q_{i}^{0}) & = {\hat{p}}(\psi _{i},p^{0})(q_{i}^{0}+\gamma _{i}(D({\hat{p}}(\psi _{i},p^{0})-D(p^{0})) \end{aligned}$$

(14)

$$\begin{aligned}&\quad -C_{i}(q_{i}^{0}+\gamma _{i}(D({\hat{p}}(\psi _{i},p^{0})-D(p^{0})). \end{aligned}$$

(15)

Equilibrium conditions⁶ are

$$\begin{aligned}&\frac{\partial {\hat{p}}(\psi _{i},p)}{\psi _{i}}\left[ q_{i}+\gamma _{i}D^{\prime }(p)(p-C_{i}^{\prime }(q_{i}))\right] =0, \end{aligned}$$

(16)

$$\begin{aligned}&\psi _{i} =p,i=1,\ldots ,n. \end{aligned}$$

(17)

$$\begin{aligned}&\sum \limits _{i=1}^{n}q_{i} =D(p). \end{aligned}$$

(18)

Since the derivative $\frac{\partial {\hat{p}}(\psi _{i},p)}{\psi _{i}}$ is strictly positive, these relations coincide with the $\gamma$-equilibrium conditions which may then hold for a wider class of matching mechanisms. This could be generalized to the case of price discrimination.

4 The monodirectional matching case

Let us examine now the more realistic case where the pricing algorithms are only used as a response to cutting the price. When the deviating firm charges a higher price, the rivals stick to the current market price. Starting from a feasible state $\left( p^{0},q^{0}\right) ,$ any deviating firm charging a price $p_{i}>p^{0}$ will lose all or part of its customers in favor of the rivals. Let us assume for simplicity that all the firms are active under the various oligopoly states considered.

Let ${\tilde{q}}_{i}(p_{i},p^{0})\ge 0$ be the output level, if any, the deviating firm i keeps once the whole profitable capacity of the rivals is fully used. ${\tilde{q}}_{i}(p_{i},p^{0})$ is computed as the difference between the potential demand for firm i at price $p_{i},\left( D(p_{i})-\sum \nolimits _{j\ne i}q_{j}^{0}\right)$ and what is recovered by the rivals and sold at price $p^{0}$, $\sum \nolimits _{j\ne i}\left( s_{j}(p^{0})-q_{j}^{0}\right) ,$ provided this difference is nonnegative. This gives

$$\begin{aligned} {\tilde{q}}_{i}(p_{i},p^{0})=\left[ D(p_{i})-\sum \limits _{j\ne i}s_{j}(p^{0}) \right] ^{+}. \end{aligned}$$

Since $p_{i}\ge p^{0},$ we have $D(p_{i})\le D(p^{0})$ and $s_{i}(p^{0})\le s_{i}(p_{1}).$ As a result,

$$\begin{aligned} {\tilde{q}}_{i}(p_{i},p^{0})\le \left[ D(p^{0})-\sum \limits _{j\ne i}s_{j}(p^{0})\right] ^{+}. \end{aligned}$$

(19)

Since $D(p^{0})\le \sum \limits _{j\ne i}s_{j}(p^{0})+s_{i}(p^{0}),$ then

$$\begin{aligned} {\tilde{q}}_{i}(p_{i},p^{0})\le s_{i}(p^{0})\le s_{i}(p_{i}), \end{aligned}$$

(20)

so that the adjusted output of firm i remains profitable at price $p_{i}$. Inequality (19) implies ${\tilde{q}}_{i}(p_{i},p^{0})\le q_{i}^{0}-\sum \nolimits _{j\ne i}(s_{j}(p^{0})-q_{j}^{0})\le q_{i}^{0}.$ Accordingly, raising the price always reduces the output of the deviating firm. Note that its rivals are better off since they all use their full profitable capacities.

Clearly if $D(p^{0})-\sum \limits _{j\ne i}s_{j}(p^{0})\le 0,$ we have $q_{i}^{0}\le$ $\sum \nolimits _{j\ne i}s_{j}(p^{0})-q_{j}^{0}.$ The current output of the deviating firm is entirely absorbed by the available capacity of the opponents. Dropping even slightly the price exposes the seller to losing all its customers. Accordingly, the profit of the deviating firm is written as : 

$$\begin{aligned} \Pi _{i}(p_{i},p^{0},q_{i}^{0})=\left\{ \begin{array}{c} \Pi _{i}^{-}(p_{i},p^{0},q_{i}^{0})\text { if }p_{i}\le p^{0}, \\ \Pi _{i}^{+}(p_{i},p^{0})\text { if }p_{i}>p^{0}, \end{array} \right. \end{aligned}$$

(21)

with $\Pi _{i}^{-}(p_{i},p^{0},q_{i}^{0})=p_{i}(q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))-C_{i}(q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))$ and $\Pi _{i}^{+}(p_{i},p^{0})=p_{i}\left[ D(p_{i})-\sum \nolimits _{j\ne i}s_{j}(p^{0})\right] ^{+}-C_{i}\left[ D(p_{i})-\sum \nolimits _{j\ne i}s_{j}(p^{0})\right] ^{+}.$ Clearly, we have $\Pi _{i}^{-}(p^{0},p^{0},q_{i}^{0})=p^{0}q_{i}^{0}-C_{i}(q_{i}^{0}).$ For $p^{0}=p^{w},$ under strictly decreasing returns to scale conditions, we have $s_{j}(p^{w})=q_{j}^{w}$ and $D(p^{w})-\sum \nolimits _{j\ne i}s_{j}(p^{w})=q_{i}^{w}.$ Hence $\Pi _{i}^{+}(p^{w},p^{w})=\Pi _{i}^{-}(p^{w},p^{w},q_{i}^{w}).\$At the competitive solution, the profit $\Pi _{i}$ is a continuous function of the deviating price. It is not in other cases, particularly in the constant returns case, where $s_{j}(p)=+\infty ,$ so that $\Pi _{i}^{+}(p^{w},p^{w})=-\infty$. Let us examine successively how the profit is maximized by down and up price moves. Establishing the conditions that makes unilateral deviations in both senses unprofitable defines the family of $\gamma ^{-}$-equilibria associated with the MCR vector $\gamma \in \left[ 0,1\right] ^{n}.\$

4.1 Downward maximization

Let us analyze the stability of a current feasible oligopoly state ($p^{0},q^{0})$ with respect to an unilateral cut of price $p_{i}.$ This comes from the following optimization program (note that $\Pi _{i}^{-}$ is right-differentiable at point $p^{0}),$ with $\gamma _{i}\in \left[ 0,1 \right] :$

$$\begin{aligned} \left\{ \begin{array}{l} \max _{p_{i}}\left[ p_{i}(q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))-C_{i}(q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))\right] , \\ p_{i}\le p^{0}, \end{array} \right. \end{aligned}$$

(22)

whose first order conditions are

$$\begin{aligned} \begin{array}{c} (q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0})) +\gamma _{i}D^{\prime }(p_{i})\left[ p_{i}-C_{i}^{\prime }(q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))\right] -\alpha _{i}=0, \\ \alpha _{i}(p^{0}-p_{i})=0,\alpha _{i}\ge 0, \end{array} \end{aligned}$$

(23)

where $\alpha _{i}$ stand for Kuhn–Tucker multiplier of the price constraint. Equilibrium conditions are met when the first order conditions hold for $p_{i}=p^{*}=p^{0},\forall i.$ As a result equilibrium $(p^{*},q^{*})$ is characterized by:

$$\begin{aligned} \begin{array}{c} q_{i}+\gamma _{i}D^{\prime }(p)\left[ p-C_{i}^{\prime }(q_{i})\right] =\alpha _{i},i=1,\ldots ,n. \\ \alpha _{i}\ge 0. \end{array} \end{aligned}$$

(24)

Let us define $\beta _{i}=-\alpha _{i}\gamma _{i}D^{\prime }(p) \left[ p-C_{i}^{\prime }(q_{i})\right] \ge 0$. Relations (24) may be rewritten as

$$\begin{aligned} \left\{ \begin{array}{c} q_{i}+g_{i}D^{\prime }(p)\left[ p-C_{i}^{\prime }(q_{i})\right] =0,i=1,\ldots ,n, \\ g_{i}\ge \gamma _{i}, \end{array} \right. \end{aligned}$$

(25)

with $g_{i}=\gamma _{i}+\beta _{i}.$ Together with the supply=demand condition $D(p)=\sum \nolimits _{i=1}^{n}q_{i},$ they give the equilibrium conditions of a g-equilibrium, extended here for values of $g_{i}\ge 0.$ It can easily be checked that this reasoning still holds when adding positivity condition to program (24) $q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))\ge 0.$ Clearly the economic interpretation of $g_{i}$ in terms of MCR does not really works when $g_{i}\ge 1$. Parameters $g_{i}$ are useful only to compute the price and the quantities associated with any equilibrium. As a result, for any given responsiveness vector $\gamma _{i}\in \left[ 0,1\right] ^{n},$ there exists a family of solutions of program (22) of the form $(p^{*}(g),q^{*}(g))$ parametrized by the $g_{i}$,  with $g_{i}\ge \gamma _{i}$.

4.2 Upward optimization

Let us compute the best response price ${\tilde{p}}_{i}(p^{0})\$firm i would charge with a positive output when the rivals use their full profitable capacities at price $p^{0}$. This results from the program:

$$\begin{aligned} \left\{ \begin{array}{l} \max _{p_{i},{\tilde{q}}_{i}}p_{i}{\tilde{q}}_{i}-C_{i}\left( {\tilde{q}} _{i}\right) \\ {\tilde{q}}_{i}+\sum \limits _{j\ne i}s_{j}(p^{0})=D(p_{i}), \\ {\tilde{q}}_{i}\ge 0. \end{array} \right. \end{aligned}$$

(26)

Let $r_{i}(p_{0})$ the unique solution of the program (26), if any. The best response price of firm i is ${\tilde{p}}_{i}(p^{0})=\max (r_{i}(p_{0}),p_{0}).\$Any upward unilateral move of price starting from oligopoly state ($p^{0},q^{0})$ is not profitable for firm i if $\Pi _{i}( {\tilde{p}}_{i}(p^{0}),p^{0}),q_{i}^{0}))\le \Pi _{i}(p^{0},p^{0},q_{i}^{0}).$ Note that this condition always holds for $r_{i}(p^{0})\le p^{0}$ as an equality.

4.3 Equilibrium conditions

These developments lead to define the family of $\gamma ^{-}$-equilibria which prevail for any given MCR vector $\gamma \in \left[ 0,1\right] ^{n},$ as follows:

Definition 7

Let $\left( p^{*}(g),q^{*}(g)\right)$ a g-equilibrium .Oligopoly state $\left( p^{*}(g),q^{*}(g)\right)$ is a $\gamma ^{-}$-equilibrium if

• 1. $g_{i}\ge \gamma _{i},\forall i,$

• 2. $\Pi _{i}^{+}({\tilde{p}}_{i}(p^{0}),p^{*}(g))\le \Pi _{i}(p^{*}(g)),p^{*}(g),q_{i}^{*}(g)),\forall i=1,\ldots n.$

Proposition 8

In the constant returns case, any g-equilibrium is a $\gamma ^{-}$-equilibrium, for $g_{i}\ge \gamma _{i}\ge 0.\$In particular the competitive solution is a $\gamma ^{-}$-equilibrium.

Proof

Under constant returns, marginal cost functions $C_{i}^{\prime }$ are not invertible and $s_{i}(p)=+\infty ,$ for all i,  Condition 2 is thus not fulfilled: as a result, program (26) has no bounded solution; no upward move of the price is therefore allowed. Equilibrium conditions reduces to condition 1 of definition (7). The competitive solution is achieved for $g=+\infty .$ $\square$

Lemma 9

The collusive solution $(p^{m},q^{m})$ is $\gamma ^{-}$- equilibrium, with $\gamma _{i}=\gamma _{i}^{m}.$

Proof

Condition 2 of definition (7) is necessarily satisfied for $p^{m}=p^{*}(\gamma ^{m}),$ as a strict inequality. Let us prove it by contradiction. Assume there exists i such that $\Pi _{i}^{+}({\tilde{p}} _{i}(p^{m}),p^{m}))>\Pi _{i}(p^{m},p^{m},q_{i}^{m}).$For the rivals, $j\ne i,$ we have the following inequalities: $\Pi _{j}({\tilde{p}}_{i}(p^{m}),\tilde{ p}_{i}(p^{m}),s_{j}(p^{m})>\Pi _{j}(p^{m},p^{m},s_{j}(p^{m}))$ $\ge \Pi _{j}(p^{m},p^{m},q_{j}^{m}),$ since ${\tilde{p}}_{i}(p^{m})\ge p^{m}$ and $s_{j}(p^{m})\ge$ $q_{j}^{m}.$ Hence, the n+1 tuple $\left( {\tilde{p}} _{i}(p^{m}),{\bar{q}}_{j}\right)$ with ${\bar{q}}_{i}=D({\tilde{p}} _{i}(p^{m})-\sum \limits _{j\ne i}s_{i}(p^{m})$ and ${\bar{q}} _{j}=s_{j}(p^{m})),j\ne i$ is an oligopoly state holding at price ${\tilde{p}} _{i}(p^{m})$ and demand $D({\tilde{p}}_{i}(p^{m})),$ which strictly dominates the collusive solution for all the firms. Hence, the contradiction. $\square$

Lemma 10

Under strictly decreasing returns, the competitive solution is never a $\gamma ^{-}$-equilibrium.

Proof

As noted above, the profit function is continuous at $p^{w}$. We have $\left. \frac{\partial \Pi _{i}(p_{i},p^{c})}{\partial p_{i}}\right| _{p_{i}=p^{w+}}=q_{i}^{w}\ge 0$ (with a strict inequality for at least one firm). Increasing even slightly price $p_{i}$ yields profit improving. This is a fortiori true at the best response price ${\tilde{p}}_{i}(p^{w})>p^{w}.$ Hence, condition 2 of proposition (7) never holds. $\square$

Theorem 11

There exists ${\bar{g}}_{i}>\gamma _{i}^{m},$ such that $\left( p^{*}(g),q^{*}(g)\right)$ is a $\gamma ^{-}$-equilibrium for any vector g such that ${\bar{g}}_{i}\ge g_{i}\ge \gamma _{i}.$ It is not for $g_{i}\ge {\bar{g}}_{i}.$

Proof

Let us consider the family of functions $\delta _{i}:\mathfrak {R}^{n}\rightarrow \mathfrak {R}$ defined by: $\delta _{i}(g)=\left[ \Pi _{i}^{+}({\tilde{p}}_{i}(p^{*}(g)),p^{*}(g))-\Pi _{i}(p^{*}(g)),p^{*}(g),q_{i}^{*}(g)) \right] ,$ for $g_{i}\in \left] \gamma _{i},+\infty \right[ .$ Under the regularity assumptions made, functions $\delta _{i}$ are continuous. Lemma 9 implies that $\delta _{i}(\gamma ^{m})<0$ and lemma (10) that $\lim _{g_{i}\rightarrow \infty }\delta _{i}(g)>0.$ By continuity, there is a vector ${\bar{g}}$ $\in \Pi _{i}[ \gamma _{i}^{m},+\infty [$ such that all functions $\delta _{i}$ are simultaneously lower or equal to 0 in hypercube ${\Pi }_{i}[ \gamma _{i}^{m},{\bar{g}}_{i}[$. Hence the result. $\square$

Theorem (11) is the key result of this section. To summarize, in the monodirectional matching case, there exists a multiplicity of equilibrium prices located in the range $\left[ p^{b},p^{*}(\gamma )\right]$, where $p^{b}=p^{*}({\bar{g}})$ is the lowest price where $\gamma ^{-}$-equilibrium may exist.

4.4 The linear-quadratic symmetric case (cont’d)

Let us illustrate these results in the linear-quadratic symmetric case. Following subsection (3.4), the g-equilibrium is defined by $p^{*}(g)=\frac{\left( 2ug+cng+1\right) }{ng+2ug+1},q_{i}^{*}(g)= \frac{g\left( 1-c\right) }{g\left( n+2u\right) +1},i=1,n$: let us compute the best response pricing ${\tilde{p}}_{1}(.)$ at this point for a price increase of firm 1. Clearly, we have $s_{i}(p^{0})=(p^{0}-c)/2u$ and $\tilde{q }_{1}(p_{1},p^{0})=D(p_{1})-(n-1)(p^{0}-c)/2u,$ so that ${\tilde{p}} _{1}(p^{0})=\arg \max _{p}(p{\tilde{q}}_{1}(p_{1},p^{0})-C_{1}({\tilde{q}} _{1}(p_{1},p^{0})))$.

Standard computations yield: ${\tilde{p}}_{1}(p^{0})=\frac{1}{4}\frac{ \left( 2u-n-2nu+1\right) p_{0}+\left( 2u-c+cn+4u^{2}+2cnu\right) }{u\left( u+1\right) }$ and ${\tilde{q}}_{1}\left( p^{0}\right) ={\tilde{q}} _{1}\left( {\tilde{p}}_{1}(p^{0}),p^{0}\right) =\frac{1}{4}\frac{ (n-1)(c-p_{0})+2u(1-c)}{u\left( u+1\right) }.$ Computing these values for $p_{0}=$ $p^{*}(g)$ gives

$$\begin{aligned} \left\{ \begin{array}{l} {\tilde{p}}_{1}(p^{*}(g))=\frac{1}{4}\frac{ -c-n+4u+2ug+8u^{2}g+8u^{3}g+cn-2nu+4u^{2}-2cug+2cnu+4cnug+4cnu^{2}g+1}{ u\left( u+1\right) \left( ng+2ug+1\right) } , \\ {\tilde{q}}_{1}((p^{*}(g)))=\dfrac{\left( 1-c\right) \left( 2u+2ug+4u^{2}g-(n-1)\right) }{4u\left( u+1\right) \left( ng+2ug+1\right) }, \\ {\tilde{\Pi }}_{1}(p^{*}(g))=\frac{1}{16}\left( 1-c\right) ^{2}\dfrac{ \left( n-2u-2ug-4u^{2}g-1\right) ^{2}}{u^{2}\left( u+1\right) \left( ng+2ug+1\right) ^{2}}. \end{array} \right. \end{aligned}$$

Firm 1 is better off when increasing price up to ${\tilde{p}}_{1}(p^{*}(g))$ if ${\tilde{P}}_{1}(p^{*}(g))>P_{1}(\left( p^{*}(g),q^{*}(g)\right) ,$ namely for

$$\begin{aligned} g>{\bar{g}}=\frac{\left( 2(n-1)u++4nu^{2}+4\sqrt{u^{3}\left( n-1\right) \left( n+1\right) \left( u+1\right) }\right) }{4u^{2}}. \end{aligned}$$

(27)

For the values of g satisfying inequality (27), we also have ${\tilde{p}}(p^{*}(g))\ge p^{*}(g)$ and ${\tilde{q}}_{1}((p^{*}(g)))\ge 0.$ Let us define $p^{b}=p^{*}({\bar{g}})\ge p^{w}.$ We have $p^{b}\le p^{C}.$ At least in the linear-quadratic symmetric case, Cournot is an equilibrium.

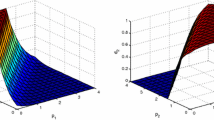
Any oligopoly state $\left( p,D(p)/n\right)$ is a $\gamma ^{-}$-equilibrium when price p $\in$ $\left[ p^{b},p^{*}(\gamma )\right]$ and $p^{*}(\gamma )\in \left[ p^{C},p^{m}\right]$. In this context, price $p^{b}$ can be viewed as the bottom price, namely the lowest (deterministic) equilibrium price under decreasing returns. Under constant returns ($u=0)$, the bottom price coincides with the perfect competition price $p^{w}=c.$ In the decreasing returns case, this is asymptotically true for $u\rightarrow \infty .$ This is illustrated in Fig. 1 where the various prices are expressed in terms of the quadratic cost factor u.

Fig. 1

Equilibrium prices in the linear-quadratic case

Hence the Bertrand–Edgeworth paradox holds only for market prices between the bottom and the competitive price.

5 Concluding remarks

Pricing algorithms generate a family of equilibria associated with the MCR parameters $\gamma _{i},$ namely a characteristic of the marginal customers behavior. For significant values of MCR parameters, pricing algorithms ensure the existence of pure strategy equilibria in oligopoly with strictly decreasing returns to scale, while bypassing the Bertrand–Edgeworth paradox. This way pricing algorithms may contribute to the internal stability of the markets.

Furthermore, pricing algorithms work as a market clearing tool that fixes the price equating supply and demand. No auctioneer is needed. Pricing algorithms substitute for intermediaries in charge of crossing demand and supply in standard markets. As such, they mitigate the intermediation cost borne by the economy as a whole. On this point, pricing algorithms are welfare-improving if the costs in terms of coding are not too high.

At least in the symmetric case, the equilibrium price is located in the range $\left[ p^{C},p^{m}\right]$. The lower bound of equilibrium values is the bottom price which is a $\gamma ^{-}$-equilibrium for any $\gamma$. It provides the best social welfare that the pricing algorithms can achieve. The loss of consumer surplus involved at equilibrium price $p^{*}$ is due to the overcharge ($p^{*}-p^{w})=(p^{*}-p^{b})+(p^{b}-p^{w})$. The overcharge between the bottom and the competitive price, ($p^{b}-p^{w}),$ is incompressible as it is due to technology conditions underpinning the cost structure of the industry. As a result, public policy should focus towards reducing $(p^{*}-p^{b}),$ in the perspective of selecting an equilibrium price as close as possible to the bottom price $p^{b}$. Some actions are working in this sense:

• Promote the bottom price as the basis of market power measurement in the digital economy.

• Set up special monitoring and alert systems that block pricing algorithms incorporating bidirectional matching mechanisms.

• Enhance the consumers’ confidence in pioneering price discounters, since they are more likely to be associated with the highest MCR $\gamma$.

• Give emphasis on antitrust policies designed to lower barriers to entry. The pressure of potential entrants remains the best way to dissipate the residual deadweight loss due to overcharge $(p^{*}-p^{b})$.

An important related issue deals with the dynamical stability of the process underlying the pricing algorithms. Our results in the linear demand and constant returns case indicate how these algorithms may enhance the external stability of the system. More research is needed to extend this result to decreasing returns and non linear demand situations.

This suggests there could be some economic advantages to let pricing algorithms be implemented in oligopolistic industries: they convey more information in the market and—last but not least—they may contribute to the internal and external stability of the industry.

Appendix

Proof of theorem 3

Let us consider an oligopoly state $(p^{0},q^{0})$ with $\sum \nolimits _{k=1}^{n}q_{k}^{0}=D(p^{0})$ and $q_{k}^{0}>0.\$Starting from this particular point, the price $p_{i}$ that maximizes firm i ’s profit solves the following program:

$$\begin{aligned} \left\{ \begin{array}{l} \max _{p_{i}}\left[ p_{i}(q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))-C_{i}(q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))) \right] \\ q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))\ge 0, \end{array} \right. \end{aligned}$$

(28)

The Lagrangian of this program is

$L_{i}=p_{i}(q_{i}^{0}+$ $\gamma _{i}(D(p_{i})-D(p^{0})))-C_{i}(q_{i}^{0}+$ $\gamma _{i}(D(p_{i})-D(p^{0})))+\lambda _{i}[q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))],$ where $\lambda _{i}$ is the Kuhn and Tucker multiplier associated with the positivity constraint; the first-order conditions are

$$\begin{aligned} \begin{array}{c} (q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0})) +\gamma _{i}D^{\prime }(p_{i})\left[ p_{i}-C_{i}^{\prime }(q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))\right] \\ +\lambda _{i}\gamma _{i}D^{\prime }(p_{i})=0, \\ \lambda _{i}[q_{i}^{0}+\gamma _{i}(D(p_{i})-D(p^{0}))]=0,\pi _{i}\ge 0. \end{array} \end{aligned}$$

(29)

The oligopoly equilibrium is defined by a vector $\left( p^{*},q_{i}^{*},\lambda _{i}^{*},\right)$ satisfying conditions (29) with $p^{0}=p^{*}$ and for any $i=1,\ldots ,n,$ namely

$$\begin{aligned} q_{i}+\gamma _{i}D^{\prime }(p)\left[ p-C_{i}^{\prime }(q_{i})\right] +\lambda _{i}\gamma _{i}D^{\prime }(p) & = 0. \end{aligned}$$

(30)

$$\begin{aligned} \lambda _{i}q_{i} & = 0,\lambda _{i}\ge 0. \end{aligned}$$

(31)

Then the equilibrium price and quantities are characterized by the conditions:

$$\begin{aligned} q_{i}+\gamma _{i}D^{\prime }(p)\left[ p-C_{i}^{\prime }(q_{i})\right] & = 0, \text { if }q_{i}>0, \end{aligned}$$

(32)

$$\begin{aligned} p-C_{i}^{\prime }(0) & \le 0,\text {if }q_{i}=0. \end{aligned}$$

(33)

$$\begin{aligned} D(p) & = \sum \limits _{i=1}^{n}q_{i}. \end{aligned}$$

(34)

Let ${A\!\!\!/}_{n}=\left\{ r\text { st.}.q_{i}^{r}\ge 0,i=1,\ldots ,r\right\} ,$ with $r\le n.\$Clearly, $A_{n}\ne \emptyset ,$ as $1\in A_{n}.$ Then $q^{r^{*}}$ always exists. Since $q_{r^{*}}^{r^{*}}\ge 0,$ we have $p^{r*}\ge C_{r^{*}}^{\prime }(0).$ Let us prove by contradiction that $p^{r^{*}}\le C_{r^{*}+1}^{\prime }(0)$. Assume that it is not true, namely

$$\begin{aligned} p^{r^{*}}>C_{r^{*}+1}^{\prime }(0). \end{aligned}$$

(35)

Let $q_{i}=h_{i}(p)$ solution of relation (9). Clearly, $h_{i}^{\prime }(p)=-(1-\gamma D^{\prime }C_{i}^{\prime \prime })/(\gamma D^{^{\prime \prime }}(p-C_{i})+\gamma D^{\prime })\ge 0.$ Let us define $f(p)=D(p)-\sum \limits _{i=1}^{r}h_{i}(p)$ and $\varphi (p)=f(p)+\gamma _{r^{*}+1}D^{\prime }(p)\left[ p-C_{r^{*}+1}^{\prime }(f(p)\right] .$ We have $f(p^{r^{*}})=0$ and $h_{i}(p^{r^{*}})\ge 0,i=1,\ldots ,r.$ We have $\varphi (p^{r^{*}})=\gamma _{r^{*}+1}D^{\prime }(p^{r^{*}}) \left[ p^{r^{*}}-C_{r^{*}+1}^{\prime }(0\right] \le 0,$ thanks to assumption (35). Clearly, we have $f^{\prime }<0$ and then $f(C_{r^{*}+1}^{\prime }(0))\ge f(p^{r^{*}})=0.$ Consequently, $\varphi (C_{r^{*}+1}^{\prime }(0))=f(C_{r^{*}+1}^{\prime }(0))\ge 0.$ In addition $\varphi ^{\prime }(p)=f^{\prime }(p)+\gamma _{r^{*}+1}D^{\prime \prime }(p)\left[ p-C_{r^{*}+1}^{\prime }(f(p)\right] +\gamma _{r^{*}+1}D^{\prime }(p)\left[ 1-C_{r^{*}+1}^{\prime \prime }(f(p)f^{\prime }(p)\right] \le 0.$ Thanks to the intermediate value theorem, there exists a value $p^{a}\in \left[ C_{r^{*}+1}^{\prime }(0),p^{r^{*}}\right]$ such that $\varphi (p^{a})=0.$ By definition, $p^{a}=$ $p^{r^{*}+1}\in \left[ C_{r^{*}+1}^{\prime }(0),p^{r^{*}} \right] .$ Let us prove by contradiction that $h_{i}(p^{r^{*}+1})\ge 0,i=1,\ldots r^{*}$. If $h_{i}(p^{r^{*}+1})<0,$ as $h_{i}(p^{r^{*}})\ge 0,$ applying again the intermediate value theorem exhibits a value ${\tilde{p}}\in \left[ p^{r^{*}+1},p^{r^{*}}\right] ,$ such that $h_{i}( {\tilde{p}})=0,$ i.e. ${\tilde{p}}=C_{i}^{\prime }(0).$ Hence, $C_{r^{*}+1}^{\prime }(0)\le p^{r^{*}+1}\le C_{i}^{\prime }(0),$ which is impossible according to (8). To summarize, we have $q_{i}^{r^{*}+1}=h_{i}(p^{r^{*}+1})\ge 0,i=1,\ldots ,r^{*}$ and $q_{r^{*}+1}^{r^{*}+1}=f(p^{r^{*}+1})\ge 0.$ This contradicts that $r^{*}$ is defined as the maximum of $\left\{ r\text { st. }q_{i}^{r}\ge 0,i=1,\ldots ,r. \right\} .$

Finally, we have $p^{r^{*}}\le C_{r^{*}+1}^{\prime }(0)\le C_{i}^{\prime }(0),i=r^{*}+1,\ldots ,n.$ Then according to (33), we state $q_{i}^{*}=0,$ for $i=r^{*}+1,\ldots ,n.$ Putting $q_{i}^{*}=q_{i}^{r^{*}}\ge 0,$ for $i=1,\ldots ,r^{*}$ completes the full characterization of the $\gamma$-equilibrium.