Two simple characterizations of the Nash bargaining solution

Abstract

We provide two alternative characterizations of the Nash bargaining solution. We introduce new simple axioms, strong undominatedness by the disagreement point, and egalitarian Pareto optimality. First, we prove that the Nash solution is characterized by symmetry, scale invariance, independence of irrelevant alternatives, and strong undominatedness by the disagreement point. Second, we replace the independence of irrelevant alternatives axiom with the sandwich axiom (Rachmilevitch in Theory Decis 80:427–442, 2016) and egalitarian Pareto optimality. We then demonstrate that the Nash solution is characterized by symmetry, scale invariance, strong undominatedness by the disagreement point, the sandwich axiom, and egalitarian Pareto optimality.

1 Introduction

As is well known, Nash (1950) proposed a solution to the two-person bargaining problem, comprising a utility possibility set and a disagreement point, and proved that it is characterized by four axioms, i.e., symmetry, scale invariance, independence of irrelevant alternatives, and weak Pareto optimality. Although the weak Pareto optimality axiom appears to be an uncontroversial requirement, it has been shown that it can be substituted by another axiom, while the other three axioms remained unchanged. Roth (1977) replaced weak Pareto optimality with strong individual rationality in characterizing the Nash solution. More recently, Anbarci and Sun (2011) showed that the Nash solution can be characterized using weakest collective rationality, which is weaker than both weak Pareto optimality and strong individual rationality.¹ In this study, we provide two characterizations of the Nash bargaining solution, which improve on Nash (1950), Roth (1977), and Anbarci and Sun (2011).

First, we introduce a new axiom, strong undominatedness by the disagreement point, which requires that the bargaining solution be neither weakly dominated by nor equal to the disagreement point. This axiom is weaker than both weak Pareto optimality and strong individual rationality, but it neither imply nor is implied by weakest collective rationality. However, strong undominatedness by the disagreement point seems more intuitive than weakest collective rationality. Moreover, if the bargaining problem allows for the case that the set of utility possibilities is not compact,² then weakest collective rationality together with three standard conditions is not sufficient for characterizing the Nash solution. We then show that the Nash solution is characterized by symmetry, scale invariance, independence of irrelevant alternatives, and strong undominatedness by the disagreement point, assuming that the set of utility possibilities is closed, convex, and bounded above.

Second, we replace the independence of irrelevant alternatives axiom with two axioms, the sandwich axiom and egalitarian Pareto optimality. The sandwich axiom, proposed by Rachmilevitch (2016), is a weakening of independence of irrelevant alternatives. Egalitarian Pareto optimality, which is another new axiom, requires that the efficient solution be chosen if the bargaining problem is such that the utilities of the two persons are equal in all utility points. We then show that the Nash solution is characterized by symmetry, scale invariance, strong undominatedness by the disagreement point, the sandwich axiom, and egalitarian Pareto optimality.

2 Preliminaries and axioms

A two-person bargaining problem is a pair (S, d), where $S\subset \mathbb {R}^{2 }$ is a closed and convex set of utility possibilities and $d \in S$ is a disagreement point, which is the utility vector that results when no agreement is reached.³ It is assumed that S is bounded above, i.e., there exists $b (S )\in \mathbb {R}_{++}$, such that b ($S ) > s_{i}$ for all $s\in S, i=1,2$, and contains a point s, such that $s \gg d$.⁴ Let $\mathcal{B}$ be the class of two-person bargaining problems satisfying the conditions above. A bargaining solution is a function $f : \mathcal{B}\rightarrow \mathbb {R}^{2 }$, such that for every ($S, d )\in \mathcal{B}, f (S, d )\in S$. The Nash bargaining solution is the solution $N : \mathcal{B}\rightarrow \mathbb {R}^{2 }$ that is defined by $N (S, d )=\hbox {argmax}_{s\in S,\,\,s\ge d} \left( {s_1 -d_1 } \right) \left( {s_2 -d_2 } \right)$.

Nash (1950) characterized the solution N by the following four axioms.

Symmetry: For all $(S, d )\in \mathcal{B}$, if $d_{1 }=d_{2}$, and ($s_{1}, s_{2 })\in S$ implies ($s_{2}, s_{1 })\in S$, then $f_{1} (S, d )=f_{2} (S, d )$.

Scale invariance: Let $\tau$ : $\mathbb {R}^{2}\rightarrow \mathbb {R}^{2 }$ be a positive affine transformation given by $\tau (x)= ( \alpha _{1}x_{1}+\beta _{1}, \alpha _{2}x_{2}+\beta _{2 })$, with $\alpha _{1}, \alpha _{2 }\in \mathbb {R}_{++ }$ and $\beta _{1}$, $\beta _{2} \in \mathbb {R}$, for all $x \in \mathbb {R}^{2}$. For all (S, d), $(S^\prime , d^\prime )\in \mathcal{B}$, if $S^{\prime } =\{s^{\prime } \in \mathbb {R}^{2}\mid {s}^{\prime }= \tau (s)$ for $s \in S \}$ and $d^{\prime }=\tau (d)$, then f ($S^{\prime }, d^{\prime })= \tau$ (f(S, d)).

Independence of irrelevant alternatives: For all ($S, d ),(S^{\prime }, d )\in \mathcal{B}$, if $S^{\prime } \subset S$ and $f (S, d )\in S^{\prime }$, then $f (S, d )= f (S^{\prime }, d )$.

Weak Pareto optimality: For all $(S, d )\in \mathcal{B}$, all $s\in \mathbb {R}^{2}$, if $s \gg f (S, d )$, then $s \notin S$.

Roth (1977) showed that the Nash solution N can be obtained by replacing weak Pareto optimality with the following axiom.

Strong individual rationality: For all ($S, d )\in \mathcal{B}, f (S,d )\gg d$.

According to Roth (1977), strong individual rationality is regarded as a more elementary requirement than weak Pareto optimality, though these two conditions do not imply each other.

Anbarci and Sun (2011) have proposed an alternative axiom, called weakest collective rationality, which is weaker than both weak Pareto optimality and strong individual rationality.

Weakest collective rationality: For all $(S, d )\in \mathcal{B}, f (S, d ) \notin \{s \in S \diagdown WP{\mid } D (s) \cap S = \{s \}\}$ where $WP =\{s \in S \mid$ for all $s^{\prime } \in \mathbb {R}^{2 }$, if $s^{\prime } \gg s$, then $s^{\prime } \notin S \}$ and $D (s )=\{r \in \mathbb {R}^{2}\mid r \le s \}$.

Weakest collective rationality states that the solution should not be included in the set of Pareto minimal points. They then showed that combining this axiom with symmetry, scale invariance, and independence of irrelevant alternatives characterizes the Nash solution.

We introduce an alternative axiom as follows.

Strong undominatedness by the disagreement point: $f (S, d ) \notin D (d )$.

Strong undominatedness by the disagreement point states that the bargaining solution should not be either weakly dominated by or equal to the disagreement point.⁵ This requirement is quite natural and its intuitive sense is clearer than the weakest collective rationality axiom.⁶ As mentioned in the Introduction, we should note that this axiom is weaker than both weak Pareto optimality and strong individual rationality, but it neither imply nor is implied by weakest collective rationality.

3 Strong undominatedness by the disagreement point and the Nash solution

In this section, we characterize the Nash solution using strong undominatedness by the disagreement point instead of weak Pareto optimality, strong individual rationality, or weakest collective rationality.

Proposition 1

A bargaining solution f satisfies symmetry, scale invariance, independence of irrelevant alternatives, and strong undominatedness by the disagreement point if and only if it is the Nash solution N.

Scale invariance and independence of irrelevant alternatives together imply a simple and important result, as is proved in Lemma 1 below.⁷

Lemma 1

Let f satisfy scale invariance and independence of irrelevant alternatives. Let $\ell ((S, d ), \pi )=(1-\pi )d +\pi f (S, d )$ for $\pi \in \mathbb {R}$. If $f (S, d )\ne d$, then for all $\pi >1$, $\ell ((S, d ), \pi ) \notin S$.

Proof

By contradiction, we suppose that for some ($S, d )\in \mathcal{B},f$ $(S, d )\ne d$ and there is some $\hat{\pi } > 1$, such that $\ell ((S, d ), \hat{\pi } )\in S$ . By scale invariance, we may let $d = \mathbf{0}\equiv (0,0)$. Therefore, $\ell ((S, \mathbf{0})$, $\hat{\pi } )=\hat{\pi } f (S, \mathbf{0})\in S$. Letting $\lambda = 1/\hat{\pi } < 1$, we consider $\lambda S = \{(\lambda s \in \mathbb {R}^{2}\mid s \in S \}$. Since $f (S, \mathbf{0})\in \lambda S \subset S$, it follows that $f (S, \mathbf{0})= f (\lambda S$, 0) by independence of irrelevant alternatives. However, by scale invariance again, it must be that $\lambda f (S, \mathbf{0}) = f (\lambda S, \mathbf{0})$, and that is a contradiction. $\square$

Since S is closed, Lemma 1 implies that the bargaining solution f(S, d) must be in the boundary of S unless it is equal to the disagreement point.

Proof of Proposition 1

(If.) N certainly satisfies symmetry, scale invariance, independence of irrelevant alternatives, and strong undominatedness by the disagreement point. (Only if.) Suppose f satisfies all axioms in Proposition 1. We consider a bargaining problem (S, d). By scale invariance, without loss of generality, we can let $d =\mathbf{0}$ and $N (S, \mathbf{0}) = (1,1)$. Let $s_{i }^\mathrm{max} = \max \{ s_{i }\mid s \in S \}$ for $i =1,2$ and $\bar{s} = \max \{ s_{1 }^\mathrm{max}, s_{2}^\mathrm{max}\}$. Since S is closed and bounded above, there exists $s_{i }^\mathrm{max}$ for $i =1,2$. Furthermore, let $T = \{ (s_{1}, s_{2 })\mid \bar{s}\ge s_{1}, \bar{s} \ge s_{2 }, s_{1 }+s_{2 }\le 2 \}$. Then, $S \subset T$, since S is convex.⁸ By symmetry, $f (T, \mathbf{0}) = (t, t)$ for some $t \in \mathbb {R}$, such that $t\le 1$. By strong undominatedness by the disagreement point, it follows that $0 < t \le 1$. Then, Lemma 1 implies $t = 1$. Therefore, by independence of irrelevant alternatives, $f (S, \mathbf{0})= f (T, \mathbf{0})=(1, 1)= N (S, \mathbf{0}$), as required. $\square$

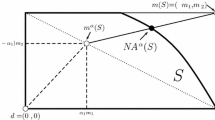
Figure 1 illustrates Proposition 1.

Fig. 1

Illustration of Proposition 1. T is a symmetric bargaining set that includes the point (1, 1) on its boundary and contains S. The solution for T is (t, t), which must be equal to (1, 1). Then, the solution for S must be (1, 1)

We show the independence of four axioms by pointing out that each of the following solutions violates one axiom while satisfying the remaining three.

The solution that for all $(S, d )\in \mathcal{B}, f (S, d )=\hbox {argmax}_{s\in S,\,\,s\ge d} ( {s_1 -d_1 } )^{\frac{1}{4}}( s_2 -d_2 )^{\frac{3}{4}}$ violates symmetry. The solution that for all $(S, d )\in \mathcal{B}, f (S, d )=\hbox {arg}\,\hbox {min} \{{\vert }s_1^*-s_2^*{\vert }{\vert } s^{*}= \hbox {argmax}_{s\in S,s\ge d} ( {s_1 +s_2 } )$} violates scale invariance. The Kalai–Smorodinsky solution, that is the maximal element of S on the segment joining d to a(S, d) where $a (S, d )= (a_{1 }(S, d ), a_{2 }(S, d ))$ with $a_{i }(S, d ) =\max \{ s_{i }{\vert }s \ge d, s \in S \}$ for $i =1, 2$,⁹ violates independence of irrelevant alternatives. The solution that for all ($S, d )\in \mathcal{B}, f (S, d )=d$ obviously violates strong undominatedness by the disagreement point.

4 Weakening of the independence of irrelevant alternatives axiom

Rachmilevitch (2016) has introduced an axiom named the sandwich axiom, which requires that for $S \subset S^{\prime } \subset S^{\prime \prime }$, if two bargaining problems (S, d) and $(S^{\prime \prime }, d )$ have the same solution, then $(S^{\prime }, d )$ should also have that solution.¹⁰ Formally, the sandwich axiom is defined as follows:

Sandwich axiom: For any $(S, d ), (S^{\prime }, d )$, $(S^{\prime \prime }, d )\in \mathcal{B}$, such that $S \subset S^{\prime } \subset S^{\prime \prime }$, if $f (S, d )= f (S^{\prime \prime }, d )=y$, then $f (S^{\prime }, d )=y$.

The sandwich axiom can be interpreted as follows¹¹: for the disagreement point d, if the solution chosen in a utility possibilities set S is also chosen in a utility possibilities set $S^{\prime \prime }$ containing S, then any alternatives in $S^{\prime \prime }/S$ are regarded as irrelevant and, therefore, the same solution should be chosen in the utility possibilities set $S^{\prime }$ that contains S and is contained in $S^{\prime \prime }$. Then, the sandwich axiom is certainly implied by independence of irrelevant alternatives.

Next, we consider a set of utility possibilities L = convexhull $\{ d , x \}$ for $d , x \in \mathbb {R}^{2 }$, such that $d_{1 }= d_{2}, x_{1 }= x_{2}$, and $x \gg d$, where convexhull $\{d, x\}$ denotes the convex hull of the set of two points, d and x, which is just a straight line segment [d, x]. Then, it is quite natural to require that the solution be efficient in such bargaining problems as $(L, d )\in \mathcal{B}$, in which the utilities at the disagreement point ($d_{1}$ and $d_{2}$ ) and the utilities at each feasible point ($u_{1}$ and $u_{2}$ for $u\in L )$ are equal between two persons. Therefore, we may assume the following axiom.

Egalitarian Pareto optimality: For any (L, d) where L = convexhull $\{d, x\}$ for $d, x \in \mathbb {R}^{2}$, if $d_{1}= d_{2}$, $x_{1}= x_{2}, x \gg d$, then $f (L, d )= x$.

Egalitarian Pareto optimality is certainly weaker than weak Pareto optimality. Note that independence of irrelevant alternatives together with scale invariance and strong undominatedness by the disagreement point implies egalitarian Pareto optimality, which is demonstrated as follows. For the bargaining problem ($L, d )\in \mathcal{B}$ where L = convexhull $\{d, x \}$, such that $x \gg d$ for $d, x \in \mathbb {R}^{2}$ with $d_{1 }= d_{2}$ and $x_{1 }= x_{2}$, we consider $\ell ((L, d ), \pi )$ for $\pi \in \mathbb {R}$. Then, by strong undominatedness by the disagreement point, it follows that $f (L, d ) \ne d$ and, by Lemma 1, it follows that $\ell ((L, d ),\pi ) \notin L$ for all $\pi >1$. Therefore, we have $f (L, d )= x$.

From this observation and the fact that the sandwich axiom is a weakening of independence of irrelevant alternatives, it follows that independence of irrelevant alternatives together with scale invariance and strong undominatedness by the disagreement point implies the sandwich axiom and egalitarian Pareto optimality. However, the sandwich axiom and egalitarian Pareto optimality together with scale invariance and strong undominatedness by the disagreement point do not imply independence of irrelevant alternatives. For example, for a given problem $(S, d )\in \mathcal{B}$, let $Z (d ) = \{z{\vert }z_{1 }> d_{1}, z_{2 }=d_{2 }\}$ and $\tilde{z} \left( S \right)$ = arg max {$z_{1}{\vert } z \in Z (d )\cap S$} if $Z (d )\cap S \ne \phi$. The solution that for any ($S, d )\in \mathcal{B}, f (S, d )$ = (1/2)($\tilde{z} \left( S \right) +d )$ if $Z (d )\cap S \ne \phi$ and $f (S, d )= N (S, d )$, otherwise satisfies those four axioms, but nevertheless violates independence of irrelevant alternatives.

We then provide a characterization of the Nash solution replacing independence of irrelevant alternatives with two axioms, the sandwich axiom and egalitarian Pareto optimality. The following result certainly improves on Proposition 1.

Proposition 2

A bargaining solution f satisfies symmetry, scale invariance, egalitarian Pareto optimality, the sandwich axiom, and strong undominatedness by the disagreement point if and only if it is the Nash solution N.

Like Lemma 1 for Proposition 1, we present the following lemma for Proposition 2.

Lemma 2

Let f satisfy scale invariance, the sandwich axiom, and egalitarian Pareto optimality. If $f (S, d ) \gg d$, then for all $\pi >1$, $\ell ((S, d ), \pi ) \notin S$.

Proof

Analogous to the proof of Lemma 1, we suppose by contradiction that for some $(S, d )\in \mathcal{B}, f$ ($S, d ) \gg d$, and there is some $\hat{\pi } > 1$, such that $\ell ((S, d ), \hat{\pi } )\in S$. Using scale invariance, we let $d =\mathbf{0 }$ and $f_{1 }(S, \mathbf{0} ) = f_{2} (S, \mathbf{0} )$, and letting $\lambda = 1/\hat{\pi } < 1$, we have $f (S, \mathbf{0})\in \lambda S$. By scale invariance again, it follows that $f (\lambda S, \mathbf{0})= \lambda f (S, \mathbf{0})$. On the other hand, for the bargaining problem (convexhull $\{\mathbf{0}, f (S, \mathbf{0 })\},\mathbf{0})\in \mathcal{B}, f$(convexhull $\{\mathbf{0}, f (S, \mathbf{0})\},\mathbf{0})= f (S, \mathbf{0})$ by egalitarian Pareto optimality. Then, since convexhull $\{\mathbf{0}, f (S, \mathbf{0})\}\subset \lambda S$ by convexity of S, it must be that $f (\lambda S, \mathbf{0})=f(S, \mathbf{0})$ by the sandwich axiom, and that is a contradiction. $\square$

Proof of Proposition 2

(If.) N certainly satisfies symmetry, scale invariance, egalitarian Pareto optimality, the sandwich axiom, and strong undominatedness by the disagreement point. (Only if.) Suppose f satisfies all axioms in Proposition 2. We consider a bargaining problem (S, d). Analogous to the proof of Proposition 1, we let $d = \mathbf{0}$ and $N (S, \mathbf{0}) = (1, 1)$, and define the set T containing S as above. By symmetry and strong undominatedness by the disagreement point, it follows that $f (T, \mathbf{0}) = (t,t)$ and $0 < t \le 1$. Lemma 2 implies $t = 1$, i.e., $f (T, \mathbf{0}) = (1, 1)$. Then, by egalitarian Pareto optimality, f (convexhull {0, (1, 1)}, 0) = (1, 1). Since (convexhull {0,(1, 1)}, 0) $\subset S \subset T$ by the sandwich axiom f(S, 0) = (1, 1) = N (S, 0), as required. $\square$

We show the independence of five axioms by pointing out that each of the following solutions violates one axiom while satisfying the remaining four.

The solution that for all ($S, d )\in \mathcal{B}, f (S, d )=\hbox {argmax}_{s\in S,\,s\ge d} ( {s_1 -d_1 } )^{\frac{1}{4}}( {s_2 -d_2 } )^{\frac{3}{4}}$ and the solution that for all $(S, d )\in \mathcal{B}, f (S, d )=\hbox {arg}\,\hbox {min}\{{\vert }s_1^*-s_2^*{\vert }{\vert }s^{*}= \hbox {argmax}_{s\in S,\,\,s\ge d} ( {s_1 +s_2 } )\}$, as defined above, violate symmetry and scale invariance, respectively. The solution that for all $(S, d )\in \mathcal{B}$, (1/2)N(S, d) violates egalitarian Pareto optimality. The Kalai Smorodinsky solution violates the sandwich axiom. The solution that for any ($S, d )\in \mathcal{B}, f (S, d )=d$, if S contains some s, such that $s_{1} <d_{1}$ or $s_{2} <d_{2}$, and $f (S, d )= N (S, d )$, otherwise violates strong undominatedness by the disagreement point.