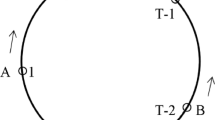A composite channel hopping algorithm for blind rendezvous in heterogeneous cognitive radio networks

Abstract

In cognitive radio networks (CRNs), rendezvous is the vital step prior to the communication between two unlicensed secondary users (SUs), where the SUs hop on the same channel at the same time to establish a link. With the dramatic fall in the cost and size of wireless transceivers, it becomes more reasonable to apply multiple radios to achieve significant improvement in the rendezvous performance. However, most of the existing multiradio rendezvous algorithms are proposed for homogeneous CRNs where all the SUs are equipped with an equal number of radios and do not possess backward compatibility to SU with a single radio. In reality, the CRNs are heterogeneous in nature as SUs may have different numbers of radios. In this paper, a composite CH algorithm is proposed for an asynchronous and heterogeneous network to achieve blind rendezvous with full rendezvous diversity. An SU with m number radios are categorized into three groups those follow different channel hopping (CH) algorithms. The upper bound of the rendezvous latency is being evaluated with a brief theoretical and mathematical analysis. Extensive simulations have conducted for different performance metrics, and the results are compared with the state-of-art algorithms. Overall, the proposed algorithm shows better performance in heterogeneous CRNs.

1 Introduction

With the exponential development of smart wireless technology and the explosive spread of wireless devices, the unlicensed spectrum has become overcrowded and a scarce resource. At the same time, a significant portion of the licensed spectrum remains underutilized. Cognitive radio (CR) has gained attention in the past decade for efficiently utilizing this underutilized licensed spectrum. The unlicensed or secondary users (SUs) in the cognitive radio networks (CRNs) opportunistically share the temporarily vacant spectrum of the primary users (PUs), also called the licensed users [1]. Each SU in the CRN is equipped with a cognitive transceiver, or CR, that is used to sense and access the idle channels of PUs for data transmission. However, before the data transmission between any pair of SUs, they must share control information and establish a link on the available channel, called the rendezvous of SUs. The conventional rendezvous is achieved using a centralized unit or dedicated common control channels (CCCs), which have security issues and also face scalability problems [2, 3]. Hence, blind rendezvous is widely adopted by the CRNs, where SUs hop on their respective available channels following certain channel hopping sequences (CHSs) until they find the same channel at the same time. This channel rendezvous is blind, as the SUs do not have any prior information about others’ presence and available channel sets. The design of the CH sequence that can achieve blind rendezvous also has the following challenges [4,5,6,7,8,9]:

• Asynchronous clock Clock synchronization is unrealistic and difficult to maintain for spatially scattered SUs in distributed CRNs. CHSs must handle asynchronous scenarios while ensuring rendezvous.

• Heterogeneity in CRN It is implicitly assumed that CRNs are homogeneous, where each SU is equipped with an equal number of CRs, and those can sense and access all the available channels in the network. Nevertheless, different SUs may have a different number of CRs, and the available channels may also differ because of different sensing capabilities. Hence, heterogeneous CRNs are needed and should be focused on.

• Symmetric CHS generation Many rendezvous algorithms use asymmetric CHSs for a pair of SUs with the preassigned roles of transmitter and receiver. This method can offer the lowest rendezvous latency, but the prior knowledge or assignment of roles is unrealistic. In practice, symmetric CHSs are generated for each SU with symmetric roles.

• Anonymous SUs’ information To achieve better rendezvous results, ID-based CH algorithms are designed with unique identifications of SUs, where the CHS length is the function of the ID string. However, with increasing numbers of SUs in the network, the rendezvous time would also increase with the increasing length of ID strings. Moreover, for security concerns, an ID independent rendezvous algorithm is preferred.

With the challenges discussed above, any randomly designed blind rendezvous algorithm cannot guarantee rendezvous. To achieve guaranteed and fast rendezvous within a finite time, the construction of CH sequences must focus on the degree and latency of rendezvous. Three primary performance metrics are Average Time to Rendezvous (ATTR), Maximum Time to Rendezvous (MTTR), and rendezvous diversity. When a pair of SUs start to hop with their CHSs, which might be asynchronous, the time required for the first rendezvous is called time to rendezvous(TTR). The expected and maximum time required for the rendezvous under all possible clock drifts between the SUs are considered as ATTR and MTTR respectively. The upper bound of MTTR is denoted as maximum conditional time to rendezvous (MCTTR) in most of the literature, and it is the MTTR value at the worst condition when only one channel is common between sensed available channel sets of SUs. Rendezvous diversity is the minimum number of distinct channels on which two SUs can rendezvous. If they can rendezvous on all the channels, they achieve optimum rendezvous diversity. Hence, with full rendezvous diversity, a pair of SUs guarantee rendezvous even in the worst conditions.

Most of the rendezvous schemes in the literature assume that SUs are equipped with a single transceiver or radio [5, 6, 10,11,12,13]. The cost of transceivers has dropped dramatically in recent years [7, 14, 15], and multiradio rendezvous has become feasible to implement. In multiradio rendezvous, SUs can hop in parallelly on multiple channels at the same time, and the TTR can be shortened significantly. Some previous works [16,17,18,19,20,21,22,23,24] attempted to design multiradio rendezvous algorithms. However, many disadvantages are still present in these works that need to be explored, such as (i) All the SUs in the CRN are assumed to have an equal number of radios, which is unrealistic for heterogeneous networks. (ii) Each SU is implicitly assumed to be equipped with more than one radio. In other words, the designed algorithms are not backward compatible with single radio rendezvous. If at least one SU is using one radio, rendezvous for a pair of SUs cannot be guaranteed. (iii) Even though some multiradio rendezvous algorithms possess backward compatibility, they have a very large MTTR for single radio rendezvous. (iv) With multiradios, a SU may hop on the same radio at the same time, which is just a waste of radio resources. Hence, by accessing different distinct channels with the radios at the same time, the possibility of rendezvous will increase in each time slot. (v) For some of the algorithms [16, 24], MTTR value is infinite as they cannot guarantee rendezvous within finite time.

CHS period describes the repeating pattern of the CHS. Studies show that it is faster to rendezvous for an SU pair with multiple radios within a short CHS period, which results in a shorter TTR value. However, if an SU only has one radio, the CHS period of the SU increases significantly, increasing TTR value and computational complexity. In this paper, the novelty lies in the use of a DDS-based CHS for a single radio as the period length can be reduced by using a disjoint difference sets with minimum elements. A composite channel hopping algorithm is introduced for heterogeneous radios, focusing on the disadvantages discussed above for guaranteed blind rendezvous. For the realistic network scenario, the SUs are considered with no pre-assigned roles, and the SUs have asynchronous local clocks, different numbers of radios, and asymmetric available channel sets. Internet of Things devices presently are constrained by their low memory and processing power, which restricts the type of computations they can perform. The limitation of resources may serve as the primary constraint that imposes restrictions on IoT devices. The suggested CHRR method would be more beneficial for device-to-device communication and IoT applications that can save time and memory in small sensors and mobile devices due to the shortest CHS period and rendezvous latency.

The contribution of this paper is summarized as follows.

• (1) A composite CHS is proposed for the two-user rendezvous, where the SUs may be equipped with a heterogeneous number of radios. For this, a DDS-based CH algorithm and a stay-jump based CH algorithm are proposed. The first one is used for single radio rendezvous, while the combined form of the two CHSs is used for multiradio rendezvous.

• (2) The upper bounds of MTTR are derived for the CHRR algorithm under all possible combinations of radios in a heterogeneous CRN.

• (3) The performance of the CHRR in terms of ATTR and MTTR is evaluated through extensive simulations and compared with other state-of-the-art multiradio and heterogeneous radio rendezvous algorithms.

The rest of this paper is organized as follows: In Sect. 2, existing multiradio rendezvous algorithms are briefly reviewed. Section 3 introduces the system model and problem formulation of our work. Section 4 presents the proposed composite multiradio rendezvous algorithm. In Sect. 5, the theoretical analysis has been done for rendezvous diversity and the upper bound of MTTR for heterogeneous networks. Section 6 demonstrates the simulation and the comparison with other algorithms. Finally, the paper is concluded in Sect. 7.

2 Related works

The existing channel-hopping rendezvous algorithms are implicitly classified based on the number of radios that the SUs have. Most of the previous works have considered single radio-based rendezvous. Several researchers are concentrating on multiple radios-based CH algorithms since multiple radios have become more realistic in recent years. The CH algorithms can be further characterized based on the CRN type: homogeneous or heterogeneous. All the SUs in the homogeneous networks are equipped with an equal number of radios, whereas the number of radios is not the same in the heterogeneous networks. The design of a CH algorithm for heterogeneous networks is more challenging since it must be a multiradio rendezvous method with single radio rendezvous backward compatibility. In this section, a detailed review of recent multiradio rendezvous algorithms is presented.

Table 1 Performance comparison of multi-radio rendezvous schemes

The role-based parallel sequence (RPS) algorithm is proposed in [16] for multiradio rendezvous in homogeneous CRNs. The primary idea behind this article is to think of one radio as a dedicated radio and the rest as jump radios for an SU with m radios. The dedicated radio stays on a specific channel for a certain number of timeslots, while the $(m-1)$ jump radios hop continuously on the available channels in a round robin manner. The ATTR and MTTR performance of the RPS algorithm is further improved in adjustable multi-radio rendezvous (AMRR) [21] by adjusting the number of dedicated radios of an SU. If $N_1$ and $N_2$ be the number of available channels of $SU_1$ and $SU_2$ respectively in a CRN with N number of total available channels, then MTTR value of RPS and AMRR depends on N and $(N_1, N_2)$, respectively. This shows that, unlike RPS, AMRR takes heterogeneity into account. The general construction for rendezvous (GCR) in [17] divides the total radios of an SU into pairs and the available channels are distributed among them. Two-prime modular clock concept is utilized here for rendezvous. The disadvantage of this method is that an even number of radios is necessary. Moreover, bounded MTTR is guaranteed for RPS, AMRR and GCR only when the number of radios is greater than one, and MTTR tends to infinity for a single radio environment.

In [18], multiradio sunflower-set based rendezvous (MSS) algorithm is suggested, which is inspired by the single-radio sunflower-set based rendezvous (SSS) algorithm. For a single radio, a periodic CH sequence is generated using the SSS algorithm. For multiradio, the SSS-generated CH sequence is assigned to the first radio, and for the remaining radios, CH sequences are generated sequentially by cyclically rotating the sequence of the previous radio by 2P timeslots. P is the smallest prime integer that is not less than three or the number of available SU channels. Though MSS can be applied to heterogeneous CRNs, the MTTR is high and increases significantly with the increase in the number of available channels. Further, two SUs cannot guarantee rendezvous when they start the rendezvous process simultaneously or when any SU has only one available channel. A Chinese remainder theorem-based multiradio rendezvous (CMR) is proposed in [25]. This algorithm guarantees rendezvous when at least two different prime numbers are used by an SU for the generation of multiradio CH sequences. If both SUs are equipped with a single radio, CMR cannot guarantee a rendezvous when both employ the same prime integer to generate their CH sequences. The adaptive rendezvous (AR) algorithm in [19] guarantees rendezvous with a high probability, but the number of radios in each SU is assumed to be equal, which makes it difficult to implement in heterogeneous CRNs.

In the algorithms [16,17,18,19], many radios of an SU may hop on the same channel at the same time, wasting radio resources. Hybrid radio rendezvous (HRR) algorithm, enhanced HRR(EHRR) algorithm, and modified enhanced heterogeneous radio rendezvous (MEHRR) algorithm in [22, 23, 26] respectively, ensure that different radios of an SU access different channels at a given time-slot. The three algorithms fully address the heterogeneity of the CRNs by designing two separate algorithms for SUs with a single radio and SUs with multiple radios. Here, rendezvous is also guaranteed when one SU is with one radio and the other is with multiple radios. However, when the two SUs are equipped with single radios, in the worst case, the upper bound of MTTR would be $5P^3$, $4P^3$, and $3P^3$ in HRR, EHRR, and MEHRR respectively. Despite the fact that these algorithms work extremely well for multiradio rendezvous, the MTTR values for single radio rendezvous scenario are notably very high. Here, P is same as refereed in other algorithms.

The computational complexities of these rendezvous algorithms are directly related to the period of the CH sequences and the upper bound of MTTR. In [16, 17, 21], faster rendezvous is guaranteed with a short CHS period, where the SUs are with multiple radios and hence, complexities are relatively lower as compared to others. In the case of heterogeneous radios, if one of the SUs is equipped with a single radio, the period length of the CH sequences for HRR, MEHRR, and CHRR would be $5P^2$, $3P^2$, and ${2P^{2}+\lfloor \frac{P}{2}\rfloor \times P}$, respectively. However, despite the fact that the period lengths of HRR and MEHRR are $O(P^2)$, their corresponding MTTR with full rendezvous diversity is $O(P^3)$, as seen in Table 1. In contrast, CHRR achieves full rendezvous diversity within the period for which its complexity is $O(P^2)$ as compared to others.

Table 1 compares state-of-the-art multiradio rendezvous algorithms in terms of the upper bound of MTTR, complexity, heterogeneity, and compatibility with single radio rendezvous.

3 System model and problem formulation

3.1 System model

We consider a heterogeneous CRN with N non-overlapping licensed channels, where the channel set $C = \lbrace 0,1, 2, 3, 4,\ldots , N-1\rbrace$. A subset of C is said to be accessible to an SU if the user can communicate over these channels without interfering with the PUs. The $SU_u$ is considered to be equipped with $m_u$ radios, where $m_u \ge 1$. The set of available channels sensed idle by the $SU_u$ is $C_u\subseteq C$ and $\mid C_u\mid =N_u$.The network divides time into timeslots of length $2t_s$, where $t_s$ is the time necessary to create a link between two users by completing the beaconing and handshaking operations. According to IEEE 802.22 standard, $t_s=10$ ms [27].

In the heterogeneous network, if SU is equipped with a single radio, i.e., $m=1$, the radio is named as main radio. When $m=2$ for an SU, first radio is termed as main radio with CHS same as that of $m=1$, and the second radio termed as stay radio. For the SU with $m\ge 3$, the radios are divided into three groups, one main radio, k stay radios, and $(m-1)-k$ jump radios. The CHS generation algorithms for different groups of radios are discussed in Sect. 4.

The rendezvous is considered between a pair of SUs, $SU_u$ and $SU_v$. Here, $m_u$ and $C_u$ may not be equal to $m_v$ and $C_v$, respectively. The available common channels between $SU_u$ and $SU_v$ is denoted by the set $G_{uv}=C_u\cap C_v$. Rendezvous is possible between the users if $G_{uv}\ne \emptyset$. The CHS of $SU_u$ is denoted as $S_u =\lbrace S_u^1, S_u^2, S_u^3,\ldots , S_u^{i_u},\ldots , S_u^{m_u} \rbrace$, where $S_u^{i_u}=\lbrace S_u^{i_u}(1), S_u^{i_u}(2), S_u^{i_u}(3),\ldots , S_u^{i_u}(t),\ldots , S_u^{i_u}(T) \rbrace$ is the CHS of ith radio with a length of T timeslots. Hence, $S_u^{i_u}(t)$ represents the channel accessed by the ith radio of $SU_u$ at tth timeslot. A clock drift of $\delta$ is considered between the CHSs of two SUs.

3.2 Problem formulation

The blind rendezvous problem for the heterogeneous CRN can be formulated as follows:

For a pair of SUs, $SU_u$ and $SU_v$, design the channel access strategy for their radios at different timeslots $S_r^{i_r}(t)$ $\in$ $C_{r}$, where r $\in$ $\lbrace$u, v$\rbrace$ and $\forall$ $C_{u}$, $C_{v}$, $\delta$, and $\forall$ $R \in G_{uv}$, $\exists$ $t',i_u, i_v$ such that $S_{u}^{i_u}(t' + \delta ) = S_{v}^{i_v}(t')=R$

Here, the CH process of $SU_v$ starts $\delta$ timeslots later than that of $SU_u$, and the rendezvous is said to be achieved on channel R at $t'$th timeslot. The ATTR is the average times required for the first occurrence of rendezvous and can be represented as $ATTR= E(\min \limits _{\forall R} t')$.

Let $\Gamma (G_{uv}, \delta )$ is the minimum TTR on all the commonly available channels. Then MTTR with full rendezvous diversity can be represented as:

$MTTR= \max \limits _{\forall \delta }( \Gamma (G_{uv}, \delta ))$

In the worst-case scenario, where $G uv=1$, the MTTR would have its upper bound. Short MTTR represents two SUs can rendezvous quickly even at the worst condition, and short ATTR means two SUs can rendezvous quickly on average. Hence, both are significant metrics for the design of a CH rendezvous algorithm.

In Fig. 1, a rendezvous process is illustrated between $SU_u$ and $SU_v$ with radios $m_u=1$ and $m_v=3$ respectively. Here, $C=\lbrace 0,1,2,3,4,5,6\rbrace$, $C_u=\lbrace 0,1,2,3,6\rbrace$, $C_v=\lbrace 0,2,3,6\rbrace$, and $G_{uv}=\lbrace 0,2,3,6\rbrace$. The CH process of $SU_v$ starts after $\delta =5$ timeslots. As TTR is calculated from the instant when both the users start their CH, local clock of $SU_v$ is considered for the TTR calculation. The rendezvous at channels $\lbrace 0,2,3,6\rbrace$ occurred for the first time at $1^{st}, 3^{rd}, 7$th, and 15th timeslots. Hence, $\min \limits _{\forall R} t'$ or the minimum $TTR=1$, and $\Gamma (G_{uv}, 5)=15$.

Fig. 1

Example of rendezvous process

4 Composite CH-based heterogeneous radio rendezvous algorithm

To achieve fast rendezvous in heterogeneous CRN, a DDS-based CH algorithm is proposed for SU with a single radio. For SU with multiple radios, a composite CH algorithm is introduced, where the DDS-based CH algorithm is used for the generation of the CHS of its first radio and a Stay-Jump CH algorithm is used for the CHSs of the remaining radios.

4.1 DDS-based channel hopping algorithm

4.1.1 Disjoint difference set

Definition 1

A set $D=\lbrace a_{0}, a_{1}, a_{2}, \cdots , a_{k-1} \rbrace$ $\subset \ Z_{n}$ is referred as a $\textit{relaxed cyclic difference set}$ or simply (n, k)-DS, if an order pair $(a_{i}$, $a_{j})$ exists $\forall$ $d \in (0, n)$ such that $(a_{i} - a_{j})$ $\equiv$ d mod n. Here, $a_{i}$, $a_{j}$ $\in D$ and $\ Z_{n}$ is the set of positive integers denoted as $\{0, 1,2,\ldots ,n-1 \}$.

Corollary 1

If D is a (n, k)-DS, under $\ Z_{n}$ then rotate(D, i) is likewise a (n, k)-DS, where i $\in$ (0, n) and rotate(D, i)= $\lbrace a_{0}+i, a_{1}+i, \ldots , a_{k-1}+i \rbrace$ mod n,

Proof

The corollary has been proved in our previous work [28]. As an illustration, if $D= \lbrace 1,4,5 \rbrace \subset Z_{6}$ is a DS, then $rotate(D, 3)=\lbrace 4, 1, 2 \rbrace$ is also a DS.

Definition 2

A set $Q=\lbrace A_{0}, A_{1} \ldots A_{n-1}\rbrace$ is referred as a cyclic quorum system (CQS), if each set $A_{i}\subseteq Z_n$ and Q has the following two properties for all i, j $\in [0, n-1]$:

• i) $A_{i}=rotate(A_{0}, i)$,

• ii) $A_{i}\bigcap A_{j} \ne \emptyset$

Corollary 2

A CQS under $Z_{n}$ can be formed with a group of n sets $\lbrace A_{0}, A_{1},\ldots A_{n-1}\rbrace$, if $A_{i}= \lbrace (a_{0}+i)mod~n, (a_{2}+i)mod~n, \ldots ,(a_{k-1}+i)mod~n\rbrace$ $\forall \textit{i}\in [0, n)$ and set $D= \lbrace$ $a_{0}, a_{1}, \ldots ,a_{k-1} \rbrace$ is a (n, k)-DS.

Proof

The corollary has been proved in our previous work [28].

Definition 3

A set $S=\lbrace D_{0}, D_{1}, \ldots ,D_{m-1}\rbrace$ denotes a group of disjoint difference sets (DDS) under $Z_{n}$, where $D_{i}$ is a DS and $D_{i}\bigcap D_{j}= \emptyset , \forall i,j\in [0, m-1]$.

Corollary 3

If $S=\lbrace D_0, D_1, \ldots , D_{m-1.}\rbrace$ is a DDS with $D_i\subset Z_n$, then the set rotate(S, i) is likewise a DDS, where $i\in (0,n)$ and $rotate(S, i)= \lbrace rotate(D_{0}, i), rotate(D_{1}, i), \ldots , rotate(D_{m-1}, i) \rbrace$.

Proof

The corollary has been proved in our previous work [28].

Corollary 4

If $S= \lbrace D_{0}, D_{1},\ldots ,D_{m-1}\rbrace$ is a DDS with $D_{i}\subset Z_{n}$, then S can be used to create a set of m number of CQS.

Proof

The corollary has been proved in our previous work [28].

4.1.2 Construction of DDS

An algorithm is established for the construction of a DDS under $Z_{n}$. In this paper, $n= Pk$, where P is the smallest prime number greater than equal to the total number of licensed channels in the CRN. k is the average number of elements per DS. The set $S=\lbrace D_{0}, D_{1}, D_{2}, \ldots , D_{P-1} \rbrace$ is constructed with P disjoint DSs, where each DS is of size k and $k= 2P+\lfloor \frac{P}{2}\rfloor$.

To start building a DDS under $Z_n$, the $Z_{n}$ is partitioned into P distinct sets of size k and is designated as $U_{0}, U_{1}, \ldots , U_{P-1}$. This procedure is depicted in Fig. 2. Here, $U_{l}= \lbrace lk, lk+1, \ldots ,(lk+k-1) \rbrace , l \in [0, P-1]$. Each $U_{l}$ is further split into two subsets, $X_{l}$ and $Y_{l}$. The subsets $X_{l}$ and $Y_{l}$ each have P and $(k-P)$ number of elements, respectively. Now, the ith DS of size k is constructed with the first P elements selected from $\{X_0, X_1,\ldots ,X_{P-1}\}$ represented with a set, $D_{Xi}$ and the rest $(k-P)$ elements are selected from $\{Y_0, Y_1,\ldots ,Y_{P-1}\}$ by using the concept of triangular number. The selected $(k-P)$ elements are presented with the set, $D_{Yi}$. The term $T_{j}$, used in Fig. 2 is a triangular number and is defined as $\frac{j(j+1)}{2}$ for any non negative integer j. Therefore, $D_{i}$ is given by

$D_{i}= D_{Xi} \cup D_{Yi}$,

where

$D_{Xi}= \lbrace x_{ip}\rbrace$, $x_{ip}= kp+ i$,

$D_{Yi} =\lbrace y_{iq}\rbrace$, $y_{iq}= k(T_{q}+ i)+ P+ q$,

$T_{q}= \frac{q(q+1)}{2}$modP,0 $\le p\le P-1$ and $0 \le q\le k-P-1$

Algorithm 1

Construction of Disjoint Difference Sets

In Algorithm 1, the construction of $D_{Xi}$ and $D_{Yi}$ are mentioned respectively in lines $4\sim 6$ and lines $8\sim 11$. The ith difference set, $D_i$ is constructed in line 13 by combining $D_{Xi}$ and $D_{Yi}$ and the final set S, obtained in line 14 is a DDS. The proof for the constructed $D_i$’s being the disjoint difference sets is given in the “Appendix”.

Fig. 2

Construction of the ith difference set $D_{i}$ under $Z_{n}$, $\forall i \in [0, P-1]$

4.1.3 CH sequence generation based on DDS for the rendezvous

As stated in Algorithm 2, a DDS-based CH sequence is generated for $SU_{u}$. If $C=\lbrace 0, 1, 2, \ldots ,P-1\rbrace$ is the set of licensed channels in the network, and $C_{u}$ is the available channel set of $SU_{u}$ then the DDS S has P number of disjoint sets $D_{i}, i\in C$. These DSs are used to construct CH sequence for the first radio with time period of n time slots as shown in lines $6\sim 13$.

Fig. 3

Rendezvous process using DDS-based CH sequences. a Illustration for channel access at different time slots using DDS S, Disjoint difference sets when $P=3$, b Rendezvous between two SUs while using DDS-based CHSs with 6 time slots drift

Algorithm 2

Generation of DDS-based CH sequence

Example A CRN network is considered with the licensed channel set $C =\lbrace 0,1,2\rbrace$. $P=3$ for the given C. The SUs $SU_{u}$ and $SU_{v}$ with $C=C_u=C_v$ generate their CH sequences using Algorithm 1 and 2. Figure 3 illustrates the relevant CH sequences and the rendezvous between them in an asynchronous environment.

Algorithm 3

Generation of Stay-Jump CH sequence

4.2 Stay-jump channel hopping algorithm

When an SU is equipped with multiple radios, and $\vert C_v \vert \le m_v$, each radio by default will act as a stay radio and access the same channel at every timeslots as shown in Fig. 4b. However, for $\vert C_v\vert > m_v$, the CHS for the first radio is generated based on DDS-based CH algorithm, and CHSs for the remaining radios are generated using Jump-Stay CH algorithm. One period of CHSs generated by the latter algorithm is consist of $\eta$ number of inner periods, each of length $\tau _{v}$. Based on the number of stay radios $(m_{vs})$ and the jump radios $(m_{vj})$, length of the periodic CHSs is $T=\eta \times \tau _{v}$, where $\eta = \frac{LCM(C_v,m_{vs})}{m_{vs}}$ and $\tau _{v}=\lceil \frac{C_v-m_{vs}}{m_{vj}}\rceil$ as shown in Fig. 4a, and the channel accessed by the radios in each time slot is derived in Algorithm 3.

For each inner period, the set $C_v$ is divided into distinct disjoint sets, $C^S_v$ and $C^J_v$, where $\vert C^S_v\vert =m_{vs}$. Throughout an inner period, each stay channel stays on a particular channel, $c\in C^S_v$, and each jump radio hops to a different channel, $c\in C^J_v$ at different timeslots. In line 8, $C^S_v$ and $C^J_v$ are initialized to null sets for each inner period. In lines $11 \sim 12$, $\vert C^S_v\vert =m_{vs}$ distinct channels from $C_v$ are assigned to the stay radios and the selected channels are taken into $C^S_v$ in line 13. $C^J_v$ is derived in line 15,and In lines $17\sim 25$, the jump radios hop on different channels of $C^J_v$ during the inner period in such a way that their accessed channels are different at one time slot. Finally, the required one period of the CHSs of all the $(m_v-1)$ radios is generated in line 29.

Algorithm 4

CHRR Rendezvous Algorithm

Fig. 4

Generation of the CHS for an SU having multiple radios. a The structure of one period of the CHSs generated by Stay-Jump CH Algorithm. b An example of of CHS generated by CHRR Algorithm when $m_v >\vert C_v\vert$ for $SU_v$. (c) An example of of CHS generated by CHRR Algorithm when $m_u <\vert C_u\vert$ for $SU_u$

4.3 CHRR algorithm

Lastly, as previously described, the composite-CH based heterogeneous radio rendezvous (CHRR) method is constructed in Algorithm 4 to achieve full rendezvous diversity. The SUs continue to access channels using their respective created CHSs using Algorithm 4 and accomplish rendezvous regardless of their asynchronous clocks.

An example is discussed in Fig. 4 to make the algorithms easier to follow. Here, the licensed channel set $C=\lbrace 0,1,2,3,4,5,6,7,8 \rbrace$ and two secondary users, say $SU_u$ and $SU_v$ are considered which are equipped with multiple radios of $m_u$ and $m_v$ respectively. The available channel sets of $SU_u$ and $SU_v$ are $C_u=\lbrace 0,1,3,4,5,7,8\rbrace$ and $C_v=\lbrace 3,4,6\rbrace$ respectively. Since $m_v >\vert C_v\vert$, each radio of $SU_v$ acts as a stay radio, and the channels in $C_v$ are assigned to each radio using the lines $6\sim 10$ of Algorithm 4. The generated CHS is shown in Fig. 4b. As $m_u <\vert C_u\vert$ for $SU_u$, the CHS of each radio is generated using the lines $12\sim 15$ of Algorithm 4. In this case, a DDS-based CHS with the period of $2P^{2}+\lfloor \frac{P}{2}\rfloor \times P=297$ timeslots is generated using Algorithm 2 for the first radio, where $P=11$ as $\vert C\vert =9$. For the rest 4 radios Stay-Jump CHS is generated using Algorithm 3 with $m_{us}=2$ and $m_{uj}=2$. Here, the length of each inner period is $\tau _u=\lceil \frac{\vert C_u\vert -m_{us}}{m_{uj}}\rceil = \lceil \frac{7-2}{2}\rceil =\lceil \frac{5}{2}\rceil =3$. The length of one outer period of the Stay-Jump CHS $= \frac{LCM(\vert C_u\vert ,m_{us})}{m_{us}}\times \tau _{u} =\frac{LCM(7,2)}{2}\times 3=21$ timeslots. For the first inner period, $C^S_u=\lbrace 0, 1\rbrace$ and $C^J_u=\lbrace 3, 4,5,7,8\rbrace$. Each stay radio stays on a distinct channel of $C^S_u$ during the inner period using lines $10\sim 13$ of Algorithm 3. Then channels of $\lbrace 3, 4,5,7,8\rbrace$ are assigned to the two jump radios sequentially using lines $16\sim 27$ of Algorithm 3. Similarly, for the next inner period the channels are assigned to the radios of $SU_u$ with $C^S_u=\lbrace 3,4\rbrace$ and $C^J_u=\lbrace 0,1,5,7,8\rbrace$.

5 Performance analysis

In this section, the theoretical analysis of the MTTR with optimal rendezvous diversity is obtained in heterogeneous CRNs, and the upper bound of the TTR is derived for the worst-case scenario. For a better understanding, Lemma 2 is presented first, and the performance is analyzed for the rendezvous between $SU_u$ and $SU_v$ under two scenarios:

(i) $m_{u} \le 2$, $m_{v} \ge 1$, ii) $m_{u} > 2$, $m_{v} > 2$.

For Lemma 2, some notations are used in the structure of two adjacent inner periods of the Stay-Jump CHS and is shown in Fig. 5. To analyze any contiguous $\tau$ time slots in the CHS, two adjacent inner periods are considered in Fig. 5, where l number of time slots fall in the front inner period and $(\tau -l)$ timeslots fall in the subsequent inner period. The channel sets covered by the Stay radios and Jump radios in the front l time slots are denoted as $C_{fS}$ and $C_{fJ}$. Similarly $C_{bS}$ and $C_{bJ}$ are the notations used for the back $(\tau -l)$ timeslots. Here, $\tau$ is the length of one inner period and $l\in [1, \tau -1]$.

Fig. 5

Rendezvous between $SU_u$ and $SU_v$ when $m_{u} > 2$, $m_{v} > 2$

Lemma 2

In the Stay-Jump CHS of an SU, all the available channels of the SU are visited at least once during any contiguous $\tau$ timeslots, where $\tau$ is the length of one inner period.

Proof

According to the Algorithm 3, the total distinct channels visited by the radios of the SU in one inner period are $\vert C \vert$, where C is the available channel set of SU. It is cleared from the Algorithm that $\vert C\vert$ is equivalent to $(S+J(\tau -1)+(\vert C \vert -S-1)$ mod $J +1)$. Hence, all the channels of set C with indexes $\lbrace 0, 1, 2, 3,\ldots , (\vert C \vert -1)\rbrace$ are assigned to stay and jump radios of SU in one inner period and the channel assignment to different radios varies in different inner periods. In the Fig. 5, let i is the index of the channel assigned to the first stay radio of the front inner period. Then according to Algorithm 3, the indexes of the channels in the following sets would be,

$\textit{(1)}$ for set $C_{fS} \Rightarrow i$ to $(i+(S-1))$ mod $\vert C \vert$

$\textit{(2)}$ for set $C_{fJ}\Rightarrow (i+S+J(\tau -l))$ mod $\vert C \vert$ to $(i+S+J(\tau -1))$ mod $\vert C \vert$

$\textit{(3)}$ for set $C_{bS}\Rightarrow (i+S)$ mod $\vert C \vert$ to $(i+(2\,S-1))$ mod $\vert C \vert$

$\textit{(4)}$ for set $C_{bJ}\Rightarrow (i+2S)$ mod $\vert C \vert$ to $(i+S+J(\tau -l)-1)$ mod $\vert C \vert$

For any value of l and i, the channel indexes covered by the set $C_{fS}\cup C_{fJ}\cup C_{bS}\cup C_{bJ}$ will be $\lbrace i, (i+1)$ mod $\vert C \vert ,\ldots ,(i+S+J(\tau -1)+(\vert C \vert -S-1))$ mod $\vert C \vert \rbrace$ which is equivalent to $\lbrace i, (i+1)$ mod $\vert C \vert ,\ldots ,(i+(\vert C \vert -1))$ mod $\vert C \vert \rbrace$ or $\lbrace 0, 1,\ldots ,(\vert C \vert -1)$. Hence, it is proved that during any $\tau$ timeslots in the CHS, all the channels in C are visited at least once.

Fig. 6

All possible CHSs constructed with Algorithm 2 with the DDS S as mentioned in Fig. 4a for available channel set, $\lbrace 0, 1, 2\rbrace$

Theorem 2

The MTTR of the proposed composite algorithm is upper bounded by $2P^{2}+\lfloor \frac{P}{2}\rfloor \times P$ time slots when $m_{u} \le 2$, $m_{v} \ge 1$ with full rendezvous diversity.

Proof

At least one radio of every SU follows DDS-based CHS. The DDS S is constructed in Algorithm 1, and by using $rotate(S, x), \forall x \in [0, n-1]$ in Algorithm 2, n distinct CH sequence can be generated that the SUs can employ. Let two SUs generate their CH sequences using rotate(S, x) and rotate(S, y) respectively, where $x, y \in [0, n-1]$. Let the second SU’s CH sequence be $\textit{d}$ time slots behind the first SU’s CH sequence in an asynchronous environment. The two non-synchronized CH sequences are equivalent to the two synchronized CH sequences generated by rotate(S, x) and $rotate(S, y+ d mod n)$. These two synchronized CH sequences can be simply examined using the example in Fig. 6. According to Algorithm 2, the n number of (n, k)-DSs $rotate(D_{i}, 0), rotate(D_{i}, 1), \ldots , rotate(D_{i}, n-1)$ are assigned to channel i, and in accordance with corollary 4, the n DSs would form a CSQ under $Z_n$, $\forall i\in [0,P-1]$. Now the two CH sequences generated using rotate(S, x) and rotate(S, y) will rendezvous on the channel i at the timeslot t $\in rotate(D_{i},x) \cap rotate(D_{i},y+ dmodn)$, $\forall i\in [0,P-1]$ within one time period of CH sequence.

The proposed rendezvous algorithm ensures rendezvous during the CH period of n timeslots on all N licensed channels. In this paper, n is the total number of elements of DDS S, which is $2P^{2}+\lfloor \frac{P}{2}\rfloor \times P$. As the algorithm has N degree of rendezvous, in the worst-case scenario, when there is just one channel common between the available channel sets of two SUs, rendezvous takes place on that channel during a CHS period. Hence, MCTTR$= n= 2P^{2}+\lfloor \frac{P}{2}\rfloor \times P$.

Theorem 3

For $m_{u} > 2$, $m_{v} > 2$, the MTTR of the proposed composite algorithm with full rendezvous diversity is upper bounded by $\tau _u\times \lceil \frac{C_u}{m_{us}} \rceil +\tau _v$ time slots when $\tau _v < \tau _u$ or $\tau _v = \tau _u$ and $\lceil \frac{C_u}{m_{us}} \rceil \le \lceil \frac{C_v}{m_{vs}}\rceil$.

Proof

The inner period length of $SU_v$ is smaller than $SU_u$ as shown in the Fig. 7. All the available channels of $SU_v$ are visited during any continuous $\tau _v$ time slots as proved in Lemma 2, and a constant channel is accessed by the stay radio of $SU_u$ during one inner period. Hence, rendezvous is guaranteed on the stay channel during the $\tau _v$ timeslots if it is a common channel between the SUs. Similar manner rendezvous occurs on all the commonly available channels during the stay periods of $SU_u$ as the stay channels are changed in different stay periods. The possibilities of rendezvous are shown by the blue-shaded regions in the figure. With $\lceil \frac{C_v}{m_{vs}}\rceil$ numbers of inner periods containing all the distinct channels, TTR for full rendezvous diversity will be $\lceil \frac{C_v}{m_{vs}}\rceil \times \tau _u$. For some of the cases, the starting overlapping timeslots between the SUs are not enough to achieve rendezvous as shown in Fig. 7 with duration $\Delta$. Hence the MTTR is upper bounded by $\tau _u \times \lceil \frac{C_v}{m_{vs}}\rceil + \tau _v$.

For $\tau _v = \tau _u$ if $\lceil \frac{C_u}{m_{us}} \rceil \le \lceil \frac{C_v}{m_{vs}}\rceil$ all the available channels of $SU_v$ will be accessed by the stay radios within $\tau _v \times \lceil \frac{C_v}{m_{vs}}\rceil$ time slots. For $SU_u$, all the available channels are visited during any $\tau _u$ time slots. Hence, the upper bound of MTTR to achieve rendezvous on all commonly available channels will be $\tau _u \times \lceil \frac{C_v}{m_{vs}}\rceil + \tau _v$.

Fig. 7

Rendezvous between $SU_u$ and $SU_v$ when $m_{u} > 2$, $m_{v} > 2$

6 Performance evaluation and simulation results

In this section, the performance of the proposed CHRR algorithm is evaluated. Extensive simulations are conducted using Matlab, and the correctness of the theoretical analysis is verified with the results. A CRN with N licensed channels denoted with channel set C is taken into account. In the network, the SU pair trying to rendezvous are denoted as $SU_u$ and $SU_v$ and they are equipped with $m_u$ and $m_v$ radios, respectively. For the heterogeneous CRN, different possibilities of $m_u$ and $m_v$ pair are considered for the simulations and the SUs may have different available channel sets denoted as $C_u$ and $C_v$ respectively, where $C_u$, $C_v \subseteq C$. The SUs achieve rendezvous on channels $c \in C_u\cap C_v$ by using their respective CHSs. Again, all the simulations are conducted in an asynchronous environment by considering random time-slots drift between the CHSs of the SUs. Thus, for a heterogeneous and asynchronous CRN, the rendezvous performance of the proposed CHRR scheme is observed under a different number of radios. In the multi radio rendezvous case, the effect of allocated jump radios and stay radios on the TTR value is evaluated. Moreover, the performance of CHRR is compared with other state-of-the-art multi-radio CH algorithms in terms of ATTR and MTTR with full rendezvous diversity.

6.1 Performance under heterogeneous numbers of radios

The performance of CHRR is evaluated for different combinations of radios $(m_u, m_v)$. The simulations are conducted by varying the total licensed channel N from 10 to 50. The number of available channels for each SU is set as 0.7N and while considering the asymmetric model, the number of common channels between the SUs is set at 0.5N. The simulated ATTR and MTTR values of the CHRR are shown in Fig. 8a,b, respectively for the radio combinations of (1, 1), (1, 3), (1, 5), (2, 2), (2, 3), (3, 3). For the multiple radios case, the number of stay radios of the $SU_u$ and $SU_v$ is set as $m_{us}=\lfloor \frac{m_u}{2}\rfloor$ and $m_{vs}=\lfloor \frac{m_v}{2}\rfloor$, respectively. The correctness of the theoretical analysis is verified with the simulated results, as the values shown in the graphs are less than the derived upper bound of the MTTR in the previous section. The ATTR and MTTR values increase as the value of N increases. The reason is that ATTR and MTTR are directly proportional to the length of one period of the CHS, and the length of the CHS of any SU is directly proportional to the number of licensed channels and the number of available channels to that SU.

Likewise, for a given N, the ATTR and MTTR for the SU pair are relatively shorter when at least one is equipped with a single radio than when both are equipped with a single radio. If we consider three distinct cases, the firstcase, where both SUs are equipped with single radios, the rendezvous is performed with the DDS-based CHSs of both users, and the TTR values are large since the CHS length is $O(N^2)$. In the second case, when one SU has a single radio and the other has multiple radios, guaranteed rendezvous happens owing to the DDS-based CHSs of both SUs. However, there is a possibility of a rendezvous between the first SU’s DDS-based CHS and the other SU’s stay radios. In the third case, if both SUs are equipped with multiple radios, the stay radios of one SU have a high chance of colliding with the radios of the other SU. Apart from these, both SUs also achieved rendezvous with their first radio using DDS-based CHSs. Furthermore, as the value of $m_u$ and $m_v$ increases in the third case, the period length of stay-jump CHSs decreases significantly, shortening the ATTR and MTTR. The correctness of the rendezvous performance for these three cases is reflected in Fig. 8a,b.

Fig. 8

Performance comparison for different numbers of radios

6.2 Performance with different allocation of radios

The influence of varied radio allocation on the performance of the CHRR is investigated in this subsection. The notation $(m_{us}, m_{vs})$ denotes the number of stay radios for $SU_u$ and $SU_v$, and the number of jump radios may be determined using the provided notation. As a result, the notation $(m_{us}, m_{vs})$ might be interpreted as different radio allocations. In the simulation, the total number of radios in $SU_u$ and $SU_v$ is set to 5 and 5, respectively. We have six distinct allocation choices here, marked as (1, 1), (1, 2), (1, 3), (2, 2), (2, 3), and (3, 3).

The performance of all the six types of allocations is compared in Fig. 9a, b for the different numbers of licensed channels varying from 10 to 50. It is observed from the graphs that the ATTR and MTTR are comparatively higher when one of the SUs is equipped with the maximum possible stay radios or the minimum possible jump radios. Here, the radio allocations (3, 3), (2, 3) and (1, 3) are showing higher values, while the allocations (1, 1), (1, 2), and (2, 2) are showing shorter TTR values. The reason is that the increase in jump radios leads to a decrease in the length of the CHS period, and MTTR is directly related to the period length. For a symmetrical model, the available channels set for all SUs are the same. Hence, the (1, 1) radio allocation can be used to achieve minimum TTR. However, the SUs have a different set of available channels in an asymmetric model. Though, the (3, 3) and (1, 1) radio allocations in Fig. 9a show higher and shorter ATTR, respectively, the same allocations may not have the maximum and minimum MTTR respectively, as shown in Fig. 9b.

Fig. 9

Performance comparison with different allocations of radios

6.3 Comparison with other algorithms

In this section, the proposed CHRR algorithm’s performance is compared to that of other current blind rendezvous methods. When one of the SU pairs is equipped with a single radio, the heterogeneous radio rendezvous techniques, the MEHRR algorithm [23], and the HRR algorithm [22] are evaluated for comparison. However, when both the SUs are equipped with multiple radios, in addition to [22, 23], the RPS algorithm [16] and the AMRR algorithm [21] are compared with the proposed algorithm. An asymmetric model is considered, where the number of available channels of each SU and the number of commonly available channels between any two SUs are set at 0.7N and 0.5N, respectively. The simulation results are obtained for various N values ranging from 10 to 50.

Figure 10a–f show the comparisons of MTTR with full rendezvous diversity for the $(m_u,m_v)$ combinations $(1, 1), (1, 3), (1, 5)$. When both SUs have a single radio, the MTTR of HRR and MEHRR are much higher than CHRR, as illustrated in Fig. 10a). The reason for this is that the CHSs of HRR and MEHRR for a single radio rendezvous have a longer period duration than CHRR, and the length of the CHS period grows significantly for HRR and MEHRR as N increases. Under the worst-case scenario of an asymmetric model, the upper bound of the MTTR is related to the CHS period, as shown in Table 1. By adopting DDS-based CHS for single radio rendezvous, the MTTR of CHRR is considerably lowered. In Fig. 10b, c, it is seen that when one of the SUs has multiple radios, the MTTR values of the algorithms are decreased, and the values decrease further as the number of multiple radios increases. Despite the fact that the MTTR values of HRR and MEHRR for the radio combinations (1, 3) and (1, 5) have reduced dramatically when compared to the combination (1, 1), they are still greater than CHRR, as seen in the graphs.

The comparisons of MTTR with complete rendezvous diversity of several multiradio rendezvous algorithms for the radio combinations (2, 2), (2, 3), (3, 3) are shown in Fig. 10d, f. In all graphs, the RPS scheme has a greater MTTR than the other schemes. The reason for this is that in PRS, CHSs are generated based on all licensed channels, but in the other four schemes, CHSs are generated based on the SUs’ available channel sets. As a result, the period length of CHS is substantially longer than that of PRS, resulting in a high MTTR. The AMRR scheme performs better with a shorter MTTR. Nevertheless, both the RPS and AMRR algorithms are inapplicable to heterogeneous CRNs where each SU may have a single radio. The figures show that MTTR grows as N increases, since the inner period length of the CHS increases as well. The inner period length of CHSs of the SUs is longer in the case of the HRR algorithm than in the MEHRR and CHRR for a particular radio combination, allocation, and available channel sets. As a result, the MTTR for HRR is greater. MEHRR has a shorter MTTR for multiradio rendezvous than the proposed CHRR scheme. The reason for this is that the greater the number of radios used to generate CHS for an SU, the shorter the inner period of the CHS. In the MEHRR scheme, all SU radios participate in the creation of stay-jump based CHS, whereas in the CHRR scheme, one SU radio follows DDS-based CHS and the remaining radios follow stay-jump based CHS. As a result, the inner period of the stay-jump based CHS is somewhat shorter in the case of MEHRR than in the case of CHRR. But, if the number of radios increases, the difference will become insignificant. Due to the small MTTR values as seen in the graphs of Fig. 10, the overall rendezvous latency for CHRR would be significantly reduced in the situation of heterogeneous radio. This improves the scheme’s suitability for device-to-device communication and Internet of Things applications by maintaining the time and memory of the tiny devices, which are constrained by their limited processing power and memory.

Fig. 10

MTTR comparison of different rendezvous algorithms

Fig. 11

ATTR comparison of different rendezvous algorithms

The ATTR of several rendezvous methods is evaluated in Fig. 11 for heterogeneous radio combinations $(1, 1), (1, 3), (2, 5), (4,4)$. Because the CHS period duration is substantially longer for the (1, 1) radio combination, the ATTR values of the schemes are larger for SUs with a single radio than SUs with multiple radios. In Fig. 11a, CHRR performs better because to its shorter CHS time. The ATTR values of the schemes are more or less near to each other in Fig. 11b–d. Despite the ATTR of CHRR is greater for situations owing to the asymmetric model, as shown in the graphs, the difference is minimal since the ATTR values for multiradio rendezvous scenarios are comparatively small.

7 Conclusion

In this paper, we have proposed a blind rendezvous scheme for heterogeneous CRNs, where the SUs may own either a single or multiple radios. The proposed CHRR algorithm, in contrast to other multiradio rendezvous schemes, exhibits backward compatibility with the single radio rendezvous method. In this scheme, the radios of an SU were assigned a combination of DDS-based CHS and Stay-jump-based CHS for this objective. When compared to the HRR and MEHRR algorithms, the CHRR algorithm resulted in a considerable reduction in MTTR with complete rendezvous diversity for the case, where at least one SU of the SU pair was equipped with a single radio. Although the MTTR for the CHRR was greater than that of the HRR and MEHRR in the context of multiradio rendezvous, the difference was not significant when compared to the difference observed in rendezvous involving SU with only one radio The CHRR algorithm has been examined theoretically for various possible combinations of radios within a pair of SU, and its performance was established by comprehensive simulations.

Appendix: Supporting Lemma and Theorem for DDS

Lemma 1

For a pair of numbers ($a_{1}, a_{2}$) under $Z_{n}$, with a difference value d such that $(a_{1}- a_{2})$mod $n= d$ and if d mod k $=d'$, there also exits a difference value $(n-d)$ for the same ($a_{1}, a_{2}$) pair, and $(n-d)$ mod k $=(k-d')$.

Proof

For any number pair, ($a_{1}, a_{2}$) under $Z_{n}$ if $(a_{1} - a_{2})$mod $n= d$, then ($a_{2} - a_{1}$) mod n will be $(-d)$ mod n which is equal to $(n-d)$. If d mod k $=d'$ then for the other difference value $(n-d)$, we can prove that

$(n-d)$mod $k= (Pk$ mod $k- d$ mod k)mod k

= $(0-d')$mod k

= $(k-d')$.

Theorem 1

In Algorithm 1, the constructed set $S= \lbrace$ $D_{0}$, $D_{1}$, $D_{2}, \ldots , D_{P-1}$ $\rbrace$ is a DDS.

Proof

The set S must satisfy the two properties stated in Definition 3. For this, we need to demonstrate that each set in S is a difference set and all are disjoint from one another.

Triangular numbers and the modular idea are used to create a set that satisfies the DS properties using the numbers picked from $Z_n$. The required range of difference values, $d\in [1, n-1]$ for each set, as stated in Definition 1 can be reduced to a narrower range of $d' \in [1, k-1]$ using the modular approach $d'= d$ mod k. Now, it has to be verified that $\forall d'\in [0, k-1]$, there exists a pair of numbers ($a_{i}, a_{j}$) in each set of S such that $(a_{i}$-$a_{j})$ mod n = $d'+ rk$, $\forall r\in [0, P-1]$.

1. For $k= 2P+\lfloor \frac{P}{2}\rfloor$:

Case 1.1 $d'=0$. All $D_{i}$ has a number pair ($a_{ij_{1}}, a_{ij_{2}}$) such that $a_{ij_{1}}, a_{ij_{2}} \in D_{Xi}$, 0$\le j_{1}, j_{2} \le P-1$ and the difference d = $(a_{ij_{1}}- a_{ij_{2}})$ mod n

$d =((kj_{1}+ i)- (kj_{2}+ i))$mod Pk

= $(k(j_{1}-j_{2})+ 0)$ mod Pk

= $(k(j_{1}-j_{2})+ 0)$, for 0$\le j_{1}- j_{2} \le P-1$

= $kr+ d'$

Case 1.2 $1 \le d' \le \lfloor \frac{P}{2}\rfloor$ and $2P\le d' \le 2P+ \lfloor \frac{P}{2}\rfloor -1$. All $D_{i}$ has a number pair ($b_{ij_{1}}, b_{ij_{2}}$) such that $b_{ij_{1}}, b_{ij_{2}}\in D_{Yi}$ and $0 \le j_{1}, j_{2} \le k-P-1$ and the difference of the numbers $b_{ij_{1}}$ and $b_{ij_{2}}$ is $d= b_{ij_{1}} - b_{ij_{2}}$ mod n

= $(k(T_{j_{1}}+i)+P +{j_{1}})- (k(T_{j_{2}}+i)+P +j_{2}$))mod n

= $(k(T_{j_{1}} -T_{j_{2}} )+ (j_{1} -j_{2})mod Pk$

= $(k(T_{j_{1}} -T_{j_{2}} )$mod $Pk+ (j_{1} -j_{2})mod Pk )mod Pk$

= $(k((T_{j_{1}} -T_{j_{2}} )$mod $P)+ (j_{1} -j_{2}))mod Pk$

= ($kr+ d'$)mod Pk

Here $r= (T_{j_{1}}- T_{j_{2}})$ mod P

= $(\frac{j_{1}(j_{1}+1)}{2}$- $\frac{(j_{1}-d')(j_{1}-d'+1)}{2})$mod P

= (${j_{1}}d'- \frac{d'^{2}-d'}{2}$)mod P

In this case, $\frac{d'^{2}-d'}{2}$ is a whole number and P is a prime number making, $d'$ and P as co-prime. Hence, r will attain all the values from 0 to $P-1$ for all P continuous values of ${j_{1}}$. For a given $d'$, if 0 $\le j_{2}\le P-1 \Rightarrow d' \le j_{1}\le (P-1)+d'$ and since the maximum value of ${j_{1}}$ is $P+\lfloor \frac{P}{2}\rfloor -1$, therefore, the range of $d'$ can be derived as $1 \le d' \le \lfloor \frac{P}{2}\rfloor$. Moreover, the range of $d'$ can be expressed as $2P\le d' \le 2P+ \lfloor \frac{P}{2}\rfloor -1$ using Lemma 1.

Case 1.3 $\lfloor \frac{P}{2}\rfloor < d'\le 2P-1$. Every $D_{i}$ has a pair of numbers, $(a_{ij_{1}}$, $b_{ij_{2}}$) such that $a_{ij_{1}}\in D_{Xi}, b_{ij_{2}} \in D_{Yi}$ and $0 \le j_{1} \le P-1, 0 \le j_{2} \le k-P-1$. The difference is given by $d= (b_{ij_{2}} -a_{ij_{1}})$mod n

= $((k(T_{j_{2}}+i)+ P + j_{2})-k(j_{1}+i))$ mod n

= $(k(T_{j_{2}}+i-j_{1})+(P+j_{2}-i)))$ mod Pk

= $(k((T_{j_{2}}+i-j_{1})mod P)+(P+j_{2}-i))$ mod Pk

= ($kr+ d'$)mod Pk

Here, $r= (T_{j_{2}}+ i-j_{1})$ mod P = $(\frac{j_{2}(j_{2}+1)}{2}+ i-j_{1})$ mod P and $d'= (P+j_{2}-i$).

For a given i and $j_{2}$, the expression $(\frac{j_{2}(j_{2}+1)}{2}+ i)$ will be a constant and a whole number. Consequently, for P continuous values of ${j_{1}}$, i.e, $0 \le j_{1} \le P-1$, r covers all values in $[0, P-1]$. For a given range of ${j_{2}}$ in set $D_{Yi}$, the range of $d'$ is derived for different values of i. If $0 \le i\le \lfloor \frac{P}{2}\rfloor$ for a given $d'$, then $d'-P \le j_{2} \le d'-P+\lfloor \frac{P}{2}\rfloor$, which denotes $P \le d' \le 2P-1$. Further, the range of $d'$ can be expressed as $\lfloor \frac{P}{2}\rfloor +1 \le d'\le P+ \lfloor \frac{P}{2}\rfloor$ using Lemma 1. Similarly, for a given $d'$ if $\lfloor \frac{P}{2}\rfloor \le i\le P-1$ then $d'-\lfloor \frac{P}{2}\rfloor -1 \le j_{2}\le d'-1$, which implies $\lfloor \frac{P}{2}\rfloor +1 \le d'\le P+ \lfloor \frac{P}{2}\rfloor$. The range can also be expressed as $P\le d'\le 2P-1$, using Lemma 1. The range of $d'$ for all $D_{i}$ is therefore, $\lfloor \frac{P}{2}\rfloor < d'\le 2P-1$.

Hence, all $D_{i}$ are DS as each has a pair of numbers with $d = d'+ rk$, $\forall d'\in [0,k-1]$ and $\forall r\in [0, P-1]$ with the three cases mentioned above.

Algorithm 1 states that $D_i= D_{Xi} \cup D_{Yi}$ and $D_j= D_{Xj} \cup D_{Yj}$ and with this the next three cases will be examined to demonstrate that $D_i\cap D_j=\emptyset$.

Case 1 Subsets X and Y are used to choose the elements of the subsets $D_{Xi}$ and $D_{Yj}$, respectively (Fig. 2) and $X \cap Y =\emptyset$. Hence, $D_{Xi}\cap D_{Yj}=\emptyset$ and $D_{Xj}\cap D_{Yi}=\emptyset$.

Case 2 $D_{Xi}=(kp_1+i)$ and $D_{Xj}=(kp_2+j)$, where $p_1,p_2\in [0,P-1]$. So any element in $D_{Xi}$ and $D_{Xj}$ are the ith and jth element of $U_{p_1}$ and $U_{p_2}$ respectively (Fig. 2). Since $i\ne j$, therefore, $D_{Xi}\cap D_{Xj}=\emptyset$.

Case 3 $D_{Yi}=(k(T_{q_1}+ i)+ P+ q_1$) and in $D_{Yj}=(k(T_{q_2}+ j)+ P+ q_2)$, where $q_1,q_2\in [0,k-P-1]$. The elements in $D_{Yi}$ and $D_{Yj}$ are therefore $(q_1+P)$th and $(q_2+P)$th elements, respectively of the set $U_{T_{q_1}+ i}$ and $U_{T_{q_2}+ j}$. To prove via contraction, assuming that there is a common element in $D_{Yi}$ and $D_{Yj}$, therefore, $(q_1+P)$th number of $U_{T_{q_1}+ i}$ is equals to $(q_2+P)$th element of $U_{T_{q_2}+ j}$ and since all U are disjoint, which implies ${T_{q_1}+ i} = {T_{q_2}+ j}$ and $q_1=q_2$. Hence, the contraction $i=j$ is formed. It concludes, $D_{Xi}\cap D_{Yj}=\emptyset$ for $i\ne j$.

As a result, the three scenarios above demonstrate that all sets in S are disjoint to one another.