1 Introduction

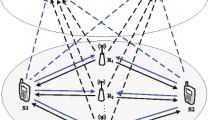
Cognitive radio (CR) has been widely recognized as a powerful means to efficiently utilize the scarce and precious frequency radio resources [1, 2]. The principle of the CR technology is to allow the secondary users (SUs) to share the spectrum bands licensed to the primary users (PUs). In general, the operation models of the CR networks can be classified into opportunistic spectrum access (OSA) or spectrum sharing (SS) models [2]. In the OSA model, the SUs can opportunistically access the spectrum if they can find the spectrum holes or white spaces in which the PUs are inactive. In contrast, in the SS model, the SUs can transmit concurrently with the PUs. However, the SUs are provided a lower priority in accessing the spectrum than the PUs. Thus, the SUs are only allowed to transmit if they do not harmfully affect the performance of the PUs [1, 3]. Due to simultaneous transmissions of the PUs and SUs, the SS model can utilize the spectrum more efficiently than the OSA provided that interference is properly managed. Thus, the design problems of the SU transmission strategies to cope with interference and to improve the secondary network performance without any degradation in the PU transmission performance are crucial in CR network designs [1, 3, 4]. The focus of the present paper is on the underlay multiple-input multiple-output (MIMO) CR networks in which the users exploit spatial dimensions for interference management.

Research works have been extensively conducted to improve the performance of the CR networks; see, for example, [1, 4,5,6,7,8,9] and references therein. Two performance metrics which are widely used in the CR designs are the sum-rate maximization (SRM) and minimum mean square error (MMSE) [4,5,6,7, 9]. The sum-rate functions are in general non-concave in the design variables of the precoding and decoding matrices and, thus, finding the optimal solutions to the sum-rate maximization problems is difficult [4,5,6]. In [4], the weighted sum-rate maximization of the SUs under the per-user transmit power constraints and CR interference constraints was considered in which the geometric programming and network duality methods were used to develop the alternative centralized algorithm for resource allocation. In addition, the semi-distributed algorithm was proposed by exploiting the primal decomposition technique. Similarly, the convex relaxation technique and the uplink-downlink duality were introduced in [5] to maximize the weighted sum-rate of the multiple-input single-output (MISO) CR network. Alternatively, to overcome the difficulty associated with the non-concavity of the sum-rate function, zero-forcing techniques were used to cancel interference between the SUs [6]. On the other hand, the MMSE-based methods for the transceiver designs in CR networks were introduced in [7, 8]. More specifically, non-iterative adaptive MMSE-block diagonalization techniques were proposed in [7] for multiuser MIMO CR networks. In [8], the alternating optimization techniques with reduced complexity were used since the MMSE design problems are not jointly convex in the design variables. Recently, interference alignment (IA) has been emerged as an effective approach to manage interference. It is enable not only to cancel interference but also to achieve the maximum degrees of freedom (DoFs) [10]. The key principle of IA is that the transmitters are cooperative with each other to align their transmitted signals into a certain interference subspace at each unintended receiver such that the desired signals can be received at the interference-free subspace. IA aims at restricting the dimension of the interference subspace while maximizing the dimension of the desired signal subspace at each receiver. The conventional IA has been widely applied into interference channels [11,12,13]. Recently, the studies of IA in CR networks have been a very active research area [1, 3, 10, 14]. In CR networks, to guarantee no harmful interference from the SUs to the PUs, the interference from the SUs should be aligned into the subspace which is orthogonal to the desired signal subspace at each primary receiver (PRx).

In general, the aforementioned designs aim mainly at optimizing the spectral efficiency by seeking the transceivers to maximize the sum-rate or the DoFs. However, the spectral efficiency schemes tend to use the maximum transmit power which may result in energy inefficiency. Recently, due to increasing global carbon dioxide (\(\text {CO}_2\)) emissions and growing energy costs, green wireless communication systems with energy efficiency have drawn increasing attention [15,16,17,18,19]. In this paper, we consider a MIMO CR network in which multiple SUs share the same frequency spectrum with multiple PUs. Different from the conventional approaches, the present paper focuses on designing the transmission strategies of the users to maximize the energy efficiency rather than the spectral efficiency. It should be emphasized that the sum-rate maximization in CR networks through IA is mathematically challenging to solve due to the nonconvexity of the design problem [10]. Thus, the design problems of the EE maximization in this paper will be more difficult since the objective functions associated with the EE are highly nonlinear and non-concave fractional functions.

In CR networks, the PUs have a higher priority to access the radio resource while the SU transmissions are required not to degrade the performance of the PUs [20]. Thus, the PUs focus on dealing with the mutual interference between the users in the primary network while the SUs handle not only interference between the users in their own network but also interference from and to the PUs. Thus, interference mitigation for the secondary network is more challenging than that in the primary network. In our proposed method, full IA is applied to the primary network to mitigate interference between the PUs and, then, the EE maximization problem for the primary network can be reformulated into a tractable fractional programming problem which can be solved by invoking the Dinkelbach method [21]. In contrast, it may be impossible to obtain perfect IA in the secondary network since the secondary receivers (SRxs) suffer from the uncoordinated interference caused by the primary transmitters (PTxs). Thus, in this paper, we propose a partial IA scheme for the secondary network in which the transceiver designs of the SUs are designed to optimize the EE while enforcing the signals transmitted from the secondary transmitters (STxs) to be aligned into the unused dimensions of the PRxs. Since the EE maximization of the secondary network is an intractable nonlinear fractional programming problem. Thus, to reformulate its objective function as a concave-convex fractional function, we propose to reformulate the numerator of the objective function as a difference of two concave functions and, then, one of them is linearized. Then, we develop an iterative algorithm by using the difference of convex functions (DC) programming combined with the Dinkelbach method. Moreover, to obtain more insights into the structures of the transceivers, we also derive the closed-form expressions for the transceivers in each iteration. We show that the convergence of the proposed iterative algorithms are guaranteed. Simulation results are provided to demonstrate the effectiveness of the proposed method in terms of the achievable EE when compared to the other methods which maximize the spectral efficiency.

The rest of the paper is organized as follows. In Sect. 2, the system model of the CR network is introduced and the transceiver design problems for the EE maximization are formulated. The transceiver design algorithms for maximizing the EE in the primary and secondary networks are proposed in Sect. 3. Section 4 provides simulation results to evaluate the effectiveness of the proposed algorithms. Finally, concluding remarks are drawn in Sect. 5.

Notations: Throughout this paper, boldface lowercase and uppercase letters denote vectors and matrices, respectively. \((\cdot )^H\) denotes the conjugate transpose operation while \(\mathbb {E}(.)\) is the statistical expectation. \(||\pmb {x}||\) and \(||\pmb {X}||_F\) denote Euclidean norm of vector \(\pmb {x}\) and the Frobenius norm of matrix \(\pmb {X}\), respectively. We define \([x]^+=\max \{0,x\}\). \([\pmb {X}]_k^\ell \) is a matrix whose columns are taken from column k to column \(\ell \) of matrix \(\pmb {X}\). \(\pmb {I}_n\) and \(\pmb {0}_{n \times m}\) represent respectively the \(n \times n\) identity and \(n \times m \) zero matrices. \(\langle \pmb {X} \rangle \), \(|\pmb {X}|\), \(\mathrm {rank}(\pmb {X})\), and \({\mathcal {N}}(\pmb {X})\) denote the trace, determinant, rank and null space of matrix \(\pmb {X}\). \(\pmb {X} \succeq 0\) means that \(\pmb {X}\) is a Hermitian positive semidefinite matrix. \({\mathcal {X}}^\bot \) denotes an orthogonal subspace of the subspace \({\mathcal {X}}\). \(\pmb {x}\sim {{\mathcal {C}}}{{\mathcal {N}}}(\bar{\pmb {x}},\pmb {R}_{\pmb {x}})\) represents a complex Gaussian random vector \(\pmb {x}\) with mean \(\bar{\pmb {x}}\) and covariance \(\pmb {R}_{\pmb {x}}\).

2 System model and problem statement

We consider a CR network where \(K_s\) SUs share the same spectrum with \(K_p\) PUs. This model can be considered as a K-user MIMO interference channel with \(K=K_s+K_p\). The set of PUs, denoted as \(\mathcal {K}_p=\{1,\ldots ,K_p\}\), forms a primary network while the set of SUs, \(\mathcal {K}_s=\{K_p+1,\ldots ,K_p+K_s\}\), forms a secondary network. Transmitter (Tx) k, where \(k\in \mathcal {K}=\{1,\ldots ,K\}\), is equipped with \(M_k\) antennas while receiver (Rx) k uses \(N_k\) antennas. Each transmitter sends its signal to an intended receiver and causes interference to the unintended users. Let \(\pmb {x}_k\in \mathbb {C}^{d_k\times 1}\) be the signal transmitted from Tx k to the intended Rx k, in which \(d_k\) is the number of data streams. The transmitted signal vectors \(\pmb {x}_k\) are assumed to be independent and identically distributed (i.i.d.) so that \(\mathbb {E}\{\pmb {x}_k\pmb {x}_k^H\}=\pmb {I}\) and \(\mathbb {E}\{\pmb {x}_\ell \pmb {x}_k^H\}=\pmb {0}, \forall \ell \ne k\). Assume that \(\pmb {H}_{k,\ell }\in \mathbb {C}^{N_k\times M_\ell }\) is the flat fading channel matrix from Tx \(\ell \) to Rx k. Then, the received signal vector at Rx k can be represented as

$$\begin{aligned} \pmb {y}_k = \underbrace{\pmb {W}_k^H\pmb {H}_{k,k}\pmb {F}_{k}\pmb {x}_k}_{\text {desired signal}}+\underbrace{\sum _{\ell \in \mathcal {K},\ell \ne k}\pmb {W}_k^H\pmb {H}_{k,\ell }\pmb {F}_\ell \pmb {x}_\ell }_{\text {interference among users}} + \underbrace{\pmb {W}_k^H\pmb {n}_k}_{\text {noise}} \end{aligned}$$
(1)

where \(\pmb {F}_k \in \mathbb {C}^{M_k \times d_k}\) is a precoding matrix (PM) applied to \(\pmb {x}_k\) before transmission; \(\pmb {n}_k\in \mathbb {C}^{N_k\times 1}\) is the complex additive white Gaussian noise (AWGN) vector at Rx k with zero mean and covariance matrix \(\sigma _k^2\pmb {I}\), i.e., \(\pmb {n}_k\sim \mathcal {CN}(\pmb {0},\sigma _k^2\pmb {I})\); and \(\pmb {W}_k\) is the decoding matrix (DM) at Rx k. Then, the achievable rate, \(\mathcal {R}_k(\{\pmb {F}_k\}, \{\pmb {W}_k\})\), of user k is given by [1, 10]

$$\begin{aligned} {\mathcal {R}}_k(\{\pmb {F}_k\}, \{\pmb {W}_k\})&= \log _2\left| \pmb {I}_{d_k} + \pmb {W}_k^H\pmb {H}_{k,k}\pmb {F}_k\pmb {F}_k^H\pmb {H}_{k,k}^H\pmb {W}_k\pmb {R}_{k}^{-1} \right| \end{aligned}$$
(2)

where \( \pmb {R}_{k} = \pmb {W}_k^H(\sum _{\ell \in \mathcal {K},\ell \ne k} \pmb {H}_{k,\ell }\pmb {F}_\ell \pmb {F}_\ell ^H\pmb {H}_{k,\ell }^H + \sigma _k^2\pmb {I}_{d_k})\pmb {W}_k\) is the covariance matrix of interference plus noise at Rx k.

The EEs of the primary and secondary networks are respectively defined as [17, 22, 23]

$$\begin{aligned} \eta _{\text {PEE}}(\{\pmb {F}_k,\pmb {W}_k\}_{k\in \mathcal {K}_p})= & {} \frac{ \sum _{k\in \mathcal {K}_p}\mathcal {R}_k(\{\pmb {F}_k\}, \{\pmb {W}_k\})}{\sum _{k\in \mathcal {K}_p} \left( \zeta _k\langle \pmb {F}_k\pmb {F}_k^H\rangle + P_{c_k}\right) } \end{aligned}$$
(3)
$$\begin{aligned} \eta _{\text {SEE}}(\{\pmb {F}_k,\pmb {W}_k\}_{k\in \mathcal {K}_s})= & {} \frac{ \sum _{k\in \mathcal {K}_s}\mathcal {R}_k(\{\pmb {F}_k\}, \{\pmb {W}_k\})}{\sum _{k\in \mathcal {K}_s} \left( \zeta _k\langle \pmb {F}_k\pmb {F}_k^H\rangle + P_{c_k}\right) } \end{aligned}$$
(4)

where \(P_{c_k}\) and \(1/\zeta _k\) are circuit power and the power amplifier efficiency parameters at Tx k. For simplicity of presentation, we assume \(\zeta _k=1\) and \(P_{c_k}=P_c\) [17, 23].

In this paper, we assume that the PUs have the perfect knowledge of the channels between the PUs in the primary network while the global knowledge of channel state information (CSI) is available at the SUs. As discussed in [24], such CSI can be obtained by exploiting the channel reciprocity, feedback channels, and learning mechanisms. Alternatively, CSI can be acquired by employing a fusion center [3]. Such an assumption on perfect CSI is also widely adopted in the literature; see, for example [24,25,26] and references therein. In any case of imperfect CSI, the results in this paper can be treated as benchmarks. Given that perfect CSI is available at the users, the problem of interest is to jointly design the PMs and DMs which adapt with the channel conditions to maximize the EE of the primary and secondary networks. The EE maximization problem for the primary network can be mathematically posed as

$$\begin{aligned} \underset{\{\pmb {F}_k,\pmb {W}_k\}_{k\in \mathcal {K}_p}}{\max }&\eta _{\text {PEE}} \end{aligned}$$
(5a)
$$\begin{aligned} \text {s.t.}\,\,\,\,\,\,\,\,\,\,\,\,&\langle \pmb {F}_k\pmb {F}_k^H\rangle \le P_{k},\forall k\in \mathcal {K}_p \end{aligned}$$
(5b)

where \(P_{k}\) is the maximum transmit power at Tx k and condition (5b) imposes the power constraint on the Txs.

In CR networks, the SU transmissions must preserve the performance of the PUs by adapting their transmission strategies to guarantee no harmful interference to the PUs. Thus, the EE maximization for the secondary network can be expressed as

$$\begin{aligned} \underset{\{\pmb {F}_k,\pmb {W}_k\}_{k\in \mathcal {K}_s}}{\max }&\eta _{\text {SEE}} \end{aligned}$$
(6a)
$$\begin{aligned} \text {s.t.}\,\,\,\,\,\,\,\,\,\,\,\,&W_{i}^H\pmb {H}_{i,k}\pmb {F}_{k}= \pmb {0},\forall k\in \mathcal {K}_s, i\in \mathcal {K}_p \end{aligned}$$
(6b)
$$\begin{aligned}&\langle \pmb {F}_k\pmb {F}_k^H\rangle \le P_{k},\forall k\in \mathcal {K}_s. \end{aligned}$$
(6c)

Here, condition (6b) ensures that the interference from the STxs must not be pilled into the PRxs. Condition (6c) represents the per-user transmit power constraints.

It should be noted that the coupling of PMs and DMs in the interference terms makes the rate function (2) highly nonlinear and nonconcave. Thus, the objective functions (5a) and (6a) are fractional functions with nonconcave numerators. Consequently, the optimization problems (5) and (6) are computationally intractable to solve directly.

3 Proposed algorithms for energy efficiency maximization

In this section, we will propose the structures of the PMs and DMs to mitigate interference and reformulate the optimization problems (5) and (6) into amenable ones. Then, we develop effective iterative algorithms to find the optimum solutions to (5) and (6).

3.1 Energy efficiency maximization for the primary network

In the CR network, the PUs have higher priority to access the spectrum and, thus, they are oblivious to the presence of the SUs. They selfishly design their transmission strategies to maximize their EE without awareness of the SU performance. To overcome the mathematical difficulties in solving problem (5) and make the optimization problem more tractable, IA is adopted to cancel the PU interference by aligning the interference signals into a reduced dimensional subspace at each PRx. To this end, the PMs of the PTxs and the DMs of the PRxs are respectively designed to have the structures as

(7)
(8)

where matrices \(\pmb {C}_k\in \mathbb {C}^{M_k\times d_k}\) and \(\pmb {G}_k\in \mathbb {C}^{N_k\times d_k}\) are designed to confine the interference signals into an interference subspace at each PRx while matrices \(\pmb {B}_k\in \mathbb {C}^{d_k\times d_k}, \pmb {A}_k\in \mathbb {C}^{d_k\times d_k}\) and \(\pmb {D}_k\in \mathbb {C}^{d_k\times d_k}\) are then designed for the EE maximization of the primary network.

Given the zero-interference from the SUs to the PUs in (6b), interference at the PRxs in (1) can be perfectly eliminated if the following IA conditions are satisfied

$$\begin{aligned}&\pmb {G}_k^H\pmb {H}_{k,\ell }\pmb {C}_\ell = \pmb {0}, \forall \ell \in \mathcal {K}_p\setminus \{k\}, k\in \mathcal {K}_p. \end{aligned}$$
(9)

To remove all interferences at PRx k, the interference signals \(\pmb {H}_{k,\ell }\pmb {C}_\ell ,\forall \ell \in \mathcal {K}_p\setminus \{k\},\) are aligned into the interference receiving subspace \({\mathcal {G}}_k^{\perp }\) which is spanned by the orthonormal basis matrix . To fulfill conditions (9), matrices can be obtained by using an iterative IA algorithm in [27]. Particularly, for fixed , \(\pmb {C}_\ell \) can be calculated by

(10)

where \(\zeta _{\min }^d\left\{ \pmb {X}\right\} \) is a matrix whose columns are the d eigenvectors corresponding to the d smallest eigenvalues of \(\pmb {X}\). Then, for given \(\{\pmb {C}_\ell \}_{\ell \in \mathcal {K}_p}\), can be computed by

(11)

where \(\zeta _{\max }^{N_k-d_k}\left\{ \pmb {X}\right\} \) is a matrix which consists of the \((N_k-d_k)\) dominant eigenvectors of matrix \(\pmb {X}\). Finally, using the singular value decomposition (SVD), one obtains and, then matrices , \(k\in \mathcal {K}_p\), are defined by

(12)

The feasible condition for the IA scheme in (9) can be derived by recalling a proper system in which the number of variables \(N_{eq}\) is no less than the number of equations \(N_{va}\) [28]. \(N_{eq}\) and \(N_{va}\) can be directly obtained from (9) and one has the feasible IA condition as follows

$$\begin{aligned} \sum _{k\in \mathcal {K}_p}d_k(N_k-d_k)+\sum _{\ell \in \mathcal {K}_p}d_\ell (M_\ell -d_\ell )\ge \sum _{\ell \ne k}d_kd_\ell . \end{aligned}$$
(13)

The next step is to design matrices \(\pmb {B}_k\) and \(\pmb {A}_k\) of the PTxs as well as matrices \(\pmb {D}_k\) of the PRxs, \(\forall k\in \mathcal {K}_p\), to maximize the EE of the primary links. Note that after applying IA, the effective channel between Tx k and Rx k is . The eigmode transmissions are proposed to design \(\pmb {B}_k\) and \(\pmb {D}_k\) [29]. Specifically, we take the SVD of the effective channel as follows

$$\begin{aligned} {\tilde{\pmb {H}}}_{k,k} = {\tilde{\pmb {\varPi }}}_k{\tilde{\pmb {\varLambda }}}_k{\tilde{\pmb {\varOmega }}}_k^H, \end{aligned}$$
(14)

where \({\tilde{\pmb {\varPi }}}_k\in \mathbb {C}^{d_k\times d_k}\) and \({\tilde{\pmb {\varOmega }}}_k\in \mathbb {C}^{d_k\times d_k}\) are unitary matrix which contains the left-singular and right-singular vectors, \({\tilde{\pmb {\varLambda }}}_k=\mathrm {diag}({\tilde{\lambda }}_{k,1}, \ldots ,{\tilde{\lambda }}_{k,d_k}) \) is a diagonal matrix where \({\tilde{\lambda }}_{k,t}\) is the t-th largest singular value of \({\tilde{\pmb {H}}}_{k,k}\). Then, matrices \({\pmb {B}}_k\), \(\pmb {D}_k\), and \(\pmb {A}_k\) are designed as follows

$$\begin{aligned} {\pmb {B}}_k&= {\tilde{\pmb {\varOmega }}}_k, \end{aligned}$$
(15)
$$\begin{aligned} \pmb {D}_k&= {\tilde{\pmb {\varPi }}}_k, \end{aligned}$$
(16)
$$\begin{aligned} \pmb {A}_k&= \mathrm {diag}(\sqrt{a_{k,1}},\ldots ,\sqrt{a_{k,d_k}}), \end{aligned}$$
(17)

where \(a_{k,t} \ge 0,\forall t\in \mathcal {S}_k=\{1,\ldots ,d_k\},\) is the power allocated to data stream t of STx k. After applying IA in (9) and using (15), (16), (17), the achievable rate of PU k in (2) reduces to

$$\begin{aligned} \mathcal {R}_k(\pmb {A}_k) = \sum _{t=1}^{d_k}\log _2(1+a_{k,t}g_{k,t}), \end{aligned}$$

where \(g_{k_t} = \frac{{\tilde{\lambda }}_{k,t}^2}{\sigma _{k}^2}\) is the channel gain to noise ratio of stream t at PRx k. Accordingly, problem (5) is rewritten as

$$\begin{aligned} \underset{\{a_{k,t}\} \ge 0}{\max }\qquad&\eta _{\text {PEE}}=\frac{ \sum _{k\in \mathcal {K}_p}\mathcal {R}_k(\pmb {A}_k)}{\sum _{k\in \mathcal {K}_p}\left( \sum _{t=1}^{d_k}a_{k,t}+P_c\right) } \end{aligned}$$
(18a)
$$\begin{aligned} \text {s.t.}\,\,\,\,\,\,\qquad&\sum \limits _{t=1}^{d_k}a_{k,t}\le P_k, \forall k\in \mathcal {K}_p. \end{aligned}$$
(18b)

The cost function (18a) is a ratio of a concave function and a convex one while constraints (18b) are convex. Thus, problem (18) is a concave-convex fractional program which can be solved by the Dinkelbach method [21]. By invoking the Dinkelbach method, our goal is to derive closed-form expressions at each iteration to solve (18). First, we introduce a parameterized problem as follows

$$\begin{aligned} \underset{\{a_{k,t}\} \ge 0}{\max }\,\,&\sum \limits _{k\in \mathcal {K}_p}\sum \limits _{t=1}^{d_k}\log _2(1+a_{k,t}g_{k,t}) {-}\tau \sum _{k\in \mathcal {K}_p}\left( \sum _{t=1}^{d_k}a_{k,t}+P_c\right) \end{aligned}$$
(19a)
$$\begin{aligned} {\mathrm {s.t.}} \quad&(\hbox {18b}). \end{aligned}$$
(19b)

Problem (19) is a convex optimization problem and satisfies the Slater’s conditions. Hence, it can be solved by its dual problem given by

$$\begin{aligned} \underset{\{\mu _k\}\ge 0}{\min }\,\,\, \underset{\{a_{k,t}\}\ge 0}{\max }\,\,\, \mathcal {L}_{p}\left( \{a_{k,t}\},\{\mu _k\}\right) , \end{aligned}$$
(20)

where the partial Lagrangian function is defined as

$$\begin{aligned}&\mathcal {L}_{p}\left( \{a_{k,t}\},\{\mu _k\}\right) = \sum \limits _{k\in \mathcal {K}_p}\sum \limits _{t=1}^{d_k}\log _2(1+a_{k,t}g_{k,t}) \nonumber \\&\quad -\tau \sum _{k\in \mathcal {K}_p}\left( \sum _{t=1}^{d_i}a_{k,t}+P_c\right) + \sum \limits _{k\in \mathcal {K}_p}\mu _k\left( P_k-\sum \limits _{t=1}^{d_k}a_{k,t}\right) \end{aligned}$$
(21)

and \(\{\mu _k\}_{k\in \mathcal {K}_p}\) are the Lagrangian multipliers corresponding to (18b).

Problem (20) are solved by an iterative algorithm in which the inner maximization and outer minimization problems are alternatively solved. For given sets of the Lagrangian multipliers \(\{\mu _k\}_{k\in \mathcal {K}_p}\), it is easily shown that the inner maximization problem in (20) can be separated into \(K_p\) independent subproblems. Specifically, in each iteration, the inner maximization subproblem to find \(a_{k,t}\), can be written as

$$\begin{aligned} \underset{\{a_{k,t}\} \ge 0}{\max }\,\, \sum \limits _{t=1}^{d_k}\log _2(1+a_{k,t}g_{k,t}) -(\tau +\mu _k)\sum \limits _{t=1}^{d_k}a_{k,t}. \end{aligned}$$
(22)

The optimal solution to problem (22) can be easily derived as

$$\begin{aligned} a_{k,t} = \left[ \frac{1}{\ln 2(\tau +\mu _k)}-\frac{1}{g_{k,t}}\right] ^{+}, \forall t\in \mathcal {S}_k. \end{aligned}$$
(23)

Now, for given \(\{a_{k,t}\}_{k\in \mathcal {K}_p,t\in \mathcal {S}_k}\), the outer minimization problem in (20) are solved using the subgradient method to obtain the optimal solutions \(\{\mu _k^{*}\}_{k\in \mathcal {K}_p}\). Particularly, at the \((q+1)\)-th iteration, \(\{\mu _k\}_{k\in \mathcal {K}_p}\) are computed by

$$\begin{aligned} \mu _k^{(q+1)}=\left[ \mu _k^{(q)}-\rho \left( P_k-\sum \limits _{t=1}^{d_k}a_{k,t}\right) \right] ^{+}, \end{aligned}$$
(24)

where \(\rho >0\) is the step size. Note that the convergence of the subgradient method is guaranteed if the step size is properly chosen [30]. Thus, the Lagrangian multipliers \(\{\mu _k\}_{k\in \mathcal {K}_p}\) are calculated iteratively until convergence.

Finally, for given \(\{a_{k,t}\}_{k\in \mathcal {K}_p,t\in \mathcal {S}_k}\), we update \(\tau \) by the Dinkelbach method. The detailed algorithm to solve (18) is summarized in Algorithm 1.

figure d

3.2 Energy efficiency maximization for the secondary network

Due to the uncoordinated interference from the PUs to the SRxs, perfect IA for the secondary network may be not obtained. Thus, we propose a partial IA scheme in which only the interference from the STxs to the PRxs is perfectly eliminated. Thus, the PMs of the STxs are designed to have structures as

$$\begin{aligned}&\pmb {F}_k = \pmb {C}_k\pmb {B}_k, \forall k\in \mathcal {K}_s \end{aligned}$$
(25)

where the orthonormal matrices \(\pmb {C}_k\in \mathbb {C}^{M_k\times d_k}\) is selected to align interference signals from the STx into the subspace which is orthogonal to the receive subspaces of the PRxs while matrices \(\pmb {B}_k\in \mathbb {C}^{d_k\times d_k}\) are then designed for the EE maximization of the secondary network.

In order to cancel interference from STx k to all the PRxs, PMs \(\pmb {F}_k\), \(\forall k\in \mathcal {K}_s,\) are designed to satisfy constraint (6b) which can be rewritten as

$$\begin{aligned} {\bar{\pmb {H}}}_{k}\pmb {F}_k&=\pmb {0}_{\left( \sum _{i\in \mathcal {K}_p}d_i\right) \times d_k}, \end{aligned}$$
(26)

where \({\bar{\pmb {H}}}_{k}\in \mathbb {C}^{\left( \sum _{i\in \mathcal {K}_p}d_i\right) \times M_k}\) is given by

$$\begin{aligned} {\bar{\pmb {H}}}_{k} =\left[ \left( \pmb {W}_1^H\pmb {H}_{1,k}\right) ^H,\ldots , \left( \pmb {W}_{K_p}^H\pmb {H}_{K_p,k}\right) ^H\right] ^H. \end{aligned}$$
(27)

Constraint (26) ensures that \(\pmb {F}_k\) lies in the null space of the interference matrix \({\bar{\pmb {H}}}_{k}\), which is satisfied if

$$\begin{aligned} M_k\ge \sum _{i\in \mathcal {K}_p}d_i + d_k, \end{aligned}$$
(28)

and, then we choose \(\pmb {C}_k={\mathcal {N}}({\bar{\pmb {H}}}_{k})\).

In the next step, the matrices \(\pmb {B}_k\) and the DMs \(\pmb {W}_k\) of the SUs are designed to suppress interference and to maximize the EE. The optimization problem (6) can be equivalently rewritten as

$$\begin{aligned} \underset{\{\pmb {Q}_k\}\succeq 0,\{\pmb {W}_k\}}{\max }\,\,\,\,\,\,\,\,\,&\eta _{\text {SEE}} =\frac{\sum _{k\in \mathcal {K}_s}\mathcal {R}_k(\{\pmb {Q}_k\},\{\pmb {W}_k\})}{\sum _{k\in \mathcal {K}_s}\left( \langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle +P_c\right) } \end{aligned}$$
(29a)
$$\begin{aligned} {\mathrm {s.t.}}\,\,\,\,\,\,\,\, \qquad&\langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle \le P_{k},\forall k\in \mathcal {K}_s \end{aligned}$$
(29b)

where \(\pmb {Q}_k=\pmb {B}_k\pmb {B}_k^H\in \mathbb {C}^{d_k\times d_k}\) while the achievable data rate \(\mathcal {R}_k(\{\pmb {Q}_k\},\{\pmb {W}_k\})\) of SU k is given by

$$\begin{aligned}&\mathcal {R}_k(\pmb {Q}_k,\pmb {W}_{k})\nonumber \\&\quad =\log _2\left| \pmb {I}_{d_k} +\pmb {W}_k^H{\pmb {H}}_{k,k}\pmb {C}_k\pmb {Q}_k\pmb {C}_k^H{\pmb {H}}_{k,k}^H\pmb {W}_k\pmb {R}_k^{-1}\right| , \end{aligned}$$
(30)

where \(\pmb {R}_{k}=\pmb {W}_k^H(\sum _{\ell \in \mathcal {K},\ell \ne k}{\pmb {H}}_{k,\ell }\pmb {C}_\ell \pmb {Q}_\ell \pmb {C}_\ell ^H{\pmb {H}}_{k,\ell }^H+\sigma _k^2\pmb {I}_{d_k})\pmb {W}_k\).

Firstly, to deal with the coupling of PMs and DMs in the design problem (29), we use an alternating optimization technique to iteratively solve problem (29). Particularly, at each iteration, the DMs \(\{\pmb {W}_k\}\) are updated by solving problem (29) for fixed PMs \(\{\pmb {F}_k\}\) and, then, \(\{\pmb {F}_k\}\) are updated by solving problem (29) for given \(\{\pmb {W}_k\}\). It should be noted that for fixed PMs \(\{\pmb {F}_k\}\), problem (29) with respect to \(\{\pmb {W}_k\}\) is exactly reduced to the sum rate maximization problem of \(K_s\)-user MIMO channels. Therefore, for given \(\{\pmb {F}_k\}\), we invoke the optimal DM solutions given in [35]

$$\begin{aligned} \pmb {W}_k^{[j]} = \frac{ \pmb {\varTheta }_{k,j}^{-1}\pmb {H}_{k,k}\pmb {F}_k^{[j]} }{ \left\| \pmb {\varTheta }_{k,j}^{-1}\pmb {H}_{k,k}\pmb {F}_k^{[j]}\right\| } \end{aligned}$$
(31)

where \(\pmb {W}_k^{[j]}\) and \(\pmb {F}_k^{[j]}\) are the j-th column vectors of \(\pmb {W}_k\) and \(\pmb {F}_k\), respectively; and

$$\begin{aligned} \pmb {\varTheta }_{k,j}&=\sum _{\ell \in \mathcal {K}}\sum _{a=1}^{d_\ell } \pmb {H}_{k,\ell }\pmb {F}_\ell ^{[a]}(\pmb {F}_\ell ^{[a]})^H\pmb {H}_{k,\ell }^H\\&\quad - \pmb {H}_{k,k}\pmb {F}_k^{[j]}(\pmb {F}_k^{[j]})^H\pmb {H}_{k,k}^H + \sigma _k^2\pmb {I} \end{aligned}$$

is the interference plus noise covariance matrix of data stream j at SRx k.

For fixed \(\{\pmb {W}_k\}\), we now update PM \(\pmb {F}_k\) by solving the precoding design problem as follows

$$\begin{aligned} \underset{\{\pmb {Q}_k\}\succeq 0}{\max }\,\,\,\,\,\,\,\,\,&\eta _{\text {SEE}} =\frac{\sum _{k\in \mathcal {K}_s}\mathcal {R}_k(\{\pmb {Q}_k\})}{\sum _{k\in \mathcal {K}_s}\left( \langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle +P_c\right) } \end{aligned}$$
(32a)
$$\begin{aligned} {\mathrm {s.t.}}\,\,\,\,\,\,\,\, \quad&\langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle \le P_{k},\forall k\in \mathcal {K}_s. \end{aligned}$$
(32b)

It is worth noting the Dinkelbach method cannot be directly applied to problem (32) since \(\sum _{k\in \mathcal {K}_s}\mathcal {R}_k(\{\pmb {Q}_k\})\) is not concave. To handle this difficulty, we rewrite the sum rate as

$$\begin{aligned} \sum _{k\in \mathcal {K}_s}\mathcal {R}_k(\{\pmb {Q}_k\})=\mathcal {R}_k(\pmb {Q}_k,\pmb {Q}_{-k})+f_k(\pmb {Q}_k,\pmb {Q}_{-k}), \end{aligned}$$
(33)

where \(\mathcal {R}_k(\pmb {Q}_k,\pmb {Q}_{-k})\) and \(f_k(\pmb {Q}_k,\pmb {Q}_{-k})\) denote the rate of user k and the sum rate of all links except for link k, respectively, which are expressed as

$$\begin{aligned} \mathcal {R}_k(\pmb {Q}_k,\pmb {Q}_{-k})&=\log _2\left| \pmb {I}_{d_k} +{\tilde{\pmb {H}}}_{k,k}\pmb {Q}_k{\tilde{\pmb {H}}}_{k,k}^H\pmb {R}_k^{-1}\right| \end{aligned}$$
(34)
$$\begin{aligned} f_k(\pmb {Q}_k,\pmb {Q}_{-k})&=\sum _{\ell \in \mathcal {K}_s\setminus k} \log _2\left| \pmb {I}_{d_\ell } +{\tilde{\pmb {H}}}_{\ell ,\ell }\pmb {Q}_\ell {\tilde{\pmb {H}}}_{\ell ,\ell }^H\pmb {R}_\ell ^{-1}\right| \end{aligned}$$
(35)

where \(\pmb {Q}_{-k}\triangleq \{\pmb {Q}_{\ell }|\ell \in \mathcal {K}\setminus k\}\), \( \pmb {R}_\ell = \sigma _\ell ^2 \pmb {W}_\ell ^H\pmb {W}_\ell + \sum _{j\in \mathcal {K}\setminus \ell } {\tilde{\pmb {H}}}_{\ell ,j}\pmb {Q}_j{\tilde{\pmb {H}}}_{\ell ,j}^H \in \mathbb {C}^{d_\ell \times d_\ell }, \) and \({\tilde{\pmb {H}}}_{k,\ell }=\pmb {W}_k^H\pmb {H}_{k,\ell }\pmb {C}_k\in \mathbb {C}^{d_k\times d_k},\forall \ell \in \mathcal {K},\forall k\in \mathcal {K}_s\). Notice that \(\mathcal {R}_k(\pmb {Q}_k,\pmb {Q}_{-k})\) is concave and \(f_k(\pmb {Q}_k,\pmb {Q}_{-k})\) is a convex function in \(\pmb {Q}_k\) whenever \(\pmb {Q}_{-k}\) is fixed, as shown in “Appendix 1”. Hence, the sum rate \(\sum _{k\in \mathcal {K}_s}\mathcal {R}_k(\{\pmb {Q}_k\})\) can be regarded as a DC function if only one variable \(\pmb {Q}_k\) is optimized for given \(\pmb {Q}_{-k}\). Thus, to recast the numerator of the objective function (32a) as a concave function, we find a tight lower bound of the convex function \(f_k(\pmb {Q}_k,\pmb {Q}_{-k})\) around a feasible point \({\tilde{\pmb {Q}}}_k\) as follows

$$\begin{aligned} f_k(\pmb {Q}_k,{\pmb {Q}}_{-k}) \ge f_k({\tilde{\pmb {Q}}}_k,{\pmb {Q}}_{-k}) + \big \langle \pmb {\mathcal {D}}_k({\tilde{\pmb {Q}}}_k)^H(\pmb {Q}_k-{\tilde{\pmb {Q}}}_k) \big \rangle \end{aligned}$$
(36)

where

$$\begin{aligned} \pmb {\mathcal {D}}_k(\pmb {Q}_k) \triangleq \nabla _{\pmb {Q}_k}f_k(\pmb {Q}_k,{\pmb {Q}}_{-k})= & {} -\frac{1}{\ln 2} \sum _{\ell \in \mathcal {K}_s\setminus k} {\tilde{\pmb {H}}}_{\ell ,k}^H \big [ \pmb {R}_\ell ^{-1}\nonumber \\&-(\pmb {R}_\ell +\pmb {X}_\ell )^{-1} \big ] {\tilde{\pmb {H}}}_{\ell ,k} \end{aligned}$$
(37)

in which \(\pmb {X}_\ell ={\tilde{\pmb {H}}}_{\ell ,\ell }\pmb {Q}_\ell {\tilde{\pmb {H}}}_{\ell ,\ell }^H\). The derivation of (37) is provided in “Appendix 2”. Therefore, for given \(\pmb {Q}_{-k}\), the sum data rate \(\sum _{k\in \mathcal {K}_s}\mathcal {R}_k(\pmb {Q}_k)\) can be approximated by its lower bound at \({\tilde{\pmb {Q}}}_k\) as follows.

$$\begin{aligned} \sum _{k\in \mathcal {K}_s}\mathcal {R}_k(\pmb {Q}_k)\ge {\tilde{\mathcal {R}}}_{sum}(\pmb {Q}_k) \end{aligned}$$
(38)

where

$$\begin{aligned}&{\tilde{\mathcal {R}}}_{sum}(\pmb {Q}_k) \triangleq \log _2\left| \pmb {I}+{\tilde{\pmb {H}}}_{k,k}\pmb {Q}_k{\tilde{\pmb {H}}}_{k,k}^H\pmb {R}_k^{-1}\right| + f_k({\tilde{\pmb {Q}}}_k,{\pmb {Q}}_{-k}) \nonumber \\&\quad + \big \langle \pmb {\mathcal {D}}_k({\tilde{\pmb {Q}}}_k)^H(\pmb {Q}_k-{\tilde{\pmb {Q}}}_k) \big \rangle . \end{aligned}$$
(39)

It should be emphasized that \({\tilde{\mathcal {R}}}_{sum}(\pmb {Q}_k)\) is a concave function in \(\pmb {Q}_k\) and the equality of (38) can be achieved at \(\pmb {Q}_k={\tilde{\pmb {Q}}}_k\). Defining

$$\begin{aligned} {\tilde{\eta }}_{\text {SEE}}(\pmb {Q}_k,{\pmb {Q}}_{-k}) =\frac{{\tilde{\mathcal {R}}}_{sum}(\pmb {Q}_k)}{\sum _{k\in \mathcal {K}_s}\left( \langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle +P_c\right) } \end{aligned}$$
(40)

inequality (38) results in

$$\begin{aligned} \eta _{\text {SEE}}(\pmb {Q}_k,{\pmb {Q}}_{-k}) \ge {\tilde{\eta }}_{\text {SEE}}(\pmb {Q}_k,{\pmb {Q}}_{-k}) \end{aligned}$$
(41)

for given \(\pmb {Q}_{-k}\), and (41) is meet at equality at \(\pmb {Q}_k={\tilde{\pmb {Q}}}_k\). Accordingly, problem (32) for given \(\pmb {Q}_{-k}\) can be decomposed into per-link problem at \({\tilde{\pmb {Q}}}_k\) as

$$\begin{aligned} \underset{\pmb {Q}_k \succeq 0}{\max }\,\,\,\,\,\,\,\,\,&{\tilde{\eta }}_{\text {SEE}} =\frac{{\tilde{\mathcal {R}}}_{sum}(\pmb {Q}_k)}{\sum _{k\in \mathcal {K}_s}\left( \langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle +P_c\right) } \end{aligned}$$
(42a)
$$\begin{aligned} {\mathrm {s.t.}}\,\,\,\,\,\,\,\, \quad&\langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle \le P_{k}. \end{aligned}$$
(42b)

We exploit the technique of nonlinear fractional programming, e.g., the Dinkelbach method, to solve problem (42). Particularly, we first define a parametric problem with respect to \(\tau \) as

$$\begin{aligned} \underset{\pmb {Q}_k\succeq 0}{\max }\qquad&g(\tau , \pmb {Q}_k)={\tilde{\mathcal {R}}}_{sum}(\pmb {Q}_k) -\tau \sum _{k\in \mathcal {K}_s}\left( \langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle +P_c\right) \end{aligned}$$
(43a)
$$\begin{aligned} {\mathrm {s.t.}}\,\qquad&\langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle \le P_{k}. \end{aligned}$$
(43b)

Let \(\pmb {Q}_k^{\star }(\tau )\) be an optimal solution to (43) for a given \(\tau \). As shown in [21], there exists \(\tau ^{\star }\) such that \(g(\tau ^{\star }, \pmb {Q}_k^{\star }(\tau ^{\star }))=0\) and, then, \(\pmb {Q}_k^{\star }(\tau ^{\star })\) is also the optimal solution to (42). \(\pmb {Q}_k^{\star }(\tau ^{\star })\) can be found by adopting the Dinkelbach method [21]. More specially, for a fixed \(\tau \), we solve (43) to obtain \(\pmb {Q}_k^{\star }(\tau )\) and, then, we use the Dinkelbach approach to update \(\tau \).

It is obvious that, for given \(\tau \), problem (43) is a convex problem and can be solved by standard convex solver packets, e.g., CVX [31]. However, to investigate insights to the structure of solution, we next solve problem (43) with a closed-form solution. Since problem (43) is convex and satisfies the Slater’s condition, it can be solved using the following dual problem

$$\begin{aligned} \underset{\nu _k\ge 0}{\min }\,\,\, \underset{\pmb {Q}_k\succeq 0}{\max }\,\,\, \mathcal {L}_s\left( \pmb {Q}_k,\nu _k\right) , \end{aligned}$$
(44)

where the dual Lagrangian function is defined as

$$\begin{aligned} \mathcal {L}_s\left( \pmb {Q}_k,\nu _k\right)&={\tilde{\mathcal {R}}}_{sum}(\pmb {Q}_k) -\tau \sum _{k\in \mathcal {K}_s}\left( \langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle +P_c\right) \nonumber \\&\quad + \nu _k\left( P_k-\langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle \right) \end{aligned}$$
(45)

and \(\nu _k\) is the Lagrangian multiplier corresponding to the constraints (43b). Substituting (39) to (45), we obtain

$$\begin{aligned}&\mathcal {L}_s\left( \pmb {Q}_k,\nu _k\right) \nonumber \\&\quad =\log _2\left| \pmb {I} +{\tilde{\pmb {H}}}_{k,k}\pmb {Q}_k{\tilde{\pmb {H}}}_{k,k}^H\pmb {R}_k^{-1}\right| \nonumber \\&\qquad + f_k({\tilde{\pmb {Q}}}_k,{\pmb {Q}}_{-k}) + \big \langle \pmb {\mathcal {D}}_k({\tilde{\pmb {Q}}}_k)^H(\pmb {Q}_k-{\tilde{\pmb {Q}}}_k) \big \rangle \nonumber \\&\qquad -\tau \sum _{k\in \mathcal {K}_s}\left( \langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle +P_c\right) + \nu _k\left( P_k-\langle \pmb {C}_k\pmb {Q}_k\pmb {C}_k^H\rangle \right) \nonumber \\&\quad =\log _2 \left| \pmb {I}+{\tilde{\pmb {H}}}_{k,k}\pmb {Q}_k{\tilde{\pmb {H}}}_{k,k}^H\pmb {R}_k^{-1} \right| \nonumber \\&\qquad -\beta ({\tilde{\pmb {Q}}}_k)-\Big \langle \big ( (\tau +\nu _k)\pmb {C}_k^H\pmb {C}_k - \pmb {\mathcal {D}}_k({\tilde{\pmb {Q}}}_k)^H \big )\pmb {Q}_k \Big \rangle \end{aligned}$$
(46)

where \( \beta ({\tilde{\pmb {Q}}}_k) \triangleq -f_k({\tilde{\pmb {Q}}}_k,{\pmb {Q}}_{-k}) + \big \langle \pmb {\mathcal {D}}_k({\tilde{\pmb {Q}}}_k)^H{\tilde{\pmb {Q}}}_k \big \rangle + \tau \sum _{\ell \in \mathcal {K}_s\setminus k} \left( \langle \pmb {C}_\ell \pmb {Q}_\ell \pmb {C}_\ell ^H\rangle +P_{c_\ell }\right) -\nu _k P_k \).

Problem (44) is solved by iteratively solving the inner maximization and outer minimization problems respectively. For given \(\nu _k\) the inner maximization problem can be rewritten as

$$\begin{aligned} \underset{\pmb {Q}_k\succeq 0}{\max }\,\,\, \log _2\left| \pmb {I}+{\tilde{\pmb {H}}}_{k,k}\pmb {Q}_k{\tilde{\pmb {H}}}_{k,k}^H\pmb {R}_{k}^{-1} \right| - \langle \pmb {\varUpsilon }_k\pmb {Q}_k\rangle , \end{aligned}$$
(47)

where \(\pmb {\varUpsilon }_k= \left( (\tau +\nu _k)\pmb {C}_k^H\pmb {C}_k -\pmb {\mathcal {D}}_k({\tilde{\pmb {Q}}}_k)^H \right) \in \mathbb {C}^{d_k\times d_k}\) and the constants having no effect on the optimal solution have been eliminated. The closed-form solution to problem (47) is derived in the following theorem.

Theorem 1

For given \(\pmb {Q}_{-k}\) and \(\nu _k\), the optimal solution to (47) has the following form

$$\begin{aligned} \pmb {Q}_k^{*} = \pmb {\varUpsilon }_k^{-1/2}\pmb {\varDelta }_k\pmb {\varGamma }_k\pmb {\varDelta }_k^H\pmb {\varUpsilon }_k^{-1/2}, \end{aligned}$$
(48)

where \(\pmb {\varDelta }_k\) is obtained from SVD \(\pmb {R}_{k}^{-1/2}{\tilde{\pmb {H}}}_{k,k}\pmb {\varUpsilon }_k^{-1/2} =\pmb {\varXi }_k\pmb {\varPhi }_k\pmb {\varDelta }_k^H\), with \(\pmb {\varPhi }_k=\mathrm {diag}(\phi _{k,1},\ldots ,\phi _{k,d_k}), \phi _{k,1}\ge \ldots \ge \phi _{k,d_k}\), and \(\pmb {\varGamma }_k=\mathrm {diag}(\gamma _{k,1},\ldots ,\gamma _{k,d_k})\), \(\gamma _{k,t}=\left[ \frac{1}{\ln 2}-\frac{1}{\phi _{k,t}^2}\right] ^{+}, \forall t\in \mathcal {S}_k=\{1,\ldots ,d_k\}\).

Proof

See “Appendix 3”. \(\square \)

Now, for given \(\pmb {Q}_k\), the outer minimization problem in (44) is solved by the subgradient method to obtain \(\nu _k\). Particularly, at iteration \((p+1)\), one has

$$\begin{aligned} \nu _k^{(p+1)} = \left[ \nu _k^{(p)}-\varrho \left( P_k-\langle \pmb {C}_k\pmb {Q}_k\pmb {C}^H\rangle \right) \right] ^{+}, \end{aligned}$$
(49)

where \(\varrho >0\) is the step size. \(\nu _k\) is updated iteratively until convergence [30]. Since the structure of the optimal solution to the inner maximization in (44) for each link has been revealed in Theorem 1, the optimal solution \(\{\pmb {Q}_k^{*}\}\) can be obtained by sequentially solving (47) for each STx until convergence. Finally, for given \(\{\pmb {Q}_k\}_{k\in \mathcal {K}_s}\), \(\tau \) can be updated using the Dinkelbach method.

According to the above analysis, we propose a three-layer iterative algorithm to solve (32) until convergence. In the first layer, parameter \(\tau \) is calculated using the Dinkelbach method. In layer 2, the intermediate matrices \({\tilde{\pmb {Q}}}_k\) are updated. In layer 3, the Lagrangian multiplier \(\nu _k\) and solutions \(\pmb {Q}_k^{*}\) to the inner maximization problem in (44) are updated. The step-by-step algorithms are summarized in Algorithm 2. The proof of the convergence of Algorithm 2 is given in “Appendix 4”.

figure e

Finally, to recover \(\pmb {F}_k\) from the optimal solution \(\pmb {Q}_k\), we take the SVD \(\pmb {Q}_k^{opt}=\pmb {\varOmega }_k\pmb {\varPsi }_k\pmb {\varOmega }_k^H\). The optimal PM \(\pmb {F}_k\) is then obtained as

$$\begin{aligned} \pmb {F}_k^{opt}=\pmb {\varOmega }_k\pmb {\varPsi }_k^{\frac{1}{2}}. \end{aligned}$$
(50)

4 Simulation results

In this section, we evaluate the EE performance of our proposed algorithms through numerical results. To the best of our knowledge, the EE maximization for the CR network model considered in the paper has not been reported in the literature. Thus, we compare the proposed method with ones in [4, 32] which aim at maximizing the spectral efficiency. Particularly, in the primary network, we compare the achievable EE of the proposed scheme in Algorithm 1 (called IA-PAA) with that of the method [32] using IA and the water-filling method for the sum rate (SR) maximization (called IA-SRMax). In the secondary network, the achievable EE of the proposed scheme from Algorithm 2 (called ZF-DCA) is compared with the the modified method in [4] for the sum rate maximization (SRMax). Simulation parameters are set as follows: \(K_s=3,K_p=2,M_k=M=9\), \(N_k=N=6\), \(d=2\), \(P_c=5\) dB, \(\epsilon _1=\epsilon _2=\epsilon _3=10^{-3}\), \(\sigma _k^2=1\), \(\rho = 0.05\) and \(\varrho = 0.01\). The Rayleigh fading channel coefficients are generated from the complex Gaussian distribution \({{{\mathcal {C}}}{{\mathcal {N}}}}(0,1)\).

First, we investigate the average achievable EE of our proposed IA-PAA scheme and ZF-DCA scheme. The maximum transmit power at all Txs is set to be the same, i.e., \(P_k=P_t,\forall k\in \mathcal {K}\). It can be seen from Fig. 1 that in the primary network, our proposed IA-PAA outperforms the IA-SRMax [32] in terms of EE, especially in the high transmit power region. When the maximum transmit power is small, the EE maximization problem in (5) is equivalent to a sum rate maximization problem and, hence, the achievable EE increases with the transmit power. With regard to the secondary network, Fig. 2 shows that the achievable EE of our proposed ZF-DCA scheme is also significantly higher than that of the SRMax method [4]. However, in the small transmit power region, the achievable EE decreases with an increase in the maximum transmit power. This is because that increasing transmit power leads to a higher level of interference from the PU Txs to the SU Rxs. For high maximum transmit power, our proposed method still maintains the same level of the EE, revealing that the EE will not be enhanced by increasing of the transmit power over a certain threshold.

Fig. 1
figure 1

The average achievable EE and sum rate of the primary network versus the maximum transmit power

Full size image
Fig. 2
figure 2

The average achievable EE and sum rate of the secondary network versus the maximum transmit power

Full size image

To investigate the mutual effect between the secondary network and the primary network, we consider a scenario in which the maximum transmit powers at the PTxs are kept unchanged, i.e., \(P_k=P_p,\forall k\in \mathcal {K}_p\), while the maximum transmit powers at the STxs \(P_k=P_s, \forall k \in \mathcal {K}_s\), will vary from 0 dB to 20 dB in the simulation. We plot the EE and sum rate versus \(P_s\) in Fig. 3 with \(P_p=\{5,10\}\) dB. It can be seen from Fig. 3 that the EE and sum rate of the primary network remains unchanged for all of the simulated configurations when increasing the maximum transmit power of the secondary network. This confirms that the performance of the primary network will not be degraded due to the SU transmissions in the proposed ZF-DCA scheme. Figure 3 also demonstrates that increasing maximum transmit power at PTxs leads to a reduction in the sum rate and EE performance of the secondary network. This is because the SRxs suffer more interference power from PTxs as \(P_p\) increases.

Fig. 3
figure 3

The average achievable EE and sum rate versus the maximum transmit power at the STxs

Full size image

5 Conclusion

This paper has developed iterative algorithms for the transceiver designs to maximize the EE in the multiuser MIMO CR network. To address interference issues in the CR network, the proposed method is to adopt full IA for the primary network and partial IA for the secondary network. Then, to tackle the mathematical challenges associated with highly nonlinear and intractable fractional programming of the EE maximization problems, the proposed method invokes the DC programming and Dinkelbach method to develop iterative algorithms with provable convergence in which the closed-form expressions are derived in each iteration. The simulation results have demonstrated that the proposed method is superior to the others in terms of the EE.