1 Introduction

Recently, the cooperative diversity technique has attracted much interest in wireless communications. This technique can increase the achievable rate region over non-cooperative schemes in fading channels, and provide a useful alternative for fading mitigation by the means of cooperation among multiple spatially distributed users or nodes [1,2,3,4]. However, most of the previous works focus on coherent detection, and assume that the destination has perfect knowledge of channel state information (CSI) of all transmission links, which can be estimated by transmitting pilot sequences or adopting blind estimation techniques [5]. With channel estimation, the system will be complicated and the transmission efficiency will also be reduced, especially in fast fading environments and multi-antenna or multi-node wireless systems since the amount of pilot or convergence time grows with the number of links [6]. Based on this, several differential cooperative diversity schemes have been proposed in the absence of CSI case. In [7], a differential modulation scheme with amplify-and-forward (AF) method for two-user cooperative diversity systems is presented, where the relay terminals utilize QPSK modulation to implement two BPSK streams transmission. The decode-and-forward (DF) method based coherent modulation and non-coherent modulation schemes for cooperative relay systems are proposed in [8] and [9], respectively, where two relays and multiple relays are, respectively, considered. By employing AF and DF methods, two repetition-based binary differential modulation schemes with BPSK are developed in [5]. According to the noncoherent orthogonal AF half-duplex protocol, the nonunitary and unitary diagonal distributed space-time coding (STC) schemes for cooperative relay systems are designed in [10], and full diversity can be obtained. However, the above schemes in [5, 10] are suitable for single relay only. By extending the scheme [5] to MPSK symbols case, [11] gives a distributed differential scheme for a two-user cooperative communication system employing the AF method, but this scheme is limited in one relay and repetition-based diversity. For this reason, [6] develops a distributed differential space-time modulation scheme for two-relay cooperative systems, but the decoding complexity is much higher (i.e. it needs \(M^{2}\) matrix calculation and comparison, M is constellation size). In [12] and [13], based on the network model in [6], two distributed differential STC (DSTC) schemes are designed for the DF based relay systems, respectively, where the relay selection are considered. With the DF method, a distributed differential encoding/decoding scheme in terms of Alamouti STC is developed in [14], where only single relay is considered. By introducing two specific STC schemes, [15] presents a partially-coherent distributed STC scheme with differential encoder and decoder, but the large-scale fading is neglected, and the presented DSTC needs to be constructed in terms of specific construction criteria, which will make it hard to use the existing DSTC schemes. Considering the same network model as [15, 16] gives distributed differential schemes in terms of AF and DF methods respectively, where the unitary STC (USTC) is adopted for differential encoding and decoding, but the schemes only work for the differential USTC whose code matrix is diagonal, and have exponential decoding complexity for DF schemes [17]. Based on analog network coding, a distributed DSTC scheme is proposed for two-way relay network in [18], and the corresponding pairwise error probability (PEP) and block error rate are analyzed. However, the proposed scheme is suitable for USTC and AF method only, and the analysis is limited in symmetric network.

According to the analysis above, the DSTC scheme in cooperative relay network is not studied well, especially in asymmetric network, the related study is much less. For this reason, we will investigate the performance of DSTC in asymmetry relay network and composite fading channel, where large-scale and small-scale fading are both considered.

Firstly, we develop an AF method based DSTC scheme with low complexity for wireless relay networks by introducing the orthogonal STC scheme. The differential space-time code matrices are produced by the source terminal, and each column of a code matrix is relayed by a relay user to the destination. The scheme does not require CSI both at the transmitter and receiver, and has linear decoding complexity. Thus, it avoids the exponential decoding complexity of some existing schemes.

Secondly, the existing DSTCs can be used for the developed scheme. Unlike some existing schemes that the data symbols for encoding matrix are limited in specific constellation, such as PSK or FSK, the data symbols in our scheme can be from different constellations.

Thirdly, according to the performance analysis, the power allocation (PA) between source and relay terminals is optimized to minimize the system PEP. The optimization is not only for symmetric network, but also for asymmetric network. Considering the complexity of optimized problems in asymmetric network, two practical calculation methods are proposed. With these methods, the optimized power is allocated and the resulting system performance is improved greatly.

Fourthly, another distributed DSTC scheme based on DF method is developed for cooperative relay network. Compared to the AF based scheme, the DF based scheme has better performance because no noise power is amplified at relay determines. At high SNR, however, the performance superiority will decrease due to the error propagation from the relay terminals.

The notations throughout this paper are as follows. Bold upper case and lower case letters denote matrices and column vectors, respectively. The superscripts \((\cdot )^{T}\), \((\cdot )^{*}\), and \((\cdot )^{H}\) are used to stand for the transpose, complex conjugate, and Hermitian transpose, respectively. The \(E\{\cdot \}\) and \(\mathbf{I}_{N}\) denote statistical expectation and \(N\times N\) identity matrix, respectively. \(\hbox {Re}\{\cdot \}\)and \(\hbox {Im}\{\cdot \}\)denote real part and imaginary part operator, respectively. \(\hbox {diag}\{\cdot \}\) denotes diagonal matrix.

2 System model and AF protocol based DSTC scheme

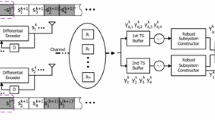
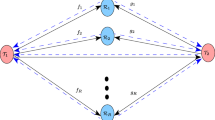
The system model for wireless relay network is shown in Fig. 1. In Fig. 1, the network consists of a source user, a destination user and R relay users, and the source user has no path access to the destination, but it can transmit the information to destination by the means of the relays. Every relay user has a single antenna, which can be used for both transmission and reception. For the source/destination user, its antenna is used for transmission/reception only. The channel from the source to the relays, and the channel from the relays to the destination are assumed to be independent flat fading, and both effects of large-scale and short-scale propagations are considered. The channel from the source to the kth relay is denoted as \(\alpha _{k} \rho _{sk}\), and the channel from the kth relay to the destination is denoted as \(\beta _{k} \rho _{kd}\), where \(\rho _{sk}\) and \(\alpha _{k}\) are the large-scale attenuation factor and small-scale fading coefficients between the source and the kth relay, respectively. \(\rho _{kd}\) and \(\beta _{k}\) are the large-scale attenuation factor and small-scale fading coefficients between the kth relay and the destination, respectively. \(\alpha _{k}\) and \(\beta _{k}\) are assumed to be independent Gaussian random variables with unit-variance and zero-mean for different k.

Fig. 1
figure 1

System model for wireless relay network

Full size image

In the following, we will give the distributed DSTC scheme in terms of AF method. Firstly, based on the transmitted symbols, using the orthogonal STC, differential coding matrices are generated for cooperative diversity. Then, each column of a coding matrix is transmitted to one relay user at different times. After that, the relay users amplify and retransmit the received signals with noise to the destination. At the receiver, the destination user collects the information sent by the relay users, and makes a final decision on the transmitted symbols or bits by differential space-time decoding.

Considering that the orthogonal STC matrix is easily constructed and has low-complexity decoding, and its differential form has better performance than differential USTC schemes [17], we introduce STC from amicable orthogonal design, and the corresponding code matrix is given by

$$\begin{aligned} \mathbf{D}_i =\frac{1}{\sqrt{L}}\sum _{l=1}^L \left( \mathbf{U}_l d_l^R +j\mathbf{V}_l d_l^I \right) \end{aligned}$$
(1)

where \(\left\{ {\mathbf{U}_l}\right\} _{l=1}^L\)and \(\left\{ {\mathbf{V}_l}\right\} _{l=1}^L\) are a set of 2L matrices of size \(K\times K\) which satisfy the orthogonal conditions in [17, Eq.(2)], and they constitute an amicable orthogonal design of order K in L variables. \(d_l^R\) and \(d_l^I\) denote the real and imaginary parts of complex symbol \(d_{l}\), respectively. The unitary signal constellation such as MPSK (similar analysis can be extended to other constellation) is first considered. Let \(\left\{ {d_l }\right\} _{l=1}^L\) be a block of L symbols to be transmitted at a time i, and they are from MPSK constellation \(\Phi \), then we have: \(\mathbf{D}_i \mathbf{D}_i^H =\sum _{l=1}^L | d_l |^{2}/L\mathbf{I}_K =\mathbf{I}_K\). Thus, \(\mathbf{D}_{i}\) is a unitary matrix.

With (1), the information matrix \(\mathbf{D}_{i}\) is firstly generated. Then, the differential encoding at the source terminal is performed. Namely, at the start of the transmission, the transmitter sends a initial code matrix \(\mathbf{S}_{0}\) (usually \(\mathbf{S}_{0}=\mathbf{I}_{K}\)) that does not carry information, the \(\mathbf{D}_{i}\) is then differentially encoded, and the corresponding encoded matrix \(\mathbf{S}_{i}\) at i-th time block is written as

$$\begin{aligned} \mathbf{S}_i =\mathbf{D}_i \mathbf{S}_{i-1}. \end{aligned}$$
(2)

Since matrix \(\mathbf{D}_{i}\) is unitary, \(\mathbf{S}_{i}\) is also unitary if \(\mathbf{S}_{i-1}\) is unitary. Because \(\mathbf{S}_{0}\) is unitary, it follows that \(\mathbf{S}_{i}\) is unitary for any i. Let the code matrix \(\mathbf{S}_{i}\) be \([\mathbf{s}_{i1},\,\mathbf{s}_{i2},\,{\ldots },\, \mathbf{s}_{iK}]\), where \(\mathbf{s}_{i1},\,{\ldots },\,\mathbf{s}_{iK}\) are the columns of \(\mathbf{S}_{i,}\) respectively. Then, we extend the above differential STC scheme to the wireless relay network. Here we assume that K relay users are available for cooperative communication, and the transmitted signals from different relays are synchronized at the destination terminal. Firstly, the first column \(\mathbf{s}_{i1}=[s_{11}{\ldots },\,\hbox {s}_{K1}]^{T}\) is transmitted to relay user 1 at the first time block. Secondly, the second column is transmitted to relay user 2 at the second time block, and so on, the K-th column \(\mathbf{s}_{iK}= [s_{1K}{\ldots },\,\hbox {s}_{KK}]^{T}\) is finally transmitted to the K-th relay user. After that, at every relay, the received signals are amplified and power-normalized. These relayed signals \(\tilde{\mathbf{s}}_{ik} (k=1,{\ldots },K)\) are transmitted to the destination user simultaneously. At the destination terminal, the receiver obtains the transmitted data by combining two adjacent received signals \(\mathbf{x}(i-1)\) and \(\mathbf{x}(i)\).

In what follows, we consider that the information symbols are from MQAM constellation. Under this case, the differential matrix \(\mathbf{S}_{i}\) is produced at the source terminal as follows:

$$\begin{aligned} \mathbf{S}_i =\mathbf{D}_i \tilde{\mathbf{S}}_{i-1} =\mathbf{D}_i \mathbf{S}_{i-1} /\xi _{i-1} \end{aligned}$$
(3)

where \(\tilde{\mathbf{S}}_{i-1}\) is the normalized value of \(\mathbf{S}_{i-1}\), and \(\xi _{i-1}\) is the amplitude of \(\mathbf{S}_{i-1}\). For the matrix \(\mathbf{S}_{i-1}\), it satisfies that \(\mathbf{S}_{i-1}^H \mathbf{S}_{i-1} =\mathbf{S}_{i-1} \mathbf{S}_{i-1}^H =\xi _{i-1}^2 \mathbf{I}_K \), and \(\xi _0 =1\) for \(\mathbf{S}_0 =\mathbf{I}_K \). Thus, \(\tilde{\mathbf{S}}_{i-1}^H \tilde{\mathbf{S}}_{i-1} =\mathbf{I}_K\) is a unitary matrix.

From (3), and considering that \(\mathbf{D}_i \mathbf{D}_i^H =\sum _{l=1}^L | d_l |^{2}/L\mathbf{I}_K \), we can obtain:

$$\begin{aligned} \mathbf{S}_i^H \mathbf{S}_i =\tilde{\mathbf{S}}_{i-1}^H \mathbf{D}_i^H \mathbf{D}_i \tilde{\mathbf{S}}_{i-1} =\tilde{\mathbf{S}}_{i-1}^H \xi _{\hbox {D}_i }^2 \mathbf{I}_K \tilde{\mathbf{S}}_{i-1} =\xi _{\hbox {D}_i }^2 \mathbf{I}_K \end{aligned}$$
(4)

where \(\xi _{\hbox {D}_i }^2 =\sum _{l=1}^L ( \left| {d_l } \right| ^{2}/L)\) is the amplitude of information matrix \(\mathbf{D}_{i}\). Hence, \(\mathbf{S}_{i}\) and \(\mathbf{D}_{i}\) have the same amplitude. After differential encoding, each column of \(\mathbf{S}_{i}\) is transmitted to the corresponding relay user.

3 Differential detection

In this section, we will give the differential detection scheme of distributed DSTC in composite fading channel. Firstly, we consider that the transmitted data symbols are from simple MPSK constellation, the initial codeword is set as \(\mathbf{S}_{0}=\mathbf{I}_{K}\), and thus \(\mathbf{S}_{i}\) is a unitary matrix according to the analysis in Sect. 2. As shown in Fig. 1, in the first transmission phase (i.e. Source to Relay), the received signal at the k-th relay terminal \((k=1,{\ldots },K)\) is written as

$$\begin{aligned} \left[ {{\begin{array}{c} {r_{i,k1} } \\ \vdots \\ {r_{i,kK} } \\ \end{array} }} \right]= & {} \sqrt{P_0 }\rho _{sk} \alpha _{ik} \mathbf{s}_{i,k} +\left[ {{\begin{array}{c} {z_{i,k1} } \\ \vdots \\ {z_{i,kK} } \\ \end{array} }} \right] \nonumber \\= & {} \sqrt{P_0 }\rho _{sk} \alpha _{ik} \left[ {{\begin{array}{c} {s_{1k} } \\ \vdots \\ {s_{Kk} } \\ \end{array} }} \right] +\left[ {{\begin{array}{c} {z_{i,k1} } \\ \vdots \\ {z_{i,kK} } \\ \end{array} }} \right] , \end{aligned}$$
(5)

where \(z_{i,kj}\) is the channel noise at the relay k at time slot \(j\,(j=1,{\ldots },K)\) within i-th time block, \(P_{0}\) is the transmit power of source terminal.

In the second transmission phase (i.e. Relay to Destination), the relay k amplifies the received signal and forwards it to the destination with transmit power \(P_{k}\). So the received signals at time slot j at the destination terminal are

$$\begin{aligned} x_{ij}= & {} \sqrt{\tilde{P}_1 }\beta _{i1} \rho _{1d} r_{i,1j} +\cdots +\sqrt{\tilde{P}_K }\beta _{iK} \rho _{Kd} r_{i,Kj} +z_{i,dj}\nonumber \\= & {} \sqrt{P_1 }\beta _{i1} \rho _{1d} \tilde{s}_{j1} +\cdots +\sqrt{P_K }\beta _{iK} \rho _{Kd} \tilde{s}_{jK} +z_{i,dj} , \end{aligned}$$
(6)

where \(z_{i,dj}\,(j=1,{\ldots },K)\) is the channel noise at time slot j at the destination terminal. The noises \(\{z_{i,dj}\}\) and \(\{z_{i,kj}\}\) are modeled as independent complex Gaussian random variables with zero-mean and variances \(N_{0}\). \(\tilde{P}_k =\mu _k P_k \,(\mu _k =1/(P_0 \rho _{sk}^2 +2N_0 ))\) is the normalized transmit power, and it ensures that the average transmit power of the relay k is \(P_{k}\). So after the normalized processing, the relay signals \(\{\tilde{s}_{uv}\}\) in (6) can be expressed as \(\tilde{s}_{uv} =\sqrt{\mu _v}r_{i,vu},\,u,\,v=1,{\ldots },K\).

Based on the analysis above, the total transmitted power is given by \(P_{t}={ KP}_{0}+P_{1}+{\ldots }+P_{K}\). With (5) and (6), using the equivalent transformation, the following received signal vector can be obtained as

$$\begin{aligned} \mathbf{x}_i =\mathbf{S}_i \mathbf{PGh}_i +\mathbf{z}_i =\mathbf{S}_i \mathbf{Pf}_i +\mathbf{z}_i \end{aligned}$$
(7)

where \(\mathbf{x}_i =[x_{i1},\ldots ,x_{iK}]^{T}\), \(\mathbf{P}=\hbox {diag}\{(P_0 P_1 \mu _1)^{1/2},\ldots ,(P_0 P_K \mu _K)^{1/2}\},\,\mathbf{h}_{i}=[h_{1},{\ldots },\,h_{K}]^{T}=[\alpha _{1i} \beta _{1i}, {\ldots } , \alpha _{Ki} \beta _{Ki}]^{T}\) is a vector that reflects small-scale fading, while \(\mathbf{G}=\hbox {diag}\{\rho _{s1}\rho _{1d},\,{\ldots },\rho _{sK} \rho _{Kd}\}\) is a diagonal matrix that reflects large-scale fading, and \(\mathbf{f}=\mathbf{Gh}_i =[\alpha _{1i} \beta _{1i} \rho _{s1} \rho _{1d},\ldots ,\alpha _{Ki} \beta _{Ki} \rho _{sK} \rho _{Kd} ]^{T}\) is a composite channel vector. As it is common to all differential schemes, here we assume that channel variation is negligible from one time block to the next, and thus we have: \(\mathbf{f}_{i}=\mathbf{f}_{i-1}\). \(\mathbf{z}_i =[z_{i1},\ldots , z_{iK} ]^{T}\) is \(K\times 1\) Gaussian noise vector with zero mean. Using the independent Gaussian distribution property of noises \(\{z_{i,dj}\}\) and \(\{z_{i,kj}\}\), the variance of the element of \(\mathbf{z}_{i}\), \(z_{ij} =\sum _{k=1}^K {\sqrt{P_k \mu _k }} \beta _{ik} \rho _{kd} z_{i,kj} +z_{i,dj} \), can be calculated as

$$\begin{aligned} E\left\{ z_{ij} z_{ij}^{*} \!\right\} \!=\!\left( \sum \nolimits _{k=1}^K {P_k } \rho _{kd}^2 \mu _k \!+\!1\!\right) N_0 \!=\!\kappa N_0 \!=\!\sigma _z^2 , \!\quad j\!=\!1,{\ldots },K.\qquad \end{aligned}$$
(8)

where \(\kappa =\sum _{k=1}^K {P_k } \rho _{kd}^2 \mu _k +1\), and thus we have: \(E\{\mathbf{z}_i \mathbf{z}_i^H \}=\sigma _z^2 \mathbf{I}_K \).

From (7), the received signal vector at time block i-1 can be expressed as

$$\begin{aligned} \mathbf{x}_{i-1} =\mathbf{S}_{i-1} \mathbf{Pf}_i +\mathbf{z}_{i-1} . \end{aligned}$$
(9)

with the obtained \(\mathbf{x}_{i}\) and \(\mathbf{x}_{i-1}\), \(\mathbf{D}_{i}\) can be detected. Specifically, substituting (4) and (9) into (7) gives

$$\begin{aligned} \mathbf{x}_i =\mathbf{D}_i \mathbf{S}_{i-1} \mathbf{Pf}+\mathbf{z}_i =\mathbf{D}_i \left( \mathbf{x}_{i-1} -\mathbf{z}_{i-1} \right) +\mathbf{z}_i =\mathbf{D}_i \mathbf{x}_{i-1} +\tilde{\mathbf{z}}_i \end{aligned}$$
(10)

where \(\tilde{\mathbf{z}}_i =\mathbf{z}_i -\mathbf{D}_i \mathbf{z}_{i-1}\) is an equivalent Gaussian noise vector with zero mean and covariance \(2\sigma _z^2 \mathbf{I}_K \), which utilizes the fact that the \(\mathbf{D}_{i}\) is an unitary matrix. According to this, we can see that the differential detection doubles the noise power, and thus the SNR loss of 3 db happens, which is also in agreement with the conventional differential modulation scheme.

Using (10), the differential detection for the information matrix \(\mathbf{D}_{i}\) can be given by

$$\begin{aligned} {\hat{\mathbf{D}}}_i= & {} \mathop {\arg \min }\limits _{\mathbf{D}_i } \left\| {\mathbf{x}_i -\mathbf{D}_i \mathbf{x}_{i-1} } \right\| ^{2}\nonumber \\= & {} \mathop {\arg \min }\limits _{\mathbf{D}_i } tr\left\{ (\mathbf{x}_i -\mathbf{D}_i \mathbf{x}_{i-1} )(\mathbf{x}_i -\mathbf{D}_i \mathbf{x}_{i-1} )^{H}\right\} \nonumber \\= & {} \mathop {\arg \max \hbox {Re}\{}\limits _{\mathbf{D}_i } tr(\mathbf{x}_{i-1} \mathbf{x}_i^H \mathbf{D}_i )\}. \end{aligned}$$
(11)

Substituting (1) into (11) yields the ML detector for the transmitted symbols \(\{d_{l}\}\,(l=1,{\ldots },L)\), i.e.,

$$\begin{aligned} \left\{ \hat{{d}}_l \right\} _{l=1}^L= & {} \mathop {\arg \max }\limits _{\left\{ d_l \right\} \in \Phi } \sum _{l=1}^L \left\{ \hbox {Re}\left\{ tr\left( \mathbf{x}_{i-1} \mathbf{x}_i^H \mathbf{U}_l \right) \right\} d_l^R \right. \nonumber \\&\left. +\,\hbox {Im}\left\{ tr\left( -\mathbf{x}_{i-1} \mathbf{x}_i^H \mathbf{V}_l \right) \right\} d_l^I \right\} . \end{aligned}$$
(12)

Thus, the ML detector of each symbol \(d_{l}\,(l=1,{\ldots },L)\) can be expressed as

$$\begin{aligned} \hat{{d}}_l= & {} \mathop {\arg \max }\limits _{d_l \in \Phi } \hbox {Re}\left\{ tr\left( \mathbf{x}_{i-1} \mathbf{x}_i^H \mathbf{U}_l \right) \right\} d_l^R \nonumber \\&+\,\hbox {Im}\left\{ tr\left( -\mathbf{x}_{i-1} \mathbf{x}_i^H \mathbf{V}_l \right) \right\} d_l^I. \end{aligned}$$
(13)

Equation (13) not only has linear decoding complexity, but also can be further changed into the detection of real part and imaginary part in parallel. Thus, this detector has a decoupled format, one scalar detector for each of the symbols \(\{d_{l}\}\). When compared with the detection method of other DSTC schemes for cooperative communication, our detection scheme has lower computational complexity. It is also due to the fact that our scheme can easily make use of the orthogonality of differential space-time code scheme. Besides, the analysis above can be extended to MQAM constellation modulation, but the encoding and decoding methods need to be changed accordingly. Namely, the encoding at the source terminal is performed in terms of Eq. (3), and the decoding at the destination terminal is done as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \hat{{d}}_l^R =\mathop {\arg \max }\limits _{d_l \in \Phi } \left\{ {\hbox {Re}\left\{ tr\left( \mathbf{x}_{i-1} \mathbf{x}_i^H \mathbf{U}_l \right) \right\} d_l^R -tr\left( \mathbf{x}_{i-1} \mathbf{x}_{i-1}^H \right) |d_l^R |^{2}/\left( \xi _{i-1} \sqrt{L}\right) } \right\} \\ \hat{{d}}_l^I =\mathop {\arg \max }\limits _{d_l \in \Phi } \left\{ {\hbox {Im}\left\{ -tr\left( \mathbf{x}_{i-1} \mathbf{x}_i^H \mathbf{V}_l \right) \right\} d_l^I -tr\left( \mathbf{x}_{i-1} \mathbf{x}_{i-1}^H \right) |d_l^I |^{2}/\left( \xi _{i-1} \sqrt{L}\right) } \right\} \\ \end{array}} \right. \end{aligned}$$
(14)

where the amplitude \(\xi _{i-1}\) can be estimated by Eq. (4) and the data symbols which have detected at the previous \((i-1)\)-th time block.

4 Power allocation for different network cases

4.1 Symmetric network case

In this section, we will give the power allocation between the source terminal and relay terminal by means of the PEP analysis. According to the analysis in Refs. [13, 19, 20], a differentially-coded system performance is well approximated at high SNR by using an equivalent coherent receiver model [i.e. Eq. (11)] with known channel matrix \(\mathbf{x}_{i-1}\) and enhanced noise power, and the corresponding performance analysis can also be obtained in terms of the PEP.

Let Pr\((\mathbf{D}\rightarrow \mathbf{E})\) be the PEP of the system, which is the probability of incorrectly decoding D as E, i.e., the probability of transmitting D and deciding in favor of another E at the detector [13, 20], and then this PEP can be given by the following (15) conditioned on equivalent channel vector \(\mathbf{x}_{i-1}\).

$$\begin{aligned} \Pr \left( \mathbf{D}\rightarrow \mathbf{E}|\mathbf{x}_{i-1} \right)= & {} Q\left( {\sqrt{E_s d^{2}(\mathbf{D},\mathbf{E})/(2N_0 )}} \right) \nonumber \\\le & {} \exp \left\{ -d^{2}\left( \mathbf{D},\mathbf{E}\right) E_s /\left( 4\sigma _z^2 \right) \right\} \nonumber \\= & {} \exp \left\{ -d^{2}\left( \mathbf{D},\mathbf{E}\right) E_s /\left( 4\kappa N_0 \right) \right\} \end{aligned}$$
(15)

where \(E_{s}\) is the averaged power per symbol period, and \(d^{2}(\mathbf{D},\mathbf{E})=\mathbf{x}_{i-1}^H \mathbf{C}^{H}{} \mathbf{Cx}_{i-1} \), \(\mathbf{C}=\mathbf{D}_i -\mathbf{E}_i \).

For high SNR, (10) can be approximately equivalent to

$$\begin{aligned} \mathbf{x}_{i-1} \approx \mathbf{S}_{i-1} \mathbf{Pf}_i =\mathbf{S}_{i-1} \mathbf{PGh}_i \end{aligned}$$
(16)

With (16), we have:

$$\begin{aligned} d^{2}\left( \mathbf{D},\mathbf{E}\right)\approx & {} \mathbf{f}^{H}{} \mathbf{PS}_{i-1}^H \mathbf{C}^{H}{} \mathbf{CS}_{i-1} \mathbf{Pf}_i \nonumber \\= & {} \mathbf{h}_i^H \mathbf{G}^{H}\mathbf{PS}_{i-1}^H \mathbf{C}^{H}{} \mathbf{CS}_{i-1} \mathbf{PGh}_i \end{aligned}$$
(17)

Substituting (17) into (15) yields

$$\begin{aligned}&\Pr \left( \mathbf{D}\rightarrow \mathbf{E}|\mathbf{x}_{i-1} \right) \nonumber \\&\quad \le \exp \left\{ -\mathbf{h}_i^H \mathbf{G}^{H}{} \mathbf{PS}_{i-1}^H \mathbf{C}^{H}{} \mathbf{CS}_{i-1} \mathbf{PGh}_i E_s /(4\kappa N_0 )\right\} \end{aligned}$$
(18)

Based on the analysis in Refs. [13, 19, 21], the received signal vector \(\mathbf{x}_{i}\) can be approximated as a linear combination of \(\mathbf{h}_{i}\), so it constitutes a set of dependent channel coefficients. As a result, \(\mathbf{x}_{i}\) is also a Gaussian vector conditioned on \(\{{\beta }_{ik}\}\).

With the derivation results under two-relay cases in “Appendix 1”, we can establish the corresponding optimized objective function on PA under the total power \(P_{t}\) constraint as

$$\begin{aligned} \mathcal{L}\left( P_0 ,P_1 ,P_2 \right)= & {} \mu _1 \mu _2 P_0^2 P_1 P_2 /\left( P_1 \rho _{1d}^2 \mu _1 +P_2 \rho _{2d}^2 \mu _2 +1\right) ^{2}\nonumber \\&+\,\eta \left( P_t -2P_0 -P_1 -P_2 \right) \end{aligned}$$
(19)

where \(\eta \) is a Lagrange multiplier. Besides, according to the analysis in “Appendix 1”, the system may obtain full diversity order, as expected.

In the following, we firstly consider the symmetric network case, where the distances between source and relay terminals are the same, and the distances between relays and destination terminal are also the same. Correspondingly, \(\rho _{s1}= \rho _{s2}\) and \(\rho _{1d}= \rho _{2d}\). Thus, we have:

$$\begin{aligned} \mu _1 =1/\left( P_0 \rho _{s1}^2 +2N_0 \right) =1/\left( P_0 \rho _{s2}^2 +2N_0 \right) =\mu _2 \end{aligned}$$
(20)

Substituting (20) into (19) gives

$$\begin{aligned} \mathcal{L}\left( P_0 ,P_1 ,P_2 \right)= & {} P_0^2 P_1 P_2 /\left( P_1 \rho _{1d}^2 +P_2 \rho _{1d}^2 +1/\mu _1 \right) ^{2}\nonumber \\&+\,\eta \left( P_t -2P_0 -P_1 -P_2 \right) \nonumber \\= & {} P_0^2 P_1 P_2 /\left( P_1 \rho _{1d}^2 +P_2 \rho _{1d}^2 +P_0 \rho _{s1}^2+2N_0\right) ^{2} \nonumber \\&+\eta \left( P_t -2P_0 -P_1 -P_2 \right) \end{aligned}$$
(21)

Due to the symmetry of \(P_{1}\) and \(P_{2}\) in (21), it is easily achievable that \(P_{1}=P_{2}\). Thus (21) is reduced to

$$\begin{aligned} \mathcal{L}\left( P_0 ,P_1 \right)= & {} P_0^2 P_1^2 /\left[ 2P_1 \rho _{1d}^2+P_0 \rho _{s1}^2 +2N_0 \right] ^{2}\nonumber \\&+\eta \left( P_t -2P_0 -2P_1 \right) \end{aligned}$$
(22)

By taking the derivatives of (22) with respect to \(\{P_{k},\,k=0,1\}\) and equating to zero yields

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\partial \mathcal{L}}{\partial P_0 }=\frac{2P_0 P_1^2 \left( 2P_1 \rho _{1d}^2 +P_0 \rho _{s1}^2 +2N_0 \right) -2P_0^2 P_1^2 \rho _{s1}^2 }{\left[ 2P_1 \rho _{1d}^2 +P_0 \rho _{s1}^2 +2N_0 \right] ^{3}}-2\eta =0 \\ \frac{\partial \mathcal{L}}{\partial P_1 }=\frac{2P_0^2 P_1 \left( 2P_1 \rho _{1d}^2 +P_0 \rho _{s1}^2 +2N_0 \right) -4P_0^2 P_1^2 \rho _{1d}^2 }{\left[ 2P_1 \rho _{1d}^2 +P_0 \rho _{s1}^2 +2N_0 \right] ^{3}}-2\eta =0 \end{array}} \right. \end{aligned}$$
(23)

With (23), the following equation is obtained, i.e.,

$$\begin{aligned} P_0^2 \rho _{s1}^2 +2N_0 P_0 -2P_1^2 \rho _{1d}^2 -2N_0 P_1 =0 \end{aligned}$$
(24)

Utilizing (24) and the condition \(2P_{0}+2P_{1}=P_{t}\), one quadratic equation on \(P_{0}\) or \(P_{1}\) is established. After solving this equation, we have the following optimal PA, i.e.,

$$\begin{aligned} \left\{ {\begin{array}{l} P_0 =\left[ \sqrt{\left( P_t \rho _{1d}^2 +2N_0 \right) \left( P_t \rho _{s1}^2 /2+2N_0 \right) }-\left( 2N_0 +P_t \rho _{1d}^2 \right) \right] \big /\left( \rho _{s1}^2 -2\rho _{1d}^2 \right) \\ P_1 =P_2 =\left[ \left( 2N_0 +P_t \rho _{s1}^2 /2\right) -\sqrt{\left( P_t \rho _{1d}^2 +2N_0 \right) \left( P_t \rho _{s1}^2 /2+2N_0 \right) }\right] \big /\left( \rho _{s1}^2 -2\rho _{1d}^2 \right) \end{array}} \right. \end{aligned}$$
(25)

Similarly, by using the above analysis and derivation method, we can achieve the optimal PA for three and four relays under symmetric network, respectively. Specifically,

(1) for three relays

$$\begin{aligned} \left\{ {\begin{array}{l} P_0 =\left[ \sqrt{\left( P_t \rho _{1d}^2 +2N_0 \right) \left( P_t \rho _{s1}^2 /3+2N_0 \right) }-\left( 2N_0 +P_t \rho _{1d}^2 \right) \right] \big /\left( \rho _{s1}^2 -3\rho _{1d}^2 \right) \\ P_1 =P_2 =P_3 =\left[ \left( 2N_0 +P_t \rho _{s1}^2 /3\right) -\sqrt{\left( P_t \rho _{1d}^2 +2N_0 \right) \left( P_t \rho _{s1}^2 /3+2N_0 \right) }\right] \big /\left( \rho _{s1}^2 -3\rho _{1d}^2 \right) \end{array}} \right. \end{aligned}$$
(26)

(2) for four relays

$$\begin{aligned} \left\{ {\begin{array}{l} P_0 =\left[ \sqrt{\left( P_t \rho _{1d}^2 +2N_0 \right) \left( P_t \rho _{s1}^2 /4+2N_0 \right) }-\left( 2N_0 +P_t \rho _{1d}^2 \right) \right] \big /\left( \rho _{s1}^2 -4\rho _{1d}^2 \right) \\ P_1 =P_2 =P_3 =P_4 =\left[ \left( 2N_0 +P_t \rho _{s1}^2 /4\right) -\sqrt{\left( P_t \rho _{1d}^2 +2N_0 \right) \left( P_t \rho _{s1}^2 /4+2N_0 \right) }\right] \big /\left( \rho _{s1}^2 -4\rho _{1d}^2 \right) \end{array}} \right. \end{aligned}$$
(27)

Based on the optimal PA above, the system performance will be improved greatly, and is obviously superior to the performance with conventional fixed PA.

4.2 Asymmetric network case

In the subsection above, the PA of the distributed DSTC under symmetric network is presented. In practice, however, the network may be asymmetric, i.e., the distances between source and relay terminals are different, or the distances between relays and destination terminal are different. Thus, we have: \(\rho _{sk} \ne \rho _{su}\) or \(\rho _{kd} \ne \rho _{ud}\) for relay k and \(u\,(k\ne u)\). According to this, it is necessary to extend the above PA to asymmetric case. Unfortunately, the related analysis and optimized design are much less due to the difficulty of optimization. For this reason, we will provide the optimization of PA to meet practical asymmetric network. For simplicity, two-relay asymmetry network (i.e. \(\rho _{s1} \ne \rho _{s2},\,\rho _{1d} \ne \rho _{2d}\)) is firstly considered.

Utilizing \(\mu _k =1/(P_0 \rho _{sk}^2 +2N_0 )\), \(k=1,2\), (19) is changed to

$$\begin{aligned}&\mathcal{L}\left( P_0 ,P_1 ,P_2 \right) =\frac{P_0^2 P_1 P_2 \left[ P_0^2 \rho _{s1}^2 \rho _{s2}^2 +2N_0 P_0 \left( \rho _{s1}^2 +\rho _{s2}^2 \right) +4N_0^2 \right] }{\left[ P_1 P_0 \rho _{1d}^2 \rho _{s2}^2 +P_2 P_0 \rho _{2d}^2 \rho _{s1}^2 +P_0^2 \rho _{s1}^2 \rho _{s2}^2 +2N_0 \left( P_1 \rho _{1d}^2 +P_2 \rho _{2d}^2 +P_0 \rho _{s1}^2 +P_0 \rho _{s2}^2 \right) +4N_0^2 \right] ^{2}} \nonumber \\&\quad +\eta \left( P_t -2P_0 -P_1 -P_2 \right) \end{aligned}$$
(28)

With (28), using the derivation in “Appendix 2”, we can obtain a cubic equation on \(P_{0}\) as follows:

$$\begin{aligned}&\left( 4\rho _{s1}^2 \rho _{s2}^2 -8\rho _{s1}^2 \rho _{2d}^2 -8\rho _{s2}^2 \rho _{1d}^2 \right. \nonumber \\&\qquad \left. +\,16\rho _{1d}^2 \rho _{2d}^2 \right) P_0^3 +\left( 12\rho _{s1}^2 N_0 +12\rho _{s2}^2 N_0 +6\rho _{s1}^2 \rho _{2d}^2 P_t\right. \nonumber \\&\qquad +\,6\rho _{s2}^2 \rho _{1d}^2 P_t -24\rho _{2d}^2 N_0 -24\rho _{1d}^2 N_0\nonumber \\&\qquad \left. -\,24\rho _{1d}^2 \rho _{2d}^2 P_t \right) P_0^2 +\left( 20\rho _{2d}^2 N_0 P_t +20\rho _{1d}^2 N_0 P_t\right. \nonumber \\&\qquad +\,32N_0^2 -2\rho _{s1}^2 N_0 P_t-2\rho _{s2}^2 N_0 P_t\nonumber \\&\qquad -\,\rho _{s1}^2 \rho _{2d}^2 P_t^2 -\rho _{s2}^2 \rho _{1d}^2 P_t^2 \nonumber \\&\qquad \left. +\,12\rho _{1d}^2 \rho _{2d}^2 P_t^2 \right) P_0 -4\rho _{1d}^2 N_0 P_t^2 \nonumber \\&\qquad -\,4\rho _{2d}^2 N_0 P_t^2 -8N_0^2 P_t -2\rho _{1d}^2 \rho _{2d}^2 P_t^3 =0 \end{aligned}$$
(29)

To obtain the solution of this cubic equation, we will resort to the Shengjin’s Formulas in [22]. For a cubic equation in one variable: \(aX^{3}+bX^{2}+cX+d=0\), \(a\ne 0\), the Shengjin’s Formulas provide the closed-form solutions. Firstly, we may use the following Shengjin’s discriminant \(\Delta \) to decide the existence condition of solutions. i.e.,

$$\begin{aligned} \Delta= & {} B^{2}-4AC,\hbox { and }A=b^{2}-3ac,\,B=bc-9ad,\nonumber \\ C= & {} c^{2}-3bd. \end{aligned}$$
(30)

From (29), the coefficients \(\{a,\,b,\,c,\,d\}\) in cubic equation can be given by

$$\begin{aligned} a= & {} 4\rho _{s1}^2 \rho _{s2}^2 -8\rho _{s1}^2 \rho _{2d}^2 -8\rho _{s2}^2 \rho _{1d}^2 +16\rho _{1d}^2 \rho _{2d}^2 , \\ d= & {} -4\rho _{1d}^2 N_0 P_t^2 -4\rho _{2d}^2 N_0 P_t^2 -8N_0^2 P_t -2\rho _{1d}^2 \rho _{2d}^2 P_t^3 ,\\ b= & {} 12\rho _{s1}^2 N_0 +12\rho _{s2}^2 N_0 +6\rho _{s1}^2 \rho _{2d}^2 P_t +6\rho _{s2}^2 \rho _{1d}^2 P_t \\&-\,24\rho _{2d}^2 N_0 -24\rho _{1d}^2 N_0 -24\rho _{1d}^2 \rho _{2d}^2 P_t ,\\ c= & {} 20\rho _{2d}^2 N_0 P_t +20\rho _{1d}^2 N_0 P_t +32N_0^2 -2\rho _{s1}^2 N_0 P_t \\&-,2\rho _{s2}^2 N_0 P_t -\rho _{s1}^2 \rho _{2d}^2 P_t^2 -\rho _{s2}^2 \rho _{1d}^2 P_t^2 +12\rho _{1d}^2 \rho _{2d}^2 P_t^2 . \end{aligned}$$

Then, according to different values of \(\Delta \), we may use the corresponding Shengjin’s Formulas to evaluate the solutions of \(P_{0}\). Considering the power constraint \((2P_{0}+P_{1}+P_{2}=P_{t}),\,P_{1}>0,\,P_{2}>0\), and \(P_{0}>0\), we have: \(P_{0}<P_{t}/2\). Utilizing these constraint conditions, we can easily obtain the appropriate solution of \(P_{0}\). With the obtained \(P_{0}\), using (56) and (55) in “Appendix 2”, \(P_{1}\) and \(P_{2}\) can be finally achieved.

For two special asymmetric network cases (1) \(\rho _{s1} \ne \rho _{s2}\), \(\rho _{1d}=\rho _{2d}\); and (2) \(\rho _{s1}=\rho _{s2}\), \(\rho _{1d} \ne \rho _{2d}\), we can employ the above formulas to obtain the corresponding optimal PA as well. Moreover, the related calculations will become simpler due to special network cases.

In addition, considering that the relay terminals are often close to the source terminal (i.e., the distances between source and relay terminals are smaller than those between relays and destination terminal), \(\rho _{sk}\) is larger than \(\rho _{kd}\) in general. Correspondingly, the value of \(\Delta \) in (30) is often smaller than zero. Hence, Shengjin’s Formula 4 [22] is used to evaluate the solution of \(P_{0}\). Based on the previous constraint condition \((0< P_{0}<P_{t}/2)\), \(P_{0}\) will take the value of \(X_{2}\) in Formula 4 [22], i.e.,

$$\begin{aligned} P_0 =\frac{-b+A^{1/2}\left[ \cos (\theta /3)+3^{1/2}\sin (\theta /3)\right] }{3a} \end{aligned}$$
(31)

where \(\theta =\hbox {arccos}T,\,T=(2{ Ab}-3{ aB})/(2A^{3/2})\), and a, b, c and d are coefficients of cubic equation. In “Appendix 3”, the derivation on Shengjin’s Formula 4 is provided, and based on this, (31) is obtained. Substituting (31) into (56) yields the \(P_{1}\), and then substituting the obtained \(P_{0}\) and \(P_{1}\) into (55), the \(P_{2}\) is finally achieved.

For the asymmetric network with more than two relay users, we employ similar analytical method above for the corresponding power optimization, and the resultant superior performance is attained. However, the related computation will be much complicated because it needs to evaluate the solution of high-order equation. For this, we will resort to the Newton method to obtain the suboptimal solution. For three relays case, the objective function corresponding to (19) is changed to

$$\begin{aligned} \mathcal{L}\left( P_0 ,P_1 ,P_2 ,P_3 \right)= & {} \mu _1 \mu _2 \mu _3 P_0^3 P_1 P_2 P_3 /\left( P_1 \rho _{1d}^2 \mu _1 \right. \nonumber \\&\left. +P_2 \rho _{2d}^2 \mu _2 +P_3 \rho _{3d}^2 \mu _3 +1\right) ^{3} \nonumber \\&+\eta \left( P_t -3P_0 -P_1 -P_2 -P_3 \right) .\nonumber \\ \end{aligned}$$
(32)

With (32), we can use the quasi-Newton method to find the solution on \(\{P_{0},\,P_{1},\,P_{2},\,P_{3}\}\), i.e.,

$$\begin{aligned} \mathbf{y}^{(n+1)}=\mathbf{y}^{(n)}-\gamma \mathbf{H}^{-1}{} \mathbf{g}^{T} \end{aligned}$$
(33)

where \(\mathbf{y}=[y_{1},\,y_{2},\,y_{3},\,y_{4},\,y_{5}]^{T}\), and \(y_{1}= P_{0},\,y_{2}=P_{1},\,y_{3}=P_{2},\,y_{4}=P_{3},\,y_{5}= \eta \). The initial value \(\mathbf{y}^{(0)}\) may take some small positive values. n is the iterative index, and the iterative times depend on the given tolerance. Once the difference of \(\mathbf{y}^{(n+1)}\) and \(\mathbf{y}^{(n)}\) is very small and satisfies the tolerance requirement, and the iteration is terminated. \(\gamma \) is adjustment step. The gradient vector g and Hessian matrix H are defined as follows:

$$\begin{aligned} \mathbf{g}= & {} \left[ {\frac{\partial \mathcal{L}}{\partial y_1 },\frac{\partial \mathcal{L}}{\partial y_2 },\frac{\partial \mathcal{L}}{\partial y_3 },\frac{\partial \mathcal{L}}{\partial y_4 },\frac{\partial \mathcal{L}}{\partial y_5 }} \right] ^{T}, \nonumber \\ \mathbf{H}= & {} \left[ {{\begin{array}{ccc} {\frac{\partial ^{2}\mathcal{L}}{\partial y_1^2 }}&{} \cdots &{} {\frac{\partial ^{2}\mathcal{L}}{\partial y_1 \partial y_5 }} \\ \vdots &{} \ddots &{} \vdots \\ {\frac{\partial ^{2}\mathcal{L}}{\partial y_5 \partial y_1 }}&{} \cdots &{} {\frac{\partial ^{2}\mathcal{L}}{\partial y_5^2 }} \\ \end{array} }} \right] . \end{aligned}$$
(34)

By using the iterative calculation above, the suboptimal PA for three-relay case can be obtained. With these PAs, the system performance will be improved greatly. Similarly, for more than three relay asymmetric case, we can also employ the Newton method above to find suboptimal PA to achieve the superior performance. All these results will provide useful guideline for the system design.

5 DF protocol based DSTC scheme

In this section, we will give another DSTC scheme based on the DF method. According to the principle of DF method, and considering that the CSI is absent at both relay terminals and destination terminal, two differential schemes are employed for decoding at relay terminals and destination terminal, respectively. Moreover, these two schemes will be different, i.e., one is based on the single-symbol differential modulation, and the other is based on differential space-time modulation.

With the analysis in Sect. 1, L information symbols \(\{d_{l,} l=1,{\ldots }L\}\) used for space-time coding will be transmitted at the source terminal (the information symbols will depend on different STC schemes). Firstly, these symbols are differentially encoded in terms of the following differential PSK modulation.

$$\begin{aligned} s_l =s_{l-1} d_l , \quad l=1,{\ldots } L, \end{aligned}$$
(35)

where the initial value \(s_{0}=1\), \(\{d_{l}\}\) are from MPSK constellation\(\Phi \). Then, these encoded symbols are transmitted to all relay terminals by broadcasting from \((L+1)\) different slots. Thus, according to (5), at k relay terminal, the received signals at the \(l-1\) and l time slots can be, respectively, written as

$$\begin{aligned} r_{l-1,k}= & {} \sqrt{P_0 }\rho _{sk} \alpha _{l-1,k} s_{l-1,k} +z_{l-1,k} \end{aligned}$$
(36)
$$\begin{aligned} r_{l,k}= & {} \sqrt{P_0 }\rho _{sk} \alpha _{l,k} s_{l,k} +z_{l,k} \end{aligned}$$
(37)

where \(z_{l-1,k}\) and \(z_{l,k}\) are relay noises at the time slot \(l-1\) and l, respectively, and they are modeled as independent complex Gaussian random variables with zero-mean and variances \(N_{0}\). \(P_{0}\) is transmit power of source terminal. Here, we assume that channel variation is negligible from one time slot to the next. Thus, we have: \(\alpha _{l-1,k}= \alpha _{l,k}\), \(k=1,{\ldots }K\). Based on this, using (35) and (36), (37) can be changed to

$$\begin{aligned} r_{l,k} =\left( r_{l-1,k} -z_{l-1,k} \right) d_l +z_{l,k} =r_{l-1,k} d_l +\tilde{z}_{l,k} \end{aligned}$$
(38)

where \(\tilde{z}_{l,k} =z_{l,k} -z_{l-1,k} d_l\) is an equivalent noise with zero-mean and variance \(2N_{0}\).

With (38), we can obtain the decision of symbol \(d_{l}\). i.e.,

$$\begin{aligned} \hat{{d}}_l =\mathop {\arg \max }\limits _{d_l \in \Phi } \hbox {Re}\left\{ r_{l,k}^{*} r_{l-1,k} d_l \right\} \end{aligned}$$
(39)

Since K relays perform independent decoding, the K decision values \(\hat{{d}}_{l,k}\,(k=1,{\ldots },K)\) for \(\{ d_{l}\}\) will be produced. At low SNR, the noise becomes a dominant factor to affect the bit error rate (BER) performance, so these K decision values will be approximately identical. Moreover, for symmetric network, these K values are also approximately the same because K channels from source to relay terminals will experience almost the same fading. For asymmetric network, at high SNR, the above K decision values may have some differences due to different fading cases, but the differences will be small since the probability of decoding error has become low at high SNR. So these decision values will be asymptotically identical, and the corresponding performance is influenced less. After that, with the obtained decision symbols, the information bits are generated by the symbol demapping accordingly, which will be employed for the space-time coding at the relay terminals.

In the second transmission phase, each relay (such as relay k) re-encodes the decoded information data in terms of the given modulation mode (this mode may be different with that at source terminal) and generates the corresponding data symbols \(\{c_{lk}\}\), and then these symbols are space-time coded according to the given STC scheme. Here, the STC matrix is constructed by (1). Thus, for relay \(k\,(k=1,{\ldots },K)\), the information code matrix at time block i is written as

$$\begin{aligned} \mathbf{C}_{i,k} =\frac{1}{\sqrt{L}}\sum _{l=1}^L \left( \mathbf{U}_l c_{lk}^R +j\mathbf{V}_l c_{lk}^I \right) \end{aligned}$$
(40)

where \(c_{lk}^R\) and \(c_{lk}^I\) denote the real and imaginary parts of \(c_{lk}\), respectively. To transmit the data in absence of CSI, the differential space-time modulation is employed, i.e.,

$$\begin{aligned} \mathbf{S}_{i,k} =\mathbf{C}_{i,k} \mathbf{S}_{i-1,k} \end{aligned}$$
(41)

where \(\mathbf{S}_{0,k} =\mathbf{I}_{K}\) is the initial code matrix. After differential modulation, the relay k only transmits the \(k\hbox {th}\) column \(\mathbf{s}_{i,k}\) of \(\mathbf{S}_{i,k}\), and these columns are transmitted simultaneously. From (41), \(\mathbf{s}_{i,k}=\mathbf{C}_{i,k}{} \mathbf{s}_{i-1,k}\) is obtained.

At the destination terminal, the received signal vector at time i can be expressed as

$$\begin{aligned} \mathbf{r}_{i,d}= & {} \left[ {\sqrt{P_1 }{} \mathbf{s}_{i,1} }\,\, {\sqrt{P_2 }{} \mathbf{s}_{i,2} } \,\, \cdots \,\,{\sqrt{P_K }{} \mathbf{s}_{i,K} } \right] \nonumber \\&\quad \left[ {h_{i,1} }\,\, {h_{i,2} }\,\,\cdots \,\, {h_{i,K} } \right] ^{T}+\mathbf{z}_{i,d} =\mathbf{Y}_i \mathbf{Ph}_i +\mathbf{z}_{i,d} \end{aligned}$$
(42)

where \(P_{k} (k=1,{\ldots },K)\) is the transmit power of relay k, \(\mathbf{P}=\hbox {diag}\{P_{1}^{1/2},{\ldots },P_{K}^{1/2}\}\), \(h_{i,k}=\rho _{kd}\beta _{i,k},\mathbf{h}_{i}=[h_{i,1},{\ldots }h_{i,K}]^{T}\), \(\mathbf{Y}_{i}=[\mathbf{s}_{i,1},\,\mathbf{s}_{i,2},\,{\ldots }{} \mathbf{s}_{i,K}]\). Note that \(\mathbf{Y}_{i}\) is different with \(\mathbf{S}_{i,k}\) in that its columns are from different relays, whereas the columns of \(\mathbf{S}_{i,k}\) are from the same relay k. \(\mathbf{z}_{i,d} =[z_{i1,d} ,\ldots ,z_{iK,d} ]^{T}\) is the noise vector, and its elements are independent complex Gaussian random variables with zero-mean and variances \(N_{0}\). Similarly, at time \(i-1\), the corresponding received signal vector is written as

$$\begin{aligned} \mathbf{r}_{i-1,d}= & {} \left[ {\sqrt{P_1 }{} \mathbf{s}_{i-1,1} } \,\, {\sqrt{P_2 }{} \mathbf{s}_{i-1,2} } \,\, \cdots \,\, {\sqrt{P_K }\mathbf{s}_{i-1,K} } \right] \nonumber \\&\quad \mathbf{h}_i +\mathbf{z}_{i-1,d} =\mathbf{Y}_{i-1} \mathbf{Ph}_i +\mathbf{z}_{i-1,d} \end{aligned}$$
(43)

where the channel is assumed to keep unchanged at two consecutive time blocks, i.e., \(\mathbf{h}_{i-1}=\mathbf{h}_{i}\) is utilized.

With the above analytical results, we may assume that \(\mathbf{C}_{i,k}\) is approximately equal to \(\mathbf{C}_{i,u}\) for different k and u, and thus the index k of \(\mathbf{C}_{i,k}\) may be dropped for analysis simplicity. Hence, with (42) and (43), using \(\mathbf{s}_{i,k}\approx \mathbf{C}_{i}{} \mathbf{s}_{i-1,k}\) for different k, we have:

$$\begin{aligned} \mathbf{r}_{i,d} \approx \mathbf{C}_i \mathbf{r}_{i-1,d} +\tilde{\mathbf{z}}_{i,d} \end{aligned}$$
(44)

where \(\tilde{\mathbf{z}}_{i,d} \approx \mathbf{z}_{i,d} -\mathbf{C}_i \mathbf{z}_{i-1,d}\) is an equivalent Gaussian noise matrix with zero mean and covariance \(2N_{0}{} \mathbf{I}_{K}\). Employing the analytical method in Eqs. (12) and (13), the approximate expression similar to (14) for ML detector of each transmitted symbol \(c_{l}\) can be obtained as

$$\begin{aligned}&\hat{{c}}_l \mathop {\approx \arg \max }\limits _{c_l \in \Phi } \left\{ tr\left( \mathbf{r}_{i-1,d} \mathbf{r}_{i,d}^H \mathbf{U}_l \right) \right\} c_l^R \nonumber \\&\quad +\hbox {Im}\left\{ tr\left( -\mathbf{r}_{i-1,d} \mathbf{r}_{i,d}^H \mathbf{V}_l \right) \right\} c_l^I \end{aligned}$$
(45)

Using the symbol demapper, the information bits are finally attained. If the decoded data are almost inerrable at relays, the decision of (45) will be more accurate, and the resulting BER becomes lower due to the full utilization of diversity gains. Considering that the decoding error does exist at the relay, the decision of (45) will be affected. Correspondingly, the BER will be increased to some extent, especially at high SNR. Besides, for symmetric network, (45) is effective. However, for asymmetric network at high SNR, it will produce some decoding errors since the approximation \(\mathbf{C}_{i,k} \approx \mathbf{C}_{i,u}\) is not strict under this case.

Based on the analysis above, the DF method will increase the computational complexity at relays due to the requirement of timely decoding, but this method can effectively avoid the amplification of relay noise from AF method. Hence, its performance will outperform that of AF method. Moreover, it can provide the flexibility of encoding scheme for the information bits at the relays in a spectrum efficient manner, which is also not implemented by the AF method. Besides, the above differential scheme is also suitable for the application of other STC schemes to implement different cooperative diversity. For example, when USTC [20] is employed, the presented scheme above will correspond to the distributed differential USTC (DDUSTC). Although [16] also gives a DDUSTC scheme, the scheme is only designed for the diagonal USTC, whereas our DDUSTC scheme has no this limitation. Thus, it will have generality. Moreover, from the view of complexity, the former needs \(M^{K}\) search times for decoding, while our DDUSTC scheme needs \(KM+M\) search times, where M is the symbol constellation size and often chosen to equal the cardinality of \(\mathcal {G}\) (i.e., the number of USTC matrix in \(\mathcal {G}\), where \(\mathcal {G}\) represents a group which consists of \(K\times K\) USTC matrices \(\{\mathbf{C}_{m}\}\) [20]). Thus, our scheme will have lower complexity.

6 Simulation results

In this section, we will use computer simulation to verify the effectiveness of the developed distributed DSTC schemes and PA scheme in composite Rayleigh channel including large-scale and small-scale fading. In simulation, Gray code is employed to map the data bits to symbol constellations. The symmetric and asymmetric networks are both considered for performance evaluation. The 2-antenna and 3-antenna orthogonal STC from amicable orthogonality are used for different STC schemes, and correspondingly, two and three relays are employed. The average BER is obtained by averaging the \(10^{7}\) Monte Carlo simulations, and the results are illustrated in Figs. 2, 3, 4, 5 and 6. In these figures, the noise variance is normalized to unit, and the total transmit power \(P_{t}\) is defined as the SNR accordingly.

Fig. 2
figure 2

BER of AF based differential and coherent DTC scheme with FPA and OPA for 2-relay symmetric network case

Full size image
Fig. 3
figure 3

BER of AF based differential and coherent DTC scheme with FPA and OPA for 3-relay symmetric network case

Full size image
Fig. 4
figure 4

BER of AF based differential and coherent DTC scheme with FPA and OPA for 2-relay asymmetric network

Full size image
Fig. 5
figure 5

BER of AF based differential and coherent DTC scheme with FPA and OPA for 3-relay asymmetric network

Full size image
Fig. 6
figure 6

BER of distributed differential DTC schemes with AF and DF methods for different network cases. a Symmetric network. b Asymmetric network

Full size image

Figure 2 shows the BER performance of the developed distributed DSTC schemes based on AF method with coherent detection and differential detection for two relays. To testify the validity of the optimized PA scheme, we also give the comparison of fixed PA (FPA) and optimal PA (OPA), where the OPA scheme is from Eq.(25), and the FPA scheme corresponds to equal PA (i.e., \(P_{0}=P_{1}=P_{2}=P_{t}/4\)). In Fig. 2, the symmetric network situation that the distance between source and relay terminals is the one-third of the distance between relays and destination terminal is considered, and thus we may assume that \(\rho _{1d}=\rho _{2d}=1\) and \(\rho _{s1}=\rho _{s2}=\sqrt{27}\), where the path-loss exponent is set as 3. QPSK and 16PSK are employed for modulations. From Fig. 2, it can be seen that our differential scheme has performance loss of about 3dB as expected when compared with the corresponding coherent scheme. To implement the coherent scheme, however, the perfect CSI is required at the receiver, whereas our differential scheme does not need CSI at both receiver and transmitter, which will greatly decrease the realization complexity and increases the transmission efficiency. Moreover, it is found that the derived OPA scheme obtains better performance than the FPA scheme, at the BER of \(10^{-3}\), it achieves close to 2 dB gain for both QPSK and 16PSK modulations. Besides, the systems with QPSK outperform those with 16PSK. This is because the constellation points of high-order constellation are densely packed and prone to errors in fading channel.

Figure 3 gives the BER performance comparison of the AF method based distributed DSTC schemes with three relays under symmetric network, the channel parameters are set similar to those in Fig. 2, i.e., \(\rho _{1d}= \rho _{2d} =\rho _{3d} =1\) and \(\rho _{s1}=\rho _{s2}=\rho _{s3}=\sqrt{27}\). The OPA scheme is from Eq. (26). The FPA scheme corresponds to equal PA (i.e. \(P_{0}=P_{1}=P_{2}=P_{3}=P_{t}/6\)). The QPSK and 16PSK are used for modulations. As shown in Fig. 3, we can obtain the same conclusions as Fig. 2. Compared to the differential scheme with OPA, the coherent scheme with OPA has about 3 dB gain at the same BER, which accords with the existing knowledge. The results indicate that our OPA scheme can be applied to coherent case and obtain superior performance. Besides, by comparing Figs. 2 and 3, it is found that the BER performance with 3 relays is better than that with 2 relays because of more cooperative diversity gains. Moreover, with the growth of the modulation size, the BER performance decreases due to the reason analyzed in Fig. 2. The above results show that the proposed DSTC scheme and optimal PA for symmetric network are valid and reasonable.

To testify the validity of the proposed PA scheme under asymmetric network, we give the BER performance comparison for distributed DSTC scheme with AF method in Figs. 4 and 5, where QPSK and 16PSK modulations are used. In Fig. 4, two-relay asymmetric network with \(\rho _{1d}=1,\,\rho _{2d}=\sqrt{3}\) and \(\rho _{s1}=\sqrt{27},\, \rho _{s2}=\sqrt{125}\) is considered. The FPA scheme is set as to equal PA (i.e. \(P_{0}=P_{1}=P_{2}=P_{t}/4\)), and the OPA scheme is based on the derivation in Sect. 4.2 [i.e., (31), (56) and (55) are used]. It is observed that the OPA scheme has obvious performance superiority over FPA scheme, and gives about 2 dB gain over the latter. Moreover, the performance of OPA scheme with 16PSK is worse than that with QPSK as expected. For further comparison, we provide the performance results under three-relay asymmetric network in Fig. 5, where \(\rho _{1d}=1,\,\rho _{2d}=\sqrt{2}\), \(\rho _{3d}=\sqrt{3}\) and \(\rho _{s1}=\sqrt{27}\), \(\rho _{s2}=\sqrt{64}\), \(\rho _{s3}=\sqrt{125}\) are considered. The optimal PA scheme is obtained by (33) and (34), i.e., it is from the iterative calculation of Newton method. As shown in Fig. 5, the derived PA scheme is also effective for three-relay asymmetric network, and its performance is superior to that with FPA scheme. At BER of \(10^{-4}\), it achieves close to 2 dB gain for QPSK or 16PSK modulation. By comparing Figs. 4 and 5, it is found that the system with 3 relays has better BER performance than that with 2 relays due to greater cooperative diversity gains. All these results indicate that the derived two OPA schemes for asymmetric network are valid and reasonable, which will provide helpful guideline for the practical system design.

Figure 6 shows the BER performance of the distributed DSTC scheme based on DF method under different fading cases, where two and three relays are considered, QPSK and equal PA are employed. For comparison, the performance of the AF method based DSTC scheme is also provided. In Fig. 6a, the symmetric network is considered, where \(\rho _{1d}= \rho _{2d} =1\) and \(\rho _{s1}=\rho _{s2}=\sqrt{64}\) for two relays, and \(\rho _{1d}= \rho _{2d} = \rho _{3d} =1\) and \(\rho _{s1}=\rho _{s2}=\rho _{s3}=\sqrt{64}\) for three relays. It is observed that the scheme with DF method outperforms that with AF method. Especially at low SNR, the noise becomes the dominant factor to affect the performance, and the performance superiority from the DF scheme becomes very obvious because no noise power is amplified. Under this case, the performance of scheme with AF method becomes worse due to the amplification of noise power. At high SNR, however, the performance superiority will decrease because of the decoding error propagation from the relay terminals for DF scheme. Besides, by comparing the BERs of two relays and three relays, three-relay system has better BER performance than two-relay system for both DF and AF schemes. This is because more cooperative diversity gains are available.

In Fig. 6b, the asymmetric network is considered, where \(\rho _{1d}=1,\,\rho _{2d}=\sqrt{2}\) and \(\rho _{s1}=\sqrt{27},\rho _{s2}=\sqrt{64}\) for two-relay cases, and \(\rho _{1d}=1,\,\rho _{2d}=\sqrt{2},\,\rho _{3d}=\sqrt{3}\) and \(\rho _{s1}=\sqrt{27},\,\rho _{s2}=\sqrt{64}\), \(\rho _{s3}=\sqrt{125}\) for three-relay cases. As shown in Fig. 6b, the developed DSTC scheme with DF method still outperforms that with AF method for two relays or three relays because of no noise power amplification, especially at low SNR. At high SNR, however, the performance superiority of the former (i.e. DF scheme) drops due to the decoding error propagation at relay terminals and approximate decoding scheme at the destination terminal. Moreover, the latter (i.e. AF scheme) can utilize the diversity gain to achieve better performance at high SNR due to less noise influence, and thus the decreasing rate of BER curve of AF scheme is faster than that of the DF scheme. The results above show that the proposed differential scheme with DF method outperforms that with AF method, but the performance superiority will decrease at high SNR.

7 Conclusions

Based on the AF and DF methods, we have presented two distributed DSTC schemes for symmetric and asymmetric relay networks, respectively. The system performance is investigated in composite fading channels with large-scale and small-scale fading. The schemes do not require the CSI at both transmitter and receivers, and have low decoding complexity. Thus, they avoid high implementation complexity and low efficiency by conventional channel estimation. Moreover, different DSTC schemes and modulation modes can be applied to the proposed schemes, and thus the flexibility of system design is increased greatly. According to the PEP analysis, the powers of source terminal and relay terminals are jointly optimized for symmetric/asymmetric network so that the PEP is minimized. Especially, for the complicated optimization problem under asymmetric network, two practical methods (one is based on Shengjin’s Formulas, the other is based on Newton method) are presented to obtain the optimal/suboptimal PA, which is seldom studied due to the optimization difficulty. Simulation results and numerical analysis indicate that the application of optimal PA does improve the performance of the proposed scheme, and the corresponding performance is superior to that with fixed PA. Besides, compared with the scheme with AF method, the scheme with DF method has better performance since no noise power is amplified. However, at high SNR, the performance superiority decreases due to the influence of error propagation from the relay terminals. Besides, in the future work, we will continue to study the performance of distributed DSTC schemes with power allocation over composite fading channels, and derive the theoretical BER expressions so that the system performance may be effectively evaluated in theory.