Abstract
This paper discusses an outstanding issue in philosophy of physics concerning the relation between quantum symmetries and the notion of physical equivalence. Specifically, it deals with a dilemma arising for quantum symmetry breaking that was posed by Baker (Philos Sci 78:128–148, 2011), who claimed that if two ground states are connected by a symmetry, even when it is broken, they must be physically equivalent. However, I argue that the dilemma is just apparent. In fact, I object to Baker’s conclusion by showing that the two thermodynamical phases of a ferromagnet, which are connected by the so-called flip-flop symmetry, are physically inequivalent, thereby providing a counter-example to his claim.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Symmetries play an important role in physics. In fact, they are employed in the construction of our most successful theories. Moreover, they prove to be a useful heuristic tool, for instance in the search for fundamental particles. Informally, a symmetry is characterized by invariance of certain properties under a specified group of transformations. If the properties that are left unchanged by the symmetry constitute the empirical content of the description of a physical system, one could argue that the transformed description ought to be physically equivalent to the original description. Nevertheless, physics also abounds with examples of symmetry breaking, as it happens in infinite quantum theory. In such cases, one has a well-defined symmetry and yet some empirically relevant property does not remain invariant. One thereby faces a thorny interpretational question, that is whether mathematically different descriptions connected by a broken symmetry are physically equivalent or physically inequivalent. The present paper takes up this issue in the context of quantum symmetry breaking. Specifically, I address a dilemma raised by Baker (2011) that concerns the relation between broken symmetries and physical equivalence, and I apply my analysis to the case of ferromagnetism in quantum statistical mechanics.
The paper is structured as follows. Section 2 introduces the definition of quantum symmetry within the algebraic approach to physical theories, which enables one to provide a sharp distinction between broken and unbroken symmetries. In Sect. 3, I discuss a puzzle put forward by Earman (2003) for quantum symmetry breaking that arises from the failure of unitary equivalence, whose solution relies on a generalized version of Wigner’s theorem. I present Baker’s dilemma in the following Sect. 4: arguably, one would run into a contradiction if one insists that physical equivalence is both necessary for a quantum symmetry and sufficient for unitary equivalence, since the latter condition does not hold when a symmetry is broken. Baker’s own solution is that one should maintain that the presence of a symmetry connecting two ground states always implies that they are physically equivalent. In particular, in his view, this claim would hold true in quantum statistical mechanics where the relevant symmetry is broken in the transition between the pure thermodynamical phases of a ferromagnet. Section 5 critically discusses some general requirements for physical equivalence that lie beneath the two horns of the dilemma. Finally, in the last Sect. 6, I will proceed to show why Baker’s dilemma is just apparent and counter his conclusion in favor of physical equivalence in the example of ferromagnetism.
2 Symmetry breaking in quantum theory
In the algebraic approach physical systems are described by algebras of observables. Such a framework proves particularly useful in order to account for infinite quantum theories where spontaneous symmetry breaking occurs. For the purpose of the present paper it is sufficient to restrict our focus to von Neumann algebrasFootnote 1 and normal (i.e. \(\sigma \)-additive) states defined on them. To fix the notation, let \({\mathcal {S}}({\mathcal {A}})\) denote the set of all normal states on the von Neumann algebra \({\mathcal {A}}\). In particular, a state \(\omega \) on \({\mathcal {A}}\) induces the so-called Gelfand–Naimark–Segal (GNS) representation \((\Omega _{\omega }, {\mathcal {H}}_{\omega }, \pi _{\omega })\), where \({\mathcal {H}}_{\omega }\) is a Hilbert space,Footnote 2\(\Omega _{\omega }\) a vector state in \({\mathcal {H}}_{\omega }\) and \(\pi _{\omega }\) a representation of \({\mathcal {A}}\) such that \(\pi _{\omega }({\mathcal {A}}) \subseteq {\mathcal {B}}({\mathcal {H}}_{\omega })\). For simplicity, in order for not to overburden the notation, throughout the text I will mostly refer to the whole triple just with \(\pi _{\omega }\). The state can thus be expressed as \( \omega (A) = <\Omega _{\omega }, \pi _{\omega }(A) \Omega _{\omega }> \) for all elements A of \({\mathcal {A}}\) and the set of vectors \(\{ \pi _{\omega }(A)\Omega _{\omega } : A \in {\mathcal {A}} \}\) is dense in the underlying Hilbert space \({\mathcal {H}}_{\omega }\). The cyclicity of the state \(\omega \) for the algebra \({\mathcal {A}}\) assures the existence (and uniqueness up to unitary equivalence) of the corresponding GNS representation. Then, a representation is said to be irreducible just in case the underlying Hilbert space contains no proper closed invariant subspace other than the null space. In particular, the GNS representation \((\Omega _{\omega }, {\mathcal {H}}_{\omega }, \pi _{\omega })\) is irreducible if and only if \(\omega \) is a pure state on \({\mathcal {A}}\), and hence it cannot be written as a mixture of other states; alternatively, any mixed state on \({\mathcal {A}}\) induces a reducible GNS representation of the algebra. Finally, let us stress that by means of the double commutant theorem one can construct the affiliated algebra \(\pi ({\mathcal {A}})''\), which corresponds to the weak-operator closure of \(\pi ({\mathcal {A}})\). In many cases of physical interest, it is actually necessary to resort to the affiliated algebra in order to define physically meaningful observables that are not contained in the original algebra.
Within the algebraic approach, one can define a symmetry as the composition of the following two bijections (Roberts and Roepstorff 1969):
-
A *-automorphism \(\alpha : {\mathcal {A}} \longrightarrow {\mathcal {A}}\) over the algebra, and
-
A mapping \(\bar{\alpha } : {\mathcal {S}}({\mathcal {A}}) \longrightarrow {\mathcal {S}}({\mathcal {A}}) \) over the set of all states of the algebra, such that \(\bar{\alpha }(\omega ) := \omega \circ \alpha ^{-1} \).
Accordingly, at the level of observables, a symmetry takes the form of an automorphism mapping each element A of \({\mathcal {A}}\) onto some other element \(\alpha (A)\) belonging to the algebra. Furthermore, its action has a counterpart \(\bar{\alpha }\) in the state space \({\mathcal {S}}({\mathcal {A}})\) that is supposed to assure preservation of all expectation values, in the sense that one has \( \bar{\alpha } (\omega \circ \alpha )(A) =\omega (A)\) for all operators \(A \in {\mathcal {A}} \). It follows that, beside the GNS representation \(\pi := (\Omega , {\mathcal {H}}, \pi )\) induced by the untransformed state \(\omega \), one also constructs the GNS representation \(\pi ' := (\Omega ', {\mathcal {H}}', \pi ')\) induced by the transformed state \(\omega ' = \bar{\alpha } (\omega )\), where \(\pi ' = \pi \circ \alpha \). Cases of interest for quantum symmetry breaking are those in which the initial GNS state \(\omega \) has special physical significance, most notably when it corresponds to the so-called ground state of some theory, like the vacuum in quantum field theory or a thermodynamical phase in quantum statistical mechanics. Then, the above definition enables one to distinguish between unbroken and broken symmetries, depending on whether or not the said state remains invariant under the relevant transformation. More to the point, if the ground state is preserved, i.e. \(\omega = \omega '\), the symmetry is unbroken; otherwise, if it is not preserved, i.e. \(\omega \ne \omega '\), the symmetry is broken.
Such a distinction can be further characterized in terms of whether or not there is any unitary operator implementing the symmetry. In this respect, the following notions are particularly useful for our discussion of quantum symmetry breaking. An automorphism \(\alpha \) of the algebra \({\mathcal {A}}\) is said to be inner if one can find some unitary \(U \in {\mathcal {A}}\) such that \(\alpha (A) = U^{*} A U \) for all elements A of \({\mathcal {A}}\). That is, at the level of the algebra of observables, the symmetry is enacted by a unitary operator. However, such a condition proves too stringent to capture the content of quantum symmetry: in fact, unless \({\mathcal {A}} \equiv {\mathcal {B}}({\mathcal {H}})\), not all automorphisms of the algebra are inner. A weaker notion, which explicitly depends on a chosen state \(\omega \) over the algebra, asserts that \(\alpha \) is a \(\omega \)-inner automorphism just in case there exists some unitary operator \(U \in {\mathcal {A}}\) such that the transformed state takes the form \(\omega (\alpha (A)) = \omega (U^{*} A U) \) for all \(A \in {\mathcal {A}}\). It means that the action of a symmetry expressed by \(\alpha \) on the state \(\omega \) can be expressed by means of a unitary operator belonging to the algebra \({\mathcal {A}}\). Furthermore, there is yet another notion characterizing an automorphism in terms of a unitary operator, although the latter is supposed to act across different GNS representations of the algebra rather than within the algebra itself. Specifically, an automorphism \(\alpha \) is said to be unitarily implementable in \(\omega \) just in case there exists a unitary \(\bar{U}\) on the Hilbert space \({\mathcal {H}}\) such that
for all \(A \in {\mathcal {A}}\). If this condition is verified, the GNS representations \(\pi \) and \(\pi '\) induced by the original state \(\omega \) and by the transformed state \(\omega '\), respectively, are said to be unitarily equivalent. An important result linking the above defined notions holds that \(\alpha \) is \(\omega \)-inner if and only if \(\pi \) and \(\pi ' = \pi \circ \alpha \) are unitarily equivalent representations (cfr. Glimm and Kadison 1960).Footnote 3 Hence, the existence of a unitary operator \(U \in {\mathcal {A}}\) implementing the symmetry expressed by \(\alpha \) at the level of the algebra of observables is closely related to the existence of a unitary operator intertwining the GNS representations induced by the states connected by \(\bar{\alpha }\).
What is more, the fact that a symmetry is unbroken proves sufficient for unitary equivalence. Indeed, the invariance of the state \(\omega \) under the automorphism \(\alpha \) implies that \(\alpha \) is \(\omega \)-inner. For, let \(\omega (A) = \omega (\alpha (A))\) for all \(A \in {\mathcal {A}}\). Then, for the sake of reductio ad absurdum, let us assume that \(\alpha \) is not \(\omega \)-inner, and hence for all \(U \in {\mathcal {A}}\) one can find some operator \(A \in {\mathcal {A}}\) such \(\omega (\alpha (A)) \ne \omega (U^{*}AU)\). By the invariance of \(\omega \) under \(\alpha \), this means \(\omega (A) \ne \omega (U^{*}AU)\), from which it follows that \(A \ne U^{*}AU\). However, that cannot be true for all unitaries U in the algebra \({\mathcal {A}}\), since in case U commutes with A, for instance if it is of the form \(U := e^{-iA}\), then \(U^{*}AU = U^{*}UA = I A\), and hence one would derive the contradiction \(A \ne A\). It follows that \(\alpha \) must be an \(\omega \)-inner automorphism (note, however, that the converse is not true: in fact, not even when \(\alpha \) is an inner automorphism does it follow that \(\omega \) remains invariant under \(\alpha \)). One can thus infer that, if \(\pi \) and \(\pi ' =\pi \circ \alpha \) are unitary inequivalent, the ground state \(\omega \) is not preserved under the automorphism \(\alpha \). This means that the corresponding symmetry is broken, that is there is some \(A \in {\mathcal {A}}\) such that \(\omega (A) \ne \omega (\alpha (A))\).
Typical examples of broken symmetries arise in quantum theory for systems with infinitely many degrees of freedom. In fact, for quantum systems with finitely many degrees of freedom the GNS representation of the algebra of bounded operators \({\mathcal {B}}({\mathcal {H}})\) induced by any cyclic state is unique up to unitary equivalence, and therefore from a mathematical point of view quantum symmetry breaking can be rigorously described just in case one takes an infinite limit. A concrete example of broken symmetry is given by the spontaneous magnetization of a ferromagnet below critical temperature, which is our case-study here.
2.1 An example of broken symmetry: the case of ferromagnetism
The spontaneous magnetization of a ferromagnet below the critical temperature \(T_{c}\), and hence above the inverse critical temperature \(\beta _{c} = \frac{1}{T_{c}}\), is a well-known instance of phase transitions, according to which a substance in equilibrium (e.g. an iron bar at \(771^{\circ }\) Celsius) passes from the paramagnetic to the ferromagnetic phase even in the absence of an external magnetic field. In order to provide a mathematical description of this phenomenon, let us focus on the Weiss-Ising model for ferromagnetism (Emch and Knops 1970) in quantum statistical mechanics. There, one considers a chain of spin-\(\frac{1}{2}\) systems arranged along the z axis, each one being indexed by an integer number. Such spins can be oriented in the up-direction or in the down-direction, depending on the external magnetic field. Since particles with half-integer spins are fermions, they obey canonical anticommutation relations: as such, the collection of relevant operators generates the so-called CAR algebra. Formally, the quantum spin resident at the given site \(k \in {\mathbb {Z}}\) of the lattice is represented by the Pauli operator \(\sigma _{k}^{z}\), and the corresponding algebra is isomorphic to the algebra of 2 by 2 complex matrices, that is \({\mathcal {A}}_{k} \simeq M_{2}( {\mathbb {C}})\). More to the point, for every finite string \(\Lambda \subset {\mathbb {Z}}\) of spins, the overall algebra is given by the tensor product \({\mathcal {A}}_{\Lambda } = \bigotimes _{k \in \Lambda } {\mathcal {A}}_{k}\), to which there is associated the Hamiltonian
where B is a homogeneous external magnetic field parallel to the z-axis and \(B_{\Lambda , k} = \frac{1}{2} \sum _{k \in \Lambda }J_{\Lambda , j k}^{\beta }\sigma _{k}^{z}\) is the “molecular” average magnetic field, with \(J_{\Lambda , j k}^{\beta } > 0\) for \(j \ne k\) and \(J_{\Lambda , j k}^{\beta } = 0\) otherwise. Spontaneous Symmetry Breaking (SSB) manifests itself in the sense that, notwithstanding the fact that external magnetic field is null, i.e. \(B = 0\), above the critical inverse temperature \(\beta _{c}\) all spins in the string align in the up-direction or in the down-direction. Accordingly, the magnetization observable \(M_{\Lambda }^{z} = \frac{1}{| \Lambda |}\sum _{k \in \Lambda } \sigma _{k}^{z}\) ought to take on the value \(+1\) or the value \(-1\), respectively. SSB then occurs when all spins spontaneously flip into one direction or into the other one.
As it turns out, though, the observed behaviour can be represented only by means of an infinitely long string of spins. In fact, the Jordan–Wigner uniqueness theorem implies that for a finite number of spins all irreducible representations of the canonical anticommutation relations are unitarily equivalent to each other, and hence one could not possibly have symmetry breaking since the ground state would be unique. If one considers an infinite number of spins, one needs to take the limit \(|\Lambda | \longrightarrow \infty \). In this case, the algebra describing the string is constructed by taking the norm closure of the union of all finite string algebras \({\mathcal {A}}_{\Lambda }\)’s, which gives rise to the quasi-local algebra \({\mathcal {A}} = \overline{\bigcup _{\Lambda \subset {\mathbb {Z}}}{\mathcal {A}}_{\Lambda }}\) representing the infinite spins chain (which is not actually a von Neumann algebra). Yet, the magnetization observable cannot be defined as an element of the quasi-local algebra \({\mathcal {A}}\), because in general the limit \(\lim _{|\Lambda | \longrightarrow \infty }M_{\Lambda }^{z}\) does not converge in the norm topology. Instead, given some appropriately chosen state \(\omega \) on \({\mathcal {A}}\), one can show that there exists an operator
that converges in the weak topology associated with the GNS representation \(\pi _{B, \beta }\) of \({\mathcal {A}}\) induced by \(\omega \). It must be stressed that the thus-defined observable actually belongs to the affiliated algebra \(\pi _{B, \beta }({\mathcal {A}})''\). Then, for vanishing external magnetic field \(B \longrightarrow 0\) and inverse temperature \(\beta > \beta _{c}\), the magnetization observable \(M^{z}_{0, \beta }\) takes on the expectation value \(+1\) in the pure state \(\omega _{+}\) representing all spins up and the expectation value \(-1\) in the pure state \(\omega _{-}\) representing all spins down. These two states are connected by the flip-flop symmetry \(\alpha _{\pm }\) on \({\mathcal {A}}\), which corresonds to a \(180^{\circ }\) rotation along an axis perpendicular to z. Such a symmetry is provably broken, in that its action is such that \(\omega _{-} = \bar{\alpha }_{\pm } (\omega _{+})\) and \(\omega _{+} = \bar{\alpha }_{\pm } (\omega _{-})\). Indeed, the GNS representation \((\Omega _{+}, {\mathcal {H}}_{+}, \pi _{+})\) induced by \(\omega _{+}\) and the GNS representation \((\Omega _{-}, {\mathcal {H}}_{-}, \pi _{-})\) induced by \(\omega _{-} \) are unitarily inequivalent.
Whether the two available phases of a ferromagnet, and in general any pair of ground states connected by a broken symmetry, are physically equivalent or physically inequivalent is a contentious issue in philosophy of physics, which has been expressed by Baker (2011) in terms of a dilemma arising for quantum symmetry breaking. Before taking it up, it is worth to discussing a related point concerning the connection between unitary (in-)equivalence and the physical content of quantum symmetries. I will do so here below.
3 Earman’s puzzle and W-Unitary equivalence
The failure of unitary equivalence between representations induced by different GNS states when symmetries are broken in quantum theory is in apparent tension with the content of a famous theorem by Wigner (1931), according to which quantum symmetries are expressed by means of unitary operators or anti-unitary operators. In fact, Wigner’s theorem shows that when \({\mathcal {A}}\) is isomorphic to the algebra of bounded operators on a Hilbert space, in order to preserve transition probabilities across the representations, a symmetry \(\alpha \) must be implemented by a unitary (or an anti-unitary) mapping from the original Hilbert space \({\mathcal {H}}\) onto the transformed Hilbert space \({\mathcal {H}}'\). Specifically, if \(W: {\mathcal {H}} \longrightarrow {\mathcal {H}}'\) is a unitary operator, which we refer to as Wigner unitary, one obtains the equality
for all vector states \(\psi \) and \( \phi \) in \({\mathcal {H}}\) and all vector states \(\psi ' = W \psi \) and \(\phi ' = W \phi \) in \({\mathcal {H}}'\), thereby assuring preservation of transition probabilities in the form of the square of the vector product between elements of each Hilbert space. More to the point, owing to the property \(W^{*} W = I\) of unitary operators, one can show that \(\langle \psi ', \phi ' \rangle = \langle W \psi , W \phi \rangle =\langle \psi , W^{*} W \phi \rangle = \langle \psi , \phi \rangle \). The physical underpinning of Wigner’s theorem is grounded on the interpretation of transition probabilities as capturing the empirical content of quantum theory. Nevertheless, in the case of quantum symmetry breaking, the lack of a unitary operator intertwining the corresponding GNS representations \(\pi \) and \(\pi '\) seems at odds with the desideratum that a Wigner unitary implementing a symmetry ought to exist.
Arguably, this would lead one to a puzzle that was posed by Earman (2003). As he pointed out:
[A broken] symmetry... is not unitarily implementable, i.e. its action is not fully represented by a unitary... But how can this be, since Wigner’s theorem has taught us that a symmetry in QM is represented by a unitary transformation? (p. 338)
For instance, in the particular case of the Weiss-Ising model for ferromagnetism, the flip-flop symmetry \(\alpha _{\pm }\) connecting the two phases \(\omega _{+}\) and \(\omega _{-}\) is a rotation along the z-axis, and as such it ought to be represented by a unitary operator; yet, the corresponding GNS representations are unitary inequivalent. Earman’s puzzle can then be expressed along the lines of the following quotation by Baker and Halvorson (2013):
The infinite CAR algebra possesses a non-unitarily implementable automorphism which represents a symmetry of the ferromagnet: namely, a 180-degree rotation which flips all of the spins in the chain. The rotation is therefore a spontaneously broken symmetry... But since \(\alpha \) is spontaneously broken, \(\pi _{+}\) must be unitarily inequivalent to \(\pi _{-}\). This is where the seeming paradox comes in.(p. 465)
The solution to the puzzle, which I myself endorse, was already outlined by Earman himself and subsequently developed by Baker and Halvorson in their (2013) paper. Here, I wish to reformulate it in a manner that unpacks the technical and conceptual subtleties involved in the treatment of quantum symmetry breaking, so as to be in a position to apply it directly to the example of ferromagnetism.
The proposed solution rests on the recognition that a weaker form of Unitary Equivalence is still sufficient to guarantee preservation of transition probabilities, just as Wigner’s theorem demands. More to the point, one can introduce a condition that I label W-Unitary Equivalence, according to which there is a unitary operator \(W : {\mathcal {H}} \longrightarrow {\mathcal {H}}'\) with the property that
where \({\mathcal {A}}\) is the von Neumann algebra describing the physical system of interest. In other words, W-Unitary Equivalence prescribes that, for any element of \({\mathcal {A}}\), its image under \(\pi '\) is mapped onto the image of some element of \({\mathcal {A}}\) under \(\pi \). This condition owes his name to the fact that it is weaker that Unitary Equivalence in the sense that the representation \(\pi \) does not need to map pointwise to the representation \(\pi '\): indeed, there may well be some element \(A \in {\mathcal {A}}\) whose image under \(\pi \) is not mapped onto its image under \(\pi '\), that is it is possible that \(\pi (A) \ne W^{*} \pi '(A) W \). As I show below, that is exactly what happens when a symmetry is broken.
The label W-Unitary Equivalence is also evocative of the fact that, as demonstrated by Wigner, a quantum symmetry \(\alpha \) is implemented by a unitary operator, and that is true even when Unitary Equivalence does not hold. That is the content of a result that Baker and Halvorson (2013) presented as the Wigner Representation Theorem: accordingly, for any symmetry \(\alpha \) on \({\mathcal {A}}\), there is a unique Wigner unitary W mapping from \({\mathcal {H}}\) onto \({\mathcal {H}}'\) such that
-
\(W \Omega = \Omega '\)
-
\(\pi (\alpha ^{-1}(A)) = W^{*} \pi '(A) W \) for all \(A \in {\mathcal {A}}\)
Provably, if the GNS representations induced by \(\omega \) and \(\omega '\) are W-unitarily equivalent, transition probabilities in the form of the inner product between vector states in the Hilbert spaces \({\mathcal {H}}\) and \({\mathcal {H}}'\), respectively, are preserved under the action of the unitary operator W. Note that the Wigner unitary does not intertwine \(\pi '\) and \(\pi \): instead, it intertwines \(\pi '\) and \(\pi \circ \alpha ^{-1}\). That assures that \(\omega '(A)\) is equal to \(\omega (\alpha ^{-1}(A))\) for all elements A of the algebra \({\mathcal {A}}\), in agreement with the definition of quantum symmetries provided in Sect. 2, whereby \(\bar{\alpha }(\omega ) := \omega \circ \alpha ^{-1}\). Indeed,
Of course, this general fact remains true even when the symmetry \(\alpha \) implemented by W turns out to be broken. Hence, the existence of a quantum symmetry connecting two ground states does not require unitary equivalence between their GNS representations but only W-unitary equivalence, thereby explaining away Earman’s puzzle.
In order to fully grasp the content of the Wigner representation theorem, it is important to carefully distinguish the meaning and the role of the different unitary operators that are used in the implementation of a quantum symmetry. If one considers the case in which the symmetry is unbroken, namely \(\omega (\alpha (A)) =\omega (A)\) for all \(A \in {\mathcal {A}}\), then, as we saw above, there are both a unitary operator belonging to the algebra \({\mathcal {A}}\) and a unitary operator acting at the level of representations of \({\mathcal {A}}\) that implement the symmetry. Indeed, the corresponding automorphism \(\alpha \) over \({\mathcal {A}}\) is \(\omega \)-inner, meaning that there is a unitary operator \(U \in {\mathcal {A}}\) implementing the symmetry with respect to the ground state \(\omega \), which extends to a unitary operator \(\bar{U}\) that intertwines the GNS representations \(\pi \) and \(\pi ' = \pi \circ \alpha \). However, it should be stressed that the intertwiner \(\bar{U}\) does not coincide with the Wigner unitary W implementing \(\alpha \) according to the Wigner representation theorem. Indeed, in the case of an unbroken symmetry, it turns out thatFootnote 4\(W = I\): so, if \(\bar{U}\) were equal to W, it would be trivial and it would then follow that \(\pi (A) = \bar{U}^{*}\pi '(A)\bar{U} = \pi '(A)\) for all A, which entails that one would have \(\pi ' = \pi \) rather than \(\pi ' = \pi \circ \alpha \). Instead, when the symmetry is broken, the intertwiner \(\bar{U}\) is not defined at all, since the representations \(\pi \) and \(\pi '\) are not unitarily equivalent, whereas the Wigner unitary W exists and in this case it is non-trivial, i.e. it is different from the identity I. More to the point, given that one has \(\pi '(A) = W^{*}\pi (\alpha ^{-1}(A))W\) for all \(A \in {\mathcal {A}}\) but \(\pi (A) \ne \pi (\alpha ^{-1}(A))\) for some element A of \({\mathcal {A}}\), the uniqueness of the Wigner unitary W implementing the broken symmetry \(\alpha \) implies that the representations \(\pi \) and \(\pi '\) can only be W-unitarily equivalent.
In the same vein, one can resolve the seeming paradox pinpointed by Baker and Halvorson in the example of ferromagnetism in quantum statistical mechanics. The flip-flop symmetry \(\alpha _{\pm }\) acts as a rotation turning all spins in the up-direction into the down-direction, and viceversa: yet, it is not represented by any unitary operator \(U_{\pm }\) in the quasi-local algebra \({\mathcal {A}}\) of the infinite spin chain, nor by any unitary operator \(\bar{U}_{\pm }\) intertwining the GNS representations of \({\mathcal {A}}\) induced by the two different ground states \(\omega _{+}\) and \(\omega _{-}\), respectively. In fact, \(\pi _{+}\) and \(\pi _{-}\) are unitarily inequivalent. However, courtesy of the Wigner representation theorem, the broken symmetry \(\alpha ^{\pm }\) must be implemented by a Wigner unitary \(W_{\pm }: {\mathcal {H}}_{+} \longrightarrow {\mathcal {H}}_{-}\), which does not map pointwise between \(\pi _{+}\) and \(\pi _{-}\). This means that the unitarily inequivalent representations \(\pi _{+}\) and \(\pi _{-}\) are just W-unitary equivalent.Footnote 5 The seeming paradox of ferromagnetism that would stem from Earman’s puzzle is thus resolved by recognizing that the flip-flop symmetry \(\alpha _{\pm }\) is implemented by a unitary operator without that requiring that the GNS representations \(\pi _{+}\) and \(\pi _{-}\) ought to be unitary equivalent. We are now in a position to turn to the dilemma concerning broken symmetries which Baker (2011) raised in connection with the example of ferromagnetism in quantum statistical mechanics.
4 A dilemma for broken symmetries
The analysis of the previous section shows how the Wigner representation theorem enables one to explain away Earman’s puzzle for broken symmetries. Nevertheless, in doing so the result raises a further challenge to our understanding of quantum symmetry breaking, especially in the case of ferromagnetism. Indeed, the existence of a Wigner unitary implementing a quantum symmetry seems to lead one to yet another problem, which is captured by a dilemma posed by Baker (2011):
[t]he apparent dilemma brings together two separate threads in recent literature. One thread suggests that the existence of a symmetry... is a mark of physical equivalence... The second thread suggests that physical equivalence... is possible only in presence of unitary equivalence. In the examples central to this paper [e.g. spontaneous magnetization in the Infinite Spins Chain], a symmetry can exist between representations without a unitary equivalence. The conflict here is obvious. (p. 129)
In order to outline the logical structure of Baker’s dilemma, let me first note that there is an underlying premise that is not explicitly stated in the above quotation, namely that the existence of a symmetry does not imply unitary equivalence. In fact, the GNS representations induced by ground states connected by a broken symmetry prove to be unitarily inequivalent. This fact can be formulated as follows:
-
(0) Symm.
 Unit.Equiv.
Unit.Equiv.
Having introduced statement (0) as a premise, the conundrum described by Baker then takes the form of a contradiction between two material conditionals, corresponding to the horns of the dilemma: that is,
-
(1) Symm. \(\Longrightarrow \) Phys.Equiv.
-
(2) Phys.Equiv. \(\Longrightarrow \) Unit.Equiv.
On the one hand, according to statement (1), whenever two GNS representations are connected by a symmetry, they must be physically equivalent; on the other hand, statement (2) maintains that physical equivalence requires such representations to be unitarily equivalent. The intended inconsistency between these claims arises once premise (0) is taken into account. For, the latter states that, given a symmetry \(\alpha \), the representation \(\pi \) and \(\pi ' = \pi \circ \alpha \) may not be unitarily equivalent, as it happens in the case of quantum symmetry breaking: yet, if there is such a symmetry, it would follow from statement (1) that \(\pi \) and \(\pi '\) ought to be physically equivalent, which in turn entails by statement (2) that \(\pi \) and \(\pi '\) are necessarily unitarily equivalent. As a result, it appears as if what enables one to explain away Earman’s puzzle concerning Wigner’s theorem, namely statement (0), is just what leads one to the above dilemma plaguing broken symmetries.
As Baker himself argues, the alleged contradiction is just apparent. Indeed, in his view, one can disarm the dilemma by giving up its second horn, while still maintaining the first one:
I think its resolution [of the dilemma], on reflection, is also obvious. The first thread should be pursued at the expense of the second. In infinite quantum theory, as elsewhere, a symmetry should be enough for physical equivalence. (p.129)
To put it within our logical scheme, Baker’s suggestion is that, when dealing with a broken symmetry \(\alpha \), in order to avoid a conflict with statement (1) one ought to deny statement (2), so as to allow for the representations \(\pi \) and \(\pi ' = \pi \circ \alpha \) to be physically equivalent without being unitarily equivalent. In other words, one would have to endorse something akin to the following statement, whereby unitary equivalence is not necessary for physical equivalence:
-
(2’) Phys.Equiv.
 Unit.Equiv.
Unit.Equiv.
Allegedly, the reason to abandon statement (2) is that the presence of a symmetry, whether unbroken or broken, must entail physical equivalence. In fact, as the quotation indicates, Baker believes that statement (1) holds in general, especially in the context of infinite quantum theory. To illustrate his claim he uses the example of ferromagnetism in quantum statistical mechanics, wherein a chain of quantum spins aligned in one direction spontaneously flips into the other direction.
While I agree that the above dilemma is merely apparent, I contend that, contra Baker, statement (1) fails in general and hence it needs to be abandoned. More to the point, I submit that spontaneous symmetry breaking as it occurs in a ferromagnet below critical temperature shows that the presence of a symmetry \(\alpha \) is not at all sufficient for two unitarily inequivalent representations \(\pi \) and \(\pi ' = \pi \circ \alpha \) to be physically equivalent. Before developing my claim in greater detail in Sect. 6, let me first expose and criticize Baker’s own reasons to favor statement (1) over statement (2).
4.1 Is symmetry sufficient for physical equivalence?
The philosophical motivation behind Baker’s (2011) claim that the presence of a symmetry, even when it is a broken one, entails physical equivalence lies in his commitment to a condition of No Primitive Identity, which has been discussed in the literature in the context of the metaphysics of spacetime (cfr. Teller 1991; Hoefer 1996). Such a condition denies that spacetime points possess (indispensable) intrinsic properties that would make them ontologically different from each other. The condition of No Primitive Identity is rooted in the principle of Leibniz equivalence, whereby spacetime symmetry transformations ought not to relate distinct possible worlds. For instance, applying a translation or a rotation within Newtonian spacetime is expected not to produce different states of affairs: to the contrary, it would merely lead one to a re-description of the same physical possibility. That is the sense in which, owing to No Primitive Identity, spacetime symmetries underwrite physical equivalence.
As an example, Baker offers an analysis of the classical Mexican Hat. There, each of the points around the lowest edge of the hat represents one of the possible ground states wherein a ball rolling down from the top of the hat can end up. Arguably, the availability of multiple ground states signals the presence of a broken symmetry. On pain of violating No Primitive Identity, these states cannot be physically inequivalent despite being represented by mathematically distinct points. For Baker, that should be true even in relativistic spacetime, irrespective of whether one adopts a substativalist or a relationist ontology. As he puts it,
Both ontologies entail that in the classical symmetry-breaking case under discussion, there is a unique possible world with least energy, although the state space of our physical theory includes multiple ground states. So there must be a many-to-one correspondence between mathematical states and physical possibilities. Mathematically distinct ground states must be physically equivalent. (p. 132)
Thus, according to Baker, the fact that different points can be connected by a spacetime symmetry guarantees that they constitute the same physical state. What is more, he seems to think that physical equivalence is established whenever there is a symmetry, even a broken one, that maps between two mathematically distinct ground states. On this basis, he goes on to claim that the above argument can be extended from classical spacetime symmetries to quantum theory. Nevertheless, he does not explain how to formulate an analogue of the classical version of No Primitive Identity in the context of quantum symmetries. Hence, it is not quite clear how exactly the purported condition should ground statement (1) in the dilemma for quantum symmetry breaking. Nor does it follow that a violation of such a statement would compel us to revise our classical notion of spacetime symmetries.Footnote 6 I will return to this point at the end of Sect. 6, after showing that the flip-flop symmetry connecting the two phases of a ferromagnet does not imply their physical equivalence.
It should also be stressed that Baker contends that symmetry breaking appears to be more elusive in the quantum case than in the classical one. In fact, in his view, physical equivalence demands that a translation scheme exists between different mathematical descriptions of the same physical possibility. In the example of the classical Mexican Hat, such a scheme is readily available: in cylindrical polar coordinates \((r, \theta , h)\), the transformation \(\theta \longrightarrow \theta + \epsilon \) translates between the ground states \(\theta = 0\) and \(\theta = \epsilon \) in which the ball may end up. Yet, the fact that different quantum states connected by a broken symmetry induce GNS representations that are unitarily inequivalent seems to impede their inter-translatability. For, Halvorson and Clifton (2001) elaborated a translation scheme designed for plausible ontologies of quantum theory, which provably requires unitary equivalence: accordingly, in the example of an infinitely long spins chain one must conclude that one cannot translate between the up-polarized and the down-polarized states. Instead, based on his conviction that the two phases of a ferromagnet ought to be regarded as physically equivalent so as not to infringe on the classical notion of spacetime symmetries, Baker’s own diagnosis for the failure of inter-translatability is that Halvorson and Clifton’s proposal appears as too restrictive. Hence, he goes on to conjecture that an alternative translation scheme may be enacted by means of a Wigner unitary mapping between different GNS representations, even when the latter are unitarily inequivalent. Unfortunately, though, he does not elaborate further on the details. Be that as it may, as I will argue in the next section, the purported translation scheme cannot be developed on the basis of the Wigner representation theorem since a unitary W implementing a broken symmetry \(\alpha \) does not fully preserve the empirical content in quantum theory.
5 What is physical equivalence?
For the sake of establishing whether statement (1) and statement (2) in Baker’s dilemma hold or not, we need to have a better grasp of the concept of physical equivalence, as well as the way in which it allegedly relates to the presence of a symmetry and/or the condition of unitary equivalence. Yet, that is not as straightforward as one may hope. In fact, while the concepts of symmetry and unitary equivalence have sharp mathematical definitions, physical equivalence can be hardly formulated in a general manner. Instead, it can be fully evaluated only within the relevant physical contexts, that is on the basis of the particular physical phenomenon under description. Hence, one cannot really sustain general statements, as Baker’s dilemma would require. Sure enough, given that in the algebraic approach certain physical theories, like quantum statistical mechanics and quantum field theory, are cast within the same formalism, one can still try to introduce some conceptually motivated, mathematical conditions that ought to be satisfied in order for physical equivalence to hold. However, such conditions must then be checked in each specific case. Furthermore, and more importantly, whether two GNS representations of the algebra of observables are to be viewed as physically equivalent or not is contingent upon what specific physical states their ground states are supposed to represent. For instance, Feintzeig (2015) analyzes the example of a classical spin chain and showed that one can interpret the two possible ground states as being equivalent or inequivalent depending on whether or not one fixes the conventional distinction between up and down. Here below, I discuss some general conditions for physical equivalence that allegedly lie beneath statements (1) and (2) in Baker’s dilemma and then, in the following section, I address the specific case of ferromagnetism for the quantum spin chain.
Let me begin by explaining the reasons why some authors, most notably Arageorgis (1995) and Ruetsche (2003, 2011, 2013), endorse statement (2), namely the claim that physical equivalence implies unitary equivalence. In principle, one would expect that, if two states \(\omega \) and \(\omega '\) are regarded as physically equivalent, one should at least be able to write \(\omega '\) in the GNS representation induced by \(\omega \), and viceversa. Specifically, the folium \({\mathcal {F}}_{\omega }\) of a state \(\omega \) is the set of states that are expressible as density matrices in the GNS representation \(\pi _{\omega }\): as such, it comprises all states that are, so to speak, “possible” relative to \(\omega \). That means that, when a state \(\omega '\) does not belong to the folium of \(\omega \), it cannot be written in the GNS representation induced by the latter. It thus seems plausible to require that for \(\omega \) and \(\omega '\) to be physically equivalent they must at least lie in each other’s folium. If their GNS representations \(\pi \) and \(\pi '\) are unitarily inequivalent, though, this requirement would be violated. One is therefore tempted to argue, as Arageorgis first does, that unitary equivalence is a necessary condition for physical equivalence.
More to the point, there is a weaker, and yet suitable, formal condition for physical equivalence that is related to unitary equivalence. Accordingly, even if states \(\omega \) and \(\omega '\) do not lie in each other’s folium, for them to be regarded as physically equivalent it must be that the intersection between their folia \( {\mathcal {F}}_{\omega }\) and \( {\mathcal {F}}_{\omega '}\) is non-empty. If that is not the case, namely if
then the states \(\omega \) and \(\omega '\) are said to be disjoint states. It means that none of the states that can be written in the GNS representation \(\pi \) can also be written in the GNS representation \(\pi '\), and viceversa. As Ruetsche (2011) argues, such a condition captures the idea that \(\omega \) and \(\omega '\) are not possible relative to each other in the sense that, if the two states are disjoint, the transition probability between them is equal to zero.Footnote 7 It thus seems rather natural to think of disjoint states as being physically inequivalent. In other words, the failure of disjointness is a necessary condition for physical equivalence. As it turns out, if \(\omega \) and \(\omega '\) are pure states and their GNS representations are unitarily equivalent, then their folia coincide, i.e. \({\mathcal {F}}_{\omega } ={\mathcal {F}}_{\omega '}\); whereas if they are not unitarily equivalent, and the algebra of observable is a factor (namely its center \({\mathcal {A}} \bigcap {\mathcal {A}}'\) is a complex multiple \(\lambda \) of the identity operator I), then \(\omega \) and \(\omega '\) are disjoint states. That reinforces Arageorgis’ claim that physical equivalence implies unitary equivalence.
Baker and Halvorson (2013) object to this conclusion on the basis of their solution to Earman’s puzzle for quantum symmetry breaking. As they write,
[the] argument includes a false premise: the assumption that the existence of a unitary operator connecting the folia of two representations implies a unitary equivalence between those representations. As we have shown, though, there is no such implication if the unitary operator is what we’ve called a Wigner unitary. [p. 468]
In fact, by means of the Wigner unitary W implementing a broken symmetry, one could connect the folia \({\mathcal {F}}_{\omega }\) and \({\mathcal {F}}_{\omega '}\) without entailing unitary equivalence between \(\pi \) and \(\pi '\). Allegedly, this casts doubts on statement (2) of the dilemma. In turn, it appears as if W-unitary equivalence between the respective GNS representations would be sufficient for the states \(\omega \) and \(\omega '\) to be physically equivalent even when a symmetry is broken, in agreement with statement (1) in Baker’s dilemma. Nevertheless, pace Halvorson and Baker, W-unitary equivalence between the GNS representations \(\pi \) and \(\pi '\) does not imply that the states \(\omega \) and \(\omega '\) cannot be disjoint. In fact, the existence of a Wigner unitary W connecting the GNS representation of \(\omega \) and the GNS representation of \(\omega '\) does not assure that the respective folia \( {\mathcal {F}}_{\omega }\) and \( {\mathcal {F}}_{\omega '}\) share some common state. For, when one deals with pure states defined over a factor algebra, if unitary equivalence fails disjointness holds true. In this case, the representations \(\pi \) and \(\pi ' = \pi \circ \alpha \) are still W-unitary equivalent since they are connected by a symmetry \(\alpha \), but the folia of the corresponding GNS states \(\omega \) and \(\omega '\) have empty intersection. Therefore, the existence of a Wigner unitary W does not prevent two (pure) states from being disjoint: as such, it cannot be a sufficient condition for their physical equivalence. In the next section I will show how this fact applies directly to the case of ferromagnetism, where the ground states \(\omega _{+}\) and \(\omega _{-}\) of the infinite spin chain prove to be disjoint states, even though they are connected by the flip-flop symmetry \(\alpha _{\pm }\) implemented by the Wigner unitary \(W_{\pm }\).
Be that as it may, Baker and Halvorson then go on to argue that the presence of a symmetry entails physical equivalence because it assures the preservation of the empirical content of quantum theory, in the sense that the Wigner unitary W implementing a symmetry \(\alpha \) always leaves transition probabilities invariant.
If we further assume (as conventional wisdom dictates) that a quantum theory’s symmetries preserve all empirical content, then the folia of at least some pairs of inequivalent representations must be empirical equivalent if spontaneous symmetry is possible. [p. 468]
Agreed, it seems quite reasonable to demand that, for two mathematical states and respective folia to be physically equivalent, the symmetry transformation connecting them must not change the empirical content. Yet, that requires one to specify what exactly is the latter. In quantum theory the empirical content is expressed in terms of the expectation values of physical observables. For our purposes, we can identify (at least) two distinct senses in which such a concept is intended in connection with quantum symmetries. According to the first sense, any symmetry is by definition supposed to preserve expectation values in that it yields \( \bar{\alpha } (\omega \circ \alpha )(A) = \omega (A) \) for all observables A in \( {\mathcal {A}} \) (see Sect. 2). In other words, the state \(\omega \) is mapped onto itself if one applies the bijection \(\bar{\alpha }\) over the state space \({\mathcal {S}}({\mathcal {A}})\) together with the automorphism \(\alpha \) of the algebra \({\mathcal {A}}\). The Wigner representation theorem then guarantees that the unitary operator W implementing a symmetry does not change the transition probabilities in the form of the inner product between vectors in the underlying Hilbert space, even when the symmetry is broken. According to the second sense, instead, one refers to the expectation values of observables as being computed in the ground state. The expectation value of the observable A computed in state \(\omega \) is thus given by \( <\Omega , \pi (A) \Omega>\). However, it turns out that in the case of quantum symmetry breaking not all expectation values remain the same under the relevant transformation from \(\omega \) into \(\omega ' = \omega \circ \alpha \): in fact, when a symmetry is broken, one has \(<\Omega , \pi (A) \Omega > \ne <\Omega ', \pi '(A) \Omega '>\) for some \(A \in {\mathcal {A}}\). So, the question whether the empirical content is unchanged by a given symmetry has a different answer depending on the particular sense in which one understands the concept of preservation of expectation values.
Baker and Halvorson just intend this concept in the first rather than in the second sense, and that is why they maintain that the preservation of the empirical content of a quantum theory is captured by the invariance of transition probabilities. Under their interpretation, a symmetry would thus be sufficient for physical equivalence. It is indeed such a presupposition that grounds both Baker’s (2011) commitment to statement (1) and his denial of statement (2) in the alleged dilemma. Nonetheless, when a symmetry is broken, the numerical disagreement between the probabilities assigned to a given physical observable by the initial state \(\omega \) and by the transformed state \(\omega '\), respectively, does make an empirically significant difference. So, even though the empirical content encoded in a quantum state certainly includes transition probabilities, it should not be merely restricted to them. It follows that the preservation of transition probabilities under a quantum symmetry proves too weak a condition to assure physical equivalence between a pair of states. As a consequence, contrary to Baker’s own conjecture, one cannot even construct a translation scheme based on the Wigner unitary W mapping between unitarily inequivalent GNS representations \(\pi \) and \(\pi '\), on pain of overriding a physically relevant part of the empirical content. That is true, in particular, in the example of a ferromagnet in quantum statistical mechanics, where empirically distinct phases assign different expectation values to the magnetization observable. Let us now proceed to develop the argument for physical inequivalence in this particular case-study.
6 Coexistence of empirically distinct thermodynamical phases
According to Baker’s dilemma, given that the presence of a symmetry does not imply unitary equivalence, i.e. statement (0), one would run into a contradiction if one maintains that physical equivalence is both necessary for a symmetry, i.e. statement (1), and sufficient for unitary equivalence, i.e. statement (2). Specifically, when dealing with a broken symmetry, for which unitary equivalence fails, the combination of the two horns of the dilemma would lead one to the false conclusion that unitary equivalence holds. It thus appears as if one is bound to choose between statement (1) and statement (2). However, in my view, the alleged conflict between these two statements is just apparent, since their truth rests on what one means exactly by physical equivalence, and that, as it was explained in the previous section, is not a matter that can be decided on the basis of purely formal conditions. In fact, the claim that two GNS representations induced by mathematically distinct states on the observable algebra be physically equivalent depends on the particular physical phenomenon under investigation. As a consequence, one cannot quite establish general statements concerning physical equivalence, as in Baker’s dilemma: rather, one must evaluate it on a case-by-case basis. Thus, in order to determine whether or not the GNS representations \(\pi \) and \(\pi ' =\pi \circ \alpha \) connected by the broken symmetry \(\alpha \) are physically equivalent one must take into account what kind of physical states their respective ground states \(\omega \) and \(\omega ' = \bar{\alpha }(\omega )\) over the algebra \({\mathcal {A}}\) correspond to. In particular, this means that the analysis of the two phases of a ferromagnet in quantum statistical mechanics is ultimately independent from other examples of broken symmetries in infinite quantum theory.
In order to enforce this fact, it is worth to start by contrasting the infinite spin chain with a case-study discussed by Baker and Halvorson (2013). Specifically, as an example of how the content of the Wigner representation theorem would allegedly cast doubts onto the claim that physical equivalence requires unitary equivalence, they cite the multiplicity of vacuum representations in quantum field theory. In a nutshell, the algebraic formulation of quantum field theory establishes a correspondence between bounded regions \({\mathcal {O}}\) of Minkowski spacetime \({\mathcal {M}}\) and local algebras \({\mathcal {A}}({\mathcal {O}})\) of observables, whose structure is determined by a set of physical and mathematical axioms [see Haag (1996) for more details, which we cannot review here]. In this context, the quasi-local algebra \({\mathcal {A}}\) is given by the norm closure of the net of all local algebras defined over the entire Minkowski spacetime, that is \({\mathcal {A}} = \overline{\bigcup _{{\mathcal {O}} \subset {\mathcal {M}}} {\mathcal {A}}({\mathcal {O}}) } \). The latter admits multiple unitarily inequivalent representations, each of which is determined by a different vacuum state. Baker and Halvorson then argue as follows:
What are the necessary conditions for physical equivalence between field-theoretic states?... [T]he existence of a symmetry is often taken to imply physical equivalence in the fullest sense (see Baker 2011). The notion that unitary equivalence is a necessary condition for physical equivalence should now appear quite suspect. Insofar as the so-called “Hilbert space conservative” interpretation of quantum field theory identifies physical equivalence with unitary equivalence (see Ruetsche 2002), that interpretation must come into question as well. (p. 467)
The view named by Laura Ruetsche “Hilbert space conservatism”, which the above quotation refers to, maintains that the observables retaining physical significance are not those belonging to the abstract quasi-local algebra \({\mathcal {A}}\), but rather those corresponding to the self-adjoint elements of the affiliated algebra \(\pi _{0}({\mathcal {A}})''\) mapping over a concrete Hilbert space, which is constructed by means of the representation \(\pi _{0}\) induced by the vacuum state \(\omega _{0}\). The vacuum is characterized as the unique state within its own GNS representation that is invariant under the Poincaré group, namely the group of relativistic spacetime symmetries of quantum field theory. So, according to Hilbert space conservatism, given any pair of distinct vacuum states \(\omega _{0}\) and \(\omega '_{0}\), their respective GNS representations \(\pi _{0}\) and \(\pi _{0}'\) being unitarily inequivalent means that they are physically inequivalent as well. Yet, as different ground states they are connected by a broken symmetry, call it \(\alpha _{0}\), and hence there exists a corresponding Wigner unitary \(W_{0}\) preserving the transition probabilities in the form of the inner product between vectors in the underlying Hilbert spaces \({\mathcal {H}}_{0}\) and \({\mathcal {H}}'_{0}\). If so, Baker and Halvorson’s criterion for physical equivalence based on the Wigner representation theorem would be satisfied in quantum field theory, at least if one endorses Hilbert space conservatism. Arguably, as it stands, this conclusion would not go through if one adopts other possible views recognized by Ruetsche, such as “Algebraic imperialism”, for which the prominent concept is the abstract observable algebra itself instead of its concrete Hilbert space representations. It is not our purpose here to settle this contentious matter in the context of quantum field theory. Rather, the issue at stake is whether or not one could extend the same argument put forward by Baker and Halvorson to the case of ferromagnetism in quantum statistical mechanics.
Recall that in the Weiss–Ising model the two ground states \(\omega _{+}\) and \(\omega _{-}\) on the quasi-local algebra \({\mathcal {A}} = \overline{\bigcup _{\Lambda \subset {\mathbb {Z}}}{\mathcal {A}}_{\Lambda }} \) describing the infinite spin chain are meant to represent different thermodynamical phases, in which all spins are oriented towards the up direction or towards the down direction, respectively. Thus, intuitively, the physical states of affairs they correspond to are not quite the same, at least once a distinction between up and down has been conventionally fixed. In what follows I will argue in favor of this claim by providing some compelling reasons why, contrary to Baker’s (2011) own argument, the states \(\omega _{+}\) and \(\omega _{-}\) inducing the respective representations \(\pi _{+}\) and \(\pi _{-}\) are to be regarded as physically inequivalent. For one, being defined as stable equilibrium Gibbs states at the same inverse temperature \(\beta \), they constitute empirically distinct pure phases in the sense that they prove to be disjoint states assigning different expectation values to the magnetization observable. That means that a significant part of the empirical content is not preserved under the flip-flop symmetry \(\alpha _{\pm }\). Furthermore, in order to model all relevant thermodynamical phenomena, one needs to be able to describe cases of co-existence of phases, which often occur in nature: accordingly, it must be possible for the ground states \(\omega _{+}\) and \(\omega _{-}\) to form a mixture, wherein the two pure phases are both present at the same time while remaining physically separated from each other. That actually leads us to a different conclusion than the one reached by Baker and Halvorson in the case of quantum field theory. Let me elaborate on these points in greater detail.
In ordinary quantum mechanics, an equilibrium state at inverse temperature \(\beta \) is given by the entropy-maximizing Gibbs state expressed by the density operator \(\rho = \frac{e^{- \beta H}}{Tr(e^{- \beta H})}\), where H denotes the Hamiltonian of the system with discrete spectrum. It is taken to represent a pure thermodynamical phase in that, beside exhibiting the stable behaviour typical of equilibrium [see Emch (2007) for a systematic review of this fact], when being computed in such a state the thermodynamical macroproperties of a physical system, like the magnetization observable in a ferromagnet, prove dispersion-free. Specifically, we say that a self-adjoint operator A is dispersion-free in the state \(\omega \) just in case \(\omega (A^{2}) =(\omega (A))^{2}\), which implies that \(\omega \) ascribes probability equal to 1 to some eigenvalues of A. For our purposes here, it is just important to stress that the requirement of assigning dispersion-free values to thermodynamical macroproperties is satisfied by factor states, namely by states whose affiliated algebras have trivial center: specifically, the state \(\omega \) on the algebra \({\mathcal {A}}\) having GNS representation \(\pi \) is a factor just in case \(\pi ({\mathcal {A}})'' \cap \pi ({\mathcal {A}})' = \{ \lambda I \}\) with \(\lambda \) being a complex number and I the identity operator. As it turns out, any pure state is a factor state, and thus it behaves like an equilibrium Gibbs state with respect to thermodynamical macroproperties. Yet, since in finite quantum statistical mechanics a Gibbs state is unique, when a ground state is assumed to have this form there cannot be symmetry breaking unless one describes the system in the thermodynamical limit. For instance, as noted in Sect. 2.1, in the Weiss–Ising model a magnetization observable \(M^{z}_{B, \beta }\) at inverse temperature \(\beta \) with external field B parallel to the z-axis is constructed only when taking the limit \(|\Lambda | \longrightarrow \infty \) for an infinitely long spin chain. That enables one to define multiple thermodynamical phases at the same inverse temperature. Indeed, given that \(\omega _{+}\) and \(\omega _{-}\) are pure states on the quasi-local algebra \({\mathcal {A}}\), they are factor states that give rise to the affiliated algebras \(\pi _{+}({\mathcal {A}})''\) and \(\pi _{-}({\mathcal {A}})''\) by means of their respective GNS irreducible representations. As such, both ground states of the infinite spin chain are interpreted as pure thermodynamical phases, assigning dispersion free values to the magnetization observable. What is more, and that is the crucial point here, they can be shown to be empirically distinct phases, which makes them physically inequivalent.
Indeed, as explained in the previous section, general claims that unitary equivalence is necessary for physical equivalence typically rest on the requirement that two states are disjoint in sense that their folia do not share any common element. The thermodynamical phases \(\omega _{+}\) and \(\omega _{-}\) fulfill such a requirement since they are pure states on the quasi-local algebra \({\mathcal {A}}\) and their GNS representations \(\pi _{+}\) and \(\pi _{-}\) are not unitarily equivalent. Granted, it is also true that the flip-flop symmetry \(\alpha _{\pm }\) is implemented by a Wigner unitary operator \(W_{\pm }\) that leaves transition probabilities invariant, as Baker and Halvorson’s alleged sufficient condition for physical equivalence would demand. Nevertheless, being a broken symmetry, \(\alpha _{\pm }\) fails to preserve the full empirical content of the theory in the sense that the expectations values of the magnetization observable computed in the ground states \(\omega _{+}\) and \(\omega _{-}\) do not agree with each other. For, such an observable takes on the value \(+1\) in \(\omega _{+}\), as well as in any other state in its folium \({\mathcal {F}}_{\omega _{+}}\); and, likewise, it takes on the value \(-1\) in \(\omega _{-}\), as well as in any other state in its folium \({\mathcal {F}}_{\omega _{-}}\). What is worse, given that \(M^{z}_{B, \beta }\) does not belong to \({\mathcal {A}}\) but rather to the affiliated algebra generated by the GNS representation of a given state, if it is constructed in \(\pi _{+}({\mathcal {A}})''\) then it is not even defined in \(\pi _{-}({\mathcal {A}})''\), and viceversa. This fact thus corroborates the claim that the pure thermodynamical phases \(\omega _{+}\) and \(\omega _{-}\) are empirically distinct.
Actually, Baker himself recognizes that the magnetization observable acquires a different physical meaning in the two representations \(\pi _{+}\) and \(\pi _{-}\), but he insists that the latter should still be regarded as physically equivalent so as to allow for a translation scheme.
This is the sort of “translating” that symmetry transformations do all the time. For example, when we take a model of a \(+z\)-polarized magnet and transform the z coordinate to \(-z\), we will change the expectation value of the observable for magnetization along z, say from 1 to \(-1\). The believer in Leibniz equivalence would say that we have thereby changed which physical quantity this operator denotes. As long as we keep that in mind, there should be no obstacle to constructing a translation scheme. [p. 145; where the notation has been suitably modified]
It thus seems that, for Baker, the flip-flop symmetry \(\alpha _{\pm }\) that transforms, say, the phase \(\omega _{+}\) into the phase \(\omega _{-}\) would just correspond to a mere change of coordinates from \(+z\) into \(-z\). However, this overlooks the fact that phase transition is a real physical phenomenon. That is, when spontaneous magnetization occurs even in the absence of an external magnetic field B, all spins in the chain align either in the up-direction or in the down-direction along the z-axis: so, once the spins are thus oriented, the distinction between the two possible states of affairs is not purely a matter of convention about how to fix the spatial direction.Footnote 8 Magnetization can then be defined as a physically meaningful observable only with respect to the particular GNS representation one chooses. Baker’s purported translation scheme based on the Wigner representation theorem does not formally capture this fact, and hence it can hardly be used to establish physical equivalence in the example of a ferromagnetism.
Be that as it may, there is another more compelling reason to deny that statement (1) in Baker’s dilemma holds in quantum statistical mechanics, namely the fact that pure thermodynamical phases can co-exist at the same time. That is a physical phenomenon typically observed when a system undergoes phase transitions. For instance, in condensed matter physics, one can have a state in which ice and water are both there. Likewise, when the critical temperature is reached, the state of a ferromagnet is expressed by a mixture of the two stable equilibrium states \(\omega _{+}\) and \(\omega _{-}\), which means that both pure phases are present together. Indeed, in the familiar Weiss–Ising model with an infinitely long spin chain, a well-defined magnetization observable \(M^{z}_{0, \beta _{c}}\) for a null external magnetic field \(B = 0\) and inverse critical temperature \(\beta _{c}\) can be constructed just as an element of the algebra \(\pi _{0, \beta }({\mathcal {A}})''\) affiliated with the GNS (reducible) representation \(\pi _{0, \beta }\) induced by the mixed stateFootnote 9\(\omega _{0, \beta } = \frac{1}{2}\omega _{+} + \frac{1}{2}\omega _{-} \) over the quasi-local algebra \({\mathcal {A}}\). It is important to stress that, just as its components \(\omega _{+}\) and \(\omega _{-}\), such a mixture \(\omega _{0, \beta }\) corresponds to a thermodynamical equilibrium state. In order to see how that is possible, we need to formalize this fact within a framework having the resources to accommodate multiple equilibria at the same temperature. The sought-after algebraic structure is provided by the Kubo–Martin–Schwinger (KMS) states, which generalize the notion of Gibbs states in infinite quantum statistical mechanics.
Let \(\sigma _{t}\) denote the one-parameter automorphism group over the algebra \({\mathcal {A}}\), representing the dynamics of the system in the course of time t. By definition, a state \(\omega \) on \({\mathcal {A}}\) is a KMS state with respect to \(\sigma _{t}\) at inverse temperature \(\beta \) just in case, for all elements \(A, B \in {\mathcal {A}}\), one has
The KMS condition thus expresses stability under the dynamical group \(\sigma _{t}\), which is a typical feature of equilibrium states. For any fixed \(\beta \), one can define a set \({\mathcal {K}}(\beta )\) of KMS states with the above property. In finite quantum mechanics where the Gibbs state is unique \({\mathcal {K}}(\beta )\) is a singleton, but in the thermodynamical limit it becomes a convex set containing more than one element. In the specific example of the infinite spin chain in the Weiss–Ising model, at the inverse critical temperature the mixed state \(\omega _{0, \beta }\) induces a one-parameter automorphism group \(\sigma _{t}\) that determines a convex set \({\mathcal {K}}(\beta _{c})\) of KMS states. The states \(\omega _{+}\) and \(\omega _{-}\) then prove to be extremal for such a set, in the sense that they cannot be written as a convex combination of other elements of \({\mathcal {K}}(\beta _{c})\). In fact, extremal states are factor states and therefore they are dispersion-free for the magnetization observable \(M^{z}_{0, \beta _{c}}\), just as pure thermodynamical phases are supposed to be. More to the point, one can find projections \(P_{+}\) and \(P_{-}\) residing in the center of the affiliated algebra \(\pi _{0, \beta }({\mathcal {A}})''\) such that one can write \(\omega _{+}(A) =\frac{\omega (P_{+}AP_{+})}{\omega (P_{+})}\) and \(\omega _{-}(A) =\frac{\omega (P_{-}AP_{-})}{\omega (P_{-})}\) for all A in the quasi-local algebra \({\mathcal {A}}\). Therefore, the fact that the mixture \(\omega _{0, \beta } = \frac{1}{2}\omega _{+} + \frac{1}{2}\omega _{-} \) represents a physically significant state demonstrates that the states \(\omega _{+}\) and \(\omega _{-}\) can co-exist as empirically distinct thermodynamical phases. As such, they must be physically inequivalent: otherwise, the mixture \(\omega _{0, \beta }\) of which they are pure components would not correspond to the observed phenomenological state of affairs it purports to describe.
In the last analysis, the possibility of co-existence of phases indicates that the previously discussed argument by Baker and Halvorson in favor of the physical equivalence between the GNS representations of different vacuum states in quantum field theory does not go through in quantum statistical mechanics. Indeed, as they claim, if one embraces Hilbert space conservatism, the empirical content is fully encoded within each GNS representation taken in isolation, and hence it should be preserved under a symmetry transformation across different GNS representations. Ultimately, the underlying idea rests on the uniqueness of the vacuum state within its own irreducible representation, namely the fact that in a concrete quantum field theory there could only be one state having the same properties ascribed to the vacuum. That presupposes (via superselection rules) that one cannot construct a state combining two distinct vacuum states \(\omega _{0}\) and \(\omega '_{0}\), for instance in the form of a superposition. Instead, as I have just argued, in quantum statistical mechanics one must be able to combine together two pure thermodynamical phases, like the ground states \(\omega _{+}\) and \(\omega _{-}\) of a ferromagnet, if one wishes to describe empirically relevant phenomena. Granted, one cannot take a superposition of \(\omega _{+}\) and \(\omega _{-}\) either, and in fact each phase is also unique within its own irreducible representation; yet, one can form a physically meaningful mixture \(\omega _{0, \beta }\) that induces a reducible GNS representation whose affiliated algebra \(\pi _{0, \beta }({\mathcal {A}})''\) enables one to reconstruct both pure states \(\omega _{+}\) and \(\omega _{-}\). Therefore, Hilbert space conservatism does not have the resources to accommodate multiple co-existing thermodynamical phases, which entails that the argument put forward by Baker and Halvorson in quantum field theory does not hold here. The account of symmetry breaking in terms of KMS states (which Liu and Emch 2005 refers to as the decompositional account) just puts us in a position to see this point clearly within the framework of algebraic quantum statistical mechanics. That enforces the fact that the putative relation between the presence of a broken symmetry and the notion of physical equivalence must be evaluated with respect to each specific physical context.Footnote 10
Finally, let me conclude with a few remarks concerning Baker’s (2011) thesis that the presence of a symmetry is sufficient for physical equivalence, that is statement (1) in his alleged dilemma for broken symmetries. Recall from Sect. 4.1 that this reflects his commitment to the metaphysical principle of No Primitive Identity rooted in the classical notion of spacetime symmetries, according to which any two spacetime points, say x and \(x'\), should not be ontologically distinct inasmuch as they can be mapped into each other by some symmetry transformation. Allegedly, it entails that when two mathematically distinct states are connected by a symmetry, even a broken one, they should represent the same physical possibility. Now, the failure of the two ground states of an infinite spin chain to be physical equivalent despite being related by the flip-flop symmetry clearly provides a counter-example to Baker’s thesis. So, one may as well wonder whether it also leads one to a violation of No Primitive Identity.
However, I submit that this is not really the case since such a condition is not directly relevant to the treatment of ferromagnetism in quantum statistical mechanics. For one, the theory is not formulated within a quadri-dimensional spacetime manifold: indeed, the quasi-local algebra \({\mathcal {A}}\) is just constructed in Euclidean three-space, whereas the temporal dimension t is introduced independently, for instance by means of the one-parameter automorphism group \(\sigma _{t}\) dictating the time-evolution of the system under description. More to the point, the covariance axiom of quantum statistical mechanics to which \({\mathcal {A}}\) is supposed to obey requires that the relevant symmetries are translations along the spin chain. That means that, if one considers two spin systems located in the spatial positions x and \(x'\), respectively, one can map one into the other by means of a translation, and yet both ground states \(\omega _{+}\) and \(\omega _{-}\) remain invariant under such a transformation. So, the relevant symmetry is not broken at all in this case. Instead, the flip-flop symmetry \(\alpha _{\pm }\) is broken, yet it is not really a spacetime symmetry of the sort contemplated by No Primitive Identity. For, in the example of the classical Mexican Hat, the ground states of the system are represented by points x and \(x'\) having distinct locations in space. Quite differently, the flip-flop symmetry has just the effect to invert the orientation of all the spins in the infinite chain: its action corresponds to a spatial rotation of 180 degrees, but it is applied at the same fixed point in space where each spin is located. In other words, rather than mapping between different spatial points x and \(x'\), the transformation \(\alpha _{\pm }\) simply flips the spin orientation of a system at point x while keeping the system in the same spatial location. Hence, we can conclude that the fact that the ground states \(\omega _{+}\) and \(\omega _{-}\) are physically inequivalent despite being connected by the quantum symmetry \(\alpha _{\pm }\) does not entail any conflict with the metaphysical principle of No Primitive Identity, even if it is in flat contradiction with statement (1) in Baker’s dilemma.
7 Conclusion
Baker’s dilemma raises important philosophical issues concerning the concepts of symmetry, unitary equivalence and physical equivalence, especially in the case of quantum symmetry breaking. However, his alleged dilemma is merely apparent. Indeed, while the relations between the existence of a symmetry, whether broken or unbroken, and the fulfillment of unitary equivalence can be determined mathematically, questions about physical equivalence ought to be settled just on a case-by-case basis, depending on the specific physical situation under description. As a consequence, one can hardly establish general facts involving physical equivalence, such as statement (1) and statement (2) in the dilemma. In particular, throughout the paper I argued that, contrary to what Baker claims, the presence of a symmetry mapping between two ground states is not at all sufficient for the latter to be physically equivalent. More to the point, by focusing on the example of ferromagnetism in quantum statistical mechanics, I showed how the pure thermodynamical phases of the Weiss–Ising model corresponding to the ground states in which all spins are oriented in the up-direction and in the down-direction, respectively, must be regarded as physically inequivalent even though they are connected by a symmetry, which in fact turns out to be a broken one.
Notes
More in general, one can describe a physical system by means of a C*-algebra, namely an algebra of observables equipped with an involution and a norm, which is closed under the uniform topology. Von Neumann algebras are a special case of C*-algebras, which are just closed under the weak operator topology. Equivalently, a von Neumann algebra coincides with its double commutant. Unless otherwise specified, throughout the paper it is assumed that the algebras of observables we deal with are all von Neumann algebras, for which the results we discuss here hold true.
Note that for the kind of GNS representations we consider in the remainder of the paper the underlying Hilbert space turn out to be separable.
In the special case of inner automorphisms, one can even show that if \(\omega \) is a pure state on \({\mathcal {A}}\) then one obtains \(\bar{U} = \pi (U)\) for the unitary operator acting across the representations.
See Baker and Halvorson (2013) for a proof of this fact, which they refer to as the Specialized Representation Wigner Theorem.
Indeed, for any \(A \in {\mathcal {A}}\) the action of \(W_{\pm }\) is such that the element \(\pi _{+}(A)\) belonging to \(\pi _{+}({\mathcal {A}}) \subseteq {\mathcal {B}}({\mathcal {H}}_{+})\) is transformed into an element \(W_{\pm }^{*}\pi _{+}(A)W_{\pm }\) belonging to \(\pi _{-}({\mathcal {A}}) \subseteq {\mathcal {B}}({\mathcal {H}}_{-})\), but the resulting operator is not equal to \(\pi _{-}(A)\). Else, if it were equal, given that \(\Omega _{-} =W_{\pm } \Omega _{+}\), the state \(\omega _{+}(A) =\langle \Omega _{+}, \pi _{+}(A) \Omega _{+} \rangle \) would become
$$\begin{aligned} \langle W_{\pm } \Omega _{-}, \pi _{+}(A)W_{\pm } \Omega _{-} \rangle = \langle \Omega _{-}, W_{\pm }^{*}\pi _{+}(A)W_{\pm } \Omega _{-} \rangle = \langle \Omega _{-}, \pi _{-}(A) \Omega _{-} \rangle \end{aligned}$$for all A in the quasi-local algebra \({\mathcal {A}}\), which is exactly the state \(\omega _{-}(A)\): consequently, the two phases \(\omega _{+}\) and \(\omega _{-} = \bar{\alpha }_{\pm } (\omega _{+})\) of the infinite spins chain would coincide, notwithstanding the fact that they are connected by the broken symmetry \(\alpha _{\pm }\). Instead, by appealing to the Wigner representation theorem we can infer that, rather than being equal to \(W_{\pm }^{*}\pi _{+}(A)W_{\pm }\), the operator \(\pi _{-}(A)\) is equal to \(W_{\pm }^{*}\pi _{+}(\alpha _{\pm }(A))W_{\pm }\) for all \(A \in {\mathcal {A}}\).
In this respect, it should be mentioned that Feintzeig (2015) argues that some of the features that Baker finds puzzling in quantum symmetry breaking are present in examples of classical broken symmetries too.
In algebraic terms the transition probability between two states \(\omega \) and \(\omega '\) is expressed by formula \(1 -\frac{1}{4} \Vert \omega - \omega ' \Vert ^{2}\), where \(\Vert \cdot \Vert \) is the norm on the state space \({\mathcal {S}}({\mathcal {A}})\) (cfr. Roberts and Roepstorff 1969).
As I stressed at the beginning of section 5, Feintzeig (2015) makes a similar point for the classical spin chain.
Note that, strictly speaking, the pure states \(\omega _{+}\) and \(\omega _{-}\) should be written in such a way to display their dependence on 0 and \(\beta \), like the mixed states of which they are the components. However, in order for not to overburden the notation, for simplicity here I drop the subscripts relative to the external magnetic field and the inverse temperature, just as I have done in the rest of the paper.
An extended discussion about the difference between the treatment of symmetry breaking between quantum statistical mechanics and quantum field theory can be found in Fraser (2012).
References
Arageorgis, A. (1995). Fields, particles and curvature. Unpublished dissertation, University of Pittsburgh.
Baker, D. (2011). Broken symmetry and spacetime. Philosophy of Science, 78, 128–148.
Baker, D., & Halvorson, H. (2013). How is spontaneous symmetry breaking possible? Understanding Wigner’s theorem in light of unitary inequivalence. Studies in History and Philosophy of Modern Physics, 44(4), 464–469.
Bargmann, V. (1964). Note on Wigner’s theorem on symmetry operations. Journal of Mathematical Physics, 5, 862–868.
Earman, J. (2003). Rough guide to spontaneous symmetry breaking. In K. Brading & E. Castellani (Eds.), Symmetries in physics: Philosophical reflections (pp. 335–346). Cambridge: Cambridge University Press.
Emch, G. G. (2007). Quantum statistical physics. In J. Butterfield & J. Earman (Eds.), Philosophy of physics (pp. 1075–1182). New York: Elsevier.
Emch, G. G., & Knops, H. J. F. (1970). Pure thermodynamical phases as extremal KMS states. Journal of Mathematical Physics, 11, 3008–3018.
Feintzeig, B. (2015). On broken symmetries and classical systems. Studies in the History and Philosophy of Modern Physics, 52B, 267–273.
Fraser, D. (2012). Spontaneous Symmetry breaking: Quantum statistical mechanics versus quantum field theory. Philosophy of Science, 79(5), 905–916.
Glimm, J. M., & Kadison, R. V. (1960). Unitary Operators in C*-algebras. Pacific Journal of Mathematics, 10, 547–556.
Haag, R. (1996). Local quantum physics: Fields, particles, algebras. Berlin: Springer.
Halvorson, H., & Clifton, R. (2001). Are rindler quanta real? Inequivalent particle concepts in quantum field theory. British Journal for the Philosophy of Science, 52, 417–470.
Hoefer, C. (1996). The metaphysics of spacetime substantivalism. Journal of Philosophy, 93, 5–27.
Liu, C., & Emch, G. G. (2005). Explaining quantum spontaneous symmetry breaking. Studies in History and Philosophy of Modern Physics, 36, 137–163.
Roberts, J. E., & Roepstorff, G. (1969). Some basic concepts of algebraic quantum theory. Communications in Mathematical Physics, 11, 321–338.
Ruetsche, L. (2002). Interpreting quantum field theory. Philosophy of Science, 69, 348–378.
Ruetsche, L. (2003). A matter of degree: Putting unitary inequivalence to work. Philosophy of Science, 70(5), 1329–1342.
Ruetsche, L. (2006). Johnny’s so long at the ferromagnet. Philosophy of Science (Proceedings), 73, 473–486.
Ruetsche, L. (2011). Interpreting Quantum Theories. New York: Oxford University Press.
Ruetsche, L. (2013). Unitary equivalence and physical equivalence in the Oxford handbook of philosophy of physics. New York: Oxford University Press. ed. Bat- terman R.
Teller, P. (1991). Substance, relations and arguments about the nature of space-time. Philosophical Review, 100, 363–97.
Wigner, E. P. (1931). Gruppentheorie und ihre Anwendung auf die Quanten mechanik der Atomspektren (in German) (pp. 251–254). Braunschweig, Germany: Friedrich Vieweg und Sohn.
Acknowledgements
The author is especially grateful to Dave Baker, Erik Curiel, John Earman and Ben Feintzeig for helpful comments and discussions. He would also like to thank the FWF der Wissenschaftsfonds for supporting him under the Lise Meitner Programme during the development of this project.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Valente, G. Quantum symmetry breaking and physical inequivalence: the case of ferromagnetism. Synthese 198, 8127–8148 (2021). https://doi.org/10.1007/s11229-020-02561-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-020-02561-y


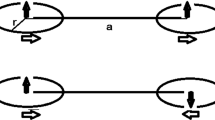

 Unit.Equiv.
Unit.Equiv. Unit.Equiv.
Unit.Equiv.