Fault-tolerant routing algorithm based on disjoint paths in 3-ary n-cube networks with structure faults

Abstract

The 3-ary n-cube network is widely used in large-scale multi-processor parallel computers. It is an important issue to design high-performance communication technology with fault tolerance. In this paper, we study the fault-tolerant routing of 3-ary n-cube without desired intersection. Firstly, we propose a fully adaptive routing algorithm for 3-ary n-cube network based on the new virtual network partition technology. The virtual channel allocation of the algorithm is given and its deadlock free property is proved. Secondly, we propose a construction of disjoint paths in 3-ary n-cube networks under the fault model. Finally, we propose a novel fault-tolerant routing algorithm for 3-ary n-cube networks based on the disjoint path with structure faults. The simulation results show that the proposed fault-tolerant routing algorithm outperforms the previous fault-tolerant routing algorithm in many situations, which has a 19–21 percent increase in throughput and the injection rate.

1 Introduction

With the rapid development of information society, high performance computing (HPC) has been the third pillar of scientific research following theoretical sciences and experimental sciences. In the research of HPC, improving operation efficiency has always been the primary goal of its development.

Parallel computing is an effective means to improve the computing speed of the systems. Interconnection networks take vital roles in parallel computing systems, the selection of an interconnection network is crucial as it can greatly affect communication performance, hardware costs and fault tolerant capabilities. The topology of interconnection network defines the connections between the processors of the parallel computing system. Numerous interconnection networks have been proposed, such as hypercubes [1], crossed cubes [2], exchanged hypercubes[3], DCell networks [4], k-ary n-cubes [5].

With the expansion of network scale and increase in complexity, the reliability and stability of the network have become more and more urgent. Ensuring the efficient and safe operation of the network has become very important. Reliability of interconnection networks is crucial for evaluating the network performance [6]. It is necessary to consider the reliability for running distributed systems, and the fault tolerance of interconnection networks has been extensively studied [7,8,9]. There are many types of failures: single node failures, link failures, and fault domains where two types of failures are connected. In reality, processors that are linked could affect each other, and the neighbors of a faulty processer might have a higher probability of becoming faulty later. It should be noted that rapid development of technology in nowadays, networks and subnetworks are made into chips [10]. That means if any node/nodes on the chip become faulty, the whole chip can be considered to be faulty. This reason motivated the research on the effect caused by some structures or subgraphs becoming faulty, instead of considering the effect of nodes or edges becoming faulty [11].

$Q^{3}_{n}$ network is an on-chip network structure widely used in multi-processor parallel computers  [12]. Performance and fault tolerance are the two main problems facing the design of large-scale multi-processor systems. Because of this, high-performance communication technology with fault tolerance has become a very challenging problem. However, fault tolerance is massively parallel processing. The most basic requirements of the device. On the one hand, although modern routers are becoming more and more robust, due to the long-term operation of the components, the probability of errors will increase [13]. Meanwhile, the scale of parallelism and multi-processors become larger, and the probability of failure chains will also increase. On the other hand, routing algorithms originally designed for fault-free networks fail under the influence of faulty nodes or faulty chains. If the message is mistransmitted, the entire network will cause congestion or even deadlock. For example, for deterministic routing algorithms, such as DOR routing algorithms, since there is only one alternative path, when this only path is caused by a failure when blocked, the message will be blocked [14,15,16]. Therefore, it is critical to design a multi-processor parallel routing fault-tolerant mechanism, especially for the $Q^{3}_{n}$ network.

Fault-tolerant routing is a common fault-tolerant mechanism for solving multi-processor parallel computers. A good fault-tolerant routing algorithm needs to well alleviate possible routing congestion to achieve load balancing, and it also needs to consider the quality of service, that is, to select the shortest routing path and minimize communication delay as much as possible [17]. Data transmission can be effectively guaranteed by finding parallel paths (disjoint paths) between the vertices of the network. The problem of disjoint paths can generally be divided into three categories: one-to-one disjoint paths, one-to-many disjoint paths and many-to-many disjoint paths [18]. One-to-one disjoint path refers to a disjoint path connecting two different vertices. One-to-many disjoint path considers the disjoint path ($k\ge 2$) connecting a vertex s and k vertices $t_1, t_2, \ldots t_k$. A many-to-many disjoint path refers to a disjoint path connecting k vertices $s_1, s_2,\ldots , s_k$ and k vertices $t_1, t_2, \ldots t_k$. Disjoint multi-path routing is an effective strategy to achieve robustness to forward data along multiple links or disjoint paths of nodes in the network.

The avoidance of deadlock is very important in the implementing an adaptive fault-tolerant routing algorithm. A common method is to divide each physical channel into a certain number of virtual channels to avoid deadlock. The resources (such as cache, bandwidth) on the physical channel will be allocated to each virtual channel [19]. Therefore, the number of virtual channels required in the deadlock avoidance mechanism will affect the efficiency of resource utilization in the routing mechanism. Under the condition of relatively limited physical resources, how to use fewer virtual channels so that each virtual channel is allocated more resources. However, using fewer virtual channels increases the difficulty of the deadlock avoidance mechanism.

In this paper, we focus on the construction of disjoint paths and fault-tolerant routing of $Q^{3}_{n}$ with structure faults. The main contributions of this paper are listed as follows:

• 1. We propose an $O(n^2)$ algorithm to give the disjoint path between any two distinct nodes in $Q_n^3$. And after analysis, the maximum length of n-disjoint paths between any two distinct nodes in $Q_n^3$ is no more than $2n-1$.

• 2. We give a disjoint path based fault-tolerant routing algorithm DPFR, which can tolerate the number of faulty nodes not exceeding the size of connectivity.

• 3. We analyse the time complexity of the algorithm DPFR is O(n) and four modes are implemented to evaluate the performance of the proposed algorithm in terms of injection rate, throughput, average delay, and buffer utilization.

The remaining of this paper is organized as below. Section 2 introduces the related work of disjoint paths and fault-tolerant routing. Section 3 provides the preliminaries used throughout this paper and gives the formal definition and properties of $Q_n^3$, and proposes an algorithm for finding n-disjoint paths between any two distinct nodes of $Q_n^3$. A fault-tolerant routing algorithm for $Q_n^3$ are given in Sect. 4. Simulation and experiment results are presented in Sect. 5. Section 6 concludes the paper.

2 Related works

The algorithm in the interconnection network needs to consider the following factors when designing: avoiding deadlock, resource allocation, self-adaptation and fault tolerance. There are two main solutions to avoid deadlock in network transmission of data packets [20]. One is to use virtual channels to divide the network into several virtual sub-networks. Another method is to limit the turn of routing messages in certain situations. To realize the efficient allocation of resources, it is necessary to make the number of virtual channels as small as possible. Meanwhile, it also needs to be adaptive to the algorithm and restrict certain turns. Fault-tolerant routing requires the support of an effective fault model, while deadlock avoidance and high self-adaptation are also necessary conditions for fault tolerance.

The routing algorithm determines the path that the data will go through in the switch fabric, so the quality of the routing algorithm has a great impact on the system performance [21]. Ren et al. [22] proposed a traffic balancing forgetting routing algorithm in 2-D grids and tori. In addition, they also provide two different granularity fault detection and analysis schemes, and ensure orderly packet delivery by assigning a unique path to each process. Zhao et al. [23] proposed a fault-tolerant minimum routing algorithm for two-dimensional grids. By calculating the fault-tolerant Manhattan path from each node to the source node or the target node, it marks these nodes as nodes with lower time complexity. In the process of path counting, no available nodes will be sacrificed under any fault distribution. Compared with the work based on fault block model, this method is not affected by fault distribution and has low computational complexity.

Zhao et al. [24] proposed a general fault-tolerant minimum routing of the grid structure. Habibian et al. [25] proposed a fault-tolerant routing algorithm for hypercube and CCC (Cube Connected Cycles) networks of any fault size and type based on the best priority search and backtracking strategy. Dong et al. [26] studied the paths and cycles embedding into 3-ary n-cubes with faulty nodes and links. Li et al. [27] studied the embedding of paths and cycles into 3-ary n-cubes with path restrictions. Francalanci et al. proposed a deadlock-free multicast routing algorithm (DFMR) for k-ary n-cube networks, which prevents deadlock by allowing nodes to send flit immediately when the link between nodes is available for transmission. Zhang et al. [28] studied the structure connectivity and substructure connectivity of bubble-sort star graph, furthermore, Zhang et al. [29] proved the structure connectivity and substructure connectivity of k-ary n-cubes.

Multi-path fault-tolerant routing means that there are multiple paths to choose from between the source and the destination. When one of the paths is interrupted due to a node failure, the other path is quickly and randomly selected with probability, so multi-path fault-tolerant routing has good fault tolerance. The disjoint path refers to a path that does not share any common nodes except for the two ends. Disjoint paths are fundamental and essential for parallel computing, fault-tolerance, and load balancing of a network [9]. Disjoint paths can ensure the stable and safe transmission of data in the network. At present, there have been a lot of researches on disjoint paths of well-known networks. Wang et al.  [30] designed an algorithm to construct at least ${\kappa }^1(G)$ disjoint paths based on any two distinct nodes in generalized hypercube under the 1-restricted connectivity. Then, Wang et al.  [31] designed an algorithm to give disjoint paths between any two distinct nodes of exchanged generalized hypercube. Lai  [32] studied the optimal construction of all shortest disjoint paths in the hypercube with applications. Wang et al. [33] constructed $n+k-1$ disjoint paths between every two distinct nodes of the k-dimensional DCell network and propose an algorithm for finding a one-to-one r-disjoint path cover in $D_{k,n}$ for any integer $1\le r\le n+k-1$ [33]. Guo et al. [34] give an $O(\kappa (G)^2)$ algorithm BuildPathSet(u, v) to get a set of $\kappa (G)$ disjoint paths between arbitrary distinct nodes u and v in BCube.

Krishnan et al. [35] proposed a fault-tolerant routing algorithm with minimum delay for grid architecture. The algorithm can find fault-tolerant paths from source to target at the minimum Manhattan distance. Otake et al. [36] proposed two methods for fault-tolerant routing in the crossed cube. Aspnes et al. [20] given the fault-tolerant routing in P2P systems, and considered the problem of designing an overlay network and routing mechanism that permits finding resources efficiently in a peer-to-peer system. Xiang et al. [37] proposed a deadlock-free unicast scheme based on minus-first routing for Dragonfly networks. Minus-first routing is a partially adaptive routing scheme in dragonfly networks without virtual channels. Furthermore, Xiang et al. [38] proposed a new deadlock-free adaptive fault-tolerant routing algorithm based on two-tier security information model. The new fault-tolerant routing algorithm can not only tolerate static and dynamic failures, but also avoid dead-zone and aimless error routing by using the new security information model. When a faulty block is encountered in the process of sending a message from the source node to the destination node, the number of virtual channels will be increased in order to avoid deadlock. In fact, some well-known deterministic strategies (XY routing, turn models, etc.) are good ways to avoid deadlock. They all send data packets through the same fixed path between each source and target pair. However, if the traffic is concentrated in the same area, congestion may occur, and multi-path routing will cause the load to concentrate on the boundary of the faulty area. Therefore, this will have a negative impact on performance and reduce the throughput of the routing algorithm.

3 System model

3.1 Preliminaries

In this section, we will give some definitions used in this paper. Interconnection networks are generally modeled with a graph $G=(V,E)$, where the vertex set V represents processors and the edge set E represents communication links between processors. A path in G is a sequence of distinct nodes, $P=(x_0,x_1,\ldots , x_{k-1},x_k)$, in which any two consecutive nodes $x_i$ and $x_{i+1}$ are adjacent for any integer $0\le i\le k$. We denoted the path P by $x_0\sim x_k$ and an edge $(a_i,a_{i+1})$ in P by $x_i\rightarrow x_{i+1}$. Let $P-a_k$ to denote the path $(a_0,a_1,\ldots , a_{k-1})$. The length of a path P is the number of edges in P.

A path P is called $f\!ault$-$f\!ree$ if all nodes in P are non-faulty. Suppose P and $P'$ are the two paths from node x to node y, if the other nodes are distinct except for nodes x and y, then we say P and $P'$ are disjoint. The distance between nodes x and y is written as dist(x, y), which is the minimum value of all path lengths from x to y. The diameter of G is the maximum distance between any two distinct nodes in G, denoted as $max\{dist(x,y)\mid x, y\in V(G)\; {\mathrm {and}}\; x\ne y\}$. Let G be a graph and F(G) be the faulty set of G. We refer to an edge $(x, y)\in E(G)$ where $x \notin {\mathcal {V}}(F(G))$ and $y\notin {\mathcal {V}}(F(G))$, as a safe crossing-edge.

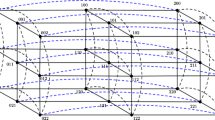
The 3-ary n-cube $Q^{3}_{n}$ ($n\ge 1$) has $N=3^{n}$ vertices, each vertex can be denoted by $x=x_{n-1}\ldots x_{1}x_{0}$, where $0\le x_{i}\le 2$ for every $0\le i\le n-1$. As shown in Fig. 1, two vertices $x=x_{n-1} \ldots x_{1}x_{0}$ and $y=y_{n-1} \ldots y_{1}y_{0}$ are adjacent if and only if there exists an integer j with $0\le j\le n-1$, such that $x_{j}=(y_{j}\pm 1)\text{ mod }$ 3 and $x_{i}=y_{i}$ for $i\in \{0,1,2, \ldots ,n-1\}-\{j\}$. Furthermore, the i-th position, from the right to the left, of the n-bit string x is called the i-dimension. For any two vertices x and y, if and only if they are different in the j-dimension, then the edge (x, y) is called a j-dimensional edge or simply a j-edge. A vertex incident to a j-edge is called a j-dimensional vertex.

Fig. 1

a The 3-ary 1-cube $Q^{3}_{1}$, b the 3-ary 2-cube $Q^{3}_{2}$, c the 3-ary 3-cube $Q^{3}_{3}$

3.2 Fault information model

In this section, We first classify the types of structural failures and extract the commonality of such failures. Then, we construct disjoint paths for such structural failure models.

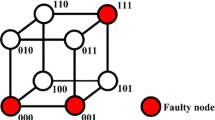
In a 3-ary n-cube network, failures are random. According to statistics [15], the following types of failure models are common in the network, and different failure domains and failure cycles can be formed at the same time. As shown in Fig. 2a, when the faulty server has a small affect on the area, the faulty structures could be $K_1$, $K_{1,1}$, and $K_{1,2}$. While when the effect of the faulty server on the area is becoming larger, the faulty structure could be $K_{1,M}$ with $M\ge 3$. In the convex fault model, there are a total of 12 types of node locations on the fault. They are: (1) North, (2) South, (3) West, (4) East, (5) North-east outer corner, (6) North-west outer corner, (7) South-east outer corner, (8) South-west outer corner, (9) South-east inner corner, (10) South-west inner corner, (11) North-east inner corner, (12) North-west inner corner. Figure 2b shows the specific locations of different fault nodes on the fault model. The faults of the $K_{1,M}$ series can be further restricted to the $C_M$ fault model. For this type of structural failure, we uniformly represent them as a convex failure model.

Fig. 2

a Structure faulty elements in a mesh-based supercomputer, b faults model

We define the following five types of messages as follows.

where $(u_0, u_1)$, $(a_0, a_1)$ and $(v_0, v_1)$ represent the source node, the current node and the destination node in the 3-ary n-cube network, respectively.

Generally, the packets that have just been injected into the network can be divided into four types, as shown in Table 1, which only belong to Dim0+, Dim0−, Dim1+ and Dim1−. Dim0+ and Dim0− messages will become Dim1+ or Dim1− messages after completing X-dimensional routing. For Horizon0− packets, it is a kind of packets after the first four packets are blocked by faults and then rerouted.

Table 1 Symbols and notations

Due to the Dimension Order Routing (DOR) routing algorithm [39], there is only one alternative route, so when this only route is blocked by a fault, the message will be blocked. Traditional DOR is very simple and efficient, but it can only be used in regular 2D mesh. Since the 3-ary n-cube network itself has surrounding channels, under the principle of the shortest route, it enables resource circulation applications among channel resources of each dimension. There may occur deadlock while using the DOR algorithm in 3-ary n-cube networks.

The virtual channel can solve the deadlock problem caused by information exchange in the network. Applying DOR routing in a 3-ary n-cube network can avoid deadlock through virtual channels. In the network, a total of two virtual channels need to be used, called $V_0$ and $V_1$, respectively. The following are the rules for the use of these two virtual channels: $V_0$ is used for routing by all packets that have not passed the wrap-around pass. If a message is routed on a certain dimension and needs to use a surround channel, it must pass through the $V_1$ virtual channel. At the same time, in the future routing process, the message will always use $V_1$ on this dimension. Meanwhile, the virtual channels $V_0$ in the same dimension will no longer have resource recycling applications between each other. Therefore, based on the DOR algorithm, we design a multi-path routing algorithm for 3-ary n-cube networks. First, we describe the routing process of the west-bound preferential turn model under the restricted convex fault model. The Dim0+, Dim0−, Dim1+ and Dim1− messages are applied.

Lemma 3.1

For Dim0+ packets, before being blocked by the fault, the packets always use the DOR dimension sequence routing algorithm. If the route on the X-dimension is completed, it will either reach the destination node or become one of Dim1+ or Dim1−.

Proof

We prove it according to the following two cases.

Case 1 There is no obstruction by the fault model in the routing process. Dim0+ packets are routed to the right according to the DOR dimension sequence, and finally Dim0+ packets will successfully complete the X-dimensional routing, either directly reach the destination node, or become Dim1+ packets or Dim1− message.

Case 2 There is failure model occurred during the routing process. When the message is routed along the X-dimension in the DOR dimension, it is blocked by the faulty node. In the fault model used in this article, the message is blocked only when it encounters a ring node of the west location type. At this point, the message will start to use the Westbound Priority Turning Model algorithm for detouring. Until the Dim0+ message reaches the node on the ring whose position type is noth-west outer corner or south-west outer corner. Subsequently, the message stops detouring on the faulty ring, but re-dos the DOR dimension sequence routing. If it is hindered by the next fault in the subsequent routing, it can be solved by a similar method, and finally the routing on the X-dimension is completed. See Fig. 3a.

Case 3 For Dim0+ messages, when the message regains the dimension order routing resource or reaches the north-west outer comer or south-west outer comer node of the structural failure model, the detour of this message will end. The similar case to Dim0−. $\square$

Fig. 3

Routing characteristics of turn model for Dim0+, Dim1+ and Dim1− messages under structural fault model

Lemma 3.2

For Dim1+ and Dim1− messages, before being blocked by the fault, the message always uses the DOR dimension sequence routing algorithm. If the routing on the Y-dimension is completed, it either directly reaches the destination node or becomes a Horizon0− message.

Proof

We have the following two cases to prove.

Case 1 There is no fault model in the routing process. When Dim1+ and Dim1− messages are routed in DOR dimension on the Y- dimension, no fault is encountered. The message will successfully complete the Y-dimensional routing and directly reach the destination node.

Case 2 There is failure model occurred during the routing process. When Dim1− message is routed south-ward in the DOR dimension on the Y-dimension, it is blocked by the faulty node. In the fault model we use, the message is blocked only when it encounters a node on the ring whose location type is north or north inner corner. At this time, the message will start to use the westbound priority turning model algorithm to make a clockwise detour. If the message does not become a Horizon0− message before reaching the easternmost node of the fault ring, it will be passed southward until it becomes a Horizon0− message. If it is hindered by the next fault in the subsequent routing, it can be solved by a similar method, and finally the routing on the Y-dimension is completed. The routing of Dim1+ packets is similar to Dim1− packets. The difference is that the detour direction on the fault ring is counterclockwise. And when it reaches the east-most node of the fault ring, it will be transmitted to the north until it becomes a Horizon0− message. See Fig. 3b. $\square$

Lemma 3.3

For Dim1+ and Dim1− messages, before being blocked by the fault, the message always uses the DOR dimension sequence routing algorithm. If the routing on the Y-dimension is completed, it either directly reaches the destination node or becomes a Horizon0− message.

Proof

We have the following two cases to prove.

Case 1 There is no fault model in the routing process. Dim0−The message is routed to the left according to the DOR dimension sequence. Finally, the Dim0− message will successfully complete the X-dimensional routing, and will either reach the destination node or become one of Dim1+ or Dim1− messages.

Case 2 There is failure model occurred during the routing process. When the message is routed along the X-dimensional DOR dimension, it is blocked by the faulty node.

In the fault model we used, only when the nodes on the ring of the east, north corner and south inner comer location types are encountered, the message is blocked. At this time, the Dim0− message will start to detour on the ring. If the node on the ring is east, the message will select its neighboring node to the north or south as the next hop node for detouring. If YoffsetY (dimension offset)>0, select the neighboring node to the north, and this message will be routed according to the routing process of Diml+ message. If Yoffset<0, the neighboring node in the south is selected, and the route will be detoured according to the routing process of Dim1− message. Eventually, the detoured Dim0− message will become Horizon0− messages. If the node on the ring is the northeast inner corner or the southeast inner corner, the routing algorithm provides 180 turns. The message can also be converted into Dim1+ message or Dim1− message for detouring. If it is in the subsequent routing, it will be blocked by the next failure. It can be solved by a similar method, and finally becomes Horizon0− message. See Fig. 4a. $\square$

Fig. 4

Routing characteristics of turn model for Dim0− and Horizon0− messages under structural fault model

Summarizing the above lemmas, we can draw the following conclusions. Through DOR dimension sequence routing and west-bound priority turn model fault-tolerant routing, Dim1− and Dim1+ messages will reach the destination node if they do not encounter failures when they are routed in the Y-dimension. Otherwise, it will be routed through Horizon0− message and finally reach the destination node. For Dim0+ messages, regardless of whether it encounters a failure during the dimension sequence routing on the X-dimension, the X -dimension routing will be completed. If the destination node has not been reached at this time, it will be routed through Dim1− or Dim1+ packets, and finally reach the destination node. For Dim0− messages, if X-dimensional routing is completed, Dim1− or Dim1+ messages can reach the destination node. Otherwise, it will be routed through Horizon0− message and finally reach the destination node. Then, if the Horizon0− message can reach the destination node smoothly when it encounters a failure, all the messages will reach the destination node smoothly. Horizon0− messages are Dim0+, Dim0−, Dim1+ and Dim1− messages. The message is blocked by a fault during the routing process, or will eventually become a message type.

Lemma 3.4

For Horizon0− message, the eastward priority turn model can be used to make a detour, and finally reach the destination node.

Proof

We have the following two cases to prove.

Case 1 There is no fault model in the routing process. The DOR dimension sequence route can be used by Horizon0− messages to complete the route on the X dimension and reach the destination node.

Case 2 There is failure model occurred during the routing process. Horizon0-message will be routed clockwise or counterclockwise along the fault ring on the faulty node. If a similar situation occurs in the subsequent routing process, it can be solved by a similar method, and the destination node will eventually be successfully reached. See Fig. 4b. $\square$

We can draw the following conclusion: for all packets injected into 3-ary n-cube network, no matter which one of the four packets belongs to, they can reach the destination node successfully under these two turning model algorithms.

3.3 Construction of disjoint paths

In this section, we will an algorithm for constructing disjoint paths between any two distinct nodes u and v in $Q_n^3$. Let P present a path between a and b where $u=(x_nx_{n-1}\cdot \cdot \cdot x_1;s)$ and $v=(y_ny_{n-1}\cdot \cdot \cdot y_1;t)$. According to the definition of $Q_n^3$, we can construct disjoint paths which end nodes are u and v.

The multi-path with disjoint links cannot be calculated by simply using the multi-pass Flody function [40]. We will illustrate this point through an example of the shortest path with two paths. As shown in Fig. 5a, this is a complete graph between four nodes, and the path length graph has been marked. Simply call the Flody algorithm (or other similar shortest path method) to find the disjoint shortest path between a and d. The process is as follows: Find the first path $a-b-c-d$ as the shortest single path, and the path length is 3. Since the paths do not intersect, the length of the second path $a-d$ is 8 and the total length of the multipath is 11. But this solution is not optimal.

In order to effectively solve this problem, we use the following methods to optimize. On the premise of finding the first path $a-b-c-d$, the first path is reversed, that is, only the reverse path is allowed, as shown in Fig. 5b.

Fig. 5

a Complete graph with 4 vertices, b complete graph after reverse optimization

At this time, call the Flody function to find the correct second shortest path, where $a-c-b-d$ path length is 7 less than $a-d$ length 8 path. After finding the two paths, the two paths need to be integrated and optimized to obtain the correct shortest path of disjoint multipath. The two paths at this time are $a-b-c-d$ and $a-c-b-d$. Obviously, the $b-c$ path in the middle has both forward and reverse paths. According to the principle of cyclic cancellation, the final shortest double paths can be obtained as $a-c-d$ and $a-b-d$. And the total length of the multi-path is 8, which is the optimal solution (as shown in Fig. 5). The principle of finding the shortest path of the multipath with more than 2 paths is exactly the same. It is only necessary to reverse all the shortest paths of the two paths found, and then call the Flody function on the new graph to find the third shortest path. Combining the previous two paths and integrating and optimizing them through the principle of circular cancellation, the shortest path of the multi-path can be obtained. The idea of the above algorithm comes from the calculation algorithm of network flow. First, consider multiple disjoint paths as a network flow from the source node to the terminal node. Then the algorithm of network flow is modified to calculate disjoint paths.

In the following disjoint path algorithms, a sub-algorithm Find_Paths is used repeatedly. This algorithm is used to get a shortest path from s to $s^i$ where $s=(x_nx_{n-1}\cdot \cdot \cdot x_1;u)$ and $s^i=(x_nx_{n-1}\cdot \cdot \cdot \overline{x_i}\cdot \cdot \cdot x_1;i)$. For convenience, we first give the sub-algorithm Generate_Paths as follows.

The first situation is that nodes s and t are adjacent in the same clique. Therefore, nodes s and t satisfy the following two conditions: (1) $x_nx_{n-1}\cdot \cdot \cdot x_1=y_ny_{n-1}\cdot \cdot \cdot y_1$ and (2) $u\not =v$. Therefore, we propose an algorithm DP_con to construct n-disjoint paths between s and t.

The following lemma will prove that the n paths constructed by the algorithm DP_con are disjoint, and the maximum length of the constructed path is 9.

Lemma 3.5

Algorithm DP_con can construct n-disjoint paths with a maximum length of 9 between nodes s and t, where s and t are adjacent in the same clique.

Proof

Since the nodes s and t are adjacent in the same clique, we let $s=(x_nx_{n-1}\cdot \cdot \cdot x_1;a)$ and $t=(x_nx_{n-1}\cdot \cdot \cdot x_1;b)$. Through the algorithm DP_con, we know that lines 4–5 construct a path from s to t through the external-neighbor of node s, lines 6–7 construct a path (s, t) and lines 8–9 construct $n-2$ paths from s to t through nodes $(x_nx_{n-1}\cdot \cdot \cdot x_1;i)$ where $i\in \langle n\rangle \backslash \{a,b\}$ is $(s, (x_nx_{n-1}\cdot \cdot \cdot x_1;i), t)$. We know that the nodes s, t and $(x_nx_{n-1}\cdot \cdot \cdot x_1;i)$ are in the same clique. Thus, these $n-2$ paths are disjoint. In summary, the n paths from s to t constructed by algorithm DP_con are disjoint. Next, we analyze the maximum length of the path constructed by the algorithm DP_con. Obviously, among the paths constructed by the algorithm DP_con, the length of the path constructed from lines 4–5 is the longest and its length is 9. In summary, the algorithm DP_con obtains n-disjoint paths from s to t, and the length of the path does not exceed 9. $\square$

4 Fault-tolerant routing algorithm

In this section, a fault-tolerant routing algorithm DPFR is proposed for the presence of faulty node in the network.

Let F be a faulty node set of $Q_n^3$. This algorithm can obtain a fault-free path between any two distinct fault-free nodes s and t in $Q_n^3$ when the faulty node set $|F|\le 2n-1$. Then the time complexity of the algorithm is analyzed and the maximal length of the fault-free paths constructed by the algorithm. An n-dimensional $Q_n^3$ can be divided into three subgraphs of the same size according to whether the i-th bit is 0, 1 or 2, and denote these three subgraphs as $S^{i=0}_{n-1}$ (0-subgraph), $S^{i=1}_{n-1}$ (1-subgraph), and $S^{i=1}_{n-1}$ (2-subgraph), respectively.

Theorem 4.1

There exists an O(n) algorithm for finding a fault-free path P between any two distinct fault-free nodes in $Q_n^3$ with a faulty node set $F\subset V(Q_n^3)$ with $|F|\le 2n-1$.

Proof

Given two nodes s and t in $Q_n^3-F$ with a faulty node set $F\subset V(Q_n^3)$ with $|F|\le 2n-1$, we propose an algorithm DPFR. In the algorithm DPFR, we will use the algorithm DPFR and its sub-algorithm DP_con. The sub-algorithm DP_con uses a loop to find the addresses of different bits in the coordinate representation of any two nodes, and stores these addresses in a list L in turn. The time complexity of sub-algorithm DPG is O(n). In the following, we use ${\mathrm {DP}}\_{\rm con}(s,t)$ to represent the obtained list Q between nodes s and t, and ${\mathrm {H}}(s,t)$ to represent the Hamming distance between nodes s and t. Next, we propose the algorithm DPFR.$\square$

And then, the time complexity of algorithm DPFR is analyzed. At the beginning of the algorithm, the Hamming distance d between nodes s and t needs to be calculated. Then, obtain a list L which contains the different bit between nodes s and t. The time complexity are both O(n). We know that the sub-algorithm Construct_d can be computed in constant time, and the core part of the algorithm DPFR is a sub-algorithm Fault-freeP, which divide $Q_n^3$ into three subgraphs $S_{2n-1}^{i=0}$, $S_{2n-1}^{i=1}$ and $S_{2n-1}^{i=2}$ such that $s\in S_{2n-1}^{i=0}$, $t\in S_{2n-1}^{i=1}$ and $t\in S_{2n-1}^{i=1}$. Assume that $S_{2n-1}^{i=1}$ contains at most $\frac{n-1}{2}$ faulty nodes of F, then obtain a fault-free path from node a to node $s^{(1)}\in S_{2n-1}^{i=1}$. Next, regard $s^{(1)}$ as s, and repeat the above method to find a fault-free path from nodes s to t in the subgraph $S_{2n-1}^{i=1}$. Assume that the fault-free path constructed by algorithm DPFR is as follows: $s\sim t= s \sim s^{(1)}\sim \cdot \cdot \cdot \sim s^{(i)}\sim s^{(i+1)}\sim \cdot \cdot \cdot \sim s'\sim t$. Since there are at most $2n-1$ faulty nodes, a fault-free path of length at most 4 can be found from node s to some node $s^{(1)}\in S_{2n-1}^{i=1}$. Then find a fault-free path from node $s^{(1)}$ to node t in $S_{2n-1}^{i=1}$. Repeat the above process, find a fault-free path of length at most 4 from node $s^{(i)}$ to node $a^{(i+1)}\in S^{i=1}_{2n-(i+1)}$, until $s^{(i+1)}=t$ or $s^{(i+1)}$ and t are divide into a fault-free subgraph. Since $|F\cap S_{2n-(i+1)}^{i=1}|\le |F\cap S_{n-i}^{i=1}|\setminus 2$ and $|F|\le 2n-1$, it can get a subgraph $S_{n-[log(n-1)]}$ which satisfy $F\cap S_{n-[log(n-1)]}=\emptyset$, node $s^{([log(n-1)])}$ is denoted as $s'$ and $t\in S_{n-[log(n-1)]}$. Then use the shortest path algorithm DP_con to find a path from $s'$ to t, and it takes O(n) time. It is clearly that routing $s^{(i)}$ to the opposite subgraph cost $O(\frac{n}{3^i})$ time since there are at most $\frac{n}{3^i}$ nodes need to be explore. Therefore, the total time complexity for finding the fault-free path from s to t in $Q_n^3$ is

$$\begin{aligned} T(n)&=O(n)+O(n)+O(n)+O(\sum _{i=0}^{\text {log}}n \frac{n}{3^i})\\&=3O(n)+O(n+\frac{n}{3}+\cdot \cdot \cdot +\frac{n}{3^{\text {log}}n})\\&=O(n). \end{aligned}$$

$\square$

Multi-path routing has better performance because it does not use the optimal path, but uses multiple sub-optimal paths. Compared to using a few sub-optimal paths, using multiple sub-optimal paths does not cause much performance degradation. Compared with the shortest path routing, multi-path routing can usually provide a better routing scheme for multiple parties participating in the game in the network. According to the network flow theory [41], the proposed disjoint paths can provide larger network flow than partially disjoint paths. Therefore, routing based on disjoint paths has better network load balancing, which is more conducive to improving the overall utilization of the network.

5 Simulation and performance evaluation

In this section, simulation experiments were carried out to compare the performance of the proposed DPFR with the two most representatives of the existing routing schemes, e.g., Minimal routing (Min) [42], Tree-based routing (Tree) [43] and DPFR. The minimal routing means that if a data packet can only jump from a node to a connected node when the movement corrects an inconsistent bit. The tree-based routing algorithm uses all header files to route along the tree. Multi-destination messages use all header flits in the message to route through the network at each intermediate node along the path of the multi-destination message. The scale of network is $8*8*8$, including 512 nodes. Each Switch is connected to four IP cores through a local port, and the number of IP cores is 256. Min and Tree adopt XYZ routing and DPFR adopt E-cube routing.

5.1 Simulation environment

The flit-level simulator [44] was used to evaluate the proposed fault-tolerant routing algorithm. The simulator uses wormhole routing mechanism. The network parameters of the flit-level simulator are set as below: the number of virtual channels in each physical channel is set to 4, and the size of each virtual channel is set to store 4 flits. The message length is set to 190 bytes and chip length is set to 150 bits. The simulation experiment runs 20,000 clock cycles each time, and the preheating period is set to the first 10% of the clock. In order to make the simulation results more accurate, the simulator runs 20 times under the same parameter configuration, and takes the arithmetic average as the output value of the simulation results.

In the flit-level simulator, the calculation methods for evaluating network performance parameters such as throughput, average delay and buffer utilization. The throughput refers to the maximum throughput of a given topology under the ideal flow control and routing mechanism. The delay is the average value of the routing delay between all communication node pairs in the whole network, assuming no congestion occurs in the routing process. The buffer utilization means that the cache is in the maximum allowable space, and the number of caches used to store microchips in the switching nodes and IP cores accounts for the proportion of the entire network cache.

5.2 Simulation results and discussion

The following four modes were used to carry out experiments: Random mode, Local mode, Hoptspot mode and Bitreversal mode. The generation of messages obeys exponential distribution. Under the random mode, the network traffic is randomly distributed, and the probability of each node receiving data packets is equal. Under local load mode, 60% of the traffic is limited to four IP cores in the cluster, 30% to six nodes with Manhattan distance of 1, and 10% of the traffic is sent to other nodes in a random distribution. Under the hotspot load mode, this paper considers the case of 300% single hotspot (hotspot receives 300% more traffic than other nodes). Min chooses the network center node as the hotspot, and (1, 1, 1) is chosen as the hotspot for the $4*4*4$ Min routing. Because of the symmetry of DPFR, a node 141 is chosen arbitrarily as the hot spot. Under the four flow modes, the DPFR algorithm is simulated in the presence of structural failures, and the average delay, average throughput, and cache utilization under different packet injection rates are recorded.

Figure 6 shows the average delay and injection rate of DPFR and Min under different modes. As shown in Fig. 6a, the delay of both structures is very low when the injection rate is less than 0.51 under random load mode. While the injection rate is greater than 0.51, the delay of Min increases rapidly. While the injection rate is greater than 0.46, the DPFR delay also increases, but the increase is smaller than that of Min. This is because DPFRs have shorter diameters than Min.

Fig. 6

Performance evaluation of average latency in different modes: a random mode, b local mode, c hotspot mode, d bitreversal mode

Figure 6b shows the delay comparison under local mode. As shown in figure, the delay growth of DPFR is flat, and when the injection rate is greater than 0.4, the delay growth begins to accelerate. DPFR have smaller buffer utilization in local mode than in random load mode, so DPFR has shorter average delay in local load mode than in random load mode. For Min, when the injection rate is small, the delay under local load is smaller than that under random load, which is also due to the smaller buffer utilization. While the injection rate is greater than 0.41, the average delay of Min in local mode increases sharply. This is because there are fewer adjacent nodes on the six outermost planes of Min. While the injection rate increases, a large number of communication gathers in fewer points, which are more prone to blocking, resulting in a significant increase in the delay of data packets waiting to be processed. In this case, the delay due to blocking is much larger than the delay due to the shortening of the buffer utilization. Therefore, when the injection rate is high, the average delay of Min under local mode is larger than that under random mode. The delay of both algorithms is low when the injection rate is small, and the average delay of DPFR is slightly less than that of Min. While the injection rate is high, the average delay of DPFR is much smaller than Min.

Figure 6c shows the average delay comparison in hotspot mode. While the injection rate is higher than 0.55, the average delay of both structures increases. Thereafter, at the same injection rate, the average delay of DPFR is always lower than that of Min. In addition, because congestion is easy to occur in hot spots, and deterministic routing algorithm is adopted in both structures, the algorithm will not adjust the routing according to the load. Therefore, some packets will wait a long time to apply for hotspot resources, so the delay of hotspot load mode increases obviously at low injection rate.

Figure 6d shows the relationship between average delay and injection rate of three algorithms under bitreversal load mode. Under bitreversal load mode and low injection rate, the average delay of DPFR and Min is lower. With the increase in data packet injection rate, the average delay of DPFR and Min also increases. While the injection rate is less than 0.52, the average delay growth of the DPFR is slightly larger than that of the Min. While the injection rate is greater than 0.55, the average delay of Min increases more than that of DPFR. This is because the node degree of the outermost node of Min is small. While the injection rate increases, these nodes are more likely to block, so the waiting time for processing data packets increases significantly. Compared with the random load mode, the average delay of the three topologies in the local load mode is larger when the injection rate is higher. This is because the increase time caused by network congestion is much longer than the decrease time caused by the shortening of buffer utilization. The average delay of the DPFR is 18.5% lower than that of the Min while the injection rate is 0.76. The average delay of the DPFR is 19.1% lower than that of the Min while the injection rate is 0.52.

Figure 7 shows the average throughput and injection rate of DPFR and Min under different load modes. As shown in Fig. 7a, in the case of random load mode, when the injection rate is less than 0.15, there is no congestion in the network. Under the same injection rate, the network throughput is basically the same. As the packet injection rate continues to increase, the network becomes busy and the throughput finally reaches saturation. For a DPFR, when the injection rate is higher than 0.2, the saturated throughput of the network is 0.27. In Min routing, when the injection rate is 0.16, the saturated throughput of the network is 0.19. The saturated throughput of DPFR is 43.2% higher than that of Min routing.

Fig. 7

Performance evaluation of average throughput in different modes: a random mode, b hotspot mode, c transpose mode, d bitreversal mode

Figure 7b shows the throughput and injection rate under local mode. While the injection rate is higher than 0.6, Min reaches saturation and saturation throughput is 0.13. The saturated throughput of DPFR is 0.35, which is 16.77% higher than that of Tree routing.

Figure 7c shows the relationship between throughput and injection rate under hotspot mode. While the injection rate is higher than 0.7, these three algorithms tend to be saturated and the throughput difference is small. The overall throughput of DPFR is slightly higher than that of Min routing. It can be seen that the single hot spot mode is more saturated than the other two modes, and the single hot spot is the bottleneck of the whole network. Meanwhile, the network throughput has little relationship with the topology.

Figure 7d shows the throughput and injection rate of the three topologies. The experimental data of network throughput of DPFR and Min are obtained by simulation under Bitreversal load mode. While the injection rate is less than 0.19, there is no congestion in the network. At the same injection rate, the network throughput is basically the same. With the increase of data packet injection rate, the network becomes busy gradually. The DPFR will reach saturation state. For DPFR, when the injection rate reaches 0.21, the network reaches saturation, and the throughput at saturation is 0.17. For Min algorithm, when the DPFR network reaches saturation, the throughput of Min is 0.21. When the DPFR is saturated, the throughput is 7.7% lower than that of the Min.

As shown in Fig. 8a, the total number of data packets increases continuously until the network reaches saturation state with the gradual increase of injection rate under the random mode. When the network reaches saturation state, the difference between the buffer utilization of DPFR and Min is small. The buffer utilization of DPFR is 12.8% less than that of Min. As shown in Fig. 8b, the buffer utilization of DPFR is close to Tree when the injection rate is 0.15 under local mode. The average hop number of DPFR is 7.2% less than that of Min. Figure 8c shows the the buffer utilization of three algorithms under hotspot mode. Under the hotspot mode, the difference between the buffer utilization of DPFR and the buffer utilization of DPFR is small. While the injection rate is 0.36, the average hop number of DPFR is 6.5% less than that of Min. Figure 8d shows the buffer utilization of three algorithms under bitreversal mode. The buffer utilization of the DPFR under this load mode is about 9.6% less than that of the Min. The buffer utilization of the three algorithms in bitreversal mode is less than the experimental values in random mode.

Fig. 8

Performance evaluation of buffer utilization in different modes: a random mode, b hotspot mode, c transpose mode, d bitreversal mode

As shown in Fig. 9, the performance of the three algorithms changes as the failure rate increases. Figure 9a–c shows the average latency, average throughput rate, and buffer utilization as the failure rate increases. Figure 9d shows the time consumed by the three algorithms in constructing a fault-free path. DPFR shows good performance in terms of average delay, throughput, cache utilization, and algorithm time overhead. Because Min and Tree routing transmit data packets along a fixed path, the DPFR algorithm transmits When data packets, the routing is evenly distributed in the rectangular space from the source node to the destination node. In the case of the same data packet injection rate, each node using the DPFR algorithm needs to process the data packets more averagely. Therefore, the delay is lower, and the greater the injection rate and the greater the congestion, the performance advantage of the DPFR algorithm is more obvious.

Fig. 9

Comparison of algorithm performance under different failure rates: a average latency, b average throughput, c buffer utilization, b the time consumption to get a fault-free path

Table 2 shows the comparison between the three algorithms and the average value of the performance parameters in the four modes. Compared with the other two algorithms, DPFR shows obvious performance advantages in terms of average delay. In terms of average throughput, it is close to the Min algorithm and has obvious advantages over the Tree algorithm. In terms of buffer utilization, DPFR has obvious advantages over Tree routing, but it is inferior to Min routing in some cases.

Table 2 Performance comparison of the three algorithms in different modes

6 Conclusions

High-performance interconnection network is a key factor that determines the performance of parallel computers. Reliability requires that the interconnection network can continue to operate normally when its routing switch node fails. In this paper, we propose a new virtual network partition scheme for 3-ary n-cube networks with structural failures. The proposed fault-tolerant routing algorithm is a deadlock free fully adaptive routing algorithm. Firstly, we classify and analyze the types of structural faults, which are expressed as convex faults. Secondly, we construct disjoint paths in 3-ary n-cube networks based on structural faults. Finally, a fault-tolerant routing algorithm based on turn model is proposed when there is a fault in 3-ary n-cube network. Each physical channel only needs four virtual channels to avoid deadlock. We gave the detailed proof process of deadlock free routing algorithm, which shows that the algorithm is feasible in 3-ary n-cube network with $2n-1$ faulty nodes. In addition, research shows that for routes that use fewer virtual channels, the lower the cost and the higher the reliability.