1 Introduction

Skyline queries have recently received substantial attention due to their wide variety of applications that involve multi-criteria decision making: for example, review evaluations with user ratings [16], product or stock recommendations [6, 17], data visualization [32] and graph analysis [35].

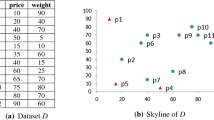
Given a set of multi-dimensional tuples, the skyline query retrieves tuples which are not dominated by any other tuples, where a tuple \(p_1\) is said to dominate a tuple \(p_2\), if \(p_1\) is no worse than \(p_2\) in any dimensions and \(p_1\) is better than \(p_2\) in at least one dimension. Figure 1a shows the item list of an online retailer, and Fig. 1b shows the result of a skyline query from the item list.

Fig. 1
figure 1

An example for a skyline query for a blouse. a An item list. b A result of skyline query

Full size image

Among the items in Fig. 1a, it is obvious that users of the online retailers have a preference for items of high quality and low prices. For instance, in Fig. 1b, it seems like that the user who wants to buy a blouse have no proper reasons to select items i and e rather than f, which has not only a better price but also a better quality. The same argument is applied to items a and b. Like this, skyline queries are helpful to retrieve preferable or interesting items that satisfy multiple criteria.

Computing the skyline is challenging today since big data is generated and processed in many applications, such as in business, social network services and scientific research. Thus, devising efficient methods for calculating skylines in a distributed and parallel environment is vital for the performance of those applications.

Skyline computation on large datasets is a both IO-consuming and CPU-intensive  [18, 33]. Therefore, a considerable number of approaches have been studied in distributed and/or parallel computing environments to process skyline queries on big data efficiently  [9, 18, 29, 30, 33]. They divide a dataset into multiple subsets and produce a local skyline for each subset. After that, they merge the local skylines and then calculate the global skyline from the merged local skylines.

However, when large datasets are dynamically generated or values of attributes in tuples are continuously changing, most of the existing distributed and/or parallel approaches become impractical [33]. Furthermore, it is hard to use the skyline algorithms of those approaches in MapReduce framework because they rely heavily on flexible inter-node communications to coordinate distributed and/or parallel processing among nodes. On the other hand, the MapReduce framework does not support inter-mapper or inter-reducer communications and the communication between a mapper and a reducer is strictly constrained by the form of key-value pairs [18].

Recently, various approaches of the skyline query processing using MapReduce framework have been proposed for the skyline computation on large datasets. However, most of the existing methods execute both the local skyline merging and the global skyline computing in a serial manner because the global skyline tuples cannot be solely determined using a single local skyline [6, 32, 33]. Consequently, those approaches cannot take a full advantage of parallelism.

To solve this problem, some researchers parallelized serial parts by distributing the additional sets of tuples needed to determine the global skyline tuples in each local skyline [14, 18]. However, all of those solutions suffered from the parallel overhead caused by computing and transmitting the additional sets of tuples, and the benefits of the parallel processing decreased as the dataset size increased. If the size of the skyline increases quickly as in anti-correlated distribution, the performance deterioration becomes more serious.

In this paper, we propose a novel two-phase skyline query processing method in MapReduce framework. Our method performs well even in an environment in which large datasets are dynamically generated. In the first phase, we start with dividing the input dataset into a number of cells (subsets of input dataset) with a grid-based partitioning scheme, and then we compute local skyline for each cell. In the set of cells, there may exist unqualified cells all of whose tuples are dominated by the tuples in other cells. To discard all tuples in unqualified cells, we design the outer-cell filter and propose a method to improve the filtering power of the outer-cell filtering technique. By using this technique, we reduce the query processing time considerably by avoiding a large number of computations for tuples in unqualified cells.

In the second phase, the computation of the global skyline is carried out using the local skylines. To determine global skyline tuples from each local skyline separately in a parallel manner, we design inner-cell filters. By distributing appropriate inner-cell filters to local skylines, we can compute the global skyline separately in a fully distributed and parallel manner. Thus, on the contrary to the existing approaches, in our method, the local skyline merging process for the global skyline computation, which is the culprit of the bottleneck, is eliminated, and it is completely parallelized using the inner-cell filters.

However, if we try to process skyline queries in a parallel manner, we must spend time to prepare and transmit the inner-cell filter to different computing nodes, which means that additional cost is needed for the parallelization. Therefore, it is important to reduce this kind of parallel overhead to avoid impairing the performance of parallel skyline query processing.

To reduce the parallel overhead for inner-cell filters, we design a method to compact the size of inner-cell filters. We also propose methods to reduce the overhead for computing the inner-cell filter, in which we remove redundant computation and reuse the computation results. Furthermore, we propose a method that groups the cells that affect each other to determine global skyline tuples in local skylines. Thereby, we further reduce the overhead for computing and transmitting inner-cell filters. With the two filtering techniques, outer-cell filtering and inner-cell filtering, we can process skyline queries fast and in a fully parallelized manner in all states of the MapReduce framework. The contribution of this paper is as follows.

  • We propose a distributed and parallel framework to compute skylines on a large amount of datasets efficiently in MapReduce. We also develop and implement new parallel skyline algorithms.

  • We design an outer-cell filter which makes fast processing of skyline queries by pruning a large number of tuples in unqualified cells.

  • We design an inner-cell filter which allows us to obtain a global skyline in a distributed and parallel manner by pruning unqualified tuples in local skylines.

  • We propose methods for computing and transmitting inner-cell filters efficiently to avoid loss of benefits for the parallel processing.

  • We seamlessly apply our filtering techniques to MapReduce by taking into consideration the nature of the MapReduce framework.

  • To show the efficiency of our approach, we conduct extensive experiments using large-scale datasets. The experimental results confirm the outstanding performance and the excellent scalability of our parallel skyline computing method.

The rest of the paper is structured as follows. In Sect. 2, we review previous methods that are related to the skyline query processing in MapReduce framework. Section 3 briefly explains the processing in MapReduce, data partitioning schemes, basic concept of the skyline computation and notations used in this paper. We propose our new outer-cell filtering and inner-cell filtering methods to efficiently compute skylines in a parallel and distributed manner in Sect. 4. Section 5 presents a series of performance optimization techniques to minimize the parallel overhead for the inner-cell filters. We present the results of performance evaluation in Sect. 6. Finally, in Sect. 7, we conclude the paper.

2 Applications of skyline queries

Computing the large-scale skyline is a challenging problem because there is an increasing trend of applications that produce large skylines as the size of data or the dimensionality of data increases. For example, suppose that we have a set of hotels, such as Fig. 2a, in which each hotel has a “price” attribute and a “distance from a beach” attribute. In general, the hotels closer to the beach have higher prices. Hence, there is an anti-correlated relationship between the price attribute and the distance attribute. If users prefer hotels with a low price and short distance, the skyline of the hotel set becomes a set of black-colored tuples in Fig. 2a, and we can speculate that the size of skylines grows quickly as the number of data items or the dimensionality increases.

Fig. 2
figure 2

An examples of skyline on various data distributions. a Skyline of a hotel set. b Skyline of an item set. c Skyline of road segments

Full size image

There are other examples of applications using skyline query processing. Suppose that we have a set of items, like in Fig. 2b, in which each item has a price attribute and a quality attribute. In general, high-quality items are more expensive than the cheaper items. Hence, the price and the quality are correlated attributes. In Fig. 2b, if users prefer items with low prices and high quality, the skyline of the item set becomes a set of black-colored tuples. In this example, we can also speculate that the size of a skyline grows quickly with increasing number of items or dimensions although the price and the quality are correlated attributes. Through the examples in Fig. 2a, b, we can know that the size of skylines rapidly increases in independent and anti-correlated distributions as the dataset size or the dimensionality grows.

We can also find examples of applications that use skyline queries for datasets with more than two dimensions. For example, in Fig. 2a, if a user wants to find a hotel that has a low price, a high star rating, a high user rating, and is close from a beach, the skyline that takes into account the four dimensions of {price, star rating, user rating, distance from a beach} can help user’s hotel choice. As another example, in Fig. 2b, if a user wants to find a product that has a low price, a high quality, and latest release year, the skyline that takes into account the three dimensions of {price, quality, release year} can help user’s choice.

Recently, with the advent of the fourth industrial revolution (4IR), we can find much more practical applications needing efficient skyline computation. Let us consider the Intelligent Transportation System (ITS) as a practical example. One of the important roles of the ITS is to manage traffic congestion to create smooth traffic flow. To do this, it monitors the traffic volume and the speed of each road segment for every unit of time using various items of equipment, such as roadside equipment (RSE), a vehicle detection system (VDS), and a general positioning system (GPS). Even in middle size cities, there are tens of thousands of road segments [7], and hence tens of gigabytes of data are collected from those monitoring devices in a single day. The ITS center periodically analyzes the collected records to detect incidents and deal with traffic problems. In this application, the traffic volume and the road segment speed are anti-correlated attributes, as in Fig. 2c, since the road segment speed is commonly low in roads with a heavy traffic volume. However, irregular situations can be observed, such as tuple \(r_1\) and \(r_2\) in Fig. 2c, which are the road segments with low traffic volume and low speed. This abnormal situation may occur for a variety of different reasons, such as cracked roads, ice on roads, spilled cargo from trucks, and road kill. To make a smooth traffic flow, we have to find those road segments that create the irregular situations and get rid of those undesirable situations. In these cases, the skyline query helps us to retrieve only the road segments that create the irregular situations.

3 Related work

In 2.1, we first review the existing approaches that process skyline queries in MapReduce framework. Then, we discuss the details of the most closely related work.

3.1 Skyline query processing in MapReduce

After skyline processing was first introduced in database management systems [3], great amount of research [2, 5, 10, 13, 22, 26, 28, 30, 34] on skyline processing was performed for parallel and distributed computing environments. However, the previous approaches were not suitable for the MapReduce framework [18]. The reason was that the skyline algorithms in those studies were heavily dependent on flexible inter-node communications to coordinate distributed and/or parallel processing among nodes. Unlike the existing computing environments, the MapReduce framework only supports communication between a mapper and a reducer, and moreover, the communication is strictly limited by the key-value form [18].

Afrati et al. [1] proposed parallel algorithms for processing skyline queries fast with load balancing and synchronization techniques among processors. They designed their algorithms based on a grid-based partitioning method, in which it is simple to roughly distribute the same amount of data to multiple nodes for computing them in parallel. They demonstrated that the proposed algorithms achieved high load balancing for skyline queries on server clusters. However, the computational models proposed in that research were substantially different from MapReduce [18].

Many researchers have proposed skyline processing algorithms designed for the MapReduce framework. Park et al. [19] proposed another skyline processing method, named SKY-MR, in the MapReduce framework. SKY-MR processes skyline queries effectively with the variation of the quadtree for filtering out non-skyline tuples in the early stage of the skyline computation. SKY-MR generates a quadtree using random samples of the entire dataset and utilizes it for data partitioning and local pruning. Then, it computes the local skyline for each region, which is divided by the sky-quadtree independently. After that, it computes a global skyline from the local skylines.

Recently, the authors of SKY-MR proposed SKY-MR+ [20] to improve the performance and scalability of SKY-MR with the adaptive quadtree generation method and techniques for workload balancing among machines. However, those approaches are unsuitable for the environments that handle large datasets that are dynamically generated. In that environment, it is hard to select a set of samples which completely represent the features of the dynamic dataset. Thus, we have to access a large portion of the dataset to make the samples represent the entire dataset well and it increases the cost.

Zhang et al. [32] proposed three MapReduce-based algorithms for skyline computation. They used Block–Nested–Loops (BNL) [3], Sort–Filter–Skyline (SFS) [8], and Bitmap [25] approaches with the MapReduce framework. The MR-BNL partitions datasets into disjoint subsets with the grid-based partitioning scheme. It distributes data partitions to multiple nodes and computes a local skyline for each partition with the BNL skyline processing method in [3]. Finally, all of the local skylines are sent to a single node and merged. After that, a global skyline is computed from the merged local skylines. The MR-SFS follows the same approaches as MR-BNL, but it uses the presorting method of [8] before computing the global skyline. The MR-Bitmap uses the bitmap algorithm for the computation of skylines and performs well regardless of data distributions. However, it can only handle data dimensions with a limited number of distinct values, although it has advantages in a multi-node environment for global skyline computing.

Chen et al. [6] proposed an angular partitioning scheme, named MR-Angle, to reduce the processing time of skyline queries in MapReduce. The MR-Angle conducts a mapping of datasets from a Cartesian coordinate space to a hyperspherical space. Then, it divides the data space using angular coordinates to shorten the processing time by eliminating redundant dominance computations. This approach reduces the total number of tuples in local skylines since all partitions share the region that is near the origin of the axes. In MR-Angle, the angle-based partitions are distributed to multiple nodes and used for computing local skylines on each partition. Finally, all local skylines are sent to a single node to be merged. After that, the global skyline is calculated from the merged local skylines.

Zhang et al. [33] introduced a parallel algorithm for skyline queries, which called PGPS, in MapReduce framework. It employs the angle-based partitioning and filtering techniques that discard unqualified tuples in each partition. After filtering unqualified tuples, PGPS calculates a local skyline for each partition in a parallel manner. Then it merges the local skylines into a single node and produces the final global skyline. To improve the merging performance of local skylines, they proposed a partial-presort technique. In the partial-presort technique, they divided again the local skylines based on grid partitioning and sorted them so as to first read the partitions that are close to the origin. This technique is good for immediately discarding tuples in the dominated partitions.

Since most of the previous studies, that process skyline queries in MapReduce, compute a global skyline serially, they do not take full advantage of parallelism. To overcome this problem, Mullesgaard et al. [18] proposed a parallel algorithm, called MR-GPMRS, which compute a skyline in a parallel manner. MR-GPMRS scans all the input data first to make a simple bitstring for filtering out tuples in unqualified partitions. After creating the bitstring, MR-GPMRS rescans all the input data again and generates local skylines for each chunk of input data while filtering out the tuples in unqualified partitions using the bitstring. It then transmits local skylines to other nodes to compute a global skyline in an distributed and parallel manner.

However, it has the following drawbacks. Although MR-GPMRS executes the serial computing parts in parallel, it suffers from performance degradation due to the redundant scans of input data and large-size local skylines because the local skylines are computed on randomly partitioned data space. In addition, the redundant transmission of local skylines seriously deteriorates the performance. This performance degradation becomes severe due to the parallel overhead which far outweighs the benefit from the parallelization as the dataset size and the dimensionality grows.

In this paper, we propose a novel method to process skyline queries efficiently in MapReduce framework. The proposed approach is completely different from the existing approaches by not only processing skyline queries in a fully parallelized manner in all states of the MapReduce framework but also minimizing the parallel overhead caused by transforming the serial processing parts to parallel processing parts.

3.2 Closely related work

Quite recently, Jia-Ling et al. [14] proposed a parallel algorithms for the skyline computation using MapReduce framework called MR-SKETCH to prevent bottlenecks from occurring when the global skyline is computed from local skylines in a serial manner. The MR-SKETCH algorithm consists of a data filtering step, a dominated subsets computing step, and a result merging step.

After a dataset is partitioned, in the filtering step, each partition of the MR-SKETCH randomly selects tuples to maintain the set of sample points. The sample points are used for calculating a skyline which is utilized as filter. After filtering out tuples which are dominated by its filters, for each partition, MR-SKETCH computes a dominated subset which consists of tuples that cannot be a global skyline. In the merging step, for each partition, it merges the surviving tuples from the filtering and dominated subset separately, and then it removes the dominated subset from the surviving tuples to determine the final global skyline.

MR-SKETCH designs rules to downsize the dominated subsets so as to decrease the network cost incurred during the distribution of them. In their experiments, MR-SKETCH performed better than other existing algorithms. However, their method still had many problems when they compute skyline in a parallel manner on the MapReduce framework.

First, MR-SKETCH applies the filtering strategy based on randomly selected filter points, whereas most filtering strategies make a deliberate choice for selecting the filter points to obtain better pruning power. Therefore, the power of its randomly selected filter points is significantly lower than other filtering strategies when we compare its filtering power with others using the same number of filter points. Consequently, the lower filtering power increases the size of map outputs and causes a higher computation cost and network cost. Moreover, that method does not consider the computing cost for dominated subsets. Therefore, as the dataset size or the dimensionality grows, it incurs a large cost for computing the dominated subsets.

Second, the performance improvement obtained by the parallel processing decreases due to the lack of scalability. Their algorithms are based on partitioning schemes that divide each data dimension into only two halves, which becomes an obstacle for scaling out the skyline computation because as the size of dataset increases, more partitions are required to process the datasets efficiently in a parallel manner. Even if we increase the number of partitions by generalizing their partitioning scheme to divide each dimension into k partitions in order to overcome the limitation, their approach still shows the limitation to scale out because the network cost for transmitting the dominated subsets increases dramatically as the number of partitions increases.

Moreover, in MR-SKETCH, when we compute dominated subsets in a reducer, we have to read the input data twice in each reducer, one for making a hash table and the other for computing dominated subsets. Due to this characteristic, we need to keep all input tuples of each reducer in the main memory because the input values of the reducers are iterable. Hence, it is difficult to process large-scale data.

Third, there is a limitation on the degree of parallelism in the MR-SKETCH method. In their method, they propose a solution to reduce the network cost since the network cost for transmitting the dominated subsets is too large to be ignored, even if they generate partitions by dividing each data dimension into only two halves. To solve this problem, they postpone part of the computations of dominated subsets after their transmission. However, this approach makes the parallel computation of dominated subsets turn back to the serial computation.

Furthermore, all the results of the reducers and dominated subsets are transmitted to a single node for the result merging at the end of MR-SKETCH. Thus, the result merging step is processed in a serial manner and becomes another bottleneck for computing the skyline as the dataset size or the dimensionality grows.

Our approach is superior to MR-SKETCH in that it provides scalable performance to massively increasing data and dimensionality by enabling the fully parallelized processing in all stages of the MapReduce jobs. Although the proposed method also has parallel overhead, it is significantly lower than that of MR-SKETCH because we reduce the parallel overhead by using various efficient methods.

4 Preliminaries

In order to fully utilize the parallelism in the MapReduce framework, it was necessary to understand its processing and devise a new computing method for skyline queries accordingly. We give a brief introduction of the processing in MapReduce in Sect. 3.1 and explain the data partitioning schemes for distributing input data to multiple nodes for the parallel processing in Sect. 3.2. Then, we review the basic concept of the skyline computation in the Sect. 3.3. Lastly, we describe the assumptions and notations used throughout this paper in Sect. 3.4.

4.1 Overview of processing in MapReduce

MapReduce [11] is a representative framework for distributed parallel computing. Under the framework, users specify a map function and a reduce function. Each map function receives key-value pairs from the input files and generates intermediate results in the form of a list of key-value pairs. After the intermediate results are emitted by map functions, the framework starts to group and sort them using the intermediate keys and sends them to reduce functions. Then, each reduce function collects all intermediate values which have the same intermediate key and produces key-value pairs as a final result.

4.2 Data partitioning schemes for distributed and parallel processing

Skyline processing methods in MapReduce framework adopt data partitioning schemes to compute a skyline in a parallel manner. There are three widely known data partitioning schemes: namely random, grid and angle-based partitioning.

In this section, a partition, a set of tuples, is denoted by \(P_i\), and a data space of \(P_i\) is denoted by \(R_{P_i}\). \(R_{P_i}\) is a d-dimensional space, and each dimension has a finite domain.

4.2.1 Random partitioning

The simplest way for partitioning a dataset is random partitioning, in which tuples are randomly assigned to partitions without considering the tuple attributes. Some researchers have employed the random partitioning scheme to compute skyline in a parallel manner [9]. In this approach, the size of a skyline of each partition is expected to be equal because each partition keeps a random sample of the dataset. Also, the same proportion of the skyline in different partitions are expected to be included in the global skyline. This method is easy for implementation without incurring computational overhead for determining which tuples will belong to which partitions.

However, because of the lack of locality information, the random partitioning scheme cannot minimize the size of the local skylines and many tuples belonging to the local skylines are not included in the global skyline. This characteristic significantly increases the communication cost between nodes when merging local skylines for the global skyline computation. Moreover, performance degradation in the random partitioning becomes severe in the case of anti-correlated distributions.

4.2.2 Grid-based partitioning

The grid-based partitioning scheme is the most prevalent approach to partition a dataset regarding skyline computation in parallel and distributed environments. In this approach, since we divide each dimension into m parts, there are a total of \(m^d\) partitions for a d-dimensional space. This approach allows us to achieve further speedup for the skyline computation by pruning unqualified partitions that cannot contain any skyline tuples. Grid-based partitioning methods have been employed in some studies on parallel skyline computation [18, 29, 30]. The data space of a grid partition can be represented by \(R_{P_i}=[\iota _1^{i-1}, \iota _1^{i}]\times \cdots \times [\iota _{d}^{i-1}, \iota _{d}^{i}]\), while \(\iota _{j}^{i-1}\) and \(\iota _{j}^{i}\) are the boundaries of the jth dimension for the ith partition.

In this approach, the number of local skyline tuples in partitions are roughly equal however, most of them have no chance to be a global skyline. Consequently, the cost for the communication and the processing for the local skylines cannot be minimized. Furthermore, partitions on the corner which is near the origin of data space mostly contribute to the global skyline, while other partitions contribute little to global skylines.

4.2.3 Angle-based partitioning

An angle-based partitioning scheme performs the mapping of a Cartesian coordinate space to a hyperspherical space and then partitioning the data space using angular coordinates. Angle-based partitioning has been employed in several studies on parallel skyline computation [6, 15, 27, 33].

It maps the Cartesian coordinates of a tuple \(p = (p[D_1], p[D_2],\ldots , p[D_d]\)) to hyperspherical coordinates, which consist of \(d-1\) angular coordinates \(\phi _1, \phi _2,\ldots , \phi _{d - 1}\) and a radial coordinator. The detailed mathematical definition of the angle-based partition can be found in [27]. The data space of an angle partition can be represented by \(R_{P_i}=[\phi _1^{i-1}, \phi _1^{i}]\times \cdots \times [\phi _{d-1}^{i-1}, \phi _{d-1}^{i}]\), where \(\phi _j^0=0\) and \(\phi _j^N=\pi /2\) (\(1 \le j \le d\)), while \(\phi _{j}^{i-1}\) and \(\phi _{j}^{i}\) are the boundaries of the angular coordinate \(\phi _{j}\) for the ith partition.

In this approach, all partitions share the region near the origin of the axes. Thus, the probability that the global skyline tuples can be assigned evenly to the partitions increases. This approach also minimizes the size of local skylines, which leads not only to a small network communication cost but also to a small merging cost of local skylines.

4.3 Skyline computation

Given a dataset P in a d-dimensional space, a tuple \(p \in P\) can be represented as \(p=({p[D_1], p[D_2], \ldots , p[D_d]}\)) where \(p[D_i]\) is the value of the tuple on the ith dimension. The dominance relationship and the skyline operator are defined as follows:

Definition 1

(Dominance relationship between tuples) Given a set of d-dimensional tuples, tuple \(p_1\) dominates \(p_2\), if \(p_1\) is no worse than \(p_2\) in any other dimensions and \(p_1\) is better than \(p_2\) in at least one dimension. It is denoted by \(p_1 \prec p_2\).

In the dominance relationship, the meaning of “better” is interpreted in accordance with the context; when the lower value is preferred (e.g., price), the tuple having lower value becomes a better one.

Definition 2

(Skyline) Given a set of tuples P in a d-dimensional space, a skyline is the set of tuples that are not dominated by any other tuples and is denoted by SKY(P).

Figure 3a illustrates an example of the dominance relationship, in which tuple \(p_1\) dominates tuples \(p_2\). Fig. 3b illustrates an example of the skyline, in which \(\{p_1, p_3, p_6\}\) becomes the skyline because each tuple in \(\{p_1, p_3, p_6\}\) is not dominated by any other tuples. The shaded areas in Fig. 3a, b are dominance regions (DRs) of \(p_1\) and \(\{p_1, p_3, p_6\}\), respectively.

Fig. 3
figure 3

An example of dominance relationship and skyline in two-dimensional space. a Dominance relationship. b Skyline

Full size image

Definition 3

(Subspace skyline) When P is a set of d-dimensional tuples and SUB is a subset of d dimensions, \(SKY_{SUB}(P)\) is the skyline of P on the subspace SUB. In the computation of \(SKY_{SUB}(P)\), we perform the dominance test using only the values of dimensions in SUB.

4.4 Notations and assumptions

In this paper, we assume that the lower value is preferred, without loss of generality. Also, we call a partition obtained by grid partitioning a cell to distinguish it from partitions generated by other partitioning schemes. Finally, Table 1 summarizes the notations used in this paper.

Table 1 Summary of notations
Full size table

5 Proposed method

In this section, we propose our parallel processing method for skyline queries in the MapReduce framework with two novel filtering techniques: outer-cell filtering and inner-cell filtering. In Sect. 4.1, we overview the framework of our method. Section 4.2 introduces the outer-cell filter and explains how to compute local skylines with it. Then, we describe how to compute the global skyline using the inner-cell filter in Sect. 4.3.

5.1 Framework overview

Our method consists of the local skyline processing step and the global skyline processing step, each of which is executed as one MapReduce job. Figure 4 gives the overview of our method which processes skyline queries in the MapReduce framework. In the figure, the dotted boxes are the mapper and the reducer and the white boxes are the output of the map and reduce functions. In the figure, the number of map tasks and reduce tasks is r.

Local skyline processing step First, the input data file F is divided into small chunks and each chunk is read by each map task. Until now, F has not been partitioned by cells. In the 1st map phase, we divide the input data by grid and make r cells and then pass the map output \(M_{c_i}\) to the reducers separately. In the 1st reduce phase, local skyline \(LS_{c_i}\) is computed from \(M_{c_i}\) as an output of each reducer. To filter out tuples in unqualified cells, we perform an outer-cell filtering in both mappers and reducers with \(OCF_{c_i}\) that is presented in detail in Sect. 4.2.

Global skyline processing step We start the global skyline processing step by reading local skylines \(LS_{c_i}\) which are the results of the local skyline processing step. In the 2nd map phase, we compute inner-cell filters \(ICF_{c_i}\) for each cell to use them for filtering out unqualified tuples in each \(LS_{c_i}\) in parallel. Then, we send the local skylines and its associated inner-cell filters to the same reducers in the shuffle phase. In the 2nd reduce phase, we compute the global skyline \(GS_{c_i}\) in each local skyline in a parallel manner with the assistance of \(ICF_{c_i}\). Finally, we generate the \(GS_{c_i}\) as a final result of skyline queries. The detailed explanation of the global skyline processing with the inner-cell filtering is given in Sect. 4.3.

In the next sections, we describe the details of the proposed method to compute skyline queries efficiently in the MapReduce framework.

Fig. 4
figure 4

An overview of our parallel skyline processing in MapReduce framework

Full size image

5.2 Local skyline processing with outer-cell filtering

Before starting MapReduce jobs, we divide the data space by the grid partitioning scheme. When the local skyline processing step begins, the framework evenly divides the input dataset and the map function processes it in a parallel manner. In each map function, for each tuple, we find a cell containing that tuple, and then we generate the map output so that tuples belonging to the same cell can be sent to the same reducer. After the tuples belonging to the same cell are transmitted to the reducer, each reduce function starts to compute local skyline for the associated cell.

5.2.1 Outer-cell filter and its principles

In the local skyline processing step, it is not necessary to compute local skylines for all non-empty cells whose tuples are dominated by tuples in other cells. We call this kind of cell an unqualified cell. To pass over the computation for local skylines in the unqualified cells, we define a new dominance relationship between two cells that is similar to the dominance relationship between two tuples.

Fig. 5
figure 5

The corner points of cells. a Two corner points of a cell. b A corner point between two cells

Full size image

The dominance relationship between two cells is based on their corner points: the worst point wp and the best point bp. Under the assumption that a lower value is better, the wp of a cell is defined as the corner point that has the highest values on all dimensions in the cell. Likewise, the bp of a cell is defined as the corner point that has the lowest values on all dimensions in the cell. Based on the definitions of the best point \(C_i.{bp}\) and the worst point \(C_i.{wp}\), the range of cell \(C_i\) is defined as [\(C_i.{bp}[D_1]\), \(C_i.{wp}[D_1]\)) \(\times \) [\(C_i.{bp}[D_2]\), \(C_i.{wp}[D_2]\)) \(\times \cdots \times \) [\(C_i.{bp}[D_d]\), \(C_i.{wp}[D_d]\)). An example of two corner points of a cell on two-dimensional space is represented in Fig. 5a. In Fig. 5a, \(C_i.{bp}\) and \(C_i.{wp}\) are the best point and the worst point of cell \(C_i\), respectively. Figure 5b shows corner point of two diagonally adjacent cells \(C_i\) and \(C_j\), in which \(C_i.{wp}\) and \(C_j.{bp}\) is the same point. In Fig. 5b, the ranges of cells \(C_i\) and \(C_j\) are [\(C_i.{bp}[D_1]\), \(C_i.{wp}[D_1]\)) \(\times \) [\(C_i.{bp}[D_2]\), \(C_i.{wp}[D_2]\)) and [\(C_j.{bp}[D_1]\), \(C_j.{wp}[D_1]\)) \(\times \) [\(C_j.{bp}[D_2]\), \(C_j.{wp}[D_2]\)), respectively.

Now, we give the definition of the total dominance relationship between two cells which can be usefully used for discarding all the tuples in unqualified cells.

Definition 4

(Total dominance relationship) A cell \(C_i\) totally dominates another cell \(C_j\), if and only if \(C_i.{bp}[D_k] < C_j.{bp}[D_k]\) for every \(D_k \in \{D_1, \ldots ,D_d\}\). It is denoted by \(C_{i} \prec _{T} C_{j}\).

For example, when there are nine cells as shown in Fig. 6a, cell \(C_1\) totally dominates cells \(C_5\), \(C_6\), \(C_8\) and \(C_9\). Given that two cells are under the total dominance relationship, the following lemma allows us to discard all tuples in unqualified cells without computing their local skyline.

Lemma 1

When non-empty cell \(C_i\) totally dominates \(C_j\), no tuples in \(C_j\) can be a part of the global skyline.

Proof

Since \(C_i\) totally dominates \(C_j\) and all data spaces of the cells do not overlap, the following inequality holds: \(C_i.bp[D_k] < C_i.wp[D_k] \le C_j.bp[D_k]\) for each \(D_k \in \{D_1,\ldots ,D_d\}\). Also, since \(C_i\) is not empty, there is a tuple p in \(C_i\) such that \(C_i.bp[D_k] \le p[D_k] < C_i.wp[D_k]\) for each \(D_k \in \{D_1,\ldots ,D_d\}\), Therefore, all tuples in \(C_j\) are dominated by p because \(p[D_k] < C_i.wp[D_k] \le C_j.bp[D_k]\) for each \(D_k \in \{D_1,\ldots ,D_d\}\). \(\square \)

By Lemma 1, if the cell \(C_1\) is not empty as shown in Fig. 6b, we do not have to compute the local skylines of the cells \(C_5\), \(C_6\), \(C_8\) and \(C_9\). When we determine the emptiness of a cell, we use the range of the cell to identify to which cell each tuple belongs.

Fig. 6
figure 6

Total dominance relationship and outer-cell filtering. a An example of cells. b Total dominance relationship. c Outer-cell filter

Full size image

To utilize Lemma 1 in the local skyline processing phase, we have to keep the information about the emptiness of cells. To keep that information, we define the outer-cell filter to represent whether or not cells are empty.

Definition 5

(Outer-cell filter) For each cell \(C_i\), the outer-cell filter of \(C_i\) is defined by the worst point of \(C_i\). It is denoted by \(OCF(C_i)\).

When the cell \(C_i\) is not empty, we maintain an outer-cell filter of \(C_i\) as a filter point and filter out tuples that are dominated by it. This method gives the same effect as we filter out all tuples in totally dominated cells.

Figure 6c shows an example of the outer-cell filtering strategy, in which \(OCF(C_1)\), the outer-cell filter of \(C_1\), is kept since \(C_1\) is not empty due to tuple p. Then, \(C_1.wp\), which is the outer-cell filter of \(C_1\) is used for filtering out all tuples in cells \(C_5\), \(C_6\), \(C_8\) and \(C_9\). Generally, by using the outer-cell filters, we can eliminate a large number of tuples that cannot be a global skyline.

5.2.2 Filtering with outer-cell filter

To design the filtering method for the MapReduce framework, we should consider the architectural characteristics of MapReduce. First, it is difficult to use the filtering methods that use predetermined filter points in MapReduce framework because scanning of the entire dataset should be completed in advance before the filter points are selected. Moreover, that job is considerably expensive [14]. Second, the input dataset is divided into small chunks and each chunk is processed separately in the MapReduce framework. Thus, the tuples in totally dominated cells may be produced because no chunk can know the information of tuples in other chunks.

figure a

Taking into account the above nature in the MapReduce framework, we propose a new filtering method called out-cell filtering. To avoid the data scanning for the predetermined filter points, we design a filtering method to keep the filter points progressively. In addition, to prevent totally dominated cells from computing the local skyline, we make both Map and Reduce functions utilizing the outer-cell filters.

The pseudocode of outer-cell filtering is shown in Algorithm 1. When a tuple has been read, it compares the input tuple p with a set of outer-cell filters SOCF (line 3). If the tuple is dominated by or equal to any outer-cell filters in SOCF, we return null which means the discarding of the tuple (lines 4–5); otherwise, we find the cell \(C_i\) that satisfies \(p \in C_i\) and update the filter set SOCF with the outer-cell filter of \(C_i\) (lines 6–7). After that, we return \(C_i\) which contains the tuple p (line 8).

The update of outer-cell filters is performed by Algorithm 2, in which the set of outer-cell filters SOCF is initially empty and progressively filled with the worst points of non-empty cells. If an outer-cell filter already exists, we terminate the filter updating process (lines 3–4); otherwise, we add the outer-cell filter to SOCF and return the SOCF (lines 5–6).

figure b

5.2.3 Applying outer-cell filtering to MapReduce

We apply the outer-cell filtering method to each map function, in which tuples surviving from the filtering method are generated as map output with the form of (cell-id, tuple). Since map functions are executed separately in a parallel manner, no map function can know the outer-cell filters in other map functions. In addition, since outer-cell filters are maintained progressively, there is a possibility that filter points may be updated later than the tuples that should be filtered out. For those reasons, it is possible for tuples that do not belong to the totally dominated cells to be generated as map output.

To prevent totally dominated cells from being produced in local skylines, we also generate outer-cell filters as map outputs at the end of the map functions in the same way as tuples. When this is done, the reduce functions are able to know the global information of outer-cell filters, and they can discard tuples in totally dominated cells. From now on, we use the terms normal tuple and filter tuple to distinguish a tuple and a filter point from map output. The pseudocodes of map and reduce functions for the local skyline processing step are shown in Algorithms 3 and 4, respectively.

figure c

In Algorithm 3, the map function takes a subset \(P_{k}\) of dataset P as input and processes each tuple p in \(P_{k}\) (line 2). For each tuple p, we examine whether or not p is filtered by Algorithm 1, which conducts outer-cell filtering (line 3). If the tuple is not dominated by any outer-cell filters, we produce the tuple p and its associated cell \(C_i\) as map output (lines 4–5). At the end of the map function, we generate outer-cell filters as a map output. If an outer-cell filter f comes from a cell C.wp in SOCF, it is responsible for filtering out the tuples in the cell \(C_j\) such that \(C.wp = C_j.bp\) (lines 6–7). Therefore, we generate a map output with \(C_j\) as its key and f as its value (line 8).

figure d

After the map phase, map outputs having the same key are transmitted to the same reduce function. A reduce function takes a map output which has \(C_j\) as the key in Algorithm 4. Since the map output contains tuples of cell \(C_j\) and may contain an outer-cell filter of \(C_j\), we check whether the value p is a normal tuple or filter tuple in an outer-cell filter for each value p in \(M_j\) (lines 1–2). If the value p is a filter tuple, that is, outer-cell filter, we terminate the reduce function without generating a local skyline (lines 3–4). The reason is that if the type of p is an outer-cell filter, the p is equal to \(C_j.bp\), which means that there is at least one tuple in the cell \(C_i\) such that \(C_i.wp \le C_j.bp\) and it totally dominates the cell \(C_j\). On the contrary, if the value p is a normal tuple, we update a local skyline of cell \(C_j\) with p using Algorithm 5 (line 5). After updating local skyline \(LS_j\), we generate the reduce output with \(C_j\) as a key and \(LS_j\) as a value (lines 6–7).

The skyline calculation is done by Algorithm 5 which works like the BNL algorithm [3]. In Algorithm 5, when a new tuple \(p_{new}\) arrives, we examine whether or not the \(p_{new}\) is dominated by existing tuples in the current local skyline (line 2). If \(p_{new}\) is dominated by existing tuple \(p_{ext}\), we discard it and return the current local skyline as a result (lines 3–4). Otherwise, we check whether or not the \(p_{new}\) dominates \(p_{ext}\) (line 5). If \(p_{new}\) dominates \(p_{ext}\), we remove it from the current local skyline (line 6). At the end of the algorithm, we insert \(p_{new}\) into the current local skyline and return it as a result (lines 7–8).

figure e

5.2.4 Further enhancement of the outer-cell filtering

In our solution, local skyline computing and outer-cell filtering are performed using a grid-based partitioning scheme. However, it is known that the grid-based partitioning scheme produces a greater number of tuples than the angle-based partitioning scheme when we compute local skylines in parallel because all partitions in the angle-based scheme share the area near the origin of the axes [33]. Thus, the tuples near the origin are split into individual partitions, and these tuples make it possible to decreases the number of tuples in a local skyline by dominating a large number of tuples.

To overcome this limitation of the grid-based partitioning scheme, we propose a further filtering strategy. We set the cell closest to the origin as the most significant cell (MSC), in which we maintain a single tuple with the largest dominance region as a filter point and we call this point a MSC filter. In Fig. 6c, the tuple p in cell \(C_1\) becomes the MSC filter. While computing local skylines, each map function uses a MSC filter for pruning out tuples that are dominated by it and transmits it to all reduce functions at the end of the map function. After all MSC filters are transmitted to reducers, each reduce function filters out tuples that are dominated by MSC filters before producing a local skyline result. Through this method, we can get an effect similar to the angle-based partitioning scheme, which shares the region near the origin of the axis.

5.3 Global skyline processing with inner-cell filtering

As we mentioned earlier in Sect. 2.1, the existing approaches merging all local skylines and computing the global skyline suffer from a bottleneck as the number of tuples of the skyline increases. To solve this problem, we design the inner-cell filter, which consists of the subsets of tuples that can immediately pick out global skyline tuples from each local skyline. By using the inner-cell filter, global skyline tuples can be determined separately in each local skyline in a parallel manner. Thus, we can efficiently parallelize the skyline query in the MapReduce framework. In this section, we assume that all tuples in totally dominated cells have been removed after the outer-cell filtering, which we described in the previous section.

5.3.1 Inner-cell filter and its principles

In the global skyline processing step, to determine global skyline tuples from local skyline in parallel, we now define another dominance relationship between two cells that is called partial dominance relationship.

Definition 6

(Partial dominance relationship) A cell \(C_i\) partially dominates the other cell \(C_j\), if and only if

  • \(C_i.{bp}[k] \le C_j.{bp}[k]\) for every \(k \in [1, d]\) and

  • \(C_i.{bp}[k] = C_j.{bp}[k]\) for at least one \(k \in [1, d]\) and

  • \(C_i.{bp}[k] < C_j.{bp}[k]\) for at least one \(k \in [1, d]\).

It is denoted by \(C_i \prec _{P} C_j\).

Figure 7a shows an example of the partial dominance relationship, in which cell \(C_4\) partially dominates \(C_5\) and \(C_7\), and \(C_2\) partially dominates \(C_5\) and \(C_5\). In Fig. 7a, gray cells represent non-empty cells.

Fig. 7
figure 7

Two types of dominance relationship between cells. a Partial dominance. b Total and partial dominance

Full size image

We define the following two types of cells using the partial dominance relationship.

Definition 7

(Partially dominated cells) Partially dominated cells of \(C_i\) is the set of cells that are partially dominated by \(C_i\) and it is denoted by \(PD(C_i)\).

Definition 8

(Partially anti-dominated cells) Partially anti-dominated cells of \(C_i\) is a set of cells that partially dominates \(C_i\) and it is denoted by \(AD(C_i)\).

When two cells are under a partial dominance relationship, we can easily derive the property in the following Observation 1 from the definitions of \(PD(C_j)\) and \(AD(C_j)\).

Observation 1

Given two cells \(C_i\) and \(C_j\), \(C_i \in PD(C_j)\) if and only if \(C_j \in AD(C_i)\).

In the example of Fig. 7a, \(PD(C_{4})\) and \(PD(C_{2})\) are {\(C_5, C_7\)} and {\(C_3, C_5\)}, respectively, and, \(AD(C_{7})\), \(AD(C_{5})\) and \(AD(C_{3})\) are {\(C_4\)}, {\(C_2, C_4\)} and {\(C_2\)}, respectively. As shown in this example, we can see that Observation 1 is satisfied between partially dominated cells and partially anti-dominated cells.

Until now, we have defined two types of relationship between cells: a totally dominance relationship and a partially dominance relationship. Figure 7b shows the two types of relationships among cells at once. By using the two relationships, we can derive the following lemma.

Lemma 2

For two tuples p and q located in different cells \(C_i\) and \(C_j\), respectively, if p dominates q, then p belongs to the cell \(C_i\) such that \(C_i \prec _{T} C_j\) or \(C_i \prec _{P} C_j\).

Proof

When two cells \(C_i\) and \(C_j\) are given, there are three cases of the dominance relationship between \(C_i.{bp}\) and \(C_j.{bp}\): \(^{1)}\) \(C_i.{bp} \prec _{} C_j.{bp}\) or \(^{2)}\) \(C_i.{bp} \succ _{} C_j.{bp}\) or \(^{3)}\) \(C_i.{bp}\) and \(C_j.{bp}\) are incomparable. In the three cases, we do not care about case 2 and case 3 because p cannot dominate q in those two cases.

In case 1 where \(C_i.{bp} \prec _{} C_j.{bp}\), we derive two cases again in terms of the relationship between \(C_i.{wp}\) and \(C_j.{bp}\): \(C_i.{wp} \preceq C_j.{bp}\) or \(C_i.{wp} \npreceq C_j.{bp}\). If \(C_i.{wp} \preceq C_j.{bp}\), then \(C_i \prec _{T} C_j\) is established by the definition of a total dominance relationship, whereas if \(C_i.{wp} \npreceq C_j.{bp}\), then \(C_i \prec _{P} C_j\) is established by definition of a partial dominance relationship.

Therefore, if p dominates q, p belongs to the cell \(C_i\) such that \(C_i \prec _{T} C_j\) or \(C_i \prec _{P} C_j\). \(\square \)

According to Lemma 2, for tuple q in cell \(C_j\), it is enough to check the tuples in cell \(C_i\) such that \(C_i \prec _{T} C_j\) or \(C_i \prec _{P} C_j\) to determine whether or not q belongs to the global skyline. Furthermore, since there are no remaining tuples in the totally dominated cells after the local skyline processing step, we need only check the tuples in cell \(C_i\) such that \(C_i \prec _{P} C_j\). Based on this observation, we make the following theorem.

Theorem 1

Given a local skyline of cell \(C_j\), its tuple q undoubtedly becomes part of the global skyline if q is not dominated by any local skylines of cells \(C_i\) such that \(C_i \in AD(C_j)\).

Proof

We prove the theorem by contradiction. When a local skyline of cell \(C_j\) is given, let us assume that the tuple q in \(C_j\) cannot be a part of the global skyline, while q is not dominated by any local skyline of the cell \(C_i\) such that \(C_i \in AD(C_j)\). By this assumption, there is at least one tuple p in \(C_k\) such that \(C_k \notin AD(C_j)\), which prevents q from becoming part of the global skyline. By Lemma 2, there are two possible cell positions of \(C_k\) : \(C_k \prec _{T} C_j\) or \(C_k \prec _{P} C_j\). Since we have already removed tuples in totally dominated cells, tuple p cannot be located in \(C_k\) such that \(C_k \prec _{T} C_j\). Therefore, tuple p is located in the cell \(C_k\) such that \(C_k \prec _{P} C_j\). Since \(C_k \prec _{P} C_j\), \(C_k\) should be included in \(AD(C_j)\) by definition of the partially anti-dominated cells, it contradicts the assumption that p is located in the cell \(C_k\) such that \(C_k \notin AD(C_j)\). \(\square \)

Figure 8 illustrates an example of Theorem 1, in which two set of tuples {\(p_1\), \(p_2\), \(p_3\), \(p_4\)} and {\(p_5\), \(p_6\), \(p_7\), \(p_8\)} are placed in cells \(C_i\) and \(C_j\), respectively. As shown in Fig. 8, all of the local skyline tuples in \(C_i\) belong to global skyline since \(AD(C_i)\) is empty. Meanwhile, the tuples \(p_5\), \(p_6\), and \(p_7\) cannot be a part of the global skyline because they are dominated by the local skyline of cell \(C_i\) such that \(C_i \in AD(C_j)\). However, tuple \(p_8\) in \(C_j\) obviously becomes the global skyline because it is not dominated by any local skylines of cells in \(AD(C_j)\).

Fig. 8
figure 8

An example of Theorem 1

Full size image

By Theorem  1, we can determine the global skyline tuples with the assistance of local skylines in its partially anti-dominated cells, which means that by using the local skylines in partially anti-dominated cells for each cell, the global skyline can be determined in parallel. We call this kind of tuple, which can filter out non-global skyline tuples, an inner-cell filter. The definition of an inner-cell filter is as follows.

Definition 9

(Inner-cell filter) Inner-cell filter of cell \(C_j\) is a set of local skylines in cell \(C_i\) such that \(C_i \in AD(C_j)\). It is denoted by \(ICF(C_j)\).

We can compute the part of global skyline of each cell in a fully parallel manner using the inner-cell filter because it prunes a large number of unqualified tuples from local skylines. However, the inner-cell filters cause network overhead since they should be transmitted to other cells. Moreover, the network overhead is naturally proportional to the number of cells because they are generated for each cell. Thus, if we take no action to reduce the network overhead, it can reduce the benefits from the parallel computing of the global skyline.

To solve this problem, we present an efficient way to reduce the number of tuples in inner-cell filters that are required to determine the global skyline tuples in parallel in the next section.

5.3.2 Compaction of the inner-cell filter

Through the following observation, when a cell \(C_i\) partially dominates a cell \(C_j\), we can see that it is unnecessary to keep all tuples in \(ICF(C_j)\) in order to determine global skyline tuples in \(C_j\).

Observation 2

Given two cells \(C_i\) and \(C_j\), when \(C_i\) partially dominates \(C_j\), there is a set of tuples whose size is less than or equal to \(LS(C_i)\) which filters out tuples that do not belong to the global skyline in \(C_j\).

For example, in Fig. 8, to filter out tuples that do not belong to the global skyline in \(C_j\), {\(p_4\)} is sufficient instead of {\(p_1\), \(p_2\), \(p_3\), \(p_4\)}.

If we exploit the properties in Observation 2, each cell can prune non-global skyline tuples with fewer tuples than the inner-cell filter. A concept similar to Observation 2 can also be found in [14].

When a cell \(C_i\) partially dominates a cell \(C_j\), there are dimensions that cannot distinguish clearly which cell has better values. To formally describe this kind of dimension, we define a set of equi-range dimensions as follows:

Definition 10

(A set of equi-range dimensions) For given two cells \(C_i\) and \(C_j\), a dimension \(D_i\) is an equi-range dimension if the ranges of \(C_i\) and \(C_j\) in dimension \(D_i\) are equal. \(ER(C_i, C_j)\) denotes a set of such dimensions for cells \(C_i\) and \(C_j\).

In Fig. 8, the set of equi-range dimensions for \(C_i\) and \(C_j\) is {\(D_2\)} since the range of dimension \(D_2\) is equal to [\(y_1\), \(y_2\)). Different from the set of equi-range dimensions, there are dimensions that can distinguish clearly which cell has better values for two cells. We define this kind of dimensions as a set of non-equi-range dimensions for two cells as follows:

Definition 11

(A set of non-equi-range dimensions) A set of non-equi-range dimensions for two cells \(C_i\) and \(C_j\) is the complement set of \(ER(C_i, C_j)\). \(NER(C_i, C_j)\) denotes a set of such dimensions for cells \(C_i\) and \(C_j\).

In the example of Fig. 8, the set of non-equi-range dimensions for \(C_i\) and \(C_j\) is {\(D_1\)}, since the range of \(C_i\) is [\(x_1\), \(x_2\)) and the range of \(C_i\) is [\(x_2\), \(x_3\)). Thus, \(C_i\) always has better values than \(C_j\) in dimension \(D_1\). In Fig. 8, \(ER(C_i, C_j)\) is \(\{D_2\}\) and \(NER(C_i, C_j)\) is \(\{D_1\}\). In this example, we can observe that even if we change the \(D_1\) dimension values of the tuples in cell \(C_i\), it does not affect whether or not the tuples of \(C_j\) is dominated. We describe this observation formally with the following lemma.

Lemma 3

When a cell \(C_i\) partially dominates a cell \(C_j\), even if we change the \(D_f\) dimension values of the tuples in cell \(C_i\) such that \(D_f \in NER(C_i, C_j)\), it does not affect whether or not the tuples of \(C_j\) is dominated.

Proof

When a cell \(C_i\) partially dominates a cell \(C_j\), by definition of the partial dominance relationship, there are dimensions \(D_f\) such that \(C_i.{bp}[D_f] < C_j.{bp}[D_f]\), and the dimension \(D_f\) belongs to \(NER(C_i, C_j)\).

In addition, since the data spaces of \(C_i\) and \(C_j\) do not overlap, the following inequality holds: \(C_i.{bp}[D_f] < C_i.{wp}[D_f] \le C_j.{bp}[D_f]\). According to the above inequality, the tuples in \(C_i\) always have better values than the tuples in \(C_j\) in the dimension \(D_f\) such that \(D_f\in NER(C_i, C_j)\). Thus, even if we change the \(D_f\) dimension values of the tuples in cell \(C_i\) within the range \([C_i.{bp}[D_f], C_i.{wp}[D_f])\), it does not change whether or not the tuples of \(C_j\) is dominated. \(\square \)

By Lemma 3, when cell \(C_i\) partially dominates \(C_j\), we know that only the values in \(D_e\) dimensions such that \(D_e \in ER(C_i, C_j)\) determine whether or not the tuples in \(C_j\) are dominated. For example in Fig. 8, only the \(D_2\) dimension values of tuples in \(C_i\) determine whether or not tuples of \(C_j\) are dominated. With this property, we describe how to obtain a set of tuples that consists of fewer tuples than the inner-cell filter but has the same dominance power in the following theorem.

Theorem 2

When a cell \(C_i\) partially dominates a cell \(C_j\), \(SKY(C_i)\) and \(SKY_{ER(C_i, C_j)}(C_i)\) dominate the same tuples in \(C_j\).

Proof

Given a set of tuples, the dominance region of the set and the dominance region of its skyline are the same. Therefore, \(^{(1)}\) \(SKY(C_i)\) and tuples in \(C_i\) have the same dominance region with respect to \(C_j\).

Now, suppose a set T made by changing the \(D_f\) dimension value of \(C_i\)’s tuple to t such that \([C_i.{bp}[D_f] \le t < C_i.{wp}[D_f])\) for each dimension \(D_f \in NER(C_i, C_j)\).

Figure 9 shows an example of T in a two-dimensional space, in which \(NER(C_i, C_j)\) is \(\{D_1\}\). By Lemma 3, \(^{(2)}\) tuples in \(C_i\) and the set T dominate the same tuples in \(C_j\). Furthermore, \(^{(3)}\) the set T and SKY(T) have the same dominance region for the reason mentioned above.

Fig. 9
figure 9

An example of the set \(T=\{p_1', p_2', p_3', p_4'\}\) whose equi-range dimension is \(D_2\)

Full size image

For each tuple \(p_i'\) in T, since the \(D_f\) dimension value of \(p_i'\) is equal to t, the result of SKY(T) is determined by the \(D_e\) dimension value of tuples in T for \(D_e \in ER(C_i, C_j)\). Therefore, \(^{(4)}\) the result of SKY(T) is the same as the result of \(SKY_{ER(C_i, C_j)}(C_i)\).

In conclusion, with (1), (2), (3) and (4), we can know that when a cell \(C_i\) partially dominates a cell \(C_j\), \(SKY(C_i)\) and \(SKY_{ER(C_i, C_j)}(C_i)\) dominate the same tuples in \(C_j\). \(\square \)

Figure 10 shows an example of Theorem 2 when cell \(C_i\) partially dominates cell \(C_j\) in two-dimensional space. When \(SKY(C_i)\) is {\(p_1\), \(p_2\), \(p_3\), \(p_4\)}, the blue-colored region in Fig. 10a shows the dominance region (DR) of \(SKY(C_i)\), and the blue-colored region in Fig. 10b shows the dominance region of \(SKY_{ER(C_i, C_j)}(C_i)\), which is {\(p_4\)}. As we see in this example, \(SKY(C_i)\) and \(SKY_{ER(C_i, C_j)}(C_i)\) dominate the same tuples {\(p_5\), \(p_6\), \(p_7\)} in the cell \(C_j\). However, \(SKY_{ER(C_i, C_j)}(C_i)\) has fewer tuples than \(SKY(C_i)\). Based on Theorem  2, we define the compact inner-cell filter as follows:

Fig. 10
figure 10

An example of Theorem 2. a DR of \(SKY(C_i)\). b DR of \(SKY_{ER(C_i, C_j)}(C_{i})\)

Full size image

Definition 12

(Compact inner-cell filter) Compact inner-cell filter of cell \(C_j\) is a set of tuples that consists of \(SKY_{ER(C_i, C_j)}(C_i)\) with respect to \(C_i \in AD(C_j)\). It is denoted by \(CICF(C_j)\).

Theorem 3 allows us to filter out non-global skyline tuples on each local skyline in a cell separately in a parallel manner using the compact inner-cell filter, which consists of significantly fewer tuples than the inner-cell filter.

Theorem 3

Given the local skyline of cell \(C_j\), its tuple q, which is not dominated by any tuples in \(CICF(C_j)\), has to be a part of the global skyline.

Proof

By Theorem  1, among the tuples of the local skyline of cell \(C_j\), a tuple that is dominated by local skylines of cells in \(AD(C_j)\) cannot be the global skyline. By Theorem  2, the local skyline

of cells in \(AD(C_j)\) has the same dominance power as \(SKY_{ER(C_i, C_j)}(C_i)\). Therefore, among the tuples of the local skyline of cell \(C_j\), the tuple that is dominated by \(CICF(C_j)\) cannot be a global skyline either. \(\square \)

Finding the compact inner-cell filter becomes more and more useful as the size of the local skyline increases.

5.3.3 Filtering with compact inner-cell filter

In the global skyline processing step, the global skyline is computed from local skylines in a parallel manner. After we read the local skyline of cell \(C_i\), we compute part of the compact inner-cell filter of \(C_j\) such that \(C_j \in PD(C_i)\) and then transmit it to the cell \(C_j\). To compute compact inner-cell filters, we first calculate the set of equi-range dimensions.

figure f

The pseudocode for calculating the set of equi-range dimensions is shown in Algorithm 6, which calculates all sets of equi-range dimensions for \(C_i\) which is the input parameter, and \(C_j\), which is partially dominated by \(C_i\). When the local skyline of cell \(C_i\) is processed, we find cells that are partially dominated by cell \(C_i\) (lines 3–4). For each cell \(C_j\) that is partially dominated by \(C_i\), we find a set of equi-range dimensions for \(C_i\) and \(C_j\) and then collect pairs of (cell \(C_j\), its corresponding set of equi-range dimensions) in erSet (lines 5–6). Finally, we return a set of those pairs (line 7).

After calculating the set of equi-range dimensions, we generate compact inner-cell filters in each cell. That is, when a cell \(C_i\) partially dominates a cell \(C_j\), we generate \(SKY_{ER(C_i, C_j)}(C_i)\) in the cell \(C_i\) for the compact inner-cell filter of cell \(C_j\).

The pseudocode in Algorithm 7 shows how to generate compact inner-cell filters. When we process the local skyline of cell \(C_i\), we generate compact inner-cell filters with erSet and \(LS_i\) as input parameters in Algorithm 7 (line 1). The erSet is a set of pairs that consist of \(C_j\) such that \(C_i \prec _{P} C_j\) and the set of equi-range dimensions for \(C_i\) and \(C_j\). The \(LS_i\) is the local skyline of the cell \(C_i\). For each pair of cell \(C_j\) and the set of equi-range dimensions ER in erSet, we compute the skyline on the subspace ER with \(LS_i\) as an input (lines 2–3). The result of this skyline computation is inserted into the map of the compact inner-cell filter (line 4). After computing the compact inner-cell filters for all pairs, the algorithm returns icfMap (line 5).

figure g

After generating compact inner-cell filters, we transmit \(SKY_{ER(C_i, C_j)}(C_i)\), which is part of \(CICF(C_j)\), to cell \(C_j\), which is partially dominated by \(C_i\). After the transmission, in the cell \(C_j\), we filter out tuples from the local skyline \(LS_j\), which are dominated by \(CICF(C_j)\). We call the inner-cell filtering process using the compact inner-cell filter compact inner-cell filtering. Further details about the compact inner-cell filtering are described in the next section.

5.3.4 Applying compact inner-cell filtering to MapReduce

The filtering method with the compact inner-cell filer is applied to the global skyline processing step. In the global skyline processing step, we start with reading the local skyline of each cell in parallel. In each map function, we generate a local skyline and compact inner-cell filter as map output.

The pseudocode of the map function for the global skyline processing is shown in Algorithm 8. In Algorithm 8, the map function takes a local skyline \(LS_{i}\) of cell \(C_i\) as input. When \(C_i\) partially dominates \(C_j\), we calculate the sets of equi-range dimensions erSet between the cell \(C_i\) and the cell \(C_j\) with Algorithm 6 (line 1). For each set of equi-range dimensions in erSet, we compute the compact inner-cell filter of \(C_j\) such that \(C_j \in PD(C_i)\) with Algorithm 7 (line 2). To transmit the compact inner-cell filter of \(C_j\) to the reduce function that processes local skyline \(LS_j\), we generate the compact inner-cell filter of \(C_j\) as map output with \(C_j\) as a key (lines 3-4). At the end of the map function, we generate the local skyline \(LS_i\) as map output with \(C_i\) as a key (line 5).

figure h

After the map phase, map outputs that have the same key are transmitted to the same reduce function. Algorithm 9 shows the pseudocode of the reduce function in the global skyline processing step. In Algorithm 9, a reduce function takes a map output \(M_j\), which has \(C_j\) as a key. In the map output \(M_j\), tuples of the local skyline \(LS_j\) and tuples of the compact inner-cell filter \(CICF(C_j)\) exist together. In this algorithm, we compute the global skyline \(GS_j\) without distinguishing whether tuples come from the local skyline or from the compact inner-cell filter (lines 2–3). Thereby, we efficiently filter out tuples that are dominated by compact inner-cell filters. After computing the global skyline \(GS_j\) with Algorithm 5, we only produce normal tuples from \(LS_j\) as a result in the tuples in \(GS_j\) (lines 4–6). As a result, we can obtain a global skyline tuples from the local skyline for each cell in a parallel manner.

figure i

6 Minimizing the parallel overhead

With the assistance of the compact inner-cell filter, we can determine global skyline tuples in each local skyline in parallel. However, when using the compact inner-cell filters, there is an additional overhead for computing and transmitting them to different nodes, and we call the cost parallel overhead. There are two types of parallel overhead in our method: computation overhead and network overhead. If we are not careful with the computation and transmission of the compact inner-cell filters, the parallel overhead may increase. Thus, it is beneficial to devise efficient methods to minimize the computation and network cost so that the cost does not outweigh the benefit of parallel processing.

For this purpose, in this section, we propose three optimization techniques for reducing the computational cost and the network cost, which are the parallel overhead, of compact inner-cell filters. Those optimization techniques are as follows:

  1. 1.

    A removing technique of the redundant computations of CICF

  2. 2.

    A reducing technique of the computational cost for each CICF

  3. 3.

    A reducing technique of the network cost for transmitting the CICF

Below we describe each one of the optimization techniques in detail.

6.1 Removing redundant computations

The calculations of the local skyline and inner-cell filter are represented as \(SKY(C_i)\) and \(SKY_{ER(C_i, C_j)}(C_i)\), respectively. Also, \(SKY(C_i)\) can be rewritten as \(SKY_{ER(C_i, C_i)}(C_i)\). Therefore, the number of calculations of skylines depends on the number of cells. Since the skyline calculation is IO-consuming and CPU-intensive job [18, 33], reducing the number of skyline calculations can improve the performance significantly.

When we divide each dimension of the input data space into m parts, the total number of cells becomes \(m^d\). Therefore, if we perform skyline calculations without utilizing the total and partial dominance relationships, the number of required skyline calculations becomes \(m^d \times m^d\) because we have to calculate the skyline for every pair of cells.

In a previous work, we can also find an attempt to reduce the number of operations, which are called dominating subset operations, that are required to compute the global skyline in a parallel manner [14]. In their study, when a dominating subset is computed for each pair of cells (\(C_i\), \(C_j\)), the authors reduced the required number of operations from \(2^d \times 2^d\) to \(\sum _{i=0}^d \left( \begin{array}{c} d \\ i \end{array}\right) \cdot 2^i\) by calculating them only for the tuples of \(C_i\) that have the possibility to dominate any tuples of \(C_j\).

If we generalize their work by dividing each dimension into m parts for applying them to calculate \(SKY_{ER(C_i, C_j)}(C_i)\), the number of required skyline calculations is as follows:

$$\begin{aligned} \sum _{i=0}^{d} \left( \begin{array}{c} d \\ i \end{array} \right) \cdot m^i \cdot \{1 + \cdot \cdot \cdot + (m-1)\}^{d-1} \end{aligned}$$
(1)

Compared to their work, in our approach, far fewer skyline calculations are required since we calculate the skyline \(SKY_{ER(C_i, C_i)}(C_i)\) only for cells in the partial dominance relationship except for the total dominance relationship. As a result, the required number of skyline calculations is as follows:

$$\begin{aligned} \sum _{i=0}^{d} \left( \begin{array}{c} d \\ i \end{array} \right) \cdot \{m^i - (m-1)^i\} \cdot \{1 + \cdot \cdot \cdot + (m-1)\}^{d-1} \end{aligned}$$
(2)

By skipping the skyline calculation between the cells in a total dominance relationship, we can reduce \(m^i\) to \(m^i-(m-1)^i\) in Eq. 2. However, even if we decrease the amount of skyline calculations, the required number of skyline calculations can increase as the number of parts m, or the dimensionality d increase. Thus, we tried to overcome this limitation by using the following observation.

When we compute the compact inner-cell filter for each cell, we observe that there are redundant sets of equi-range dimensions among cells. For example, consider the case in which three cells are given in two-dimensional space, as shown in Fig. 11. In Fig. 11, we have to calculate \(CICF(C_j)\) and \(CICF(C_k)\) to compute a global skyline. Since the cell \(C_i\) is included in both \(AD(C_j)\) and \(AD(C_k)\), the \(CICF(C_j)\) should consist of \(SKY_{ER(C_i,C_j)}(C_i)\). Similarly, \(CICF(C_k)\) should consist of \(SKY_{ER(C_i,C_k)}(C_i)\) and \(SKY_{ER(C_j,C_k)}(C_j)\). In the above skyline calculation, \(SKY_{ER(C_i,C_j)}(C_i)\) and \(SKY_{ER(C_i,C_k)}(C_i)\) make the same result since \(ER(C_i, C_j)\) and \(ER(C_j, C_k)\) is equal to {\(D_2\)}. Therefore, by calculating \(SKY_{\{D_2\}}(C_i)\) only once and providing the result to \(C_j\) and \(C_k\) respectively, we can decrease the number of skyline calculations. It is the great advantage of our approach which decreases the number of skyline calculations significantly.

Fig. 11
figure 11

An example of three cells in two-dimensional space

Full size image

Algorithm 10 shows the pseudocode that avoids redundant computations of compact inner-cell filters. In the algorithm, we find the cells that are partially dominated by input cell \(C_i\). If the input cell \(C_i\) partially dominates cell \(C_j\), we calculate the set of equi-range dimensions between \(C_i\) and \(C_j\) (lines 4–5). After that, we collect the cells that produce the same ER into cellList and then put (\(C_j\), its cellList) to erMap (lines 6–9). Finally, we can get a map that consists of (set of equi-range dimensions, list of cells) pairs (line 13). In each pair of the map, all cells in the cellList are partially dominated by the input cell \(C_i\), and each of them produces the same set of equi-range dimensions ER with the input cell \(C_i\).

figure j

By replacing Algorithm 6 with Algorithm 10 in the map function of the global skyline processing step, we can remove any redundant compact inner-cell filter computation. As a result, we can further reduce the number of skyline calculations as shown in Eq. 3. In Eq. 3, we assume that totally dominated cells are also removed in advance by the outer-cell filtering.

$$\begin{aligned} \sum _{i=0}^{d} \left( \begin{array}{c} d \\ i \end{array} \right) \sum _{i=0}^{d-1} \left( \begin{array}{c} {d-i} \\ j \end{array} \right) \cdot (2^{d-i} - 2^j) \cdot (m-2)^{j} \end{aligned}$$
(3)

In summary, Eq. 1 estimates the number of skyline computations by generalizing the partitioning method of MR-SKETCH. Equation 2 estimates the largely reduced number of skyline computations by using our outer-cell filtering technique which eliminates totally dominated cells. Lastly, Eq. 3 also estimates the number of skyline computations which is further reduced by using the outer-cell filtering technique and optimization technique 1, which removes the redundant computations of compact inner-cell filters among the cells that have the same set of equi-range dimensions.

Figure 12a, b shows the theoretically measured number of skyline calculations according to Eqs. 1, 2 and 3. The number of skyline calculations is represented in logarithmic scale (base 2) in the two figures. Figure 12a shows the number of skyline calculations by increasing the number of parts. In this figure, we can see that the proposed method largely reduces the number of skyline calculations by 87–93% compared to Eq. 1 which is derived from the previous work [14]. Moreover, our method needs a much smaller number of skyline calculations than the previous work as the number of parts increases.

Fig. 12
figure 12

The number of required skyline calculations (logarithmic scale). a Varying the number of parts. b Varying the dimensionality

Full size image

Figure 12b shows the number of required skyline calculations by varying the dimensionality of datasets. The number of skyline calculations is reduced by 20–98% compared to Eq. 1 as shown in the figure. Similar to the results of Fig. 12a, our method further decreases the number of skyline calculations from the results of the previous study with increasing dimensionality.

6.2 Reducing the computational overhead

In our approach, we have to compute two types of skylines for each cell \(C_i\): one for local skyline of cell \(C_i\) and the other for compact inner-cell filters for the cell \(C_j\) such that \(C_j \in PD(C_i)\). In Sect. 5.1, we considerably reduced the number of skyline calculations by removing the redundant compact inner-cell filter computation. We now propose an efficient method to reduce the cost of each compact inner-cell filter computation.

Fig. 13
figure 13

An example of cells and sets of equi-range dimensions in 3D space. a Five cells in 3D space. b Sets of equi-range dimensions

Full size image

Suppose that there are five cells in three-dimensional space as shown in Fig. 13a, in which cell \(C_1\) partially dominates \(C_2\), \(C_3\), \(C_4\) and \(C_5\). According to their partial dominance relationships, we can calculate sets of equi-range dimensions for \(C_1\) and each of the other cells as shown in Fig. 13b.

Table 2 Tuples and required calculations for cell C1
Full size table

When the tuples in \(C_1\) are given as shown in Table 2a, we must compute the local skyline of cell \(C_1\) and the inner-cell filters for \(C_2\), \(C_3\), \(C_4\) and \(C_5\) as shown in Table 2b. In Table 2, if we compare \(SKY_{\{D_2, D_3\}}(C_1)\) and \(SKY_{\{D_3\}}(C_1)\), we can observe the property described in the following Observation 3. For the convenience of explanation, we denote the results of \(SKY_{\{D_2, D_3\}}(C_1)\) and \(SKY_{\{D_3\}}(C_1)\) as \(S_{\{D_2, D_3\}}\) and \(S_{\{D_3\}}\), respectively.

Observation 3

If we consider only the \(\{D_3\}\) dimension values, \(S_{\{D_2, D_3\}}\) is represented as \(\{(*,*,2)\}\). Similarly, \(S_{\{D_3\}}\) is represented as \(\{(*,*,2)\}\) because \(\{p_2, p_3, p_5\}\) has the same \(\{D_3\}\) dimension values. With these results, we observe that all the \(\{D_3\}\) dimension values of tuples in \(S_{\{D_3\}}\) are preserved in that of tuples in \(S_{\{D_2, D_3\}}\) when we consider only the \(\{D_3\}\) dimension values and \(\{D_3\}\) is a subset of \(\{D_2, D_3\}\).

In Observation 3, we derive the following theorem which reduces the cost of compact inner-cell computation.

Theorem 4

Given two dimension sets U and V, if V is a subset of U, then the values of tuples in \(SKY_{V}(C_i)\) are preserved in \(SKY_{U}(C_i)\) on subspace V.

Proof

When a tuple p in \(SKY_V(C_i)\) is also included in \(SKY_U(C_i)\), we omit the proof of the theorem because it naturally holds.

Now, consider a tuple p in \(C_i\) that is included in \(SKY_V(C_i)\) but not in \(SKY_U(C_i)\). Since the tuple p is not included in \(SKY_U(C_i)\), there is at last one tuple q in \(SKY_U(C_i)\) that dominates p. That is, q dominates p in subspace U. Also, q does not dominate p in subspace V since if q dominates p in subspace V, then p cannot be included in \(SKY_V(C_i)\) due to q.

Since q does not dominate p in subspace V, q is worse than p in at least one dimension in V, or q is worse than or equal to p in all dimensions in V by the definition of skyline. In the former case, q cannot dominate p in subspace U. Thus, this case cannot be established since we have already selected q which dominates p. Therefore, the latter case is established. That is, q is worse than or equal to p in all dimensions in V (condition 1).

On the other hand, since q dominates p in subspace U, by the definition of skyline, q is not worse than p in any other dimensions in U and q is better than p in at least one dimension of U (condition 2). To satisfy both condition 1 and condition 2, q must be equal to p in all dimensions in V and better than p in at least one dimension in \(U-V\).

Therefore, although p is not included in \(SKY_U(C_i)\), there is always a tuple q in \(SKY_U(C_i)\) which has the same values with p on all dimensions in V.

Thus, from the proof, the values of tuples in \(SKY_{V}(C_i)\) are preserved in \(SKY_{U}(C_i)\) on subspace V. \(\square \)

Corollary 1

When a cell \(C_i\) partially dominates cell \(C_j\) and cell \(C_k\), \(SKY_{V}(C_i)\) and \(SKY_{V}(SKY_{U}(C_i))\) dominate the same tuples in \(C_k\) if V is a subset of U for two dimension sets U and V such that \(U=ER(C_i, C_j)\) and \(V=ER(C_i, C_k)\).

Proof

By Lemma 3, even if we change the values in \(V^C\) of the tuples in cell \(C_i\), it does not affect whether or not the tuples of \(C_k\) are dominated, which means that tuples in \(SKY_{V}(C_i)\) do not lose the dominance power as a compact inner-cell filter for \(C_k\) even if we preserve only the values in V of the tuples in \(SKY_{V}(C_i)\). By Theorem 4, since the values of tuples in \(SKY_{V}(C_i)\) are preserved in \(SKY_{U}(C_i)\) on subspace V, the values of tuples in \(SKY_{V}(C_i)\) are also preserved in \(SKY_{V}(SKY_{U}(C_i))\) on subspace V. Therefore, \(SKY_{V}(SKY_{U}(C_i))\) does not lose the dominance power as an inner-cell filter for \(C_k\). \(\square \)

By using Corollary 1, we significantly reduce the cost of compact inner-cell filter computation. For example in Table 2b, when we compute the compact inner-cell filter for \(C_5\), we can calculate skyline on subspace \(\{D_3\}\) using the result of \(SKY_{\{D_2, D_3\}}(C_1)\) as input instead of using tuples of \(C_1\) because \(SKY_{\{D_3\}}(C_1)\) and \(SKY_{\{D_3\}}(SKY_{\{D_2, D_3\}}(C_1))\) dominate the same tuples in \(C_5\) by Corollary 1. In general, we can significantly reduce the cost of compact inner-cell filter computations for \(C_5\) since the result of \(SKY_{\{D_2, D_3\}}(C_1)\) has a much smaller number of tuples than \(C_1\).

To efficiently compute compact inner-cell filters using Theorem 4, we design an ER-Cube that consists of a local skyline and skylines for the compact inner-cell filters. The structure of the ER-Cube can be visualized as a lattice structure similar to the Skycube in [31]. Figure 14a shows an example for the ER-Cube of cell \(C_1\) in Fig. 13, in which we denote the skyline calculation \(SKY_U(C)\) as a cuboid U and represent it as a rectangle. In Fig. 14, we do not have to calculate \(SKY_{\{D_1, D_2\}}(C_1)\), \(SKY_{\{D_1\}}(C_1)\) and \(SKY_{\{D_2\}}(C_1)\) since \(C_1\) partially dominates only \(C_2\), \(C_3\), \(C_4\) and \(C_5\). We represent those unnecessary cuboids with dotted rectangles.

For the two cuboids U and V in the ER-Cube, we call U the ancestor cuboid and V the descendant cuboid if \(V \subset U\). When the length difference between U and V is one, we call those cuboids the parent cuboid and the child cuboid instead of the ancestor cuboid and the descendant cuboid, respectively.

Fig. 14
figure 14

Computation of the compact inner-cell filter for cell \(C_1\) using ER-Cube. a Lattice structure of an ER-Cube. b Path for filling cuboids in an ER-Cube. c Comparison of the required skyline calculations in cuboids

Full size image

Algorithm 11 shows how to compute the compact inner-cell filters with a significantly lower cost using the ER-Cube for a cell. Since the local skyline of a cell is the skyline calculated on a data space D = {\(D_1\),...,\(D_d\)}, we use the local skyline of the cell as a root cuboid of the ER-Cube.

figure k

In Algorithm 11, we assume that erMap, which is the result of Algorithm 10, and \(LS_i\), which is the local skyline of cell \(C_i\), are provided as an input parameter. The pseudocode of Algorithm 11 consists of two parts: one for the building structure of ER-Cube and the other for filling cuboids with associated skylines. To build a structure for ER-Cube, for each pair (er,  cells), we create a cuboid from er and assign cells to a target field of the cuboid (lines 4-5). The target field indicates the cells that are partially dominated by cell \(C_i\). The created cuboid is added to ER-Cube (line 6). After all cuboids are added to ER-Cube, we sort cuboids of ER-Cube by the length of the cuboid in descending order (line 7). With this sorting, we obtain an ER-Cube with a topology similar to Fig. 14a. After the sorting, we fill cuboids with associated skylines. The root cuboid of ER-Cube is filled with the local skyline of cell \(C_i\) (lines 8–9). After that, we fill the cuboids with associated skylines from the (top+1) level to the bottom level (line 10). In this algorithm, we assume that the level of top cuboid is 0. When we fill the cuboid V, we find the closest ancestors of V (line 12). Since there are a number of cuboids in the ancestors, we select the ancestor with the minimum number of tuples and use it as the input of the skyline calculation on subspace V (lines 13–14). Finally, we return ER-Cube after filling all cuboids (line 15). By replacing Algorithm 7, which is in the map function of the global skyline processing step shown in Algorithm 8, with Algorithm 11, we considerably reduce the computation cost for compact inner-cell filters.

The great advantage of this method is that we can compute the compact inner-cell filter for each cell at an even lower cost by reusing the computation result of its ancestor cuboids. Thus, in our approach, the computational overhead of compact inner-cell filters does not increase significantly as the number of dimensions and data increase.

Figure 14c compares the results of the calculation when we use Algorithm 11 and when we do not use it. The original calculation shows the skyline calculations required for \(C_1\) using Algorithm 7 instead of Algorithm 11 which is its advanced version.

If we do not use Algorithm 11, we need to calculate the skyline using all the tuples of \(C_1\) as input for each cuboid. However, if we use Algorithm 11, we can calculate the skyline using the computation result of its ancestor cuboid, which has the minimum number of tuples. Figure 14b shows the path for filling the cuboids in Algorithm 11, in which cuboids at the tail of arrows are used as input for the CICF computation for cuboids at the head of arrows. In this figure, when we calculate skylines for cuboid \(D_1D_3\) and \(D_2D_3\), we can use the result of cuboid \(D_1D_2D_3\), which is denoted as \(\alpha \), as input for the calculations instead of tuples of \(C_1\). Similarly, when we calculate the skyline for cuboid \(D_3\), we can use the results of cuboid \(D_1D_3\) or cuboid \(D_2D_3\) as input for the calculation. In this case, since cuboid \(D_2D_3\) has fewer tuples than cuboid \(D_1D_3\), we select the result of cuboid \(D_2D_3\), which is denoted as \(\gamma \), as the input of \(SKY_{\{D_3\}}(\gamma )\).

Although the result of cuboid V changes depending on whether or not Algorithm 11 is used, we can see that values of tuples in the result are completely preserved when we consider only the values on dimensions in V. For example, the values of \({\{p_2, p_4, p_5\}}\) and \({\{p_2, p_4\}}\), which are the results of \(SKY_{\{D_1, D_3\}}(C_1)\) and \(SKY_{\{D_1, D_3\}}(\alpha )\), are equal to \(\{(3, *, 2), (2, *, 3)\}\) on dimension \({\{D_1, D_3\}}\), and the values of \({\{p_2, p_3, p_5\}}\) and \({\{p_3\}}\), which are the results of \(SKY_{\{D_3\}}(C_1)\) and \(SKY_{\{D_3\}}(\gamma )\), are equal to \(\{(*, *, 2)\}\) on dimension \({\{D_3\}}\). Through the experiments in Sect. 6, we ensure that Algorithm 11 dramatically reduces the cost for computing compact inner-cell filters.

6.3 Reducing the network overhead

Our approach performs the global skyline processing in a parallel manner for each cell with its compact inner-cell filter. Although we already have decreased the network overhead using the compact inner-cell filters, in this section, we devise an advanced technique to maximize the benefit of parallelism by reducing the number of transmissions of them.

A simple way to reduce the network cost is to produce a small number of cells as proposed in [14]. To generate a small number of cells, the authors in [14] divided the data space into large cells. After the transmission of the filter, which pruned non-global skyline tuples, they produced cells again by dividing the large cells into small cells. Then they performed filtering and global skyline computing with the newly produced cells. Thus, the network cost caused by the transmission decreased. However, the benefit of parallel processing was reduced because the processing on each large cell was executed in a serial manner. Unlike the existing methods, we propose an efficient way to reduce the network cost without loss of benefit from parallel processing.

Suppose that there are seven non-empty cells in a two-dimensional space as shown in Fig. 15a. The dashed arrow in Fig. 15a indicates the partial dominance relationship. For example, a dashed arrow between cell \(C_4\) and cell \(C_3\) indicates that cell \(C_4\) partially dominates cell \(C_3\).

Fig. 15
figure 15

A comparison of the network transmission. a An example of cells. b Without cell grouping. c With cell grouping

Full size image

In the global skyline processing, more than one cell is processed in one computing node since it is common that the number of computing nodes is smaller than the number of cells. Figure 15b, c shows two examples where the cells in Fig. 15a are placed to three computing nodes. In the two figures, each arrow represents the delivery of the compact inner-cell filters within a node or across nodes. The key observation is as follows.

Observation 4

In the two figures Fig. 15b, c, the network cost varies depending on the placement of cells since there is no network cost to deliver inner-cell filters between cells in the same node.

For example, there are six transmissions of inner-cell filters over the network in Fig. 15b, whereas there are only two transmissions over the network in Fig. 15c. Through Observation 4, we know that we should place the cells that send and receive inner-cell filters on the same node to reduce the network cost caused by transmitting the compact inner-cell filter. To place the cells that send and receive inner-cell filters into the same node, we group the cells without overlapping after the local skyline processing step, in which we obtain information about cells and their local skylines.

To solve this cell placement problem, we represent cells and their partial dominance relationships as graph \(G = (V, E)\), wherein each cell represents a node and each partial dominance relationship represents an edge. For example, when a cell \(C_i\) partially dominates a cell \(C_j\), we represent cells \(C_i\) and \(C_j\) as nodes \(v_i\) and \(v_j\), and then connect two nodes with an edge \((v_i, v_j)\). The weight of edge \(w(v_i, v_j)\) is the number of tuples in the compact inner-cell filter for \(C_j\), that is, the number of tuples in \(SKY_{ER(C_i, C_j)}(LS_{C_i})\). Although we have a limit on obtaining the exact number of tuples in compact inner-cell filters without skyline calculation, we can obtain the approximate number of tuples in inner-cell filters by calculating them by [4, 24] in advance.

In the above problem formulation, the cell placement problem is reduced to the well-known minimum k-cut problem, in which k is the number of cell groups. The minimum k-cut problem finds a set \(S \subseteq E\) of minimum weight whose removal leaves k connected components. Since solving this problem exactly is NP hard [23], we use the approximation algorithm in [12] which finds a k cut which has weight within a factor of \((2 - 2/k)\) of the optimal. As a result of the algorithm in [12], we obtain the cut of edges, and we can get k components (\(g_1,\ldots , g_k\)) by removing the cut in the graph G. For each component \(g_i\), we make a cell group \(S_i\) which consists of cells corresponding to nodes of \(g_i\).

It shows good performance when K is similar to the number of dimensions in independent distribution. In anti-correlated distribution, it provides good performance when k is similar to \(\frac{m^d}{d}\), where d is the number of dimensions and m is the number of parts.

In the global skyline processing step, we start with loading information of the cell groups. In each map function, for the cells in the same group, we skip the computation and transmission of the compact inner-cell filters. Then, when we produce map outputs, we change the key of the map output from the cell ID to the group ID to which it belongs. By skipping the transmission of cells in the same group, we significantly reduce the network cost due to the compact inner-cell filter transmission. That is, the compact inner-cell filters are transmitted only between cells belonging to different cell groups. In each reduce function, we compute a part of the global skyline using Algorithm 9, in which the tuples in the same cell group are provided as input.

In Algorithm 9, we calculate the skyline for the cell group instead of calculating inner-cell filters and filtering out non-global skyline tuples. Consequently, we skip the calculations for the compact inner-cell filters instead of postponing the calculations like in the previous work. That is, we even further reduce the number of computations as well as the network cost for the compact inner-cell filters.

7 Performance evaluation

We perform extensive experiments to show the superiority of our parallel processing methods for the skyline computation in MapReduce framework. Section 6.1 describes the experimental environment and dataset and Sect. 6.2 presents the experimental results.

7.1 Experimental data and environment

The purpose of experiments is to evaluate the efficiency of our parallel skyline processing method. We conduct a performance comparison between our method and several state-of-the-art methods, including MR-BNL, MR-Angle, PGPS, MR-GPMRS and MR-SKETCH. Our implementation of the proposed methods and the related algorithms are written in Java.

The experiments were performed on a cluster with eleven commodity machines, 1 master and 8 slave nodes connected by a gigabit switching hub. Each machine is equipped with Intel Core i5-Haswell 3.5GHz CPU and 7200RPM HDD, and 16GB main memory, running on CentOS 7.0. We use Hadoop version 1.0.2 to build the MapReduce environment on the cluster.

For the input datasets, we use both synthetic datasets and real-world datasets collected from Airbnb [21]. For the synthetic datasets, we randomly generated data by independent and anti-correlated distributions, which are typically used for evaluating the performance of the skyline computation. The detailed explanation about the real-world dataset is given in Sect. 6.2.8.

The default parameter values of experiments are as follows: the dimensionality of datasets is 4, the number of tuples in datasets is 60 millions (almost 10GB), the number of divided parts per dimension is 4, and the cluster size is 8.

We classify the methods in our experiments into three categories: (1) MR-BNL, MR-ANGLE and PGPS which perform the local skyline processing step in a parallel manner and the global skyline processing step in a serial manner on the MapReduce framework. (2) MR-GPMRS and SKY-IOC which compute the local and global skyline processing step in a parallel manner on the MapReduce framework. (3) MR-SKETCH which computes the skyline in a parallel manner on the MapReduce framework accompanying with the additional serial merging step, which is not a MapReduce job, for generating the final result.

7.2 Results of the experiments

7.2.1 Effect of data dimensionality

Figure 16 shows the comparison of the execution time in seconds as the dimensionality of dataset is varied from 2 to 6. In independent datasets, as shown in Fig. 16a, SKY-IOC shows 17–43 percent faster than the fastest method for each dimension of the existing five methods except when the dimension is 2. When the dimensionality is 2, MR-SKETCH is once faster than other methods. However, with the growth of the number of dimensions, it shows the worst performance among all methods. This is because as the dimensionality increases, the size of dominated subsets increases exponentially since they consist of sets of tuples that cannot be a global skyline, while other methods use local skylines for computing global skyline tuples. As a result, it spends a considerable amount of time for its merging step.

Fig. 16
figure 16

Execution time varying the dimensionality. a Independent dataset. b Anti-correlated dataset

Full size image

As can be seen in Fig. 16b, for anti-correlated datasets, the difference of execution time between our method and other methods is much larger than that for the independent datasets. In Fig. 16b, SKY-IOC executes 42–3906 percent faster than MR-GPMRS which is the fastest method among existing methods.

Even in the low dimensionality (2 and 3), MR-BNL, MR-ANGLE, PGPS, which are the methods in category 1, make extremely long execution time. This low performance is because of the large local skylines in anti-correlated distribution which incurs considerable time to merge them and to compute the global skyline with a single reducer. We cannot plot MR-SKETCH due to its bad performance.

For MR-GPMRS, it exhibits better performance than the methods in category 1 in Fig. 16b since it computes the global skyline in a parallel manner. However, the execution time increases sharply when the dimensionality is 4. This is because it produces lager size of local skylines than other methods due to its random partitioning scheme and transmits them redundantly.

In both independent and anti-correlated distributions, SKY-IOC shows the best performance in most cases with increasing number of dimensions, because it not only processes the local and global skyline processing in a parallel manner, but also minimizes the parallel overhead with the optimization techniques mentioned in Sect. 5. From the results of experiments, we see the excellent performance of SKY-IOC which has great advantages when processing datasets with large number of dimensions.

Fig. 17
figure 17

Execution time varying the dataset size. a Independent dataset. b Anti-correlated dataset

Full size image

7.2.2 Effect of dataset size

Figure 17 shows the comparison of execution time in seconds for the six methods when the dimensionality is 4 and the number of tuples in datasets is varied from 20 million tuples to 100 million tuples. The results show that SKY-IOC performs the best on both distributions. It executes 12–52 percent faster than the fastest methods for each dataset size of the existing five methods in the independent distribution, and 161–298 percent faster than MR-GPMRS in anti-correlated distribution. Overall, SKY-IOC always shows the best execution time with the increasing size of datasets.

The reason why our approach is superior to all other methods is due to the following reason. SKY-IOC computes the global skyline in parallel on multiple nodes, while MR-BNL, MR-ANGLE and PGPS which belong to the category 1 do not. Therefore, those three methods suffer from the performance degradation because they merge local skyline and compute the global skyline in a single node in a serial manner. As shown in Fig. 17b, this performance degradation becomes worse as the size of skylines increases in anti-correlated datasets.

MR-GPMRS well handles large size of skyline better than three methods in category 1 since it computes the global skyline in a parallel manner as shown in Fig. 17b. However, the redundant scanning of input data for bit string generation and the redundant transmission of relatively large local skylines make the performance degradation as the dataset size increase.

MR-SKETCH shows the worst performance in both independent and anti-correlated datasets. In particular, in the anti-correlated dataset, we cannot plot it in Fig. 17b due to its bad performance. The performance of MR-SKETCH is deteriorated due to the serious bottleneck occurred during the result merging step for its dominated subsets. The reason of this bottleneck is that MR-SKETCH makes the dominated subsets with tuples that cannot be a global skyline. In general, the number of tuples that cannot belong to a skyline is substantially larger than the number of tuples which belongs to skyline. Thus, MR-SKETCH is inevitable to compute and transmit far more number of tuples than other methods. The result of this experiment clearly shows that our method consistently provides the low execution time with the increasing size of datasets.

Fig. 18
figure 18

Experiments on much larger datasets. a Independent dataset. b Anti-correlated dataset

Full size image

In Fig. 18, we have carried out further intensive experiments using much larger datasets (consisting of 200 million to 1 billion tuples). As shown in Fig. 18a, SKY-IOC executes 48 to 60 percent faster than the fastest methods for each dataset size of existing five methods in the independent distribution.

Meanwhile, in the anti-correlated distribution in Fig. 18b, SKY-IOC executes 1,417 to 3,236 percent faster than MR-ANGLE which is the fastest method among existing methods even if we only use up to 600M tuples. MR-SKETCH in Fig. 18 and MR-BNL and MR-GPMRS in Fig. 18b could not be plotted since they were not completed in a reasonable time. From the experimental result, we can see that the performance gap much more increases as the size of datasets gets larger.

7.2.3 Effect of cluster size

Fig. 19
figure 19

Execution time varying the number of nodes. a Independent dataset. b Anti-correlated dataset

Full size image

In this experiment, we measure the execution time of SKY-IOC by scaling up the cluster size. For independent and anti-correlated distributions, we use a 4-dimensional dataset with 60 million tuples. Figure 19 shows the execution time of SKY-IOC and other methods by scaling up the cluster size from 2 to 8. In both distributions, SKY-IOC shows the best performance steadily regardless of the cluster size. The reason is that our method fully utilizes the growing number of computing resources by computing the local and the global skyline in a fully parallelized manner with the help the of the compact inner-cell filters. Also, with the outer-cell filtering, we can remove a large number of unqualified tuples at the early stage of the skyline query processing. Moreover, we do not decrease the gain of the parallelism by using a series of optimization techniques for minimizing the parallel overhead. Through this experiment, we clearly observe that SKY-IOC has good scalability with the increasing cluster size.

7.2.4 Maximum number of processed tuples

In the global skyline processing step, the reducer that processes a large number of tuples has a possibility to cause a bottleneck which makes the overall performance degradation. Therefore, we can expect the better performance as we decrease the maximum number of processed tuples in reducers. Figure 20 illustrates the comparison of the maximum number of tuples processed in reducers at the global skyline processing step by increasing the dataset size and the dimensionality.

The results show that SKY-IOC processes the smallest number of tuples in reducers on both distributions at the global skyline processing step. In Fig. 20a, b, we find out that, by experiments, the maximum number of processed tuples in reducers of SKY-IOC is almost 1.7 times smaller than that of PGPS in the independent dataset and almost 16 times smaller than PGPS in the anti-correlated dataset as the dataset size increases. In Fig. 20c, d, when we varying the dimensionality, we observe much larger gap of the number of processed tuples between SKY-IOC and other existing methods. When the dimensionality is just 4, the maximum number of processed tuples in reducers of SKY-IOC is 1.7 times smaller than that of PGPS in the independent dataset and 15 times smaller than that of PGPS in anti-correlated datasets. The main reason why the maximum number of processed tuples in SKY-IOC is much smaller than that of other methods is because we have performed the global skyline computation in a parallel manner using the small size compact inner-cell filter.

Fig. 20
figure 20

The maximum number of tuples processed in reducers. a Varying dataset size (independent). b Varying dataset size (anti-correlated). c Varying dimensionality (independent). d Varying dimensionality (anti-correlated)

Full size image

In this figure, in all the experimental results, MR-BNL, MR-ANGLE, and PGPS, belonging to category 1, exhibit the larger number of tuples processed in reducers than that of SKY-IOC since they merge local skylines and compute the global skyline in a single reducer. Thus, only the specific single node is heavily loaded to compute the global skyline and it causes a long execution time as shown in Figs. 16 and 17. Also in this experiment, MR-SKETCH gives the worst result and we cannot plot it in Fig. 20b–d. As noted previously, MR-SKETCH handles huge number of tuples that cannot be a global skyline, while other methods handle much smaller number of tuples that are likely to be a global skyline.

In the case of MR-GPMRS, we see that the maximum number of tuples processed in reducers is relatively large although it achieved the second shortest execution time of previous experiments in Figs. 16b and 17b. This is because each reducer of MR-GPMRS determines global skyline tuples of multiple partitions, while that of other methods such as MR-BNL, MR-ANGLE, and PGPS computes a global skyline. Since it takes much more time for computing a single skyline of a large input data than multiple skylines for several small input data, MR-GPMRS can provide a relatively short execution time although the number of tuples in its reducers is larger than that of other methods in category 1. From this experiment, we can conclude that SKY-IOC is obviously profitable to process large skylines with high dimensionality datasets in a parallel and distributed framework.

Fig. 21
figure 21

Network overhead measured in terms of tuples exchanged. a Varying dataset size (independent). b Varying dataset size (anti-correlated). c Varying dimensionality (independent). d Varying dimensionality (anti-correlated)

Full size image

7.2.5 Network overhead

As mentioned earlier, in order to perform the global skyline processing in a parallel, additional information must be provided to the local skyline of each partition to indicate which tuple belongs to the global skyline. Because this additional information is transmitted over the network, we call it network overhead. Figure 21 shows the network overhead, which is measured by the number of tuples that are transferred through the network while varying the number of input tuples and dimensionality. In order to measure the network overhead fairly, we perform experiments using cell groups, each of them have only one cell in SKY-IOC.

In the experiments in Fig. 21a, b, SKY-IOC transmits 75 times smaller tuples that cause network overhead than MR-GPMRS in an independent dataset, and 126 times smaller tuples than MR-GPMRS in an anti-correlated dataset.

The gap of network overhead between SKY-IOC and MR-GPMRS becomes larger when the dimensionality increases from 2 to 6. It reaches up to 241 times in an independent dataset and 5886 times in an anti-correlated dataset, as shown in Fig. 21c, d.

Through this experiment, we can see that our method causes extremely less network overhead than MR-GPMRS and MR-SKETCH. The main reason for the small network overhead is attributed to our compact inner-cell filter. Moreover, as we explained in Sect. 5.3, if we use the cell grouping method, the network overhead will be further reduced. Since MR-GPMRS produces relatively large local skylines due to its random partition scheme and performs the redundant transmission of its local skyline, it incurs the higher network overhead than SKY-IOC. The large network overhead of MR-SKETCH is due to the large-size dominated subsets which is previously mentioned. From this experiment, we can see that the network overhead of SKY-IOC is much smaller than that of other parallel processing methods.

7.2.6 Computational overhead

Fig. 22
figure 22

Execution time with and without the optimization techniques. a Varying the dataset size (anti-correlated). b Varying the dimensionality (anti-correlated)

Full size image

In this experiment, we measure the execution time of two cases, that is, with and without the optimization technique 1 and 2 for anti-correlated datasets. A comparison of the execution time shows how much our optimization techniques reduce the computational overhead. Figure 22a, b shows the comparison of the execution time for those two cases when the dimensionality is 4 and the number of input tuples is varied from 20 million tuples to 100 million and the dimensionality of dataset is varied from 2 to 6, respectively. In those cases, the optimization techniques reduce the computation overhead by 25 percent and by 58 percent, respectively. This experiment reveals that our optimization techniques considerably reduce the computational overhead of SKY-IOC.

Figure 23 compares the theoretically estimated number of skyline calculations with the actual number of skyline calculations in experiments. We note that there is a consistency between the dashed line of Eq. 3 which indicates the results obtained from the theoretical analysis and the solid line which is the results obtained from real experiments. Thus, we can see that the experimental results corroborate our theoretical analysis in Sect. 5.1. We can once again confirm that the proposed optimization techniques effectively reduce the computational overhead of SKY-IOC.

Fig. 23
figure 23

The number of required skyline calculations. a Varying the number of parts (independent). b Varying the dimensionality (independent)

Full size image

7.2.7 Filtering power

In this experiment, we measure the filtering power of SKY-IOC and other methods. Since the filtering of unqualified tuples is performed at the early stage of the skyline query processing, if we filter out the more tuples, we can get the better performance.

Table 3 describes the number of filtered tuples in PGPS, MR-GPMRS, MR-SKETCH and SKY-IOC for 60 million tuples in a 4-dimensional independent dataset. In this experiment, we measure TFT and FPP while varying the number of parts on each dimension from 2 to 5. TFT means the total number of filtered tuples, and FPP means the number of filtered tuples per filter point.

Table 3 The number of filtered out tuples (10 K)
Full size table

Since filtering methods select filter points for each partition, the filtering power depends on their partitioning scheme. Therefore, MR-GPMRS filters out the smallest number of tuples because it uses a grid-based partitioning scheme. On the other hand, SKY-IOC filters out the similar number of tuples to PGPS which uses an angle-based partitioning scheme from the point of view of TFT.

The main reason of this outstanding filtering power, that is comparable to PGPS, is that SKY-IOC filters out huge number of tuples in totally dominated cells by using the outer-cell filters, and further enlarges its filtering power with the MSC filter which filters out numerous tuples in cells by sharing the area close to the origin of the axis.

In the case of MR-SKETCH, it shows the largest number of filtered tuples from the point of view of TFT. However, it keeps about 1 percent input tuples, which is the large number of tuples, to make its filter. Thus, MR-SKETCH makes a significantly low FPP. On the contrary, SKY-IOC shows a similar performance to PGPS, in terms of FPP. This experimental result clearly shows the superiority of our method in terms of the filtering power.

7.2.8 Performance on real-world datasets

To validate the performance of our approach on real-world environment, we have performed additional experiments with Airbnb data collections that are taken from Rajit Dasgupta et al. [21]. Airbnb is a global online platform that hosts 150 million users and provides the lease and rental service of accommodations. The Airbnb dataset has over 9 million tuples (items) in 113 cities. Each tuple contains 21 attributes: room id, city name, price, capacity for guests, the number of reviews, overall satisfaction, the number of bedrooms, the number of bathrooms, the minimum stay for a visit, and so on.

Fig. 24
figure 24

Execution time on real-world datasets. a Varying the dataset size. b Varying the dimensionality

Full size image

Figure 24a shows the comparison of execution time in seconds for the six methods while increasing the number of tuples in the dataset when the dimension is 4. Since Airbnb dataset which we collected are relatively small to be experimented in a cluster of eight nodes, we performed experiments by generating data with the same distribution from Airbnb dataset. In the experiment of Fig. 24a, we assume that the user wants to find an accommodation that has a low price, many reviews, a high overall satisfaction, and a large capacity for guests. The graph of Fig. 24a is similar to Fig. 17a, where we have performed experiments with synthetic datasets, and confirmed that SKY-IOC performed best. It executes 12–30 percent faster than the fastest methods for each dataset size of the existing five methods.

Figure 24b shows the comparison of the execution time in seconds as the dimensionality varies from 2 to 6. In addition to previous assumptions about the user’s preferences, we assume that the user prefers a large number of bedrooms and bathrooms. The graph of Fig. 24b is similar to Fig. 16a, where we have performed experiments with synthetic datasets. From this experiment, we can see that the performance gap between SKY-IOC and existing methods becomes slightly larger than the experimental results in Fig. 16a. It executes 30–76 percent faster than the fastest methods for each dimension of the existing five methods except when the dimension is 2.

The reason is that there are some dimensions that are anti-correlated such as “the capacity for guests” and “the number of reviews”. In Airbnb service, since users tend to rent rooms having small capacity of guests, those rooms get more reviews. Therefore, those two dimensions are anti-correlated since the smaller capacity of guests creates the more number of reviews. Through these experiments, we can confirm the excellent performance of SKY-IOC in real-world datasets as well as synthetic datasets.

8 Conclusion

In this paper, we proposed an efficient parallel processing method for skyline queries in MapReduce framework. Specifically, we designed two novel filtering methods, an outer-cell filtering technique and an inner-cell filtering technique. The main objective of the outer-cell filtering technique was to discard a large number of tuples in unqualified cells at the early stage of the query processing. Hence, we achieved significant performance improvement by eliminating the I/O, network, and CPU computation costs caused by tuples in unqualified cells. We also confirmed that our MSC filter boosts up the filtering power of the inner-cell filtering technique.

The inner-cell filtering technique made it possible to compute the global skyline in a parallel manner, with which we discriminated the global skyline tuple from local skylines by computing and distributing the compact inner-cell filters. By using the compact inner-cell filtering technique, we avoided the bottleneck which occurs when local skylines are merged and the global skyline is computed from the local skylines. Based on these methods, we significantly improved the performance of skyline query processing by executing the serial computing parts in a parallel manner. Furthermore, we made significant headway in minimizing the parallel overhead caused by computing and transmitting the inner-cell filters, and we reduced the I/O, network, and CPU computation costs that are caused by the inner-cell filter.

In summary, with the support of the outer-cell filtering technique and inner-cell filtering technique, our method processed skyline queries in a fast and fully parallel manner with excellent performance in the MapReduce framework. The results of experiments clearly showed that our approach consistently outperformed existing state-of-the-art methods in terms of efficiency and scalability. In particular, our method performed significantly better as the size of the skyline increased.

As future work, we plan to (1) extend this work by developing workload balancing methods for both the outer-cell filtering and the inner-cell filtering process, which are solutions for the problem of severe data skew and (2) generalize and apply the proposed method of processing the skyline query in a distributed and parallel manner not only to MapReduce but also to any other distributed and parallel computing frameworks, such as Apache Spark. We expect that the further research will lead to more effective parallelization of the skyline query processing.