1 Introduction

Simulation of Gaussian random fields (GRFs) is important for the use of Monte Carlo techniques. Considerable work has been done to simulate GRFs defined over the d-dimensional Euclidean space, \(\mathbb {R}^{d},\) with isotropic covariance functions. The reader is referred to Wood and Chan (1994), Dietrich and Newsam (1997), Gneiting et al. (2006) and Park and Tretyakov (2015) with the references therein. See also Emery et al. (2016) for extensions to the anisotropic and non-stationary cases. Yet, the literature on GRFs defined over the two-dimensional sphere or the sphere cross time has been sparse. Indeed, only few simulation methods for random fields on the sphere can be found in the literature. Among them are Cholesky decomposition and Karhunen–Loève expansion (Lang and Schwab 2015). More recently, Creasey and Lang (2018) proposed an algorithm that decomposes a random field into one-dimensional GRFs. Simulations of the 1d process are performed along with their derivatives, which are then transformed to an isotropic Gaussian random field on the sphere by Fast Fourier Transform (FFT). Following Wood and Chan (1994), Cholesky decomposition is considered as an exact method, that is, the simulated GRF follows an exact multivariate Gaussian distribution. Simulation based on Karhunen–Loève expansion or Markov random fields is considered as approximated methods, because the simulated GRF follows an approximation of the multivariate Gaussian distribution (see Lang and Schwab 2015; Møller et al. 2015). Extensions to the spatially isotropic and temporally stationary GRF on the sphere cross time using space-time Karhunen–Loève expansion were considered in Clarke et al. (2018).

It is well known that the computational cost to simulate a random vector at n space-time locations using the Cholesky decomposition is \({\mathcal {O}}(n^{3}),\) which is prohibitively expensive for large values of n. Karhunen–Loève expansion requires the computation of Mercer coefficients of the covariance function (Lang and Schwab 2015; Clarke et al. 2018) which are rarely known. Finally, the method proposed by Creasey and Lang (2018) is restricted to a special case of spectral decomposition, which makes the method lacking generality.

One way to reduce the computational burden is through the relationship between torus-wrapping, block circulant matrices and FFT. The use of this relationship has been introduced by Wood and Chan (1994) and Dietrich and Newsam (1997) when developing circulant embedding methods to simulate isotropic GRFs over regular grids of \(\mathbb {R}^{d}\). Regular polyhedra are good candidates to be used as meshes for the sphere. However, on the sphere there exist only five regular polyhedra, the Platonic solids. The regular polyhedron with most edges and faces is the icosahedron with 12 vertices, 20 faces and 30 edges (Coxeter 1973), from which we can draw at most 30 regular points on the spheres, defined as the intersections of the lines joining the midpoints of two opposite edges.

For a GRF on the sphere, using spherical coordinates, Jun and Stein (2008) make use of circulant matrices to compute the exact likelihood of non-stationary covariance functions when the GRF is observed on a regular grid over \((0,\pi )\times (0,2\pi )\).

In this paper, we revisit the circulant structure obtained by Jun and Stein (2008) and we use it to develop a fast and exact simulation method for isotropic GRFs on the sphere. Moreover, such simulation method is extended to simulate spatially isotropic and temporally stationary GRFs on the sphere cross time. The proposed method requires an isotropic covariance function on the sphere or a spatially isotropic and temporally stationary covariance function on the sphere cross time. One of the advantages of this method is the huge reduction in the computational cost to \({\mathcal {O}}(n\log (n))\).

The paper is organized as follows. Section 2 details how to obtain circulant matrices on the sphere for isotropic covariance functions. In Sect. 3, we extend the simulation method to the case of the sphere cross time for spatially isotropic and temporally stationary covariance functions. The algorithms are detailed in Sect. 4, and in Sect. 5 we provide a simulation study. Finally, Sect. 6 contains some concluding remarks.

2 Circulant matrices over two-dimensional spheres

Let \({\mathbb {S}}^{2} = \{s \in \mathbb {R}^{3}: \Vert s\Vert = 1\} \subset \mathbb {R}^{3}\) be the unit sphere centered at the origin, equipped with the geodesic distance \(\theta (s_1,s_2) := \arccos (\langle s_1,s_2 \rangle )\), for \(s_1,s_2 \in {\mathbb {S}}^{2}\). We propose a new approach to simulate a finite-dimensional realization from a real-valued and zero mean, stationary, geodesically isotropic GRF \(\mathbf{X } = \{X(s): s \in {\mathbb {S}}^{2}\}\) with a given covariance function

$$\begin{aligned} R(s_1,s_2) = {\mathbb {E}} \left[ X(s_1) X(s_2) \right] = r(\theta (s_1,s_2)), \quad s_1,s_2 \in {\mathbb {S}}^2. \end{aligned}$$

Through the paper, we equivalently refer to R or r as the covariance function of \(\mathbf{X }\). A list of isotropic covariance functions is provided in Gneiting (2013). In what follows, we use the shortcut \(\theta \) for \(\theta (s_1,s_2)\) whenever there is no confusion.

Fig. 1
figure 1

Example of the grid with \(N=24\) and \(M=9\)

Full size image

For a stationary isotropic random field on \({\mathbb {S}}^{2},\) the covariance functions and variograms are uniquely determined through the relation (Huang et al. 2011)

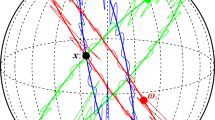
$$\begin{aligned} \gamma (\theta ) = \sigma ^{2} \Big ( 1 - r(\theta ) \Big ), \quad 0\le \theta \le \pi , \end{aligned}$$
(1)

where \(\sigma ^{2} = r(0)\). The basic requirements to simulate a GRF with the proposed method are a grid, being regular over both longitude and latitude, and the computation of the covariance function over this grid. For two integers \(M,N \ge 2\) let \(I = \{1,\ldots ,N \}\)\(J = \{1,\ldots ,M \},\) and define \(\lambda _{i} = 2\pi i/N\) and \(\phi _{j} = \pi j/M\) for \(i \in I\) and \(j \in J \), respectively. In the following, \(s_{ij}=(\lambda _i,\phi _j)\) will denote the longitude–latitude coordinates of the point \(s_{ij} \in {\mathbb {S}}^{2}\) and the set \(\varOmega _{MN} = \{(\lambda _{i},\phi _{j}): i \in I, j \in J \}\) defines a regular grid over \({\mathbb {S}}^{2}\) (see Fig. 1). The Cartesian coordinates of \(s_{ij}\), expressed in \(\mathbb {R}^{3}\), are

$$\begin{aligned} s_{ij} = (x_{ij},y_{ij},z_{ij}) = (\cos \lambda _{i} \sin \phi _{j} , \sin \lambda _{i} \sin \phi _{j}, \cos \phi _{j}).\nonumber \\ \end{aligned}$$
(2)

Let us now define the random vector

$$\begin{aligned} \mathbf{X }_{i} = [X(s_{i1}), X(s_{i2}), \ldots , X(s_{iM})], \end{aligned}$$

and the random field restricted to \(\varOmega _{MN}\) by \(\mathbf{X }_\varOmega = [\mathbf{X }_{1}, \mathbf{X }_{2}, \ldots , \mathbf{X }_{N}]\). The matrix \(\pmb \varSigma = \text{ Var }[\mathbf{X }_{\varOmega }]\) has a block structure

$$\begin{aligned} \pmb \varSigma = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \pmb \varSigma _{1,1} &{} \pmb \varSigma _{1,2} &{} \ldots &{} \pmb \varSigma _{1,N}\\ \pmb \varSigma _{1,2} &{} \pmb \varSigma _{2,2} &{} \ldots &{} {\pmb \varSigma _{2,N}}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \pmb \varSigma _{1,N}&{} {\pmb \varSigma _{2,N}} &{} \cdots &{} \pmb \varSigma _{N,N} \end{array} \right] , \end{aligned}$$

where \(\pmb \varSigma _{i,j} = \text{ cov }(\mathbf{X }_{i},\mathbf{X }_{j}) = \pmb \varSigma _{j,i}\). Notice that the grid \(\varOmega _{MN}\) assumes that the north pole \(e_{N} = (0,0,1)\). However, under isotropy assumption, the elements of \(\pmb \varSigma \) depend only on the geodesic distance, and so, the north pole does not play any role here. Moreover, the geodesic distance can be written as

$$\begin{aligned} \theta (s_{ik},s_{jl})&= \arccos (x_{ik} x_{jl} + y_{ik} y_{jl} + z_{ik} z_{jl}) \nonumber \\&= \arccos (\sin \phi _{k}\sin \phi _{l}(\cos \lambda _{i}\cos \lambda _{j}\nonumber \\&\quad + \sin \lambda _{i}\sin \lambda _{j}) + \cos \phi _{k}\cos \phi _{l})\nonumber \\&=\arccos (\sin \phi _{k}\sin \phi _{l}\cos (\lambda _{j} - \lambda _{i}) \nonumber \\&\quad + \cos \phi _{k}\cos \phi _{l}). \end{aligned}$$
(3)

Equation (3) implies \(\pmb \varSigma _{i,j} = \pmb \varSigma _{1,|j-i|+1} = \pmb \varSigma _{1,N - (|i-j| +1)}\). Thus, writing \(\pmb \varSigma _{i} = \pmb \varSigma _{1,i}\), we get

$$\begin{aligned} \pmb \varSigma = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \pmb \varSigma _{1} &{} \pmb \varSigma _{2} &{} \ldots &{} \pmb \varSigma _{N}\\ \pmb \varSigma _{N} &{} \pmb \varSigma _{1} &{} \ldots &{} \pmb \varSigma _{N-1}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \pmb \varSigma _{2}&{} \pmb \varSigma _{3} &{} \cdots &{} \pmb \varSigma _{1} \end{array} \right] . \end{aligned}$$
(4)

Equation (4) shows that \(\pmb \varSigma \) is a symmetric block circulant matrix (Davis 1979) related to the discrete Fourier transform as follows. Let \(\varvec{I}_{M}\) be the identity matrix of order M and \(\varvec{F}_{N}\) be the Fourier matrix of order N, that is, \([\varvec{F}_{N}]_{i,k} = w^{(i-1)(k-1)}\) for \(1\le i,k \le N\) where \(w = \hbox {e}^{-2\pi \imath /N}\) and \(\imath = \sqrt{-1}\). Following Zhihao (1990), the matrix \(\pmb \varSigma \) is unitary block diagonalizable by \(\varvec{F}_{N} \otimes \varvec{I}_{M}\), where \(\otimes \) is the Kronecker product. Then, there exist N matrices \(\pmb \varLambda _{i}\), with \(i\in I\), having dimension \(M\times M,\) such that

$$\begin{aligned} \pmb \varSigma = \frac{1}{N} (\varvec{F}_{N} \otimes \varvec{I}_{M}) \pmb \varLambda (\varvec{F}_{N} \otimes \varvec{I}_{M})^{*}, \end{aligned}$$
(5)

with

$$\begin{aligned} \pmb \varLambda = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \pmb \varLambda _{1}&{} \mathbf{0 } &{} \ldots &{} \mathbf{0 } \\ \mathbf{0 } &{}\pmb \varLambda _{2} &{} \ldots &{}\mathbf{0 } \\ \vdots &{} \vdots &{} \ddots &{}\vdots \\ \mathbf{0 } &{} \mathbf{0 } &{} \ldots &{}\pmb \varLambda _{N} \\ \end{array} \right] , \end{aligned}$$

where \(\varvec{B}^{*}\) denotes the conjugate transpose of the matrix \(\varvec{B}\) and \(\mathbf 0\) is a matrix of zeros of adequate size. The decomposition (5) implies that the block matrix \(\pmb \varLambda \) can be computed through the discrete Fourier transform of its first block row, that is,

$$\begin{aligned} \left[ \begin{array}{cccc} \pmb \varSigma _{1}&\pmb \varSigma _{2}&\cdots&\pmb \varSigma _{N} \end{array} \right] (\varvec{F}_{N}\otimes \varvec{I}_{M}) = \left[ \begin{array}{cccc} \pmb \varLambda _{1}&\pmb \varLambda _{2}&\cdots&\pmb \varLambda _{N} \end{array} \right] . \end{aligned}$$
(6)

Componentwise, (6) becomes

$$\begin{aligned} \left[ \begin{array}{cccc} \pmb \varSigma _{1}^{jl}&\pmb \varSigma _{2}^{jl}&\cdots&\pmb \varSigma _{N}^{jl} \end{array} \right] \varvec{F}_{N} = \left[ \begin{array}{cccc} \pmb \varLambda _{1}^{jl}&\pmb \varLambda _{2}^{jl}&\cdots&\pmb \varLambda _{N}^{jl} \end{array} \right] , \end{aligned}$$
(7)

where \(j,l \in J.\) Since \(\pmb \varSigma \) is positive definite (semi-definite), it is straightforward from the decomposition (5) that the matrix \(\pmb \varLambda \) is positive definite (semi-definite) and thus that each matrix \(\pmb \varLambda _i\) is also positive definite (semi-definite), for \(i \in I\). Hence, we get

$$\begin{aligned} \pmb \varSigma ^{1/2} = \frac{1}{\sqrt{N}} (\varvec{F}_{N} \otimes \varvec{I}_{M}) \pmb \varLambda ^{1/2}, \end{aligned}$$
(8)

which is what is needed for simulation. A simulation algorithm based on Eq. (8) is provided in Sect. 4.

3 Circulant embedding on the sphere cross time

We now generalize this approach on the sphere cross time for a spatially isotropic and temporally stationary GRF \(\mathbf{X } = \{X(s,t) : (s,t) \in {\mathbb {S}}^{2}\times {\mathbb {R}} \}\) with zero mean and a given covariance function, R, defined as

$$\begin{aligned} R \Big ( (s_1,t_1),(s_2,t_2) \Big ) := r(\theta (s_1,s_2),|t_1-t_2|), \end{aligned}$$

\((s_i,t_i) \in {\mathbb {S}}^2 \times \mathbb {R}, \quad i=1,2\). We analogously define the space-time stationary variogram \(\gamma : [0,\pi ] \times {\mathbb {R}} \mapsto \mathbb {R}\) as

$$\begin{aligned} \gamma (\theta , u) = \sigma ^{2}(1 - r(\theta ,u)), \qquad \theta \in [0,\pi ], u \in {\mathbb {R}}. \end{aligned}$$
(9)

Let \(H>0\) be the time horizon at which we wish to simulate. In addition, let T be a positive integer and define the regular time grid \(t_{\tau } = \tau H/T\) with \(\tau \in \{0,\ldots ,T\}\). Define the set \(\varOmega _{NMT} = \{(\lambda _{i},\phi _{j},t_{\tau }): i \in I, j\in J,\tau \in \{{0},\dots ,T\} \},\) and the random vectors

$$\begin{aligned} \mathbf{X }_{i,\tau }&= [X(s_{i1},t_{\tau }),~X(s_{i2},t_{\tau }),~\ldots ,~X(s_{iM},t_\tau )], \\ \mathbf{X }_{\varOmega ,\tau }&= [\mathbf{X }_{1,\tau },~\mathbf{X }_{2,\tau },~\ldots ,~\mathbf{X }_{N,\tau }], \\ \mathbf{X }_{\varOmega }&= [\mathbf{X }_{\varOmega ,0},~\mathbf{X }_{\varOmega ,1},~\ldots ,~\mathbf{X }_{\varOmega ,{T}}]. \end{aligned}$$

The associated covariance matrices are

$$\begin{aligned} \pmb \varPsi _{i,k}(\tau ,\tau ')&= \text{ cov }(\mathbf{X }_{i,\tau },\mathbf{X }_{k,\tau '}),\\ \pmb \varPsi (\tau ,\tau ')&= \text{ cov }(\mathbf{X }_{\varOmega ,\tau },\mathbf{X }_{\varOmega ,\tau '}),\nonumber \\ \pmb \varPsi&= \text{ Var }(\mathbf{X }_\varOmega ),\nonumber \end{aligned}$$

with \(i,k \in I\) and \({0} \le \tau ,\tau ' \le T\). The assumption of temporal stationarity implies that \(\pmb \varPsi _{i,k}(\tau ,\tau ') = \pmb \varPsi _{i,k}(|\tau '-\tau |).\) Therefore, \(\pmb \varPsi (\tau ,\tau ') = \pmb \varPsi (\tau ',\tau ) = \pmb \varPsi (|\tau '- \tau |).\) As a consequence, for fixed \(\tau ,\tau '\) the matrix \(\pmb \varPsi (|\tau '-\tau |)\) is a block circulant matrix with dimension \(NM\times NM\), however, \(\pmb \varPsi \) is not. To tackle this problem, we consider the torus-wrapped extension of the grid \(\varOmega _{MNT}\) over the time variable which is detailed as follows. First, let \(\kappa \) be a positive integer and let \(g: \mathbb {R}\mapsto \mathbb {R}\) be defined as

$$\begin{aligned} g({t}) = \left\{ \begin{array}{lll} \frac{{t} H}{T}&{} \text{ if } &{} 0 \le {t} \le \kappa T,\\ \\ \frac{(2 \kappa T - {t})H}{T}&{} \text{ if } &{} \kappa T< {t} \le (2\kappa T - 1).\\ \end{array}\right. \end{aligned}$$
(10)

Then, the matrix

$$\begin{aligned} {\tilde{\pmb \varPsi }}&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \pmb \varPsi (g(0)) &{} \pmb \varPsi (g(1)) &{} \ldots &{} \pmb \varPsi (g(\kappa T)) &{} \ldots &{} \pmb \varPsi (g(2\kappa T - 1))\\ \pmb \varPsi (g(1)) &{} \pmb \varPsi (g(0)) &{} \ddots &{} \pmb \varPsi (g(\kappa T-1)) &{} \ldots &{} \pmb \varPsi (g(2\kappa T - 2))\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \pmb \varPsi (g(1))&{} \pmb \varPsi (g(2)) &{} \cdots &{} \pmb \varPsi (g(\kappa T+1)) &{} \ldots &{} \pmb \varPsi (g(0)) \end{array} \right] \nonumber \\&&&\nonumber \\&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \pmb \varPsi (0) &{} \pmb \varPsi (1) &{} \ldots &{} \pmb \varPsi (\kappa T) &{} \ldots &{} \pmb \varPsi (1)\\ \pmb \varPsi (1) &{} \pmb \varPsi (0) &{} \ddots &{} \pmb \varPsi (\kappa T-1) &{} \ldots &{} \pmb \varPsi (2)\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots \\ \pmb \varPsi (1)&{} \pmb \varPsi (2) &{} \cdots &{} \pmb \varPsi (\kappa T-1) &{} \ldots &{} \pmb \varPsi (0) \end{array} \right] \end{aligned}$$
(11)

is a \((NM(2\kappa T - 1))\times (NM(2\kappa T - 1))\) block circulant matrix. Considering that each \(\pmb \varPsi (g({t}))\) is a block circulant matrix for \(0 \le {t} \le (2\kappa T - 1)\) and using decomposition (5), we get

$$\begin{aligned} {\tilde{\pmb \varPsi }}= & {} [\varvec{I}_{2\kappa L - 1}\otimes (\varvec{F}_{N} \otimes \varvec{I}_{M})][\varvec{F}_{2\kappa L - 1}\otimes \varvec{I}_{MN}] \pmb \Upsilon \nonumber \\&\times [\varvec{I}_{2\kappa L - 1}\otimes (\varvec{F}_{N} \otimes \varvec{I}_{M})]^{*}[\varvec{F}_{2\kappa L - 1}\otimes \varvec{I}_{MN}]^{*}, \end{aligned}$$
(12)

with

$$\begin{aligned} \pmb \Upsilon = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \pmb \Upsilon _{0}&{}\mathbf{0 } &{}\cdots &{}\mathbf{0 }\\ \mathbf{0 }&{}\pmb \Upsilon _{1} &{}\cdots &{}\mathbf{0 }\\ \vdots &{}\vdots &{} \ddots &{}\vdots \\ \mathbf{0 }&{}\mathbf{0 } &{}\cdots &{} \pmb \Upsilon _{(2\kappa T - 1)N } \end{array}\right] , \end{aligned}$$

where \(\pmb \Upsilon _{i}\) is a \(M\times M\) matrix for all \(i \in I\). When \({\tilde{\pmb \varPsi }}\) is a positive definite matrix, this decomposition allows to compute the square root of \({\tilde{\pmb \varPsi }}\) using the FFT algorithm twice.

There is no way to guarantee that \({\tilde{\pmb \varPsi }}\) is a positive definite matrix; however, Møller et al. (1998) and Davies et al. (2013) remark that this has rarely been a problem in practice. In the case that \({\tilde{\pmb \varPsi }}\) is not a positive definite matrix, we adopt the two methods proposed by Wood and Chan (1994):

  1. 1.

    Let assume that \(\kappa = 2^{\zeta }\) for \(\zeta > 0\). Then, we find the minimum value of \(\zeta \) such that \({\tilde{\pmb \varPsi }}\) is a positive definite matrix.

  2. 2.

    If the resulting \(\kappa \) is a very large number to be computable, then we approximate the square root of \({\tilde{\pmb \varPsi }}\) by computing the generalized square root of \(\Upsilon \).

In practice, \(\kappa \) depends on the covariance function model and the grid (Gneiting et al. 2006). Even though \(\kappa \) increases the computational burden, the simulation procedure is still exact. The use of generalized square roots solves the problem, at expenses of a not exact simulation method (see Wood and Chan 1994).

4 Simulation algorithms

Sections 2 and 3 provide the mathematical background for simulating GRFs on a regular (longitude, latitude) grid based on circulant embedding matrices. Algorithms 1 and 2 presented in this section detail the procedures to be implemented for simulation on \({\mathbb {S}}^{2}\) and \({\mathbb {S}}^{2}\times \mathbb {R}\), respectively. The suggested procedure is fast to compute and requires moderate memory storage since only blocks \(\pmb \varSigma _{i}\) (resp. \(\pmb \varPsi (i)\)) and their square roots, of size \(M \times M\) each, need to be stored and computed. FFT algorithm is used to compute the matrices \(\pmb \varLambda \) and \(\pmb \Upsilon \) by Eq. (12). The last step of both Algorithms can be calculated using FFT, generating a complex-valued vector \(\mathbf{Y }\) where the real and imaginary parts are independent. In addition, both algorithms can be parallelized. Also, a small value of \(\kappa \) means that less memory is required to compute Algorithm 2.

Some comments about the computation of \(\pmb \varLambda ^{1/2}\) and \(\pmb \Upsilon ^{1/2}\) are worth to mention. For a random field over \({\mathbb {S}}^{2}\) or \({\mathbb {S}}^{2} \times \mathbb {R},\) the matrices \(\pmb \varLambda \) and \(\pmb \Upsilon \) can be obtained through Cholesky decomposition if the underlying covariance function r is strictly positive definite on the appropriate space. In the case of a positive semi-definite covariance function, both matrices become ill-conditioned and thus generalized square roots must be used.

figure a
figure b

5 Simulations

Through this section, we assume that \(r(0) = 1\) and \(r(0,0) = 1\) for covariance functions in \({\mathbb {S}}^{2}\) and \({\mathbb {S}}^{2}\times \mathbb {R}\), respectively. For the case \({\mathbb {S}}^{2}\), we use the following covariance function models:

  1. 1.

    The exponential covariance function defined by

    $$\begin{aligned} r_{0}(\theta ) = \exp \left( -\frac{\theta }{\phi _{0}}\right) , \quad \theta \in [0,\pi ], \end{aligned}$$
    (13)

    where \(\phi _{0} > 0.\)

  2. 2.

    The generalized Cauchy model defined by

    $$\begin{aligned} r_{1}(\theta ) = \left( 1+ \left( \frac{\theta }{\phi _{1}}\right) ^{\alpha }\right) ^{-\frac{\beta }{\alpha }}, \end{aligned}$$

    where \(\alpha \in (0,1]\) and \(\phi _{1}, \beta > 0.\)

  3. 3.

    The Matérn model defined as

    $$\begin{aligned} r_{2}(\theta ) = \frac{2^{1-\nu }}{\varGamma (\nu )} \left( \frac{\theta }{\phi _{2}}\right) ^{\nu } K_{\nu }\left( \frac{\theta }{\phi _2}\right) , \end{aligned}$$

where \(\nu \in (0,1/2], \phi _{2} > 0 \), \(K_{\nu }(\cdot )\) is the Bessel function of second kind of order \(\nu \) and \(\varGamma (\cdot )\) is the Gamma function. In this simulation study, we use \(\phi _0 = 0.5243\), \(\alpha = 0.75\), \(\beta = 2.5626\), \(\phi _{1} = 1\), \(\nu = 0.25\) and \(\phi _{2} = 0.7079\). Such setting ensures that \(r_{i}(\pi /2) = 0.05\) for \(i=0,1,2\). Note that the regularity parameter is restricted to the interval (0, 1 / 2] to ensure positive definiteness on \({\mathbb {S}}^2\) (Gneiting 2013).

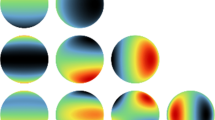
To illustrate the speed and accuracy of Algorithm 1, we compare it with Cholesky and eigenvalue decompositions, to obtain a square root of the covariance matrix (Davies et al. 2013). Because Algorithm 1 only needs the first block row of the covariance matrix, a fair comparison is made by measuring the time of the calculation after the covariance matrix was calculated. To reduce time variations, we repeat, for each grid, 25 simulations and we report the average time. Reported times are based on a server with 32 cores 2x Intel Xeon e52630v3, 2.4 GHz processor and 32 GB RAM. Tables 1, 2, and 3 show the computational time (in seconds) needed for each method to generate the GRF on each grid using the exponential, generalized Cauchy and the Matérn covariance function models, respectively. Except for the smallest grid Algorithm 1 is always faster. For the largest mesh, the eigenvalue and the Cholesky decomposition methods do not work because of storage problems. An example of a realization of the GRF using an exponential covariance function is shown in Fig. 2.

Table 1 Average time (in seconds) needed for each algorithm to be completed using an exponential covariance function model
Full size table
Table 2 Same as in Table 1 when simulating from a generalized Cauchy covariance function model
Full size table
Table 3 Same as in Table 1 when simulating from a Matérn covariance function model
Full size table

To study the simulation accuracy, we make use of variograms as defined through (1). Specifically, we estimate the variogram nonparametrically through

$$\begin{aligned} {\hat{\gamma }}(\theta ) = \frac{1}{2|N_{l}(\theta )|} \sum _{i,j,i^{\prime },j^{\prime }}(X(s_{ij}) - X(s_{i^{\prime }j^{\prime }}))^{2}{\mathbb {I}}_{N_{l}(\theta )}(s_{ij},s_{i^{\prime }j^{\prime }}),\nonumber \\ \end{aligned}$$
(14)

where \({\mathbb {I}}_{A}(x)\) is the indicator function of the set A, l is a bandwidth parameter and

$$\begin{aligned} N_{l}(\theta ) = \{(s_{1},s_{2}) \in {\mathbb {S}}^{2}: |\theta (s_{1},s_{2}) - \theta |\le l\}. \end{aligned}$$

We perform our simulations, using \(M = 30, N = 60\) (that is, \(n = 1800\)), corresponding to a \(6~\times ~6\) degree regular longitude-latitude grid on the sphere, under the three covariance models described above.

Fig. 2
figure 2

Realization of a GRF with covariance function given by Eq. (13). The parameters of the simulations are \(M=180\), \(N=360\)

Full size image
Fig. 3
figure 3

Variogram estimates for 100 simulations of different random fields with different models using circulant embedding. a–c Each realization, and d–f envelopes for simulations using Cholesky (blue envelope) and circulant embedding (red envelope). The black line is the true variogram function, gray lines are the estimated functions, while dot-dashed and dashed lines are the mean of the simulations obtained using Cholesky and Circulant Embedding, respectively. (Color figure online)

Full size image

For each simulation, Cholesky decomposition is used to compute \(\varLambda ^{1/2}\) and the variogram estimates in Eq. (14) are computed. 100 simulations have been performed for each covariance model using Algorithm 1 and using direct Cholesky decomposition for comparison. Figure 3a–c shows the estimated variogram for each simulation and the average variogram as well. Also, global rank envelopes (Myllymäki et al. 2017) were computed for the variogram under each simulation algorithms. The theoretical variogram matches the average variogram perfectly. The superimposition of the envelopes shows that our approach generates the same variability as the Cholesky decomposition.

A similar simulation study is provided for a temporal stationary and spatially isotropic random field on \({\mathbb {S}}^{2}\times {\mathbb {R}}.\) We provide a nonparametric estimate of (9) through

$$\begin{aligned} {\widehat{\gamma }}(\theta ,u)= & {} \frac{1}{2|N_{l,l^{\prime }}(\theta ,u)|} \sum _{i,j,k,i^{\prime },j^{\prime },k^{\prime }} \Big (X(s_{ij},t_{k}) - X(s_{i^{\prime }j^{\prime }},t_{k^{\prime }}) \Big )^{2} \\&{\mathbb {I}}_{N_{l,l^{\prime }}(\theta ,u)}\Big ( (s_{ij},t_k), (s_{i^{\prime }j^{\prime }},t_{k^{\prime }}) \Big ), \end{aligned}$$

where \(\theta \in [0,\pi ], u \in \mathbb {R}\) and

$$\begin{aligned}&N_{l,l^{\prime }}(\theta ,u) = \{(s_{i},t_i) \in {\mathbb {S}}^{2}\times {\mathbb {R}}, i=1,2 \; \\&\text {such that}\quad |\theta (s_{1},s_{2}) - \theta |\le l, ||t_1 - t_2| - u|\le l^{\prime } \}.\end{aligned}$$

We simulate using the spherical grid \(M = 30, N = 60\) and the temporal grid \(\tau = \{1, 3/2, \ldots , T-1/2, T \}\) where \(T = 8\), that is, \(n = 28{,}800\) and \(\kappa = 1\). We use the following family of covariance functions (Porcu et al. 2016):

$$\begin{aligned}&C_{i}(\theta ,u) = \left( \frac{1 - \delta }{1 - \delta g_{i}(u)\cos (\theta ) }\right) ^{\tau }, \quad \nonumber \\&\quad \theta \in [0,\pi ], u \in \mathbb {R}, i = 0,1 \end{aligned}$$
(15)

where \(\delta \in (0,1)\), \(\tau > 0\) and \(g_{i}(u)\) is any temporal covariance function. In this case, we consider \(g_{0}(u) = \exp (-u/c_{0})\) and \(g_{1}(u) = (1+(u/c_{1})^{2})^{-1}\). We set \(\delta = 0.95, \tau = 1/4\), \(c_{0} = 1.8951\) and \(c_{1} = 1.5250\). Such setting ensures that \(0.0470< C_{0}(\theta ,3) = C_{1}(\theta ,3) < 0.0520\) for \(\theta \in [0,\pi ]\). Following Porcu et al. (2016), Equation (15) is a positive semi-definite covariance function, and so we use SVD decomposition to compute \(\varLambda ^{1/2}\). In addition to Tables 1, 2, and 3, the number of points used in this experiment does not allow to use Cholesky decomposition, and so envelopes were not computed this time. Figure 4 shows the empirical variogram for 100 simulations. Some amount of variations is to be expected since each realization is different. Their magnitude depends on the space and timescale parameters of the covariance compared to the dimension of the simulation grid. As a proxy to the measure of variations on the empirical variograms, we will use

$$\begin{aligned} \sigma _{0}^{2} = (\varvec{1}^{T} \pmb \varPsi (0)^{-1} \varvec{1})^{-1}, \end{aligned}$$

which is the variance of the prediction of the mean of the simulation, at one time step. The values of \(\sigma _0^{2}\) are \(1/1800 \simeq 0.0006\), 0.166 and 0.117 for the independent case, \(g_{0}\) and \(g_{1}\), respectively. This shows that for the spatial margin we expect larger variations for simulations with \(g_0\) than with \(g_1\), as illustrated in Figure 4a, d. Regarding the temporal margin, we must consider that in time there is only 16 grid points, which is considerably smaller than the number of grid points in space, equal to \(30 \times 60 = 1800\). Variations could be reduced by increasing the number of temporal lags, but this is not the aim of this simulation experiment.

Finally, we use the method to simulate a spatiotemporal process with \(N = 180\), \(M = 360\), \(\tau = \{0, 0.1, \ldots , 7.9, 8.0\}\) where \(T = 8\), that is, \(n = 5,248,800\), and \(\kappa = 1\) for \(C_{0}(\theta ,u)\) and \(C_{1}(\theta ,u)\), respectively. Such realizations are shown in Movie 1 and Movie 2, respectively (Fig. 5).

Fig. 4
figure 4

Plots of the spatial margin, temporal margin and residuals with respect to the mean variogram for 100 simulated random fields. a–f The behavior of the variogram when the true covariance function is given by (15) using \(g_{0} = \exp (-u/c_{0})\) and \(g_{1} = (1+(\theta /c_{1})^{2})^{-1}\), respectively. The black line is the true variogram function, gray lines are the estimated variogram function for each simulation, and black dot-dashed points are the mean of the simulations

Full size image
Fig. 5
figure 5

Movies 1 and 2 show a realization of a spatiotemporal GRF with covariance function given by (15) using \(g_{0} = \exp (-u/c_{0})\) and \(g_{1} = (1+(\theta /c_{1})^{2})^{-1}\), respectively

Full size image

6 Discussion

Circulant embedding technique was developed on \({\mathbb {S}}^{2}\) and \({\mathbb {S}}^{2} \times {\mathbb {R}}\) for an isotropic covariance function and for a spatially isotropic and temporally stationary covariance function, respectively. All the calculations were done using the geodesic distance on the sphere. However, this method can be used with the chordal distance and axially symmetric covariance functions (Huang et al. 2012). As shown in our simulation study, this method allows to simulate seamlessly up to \(5 \times 10^6\) points in a spatiotemporal context. Traditional functional summary statistics, like the variogram, require a high computational cost, which motivates the development of different functional summary statistics or algorithms that can deal with a huge number of points.

We have several possibilities if we wish to simulate a GRF, say \(\varvec{X}\), in some specific area at some specific locations that are not on the regular grid for both \({\mathbb {S}}^{2}\) and \({\mathbb {S}}^{2}\times {\mathbb {R}}\). For example, Dietrich and Newsam (1996) consider the extended grid \(\varOmega = \varOmega _{MN} \cup {\tilde{\varOmega }},\) where \(\varOmega _{MN}\) is obtained by (2). The covariance matrix of \(\varvec{X}\) over \(\varOmega \), say \(\pmb \varSigma \), can be partitioned. Thus, the computation of \(\pmb \varSigma ^{1/2}\) can be done efficiently. Another way to simulate \(\varvec{X}\) on \({\tilde{\varOmega }}\) is by performing simulations on \(\varOmega _{MN}\) using the procedure detailed in Sect. 2. Then, perform a local conditional simulation using classical techniques Chiles (1999).

The procedures detailed in Sects. 2 and 3 should be investigated to compute different powers of the covariance function matrix. That is, for an integer k, \(\varSigma ^{k}\) can be obtained using circulant embedding by computing \(\pmb \varLambda ^{k}\) or \(\pmb \Upsilon ^{k}\). Such result is also useful to compute \(\varSigma ^{k}\) with \(k = -1\) which corresponds to the inverse of a matrix (Jun and Stein 2008). Indeed, this case is important for the computation of maximum likelihood estimators and Kriging predictors (Stein 2012).