Modified Cholesky Riemann Manifold Hamiltonian Monte Carlo: exploiting sparsity for fast sampling of high-dimensional targets

Abstract

Riemann manifold Hamiltonian Monte Carlo (RMHMC) has the potential to produce high-quality Markov chain Monte Carlo output even for very challenging target distributions. To this end, a symmetric positive definite scaling matrix for RMHMC is proposed. The scaling matrix is obtained by applying a modified Cholesky factorization to the potentially indefinite negative Hessian of the target log-density. The methodology is able to exploit the sparsity of the Hessian, stemming from conditional independence modeling assumptions, and thus admit fast implementation of RMHMC even for high-dimensional target distributions. Moreover, the methodology can exploit log-concave conditional target densities, often encountered in Bayesian hierarchical models, for faster sampling and more straightforward tuning. The proposed methodology is compared to alternatives for some challenging targets and is illustrated by applying a state-space model to real data.

1 Introduction

Markov chain Monte Carlo (MCMC) methods have by now seen widespread use for sampling from otherwise intractable distributions in statistical applications for close to three decades (Gelman et al. 2014). Still the development of new and improved MCMC methods for tackling ever more challenging sampling problems is a highly active field (see, e.g., Andrieu et al. 2010; Girolami and Calderhead 2011; Calderhead 2014; Hoffman and Gelman 2014). The contribution of the present work is a new metric tensor, deriving directly from the Hessian of the log-target density that, together with RMHMC (Girolami and Calderhead 2011), enables fast and robust sampling from target distributions with strong nonlinear dependencies. Such target distributions arise, for instance, as the joint posterior distribution of latent variables and parameters in nonlinear and/or non-Gaussian Bayesian hierarchical models.

Current MCMC strategies for Bayesian inference in such hierarchical models can informally be split into three categories (see also Betancourt and Girolami 2013, for a similar discussion): (1) variants of Gibbs sampling, (2) pseudo-marginal methods and (3) methods that update latent variables and parameters jointly. Gibbs sampling (see, e.g., Liu 2001; Robert and Casella 2004) is widely used as it is, in many cases, relatively easy to implement. However, it is well known that naive Gibbs sampling for hierarchical models, where, e.g., the latent variables are in one block and the variance parameter of the latent variables is in another block, can lead to poor mixing due to strong nonlinear dependencies across the blocks.

Pseudo-marginal methods (see, e.g., Andrieu et al. 2010; Pitt et al. 2012), on the other hand, seek to avoid such poor mixing by targeting directly the marginal posterior of the parameters (i.e., with the latent variables integrated out). However, such methods hinge on the ability to Monte Carlo simulate an unbiased, low-variance estimate of marginal posterior density of the parameters, which can often be extremely computationally demanding (Flury and Shephard 2011), or even infeasible for larger models.

Finally, methods that update the latent variables and parameters jointly are attractive in theory as they also avoid the nonlinear dependency problems of Gibbs sampling, and they do not need computationally demanding marginal density estimates. However, such methods need mechanisms for aligning the proposals with the local geometry of the target, in particular for high-dimensional problems. Currently, popular methods within this category are Metropolis-adjusted Langevin methods (see, e.g., Roberts and Stramer 2002; Girolami and Calderhead 2011; Xifara et al. 2014; Kleppe 2016) and various variants of Hamiltonian Monte Carlo (see, e.g., Duane et al. 1987; Neal 1996, 2010; Girolami and Calderhead 2011; Betancourt 2013a; Lan et al. 2015). Both use derivative information from the target log-density to guide the MCMC proposals. However, it has become clear (see, e.g., Betancourt 2013a) that methods based on first-order derivatives only [as is done in the default MCMC method in the popular Bayesian computation software Stan (Carpenter et al. 2017)] can be inefficient if one fails to take the local scaling properties of the target into account. This mirrors the relation between the method of steepest descent and Newton’s method in numerical optimization (Nocedal and Wright 1999).

Joint updating of latent variables and parameters in Bayesian hierarchical models is also the main motivation of this paper, even though the methodology is applicable for any continuous target distribution under some regularity conditions. Here a particular modified Cholesky factorization is proposed that, when applied to a potentially indefinite negative Hessian of the log-target, produces useful scaling information for RMHMC. In conjunction, RMHMC and the proposed methodology enables MCMC sampling where the proposals are far from the current configuration, and that is robust to significantly different scaling properties across the support of the target, a property often seen in Bayesian hierarchical models. It is worth noticing that applying modified negative Hessians in RMHMC (Betancourt 2013a) or when scaling MCMC proposals in general (Geweke and Tanizaki 1999, 2003; Qi and Minka 2002; Martin et al. 2012; Kleppe 2016) is not new per se. However, the proposed modified Cholesky approach is, by exploiting sparsity of the negative Hessian, computationally fast and scalable in the dimension of the target.

The exploitation of sparsity is increasingly important in the numerical linear algebra involved in modern statistical computing associated with hierarchical models, as the dimension of matrices to be factorized can easily reach $\sim$ $10^{5}$ (see, e.g., Rue 2001; Rue and Held 2005; Rue et al. 2009). The sparsity of involved Hessian matrices arises due to conditional independence assumptions used in the modeling. Examples include block-diagonal structures associated with nonlinear mixed effect regressions, banded structures for Markovian dynamic models with unobserved factors such as state-space models and less structured sparse matrices for spatial/spatial-temporal models that involve Gaussian Markov random fields (see, e.g., Lindgren et al. 2011). Currently, the integrated nested Laplace approximation (INLA) (Rue et al. 2009) is a widely used methodology for fast approximate Bayesian inference in the latent Gaussian model (LGM) subclass of Bayesian hierarchical models. Like the proposed methodology, INLA relies heavily on exploiting sparsity in order to speed up computations, and in the context of LGMs, the proposed methodology can also benefit from the fact that conditional posterior log-densities of the latents are concave. However, the proposed methodology is more general with respect to models that can be handled and in particular does not require the LGM assumption that the latent variables have a joint Gaussian prior (see Sect. 5), or the INLA assumption that the number of parameters is small.

The remainder of the paper is laid out as follows: Sect. 2 fixes notation and reviews RMHMC. Section 3 describes and discusses the proposed methodology. In Sect. 4, the proposed methodology is compared to Gibbs sampling, Euclidian metric Hamiltonian Monte Carlo (EHMC), The no-u-turn sampler (NUTS) of Stan and RMHMC based on spectral decompositions for two challenging target distributions. Section 5 describes an application to a nonlinear, non-Gaussian state-space model, and finally Section 6 provides some discussion.

2 Riemann manifold HMC

This section fixes notation and reviews RMHMC (Girolami and Calderhead 2011) in order to set the stage. Denote by $\nabla _{\mathbf {y}}$ the gradient/Jacobian operator with respect to vector $\mathbf {y}$, |A| the determinant of square matrix A, and $I_{d}$ denotes the d-dimensional identity matrix. A natural matrix norm is denoted by $\Vert \cdot \Vert$ and $\Phi$ is the standard normal cumulative distribution function.

Let $\tilde{\pi }(\mathbf {x})$ denote a density kernel associated with the target density $\pi (\mathbf {x}):\Omega \rightarrow \mathbb {R}^{+}$ where $\Omega \subseteq \mathbb {R}^{d}$. It is assumed that $\tilde{\pi }(\mathbf {x})$ is continuous and has continuous derivatives up to order 3. Moreover, let the metric tensor $G(\mathbf {x})$ be a symmetric positive definite $d\times d$ matrix for all $\mathbf {x} \in \Omega$, where $G_{i,j}(\mathbf {x}):\Omega \rightarrow \mathbb {R}$ are smooth functions for all $i,j=1,\ldots ,d$. Particular choices of $G(\mathbf {x})$ will be discussed in detail in Sect. 3.

Like for other Hamiltonian Monte Carlo methods, RMHMC relies on defining a synthetic Hamiltonian dynamical system that evolves over fictitious time $\tau$, where $\mathbf {x}$ plays the role of position variable and $\mathbf {p}\in \mathbb {R}^{d}$ is the (auxiliary) momentum variable. The total energy in the system is given by the Hamiltonian $H(\mathbf {x},\mathbf {p})$, which for RMHMC is taken to be

$$\begin{aligned} H(\mathbf {x},\mathbf {p})=-\log \tilde{\pi }(\mathbf {x})+\frac{1}{2}\log (|G(\mathbf {x})|)+\frac{1}{2}\mathbf {p}^{T}G(\mathbf {x})^{-1}\mathbf {p}. \end{aligned}$$

(1)

The time evolution of $(\mathbf {x}(\tau ),\mathbf {p}(\tau ))$ is described by Hamilton’s equations

$$\begin{aligned} \frac{\partial }{\partial \tau }\mathbf {x}(\tau )= & {} \nabla _{\mathbf {p}}H(\mathbf {x}(\tau ),\mathbf {p}(\tau ))=G(\mathbf {x}(\tau ))^{-1}\mathbf {p(\tau )}, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial }{\partial \tau }\mathbf {p}(\tau )= & {} -\nabla _{\mathbf {x}}H(\mathbf {x}(\tau ),\mathbf {p}(\tau )). \end{aligned}$$

(3)

Let $\mathbf {z}(\tau )=(\mathbf {x}(\tau )^T,\mathbf {p}(\tau )^T)^T \in \mathbb {R}^{2d}$ be the state of the system at time $\tau$ and likewise define $H(\mathbf {z}(\tau ))=H(\mathbf {x}(\tau ),\mathbf {p}(\tau ))$. Moreover, let $\varphi _{\tau }(\cdot ):\mathbb {R}\times \Omega \rightarrow \Omega$ denote the flow of $\mathbf {z}$ associated with (2, 3) so that $\mathbf {z}(r+s)=\varphi _{s}(\mathbf {z}(r))\;\forall r,s\in \mathbb {R}$ whenever $\mathbf {z}(\tau )$ solves (2, 3). The following properties of the Hamiltonian flow $\varphi _{\tau }$ can be established (see, e.g., Leimkuhler and Reich 2004)

• Energy conservation, i.e., $H(\varphi _{\tau }(\mathbf {z}))$ is constant as a function of $\tau$ for any $\mathbf {z}\in \Omega$.

• Time reversibility, i.e., the inverse of $\varphi _{\tau }$ is $\varphi _{-\tau }$ so that $\varphi _{-\tau }(\varphi _{\tau }(\mathbf {z}))=\mathbf {z}$ for any $\mathbf {z}\in \Omega$.

• $\varphi _{\tau }$ is said to be symplectic, namely for each $\tau$, $(\nabla _{\mathbf {z}}\varphi _{\tau }(\mathbf {z}))^{T}J(\nabla _{\mathbf {z}}\varphi _{\tau }(\mathbf {z}))=J$ where

  $$\begin{aligned} J=\left[ \begin{array}{cc} 0 &{}\quad I_{d}\\ -I_{d} &{}\quad 0 \end{array}\right] . \end{aligned}$$

  In particular, the symplecticity implies that $\varphi _{\tau }$ is a volume-preserving map so that the Jacobian $\nabla _{\mathbf {z}}\varphi _{\tau }(\mathbf {z})$ has unit determinant.

Based on these properties, it is relatively straightforward to verify that $\varphi _{\tau }$ preserves the Boltzmann distribution

$$\begin{aligned} \pi (\mathbf {z})=\pi (\mathbf {x},\mathbf {p})\propto \exp (-H(\mathbf {x},\mathbf {p})). \end{aligned}$$

Namely, provided that $\mathbf {z}\sim \pi (\mathbf {z})$, then also $\varphi _{\tau }(\mathbf {z})\sim \pi (\mathbf {z})$ for any $\tau \in \mathbb {R}$. Given the particular specification of the Hamiltonian (1), the Boltzmann distribution admits the target distribution $\pi (\mathbf {x})$ as the $\mathbf {x}$-marginal. To see this, observe that

$$\begin{aligned}&\int \pi (\mathbf {x},\mathbf {p})d\mathbf {p} \nonumber \\&\quad \propto \tilde{\pi }(\mathbf {x})|G(\mathbf {x})|^{-\frac{1}{2}} \int \exp \left( -\frac{1}{2}\mathbf {p}^{T}G(\mathbf {x})^{-1}\mathbf {p}\right) d\mathbf {p\nonumber }\\&\quad \propto \tilde{\pi }(\mathbf {x}). \end{aligned}$$

(4)

Granted the above constructions, an ideal MCMC algorithm for obtaining (dependent) samples $\{(\mathbf {x}_{t},\mathbf {p}_{t})\}_{t}\sim \pi (\mathbf {x},\mathbf {p})$ would be to alternate between (1) sample $\mathbf {p}_{t-1}\sim \pi (\mathbf {p}|\mathbf {x}_{t-1})=N(0,G(\mathbf {x}_{t-1}))$, and (2) compute $(\mathbf {x}_{t},\mathbf {p}^{*})=\varphi _{\tau }((\mathbf {x}_{t-1},\mathbf {p}_{t-1}))$ for some $\tau$. However, for most non-trivial target distributions and metric tensors, such an algorithm is infeasible as the corresponding $\varphi _{\tau }$s do not admit closed form expressions. Instead, RMHMC relies on approximate numerical simulation of the flow and correcting for the numerical error using an accept–reject step.

2.1 Numerical simulation of the flow and RMHMC

In order to simulate the flow numerically, the splitting method integrator of Betancourt (2013a) was used. This integrator preserves the time reversibility and symplectic nature of the flow, but only approximately preserves the total energy. Though alternative, potentially less computationally intensive, non-symplectic implementations exist (see, e.g., Lan et al. 2015), a symplectic integrator was chosen, as it admits stable and accurate numerical simulation of the flow for large d and potentially long time spans. Moreover, using a symplectic and time-reversible integrator leads to simple expressions for the acceptance probability used in the accept/reject step.

The integrator of Betancourt (2013a) for approximating $\varphi _{\varepsilon }(\mathbf {z}(\tau ))$, for some small time step $\varepsilon$, is characterized by

$$\begin{aligned}&\hat{\mathbf {p}}_{*} = \mathbf {p}(\tau )-\frac{\varepsilon }{2}\nabla _{\mathbf {x}}\left[ -\log \tilde{\pi }(\mathbf {x}(\tau ))+\frac{1}{2}\log (|G(\mathbf {x}(\tau ))|)\right] ,\nonumber \\ \end{aligned}$$

(5)

$$\begin{aligned}&\hat{\mathbf {p}}_{**} = \hat{\mathbf {p}}_{*}-\frac{\varepsilon }{2} \nabla _{\mathbf {x}}\left[ \frac{1}{2}{{\hat{\mathbf {p}}_{**}}}^{T}G(\mathbf {x}(\tau ))^{-1}\hat{\mathbf {p}}_{**}\right] , \end{aligned}$$

(6)

$$\begin{aligned} \hat{\mathbf {x}}(\tau +\varepsilon )= & {} \mathbf {x}(\tau )+\frac{\varepsilon }{2}G^{-1}(\mathbf {x}(\tau ))\hat{\mathbf {p}}_{**}\nonumber \\&+\,\frac{\varepsilon }{2}G^{-1}(\hat{\mathbf {x}}(\tau +\varepsilon ))\hat{\mathbf {p}}_{**}, \end{aligned}$$

(7)

$$\begin{aligned} \hat{\mathbf {p}}(\tau +\varepsilon )= & {} \hat{\mathbf {p}}_{**}-\frac{\varepsilon }{2}\nabla _{\mathbf {x}}H(\mathbf {x}(\tau +\varepsilon ),\hat{\mathbf {p}}_{**}), \end{aligned}$$

(8)

where $\hat{\mathbf {x}}(\tau )$ and $\hat{\mathbf {p}}(\tau )$ denote the approximations to $\mathbf {x}(\tau )$ and $\mathbf {p}(\tau )$, respectively. Applying the integrator (5–8) sequentially $l=1,2,\ldots$ times produces approximations to the flow after $\varepsilon l$ time has passed. A single transition $\mathbf {x}_{t-1}\rightarrow \mathbf {x}_{t}$ of the basic RMHMC algorithm used throughout this paper can be summarized by the steps:

• 1. Resample the momentum vector $\mathbf {p}_{t-1}\sim \pi (\mathbf {p}|\mathbf {x}_{t-1})=N(0,G(\mathbf {x}_{t-1}))$.

• 2. Sample l and $\varepsilon$, and perform l integrator steps with step size $\varepsilon$ starting at $({\mathbf {x}}_{t-1},\mathbf {p}_{t-1})$. This process results in the proposal $(\mathbf {x}_{t}^{*},\mathbf {p}_{t}^{*})$.

• 3. With probability $\min (1,\exp (-H(\mathbf {x}_{t}^{*},\mathbf {p}_{t}^{*})+H({\mathbf {x}}_{t-1},\mathbf {p}_{t-1})))$ set $\mathbf {x}_{t}=\mathbf {x}_{t}^{*}$, and with remaining probability set $\mathbf {x}_{t}=\mathbf {x}_{t-1}$.

Other, more complicated and potentially more efficient variants of the overarching RMHMC algorithm, such as algorithms choosing the number of integration steps dynamically (Betancourt 2013b, 2016), are also conceivable in this framework. Such dynamic selection is likely to be required in more automated implementations of the proposed methodology. However, the basic RMHMC method outlined above was used, as the focus of the present paper is on the particular metric tensor advocated.

It is worth noticing that (6, 7) are implicit and therefore necessitate computationally costly fixed point iterations (Leimkuhler and Reich 2004). In fact, the bulk part of the computation is spent computing the derivatives of H needed for solving (6, 7), and therefore, implementing the solution process in an efficient manner is of high importance. In the present implementation, the fixed point iterations are continued until the infinity norm of the difference between successive iterates is ${<}1.0\text {e}-6$. To meet this tolerance in the real application with $d=3087$ considered in Sect. 5, 5–6 iterations are required in (6) and 3–4 iterations are required in (7).

3 Metric tensor based on a modified Cholesky factorization

This section describes the proposed metric tensor, and thereby the implied Riemann manifold intended for RMHMC and related methods. By now, a rich literature considering the differential geometric properties of RMHMC has appeared (see, e.g., Betancourt et al. 2017). In this paper, a slightly less mathematically inclined approach is taken, and rather focus lies on some intuition and how to implement RMHMC for a general target distribution.

3.1 Metric tensor from the negative Hessian

For EHMC, a rule of thumb is that a constant G should be taken as the precision matrix of the target for near-Gaussian targets (Neal 2010). For RMHMC, several papers have argued for a metric tensor deriving from (negative) second derivative information, specifically the Fisher information matrix (Girolami and Calderhead 2011; Lan et al. 2015) or a regularized version of the negative log-target density Hessian (see, e.g., Sanz-Serna 2011; Guerrera et al. 2011; Jasra and Singh 2011). Modulus regularization, the latter fulfills the rule of thumb for EHMC and Gaussian targets. For a model where the Fisher information matrix is available, it is likely that the information matrix approach is preferable, as the information matrix is by construction positive definite. However, for a general model, the information matrix is either not available in closed form or requires substantial analytic calculations for each model instance. In the reminder of the paper, unavailable Fisher information matrix is taken as a premise for the discussion.

In deriving the metric tensor directly from the negative Hessian, computing expectations is no longer needed, but on the other hand, accounting for the fact that the negative Hessian is often not positive definite in non-negligible subsets of $\Omega$ is required. Betancourt (2013a) introduced the softmax metric, which is based on a full spectral decomposition of the negative Hessian and a subsequent regularization of the eigenvalues. This method is attractive as it retains the eigenvectors of the negative Hessian, but is very computationally demanding for large models. The present work is similar to Betancourt (2013a) in deriving G directly from the Hessian, but the computational details are different.

An additional rationale for choosing G to be a regularized approximation to the negative Hessian is as follows. It is relatively straightforward to verify that a RMHMC proposal for $\mathbf {x}$ using a single time integration step (using the generalized leapfrog integrator (Girolami and Calderhead 2011; Leimkuhler and Reich 2004, page 156)), starting at $\mathbf {x}(0)$ will have the mean

$$\begin{aligned}&E(\hat{\mathbf {x}}(\varepsilon )|\mathbf {x}(0)) \nonumber \\&\quad = \mathbf {x}(0)+\frac{\varepsilon ^{2}}{2}\left[ G^{-1}(\mathbf {x}(0))\left[ \nabla _{\mathbf {x}}\log \tilde{\pi }(\mathbf {x}(0))\right] +\,\Lambda (\mathbf {x}(0))\right] \nonumber \\&\qquad +\,O(\varepsilon ^{4}), \end{aligned}$$

(9)

where

$$\begin{aligned} \Lambda _{i}(\mathbf {x}) = \sum _{j=1}^{d}\frac{\partial }{\partial x_{j}}G_{i,j}^{-1}(\mathbf {x}),\quad i=1,\ldots ,d. \end{aligned}$$

It is seen that the $O(\varepsilon ^{2})$ term scales the gradient of the log-target with the inverse of G. Therefore, choosing G as a regularized version of the negative Hessian will turn the former part of the $O(\varepsilon ^{2})$ term into a modified Newton (numerical optimization) direction, which is known to be a well-scaled search direction in the numerical optimization literature (Nocedal and Wright 1999, Chapter 6). In fact, modulus the effect of the additional term $\Lambda$, choosing G in this manner makes time $\tau$ and the time step $\varepsilon$ effectively dimensionless (Girolami and Calderhead 2011, Page 132) as there is a unit “natural” step length (Nocedal and Wright 1999, Page 23) associated with a Newton step. In the present setup, this corresponds to $\tau =O(\sqrt{2})$ is the time needed to traverse to the mode from any region close to a mode.

It is also worth noticing that the additional term $\Lambda$ in (9) is a correction term that accounts for the non-constant curvature of the implied manifold, while retaining the correct Boltzmann distribution associated with (1). In particular, the explicit terms of (9), along with the leading term of

$$\begin{aligned} Var(\hat{\mathbf {x}}(\varepsilon )|\mathbf {x}(0))=\varepsilon ^{2}G^{-1}(\mathbf {x}(0))+O(\varepsilon ^{4}), \end{aligned}$$

are identical to the first two moments of the proposal associated with the time discretized position dependent metric Langevin diffusion (with $\pi (\mathbf {x})$ as stationary distribution due to the $\Lambda$ term in the drift) of Xifara et al. (2014, Equation 9). This observation mirrors the well-known fact that one (Euclidian metric) Metropolis-adjusted Langevin algorithm proposal is identical to the proposal of one EHMC time integration step, but in the general Riemann manifold case, this correspondence is only asymptotical as $\varepsilon \rightarrow 0$.

At this point, it is also worth contrasting a variable $G(\mathbf {x})$ to a constant G, which corresponds to EHMC. The latter is currently used (either identity, diagonal or dense matrix) in tandem with the NUTS (Hoffman and Gelman 2014) as the default sampling algorithm in the widely applied Bayesian computation software Stan (Carpenter et al. 2017). In the constant G-case, $\Lambda$ and the higher-order terms of (9) vanish, and thus the proposal means are $E(\hat{\mathbf {x}}(\varepsilon )|\mathbf {x}(0)) = \mathbf {x}(0) +\frac{\varepsilon ^{2}}{2}G^{-1}\left[ \nabla _{\mathbf {x}}\log \tilde{\pi }(\mathbf {x}(0))\right]$. For targets with close to constant curvature (i.e., in practice close to Gaussian, often seen for posteriors in non-hierarchical models), this works well and is substantially faster than the proposed methodology as explicit integrators may be employed. However, for targets exhibiting substantial variation in the curvature, such fixed scaling of the gradient may, for non-negligible subsets of $\Omega$, produce either one of:

• Too aggressive proposals, leading to inaccurate simulation of the flow and subsequent rejections of the proposals. In turn, this leads in practice to that subsets of $\Omega$ are left unexplored (Betancourt 2013a).

• Too defensive proposals, leading to slow exploration of subsets of $\Omega$. In particular, defensive proposals often lead to premature termination of the doubling of l process in NUTS-like algorithms (Betancourt 2013b), which in turn further slows down the exploration.

In Sect. 4, it is shown that Stan and EHMC may exhibit such pathologies when MCMC samples are compared to known marginals of the target. However, in practice it is difficult to determine whether such pathologies are active in a given MCMC simulation.

The remainder of this section is devoted to the particular form of metric tensor advocated here.

3.2 A smooth modified Cholesky factorization

This section develops a metric tensor in the form of a regularized approximation of the negative Hessian matrix, which is guaranteed to be positive definite. The approach is similar to the modified Cholesky factorization approach for modified Newton optimization algorithms of Gill and Murray (1974) and Gill et al. (1981). The differences amount primarily to making sure that each element of G is a smooth function of $\mathbf {x}$ so that the implied manifold is also smooth. Through a large number of numerical optimization applications, the modified Cholesky approach has proven to be a trusted and frequently used technology (Nocedal and Wright 1999), and the approximation has also served as the basis for further refinements (Schnabel and Eskow 1990, 1999). A further motivation for working with modified Cholesky factorizations, as opposed to say methods based on full spectral decompositions, is that this method can be implemented while exploiting sparsity patterns (Davis 2006) of the negative Hessian often found in statistical models (see, e.g., Rue 2001; Rue et al. 2009).

Denote by A a symmetric matrix (e.g., the negative Hessian) for which a positive definite approximation is sought. The approach for finding G takes as vantage point a square root free Cholesky factorization which produces the (LDL-)decomposition

$$\begin{aligned} \bar{L}\bar{D}\bar{L}^{T}=A. \end{aligned}$$

(10)

Here, $\bar{L}$ is unit lower triangular (i.e., 1s on the diagonal) and $\bar{D}$ is a diagonal matrix (Golub and van Loan 1996, section 4). When A is positive definite, the diagonal elements of $\bar{D}$ are positive, whereas in the indefinite case, the factorization may not exist or it may be numerically unstable and produce arbitrary large elements in $\bar{L}$ and $\bar{D}$ (Nocedal and Wright 1999, section 6.3). The insight of Gill and Murray (1974) and Gill et al. (1981) was that $\bar{D}_{j,j}$ (and consequently the resulting $\bar{L}$) can be modified online to produce a square root free Cholesky factorization $\tilde{L}D\tilde{L}=A+J$ of the symmetric positive definite matrix $A+J$, where J is a diagonal matrix with nonnegative diagonal elements. Here, $\tilde{L},D$ are equal to $\bar{L},\bar{D}$ when the original decomposition (10) is applied to $A+J$. The diagonal elements of J are chosen by the modified Cholesky algorithm to be large enough to ensure that $A+J$ is positive definite when A is indefinite. On the other hand, when A is sufficiently positive definite, J is taken to be the zero matrix by the modified Cholesky algorithm.

In the present paper, the elements of $\tilde{L}$ and D are chosen by the modified Cholesky algorithm according to the following principles

• 1. If it is known that the upper left sub-matrix $A_{1:K,1:K},$ for some $1\le K\le d$, is positive definite, then $J_{j,j}=0$ for $j=1,\ldots ,K$ and consequently $(\tilde{L}D\tilde{L}^{T})_{1:K,1:K}=A_{1:K,1:K}$. If no such information is available, then $K=0$.

• 2. The off-diagonal elements of $\tilde{L}D\tilde{L}^{T}$ are identical to those of A.

• 3. If the finalized $D_{j,j}$, $j>K$ is found to be negative during the modified Cholesky factorization, which correspond to A being negative or indefinite, $D_{j,j}$ is substituted by a smooth approximation to $\max (|D_{j,j}|,u_{j})$ where $u_{j}$ is a tunable lower bound. This approach is analogous to the flipping of signs of negative eigenvalues used in the softmax metric of Betancourt (2013a) (see also Nocedal and Wright 1999, in the context of numerical optimization), but dissimilar in that $\tilde{L}$ is only a unit determinant transformation, whereas the corresponding transformation in the softmax metric is orthonormal.

Gill and Murray (1974) and Gill et al. (1981) included a further principle for controlling numerical instabilities that can occur when $\{u_{j}\}_{j>K}$ are chosen to be close to machine precision (see, e.g., Gill et al. 1981, page 108–109). In the present context, where $\{u_{j}\}_{j>K}$ are tunable parameters that typically take substantially higher values, these numerical instabilities are not produced. A further rationale for not including the numerical stability-inducing principle of Gill and Murray (1974) and Gill et al. (1981) is that it can introduce artificially high values of $D_{j,j}$ in situations where the target exhibits substantially different scales in different directions, and consequently lead to slow exploration of the target.

Moreover, Gill and Murray (1974) and Gill et al. (1981) do not include principle 1. This principle is, when applicable, very useful in the context of RMHMC applied for hierarchical models such as LGMs where the posterior of the latent variables ($x_{1},\ldots ,x_{K}$), conditional on parameters ($x_{K+1},\dots ,x_{d})$, is log-concave, as unnecessary regularization in the form of lower bounds on $D_{j,j},\;j\le K$ is not imposed.

The modified Cholesky factorization is summarized in Algorithm 1. Steps 0–3 and 5 produce a standard $\bar{L}\bar{D}\bar{L}^{T}$, whereas step 4 is specific to the modified Cholesky factorization. Assume first that $K>0$. Then, after $j\le \min (K,d-1)$ iterations are completed, the sub-matrices $\tilde{L}_{1:j,1:j}$ and $D_{1:j,1:j}$ are not written to in the remaining iterations, and the intermediate values stored in $\tilde{L}_{j+1:d,1:d}$ and $D_{j+1:d,j+1:d}$ are not used for calculating $\tilde{L}_{1:j,1:j}$ and $D_{1:j,1:j}$. Thus, after iteration $j\le \min (K,d-1)$, $\tilde{L}_{1:j,1:j}D_{1:j,1:j}(\tilde{L}_{1:j,1:j})^{T}=A_{1:j,1:j}$, which is in agreement with principle 1. Further, principle 2 is fulfilled as the diagonal elements of A enter only in step 0,2 and the operations on $D_{k,k},\;k>j$ in step 5 are strictly additive. Therefore, increasing $D_{j,j}$ in step 4 effectively adds the difference between after and before step 5 to the diagonal of the matrix being factorized, i.e., this difference is identical to $J_{j,j}$ (Gill et al. 1981). Principle 3 follows directly from the application of the smooth absolute value function $\text {sabs}$ in step 4, as $\text {sabs}(x;u)\ge u$ for $|x|<\infty$.

In what follows, the metric tensor is taken to be of the form

$$\begin{aligned} G_{\mathbf {u}}(\mathbf {x})= & {} L(\mathbf {x})L(\mathbf {x})^{T}=\tilde{L}(\mathbf {x})D(\mathbf {x})\tilde{L}(\mathbf {x})^{T}\nonumber \\= & {} -\nabla _{\mathbf {x}}^{2}\log \tilde{\pi }(\mathbf {x})+J(\mathbf {x}), \end{aligned}$$

(11)

and

$$\begin{aligned} L(\mathbf {x}) = \tilde{L}(\mathbf {x})\;\text {diag}\left( \sqrt{D(\mathbf {x})_{1,1}},\dots ,\sqrt{D(\mathbf {x})_{d,d}}\right) \end{aligned}$$

where $\tilde{L}(\mathbf {x}),\;D(\mathbf {x})$ originate from applying Algorithm 1 to $-\nabla _{\mathbf {x}}^{2}\log \tilde{\pi }(\mathbf {x})$ with regularization parameter $\mathbf {u}$. Notice in particular that the log-determinant $\log |G_{\mathbf u}(\mathbf {x})|$ required in (1) is easily found as $\sum _{j=1}^d \log D(\mathbf {x})_{j,j}$. The resulting RMHMC method is referred to as modified Cholesky RMHMC (MCRMHMC).

3.3 Low-dimensional illustration

To illustrate the proposed methodology, consider a bivariate version of the Neal (2003) funnel distribution, given as

$$\begin{aligned} \log \tilde{\pi }(\mathbf {x})=-\frac{x_{1}^{2}}{2\exp (x_{2})}-\frac{x_{2}}{2}-\frac{x_{2}^{2}}{18}. \end{aligned}$$

(12)

Namely, $x_{1}|x_{2}\sim N(0,\exp (x_{2}))$, $x_{2}\sim N(0,3^{2})$. This model displays substantially different scales in $x_{1}$ depending on the value of $x_{2}$ and therefore illustrates how joint sampling of variables along with the variance parameter of these variables (e.g., latent field and the variance of the latent field) poses substantial problems for MCMC methods that do not adapt to local scaling properties.

Fig. 1

Illustration of the effect of modified Cholesky manifold scaling on RMHMC proposals for the bivariate funnel distribution (12). The MCRMHMC uses the tuning parameters $K=1,u_{2}=1.0,$ $\varepsilon =0.15$. Only the right half-plane is considered due to symmetry. Contours of the log-target (12) are indicated by gray lines. Dots indicate initial states $\mathbf {x}(0)$, and closed black curves indicate corresponding 95% probability regions for $\hat{\mathbf {x}}(\varepsilon )|\mathbf {x}(0)$. The negative Hessian $-\nabla _{\mathbf {x}}^{2}\log \tilde{\pi }(\mathbf {x})$ is positive definite in the region shaded with light gray. Note that corresponding 95% probability region curves for EHMC methods (such as the Stan NUTS) would have the same (elliptical) shape for all initial states

Methods based on mode and (negative inverse) Hessian at the mode (Gelman et al. 2014, Chapter 13.3) for scaling MCMC proposals are not reliable for such targets. That is, the target has mode at $\left[ 0,-4.5\right] ^{T}$, whereas $E(\mathbf {x})=\left[ 0,0\right] ^{T}$. The negative inverse Hessian at the mode variance approximation yields $\text {diag}(0.0111,9)$, whereas $Var(\mathbf {x})=\text {diag}(90.01,9).$ It is seen that the mode is shifted in the $x_{2}$-direction toward the smaller scale region (negative $x_{2}$) as smaller scales yield higher values of $p(x_{1}|x_{2})$. The variance in $x_{1}$-direction indicated by the inverse negative Hessian at the mode is also very different from $Var(x_{1})$, but one can argue that none of these variances are very informative for globally scaling MCMC proposals due to the different scales in $x_{1}$-direction determined by $x_{2}$.

Since $x_{1}|x_{2}$ is Gaussian, it is clear that $(-\nabla _{\mathbf {x}}^{2}\log \tilde{\pi }(\mathbf {x}))_{1,1}>0$, and therefore, $K=1$ is used to implement MCRMHMC for this model. Figure 1 shows 95% probability regions for single (time integration) step proposals of MCRMHMC, for a selection of initial configurations (indicated by dots) for target (12). It is seen that the metric tensor of MCRMHMC appropriately scales the proposals and aligns the proposal distributions to the local geometry of the target. The negative Hessian is positive definite only in region shaded with light gray ($x_{1}\in (\mp (\sqrt{2}/3)\exp (x_{2}/2))$), and it is seen that the negative Hessian in conjunction with the modified Cholesky factorization also produces useful scale information when the Hessian is indefinite. This latter observation is very much in line with the numerical optimization literature on modified Newton methods (Nocedal and Wright 1999, Chapter 6). Moreover, due to the relatively high degree of regularization in the $x_{2}$-direction ($u_{2}=1.0$), no problems related to close to zero eigenvalues near boundaries of the shaded region are seen (Kleppe 2016).

3.4 Discussion of the modified Cholesky factorization

Several issues related to the modified Cholesky factorization in Algorithm 1 and its application in the RMHMC context require further clarification at this point. First, it is clear that Algorithm 1 is not invariant to reordering of the variables in $\mathbf {x}$, a property that is often imposed in optimization contexts via symmetric row and column interchanges (Gill et al. 1981; Nocedal and Wright 1999). Such row and column interchanges are not applied here as they (1) introduce discontinuities in $\nabla _{\mathbf {x}}H$ which in turn makes simulating the flow associated with (2, 3) more difficult, (2) disturb any exploitation of $(K\times K$) positive definite upper left sub-matrices, (3) make exploitation of sparsity of the negative Hessian substantially less effective as the sparsity pattern of the modified Cholesky factorizations changes. Moreover, a further rationale for including such symmetric row and column interchanges is to avoid numerical instabilities associated with small finalized $D_{j,j}$s, but in the present context such problems can be tuned away by appropriate increases in $u_{j}$.

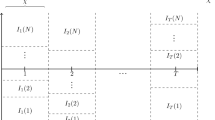
Given that Algorithm 1 is not invariant to reordering of variables, it is reasonable to ask what is an appropriate ordering of the variables? The short answer is that this is a tradeoff between exploiting any possible positive definite sub-matrices by putting the associated variables first in $\mathbf {x}$, and using orderings of the variables so that $L(\mathbf {x})$ is as sparse as possible (Davis 2006). Fortunately, in the context of hierarchical models and especially for LGMs, the means to these two objectives often align well, in the sense that the latent vector, conditional on parameters, often is both associated with a positive definite negative Hessian and (possibly after an appropriate internal reordering using, e.g., the AMD algorithm of Davis 2006, Chapter 7) has a Cholesky factorization with exploitable sparsity structure (see Rue et al. 2009, where both of these properties are exploited in the LGM context in the Laplace approximation used for calculating marginal posteriors of the parameters). Thus, assuming the above situation, a rule of thumb will be to put the latent variables first in $\mathbf {x}$ and let the last elements of $\mathbf {x}$ be the parameters. This strategy leads to the rows of $L(\mathbf {x})$ corresponding to the latent variables being sparse, and the remaining (typically few) rows corresponding to parameters being dense. To illustrate this rule of thumb procedure, Fig. 2 displays the sparsity patterns of the log-target negative Hessian and associated Cholesky factor $L(\mathbf {x})$ for the nonlinear state-space model discussed in detail in Sect. 5. The model consists of 3082 latent variables with first-order (time series) Markov structure (put first in $\mathbf {x}$), and 5 parameters (put last in $\mathbf {x}$). Due to the Markovian structure, the sub-matrix corresponding to the latent variables is tri-diagonal, and consequently the Cholesky factor has only nonzero elements on the diagonal and the first sub-diagonal. This property is retained for the Cholesky factor of the complete negative Hessian, where only the rows corresponding to the parameters are dense.

We now turn attention to a discussion of the vector of regularization parameters $\mathbf {u}$. Recall that Algorithm 1 requires $d-K$ regularization parameters, where the $\left\{ u_{j}\right\} _{j=K+1}^{d}$ should reflect the potentially very different scaling of $\left\{ x_{j}\right\} _{j=K+1}^{d}$. Including a potentially large number of regularization parameters naturally comes both with added flexibility and potential for very high-fidelity sampling when tuned properly. On the other hand, including many regularization parameters may lead to time-consuming tuning efforts, in particular since the interpretation of $\left\{ u_{j}\right\} _{j=K+1}^{d}$ is not as straightforward as in the softmax metric based on full spectral decompositions (Betancourt 2013a). Though, of course, all active regularization parameters can be set equal and thus reduce to a single regularization parameter as is the case in the softmax metric of Betancourt (2013a), in many cases this may lead to suboptimal sampling in a RMHMC context as unnecessary regularization will lead to slower and more oscillating exploration of the target.

Fig. 2

Sparsity patterns for the log-target Hessian and its associated modified Cholesky factor $L(\mathbf {x})$ for the model considered in Sect. 5. Nonzero elements are indicated by dots. In order to improve readability, only the lower right (3050:3087,3050:3087) sub-matrix is shown in both cases. The patterns repeats along the borders and (sub, sup)-diagonals in the complete matrices. For the Hessian, only 0.4% of the elements are nonzero, whereas only 0.5% of the lower triangular elements of $L(\mathbf {x})$ are nonzero

To further illustrate the advantages of this regularization scheme, consider the toy model discussed in detail in Sect. 4.2, consisting of a Gaussian zero mean AR(1) model with autocorrelation 0.999 as $\mathbf {x}_{1:d-1}$, and let $x_{d}$ be the logarithm of the innovation precision of said AR(1) model. For $d=1000$, $x_{d}=-3.0$ and $\mathbf {x}_{1:d-1}$ simulated from the true model, the eigenvalues of the negative Hessian are (in ascending order) $(-0.067,\;1.35\times 10^{-7},\;7.22\times 10^{-7},\dots )$, whereas the eigenvalues of the negative Hessian associated with $\mathbf {x}_{1:d-1}$ are $(1.35\times 10^{-7},\;7.22\times 10^{-7},\dots )$. Given that $\mathbf {x}_{1:d-1}$ is jointly Gaussian, the negative Hessian of $\mathbf {x}_{1:d-1}$ is by construction positive definite, but with smallest eigenvalue several orders of magnitude smaller than the absolute value of the single negative eigenvalue associated with $\mathbf {x}$. The modified Cholesky approach, with $K=d-1$, will exactly reproduce the precision matrix of $\mathbf {x}_{1:d-1}$ in $G_{1:d-1,1:d-1}$ and only apply regularization in the dimension corresponding to the log-precision parameter. Regularization in eigenspace, on the other hand, is likely to disturb the representation of the precision matrix of $\mathbf {x}_{1:d-1}$ in G substantially, as it is likely that regularization at least a few orders of magnitude smaller than the negative eigenvalue needs to be applied. The disturbed representation of these eigenvalues will lead to less efficient sampling as the resulting RMHMC algorithm will to a lesser degree align the Hamiltonian dynamics with the strong dependence among $\mathbf {x}_{1:d-1}$.

3.5 Implementation and tuning

The prototype large-scale code used in the reminder of this paper is implemented in C++ and uses a sparsity-exploiting implementation of Algorithm 1 that is derived from the function cs_chol of the csparse library (Davis 2006). Since the sparsity pattern of L is identical to that of a conventional sparse Cholesky factorization, the functions of the csparse library for calculating sparsity patterns, speeding up computations (elimination trees) and other numerical tasks such as triangular solves can be used directly.

The code makes use of the template capabilities of the C++ language so that a single code is maintained both for double numerics for calculating H and $\nabla _{\mathbf {p}}H$, and with automatic differentiation (AD) types for calculating $\nabla _{\mathbf {x}}H$. Specifically, the AD tool adept (Hogan 2014) is used for the latter task. Finally, in the current version, $-\nabla _{\mathbf {x}}^{2}\log \tilde{\pi }(\mathbf {x})$ is hand-coded. Future work will address the task of automatic this using AD software capable of exploiting the sparsity of the Hessian (Griewank 2000).

As discussed above, the methodology involves a number of tuning parameters, which need to be adjusted for each particular target distribution. Here, a method for such adjustment during a burn-in phase is provided, which has been used for the computations described in the reminder of the paper. Firstly, the ordering of variables and selection of K is done mainly based on insight into the problem at hand, with K latent variables typically taken first in $\mathbf {x}$, and parameters, in particular scales and correlations, put last in $\mathbf {x}$. Subsequently, too high initial guesses of K can be reduced to $j-1$ during burn-in if $D_{j,j}<0,j\le K$ at step 4 of algorithm for some $\mathbf {x}$. If such a situation is encountered during the post-burn-in phase, the MCMC simulation needs to be restarted with reduced K.

Secondly, the joint tuning of $\varepsilon$, l and $\left\{ u_{j}\right\} _{j=K+1}^{d}$ requires some more attention. The heuristic strategy adopted here is based on the following three steps:

• Select some reference $\varepsilon$ and l, e.g., $\varepsilon =0.5d^{-0.25}$ and $E(l)=\lfloor 1.5/\varepsilon \rfloor$. The expressions for $\varepsilon$, l are informed firstly by the fact that for any Gaussian target, say $N(\mu ,\Sigma )$, then $G(\mathbf {x})=\Sigma ^{-1}$ and the integrator (5–8) reduces to the conventional leap frog integrator for separable Hamiltonian systems. In this situation, it is known that an asymptotic expression for the expected acceptance probabilities for proposals independent of current configuration ($\varepsilon l\approx \pi /2)$ is $2-2\Phi (\varepsilon ^{2}\sqrt{d}/8)$ (see, e.g., Beskos et al. 2013; Mannseth et al. 2017), which when solved for $\varepsilon$ with acceptance probability 0.95 yields $\varepsilon \approx 0.7d^{-0.25}$. In practice, it is usually the case that slightly smaller values of $\varepsilon$ are needed for models with non-constant curvature and hence $\varepsilon =0.5d^{-0.25}$ is taken as a reasonable step size. Secondly, the reference expression for the number of integration steps is informed by the $l\varepsilon \approx \pi /2$ needed in the Gaussian case, whereas the connection to Newton’s method in optimization indicates $l\varepsilon \approx \sqrt{2}$.

• Tune $\left\{ u_{j}\right\} _{j=K+1}^{d}$ using the reference values of $\varepsilon$ and l, with the objective of taking $\left\{ u_{j}\right\} _{j=K+1}^{d}$ as small as possible while ensuring that the Hamiltonian is well-behaved enough for the fixed point iterations associated with (6–7) to converge. In practice, this tuning is implemented by initially setting each active $u_{j}$ to a small number, say $\exp (-20)$, to avoid unnecessary and computationally wasteful regularization, and run a number of burn-in iterations while increasing the relevant $u_{j}$ by a factor say $\exp (1)$ whenever a divergence in the fixed point iterations is encountered. Divergences in the fixed point iterations for both (6) and (7) indicate that $\Vert J(\mathbf {x},\mathbf {p})\Vert >1$ where $J(\mathbf {x},\mathbf {p})=\frac{\varepsilon }{2}\nabla _{\mathbf {x},\mathbf {p}}^{2}H(\mathbf {x},\mathbf {p})=\frac{\varepsilon }{2}\nabla _{\mathbf {x}}[G^{-1}(\mathbf {x})\mathbf {p}]$ around the sought fixed point. Moreover, for small $|D_{j,j}|/u_{j}$ (relative to say 10) and small $u_{j}$, $\frac{d}{dz}[\text {sabs}(z;u_{j})]^{-1}|_{z=D_{j,j}}$ contributes substantially to $\Vert J(\mathbf {x},\mathbf {p})\Vert$ and an ideal approach for choosing which $u_{j}$ to increase would be to measure the sensitivity of $\Vert J(\mathbf {x},\mathbf {p})\Vert$ to each of the active $u_{j}$s. Rather than computing the norm of the complete Jacobian, a heuristic approach is taken, which involves increasing $u_{\hat{j}}$ for $\hat{j}=\arg \max _{K<j\le d}|\frac{d}{dz}[\text {sabs}(z;u_{j})]^{-1}|_{z=D_{j,j}}|$ whenever a divergence is detected. It is worth noticing that, in failing to take into account the sensitivity of the negative Hessian on $\mathbf {x}$ and the fact that $D_{j,j}$ is also used in subsequent iterations in Algorithm 1, this approach is likely to be suboptimal with respect to selecting the relevant $u_{j}$. This is in particular the case when the target under consideration contains strong dependencies, and thus basing such a selection mechanism on a more direct approximation to $\Vert J(\mathbf {x},\mathbf {p})\Vert$ is scope for future research.

• Tune $\varepsilon$ and l for fixed $\left\{ u_{j}\right\} _{j=K+1}^{d}$, with the objective of controlling the acceptance probability and producing low-autocorrelation samples using standard procedures. In particular, this part of the tuning is readily automated using dynamic selection of l (Betancourt 2013b; Hoffman and Gelman 2014; Betancourt 2016) and tuning $\varepsilon$ toward a given acceptance probability, e.g., using the dual averaging algorithm of Hoffman and Gelman (2014).

4 Simulation study

To benchmark the proposed methodology against common, general purpose MCMC methods, two challenging toy models are considered. These exhibit, in the first case, strong nonlinear dependence, and in the second case, a “funnel” effect. The contending methods are chosen as they are routinely used in diverse high-dimensional applications. Throughout this section, all methods except Stan were implemented in C++ and compiled with the same compiler and with the same compiler settings. The Stan computations were done using the R interface rstan, version 2.15.1, running under R version 3.3.3. The computer used for all computations in this section was a 2014 MacBook Pro with a 2.0 GHz Intel Core i7 processor.

4.1 Twisted Gaussian mean AR(1) model

This first toy model is given by

$$\begin{aligned} x_{i}|x_{i-1},x_{d}&\sim N\left( (x_{d}^{2}-1)+0.95(x_{i-1}\right. \nonumber \\&\quad \left. -(x_{d}^{2}-1)),\frac{1-0.95^{2}}{100}\right) ,\nonumber \\&\quad \;i=2,\dots ,d-1, \end{aligned}$$

(13)

$$\begin{aligned}&x_{1}|x_{d} \sim N\left( x_{d}^{2}-1,\frac{1}{100}\right) ,\end{aligned}$$

(14)

$$\begin{aligned}&x_{d} \sim N(0,1). \end{aligned}$$

(15)

That is, conditionally on $x_{d}$, $\mathbf {x}_{1:d-1}$ is a Gaussian AR(1) process with autocorrelation 0.95, marginal standard deviation 0.1 and mean $x_{d}^{2}-1$. Similar specifications, but without autocorrelation, have previously been considered as test cases for MCMC algorithms (Haario et al. 1999; Betancourt 2013b). The model may be considered as a very simple hierarchical model, where $\mathbf {x}_{1:d-1}$ are latent variables, $x_d$ is a parameter, and no observations are modeled (in order to retain analytical marginals).

Table 1 Results for the twisted Gaussian mean AR(1) model experiment

Fig. 3

Traceplots (left), sample autocorrelation functions (center) and pdf-scaled histograms (right) of MCMC iterations for $x_{d}$ for $d=10$. Under target characterized by (13–15), $x_{d}$ has a standard Gaussian marginal distribution, which is indicated as a reference for the histograms

Fig. 4

Traceplots (left), sample autocorrelation functions (center) and pdf-scaled histograms (right) of MCMC iterations for $x_{d}$ for $d=100$. Under target characterized by (13–15), $x_{d}$ has a standard Gaussian marginal distribution, which is indicated as a reference for the histograms

Fig. 5

Traceplots (left), sample autocorrelation functions (center) and pdf-scaled histograms (right) of MCMC iterations for $x_{d}$ for $d=1000$. Under target characterized by (13–15), $x_{d}$ has a standard Gaussian marginal distribution, which is indicated as a reference for the histograms

The contending methods are chosen as they share scope with respect to generality. Specifically, Gibbs sampling, EHMC with identity mass matrix, Stan and RMHMC using full spectral decomposition (EigenRMHMC) similar to Betancourt (2013a), in addition to the proposed methodology were considered. The Gibbs sampler (Gibbs) was implemented using single dimension updates in order to mimic a situation where $\mathbf {x}_{1:d-1}$ are latent variables with intractable joint conditional posterior. Specifically, for updating $x_{i}|\mathbf {x}_{-i},\;i=1,\dots ,d-1$, exact Gaussian updates were used. For updating $x_{d}|\mathbf {x}_{1:d-1}$, a Gaussian random walk Metropolis Hastings method, with proposal standard deviation $r_{Gibbs}$ was used. Here, $r_{Gibbs}$ was tuned to produce update rates of 20–30%. Due to the slow mixing, but low per iteration computational cost, only every 1000th Gibbs iteration was recorded.

For EHMC, uniformly distributed numbers of time integration steps l were used, where the notation U(a, b) denotes uniform on the integers between a and b including a, b. In addition, the integration step sizes were jittered with ${\pm }15\%$ uniform noise (Neal 2010). The distributions for l and $\varepsilon$ were tuned to target an acceptance rate around 60% and to produce MCMC samples that were well separated in the $x_{n}$-direction.

Stan was run using 10,000 iterations, where the first 5000 burn-in iterations were used for tuning the sampler. The diag_e metric (i.e., general fixed diagonal scaling matrix) and otherwise default settings were used. The burn-in iterations are not included in the reported CPU times.

The negative Hessian of the log-density of $\mathbf {x}_{1:d-1}|x_{d}$ is positive definite, which enables $K=d-1$ for MCRMHMC. The sparsity patterns of the negative Hessian and modified Cholesky factor L are similar to those of Fig. 2 with the exception that this model only has one “parameter” with corresponding dense dth row in Hessian and L. The values for $u_{d}$ were found by successively increasing $u_{d}$ until the iterative solvers in the time integrator no longer diverged for a reference value of $\varepsilon$. Also here, uniformly distributed numbers of time integration steps and 15% jittered step sizes were used. The integration step size was taken to produce acceptance rates of around 95%, and the tuning of the distribution of l was again taken to produce high-fidelity samples for $x_{d}$.

EigenRMHMC was implemented using full spectral decomposition, followed by applying the sabs function (see Algorithm 1) with parameter u to each eigenvalue to produce a positive definite metric tensor. Other than the metric tensor, MCRMHMC and EigenRMHMC are identical. In particular u was tuned by increasing u until the iterative solvers no longer diverged and the integration step size was tuned toward acceptance rates around 95%. For both MCRMHMC and EigenRMHMC, AD was applied to the complete code (i.e., including modified Cholesky factorization- and spectral factorization codes).

The experiment was run for each of $d\in \{10,100,1000\}$. EigenRMHMC was only considered in the $d=10$ case, as very long computing times were required in higher dimensions. In all considered cases, each method was run 10 independent times. For each method except Stan, realizations from the target distribution were used as initial values for the MCMC methods, and therefore, no burn-in iterations was performed. To compare the performances of the MCMC methods, the effective sample size (ESS) calculated using the monotone sample autocorrelation estimator of Geyer (1992).

The results are presented in Table 1, and trace plots, sample autocorrelation functions and histograms for $x_{d}$ are presented in Figs. 3, 4 and 5. In addition, Table 2, upper panel, presents median (across replica) p-values from Kolmogorov–Smirnov tests with null hypothesis being that the MCMC samples representing $x_d$ have the correct standard Gaussian distribution. The Kolmogorov–Smirnov tests were only performed for MCRMHMC and Stan, as these methods produce close to iid MCMC samples.

First, it is seen from Figs. 4 and 5 that the Gibbs samplers, $d=100,1000$, even after 5 million iterations, fail to properly explore the target distributions. Also Stan appears to produce samples that do not correspond to the target distributions in all cases, as seen from Table 2, upper panel, and also quite clearly from Fig. 5.

Thus, only MCRMHMC, EHMC, and in the $d=10$ case, EigenRMHMC and Gibbs, appear to produce accurate representations of the target distribution. MCRMHMC produces uniformly highest ESSs and ESSs per computing time for $d=100,1000$, both in minimum and in mean across replica. The performance of MCRMHMC is comparable with EHMC, and better than the remaining methods in the $d=10$ case. Moreover, the relative ESS per CPU time for MCRMHMC and EHMC appears to increase with increasing dimension, with MCRMHMC being a factor 4 faster for $d=1000$. Further, visual inspection of the Hamiltonian dynamics trajectories (unreported) shows a very coherent and fast exploration of the target by the MCRMHMC, whereas the trajectories of EHMC and EigenRMHMC are oscillating due to the strong dependency structure and therefore lead to a slow exploration of the target. In the case of EigenRMHMC, a rather large regularization parameter was needed to make the fixed point iterations of integrator converge. However, this choice appears also to disturb the representation of the AR(1) model precision in the implied $G(\mathbf {x})$, which slows down the exploration.

4.2 Funnel AR(1) model

The second toy model considered is a zero mean Gaussian AR(1) model with autocorrelation 0.999 jointly with the innovation precision parameter, where the latter has a gamma(1,0.1) prior:

$$\begin{aligned} x_{i}|x_{i-1},x_{d}&\sim N\left( 0.999x_{i-1},\frac{1}{\exp (x_{d})}\right) ,\nonumber \\&\quad \;i=2,\dots ,d-1, \end{aligned}$$

(16)

$$\begin{aligned}&x_{1}| x_{d}\sim N\left( 0,\frac{1}{\exp (x_{d})(1-0.999^{2})}\right) , \end{aligned}$$

(17)

$$\begin{aligned}&\exp ( x_{d})\sim \text {gamma}(1,0.1). \end{aligned}$$

(18)

Table 2 Median (across replica) p-values for Kolmogorov–Smirnov tests with null hypothesis being that the MCMC output for the indicated marginals [after appropriate transformations in case of model (16–18)] is distributed according to the standard Gaussian distribution

This model exhibits a “funnel” nature (Neal 2003; Betancourt 2013b) as the marginal standard deviation of $x_{i},\;i=1,\dots ,d-1$ varies by two orders of magnitude between the 0.001 and 0.999 quantiles of $x_{d}$. Moreover, there are very strong dependencies among the $x_{i},\;i=1,\dots ,d-1$, which adds further complications for many MCMC methods. Thus, also this target distribution shares many of the features of the (joint latent variables and parameters) target distribution associated with hierarchical models.

Table 3 Results for the funnel AR(1) model (Eqs. 16–18) experiment

Fig. 6

Trace plots and histograms for the funnel AR(1) model experiment, $d=10$. Left column displays trace plots of $\Phi ^{-1}(F_{x_{d}}(x_{d}))$, which should have a standard Gaussian distribution. The middle column displays density-scaled histograms of $\Phi ^{-1}(F_{x_{d-1}}(x_{d-1}))$, along with a standard Gaussian density. The right column displays density-scaled histograms of $\Phi ^{-1}(F_{x_{d}}(x_{d}))$ along with a standard Gaussian density

Fig. 7

Trace plots and histograms for the funnel AR(1) model experiment, $d=100$. Left column displays trace plots of $\Phi ^{-1}(F_{x_{d}}(x_{d}))$, which should have a standard Gaussian distribution. The middle column displays density-scaled histograms of $\Phi ^{-1}(F_{x_{d-1}}(x_{d-1}))$, along with a standard Gaussian density. The right column displays density-scaled histograms of $\Phi ^{-1}(F_{x_{d}}(x_{d}))$ along with a standard Gaussian density

Fig. 8

Trace plots and histograms for the funnel AR(1) model experiment, $d=1000$. Left column displays trace plots of $\Phi ^{-1}(F_{x_{d}}(x_{d}))$, which should have a standard Gaussian distribution. The middle column displays density-scaled histograms of $\Phi ^{-1}(F_{x_{d-1}}(x_{d-1}))$, along with a standard Gaussian density. The right column displays density-scaled histograms of $\Phi ^{-1}(F_{x_{d}}(x_{d}))$ along with a standard Gaussian density

Also here, four alternatives to the proposed methodology were considered, namely Gibbs sampling, EHMC, Stan and EigenRMHMC (only for $d=10$). The model allows for a full set of univariate conditional posteriors with standard distributions, which are applied in the Gibbs sampler. For the Gibbs sampler, only every 1000th iteration was recorded due to the very slow mixing. Also here, the Euclidian metric HMC was implemented using an identity mass matrix. Due to the substantial “funnel” nature of the target, the integrator step size for EHMC must be chosen quite small to be able to explore the low-variance region of the target, which in turn leads to very high acceptance probabilities (Betancourt 2013a). However, finding a reasonable distribution for l that simultaneously leads to MCMC samples with low autocorrelation seems impossible. Also for Stan, small step sizes were imposed to account for differences in scales via setting the acceptance rate target adapt_delta equal to 0.999. For MCRMHMC, again $\mathbf {x}_{1:d-1}|x_d$ is Gaussian which suggest $K=d-1$, and the sparsity structure and tuning strategy are identical as for the model in Sect. 4.1. For EigenRMHMC, again the regularization parameter u was chosen in order to produce few divergences in the integrator fixed point iterations. However, for this u, it appears that the regularization interferes with representation of the AR(1) process precision and thus precludes finding small values of l that produce high-fidelity samples (see Sect. 3.4). The applied values of l are larger than those required for MCRMHMC. The experimental setup is otherwise identical to that of Sect. 4.1.

Due to the simple structure of the target, it is clear that the marginal cumulative distribution functions of $x_{i}$, say $F_{x_{i}}$, are easily determined from $\exp (x_{d})\sim \text {gamma}(1,0.1)$ and $\sqrt{0.1(1-0.999^{2})}x_{i}\sim t_{2}$, $i=1,\dots ,d-1$. This information can be exploited to determine the quality of the convergence for the different methods. Results from the simulation experiment for $d\in \{10,100,1000\}$ are presented in Table 3, Figs. 6, 7 and 8. In addition, the middle and lower panels of Table 2 present median p-values from Kolmogorov–Smirnov tests applied to MCMC output representing $\Phi ^{-1}(F_i(x_i)),\;i=d-1,d$. Looking first at Figs. 6–8, where the middle and right columns present density-scaled histograms of the MCMC output for a representative replica, transformed to have standard Gaussian marginal distribution via the $\Phi ^{-1}\circ F_{x_{i}}$ transformation for $x_{d-1}$ and $x_{d}$, respectively. Firstly, it is seen that EHMC, even with very large E(l) and very high acceptance rates, is unable to fully explore the target for all considered ds for this model. Secondly, this appears also to be the case for the Gibbs sampler for $d=100,1000$. Also Stan fails to explore the target fully in all cases, as seen from Table 2, middle and lower panels (and also seen clearly from Figs. 7 and  8).

From Table 3 it is seen that MCRMHMC produces high-fidelity samples in all cases, but that in the $d=10$ case, Gibbs sampling produces effective samples faster than MCRMHMC. EigenRMHMC is four orders of magnitude slower than MCRMHMC and Gibbs in the $d=10$ case.

Overall, the simulation studies for models (13–15) and (16–18) indicate that MCRMHMC is capable of producing reliable results for challenging models with diverse forms of nonlinearities and strong dependency structures. On the other hand, the contending methods may require prohibitively long MCMC chains to accurately represent the target distribution. Having said that, one can argue that the conditional Gaussian AR(1) models in (13–15) and (16–18) pose too small challenges for MCRMHMC. Therefore, also a nonlinear state-space model where the prior for the latent variables is far from jointly Gaussian is considered.

Table 4 Results for Bayesian inference for model (19–21) applied to a dataset of Eurodollar interest rates with $T=3082$

5 Application to a state-space model

In this section, a Euler–Maruyama-discretized version of the Chan et al. (1992) constant elasticity of variance model for short-term interest rates, observed with Gaussian noise, is considered. The model is fully specified by

$$\begin{aligned} y_{t}= & {} x_{t}+\sigma _{y}\eta _{t},\;\eta _{t}\sim i.i.d.\;N(0,1),\;t=1,\dots ,T, \end{aligned}$$

(19)

$$\begin{aligned} x_{t}= & {} x_{t-1}+\Delta (\alpha -\beta x_{t-1})+\sigma _{x}\sqrt{\Delta }x_{t-1}^{\gamma }\varepsilon _{t},\nonumber \\&\;\varepsilon _{t}\sim i.i.d.\;N(0,1),\;t=2,\dots ,T \end{aligned}$$

(20)

$$\begin{aligned} x_{1}\sim & {} N(0.09569,0.01^{2}), \end{aligned}$$

(21)

where $\Delta =1/252$ correspond to a daily sampling frequency for a yearly time scale. Here $\mathbf {x}_{1:T}$ models an unobserved short-term interest rate, which is observed with noise in $\mathbf {y}_{1:T}$. The prior mean of $x_{1}$ is set equal to the first observation $y_{1}$. Due to the non-constant volatility term in the $x_{t}$ process, the joint prior for $\mathbf {x}_{1:T}$ deviates strongly from being Gaussian. The model is completed with the following, (improper) prior assumptions and transformations to prepare for MCRMHMC sampling:

$$\begin{aligned} x_{T+1}&=\alpha \sim N\left( 0,\frac{100}{\Delta ^{2}}\right) ,\\ x_{T+2}&=\beta \sim N\left( \frac{1}{\Delta },\frac{100}{\Delta ^{2}}\right) ,\\ x_{T+3}&=\log (\sigma _{x}^{2})\sim \text {uniform}(-\infty ,\infty ),\\ x_{T+4}&=\gamma \sim \text {uniform}(0,\infty ),\\ x_{T+5}&=\log (\sigma _{y}^{2})\sim \text {uniform}(-\infty ,\infty ), \end{aligned}$$

(the priors for $\alpha ,\beta$ correspond to N(0, 100) priors on $\alpha ^{\prime },\beta ^{\prime }$ in the parameterization $E(x_{t}|x_{t-1})=\alpha ^{\prime }+\beta ^{\prime }x_{t-1}$). Based on experience, the dataset considered strongly disfavors values of $\gamma$ close to zero, and therefore no transformation to $\mathbb {R}$ is introduced (in order to avoid derivative calculations associated with such transformations).

The dataset considered was $T=3082$ observations of 7-day Eurodollar deposit spot rates from January 2, 1983, to February 25, 1995. The dataset has previously been used in Aït-Sahalia (1996) and, in the context of model (19–21), in Grothe et al. (2016). To implement MCRMHMC with $d=T+5$, it is first observed that even though $p(x_{1:T}|x_{T+1:T+5})$ is not uniformly log-concave, it appears that $K=T+2$ is a suitable choice since the observations are highly informative with respect to the latent process, and further that $\alpha ,\beta$ interacts only linearly with $\mathbf {x}_{1:T}$. The remaining active regularization parameters were taken to be $u_{T+3}=\exp (6.0)$, $u_{T+4}=\exp (0.0)$, $u_{T+5}=\exp (6.0)$, which were determined using the heuristic detailed in Sect. 3.5. Moreover, $l\sim U(90,180)$ and $\varepsilon =0.03$ with 15% jittering of step size were used, which correspond to integration times ranging between $\approx 2.3$ and $\approx 6.2$. The applications of MCRMHMC were done using 1100 MCMC iterations where the first 100 iterations were discarded as burn-in.

Fig. 9

Trace plots, Sample autocorrelation functions and histograms for the CEV model (19–21) based on MCRMHMC. The reported plots are for a representative replica and depicts only the 1000 post-burn-in samples

Fig. 10

Trace plots, Sample autocorrelation functions and histograms for the CEV model (19–21) based on particle Gibbs. The reported plots are for a representative replica and depicts only the 80,000 post-burn-in samples

As a reference for the proposed methodology, a Particle Gibbs sampler (Andrieu et al. 2010) using the Particle EIS filter (Scharth and Kohn 2016) with Ancestor Sampling (Lindsten et al. 2014) was used. This methodology is discussed in detail in Grothe et al. (2016) and should be regarded as a “state-of-the-art” Gibbs sampling procedure for state-space models where the latent state ($x_{1:T}$ in current notation) is updated in a single Gibbs block with close to perfect mixing. The Gibbs sampler was implemented fully in C++, and with a Gaussian random walk MH updating mechanism for $\gamma$ (with proposal standard deviation 0.025 corresponding to acceptance rates of 20–30%), but is otherwise identical to the one described in Grothe et al. (2016). A total of 100,000 Gibbs iterations were performed, with the first 20,000 iterations discarded as burn-in. All experiments in this section were run on a 2016 iMac with a 3.1 GHz Intel Core i5 processor and 8 Gb of RAM, and each experiment was repeated 10 times using different random number seeds.

It is well known that Gibbs sampling for latent variable models often lead to poor mixing for the parameters determining the volatility of the latent process. This is at least partly due to “funnel”-like nonlinear dependencies between the relevant parameters and the complete latent state. Thus, of particular interest is whether MCRMHMC is able to improve the sampling of these parameters by including both parameters and latents in the same updating block.

Results for MCRMHMC and Particle Gibbs sampling for the CEV model are presented in Table 4 and Figs. 9 and 10. It is seen from Table 4 that both methods produce close to perfect sampling for parameters $\alpha ,\;\beta ,$ $x_{1},\;x_{T}$, and indeed also the other latents (not reported). However, for $\sigma _{x},\;\gamma$ and to some degree $\sigma _{y}$, the performance of the Particle Gibbs sampler deteriorates substantially, and for $\sigma _{x}$ and $\gamma$, MCRMHMC produces effective samples at a faster rate than the Particle Gibbs (both in mean and minimum across the replica). Thus, looking at the minimum (across d dimensions) ESS per computing time, MCRMHMC performs better than Particle Gibbs, even if the Particle Gibbs updating mechanism for $\mathbf {x}_{1:T}$ is both fast and produces close to independent updates.

From Fig. 9, it is seen that the samples from MCRMHMC explores the relevant support extremely fast for all dimensions, and it appears that only a few hundred iterations would be sufficient to produce a good representation of the joint posterior. A further, interesting artifact, is that for the conditionally log-concave latents/parameters ($\mathbf {x}_{1:T+2}$), the applied distributions for l and $\varepsilon$ produce mildly negatively autocorrelated MCMC iterations, whereas there is a small positively correlated dependence for the parameters in need of regularization ($\mathbf {x}_{T+3:T+5}$). This indicates that there is potentially scope for further improvement of the tuning of the sampler, where it should be possible to align better the integration times needed to produce close to zero autocorrelation in all dimensions at the same time by a more refined selection of $\mathbf {u}_{T+3:T+5}$.

From Fig. 10, the poor performance of Particle Gibbs for the volatility-determining parameters $\sigma _{x}$, $\gamma$ is clearly seen from the trace plots and autocorrelation functions, and it is not mitigated by extremely fast mixing of the latents and the mean structure of (20). Rather, the poor mixing is an artifact of handling the model in Gibbs manner. Moreover, it is seen from the trace plots that $\sigma _{x}$ and $\gamma$ are strongly correlated a posteriori ($\text {corr}(x_{T+3},x_{T+4})\simeq 0.99$) which is handled very well by MCRMHMC, but poses problems for Gibbs sampling.

6 Discussion

This paper has presented a modified Cholesky factorization suitable for turning the log-target Hessian matrix into a suitable metric tensor for Riemann manifold Hamiltonian Monte Carlo. The resulting modified Cholesky RMHMC is shown, both in a simulation study and in a real data experiment, to be competitive, in particular for high-dimensional, challenging sampling problems. The method is in particular well suited for sampling problems where the Hessian is sparse, as unlike methods based on spectral decomposition, the modified Cholesky factorization can exploit sparsity, which holds the potential for speeding up computations drastically. Moreover, the method can exploit that the conditional posterior of some subset of the state vector $\mathbf {x}$ is log-concave, e.g., latents conditional on scale (Shephard and Pitt 1997; Rue et al. 2009), and thereby forego unnecessary regularization that slows down exploration of the target.

This paper focusses in particular on how to turn potentially indefinite Hessian matrices into useful scaling information. However, to make the proposed methodology more automatic and thus be suitable for inclusion general purpose softwares (e.g., Stan), further work is in order. In particular, the methodology would likely benefit from dynamic selection of integration times (Hoffman and Gelman 2014; Betancourt 2016) and automatic selection of integration step sizes (e.g., Hoffman and Gelman 2014). Also a more refined and automated tuning of the active regularization parameters during burn-in, which takes into account dependencies in the target, holds scope for further work. One potential such direction is to measure the sensitivity with respect to the regularization parameters on the first iterate of the fixed point iterations for (6–7). Finally, internal reordering of the variables and selection of K may also be done more automatically provided that a robust selection of the active regularization parameters is in place, as one may put the variables requiring the largest regularization parameters last in $\mathbf {x}$, whereas those not requiring regularization could be put first in $\mathbf {x}$ and K could be chosen accordingly. However, such a reordering must be weighed against the impact it has on exploitable sparsity of $L(\mathbf {x})$, and therefore, optimal, automatic selection of K and reordering of the variables for a general target also holds scope for further work.

In addition, to make the methodology more user friendly, some form of sparse automatic differentiation for calculating the Hessian of the log-target should be implemented, while retaining automatic differentiation of the Hamiltonian with respect to $\mathbf {x}$. Interestingly, these calculations are similar to the practice of differentiating Laplace approximations (for integrating out latents) with respect to parameters (Skaug and Fournier 2006; Kristensen et al. 2016). In particular, at least two avenues must be explored: (1) apply first-order backward AD to both the modified Cholesky code and the second-order AD code for the Hessian of the log-target by differentiating the internal Hessian AD computations and (2) directly compute gradient, sparse Hessian and third-order sparse derivative tensor of the log-target using AD, and combine these and the differential of the modified Cholesky factorization to find $\nabla _{\mathbf {x}}H$ similarly to Betancourt (2013a). Finding the best method among these requires further work.