Sequential Monte Carlo methods for mixtures with normalized random measures with independent increments priors

Abstract

Normalized random measures with independent increments are a general, tractable class of nonparametric prior. This paper describes sequential Monte Carlo methods for both conjugate and non-conjugate nonparametric mixture models with these priors. A simulation study is used to compare the efficiency of the different algorithms for density estimation and comparisons made with Markov chain Monte Carlo methods. The SMC methods are further illustrated by applications to dynamically fitting a nonparametric stochastic volatility model and to estimation of the marginal likelihood in a goodness-of-fit testing example.

1 Introduction

The nonparametric mixture model has become a popular method for Bayesian nonparametric density estimation and clustering. It is assumed that a random sample $y_1,\ldots ,y_n$ are independent and that

$$\begin{aligned}&y_t\vert \gamma _t\sim k(y_t\mid \gamma _t,\phi )\quad&(t=1,\ldots ,n)\\&\gamma _t \mathop {\sim }\limits ^{i.i.d.} G\quad&(t=1,\ldots ,n)\nonumber \end{aligned}$$

(1)

where $k(x\mid \gamma ,\phi )$ is a probability density function for x with parameters $\gamma$ and $\phi$, and G is a distribution which is given a nonparametric prior. The most popular instance of this model is the Dirichlet process (DP) mixture model (Escobar and West 1995) where G is given a DP prior. This prior is computationally attractive but the choice can be restrictive and so tractable generalizations have been proposed. Ishwaran and James (2001) described the construction of stick-breaking priors (such as the Poisson–Dirichlet process) and James et al. (2009) discussed inference in the class of normalized random measures with independent increments (NRMI). In all these priors, G is a discrete distribution so that

$$\begin{aligned} G=\sum _{k=1}^{\infty } w_k\delta _{\theta _k} \end{aligned}$$

(2)

where $\delta _{\theta }$ represents the Dirac measure that places measure 1 at $\theta$, $w_k>0\quad (k=1,2,\ldots )$ and $\sum _{k=1}^{\infty } w_k=1$. I will write $\theta =(\theta _1,\theta _2,\theta _3,\ldots )$ and $w=(w_1,w_2,w_3,\ldots )$. Standard choices of prior often imply that $\theta _1,\theta _2,\ldots \mathop {\sim }\limits ^{i.i.d.} H$ (whose density is h if H is continuous) and that $\theta$ and w are independent. The discreteness of G implies that the density of $y_t$ is

$$\begin{aligned} p(y_t)=\sum _{k=1}^{\infty } w_k\, k(y_t\mid \theta _k,\phi )\quad (t=1,\ldots ,n). \end{aligned}$$

The construction of methods for posterior inference in nonparametric mixture models is challenging since an infinite number of parameters is involved and the posterior is typically analytically intractable. Many Markov chain Monte Carlo (MCMC) methods have been proposed using different representations of the nonparametric prior including: Pólya urn scheme representations (Escobar and West 1995; MacEachern and Müller 1998; Neal 2000; Favaro and Teh 2013), stick-breaking representations (Ishwaran and James 2001; Papaspiliopoulos and Roberts 2008; Walker 2007; Kalli et al. 2011) and normalized Lévy process representations (Griffin and Walker 2011). These allow effective inference for a wide-range of nonparametric prior for both conjugate model (where k and H are conjugate) and non-conjugate models in static inference problems.

The increasing range of applications of nonparametric models has lead to inferential problems and modelling situations which are not well-suited to MCMC methods. For example, in economics, Bayesian nonparametric mixture models have been applied to stochastic volatility modelling (Jensen and Maheu 2010; Delatola and Griffin 2011, 2013; Jensen and Maheu 2014) for a financial time series $y_1,\ldots ,y_n$. These models assume a nonparametric mixture model for the unknown distribution $p(y_t\vert \sigma _t)$ where $\sigma _t$ is a scale parameter which evolves according to a stochastic process. More generally, Caron et al. (2008) consider the use of DP mixtures in dynamic linear models. In these models, we may be interested in making inference about the unknown distribution at different time points. These results can be used either to perform dynamic inference or to compute model comparison measures such as log predictive scores (Geisser and Eddy 1979) or h-step ahead root mean squared error. The calculation of model marginal likelihoods, used in the calculation of Bayes factors, is another inferential problem that is difficult with MCMC methods and the estimation of marginal likelihoods for nonparametric models has been particularly challenging. Basu and Chib (2003) describe a method for approximating marginal likelihood from MCMC output but this can be time-consuming. Both these problems can be addressed using sequential Monte Carlo (SMC) methods.

In this paper, I will develop SMC methods for the wide-class of NRMI mixtures. SMC methods build an approximation of the posterior with observations $y_1,\ldots ,y_t$ from an approximation of the posterior with observations $y_1,\ldots ,y_{t-1}$. These have been heavily used with non-linear state space models in dynamic problems where the posterior distribution at each time point is needed for inference and prediction. Repeated application of this process leads to the posterior conditional on the full sample $y_1,\ldots ,y_n$ and has been proposed as an alternative to MCMC methods for static problems (e.g.Chopin 2002). The model in (1) can be represented in terms of allocation variables $s_1,\ldots ,s_n$ which link the observations to the components of the mixture model by $\gamma _t=\theta _{s_t}$. This alternative representation is

$$\begin{aligned}&y_t\vert s_t=k\sim k(y_t\mid \theta _k,\phi )\quad (t=1,\ldots ,n)\\&p(s_t=k)=w_k\quad (t=1,\ldots ,n;\;k=1,2,\ldots )\nonumber . \end{aligned}$$

(3)

This representation allows the nonparametric mixture model to be written in the form of a state space model where $k(y_t\mid \theta _{s_t},\phi )$ is the observation equation, $s_t$ is the state and w, $\theta$ and $\phi$ are static parameters. SMC methods for DP mixture models were initially developed by Liu (1996) and MacEachern et al. (1999). They described sequential importance sampling methods which exploited the Pólya urn scheme representation of the DP and involved expensive numerical integrations for non-conjugate models. In practice, these algorithms can often perform poorly and lead to estimates with large variances. Fearnhead (2004) extended their algorithm to a Sampling-Importance-Resampling algorithm (also known as a particle filter). Chopin (2002) described the application of a similar algorithm to finite mixture models. There has recently been renewed interest in SMC methods for nonparametric mixture models. Ulker et al. (2010) described elaborations of the algorithm of Fearnhead (2004) and Carvalho et al. (2010) described particle learning methods.

The paper is organised as follows. Section 2 reviews some previous work on SMC methods for DP mixture models and the wide class of NRMI’s which generalise the DP. Section 3 discusses SMC methods for conjugate and non-conjugate NRMI mixtures. Section 4 briefly discusses the use of these algorithms in particle Markov chain Monte Carlo (PMCMC) samplers. Section 5 illustrates the use of these methods in a range of situations. Section 6 gives a brief discussion of the idea developed in the paper. The Online Appendix contains implementation details for two commonly used classes of NRMI’s: the DP and the normalized generalized gamma process.

2 Background

In this section, I will review the use of SMC methods for DP mixture models and the wide class of NRMI’s before considering the application of SMC methods to NRMI mixture models in Sect. 3. The notation $x_{i:j}=(x_i,\ldots ,x_j)$ will be used as shorthand for vectors.

2.1 Sequential Monte Carlo methods for Dirichlet process mixture models

Fearnhead (2004) described an SMC algorithm for the model in (1) where G is a given a DP prior to define a DP mixture model. The Pólya urn scheme representation of the DP (Blackwell and MacQueen 1973) allows us to write the model in (3) as

$$\begin{aligned}&y_t\vert s_t^{\star }=k\sim k(y_t\mid \theta ^{\star }_{k},\phi )\quad (t=1,\ldots ,n)\\&\text{ pr }\left( s^{\star }_t=k\vert s^{\star }_{1:(t-1)}\right) \nonumber \\&\quad =\left\{ \begin{array}{ll} \frac{m_{t-1,k}}{M+t-1}&{}\quad \text{ if } 1\le k\le K_{t-1}\\ \frac{M}{M+t-1} &{}\quad \text{ if } k=K_{t-1}+1 \end{array} \right. \quad (t=1,\ldots ,n)\nonumber . \end{aligned}$$

(4)

where $\theta ^{\star }_{1:K_t}$ are the distinct values of $\gamma _{1:t}$, $m_{t,k}=\sum _{k=1}^{t} {\text{ I }}\left( \gamma _k=\theta ^{\star }_{k}\right)$ and $s^{\star }_{1:t}$ are defined by $\gamma _t=\theta ^{\star }_{s^{\star }_t}$. The allocation variables $s^{\star }_{1:n}$ are just a re-numbering of $s_{1:n}$ and $\theta ^{\star }_{1:K_t}$ is a finite subset of $\theta$.

If k and H are conjugate, we say that the DP mixture model is conjugate. In this case,

$$\begin{aligned}&\text{ pr }\left( s^{\star }_t=k\vert s^{\star }_{1:(t-1)},y_{1:t}\right) \\&\quad \propto \left\{ \begin{array}{ll} m_{t-1,k} \,k^{\star }_k(y_t\mid s^{\star }_{1:(t-1)}) &{}\quad \text{ if } 1\le k\le K_{t-1}\\ M \,k^{\star }_{new}(y_t) &{}\quad \text{ if } k=K_{t-1}+1 \end{array}\right. \end{aligned}$$

where

$$\begin{aligned}&k^{\star }_k\left( y_t\vert s^{\star }_{1:(t-1)}\right) \\&\quad =\frac{\int k(y_t\vert \theta ) \prod _{\{j\vert s^{\star }_j=k, 1\le j\le t-1\}} k(y_j\mid \theta )dH(\theta )}{\int \prod _{\{j\vert s^{\star }_j=k, 1\le j\le t-1\}} k(y_j\mid \theta )dH(\theta )} \end{aligned}$$

and

$$\begin{aligned} k^{\star }_{new}(y_t)=\int k(y_t\mid \theta )dH(\theta ). \end{aligned}$$

The availability of this distribution allows an algorithm to be defined where N values $s_{1:t}^{(1)},\ldots ,s_{1:t}^{(N)}$ are sampled from $p(s_{1:t}\vert y_{1:t})$ sequentially in t. The value $s_{1:t}^{(i)}$ is called the value of $s_{1:t}$ in the ith particle and the notation $z^{(i)}$ is used generally to represent the value of z in the ith particle. The details are given in Algorithm 1. The algorithm can be very computationally efficient if $k^{\star }_k\left( y_t\mid s^{\star }_{1:(t-1)}\right)$ can be calculated using sufficient statistics (Fearnhead 2004).

The algorithm can be extended to non-conjugate mixture models in several ways. Firstly, Algorithm 1 can be directly used if $k^{\star }_k\left( y_t\mid s^{\star }_{1:(t-1)}\right)$ and $k^{\star }_{new}\left( y_t\right)$ can be efficiently approximated (using methods such as Monte Carlo integration). This typically restricts us to problems where $\theta$ is low-dimensional, often one-dimensional. Secondly, values of $\theta ^{\star }_{1:K_t}$ can be included directly in the algorithm (rather than integrating over their values) and a potential value of $\theta ^{\star \,(i)}_{K^{(i)}_{t-1}+1}$ is generated from H (which is called $\theta _{new}$ here). This algorithm is summarized in Algorithm 2. The algorithm avoids the need to approximate some integrals but introduces static parameters into the SMC sampler with the associated potential problem of particle degeneracy (where the number of distinct particles is far less than N). Chopin (2002) suggests alleviating this problem by introducing an extra Step 3) in which $\theta ^{\star \,(i)}_{j}$ for $j=1,\ldots ,K^{(i)}_t$ are updated for $i=1,\ldots ,N$ using an MCMC step such as a Metropolis-Hastings random walk step or a Gibbs step.

The problem of particle degeneracy is most pronounced in Algorithm 2 where static parameters $\theta ^{\star }_{1:K_t}$ are introduced but there is always a potential problem of particle degeneracy in all SMC methods for mixture models since $s^{\star \,(i)}_{1:t}$ act as static parameters when moving beyond the tth iteration. Ulker et al. (2010) suggest sampling a block $s^{\star }_{(t-r):t}$ conditional on $s^{\star }_{1:(t-r-1)}$ at the tth iteration to rejuvenate the particles. Alternatively $s^{\star }_{1:t}$ can be updated in Step 2.

Computational methods for approximating the marginal likelihood $p(y_1,\ldots ,y_n)$ are useful in the calculation of Bayes factors for hypothesis testing and can be used in PMCMC methods (Andrieu et al. 2010). Del Moral (2004) shows that the marginal likelihood can be a simply, unbiasedly estimated by

$$\begin{aligned} \prod _{t=1}^n \left( \frac{1}{N}\sum _{i=1}^N \xi _t^{(i)}\right) . \end{aligned}$$

which only uses the weights in an SMC sampler.

2.2 Normalized random measures with independent increment mixtures

Bayesian inference for NRMI mixtures was discussed by James et al. (2009). Only the class of homogeneous NRMI will be considered in this paper where

$$\begin{aligned} G(B) = \frac{\mu (B)}{\mu (\mathbb {Y})} \end{aligned}$$

where $\mathbb {Y}$ is the support of G and $\mu$ is a completely random measure. If the completely random measure is suitably defined, this implies that

$$\begin{aligned} \mu =\sum _{k=1}^{\infty } J_k\delta _{\theta _k} \end{aligned}$$

where $J_1,J_2,\ldots$ are the jumps of a non-Gaussian Lévy process (i.e. a subordinator) with Lévy density $\rho (x)$ and $\theta$ is independent of J. In this case, G can be written in the form of (2) with $w_1,w_2,w_3,\ldots$ defined by

$$\begin{aligned} w_k=\frac{J_k}{\sum _{l=1}^{\infty } J_l}. \end{aligned}$$

The process is well-defined if $0<\sum _{l=1}^{\infty } J_l<\infty$ which occurs if $\int _0^{\infty } \rho (x)\,dx=\infty$. The choice of $\rho (x)$ controls the rate at which the jumps of the Lévy process decay and this interpretation can be used to define a prior. Several previously proposed priors fit into this class. The Dirichlet process (Ferguson 1973) with mass parameter M arises by taking $J_1,J_2,J_3,\ldots$ to be the jumps of a gamma process which has Lévy density $\rho (x)=Mx^{-1}\exp \{-x\}$ (where $M>0$). The normalized generalized gamma (NGG) process (Lijoi et al. 2007) occurs as the normalization of a generalized gamma process (Brix 1999) which has Lévy measure $\rho (x)=\frac{M}{\Gamma (1-\gamma )}x^{-1-\gamma }\exp \{-\lambda x\}$ (where $M>0$, $0<\gamma <1$ and $\lambda >0$). A special case of this class is the Normalized Inverse Gaussian process (Lijoi et al. 2005) which occurs when $\gamma =1/2$ and $\lambda =1$.

The joint distribution of the allocations $s^{\star }_1,\ldots ,s^{\star }_t$ is particularly useful for the conjugate mixture model and can be written

$$\begin{aligned} \text{ pr }(s^{\star }_{1:t})={\text{ E }}\left[ \prod _{k=1}^{K_t} w_k^{m_{k,t}}\right] . \end{aligned}$$

This is referred to as the Exchangeable Product Partition Formula (EPPF) and it only depends on the values of $s^{\star }_{1:t}$ through $m_{1,t},\ldots ,m_{K_t,t}$ and $K_t$. Following James et al. (2009), it is useful to define the notation

$$\begin{aligned} \tau _n(u)=\int s^n \exp \{-u s\}\rho (s)\,ds \end{aligned}$$

and

$$\begin{aligned} \psi (u) = \int (1 - \exp \{-u s\})\rho (s)\,ds. \end{aligned}$$

James et al. (2009) used the identity $\int _0^{\infty } \exp \{-vx\}\,dv=\frac{1}{x}$ to show that the EPPF can be conveniently written as

$$\begin{aligned} \text{ pr }(s^{\star }_{1:t})&=\int _0^{\infty }\cdots \int _0^{\infty } {\text{ E }}\left[ \prod _{k=1}^{K_t} J_k^{m_{k,t}}\exp \left\{ -\sum _{j=1}^t v_j\sum _{l=1}^{\infty } J_l\right\} \right] \nonumber \\&\quad \times \, dv_1\cdots \,dv_t\nonumber \\&=\Gamma (t)^{-1}\int _0^{\infty }\cdots \int _0^{\infty } \exp \left\{ -\psi \left( U_t\right) \right\} \prod _{k=1}^{K_t} \tau _{m_{k,t}}\left( U_t\right) \nonumber \\&\quad \times \, dv_1\ldots dv_t \end{aligned}$$

(5)

$$\begin{aligned}&=\Gamma (t)^{-1}\int _0^{\infty } U_t^{t-1}\exp \left\{ -\psi \left( U_t\right) \right\} \prod _{k=1}^{K_t} \tau _{m_{k,t}}\left( U_t\right) \nonumber \\&\quad \times \, dU_t \end{aligned}$$

(6)

where $U_t = \sum _{j=1}^t v_j$. This result is particularly important for deriving a tractable expression for the predictive distribution of $s_t^{\star }$ which can be expressed as

$$\begin{aligned} \text{ pr }\left( s^{\star }_t\mid s^{\star }_{1:(t-1)}\right) =\frac{\text{ pr }\left( s^{\star }_{1:t}\right) }{\text{ pr }\left( s^{\star }_{1:(t-1)}\right) }. \end{aligned}$$

(7)

In the MCMC literature (Favaro and Teh 2013), it is common to sample $s^{\star }_{1:t}$ and $U_t$ from the distribution proportional to

$$\begin{aligned} U_t^{t-1}\exp \left\{ -\psi \left( U_t\right) \right\} \prod _{k=1}^{K_t} \tau _{m_{k,t}}\left( U_t\right) . \end{aligned}$$

The result in (6) implies that the marginal distribution of $\text{ pr }\left( s^{\star }_{1:t}\right)$ with this distribution is the EPPF. The Pólya urn scheme conditional on $v_{1:t}$ is

$$\begin{aligned} \text{ pr }\left( s^{\star }_t\mid s^{\star }_{1:(t-1)},v_{1:t}\right) =\frac{\text{ pr }\left( s^{\star }_{1:t}\vert U_t\right) }{\text{ pr }\left( s^{\star }_{1:(t-1)}\vert U_t\right) }. \end{aligned}$$

(8)

In the case of the NGG process, this leads to the following expression for the conditional Pólya urn scheme (full details are provided in Sect. 2 of Online Appendix)

$$\begin{aligned}&p\left( s^{\star }_t=k \mid s^{\star }_{1:(t-1)}, v_{1:t}\right) \\&\quad =\left\{ \begin{array}{ll} \frac{ m_{k,t-1}-\gamma }{ M\left( \lambda + U_t\right) ^{\gamma } +(t-1)-K_{t-1}\gamma } &{}\quad \text{ if } k \le K_{t-1}\\ \frac{ M \left( \lambda +U_t \right) ^{\gamma }}{ M\left( \lambda + U_t \right) ^{\gamma } +(t-1)-K_{t-1}\gamma } &{}\quad \text{ if } k = K_{t-1}+1 \end{array}\right. . \end{aligned}$$

If $\gamma =0$ and $\lambda =1$, this reduces to the Pólya urn scheme familiar from the DP. The probability of joining a previously defined component is proportional to $m_{k,t-1}$ which is the number of observations previously allocated to that component. The probability of joining a new cluster is proportional to M. As $\gamma$ increases, the probability of allocating to a previously defined component is reduced and the probability of allocating to a new component is increased. This leads to a prior distribution for the number of clusters in a sample of size n which becomes increasingly dispersed.

A second important result derived by James et al. (2009) is the posterior distribution of $\mu$. Let $y_1,\ldots ,y_t$ be independent and identically distributed according to G then the posterior of $\mu$ conditional on $U_t$ and $y_1,\ldots ,y_t$ is a combination of a finite set of fixed points $(\hat{J},\hat{\theta })$ where $\hat{\theta }_k$ is equal to the kth distinct value of $y_1,\ldots ,y_t$ and $p(\hat{J}_k\mid y)\propto \rho (\hat{J}_k)\hat{J}_k^{m_{k,t}}\exp \{-\hat{J}_k U_t\}$ and $(\tilde{J},\tilde{\theta })$ where $\tilde{J}$ is a Poisson process with intensity $\rho (J)\exp \{-J U_t\}$ and $\tilde{\theta }_k\mathop {\sim }\limits ^{i.i.d.} H\quad (k=1,2,\ldots )$.

3 Sequential Monte Carlo methods for NRMI mixtures

3.1 Conjugate NRMI mixtures

An SMC algorithm for conjugate NRMI mixture models could be defined by extending the methods for DP mixtures described in Sect. 2.1. An expression for the conditional distribution of $s^{\star }_t$ given $s^{\star }_{1:(t-1)}$ and $v_{1:t}$ for any NRMI mixture is available using (7). This is a finite, discrete distribution but it can be difficult to compute the probabilities of different values of $s^{\star }_t$ for many choices of $\rho (x)$. Therefore, the proposed SMC algorithm for conjugate NRMI mixtures uses the extended state $(s^{\star }_t, v_t)$ whose joint prior distribution is

$$\begin{aligned} \text{ pr }(s^{\star }_{1:t},v_{1:t})&= \Gamma (t)^{-1} \exp \left\{ -\psi \left( U_t\right) \right\} \prod _{k=1}^{K_t}\tau _{m_{k,t}}\left( U_t\right) . \end{aligned}$$

(9)

The predictive distribution of $s^{\star }_t$ and $v_t$ can be expressed as

$$\begin{aligned}&\text{ pr }\left( s^{\star }_t,v_t\mid s^{\star }_{1:(t-1)},v_{1:(t-1)}\right) \\&\quad =\text{ pr }\left( s^{\star }_t\mid s^{\star }_{1:(t-1)},v_{1:t}\right) \text{ pr }\left( v_t\mid s^{\star }_{1:(t-1)},v_{1:(t-1)}\right) \end{aligned}$$

where

$$\begin{aligned} \text{ pr }\left( v_t\mid s^{\star }_{1:(t-1)},v_{1:(t-1)}\right) =\frac{\text{ pr }\left( s^{\star }_{1:(t-1)},v_{1:t}\right) }{\text{ pr }\left( s^{\star }_{1:(t-1)},v_{1:(t-1)}\right) } \end{aligned}$$

and

$$\begin{aligned} \text{ pr }\left( s^{\star }_t\mid s^{\star }_{1:(t-1)},v_{1:t}\right) =\frac{\text{ pr }\left( s^{\star }_{1:t},v_{1:t}\right) }{\text{ pr }\left( s^{\star }_{1:(t-1)},v_{1:t}\right) }. \end{aligned}$$

(10)

It follows from (6) and (9) that

$$\begin{aligned}&\text{ pr }\left( s^{\star }_{1:(t-1)},v_{1:t}\right) \\&\quad = \sum _{s^{\star }_t=1}^{K_{t-1}+1} \text{ pr }\left( s^{\star }_{1:t},v_{1:t}\right) \\&\qquad \times \sum _{s^{\star }_t=1}^{K_{t-1}+1} {\text{ E }}\left[ \prod _{k=1}^{K_t} J_k^{m_{k,t}}\exp \left\{ -U_t\sum _{l=1}^{\infty } J_l\right\} \right] \\&\quad = {\text{ E }}\left[ \sum _{l=1}^{\infty } J_l \prod _{k=1}^{K_{t-1}} J_k^{m_{k,t-1}} \exp \left\{ -U_t\sum _{l=1}^{\infty } J_l\right\} \right] \\&\quad =-{\text{ E }}\left[ \prod _{k=1}^{K_{t-1}} J_k^{m_{k,t-1}} \frac{d}{dv_t}\exp \left\{ -U_t\sum _{l=1}^{\infty } J_l\right\} \right] \\&\quad =-\frac{d}{dv_t} \left[ \exp \left\{ -\psi \left( U_t\right) \right\} \prod _{k=1}^{K_{t-1}} \tau _{m_{k,t-1}}\left( U_t\right) \right] . \end{aligned}$$

This implies that

$$\begin{aligned}&\text{ pr }\left( v_t\mid v_{1:(t-1)},s^{\star }_{1:(t-1)}\right) \propto \\&\quad -\frac{d}{dv_t}\left[ \prod _{k=1}^{K_{t-1}} \tau _{m_{k,t-1}}\left( U_t\right) \exp \left\{ -\psi \left( U_t \right) \right\} \right] \end{aligned}$$

and, clearly, its distribution function is

$$\begin{aligned} \frac{\prod _{k=1}^{K_{t-1}} \tau _{m_{k,t-1}}\left( U_t\right) \exp \left\{ -\psi \left( U_t\right) \right\} }{\prod _{k=1}^{K_{t-1}} \tau _{m_{k,t-1}}\left( U_{t-1}\right) \exp \left\{ -\psi \left( U_t\right) \right\} }. \end{aligned}$$

Values of $v_t$ can always be simulated using inversion sampling. The conditional distribution of $s^{\star }_t$ is

$$\begin{aligned} \text{ pr }\left( s^{\star }_t=k\mid s^{\star }_{1:(t-1)},v_{1:t}\right) = \frac{\text{ pr }\left( s^{\star }_{1:(t-1)},s^{\star }_t=k,v_{1:t}\right) }{p\left( s^{\star }_{1:(t-1)},v_{1:t}\right) } \end{aligned}$$

which is a finite, discrete distribution and so can be sampled easily. The full algorithm for the conjugate NRMI mixture model is shown in Algorithm 3. Unlike the algorithm for DP mixtures described in Sect. 2.1, an adaptive resampling step is introduced which can lead to more accurate estimates from the SMC method than resampling at every step (see e.g. Del Moral et al. 2006). The resampling step uses the effective sample size (ESS) which can be loosely interpreted as the number of independent samples needed to produce estimates with the same Monte Carlo error as the SMC algorithm. In this (and subsequent algorithms), resampling only occurs if the ESS is below some threshold aN (where $a=0.5$ is a standard value used throughout the SMC literature and in this paper). Posterior summaries are calculated as weighted average so that e.g.

$$\begin{aligned} {\text{ E }}[f(s^{\star }_{1:t})\vert y_{1:t}]=\frac{\sum _{i=1}^N \xi _t^{(i)}f\left( s^{\star \,(i)}_{1:t}\right) }{\sum _{i=1}^N \xi _t^{(i)}}. \end{aligned}$$

3.2 Non-conjugate NRMI mixtures

The algorithm defined in the previous subsection exploit the conjugacy of the mixture model and some properties of NRMI priors to define an algorithm that works directly on the allocation variables $s^{\star }_{1:t}$ and $v_{1:t}$. Non-conjugate nonparametric mixture models typically lead to additional computational effort since the random measure cannot be analytically integrated from the model.

Two SMC methods for non-conjugate NRMI mixture models will be considered. The first directly extends the samplers defined in Sect. 3.1 by integrating out the sizes of the jumps, $J_1,J_2,\ldots$ and so extends Favaro and Teh (2013) from MCMC to SMC. The second extends slice sampling methods for NRMI mixture models (Griffin and Walker 2011) from MCMC to SMC.

The first method for non-conjugate mixture models is defined in the spirit of Favaro and Teh (2013) who extend Algorithm 8 of Neal (2000) for DP mixture models to NRMI mixtures by including $U_t$ as an auxiliary variable in an MCMC framework. Algorithm 2 can be extended by sampling m values $\theta _{new,1},\ldots ,\theta _{new,m}\mathop {\sim }\limits ^{i.i.d.}H_t^{\star }$ in Step 1(a) in place of $\theta _{new}$. The algorithm allows for values of $\theta _{new}$ drawn from a distribution $H_t^{\star }$ which can be chosen to reflect the centring measure H and $y_t$. The choice $H_t^{\star }=H$ leads to a simplification of the proposal distribution for $s_t^{(i)}$ and the weight. The auxiliary particle filter (Pitt and Shephard 1999) would choose $h^{\star }_t\left( \tilde{\theta }^{(i)}_k\right) \propto h\left( \tilde{\theta }^{(i)}_k\right) k\left( y_t\vert \tilde{\theta }^{(i)}_k\right)$. If this choice cannot be sampled straightforwardly then a choice of $h^{\star }_t\left( \tilde{\theta }^{(i)}_k\right)$ that approximates this distribution could be used. The full algorithm is presented as Algorithm 4. Step 1(a) can be completed using the methods developed for conjugate NRMI mixture models and the updating in Step 3 can be completed using the MCMC methods described in Favaro and Teh (2013).

The second method is based on slice sampling. Slice samplers are auxiliary variable MCMC methods which introduce latent variables that make all steps of the Gibbs sampler involve only a finite number of the distinct values of G. Griffin and Walker (2011) described two Gibbs samplers which efficiently simulate from any NRMI mixture models without truncation error. They define their Slice 1 sampler using the allocation variables $s_1,\ldots ,s_n$ (rather than $s^{\star }_1,\ldots ,s^{\star }_n$ used in the previous section) by writing the likelihood contribution $\prod _{j=1}^t w_{s_j} k(y_j\mid \theta _{s_j})$ in the following way

$$\begin{aligned} \prod _{j=1}^t {\text{ I }}(\kappa _j<J_{s_j})k(y_j\mid \theta _{s_j})\exp \left\{ -v_j\sum _{k=1}^{\infty } J_k\right\} \end{aligned}$$

(11)

where ${\text{ I }}(\cdot )$ is the indicator function. Integrating out $v_1,\ldots ,v_t$ and $\kappa _1,\ldots ,\kappa _t$ leads to the original likelihood contribution. They defined their Slice 2 sampler by writing the likelihood contribution in the alternative form

$$\begin{aligned} \prod _{j=1}^t \frac{{\text{ I }}(\kappa <\alpha _t)}{\alpha _t}J_{s_j}k(y_j\mid \theta _{s_j})\exp \left\{ -v_j\sum _{k=1}^{\infty } J_k\right\} . \end{aligned}$$

where $\alpha _t=\min \{J_{s_j}\mid j=1,\ldots ,t\}$. The introduction of the latent variables $\kappa _1,\ldots ,\kappa _t$ in Slice 1 and $\kappa$ in Slice 2 leads to likelihood contributions that only depend on a finite number of jumps and locations. A finite dimensional representation of the posterior which is suitable for simulation can be defined by integrating out all other jumps and locations.

The forms of the likelihood introduced in Slice 1 and Slice 2 are also convenient for SMC methods since the number of latent parameters grows with the number of observations. In addition to $s_t$, there are states $\kappa _t$ and $v_t$ in sampler 1 and $v_t$ in sampler 2 (with $\kappa$ treated as a static parameter). However, it is not immediately clear how to sample from their joint predictive distributions. The following method is a simple solution which works for both Slice 1 and Slice 2. In Slice 1, we firstly integrate all jumps ($\hat{J}$ and $\tilde{J}$ defined at the end of Sect. 3) from the model then the latent variable $v_t$ is sampled using the method for a conjugate model. The latent variable $\kappa _t$ is sampled by first simulating another latent variable $d_t$ according to the conditional distribution of $s_t$ given in (10). If $d_t$ is associated with a new jump then a new value is drawn from the centring distribution H and added to $\hat{\theta }$. A random variable $\nu _t$ is introduced with $\nu _t=1$ if $d_t$ is associated with a new jump and $\nu _t=0$ otherwise. The points in $\hat{J}$ are then simulated conditional on $s_{1:(t-1)}$ and $\nu _t$ and associated with $\hat{\theta }$. Finally, $\kappa _t$ is simulated from ${\text{ U }}\left( 0, \hat{J}_{d_t}\right)$. This allows us to simulate the $R_t$ jumps with size in $(\kappa _t,\infty )$ and no observation allocated. These are denoted $\tilde{J}_1,\ldots ,\tilde{J}_{R_t}$ which follow a Poisson process with intensity $\exp \left\{ -J\ U_t\right\} \rho (J)$. Values of $\tilde{\theta }$ are simulated from H and associated with each point of $\tilde{J}$. The sample of $\kappa _t$, $\hat{J}$ and $\tilde{J}$ are from the joint distribution of $\kappa _t$ and J (restricted to $(\kappa _t,\infty )$) conditional on previous values. This allows us to sample $s_t$ from its conditional distribution defined by (11).

Once all particles have been sampled, they are re-weighted. Algorithm 5 describes all necessary steps. The algorithm for Slice 1 can be easily adapted to the latent variables construction in Slice 2. Firstly, the sampling step for $\kappa _t$ in Slice 1 can be replaced by the following sampling step for $\kappa$, simulated according to $\kappa \sim {\text{ U }}(0,\beta _t)$ where $\beta _t$ is the minimum of $J_{s_1},\ldots ,J_{s_{t-1}}$ and $J_{d_t}$ and $\tilde{J}$ is now from a Poisson process with intensity $\exp \{-J U_t\}\rho (J)$ restricted to the interval $(\kappa ,\infty )$. The allocation $s_t$ is then simulated from the conditional distribution $q\left( s_t=k\right) \propto \max \left\{ J_k,\alpha _{t-1}\right\} k\left( y_t\mid \theta _k\right)$. Once all particles have been sampled, they are re-weighted. Algorithm 6 describes the full method.

3.3 Estimating hyperparameters

In many applications of Bayesian nonparametric methods, there are static parameters which we would like to infer. For example, the parameter $\phi$ in (1) is a static parameter. Similarly, there may be parameters that control the random probability measure (such as the mass parameter M in the Dirichlet process) or the centring distribution H may have parameters. The estimation of static parameters in SMC samplers is difficult. The simplest method include the parameters as extra dimensions of the particle. However, this can lead to particle degeneracy and poor estimation of the posterior distribution of the parameters. Alternatively, the parameters could be integrated out from the model. This paper adopts the alternative method of updating the static parameters using a Gibbs step when the particles are resampled.

4 Particle Markov chain Monte Carlo methods

Particle Markov chain Monte Carlo methods (Andrieu et al. 2010) use SMC methods in MCMC algorithms for static inference. There are two main cases of method: particle Metropolis–Hastings and particle Gibbs sampler. Consider the model in (4). The marginal posterior distribution of $\phi$ can be sampled using a particle Metropolis–Hastings method. An SMC method is used to unbiasedly estimate the marginal likelihood $p(y\vert \phi )$. This estimate is used in place of the actual marginal likelihood in the usual Metropolis–Hastings sampler. Algorithm 7 gives further details and Andrieu et al. (2010) show that this sampler produce draws from the posterior distribution of $\phi$.

In order to perform cluster or density estimation, a posterior sample from $s^{\star }_{1:n}$ is needed and so I will concentrate on particle Gibbs methods which can produce such a sample. Particle Gibbs methods use an SMC algorithm to jointly update states in a Gibbs sampler. In MCMC samplers where the Pólya urn scheme representation is used such as methods for conjugate mixtures and auxiliary variable samplers (Favaro and Teh 2013), particle Gibbs methods can be used to jointly update the allocations $s^{\star }_{1:n}$. In so-called conditional methods, the allocations are jointly updated conditional on some jumps of the mixing measure (e.g. Papaspiliopoulos and Roberts 2008; Kalli et al. 2011; Griffin and Walker 2011) and so particle Gibbs methods offer no benefit.

It is assumed that the posterior distribution of $s^{\star }$ and $\phi$ for the model in (4) is to be sampled using a Gibbs sampler. In particle Gibbs sampling, $\phi$ is updated from its full conditional distribution and $s^{\star }$ is updated using a conditional particle filter (Andrieu et al. 2010) which uses the current value of $s^{\star }$ as a reference trajectory in an SMC algorithm. A conditional particle filter for a conjugate NRMI mixture model is described in Algorithm 8. The first particle is the reference trajectory which is fixed in the particle filter. Otherwise, the algorithm evolves according to Algorithm 3 with new states proposed and weights calculated (for all states including the reference trajectory). This algorithm generalizes the original CPF method by allowing different re-weighting schemes (as discussed by Chopin and Singh 2013) and using adaptive resampling (e.g. Andrieu et al. 2010). The basic algorithm of Andrieu et al. (2010) arises if $a=1$ and the particles are re-weighted using multinomial sampling. A full description of extension to stratified and residual resampling schemes is given by Chopin and Singh (2013). Other variations on the conditional particle filter have been proposed including backward sampling (Whiteley 2010; Whiteley et al. 2010) and updating of the trajectory in the SMC algorithm (Lindsten et al. 2014).

5 Illustrations

5.1 Comparison of SMC methods

The infinite mixture of normals model is one of the most popular in Bayesian nonparametrics and was a natural testing ground for the methods developed in this paper. The infinite mixture model introduced by Griffin (2010) was used

$$\begin{aligned} y_t\vert \mu _t&\sim {\text{ N }}(\mu _t,a\sigma ^2),\quad t = 1,\ldots ,n \\ \mu _t&\sim G,\quad t = 1,\ldots ,n\nonumber \\ G&\sim \text{ NGG }(\gamma , 1, M, H)\nonumber \end{aligned}$$

(12)

where H is a normal distribution with mean $\mu _0$ and variance $(1-a)\sigma ^2$. Inference for the posterior distribution on the full sample $y_1,\ldots ,y_n$ only was considered to allow comparsion to MCMC methods. SMC methods for this model were applied to two datasets: the ever-popular galaxy data and the log acidity data. The data were standardized to have mean 0 and variance 1 and the parameter values $\mu _0=0$ and $\sigma =1$ were chosen. The parameter a was fixed to 0.03 for the galaxy data and 0.16 for the log acidity (these are similar to the values estimated by Griffin 2010). The data were randomly permuted and the SMC algorithms was run with 5000 particles.

Initially, a comparison of the methods for conjugate Dirichlet process mixture model was performed. The methods considered were Algorithms 3, 4 (with $m=3, 27, 250$) and 5. The number of clusters was used as the parameter of interest to calculate the effective sample size (ESS) using the method of Carpenter et al. (1999). They assumed that the posterior expectation to be approximated was $\xi ={\text{ E }}[g(\eta )\vert y_{1:t}]$ where $\eta$ were parameters of the model being estimated and that R runs of the SMC method were performed. If the estimate of $\xi$ on the rth run was $z_r=\sum _{i=1}^N \zeta _r^{(i)} g\left( \eta _r^{(i)}\right)$ and $v_r=\sum _{i=1}^N \zeta _r^{(k)} g\left( \eta _r^{(i)}\right) ^2 - z_r^2$, the ESS was estimated by $\frac{M \bar{\nu }}{\sum _{r=1}^R (z_r - \bar{z})^2}$ where $\bar{\nu }$ and $\bar{z}$ were the sample means of $\nu _1,\ldots ,\nu _R$ and $z_1,\ldots ,z_R$ respectively. The computational time was calculated using the “tic-toc” function of Matlab. The relative efficiency (R.E.) was defined to be the ratio of the ESS and the computational time and so represented the effective number of samples per unit of computational time.

Results are presented in Table 1. Algorithm 3 gave the largest ESS for both data sets and was used as a benchmark against which the non-conjugate samplers (Algorithms 4 and 5) which do not exploit the conjugacy of the mixture model were compared. Algorithm 4 outperformed Algorithm 5 for both data sets. The value of m in Algorithm 4 had a substantial effect on the ESS which was roughly three times larger for $m=250$ compared to $m=3$ and was much closer to the ESS for Algorithm 3. The effect on average computational time of increasing m is small and so large values of m are preferable.

Table 1 The ESS of estimating the posterior mean number of clusters from 5000 particles with a DP mixture model

Results for the same model with an NGG process prior with $\gamma = 0.2$ for the mixing distribution are given in Table 2. The relative performances of algorithms were broadly similar to those with a DP mixture model. Algorithm 3 outperformed both Algorithms 4 and 5 with m playing a crucial role in determining the ESS in Algorithm 4. In this case, the Algorithms 4 and 6 have similar ESS’s if m is small (in fact, Algorithm 4 with $m=9$ (results not shown) had a similar ESS to Algorithm 5 for both data sets).

Table 2 The ESS of estimating the posterior mean number of clusters from 5000 particles with an NGG process prior

The previous results assumed a fixed value for the parameter a which effects the modality and shape of the unknown density of the data. Often, we would want to estimate this parameter with the unknown density. Table 3 shows results for the DP mixture model with a given a uniform prior on (0, 1). The ESS was now calculate with the posterior mean of a as the parameter of interest. The ESS’s for the non-conjugate methods (Algorithms 4 and 6) were noticeably smaller relative to the ESS for Algorithm 3 compared to the case where a was known. Between the methods for non-conjugate mixtures, Algorithm 4 provided the largest ESS for the two data sets but only when m was large and the Algorithm 5 method provided a much ESS to Algorithm 4 than the case where a was known.

Table 3 The ESS of estimating the posterior mean number of a from 5000 particles with a DP mixture model

The parameter $\gamma$ in the NGG process prior controls the flatness of the prior on the number of clusters in a sample of size n (Lijoi et al. 2007). Larger values of $\gamma$ favouring a larger number of clusters of which many have a small size. The results with an NGG proces prior with $\gamma =0.2$ on the mixing distribution are shown in Table 4. These indicated a broadly similar pattern of results to those for the DP mixture model but with slightly larger ESS values. These results indicated that all SMC algorithms gave good performance for posterior computation and that a large value of m was preferable for Algorithm 4.

Table 4 The ESS of estimating the posterior mean number of a from 5000 particles with a NGG process prior

Table 5 shows the ESS (estimated using the initial positive sequence estimator of Geyer 1992) and computational times for three MCMC methods for NRMI mixtures: Conjugate marginalized sampler (Favaro and Teh 2013), the generalization of Neal’s algorithm 8 method to NRMI mixture models with m auxiliary variables (Favaro and Teh 2013) and the Slice 2 sampler (Griffin and Walker 2011) for non-conjugate mixture models. The results clearly showed that the MCMC methods dominated the SMC methods in terms of the relative efficiency for both conjugate and non-conjugate DP mixture model samplers. The results for posterior inference about the parameter a in the DP mixture models using MCMC are shown in Table 6. In the conjugate methods, the SMC method had a larger relative efficiencies than the MCMC method for both data sets. The SMC method was 1.9 times more efficient for the log acidity data and 4.5 times more efficient for the galaxy data. However, in non-conjugate methods, all MCMC methods were more efficient than all SMC methods for both data sets. The difference in ordering of relative efficiency performance of SMC and MCMC methods for conjugate and non-conjugate models can be explained by two factors. Firstly, the non-conjugate SMC methods have between two and three time longer computational times than MCMC methods. This difference is not explained by differences in computational complexity and is probably due to implementation issues in Matlab. Secondly, the MCMC methods have similar ESS for conjugate and non-conjugate mixture models but SMC methods have much larger ESS for conjugate than non-conjugate mixture models.

Table 5 The ESS of estimating the posterior mean number of clusters with DP mixture model using different MCMC samplers

Table 6 The ESS of estimating the posterior mean of a with DP mixture model using different MCMC samplers

Particle Gibbs methods were described in Sect. 4. Gibbs sampler with four conditional particle filters were considered with different resampling schemes: multinomial resampling, stratified resampling, adaptive multinomial resampling and adaptive stratified resampling. The methods were run on the infinite mixture model in (12) with a fixed value of a (chosen as in the SMC examples). The results are shown in Fig. 1. Some results with a small number of particles have been excluded due to biased results produced in the runs. Multinomial resampling (Andrieu et al. 2010) led to relatively low ESS’s for both data sets. Stratified resampling (Chopin and Singh 2013) led to much larger ESS’s with a roughly ten-fold increase in the ESS’s compared to multinomial resampling. The addition of an adaptive updating step led to improved ESS’s for both resampling methods. The addition of adaptive updating led to a larger improvement for stratified resampling with the log acidity data than the galaxy data. Overall, the difference between the two resampling schemes is small if adaptive updating is included. The methods with adaptive updating led to ESS’s in the thousands with only $m=5$ particles. The ESS is larger than the ESS for the conjugate methods with either SMC or MCMC. However, the computational time is much larger in the current implementation. Interestingly, the ESS’s with adaptive resampling and 60 particles were over 4000 indicating that the draws were close to independent (Tables 7, 8).

Table 7 The ESS of estimating the posterior mean number of clusters with NGG process prior using different MCMC samplers

Table 8 The ESS of estimating the posterior mean of a with an NGG process prior using different MCMC samplers

Fig. 1

The ESS and relative efficiencies of estimating the posterior mean number of clusters with DP mixture model particle Gibbs samplers with different re-weighting schemes with m particles. The schemes were: multinomial (diamond), stratified (circle), adaptive multinomial (plus), and adaptive stratified (times)

5.2 Nonparametric stochastic volatility modelling

Stochastic volatility models are a popular approach to modelling a time series of prices of a financial asset, $p_1,\ldots ,p_T$ recorded over a fixed period time (e.g. daily). In a simple stochastic volatility model, the log returns $r_t = \log p_{t+1} - \log p_t$ are modelled as

$$\begin{aligned} r_t= \beta \exp \{h_t/2\} \epsilon _t \end{aligned}$$

and

$$\begin{aligned} h_{t+1} = \mu + \phi (h_t-\mu ) + \nu _t \end{aligned}$$

where $(\epsilon _t,\nu _t)\mathop {\sim }\limits ^{ind.} F$. The variance of $r_t$ conditional on $h_t$ is $\beta ^2\psi \exp \{h_t\}$ where $\psi ={\text{ V }}[\epsilon _{t}]$ and so $h_t$, which is called the log volatility, allows the conditional variance of $r_t$ to change over time. The model is usually made identifiable by setting $\beta =1$ or $\mu =0$. The distribution G is often assumed to be a bivariate normal distribution. A non-zero correlation between $\epsilon _t$ and $\nu _t$ allows modelling of the leverage effect, which is the empirically observed difference in the effect on log volatility of negative and positive log returns of the same magnitude. Bayesian nonparametric approaches to estimating the distribution of $\epsilon _t$ are described in Jensen and Maheu (2010) and Delatola and Griffin (2011) and to the estimation of the joint distribution of $\epsilon _t$ and $\nu _t$ are described by Jensen and Maheu (2014) and Delatola and Griffin (2013). I consider a slight variation on the model of Jensen and Maheu (2014)

$$\begin{aligned}&\left. \left( \begin{array}{c}\epsilon _t\\ \nu _t\end{array} \right) \right| \mu _{t,1:2},\rho _t\\&\quad \sim {\text{ N }}\left( \left( \begin{array}{c}\mu _{t,1}\\ \mu _{t,2}\end{array} \right) , \left( \begin{array}{cc} a_1\sigma ^2 &{} \sqrt{a_1a_2}\sigma \sigma _h\rho _t\\ \sqrt{a_1a_2}\sigma \sigma _h\rho _t &{} a_2\sigma _h^2 \end{array} \right) \right) ,\\&\quad (\mu _{t,1:2},\rho _t)\sim G \end{aligned}$$

where G is a given a DP prior with $M=1$ and centring measure

$$\begin{aligned}&{\text{ N }}\left( \left( \begin{array}{c}\mu _{1}\\ \mu _{2}\end{array}\right) \left| \left( \begin{array}{c}0\\ 0\end{array}\right) , \left( \begin{array}{cc} (1-a_1)\sigma ^2 &{} \left( 1-\sqrt{a_1a_2}\right) \sigma \sigma _h\rho \\ \left( 1-\sqrt{a_1a_2}\right) \sigma \sigma _h\rho &{} (1-a_2)\sigma _h^2 \end{array} \right) \right. \right) \\&\quad \times \text{ TN }_{-1,1}(\rho \vert \mu _{\rho }, \sigma ^2_{\rho }), \end{aligned}$$

$\text{ TN }_{a,b}(\mu ,\sigma ^2)$ represents a normal distribution with mean $\mu$ and variance $\sigma ^2$ truncated to (a, b) and $0<a_1<1$ and $0<a_2<1$. The model allows different values of $\mu _1$, $\mu _2$ and $\rho$ (which is the correlation) in each component and so allows for a non-normal joint distribution of $\eta _t$ and $\nu _t$ and a non-linear leverage effect. The priors are $\phi \sim {\text{ Be }}(20, 1.5)$, $\sigma ^{-2}_h\sim {\text{ Ga }}(0.1, 0.1)$, $\sigma ^{-2}\sim {\text{ Ga }}(0.1, 0.1)$, $\mu _{\rho }\sim {\text{ U }}(-1,1)$ and $\sigma ^2_{\rho }\sim {\text{ Ga }}(1,100)$. This implies that the prior mean of $\sigma ^2_{\rho }$ is 0.01 and supports small differences in the correlation between different components.

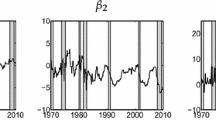
The model is non-conjugate and an extension to Algorithm 5 to allow parameter updating was used to fit data from the FTSE 100 index from 17 May 2008 to 1 May 2012, which had 1000 observations. We use $a_1=a_2=0.1$ which allows quite substantial departures from bivariate normality (see Griffin 2010, for more details in the univariate context) and 5000 particles. The posterior distribution of the log volatility and the posterior mean joint density of $\eta _t$ and $\nu _t$ are shown at three dates: 14 December 2009, 22 February 2011 and 1 May 2012 which are the 400th, 700th and 1000th (final) returns. The posterior mean densities show clear dependence and so accommodate the leverage effect. The results also show a much stronger negative dependence for more extreme values of $\epsilon _t$. However, the estimates seem to be very similar at the three different time points.

5.3 Testing a parametric model against a nonparametric alternative

The problem of testing a parametric model against a nonparametric alternative using Bayesian methods has received some attention in the literature. Carota and Parmigiani (1996) use a DP based (rather than mixture of DP based) method whereas Berger and Guglielmi (2001) uses a method based on Polya trees. Consistency issue are considered by Dass and Lee (2004). More recently, McVinish et al. (2009) have proposed a method using mixtures of triangular distributions and considered its consistency (Fig. 2).

Fig. 2

Estimated return distribution and log volatility at three dates: 14/12/2009, 22/2/2011 and 1/5/2012. The top row shows the filtered median log volatility (solid line) with 95 % credible interval estimated at each date and the bottom row shows the filtered mean return distribution at each date

The “schoolgirls” data set of the DPpackage in R records the heights of 20 girls at ages 6–10 (in years). We consider the problem of specifying a random effects model which has the form

$$\begin{aligned} y_{i,t}= & {} \beta _0 + (t-\bar{t})\beta _1 + \gamma _i + \epsilon _{i,t},\\ i= & {} 1,\ldots ,n,\quad t=1,\ldots ,T \end{aligned}$$

where t is the age, $\bar{t}=8$ is the average age, $\gamma _i\sim F$ is a random effect and $\epsilon _{i,t}\sim {\text{ N }}(0,\sigma ^2)$. A parametric specification where F is a normal distribution with mean zero and variance $\sigma _{\gamma }^2$ is tested against a nonparametric alternative where

$$\begin{aligned} \gamma _i\sim {\text{ N }}\left( \mu _i,a\sigma ^2_{\gamma }\right) ,\quad \mu _i\sim G,\quad G\sim {\text{ DP }}(MH) \end{aligned}$$

and H is a normal distribution with mean 0 and variance $(1-a)\sigma ^2_{\gamma }$. The parameter a is set equal to 0.03 to allow for a wide-range of distributions of the random effects. The other priors are common to both models: $\beta =(\beta _0,\beta _1)^T\sim {\text{ N }}(0,100^2)$, $\sigma ^{-2}\sim {\text{ Ga }}(0.01, 0.01)$ and $\sigma ^{-2}_{\gamma }\sim {\text{ Ga }}(0.01, 0.01)$. The posterior mean of F for the nonparametric model is shown in Fig. 3 and indicates a departure from a normal distribution. To test the strength of this effect, we run Algorithm 3 to calculate the log marginal likelihood for the nonparametric model which is estimated to be $-219.8$. The log marginal likelihood for the parametric model can be estimated using a SMC giving a value of $-218.5$. This implies that the Bayes factor in favour of the parametric model is $e^{1.3} = 3.7$ which represents weak evidence against the nonparametric model.

Fig. 3

The posterior mean distribution of the random effects in the nonparametric model applied to the “schoolgirl” data set

6 Discussion

There has been little work on the use of SMC methods for fitting nonparametric mixture models which are not based on Dirichlet processes. This paper has described SMC methods for the wide-class of NRMI mixture models with both conjugate and non-conjugate structure. These can be used to estimate nonparametric mixture models sequentially, estimate marginal likelihoods or as components in particle Gibbs samplers. The results suggest that SMC methods work well in conjugate mixture models. In particular, SMC methods can outperform Gibbs samplers for parameter estimation problems in static inference problems. I have considered two methods for non-conjugate mixture models: one based on slice sampling (Algorithms 5 and 6) and one based on marginalization (Algorithm 4). The marginalization method tends to outperform the slice sampling methods. Both methods provide useful inference in the problems considered. The number of auxiliary variables (m) plays an important role in the sampler. Suitable choice will depend on the problem at hand but large values of m (in the hundreds) seem appropriate if values from $H^{\star }_t$ can be generated cheaply. Particle Gibbs methods are an interesting approach for mixture models since these can jointly update $s^{\star }_1,\ldots ,s^{\star }_n$ in marginalized samplers. The results in this paper indicate that the resampling mechanism can have a substantial effect on the performance of the algorithm. Adaptive resampling methods perform best in the examples considered in this paper. These can produce relatively uncorrelated samples with small numbers of particles (an ESS over 1000 with five particles in both examples) and near independent samples with a relatively small number of particles. This is encouraging and is a promising direction for future research. The NRMI class of priors underlies recently developed time-series and spatial nonparametric priors (see e.g. Griffin et al. 2013; Chen et al. 2013; Lijoi et al. 2014; Bassetti et al. 2014) and extensions of SMC methods to these models will be an area of future research.