Machine-Learning-Based Numerical Solution for Low and Lou’s Nonlinear Force-Free Field Equilibria

Abstract

Low and Lou (Astrophys. J. 352, 343, 1990) presented a family of nonlinear force-free magnetic fields that have established themselves as the gold standard for extrapolating force-free magnetic fields in solar physics. Building upon this important work, our study introduces a novel grid-free machine-learning-based method to effectively solve the equilibria proposed by Low and Lou. Through extensive numerical experiments, our results unequivocally demonstrate the efficient capability of the machine-learning algorithm in deriving numerical solutions for Low and Lou’s equilibria. Furthermore, we explore the opportunities and challenges of applying artificial-intelligence technology to real observed solar active regions.

1 Introduction

Knowledge of the magnetic-field structure is significant for understanding solar phenomena on the Sun, for example coronal mass ejections, flares, and filaments. However, it is difficult to measure the solar magnetic field with high accuracy except in the photosphere. Therefore, there are several models of magnetic-field extrapolation that are proposed, such as potential fields (PF) (Schmidt 1964; Altschuler and Newkirk 1969), linear force-free fields (LFFF) (Nakagawa and Raadu 1972; Chiu and Hilton 1977), and nonlinear force-free fields (NLFFF) (Sakurai 1989; Neukirch 2005; Wiegelmann and Sakurai 2021).

The PF model is charaterized by

$$ \begin{aligned} \Delta \phi & = 0 \ \ \text{in} \ \Omega \\ \frac{{\partial \phi }}{{\partial n}} & = {B_{z_{0}}} \ \ \text{on} \ \partial \Omega \end{aligned} \ \ , $$

(1)

where ${\boldsymbol{B}} = {\boldsymbol{B}}\left (x,y,z\right ) = \left (B_{x},B_{y},B_{z} \right )$ is the field, $\Omega$ is the open space above the solar surface, and $\partial \Omega$ is its boundary. Finally, the magnetic field can be formulated as ${\boldsymbol {B}} = \nabla \phi$.

The solution of Equation 1 is unique. The solution is a good approximation of the large-scale topology of a solar active region, but it is not suitable for a small-scale topology such as that discussed by Aulanier, Pariat, and Démoulin (2005).

The force-free field model can be written as

$$ \begin{aligned} \nabla \times {\boldsymbol {B}} & = \alpha {\boldsymbol {B}} \ \ \text{in} \ \Omega \\ \nabla \cdot {\boldsymbol {B}} & = 0 \ \ \text{in} \ \Omega \\ {\boldsymbol {B}} & = {\boldsymbol{B_{0}}} \ \ \text{on} \ \partial \Omega \end{aligned} \ \ , $$

(2)

where ${\boldsymbol{B_{0}}}$ is the observed magnetic field in the photosphere. When $\alpha$ is a constant, Equation 2 represents the LFFF model, which can be solved analytically using the Green’s function method or the Fourier method, as discussed by Wiegelmann and Sakurai (2021). In particular, when $\alpha = 0$, Equation 2 describes the PF model, which can also be solved using these analytical methods.

In the LFFF model, $\alpha$ is a global free parameter. As observed by Démoulin et al. (2002) and Valori et al. (2010), a large $\alpha$ may lead to overestimation, while a small $\alpha$ may lead to under-estimation. When the assumption of a constant $\alpha$ is relaxed, Equation 2 becomes the NLFFF model, where $\alpha$ is a spatially dependent scalar function. With a variable $\alpha$, a closed-form solution to Equation 2 is no longer feasible. This has prompted the development of various numerical algorithms to solve Equation 2. These numerical algorithms include the works by Grad and Rubin (1958), Nakagawa (1974), Mikić and McClymont (1994), Amari et al. (1997), Wheatland, Sturrock, and Roumeliotis (2000), Yan and Sakurai (2000), Régnier, Amari, and Kersalé (2002), Wiegelmann and Neukirch (2003), Wiegelmann, Inhester, and Sakurai (2006), and Yan and Li (2006).

However, without ground-truth 3D magnetic fields, the performance, stability, and accuracy of these algorithms cannot be objectively evaluated. Fortunately, assuming an axially symmetric configuration of the magnetic field, i.e. $\frac{\partial }{{\partial \phi }} = 0$ in the spherical coordinate system $(r,\theta ,\phi )$, Low and Lou provided a set of separable and semi-analytical solutions to Equation 2:

$$ {\boldsymbol {B}} = \frac{{{B_{0}}}}{{{R^{n + 2}}}}\left [ { - \frac{{{\mathrm{d}}F}}{{\mathrm{d}\mu }}\widehat {{\boldsymbol {r}}} + \frac{{nF}}{{{{\left ( {1 - {\mu ^{2}}} \right )}^{\frac{1}{2}}}}} \widehat {{\boldsymbol{\theta}}} + \frac{{\eta A}}{{{{\left ( {1 - {\mu ^{2}}} \right )}^{\frac{1}{2}}}}} \widehat { {\boldsymbol{\phi}}} } \right ] , $$

(3)

where

$$ A = \textstyle\begin{cases} {{F^{1+{\frac{1}{n}}}},}&{n = 1} \\ {F{{\left | F \right |}^{\frac{1}{n}}},}&{n \geqslant 3} \end{cases} $$

(4)

and $F$ satisfies

$$ \left ( {1 - {\mu ^{2}}} \right ) \frac{{{\mathrm{d}^{2}}F}}{{\mathrm{d}{\mu ^{2}}}} + n\left ( {n + 1} \right )F + C = 0, $$

(5)

where

$$ C = \textstyle\begin{cases} {\left ( {1 + \frac{1}{n}} \right ){a^{2}}{F^{1 + \frac{2}{n}}},}&{n = 1} \\ {\left ( {1 + \frac{1}{n}} \right ){a^{2}}F{\left ( {{F^{2}}} \right )^{ \frac{1}{n}}},}&{n \geqslant 3.} \end{cases} $$

(6)

For a comprehensive and in-depth analysis of the mathematical framework of Low and Lou’s equilibria, please consult Appendix A for detailed discussions.

In fact, $n = 1$ and $n \ge 3$ can be generalized, as $\frac{2}{n}$ is positive and not necessarily an integer in both Equations 4 and 6. For example, $n = \frac{4}{3}$, i.e. $\frac{2}{n} = \frac{3}{2}$ is not a positive integer, but $n = \frac{2}{9}$, i.e. $\frac{2}{n} = 9$ is a positive integer.

It is to be observed that ${F^{1 + \frac{2}{n}}}$ is not always equal to $F{\left ( {{F^{2}}} \right )^{\frac{1}{n}}}$. For example, ${F^{\left ( {1 + \frac{2}{n}} \right )}} > 0$, but $F{\left ( {{F^{2}}} \right )^{\frac{1}{n}}} < 0$ when $F = -0.1$, $n = \frac{2}{9}$. In this article, we take $n = 5$, 3, 1.5, 1, 0.9, 0.7, 0.5, 0.3, and 0.1, respectively.

Equation 5 is a second-order, nonlinear, ordinary differential equation (ODE). Solving ODEs is an important topic in mathematics and engineering. In general, most of the existing research for finding solutions to ODEs falls into two main categories: analytical techniques and numerical methods. The analytical techniques include, e.g., separation of variables and the method of integrating factors. The numerical methods include, e.g., Euler’s method and the Runge–Kutta (RK) method. The numerical method is usually expressed in terms of the discretization parameters. Artificial-intelligence-based methods are also currently being used in solving ODEs, such as that discussed by Raissi, Perdikaris, and Karniadakis (2019), Dufera (2021), and Cuomo et al. (2022).

Several works have extended Low and Lou’s equilibria in the last 30 years, such as Low and Flyer (2007), Lerche and Low (2014), and Prasad, Mangalam, and Ravindra (2014) redefined Equations 6, 7, and 9 of Low and Lou (1990) in different ways. To the best of our knowledge, there is no discussion about the existence and uniqueness of analytical solutions to Equation 5. The most commonly used numerical method to solve Equation 5 is the RK fourth-order method (RK4). RK4 provides the approximate value of ${{F}}\left ( {{\mu _{i}}} \right )$ at the discrete sampling points $\mu _{i}$s. If $\mu_{j}$ is not included in the set of $\mu _{i}$, we will not be able to directly determine the value of $F\left ( {{\mu _{j}}} \right )$. In this article, a neural network can compute $F\left ( {{\mu _{j}}} \right )$ and ${F^{\prime}}\left ( {{\mu _{j}}} \right )$ at any ${\mu _{j}}$ in $\left [ { - 1,1} \right ]$ directly.

The remainder of this article is organized as follows: Section 2 provides a RK-based method for solving for the parameter $a$ in Equation 6. Section 3 develops the corresponding numerical algorithm. The data-driven numerical method for the parameters $n$ and $a$ is presented in Section 4. The conclusion is given in Section 5.

2 RK-Based Method for the Parameter $a$ in Equation 5

Returning to Equations 3 and 5, there is one parameter $a$ and two unknowns $\left ( {F,\frac{{\mathrm{d}F}}{{\mathrm{d}\mu }}} \right )$ with ${B_{0}} = 1$ and ${r_{0}} = 1$ in Low and Lou’s equilibria. In this section, we study numerical methods for solving for $a$.

The basic idea for solving Equation 5 with initial conditions is to rewrite it as a system of first-order ODEs. Introducing the variables

$$ {f_{1}} = F\left ( \mu \right ) \ \ \text{and} \ \ {f_{2}} = {F^{ \prime}}\left ( \mu \right ), $$

we obtain a system of two first-order ODEs:

$$ \textstyle\begin{cases} f_{1}^{\prime }= {f_{2}}, \\ f_{2}^{\prime }= - \frac{{n\left ( {n + 1} \right ){f_{1}} + D}}{{1 - {\mu ^{2}}}}, \end{cases} $$

where

$$ D = \textstyle\begin{cases} \left ( {1 + \frac{1}{n}} \right ){a^{2}}f_{1}^{1 + \frac{2}{n}},&{\text{if $\frac{2}{n}$ is an integer},} \\ \left ( {1 + \frac{1}{n}} \right ){a^{2}}{f_{1}}{\left ( {f_{1}^{2}} \right )^{\frac{1}{n}}}, &{\text{otherwise},} \end{cases} $$

with initial values at $\mu = - 1$

$$ {f_{1}}\left ( { - 1} \right ) = 0 \ \ \text{and} \ \ {f_{2}}\left ( { - 1} \right ) = 10. $$

The RK method is an effective method for solving the initial-value problem of Equation 5 with an unknown parameter $a$ if $f_{1}(1) = 0$.

We divide the interval $\left [ {a_{0},a_{\mathrm{max}}} \right ]$ into $N$ equal parts, choosing a step $h = \frac{{{a_{\max }} - {a_{0}}}}{N}$. Then, $a_{i} = a_{0} + \left ( {i - 1} \right )h \left ( {1 \leqslant i \leqslant N} \right )$. Without loss of generality, we choose $a_{0} = {10^{ - 5}}$, $a_{\max } = 10$, $N = 999$.

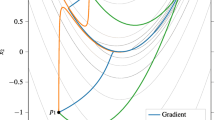
Note that $\mu = -1$ is a singular point of $f_{2}^{\prime }$ in Equation 5. The value of $f_{2}^{\prime}\left ( { - 1} \right )$ depends on the parameter $a$, as shown Figure 1, for $n = 1$, $f_{2}^{\prime}\left ( { - 1} \right ) = 0$, and $10^{6}$.

Figure 1

The curves of $F\left (a, 1\right )$ with the variable $a$ for $F^{\prime \prime} \left (-1\right )=0$ and $F^{\prime \prime} \left (-1\right )=10^{6}$, where the points of intersection between $F\left (a, 1\right )$ and the horizontal axis can determine the values of $a$ for $F\left (a, 1\right )=0$.

We take $f_{2}^{\prime}\left ( { - 1} \right ) = 0$ in this section. It helps us to find the interval that contains zeros when we plot $F\left ( {a_{i},\mu = 1} \right )$ against $a$, as shown in Figure 2. Finally, we find $F\left ( {a_{i},\mu = 1} \right ) = 0$ by the bisection method, and we find $a_{n,m}$s ($1 \le m \le 3$) as presented in Table 1.

Figure 2

$F(a,1)$ with the variable $a$ for different $n$.

Table 1 $a_{n,m}$ for the $m$th-order root of $F\left ( {a_{i},\mu = 1} \right )$ for a given $n$.

3 Machine-Learning-Based Method for $F$ and $\frac{{\mathrm{d}F}}{{\mathrm{d}\mu }}$

Most of the classical numerical methods compute an approximate value for the solution at discrete sampling points. In this section, we propose a grid-free method based on a neural network to obtain a numerical solution at any point in $\left [ { - 1,1} \right ]$.

The following theorem provides a solid theoretical basis for using multi-layer perceptrons (MLP) in scientific computing.

Theorem 1

(Universal approximation theorem (Cybenko 1989 and Hornik 1991)) Let $K \subseteq {\mathbb{R}^{d}}$ be compact, $f:K \to \mathbb{R}$ be continuous, $\rho :\mathbb{R} \to \mathbb{R}$ be continuous and not a polynomial. Then, for $\forall \epsilon > 0$, there exists $N \in \mathbb{N}, a_{k}$, $b_{k} \in \mathbb{R}$, $w_{k} \in \mathbb{R}^{d}$ with

$$ {\left \| {f - \sum \limits _{k = 1}^{N} {{a_{k}}\rho \left ( {\left \langle {{w_{k}}, \cdot } \right \rangle - {b_{k}}} \right )} } \right \|_{\infty }} < \epsilon . $$

Remark 1

The universal approximation theorem also exists when $f:K \to \mathbb{R}^{m}$.

Therefore, we use an MLP architecture with three fully connected operations to solve Equation 5 as shown in Figure 3. The first fully connected operation has one input channel corresponding to the inputs $\mu$. The second fully connected operation has $N$ hidden neurons. The last fully connected operation has two outputs $F$ and $\frac{{\mathrm{d}F}}{{\mathrm{d}\mu}}$. It can be formulated as

$$ {\boldsymbol {f} \left ( {\mu ;\theta } \right )} = {\left [ {{f_{1}},{f_{2}}} \right ]^{T}} = {W_{2}}Y + {b_{2}} = {{W_{2}}\left [ {\sigma \left ( {{W_{1}} \mu + {b_{1}}} \right )} \right ] + {b_{2}}}, $$

(7)

where ${W_{1}},{b_{1}} \in {\mathbb{R}^{N \times 1}}$, ${W_{2}} \in { \mathbb{R}^{2 \times N}}$, ${b_{2}} \in {\mathbb{R}^{2 \times 1}}$, ${\left [ \cdot \right ]^{T}}$ is the transpose operator in linear algebra, $Y = {\left [ {{y_{1}}, \ldots ,{y_{N}}} \right ]^{T}}$, and $\sigma$ is the hyperbolic tangent sigmoid (tanh) elementwise operator

$$ {\mathrm{{tanh}}}\left ( x \right ) = \frac{{1 - {\text{e}^{ - x}}}}{{1 + {\text{e}^{ - x}}}}, $$

(8)

where $x$ is an element of the column vector ${W_{1}}\mu + {b_{1}}$.

Figure 3

The MLP has an input layer, one hidden layer, and an output layer. A layer consists of small individual units called neurons. The letter $N$ is used for the number of neurons in the hidden layer. The loss function contains information from the differential equation and the initial conditions.

Theorem 1 ensures the existence of a neural-network solution ${\boldsymbol {f}} \left ( {\mu ;\theta } \right )$ that can approximate the solution of Equation 5 arbitrarily closely. Then, we find ${\boldsymbol {f}} \left ( {\mu ;\theta } \right )$ by minimizing the loss function

$$ \mathcal{L}\left ( {\mu ;\theta } \right ) = {\lambda _{1}}{ \mathcal{L}_{1}}\left ( {\mu ;\theta } \right ) + {\lambda _{2}}{ \mathcal{L}_{2}}\left ( {\mu ;\theta } \right ) + {\lambda _{3}}{ \mathcal{L}_{3}}\left ( {\mu ;\theta } \right ), $$

(9)

where

$$ \begin{aligned} {\mathcal{L}_{1}}\left ( {\mu ;\theta } \right ) & = \frac{1}{M}\sum \limits _{\mu = {\mu _{j}},j = 1}^{j=M} {{{\left ( { \left ( {1 - {\mu ^{2}}} \right ) \frac{{\mathrm{d}{f_{2}}}}{{\mathrm{d}\mu }} + n\left ( {n + 1} \right ){f_{1}} + E} \right )}^{2}}} \\ {\mathcal{L}_{2}}\left ( {\mu ;\theta } \right ) & = \frac{1}{M}\sum \limits _{\mu = {\mu _{j}},j = 1}^{M} {{{\left ( { \frac{{\mathrm{d}{f_{1}}}}{{\mathrm{d}\mu }} - {f_{2}}} \right )}^{2}}} \\ {\mathcal{L}_{3}}\left ( {\mu ;\theta } \right ) & = {\left ( {{f_{1}} \left ( { - 1;\theta } \right )} \right )^{2}} + {\left ( {{f_{2}} \left ( { - 1;\theta } \right ) - 10} \right )^{2}}, \end{aligned} $$

where $M$ is the sample size and where

$$ E = \textstyle\begin{cases} {a^{2}}\left ( {1 + \frac{1}{n}} \right )f_{1}^{\left ( {1 + \frac{2}{n}} \right )},& {\text{if}} \ \frac{2}{n} \ \text{is a positive integer}, \\ {a^{2}}\left ( {1 + \frac{1}{n}} \right ){f_{1}}{\left ( {f_{1}^{2}} \right )^{\frac{1}{n}}},& \text{otherwise} \end{cases} $$

and where ${\boldsymbol {\theta}} \in \mathbb{R}^{(4N+2)\times 1}$ is a learnable parameter, which is reshaped by the collecting set $\left \{ {{W_{1}},{b_{1}},{W_{2}},{b_{2}}} \right \}$. Clearly, if Equation 9 does reduce to zero, then Equation 5 holds.

In order to compute $\frac{{\mathrm{d}{f_{1}}}}{{\mathrm{d}\mu }}$, $\frac{{\mathrm{d}{f_{2}}}}{{\mathrm{d}\mu }}$, and $\frac{{\partial \mathcal{L}}}{{\partial \theta }}$ we use automatic differentiation (AD) (Baydin et al. 2018), rather than numerical differentiation or integration (Kincaid and Cheney 2002, Chapter 7) based on the assigned grid. AD is a set of techniques for evaluating the derivatives numerically. AD uses symbolic rules for differentiation, however AD evaluates derivatives at particular numeric values, and it does not construct symbolic expressions for derivatives. Automatic differentiation is a powerful tool to automate the calculation of derivatives and is preferable to more traditional methods, especially when differentiating complex algorithms and mathematical functions (Baydin et al. 2018). In Matlab, a dlgradient command takes derivatives with respect to the input or to the parameters.

In practice, we use the mini-batch ADAM (Chen et al. 2022) that is a batch of $Nb$ randomly sampled points at every training iteration to minimize ℒ. The $M$ data points are randomly divided into $\frac{M}{{Nb}}$ batches of size $Nb$. When all $\frac{M}{{Nb}}$ batches of data are used for optimization once an epoch is completed. The mini-batch ADAM is an optimization algorithm that can minimize the loss function ℒ.

Select $M =$ 100,000 points from −1 to 1 at random to train the MLP. Set the $m = 1$, $\beta _{1} = 0.9$, and $\beta _{2} = 0.999$ for all $n$s. Set $\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$, $N$, $Nb$, and $\eta$, as Table 2, for different $n$ at the same time. Then, update ${\boldsymbol {\theta}}$ using the mini-batch ADAM algorithm, which is shown as Algorithm 1.

Algorithm 1

Mini-batch ADAM Algorithm.

Table 2 Hyperparameters Setting of the MLP.

Finally,

$$ {{{\boldsymbol {\theta}}} ^{*}} = \mathop {\arg \min }\limits _{{ \boldsymbol {\theta}}} Loss . $$

For values of ${\mu _{i}} = - 1 + \left ( {i - 1} \right )\frac{2}{{9999}} \ \left ( 1 \leqslant i \leqslant 10{,}000 \right )$, compare the predicted values (${F_{\mathrm{MLP}}}$) of the MLP with the numerical solutions (${F_{\mathrm{RK}}}$) of Equation 2 using the classical RK4.

Define the mean square error (MSE):

$$ \begin{aligned} {\mathrm{MSE}}(F) & = \frac{1}{{10{,}000}}\sum \limits _{i = 1}^{10{,}000} {{{\left [ {{F_{\mathrm{MLP}}}\left ( {{\mu _{i}}} \right ) - {F_{\mathrm{RK}}} \left ( {{\mu _{i}}} \right )} \right ]}^{2}}}, \\ {\mathrm{MSE}}(\frac{{\mathrm{d}F}}{{\mathrm{d}\mu }}) & = \frac{1}{{10{,}000}}\sum \limits _{i = 1}^{10{,}000} {{{\left [ {{{ \frac{{\mathrm{d}F}}{{\mathrm{d}\mu }}}_{\mathrm{MLP}}}\left ( {{\mu _{i}}} \right ) - {{\frac{{\mathrm{d}F}}{{\mathrm{d}\mu }}}_{\mathrm{RK}}}\left ( {{ \mu _{i}}} \right )} \right ]}^{2}}}, \end{aligned} $$

to measure how close the ${F_{\mathrm{MLP}}}\left ( {{\mu _{i}}} \right )$ is to the ${F_{\mathrm{RK}}}\left ( {{\mu _{i}}} \right )$ and the $\left ( {{{\frac{{\mathrm{d}F}}{{\mathrm{d}\mu }}}_{\mathrm{MLP}}}} \right )\left ( {{\mu _{i}}} \right )$ is to the ${\left ( {\frac{{\mathrm{d}F}}{{\mathrm{d}\mu }}} \right )_{\mathrm{RK}}} \left ( {{\mu _{i}}} \right )$, respectively. The MSEs are shown in Tables 3 and 4. This shows that the MLP approach is efficient, compared with the RK4.

Table 3 Test performance of the numerical solutions generated by the MLP when $n > 1$.

Table 4 Test performance of the numerical solutions generated by the MLP when $n < 1$.

Figures 4 and 5 show how close the solutions generated by MLPs are to the RK method. Therefore, they illustrate that MLP works reasonably well.

Figure 4

$F$, $\frac{{\mathrm{d}F}}{{\mathrm{d}\mu }}$ generated by MLP and RK methods when $n \ge 1$.

Figure 5

$F$, $\frac{{\mathrm{d}F}}{{\mathrm{d}\mu }}$ generated by MLP and RK methods when $n < 1$.

We developed a numerical algorithm that can effectively solve a specific class of ODEs, particularly those derived from $\frac{\partial }{{\partial \phi }} = 0$. One notable aspect of our algorithm is its remarkable adaptability, which facilitates effortless adjustments to a wide range of initial and boundary conditions through simple modifications of the loss function in our proposed artificial-intelligence (AI) neural-network model. Lerche and Low (2014) generalized the equilibria proposed by Low and Lou (1990) and made modifications to the initial conditions. In this scenario, our numerical algorithm remains valid and applicable. To avoid unnecessary repetition, we have included it as Appendix B.

4 Data-Driven Approach for Identifying the Parameters $n$ and $a$

The objective is to identify the optimum parameters of Low and Lou’s equilibria to match the observations of an active region at the photosphere. This process concerns an inverse problem: given a measured magnetic field ${\boldsymbol {B}}$ at the photosphere, or its value $P{\boldsymbol {B}}$ under a measurement operator $P$, determine a corresponding parameter set $\left \{ {a,n} \right \}$ such that the neural-network solution $f\left ( {{r_{i},\mu _{i}};a,n} \right )$ can approximate the field ${\boldsymbol {B}}$.

To analyze a force-free field ${\boldsymbol {B}}$ with the additional condition $\frac{\partial }{{\partial \phi }} = 0$ imposed in the spherical coordinate system, we consider the transformation matrix $P$ defined as $P=\left[\begin{array}{ccc}0& \frac{r^{n+2}{(1-{\mu }^2)}^{\frac{1}{2}}}{n}& 0\end{array}\right]$, see Equation 19, then one obtains that

$$P\mathit{B}=\left[\begin{array}{ccc}0& \frac{r^{n+2}{(1-{\mu }^2)}^{\frac{1}{2}}}{n}& 0\end{array}\right]{\left[\begin{array}{ccc}{B}_r& B_{\theta }& B_{\varphi }\end{array}\right]}^T=F.$$

The loss function of the neural network can be designed as

$$ \mathcal{L} = \lambda _{1} \mathcal{L}_{1} + \lambda _{2} \mathcal{L}_{2}, $$

where

$$ \mathcal{L}_{1} = \frac{1}{M}\sum \limits _{i = 1}^{M} {{{\left ( { \left ( {1 - {\mu _{i}^{2}}} \right ) \frac{{{\mathrm{d}^{2}}G}}{{\mathrm{d}{\mu ^{2}}}} + {\theta _{2}} \left ( {{\theta _{2}} + 1} \right )G + {\theta _{3}}\left ( {1 + \frac{1}{{{\theta _{2}}}}} \right )G{{\left ( {{G^{2}}} \right )}^{ \frac{1}{{{\theta _{2}}}}}}} \right )}^{2}} } $$

and

$$ {\mathcal{L}_{2}} = \frac{1}{M}\sum \limits _{i = 1}^{M} {{{\left ( {1 - {\mu _{i}^{2}}} \right )}^{\frac{1}{2}}} \frac{{{r^{{\theta _{2}} + 2}}}}{{{\theta _{2}}}}{{\left ( {{{\left ( {{B_{ \theta }}} \right )}_{i}} - f\left ( {{\mu _{i}};{\theta _{1}}} \right )} \right )}^{2}}} $$

and

$$ G\left ( {{\mu _{i}}} \right ) = \frac{{{r^{n + 2}}}}{n}{\left ( {1 - { \mu _{i}^{2}}} \right )^{\frac{1}{2}}}f\left ( {{\mu _{i}};{\theta _{1}}} \right ). $$

In the above equations, $\lambda _{1}$ and $\lambda _{2}$ are two trade-off parameters: $M$ represents the sample size, and ${\boldsymbol {\theta}}_{1}$ is a learnable vector for $B_{\theta}$. Furthermore, $\theta _{2}$ and $\theta _{3}$ are two learnable parameters associated with $n$ and $a$, respectively.

For a simple case, the active region is generated by Low and Lou’s approach with $n = 5$ and $a = 3.9341$ ($n{a_{1}} = \left \{ {n = 5,a = 3.9341} \right \}$). We use an MLP with five layers to identify the parameters $n$ and $a$. The first layer has three inputs corresponding to the $r$, $\mu$, and $B_{\theta}$. There are 64 neurons for each hidden layer. The last layer has three outputs: the estimated values of the $n$, $a$, and $B_{\theta}$. Set $\lambda _{1} = \lambda _{2} = 1$ and $M = 65{,}536$. After training the MLP, the outputs $n$ and $a$ are 4.9042 and 3.9830 ($n{a_{2}} = \left \{ {n = 4.9042,a = 3.9830} \right \}$), respectively.

Figure 6 shows the magnetogram $B_{x}$ that is generated by ${na}_{1}$ and ${na}_{2}$, respectively. The magnetic-field intensity in Figure 6 is visualized in the range of −5000 to 5000. Any values exceeding 5000 are limited to 5000, and any values below −5000 are set to −5000. Figure 7 shows the contours of $B_{x}$ that are generated by ${na}_{1}$ and ${na}_{2}$, respectively. They are highly compatible in visual representation. In Figure 7, the colorbars are displayed in arbitrary units. It is worth noting that magnetograms can be represented as matrices in Cartesian coordinates $(x,y)$. Figure 8 illustrates a visual representation of the quantity $\frac{{{{\left ( {{B_{n2}}} \right )}_{x}} - {{\left ( {{B_{n1}}} \right )}_{x}}}}{{\max \left | {{{\left ( {{B_{n1}}} \right )}_{x}}} \right |}}$. However, the largest differences occur close to the magnetic nulls in Figure 8 since the error propagation rapidly increases in Equation 3 when $r$ is too small. The cosine similarity (Brockmeier et al. 2017) between the magnetograms generated by ${na}_{1}$ and ${na}_{2}$ is 0.9909. Cosine similarity is a measure that calculates the cosine value of the angle between two matrices. It ranges from −1 to 1, with a value closer to 1 indicating a higher degree of similarity between the two magnetograms.

Figure 6

The magnetogram $B_{x}$ that is generated by ${na}_{1}$ and ${na}_{2}$, respectively. Please note that the magnetograms are derived from the equilibria by Low and Lou and are dimensionless.

Figure 7

The contour of $B_{x}$ that is generated by ${na}_{1}$ and ${na}_{2}$, respectively. Please note that the contours are derived from the equilibria by Low and Lou and are dimensionless.

Figure 8

The normalized differences generated by ${na}_{1}$ and ${na}_{2}$.

If Low and Lou’s equilibria can effectively approximate the solar photospheric observational data, we can utilize a neural network to determine the parameters and initial values of the Low and Lou’s equilibria. Therefore, a neural network as shown in Figure 9 is applied to NOAA active regions (ARs) 11158 and 11302. This process can be written as:

$$\left[\begin{array}{c}{B}_r\\ B_{\theta }\\ B_{\varphi }\end{array}\right]=W^4\sigma (W^3\sigma (W^2\sigma (W^1\left[\begin{array}{c}r\\ \mu \end{array}\right]+b^1)+b^2)+b^3)+b^4,$$

where $W^{1}$, $W^{2}$, $W^{3}$, and $W^{4}$ represent the weight matrices for each layer, while $\sigma$ represents the activation function. The biases are represented by $b^{1}$, $b^{2}$, $b^{3}$, and $b^{4}$.

Figure 9

Neural-network architecture for the observational data.

The outputs of the neural network are shown in Figures 10c and d for NOAA ARs 11158 and 11302 from the Solar Dynamics Observatory/Helioseismic and Magnetic Imager (SDO/HMI), respectively. It can be observed that we cannot obtain effective magnetic fields referring to Figures 10a and b. With only the data-loss term $\mathcal{L}_{2}$, we can obtain reasonable outputs as shown in Figures 10e and f for NOAA ARs 11158 and 11302, respectively.

Figure 10

The neural-network outputs for NOAA ARs 11158 and 11302.

According to Wiegelmann and Sakurai (2021), the necessary conditions for determining whether the solar photospheric magnetic field is a nonlinear force-free field are:

$$ \int _{S} {{B_{z}}\left ( {x,y,0} \right )\mathrm{d}x \hspace{0.08cm} \mathrm{d}y} = 0, \quad \frac{{\left | {{F_{x}}} \right |}}{{{F_{p}}}} \ll 1, \frac{{\left | {{F_{y}}} \right |}}{{{F_{p}}}} \ll 1, \frac{{\left | {{F_{z}}} \right |}}{{{F_{p}}}} \ll 1, $$

where

$$ \begin{aligned} {F_{x}} = - \frac{1}{{4\pi }}\int _{S} {{B_{x}}{B_{z}} \mathrm{d}x \hspace{0.08cm} \mathrm{d}y},\ \ & \ \ {F_{y}} = - \frac{1}{{4\pi }}\int _{S} {{B_{y}}{B_{z}} \mathrm{d}x \hspace{0.08cm} \mathrm{d}y} , \\ {F_{z}} = \frac{1}{{8\pi }}\int _{S} {\left ( {B_{x}^{2} + B_{y}^{2} - B_{z}^{2}} \right )\mathrm{d}x \hspace{0.08cm} \mathrm{d}y},\ \ & \ \ {F_{p}} = \frac{1}{{8\pi }}\int _{S} {\left ( {B_{x}^{2} + B_{y}^{2} + B_{z}^{2}} \right )\mathrm{d}x \hspace{0.08cm} \mathrm{d}y}. \end{aligned} $$

For practical computations, the acceptable conditions for flux imbalance, as stated by Moon et al. (2002), are defined as:

$$ \frac{{\left | {{F^{+} } - {F^{-} }} \right |}}{{{F^{+} } + {F^{-} }}} \leqslant 0.1 , $$

where $F^{+}$ and $F^{-}$ represent the upward and downward magnetic fluxes, respectively. Additionally, the vertical-force condition, as mentioned by Liu et al. (2013), is given by

$$ \frac{{\left | {{F_{z}}} \right |}}{{{F_{p}}}} < 0.1, $$

where $F_{z}$ denotes the vertical force and $F_{p}$ represents the total magnetic pressure. If these conditions are satisfied, the magnetic field can be approximated as a force-free field $\left ( {\nabla \times {\boldsymbol {B}} } \right ) \times {\boldsymbol {B}} = 0$. The active-region data that we used in our study meets these requirements. One possible reason for the code not working is that Low and Lou’s equilibria may not accurately approximate certain observational data, such as for NOAA AR 11158. To effectively utilize Low and Lou’s equilibria, it is crucial to regularize the observational data to approximate the condition $\frac{\partial }{{\partial \phi }} = 0$. This regularization term is also essential to ensure that the modified data closely resembles the original data. As is evident from Figures 10c and d, including this regularization term is indispensable. However, the specific form of this regularization term has not yet been determined. In our future work, we will continue to explore and optimize this regularization term.

5 Conclusion

In this article, testing a numerical algorithm for solar magnetic-field extrapolation using Low and Lou’s equilibria proves to be beneficial. We have presented a machine-learning-based numerical method that effectively determines the parameter $a$ and the function $F$ in Low and Lou’s equilibria. By employing the MLP neural network, we successfully implemented this algorithm. An area of crucial investigation lies in the adaptive selection of MLP’s width and the parameters $\lambda _{1}$, $\lambda _{2}$, and $\lambda _{3}$ in Equation 9.

Furthermore, we have proposed a machine-learning algorithm to address the inverse problem of Low and Lou’s equilibria. While it performs well on generated data, it falls short when applied to observational data. An intriguing avenue for future research involves optimizing the parameters of the generalized equilibria proposed by Low and Lou to better align with observations of active regions on the photosphere.

Moreover, a promising direction for the future is to combine solar photospheric observation data with artificial-intelligence techniques for coronal magnetic-field extrapolation. This integration holds potential for further advancements in understanding and predicting solar phenomena.

Appendices

Appendix A

We focus here on mathematical concepts and derive Equations 3 and 5.

The following two theorems are commonly used in the formulation and analysis of magnetic fields.

Theorem 2

(Davis, Snider, and Davis 1979) A vector field ${\boldsymbol {B}}$ is continuously differentiable in a simply connected domain $D$, $\nabla \cdot {\boldsymbol {B}} = 0$ if, and only if, there is a vector field ${\boldsymbol {A}}$ such that ${\boldsymbol {B}} = \nabla \times {\boldsymbol {A}}$ throughout $D$.

Remark 2

${\boldsymbol {A}}$ is not unique, in fact, $\nabla \cdot \left [ {\nabla \times \left ( {\beta {\boldsymbol {A}} } \right )} \right ] = 0$ for any $\beta \in \mathbb{R}$.

Theorem 3

(Davis, Snider, and Davis 1979) Given any position vector ${\boldsymbol {r}} = x\widehat {{\boldsymbol {x}}} + y \widehat {{\boldsymbol {y}}} + z\widehat {{\boldsymbol {z}}}$, if $x = x\left ( {{u_{1}},{u_{2}},{u_{3}}} \right )$, $y = y\left ( {{u_{1}},{u_{2}},{u_{3}}} \right )$, $z = z\left ( {{u_{1}},{u_{2}},{u_{3}}} \right )$, let ${\boldsymbol{e_{i}}} = \frac{1}{{{h_{i}}}} \frac{{\partial {\boldsymbol {r}} }}{{\partial {u_{i}}}}$, where ${h_{i}} = \left | { \frac{{\partial {\boldsymbol {r}} }}{{\partial {u_{i}}}}} \right | \left ( {i = 1,2,3} \right )$. If $\left \{ {{\boldsymbol{e_{1}}} ,{\boldsymbol{e_{2}}} ,{\boldsymbol{e_{3}}} } \right \}$ are orthogonal curvilinear coordinates in $\mathbb{R}^{3}$, then for $\forall {\boldsymbol {A}} = {A_{x}}\widehat {{\boldsymbol {x}}} + {A_{y}} \widehat {{\boldsymbol {y}}} + {A_{z}}\widehat {{\boldsymbol {z}}} = {A_{1}}{ \boldsymbol{e_{1}}} + {A_{2}}{\boldsymbol{e_{2}}} + {A_{3}}{ \boldsymbol{e_{3}}}$ we have that

$$\mathrm{\nabla }\times \mathit{A}=\frac{1}{h_1{h}_2{h}_3}\left|\begin{array}{ccc}{h}_1{\mathit{e}}_{\mathbf{1}}& h_2{\mathit{e}}_{\mathbf{2}}& h_3{\mathit{e}}_{\mathbf{3}}\\ \frac{\partial }{\partial u_1}& \frac{\partial }{\partial u_2}& \frac{\partial }{\partial u_3}\\ h_1{A}_1& h_2{A}_2& h_3{A}_3\end{array}\right|.$$

Let ${u_{1}} = r$, ${u_{2}} = \theta$, ${u_{3}} = \phi$, and $x = r\sin \theta \cos \phi$, $y = r\sin \theta \sin \phi$, $z = r\cos \phi$. By the assumption of Low and Lou

$$ \frac{\partial }{{\partial {u_{3}}}} = \frac{\partial }{{\partial \phi }} = 0 $$

and using Theorems 2 and 3, we obtain the axisymmetric magnetic NLFFF ${\boldsymbol{B}}$

$$ \begin{aligned} & {\boldsymbol {B}} = \nabla \times {\boldsymbol {A}} \\ = & \frac{1}{{r\sin \theta }}\left ( {\frac{1}{r} \frac{\partial }{{\partial \theta }}\left ( {r\sin \theta {A_{\phi }}} \right )\widehat {{\boldsymbol {r}} } - \frac{\partial }{{\partial r}} \left ( {r\sin \theta {A_{\phi }}} \right ) \widehat {{\boldsymbol{\theta}}} + \sin \theta \left ( { \frac{\partial }{{\partial r}}\left ( {r{A_{\theta }}} \right ) - \frac{{\partial {A_{r}}}}{{\partial \theta }}} \right ) \widehat { {\boldsymbol{\phi}}}} \right ) \end{aligned} . $$

It is convenient to introduce $\widetilde{A} = r\sin \theta {A_{\phi }}$, ${b_{\phi }} = \sin \theta \left ( {\frac{\partial }{{\partial r}}\left ( {r{A_{\theta }}} \right ) - \frac{{\partial {A_{r}}}}{{\partial \theta }}} \right )$, then

$$ {\boldsymbol {B}} = \frac{1}{{r\sin \theta }}\left ( {\frac{1}{r} \frac{{\partial \widetilde{A}}}{{\partial \theta }} \widehat {{\boldsymbol {r}} } - \frac{{\partial \widetilde{A}}}{{\partial r}} \widehat {{\boldsymbol{\theta}}} + {b_{\phi }} \widehat { {\boldsymbol{\phi}}} } \right ) . $$

(10)

Substituting Equation 10 into ${\boldsymbol {B}} = \alpha {\boldsymbol {B}}$ and simplifying, we obtain

$$ \frac{1}{r}\frac{{\partial {b_{\phi }}}}{{\partial \theta }} = \alpha \frac{1}{r}\frac{\partial }{{\partial \theta }}\widetilde{A}, $$

(11)

$$ \frac{{\partial {b_{\phi }}}}{{\partial r}} = \alpha \frac{\partial }{{\partial r}}\widetilde{A}, $$

(12)

$$ - \left ( {\frac{\partial }{{\partial r}}\left ( { \frac{{\partial \widetilde{A}}}{{\partial r}}} \right ) + \frac{1}{{{r^{2}}}}\sin \theta \frac{\partial }{{\partial \theta }} \left ( {\frac{1}{{\sin \theta }} \frac{{\partial \widetilde{A}}}{{\partial \theta }}} \right )} \right ) = \alpha b_{\phi}. $$

(13)

Combining Equations 11 and 12 to eliminate $\alpha$,

$$\frac{\frac{\partial b_{\varphi }}{\partial \theta }}{\frac{\partial \tilde{A}}{\partial \theta }}=\frac{\frac{\partial b_{\varphi }}{\partial r}}{\frac{\partial \tilde{A}}{\partial r}}\Rightarrow 0=\frac{\partial b_{\varphi }}{\partial \theta }\frac{\partial \tilde{A}}{\partial r}-\frac{\partial b_{\varphi }}{\partial r}\frac{\partial \tilde{A}}{\partial \theta }=\left|\begin{array}{cc}\frac{\partial b_{\varphi }}{\partial r}& \frac{\partial b_{\varphi }}{\partial \theta }\\ \frac{\partial \tilde{A}}{\partial r}& \frac{\partial \tilde{A}}{\partial \theta }\end{array}\right|=J(b_{\varphi },\tilde{A}).$$

The following theorem provided us with the relationship between $b_{\phi }$ and $\widetilde{A}$.

Theorem 4

(Tolstykh 2020) If ${f_{3}}$, ${f_{4}}$ are continuously differentiable functions from $\left ( {x,y} \right ) \to \mathbb{R}$ such that the determinant of the Jacobian vanishes everywhere, then ${f_{4}}\left ( {x,y} \right ) = {H}\left ( {{f_{3}}\left ( {x,y} \right )} \right )$ or ${f_{3}}\left ( {x,y} \right ) = H\left ( {{f_{4}}\left ( {x,y} \right )} \right )$, where $H$ is a continuously differentiable function.

Therefore, ${b_{\phi }} = {b_{\phi }}\left ( {\widetilde{A}} \right )$, i.e. ${b_{\phi}}$ is an arbitrary function of ${\widetilde{A}}$.

Taking derivatives of ${b_{\phi }}$ with respect to $r$, we obtain

$$ \frac{{\partial {b_{\phi }}}}{{\partial r}} = \frac{{\partial {b_{\phi }}}}{{\partial \widetilde{A}}} \frac{{\partial \widetilde{A}}}{{\partial r}} = \frac{{\text{d}{b_{\phi }}}}{{\text{d}\widetilde{A}}} \frac{{\partial \widetilde{A}}}{{\partial r}}. $$

(14)

Combining Equations 14 and 12 to obtain $\alpha$,

$$ \alpha = \frac{{\text{d}{b_{\phi }}}}{{\text{d}\widetilde{A}}}. $$

(15)

Substituting Equation 15 into 13, we obtain

$$ \frac{{{\partial ^{2}}\widetilde{A}}}{{\partial {r^{2}}}} + \frac{{\sin \theta }}{{{r^{2}}}}\frac{\partial }{{\partial \theta }} \left ( {\frac{1}{{\sin \theta }} \frac{{\partial {\text{ }}\widetilde{A}}}{{\partial \theta }}} \right ) + \frac{\text{d}}{{\text{d}\widetilde{A}}}\left ( {\frac{1}{2}b_{\phi }^{2}} \right ) = 0, $$

(16)

known as the Grad–Shafranov equation.

Low and Lou found a set of solutions to Equation 16 if

$$\tilde{A}=\tilde{A}(r,\theta )=F(cos\theta )r^{-n},b_{\varphi }=\{\begin{array}{c}a{\tilde{A}}^{1+\frac{1}{n}},n=1\\ a\tilde{A}{\left|\tilde{A}\right|}^{\frac{1}{n}},n>1\\ \end{array}$$

(17)

for odd $n$, and a real constant $a$. Equation 16 then reduces to

$$ \begin{aligned} & \left ( {1 - {\mu ^{2}}} \right ) \frac{{{\mathrm{d}^{2}}F}}{{\mathrm{d}\mu ^{2} }} + n(n + 1)F + {a^{2}} \left ( {1 + \frac{1}{n}} \right ){F^{1 + \frac{2}{n}}} = 0, \ \ n = 1, \\ & \left ( {1 - {\mu ^{2}}} \right ) \frac{{{\mathrm{d}^{2}}F}}{{{\mathrm{d}}\mu ^{2} }} + n(n + 1)F + {a^{2}} \left ( {1 + \frac{1}{n}} \right )F{\left ( {{F^{2}}} \right )^{ \frac{1}{n}}} = 0, \ \ n > 1, \end{aligned} $$

where $\mu = \cos \theta$. Thereby, a family of axisymmetric NLFFF can be generated as Equation 3.

Moreover, substituting Equation 17 into Equation 10, we obtain

$$ \begin{aligned} {B_{r}} = \frac{1}{{r\sin \theta }}\left [ {\frac{1}{r} \frac{\partial }{{\partial \theta }}\left ( { \frac{{F\left ( {\cos \theta } \right )}}{{{r^{n}}}}} \right )} \right ] = \frac{1}{{{r^{n}}\sin \theta }}\frac{1}{{{r^{2}}}} \frac{{\partial F}}{{\partial \cos \theta }} \frac{{\partial \cos \theta }}{{\partial \theta }} = - \frac{1}{{{r^{n + 2}}}}\frac{{\partial F}}{{\partial \mu }} \end{aligned} , $$

(18)

$$ \begin{aligned} {B_{\theta }} = \frac{1}{{r\sin \theta }}\left [ { - \frac{\partial }{{\partial r}}\left ( { \frac{{F\left ( {\cos \theta } \right )}}{{{r^{n}}}}} \right )} \right ] = \frac{n}{{{r^{n + 2}}\sin \theta }}F = \frac{n}{{{r^{n + 2}}}} \frac{1}{{{{\left ( {1 - {\mu ^{2}}} \right )}^{\frac{1}{2}}}}}F \end{aligned} $$

(19)

and

$$B_{\varphi }=\{\begin{array}{c}a\frac{1}{r^{n+2}}\frac{1}{{(1-{\mu }^2)}^{\frac{1}{2}}}{F}^{1+\frac{1}{n}},n=1,\\ a\frac{1}{r^{n+2}}\frac{1}{{(1-{\mu }^2)}^{\frac{1}{2}}}F{\left|F\right|}^{\frac{1}{n}},n>1.\\ \end{array}$$

(20)

Finally, combining Equations 18, 19, and 20, we obtain

$$ {\boldsymbol {B}} = \frac{1}{{{r^{n+2}}}}\left ( { - \frac{{\text{d}F}}{{\text{d}\mu }} \widehat {{\boldsymbol {r}} } + \frac{nF}{{{{\left ( {1 - {\mu ^{2}}} \right )}^{\frac{1}{2}}}}} \widehat {{\boldsymbol{\theta}}} + {{r^{n + 2}}{B_{\phi }}} \widehat { {\boldsymbol{\phi}}} } \right ). $$

(21)

Next, we multiply Equation 21 by ${B_{0}}r_{0}^{n+2}$ using Remark 2, and some constant, and obtain Equation 3, where $\eta = a{B_{0}}r_{0}^{n+2}$.

This completes the derivation of Equations 3 and 5 in detail.

Appendix B

By conveniently adjusting the corresponding loss-function term in our model, we can tailor our approach to effectively solve various types of numerical ODE problems. With this in mind, we are actively engaged in the pursuit of solutions of the type of those of Lerche and Low (2014), i.e.

$$ (1 - {\mu ^{2}}) \frac{{{\mathrm{d}^{2}}{A_{n}}}}{{\mathrm{d}{\mu ^{2}}}} + n\left ( {n + 1} \right ){A_{n}} + \lambda {A_{n}}{\left ( {A_{n}^{2}} \right )^{ \frac{1}{n}}} = 0, $$

(22)

where $\lambda = \frac{{n + 1}}{n}{a^{2}}$.

The boundary condition for Equation 22 is

$$ {A_{n}}\left ( { - 1} \right ) = 0,\quad {A_{n}}\left ( 1 \right ) = 0 $$

(23)

and the initial condition for Equation 22 is

$$ \textstyle\begin{cases} {A_{n}}\left ( 0 \right ) = 1, \ A_{n}^{\prime}\left ( 0 \right ) = 0; & \text{if} \ {A_{n}}\left ( \mu \right ) \text{ is an even function}, \\ {A_{n}}\left ( 0 \right ) = 0, \ A_{n}^{\prime}\left ( 0 \right ) = 1; & \text{if} \ {A_{n}}\left ( \mu \right ) \text{ is an odd function}. \end{cases} $$

(24)

Regarding the aforementioned problem, the loss function in Equation 9 of the AI model that we proposed is modified as follows:

$$ \mathcal{L}\left ( {\mu ;\theta } \right ) = {\lambda _{1}}{ \mathcal{L}_{1}}\left ( {\mu ;\theta } \right ) + {\lambda _{2}}{ \mathcal{L}_{2}}\left ( {\mu ;\theta } \right ) + {\lambda _{3}}{ \mathcal{L}_{3}}\left ( {\mu ;\theta } \right ), $$

(25)

where

$$\begin{array}{rl}{\mathcal{L}}_1(\mu ;\theta )& =\frac{1}{M}\sum _{\mu ={\mu }_j,j=1}^{j=M}{((1-{\mu }^2)\frac{\mathrm{d}{f}_2}{\mathrm{d}\mu }+n(n+1)f_1+\lambda f_1{\left(f_1^2\right)}^{\frac{1}{n}})}^2,\\ {\mathcal{L}}_2(\mu ;\theta )& =\frac{1}{M}\sum _{\mu ={\mu }_j,j=1}^M{(\frac{\mathrm{d}{f}_1}{\mathrm{d}\mu }-f_2)}^2,\\ {\mathcal{L}}_3(\mu ;\theta )& =\{\begin{array}{c}{(f_1(0;\theta )-1)}^2+{\left(f_2(0;\theta )\right)}^2,\\ {\left(f_1(0;\theta )\right)}^2+{(f_2(0;\theta )-1)}^2,\end{array}\begin{array}{c}\text{if}{f}_1\text{is an even function},\\ \text{if}{f}_1\text{is an odd function}.\end{array}\end{array}$$

We have obtained the values for $\lambda$, which are listed in Tables 5 and 6. It is important to note that these corresponding values are extracted from the captions of Figures 2, 3, and 4 in Lerche and Low (2014). It can be observed that they are very close but still exhibit subtle differences, which can be attributed to factors such as grid partitioning or machine precision.

Table 5 The values of $\lambda$ in Lerche and Low (2014) and our numerical algorithm for the even functions.

Table 6 The values of $\lambda$ in Lerche and Low (2014) and our numerical algorithm for the odd functions.

For the values of ${\mu _{i}}$ ($- 1 \le {\mu _{i}} \le 1$), we compare the numerical values of the AI solver we proposed with the numerical solutions (${A_{\mathrm{LL}}}$) to Equation 22 in Lerche and Low (2014). The MSEs are listed in Tables 7 and 8. Figures 11, 12, and 13 show how close the solutions generated by the AI solver are to the RK solver of Lerche and Low (2014). They illustrate that the AI solver works reasonably well.

Figure 11

The values of $A_{n}$ and $A_{n}^{\prime}$ obtained by the AI solver that we proposed and the RK solver of Lerche and Low (2014), respectively, when $n = 0.5$.

Figure 12

The values of $A_{n}$ and $A_{n}^{\prime}$ obtained by the AI solver that we proposed and the RK solver of Lerche and Low (2014), respectively, when $n = 1$.

Figure 13

The values of $A_{n}$ and $A_{n}^{\prime}$ obtained by the AI solver that we proposed and the RK solver of Lerche and Low (2014), respectively, when $n = 4$.

Table 7 The MSEs of $A_{n}$ and $A_{n}^{\prime}$ generated by the AI solver we proposed and the RK solver of Lerche and Low (2014) when $A_{n}$ is an even function.

Table 8 The MSEs of $A_{n}$ and $A_{n}^{\prime}$ generated by the AI solver we proposed and the RK solver of Lerche and Low (2014) when $A_{n}$ is an odd function.